Micro-Analytical Study of a Zeolites/Geo-Polymers/Quartz Composite, Dielectric Behaviour and Contribution to Brønsted Sites Affinity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Brick Characterisation
2.2. Chemicals
2.3. ICP-AES Analyses
2.4. Electron Microscopy Analysis
2.5. 1H MAS NMR Analysis
2.6. Surface Electrochemical Study
3. Results
3.1. ESEM/EDS Analysis
3.2. Protonation of Brick Surfaces in Water
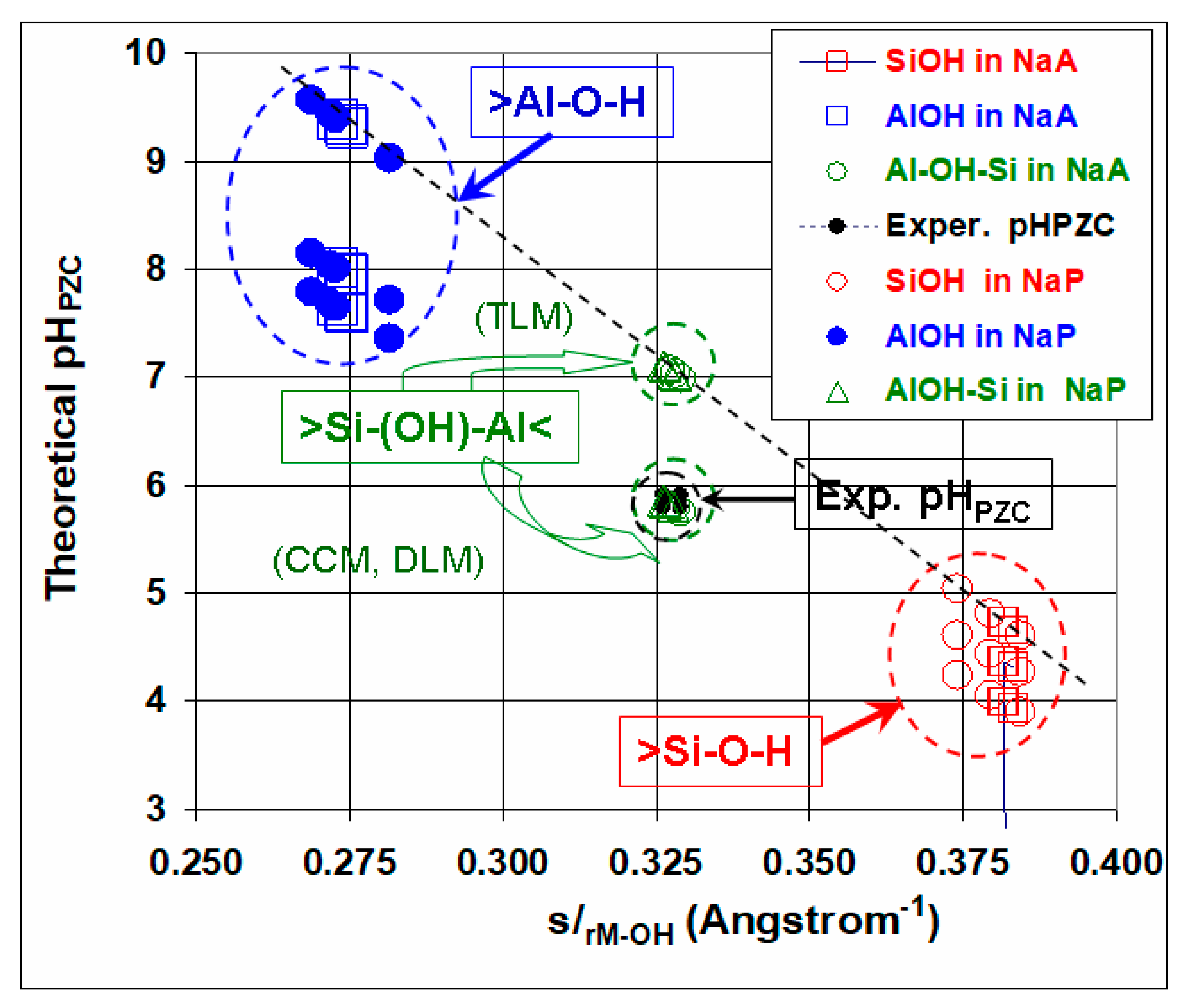
3.2.1. Pauling Bond Strengths in Zeolitic Brick Frameworks
3.2.2. Global Dielectric Constant of Surface Alkali-Brick
3.2.3. Surface-Protonation Equilibria at Composite Surfaces
3.2.4. 1H MAS NMR Analysis of Brønsted Acid Sites of Brick Composite
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Almas Dutt, M.; Asif Hanif, M.; Nadeem, F.; Bhatti, H.N. A review of advances in engineered composite materials popular for wastewater treatment. J. Environ. Chem. Eng. 2020, 8, 104073. [Google Scholar] [CrossRef]
- Roshanfekr Rad, L.; Anbia, M. Zeolite-based composites for the adsorption of toxic matters from water: A review. J. Environ. Chem. Eng. 2021, 9, 106088. [Google Scholar] [CrossRef]
- Labidi, N.S. Removal of mercury from aqueous solutions by waste brick. Inter. J. Environ. Res. 2008, 2, 275–278. [Google Scholar]
- Witharana, A.; Jayaweera, M.; Manatunge, J. Zinc adsorption by low cost sorbent materials: Clay title, brick, sawdust and rice husk. In Proceedings of the International Conference on Sustainable Built Environment (ICSBE-2010), Kandy, Lanka, 13–14 December 2010; pp. 21–28. [Google Scholar]
- Gandhi, N.; Sirisha, D.; Chandra Sekhar, K.B. Adsorption studies of chromium by using low cost adsorbents. Our Nat. 2013, 11, 11–16. [Google Scholar] [CrossRef] [Green Version]
- Hemalatha, P.V.; Prasada Rao, P.V.V. Adsorption batch studies on calcined brick powder in removing chromium and nickel ions. Inter. J. Adv. Res. Chem. Sci. 2014, 1, 14–21. [Google Scholar]
- Krishna, R.H.; Swamy, A.V.V.S. Physico-chemical key parameters, Langmuir and Freundlich isotherm and Lagergren rate constant studies on the removal of calcined brick. Inter. J. Eng. Res. Dev. 2012, 4, 29–38. [Google Scholar]
- Allahdin, O.; Dehou, S.C.; Wartel, M.; Recourt, P.; Trentesaux, M.; Mabingui, J.; Boughriet, A. Performance of FeOOH-brick based composite for Fe(II) removal from water in fixed bed column and mechanistic aspects. Chem. Eng. Res. Des. 2013, 91, 2732–2742. [Google Scholar] [CrossRef]
- Allahdin, O.; Wartel, M.; Recourt, P.; Revel, B.; Ouddane, B.; Billon, G.; Mabingui, J.; Boughriet, A. Adsorption capacity of iron oxyhydroxide-coated brick for cationic metals and nature of ion surface interactions. Appl. Clay Sci. 2014, 90, 141–149. [Google Scholar] [CrossRef]
- Allahdin, O.; Wartel, M.; Mabingui, J.; Boughriet, A. Kinetics of divalent Metals (Cd2+, Cu2+, Pb2+, Zn2+) adsorption onto a modified brick. Am. Chem. Sci. J. 2014, 4, 687–705. [Google Scholar] [CrossRef]
- Allahdin, O.; Wartel, M.; Mabingui, J.; Boughriet, A. Implication of electrostatic forces on the adsorption capacity of a modified brick for the removal of divalent cations from water. Am. J. Anal. Chem. 2015, 6, 11–25. [Google Scholar] [CrossRef] [Green Version]
- Allahdin, O.; Poumaye, N.; Wartel, M.; Boughriet, A. Correlation analysis between cationic metal characteristics and ion-exchange performance of brick-derived zeolites: A comprehensive mechanistic explanation. Mater. Chem. Phys. 2022, 276, 125353. [Google Scholar] [CrossRef]
- Qalyoubi, L.; Al-Othman, A.; Al-Asheh, S. Recent progress and challenges of adsorptive membranes for the removal of pollutants from wastewater. Part II: Environmental applications. Case Stud. Chem. Environ. Eng. 2021, 3, 100102. [Google Scholar] [CrossRef]
- Hao, S.; Jia, Z.; Wen, J.; Li, S.; Peng, W.; Huang, R.; Xu, X. Progress in adsorptive membranes for separation—A review. Sep. Purif. Technol. 2021, 255, 117772. [Google Scholar] [CrossRef]
- Venkatraman, A.; Montes de Oca Zapiain, D.; Lim, H.; Kalidindi, S.R. Texture-sensitive prediction of micro-spring performance using Gaussian process models calibrated to finite element simulations. Mater. Des. 2021, 197, 109198. [Google Scholar] [CrossRef]
- Wong, D.W.-C.; Chen, T.L.-W.; Peng, Y.; Lam, W.-K.; Wang, Y.; Ni, M.; Niu, W.; Zhang, M. An instrument for methodological quality assessment of single-subject finite element analysis used in computational orthopaedics. Med. Nov. Technol. Devices 2021, 11, 100067. [Google Scholar] [CrossRef]
- Ammarullah, M.I.; Afif, I.Y.; Izzur Maula, M.; Winarni, T.I.; Tauviqirrahman, M.; Jamari, J. Tresca stress evaluation of Metal-on-UHMWPE total hip arthroplasty during peak loading from normal walking activity. Mater. Today Proc. 2022, 63, S143–S146. [Google Scholar] [CrossRef]
- Song, Y.; Shao, E.; Bíro, I.; Baker, J.S.; Gu, Y. Finite element modelling for footwear design and evaluation: A systematic scoping review. Heliyon 2022, 8, e10940. [Google Scholar] [CrossRef]
- Ortega, A.; Roubin, E.; Malecot, Y.; Daudeville, L. An analysis of embedded weak discontinuity approaches for the finite element modelling of heterogeneous materials. Comput. Struct. 2022, 273, 106894. [Google Scholar] [CrossRef]
- Donik, Z.; Necemer, B.; Glodez, S.; Kramberger, J. Finite element analysis of the mechanical performance of a two-layer polymer composite stent structure. Eng. Fail. Anal. 2022, 137, 106267. [Google Scholar] [CrossRef]
- Hsu, T.; Kim, H.; Mason, J.H.; Mahbub, R.; Epting, W.K.; Abernathy, H.W.; Hackett, G.A.; Litster, S.; Rollett, A.D.; Salvador, P.A. High performance finite element simulations of infiltrated solid oxide fuel cell cathode microstructures. J. Power Sources 2022, 541, 231652. [Google Scholar] [CrossRef]
- Esfandian, H.; Samadi-Maybodi, A.; Khoshandam, B.; Parvini, M. Experimental and CFD modeling of diazinon pesticide removal using fixed bed column with Cu-modified zeolite nanoparticle. J. Taiwan Inst. Chem. Eng. 2017, 75, 164–173. [Google Scholar] [CrossRef]
- Lehmann, C.; Kolditz, O.; Nagel, T. Modelling sorption equilibria and kinetics in numerical simulations of dynamic sorption experiments in packed beds of salt/zeolite composites for thermochemical energy storage. Int. J. Heat Mass Transf. 2019, 128, 1102–1113. [Google Scholar] [CrossRef]
- Xiao, Y.; Qiu, S.; Zhao, Q.; Zhu, Y.; Godiya, C.B.; He, G. Numerical simulation of low-concentration CO2 adsorption on fixed bed using finite element analysis. Chin. J. Chem. Eng. 2021, 36, 47–56. [Google Scholar] [CrossRef]
- Boumya, W.; Khnifira, M.; Abdennouri, M.; Kaya, S.; Achak, M.; Barka, N. Molecular dynamic simulations and computational DFT of adsorption performances of malachite green on the metal fluorides in aqueous medium. J. Mol. Struct. 2022, 1270, 133924. [Google Scholar] [CrossRef]
- Yee, C.Y.; Lim, L.G.; Sow Mun Lock, S.; Jusoh, N.; Yiin, C.L.; Fui Chin, B.L.; Chan, Y.H.; Minh Loy, A.C.; Mubashir, M. A systematic review of the molecular simulation of hybrid membranes for performance enhancements and contaminant removals. Chemosphere 2022, 307, 135844. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, Y.; Yin, L.; Ding, D.; Jing, W.; Gu, X. Electrochemical impedance spectroscopy for analyzing microstructure evolution of NaA zeolite membrane in acid water/ethanol solution. Chem. Eng. Sci. 2016, 153, 1–9. [Google Scholar] [CrossRef]
- Silaghi, M.-C.; Chizallet, C.; Raybaud, P. Challenges on molecular aspects of dealumination and desilication of zeolites. Microporous Mesoporous Mater. 2014, 191, 82–96. [Google Scholar] [CrossRef]
- James, R.O.; Healy, T.W. Adsorption of hydrolyzable metal ions at the oxide-water interface III. A thermodynamic model of adsorption. J. Colloid Interface Sci. 1972, 40, 65–81. [Google Scholar] [CrossRef]
- Stilling, L.L.; Brantley, S.L.; Machesky, M.L. Proton adsorption at an adularia feldspar surface. Geochimica et Cosmochimica Acta 1995, 59, 1473–1482. [Google Scholar] [CrossRef]
- Stilling, L.L.; Brantley, S.L. Feldspar dissolution at 25 °C and pH 3: Reaction stoichiometry and the effect of cations. Geochim. Et Cosmochim. Acta 1995, 59, 1483–1496. [Google Scholar] [CrossRef]
- Huang, J.; Vegten, N.; van Jiang, Y.; Hunger, M.; Baiker, A. Increasing the Brønsted acidity of flame-derived silica/alumina up to zeolitic strength. Angew. Chem. 2010, 122, 7942–7947. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, J.; Dai, W.; Hunger, M. Solid-state nuclear magnetic resonance investigations of the nature, property, and activity of acid sites on solid catalysts. Solid State Nucl. Magn. Reson. 2011, 39, 116–141. [Google Scholar] [CrossRef] [PubMed]
- Dyballa, M.; Obenaus, U.; Lang, S.; Gehring, B.; Traa, Y.; Koller, H.; Hunger, M. Brønsted sites and structural stabilization effect of acidic low-silica zeolite A prepared by partial ammonium exchange. Microporous Mesoporous Mater. 2015, 212, 110–116. [Google Scholar] [CrossRef]
- Wang, C.; Dai, W.; Wu, G.; Guan, N.; Li, L. Application of ammonia probe-assisted solid-state NMR technique in zeolites and catalysis. Magn. Reson. Lett. 2022, 2, 28–37. [Google Scholar] [CrossRef]
- Uehara, G.; Gillman, G. The Mineralogy, Chemistry and Physics of Tropical Soils with Variable-Charge Clays; West View Press: Boulder, Colorado, 1981; p. 188. ISBN 0891584846. [Google Scholar]
- Seliem, M.K.; Komarneni, S. Equilibrium and kinetic studies for dissociation of iron from aqueous solution by synthetic Na-A zeolites: Statistical modelling and optimization. Microporous Mesoporous Mater. 2016, 228, 266–274. [Google Scholar] [CrossRef]
- Tontisirin, S. Synthesis and characterization of co-crystalline zeolite composite of LSX/A. Microporous Mesoporous Mater. 2016, 239, 123–129. [Google Scholar] [CrossRef]
- Sathupunya, M.; Glari, E.; Wongkasemjit, S. ANA and GIS zeolite synthesis directly from alumatrane and silatrane by sol-gel process and microwave technique. J. Eur. Ceram. Soc. 2002, 22, 2305–2314. [Google Scholar] [CrossRef]
- Zubowa, H.-L.; Kosslick, H.; Müller, D.; Richter, M.; Wilde, L.; Fricke, R. Crystallization of phase-pure zeolite NaP from MCM-22-type gel compositions under microwave radiation. Microporous Mesoporous Mater. 2007, 109, 542–548. [Google Scholar] [CrossRef]
- Khabuanchalad, S.; Khemthong, P.; Prayoonpokarach, S.; Wittayakun, J. Transformation of zeolite NaY synthesized from rice husk silica to NaP during hydrothermal synthesis. Suranaree J. Sc. Technol. 2008, 15, 225–231. [Google Scholar]
- Behin, J.; Kazemian, H.; Rohani, S. Sonochemical synthesis of zeolite NaP from clinoptilolite. Ultrason. Sonochemistry 2016, 28, 400–408. [Google Scholar] [CrossRef]
- Treacy, M.M.J.; Higgins, J.B. Collection of Simulated XRD Powder Patterns for Zeolites, 5th ed.; Elsevier: New York, NY, USA, 2007; pp. 1–762. [Google Scholar] [CrossRef]
- Sverjensky, D.A.; Sahai, N. Theoretical prediction of single-site surface-protonation equilibrium constants for oxides and silicates in water. Geochim. Cosmochim. Acta 1996, 60, 3773–3797. [Google Scholar] [CrossRef]
- Sverjensky, D.A. Crystal chemical basis for surface protonation and reaction rates. Geol. Soc. Amer. Ann. Meet. Abstr. 1994, 26, 350. [Google Scholar]
- Fischer, R.X.; Sehovic, M.; Baur, W.H.; Paulmann, C.; Gesing, T.M. Crystal structure and morphology of fully hydrated zeolite Na-A. Z. Kristallogr. 2012, 227, 438–445. [Google Scholar] [CrossRef]
- Albert, B.R.; Cheetham, A.K.; Stuart, J.A.; Adams, C.J. Investigations on P zeolites: Synthesis, characterisation, and structure of highly crystalline low-silica NaP. Microporous Mesoporous Mater. 1998, 21, 133–142. [Google Scholar] [CrossRef]
- Yoon, R.H.; Salman, T.; Donnay, G. Predicting points of zero charge of oxides and hydroxides. J. Colloid Lnterface Sci. 1979, 70, 483–493. [Google Scholar] [CrossRef]
- Quartz Mineral Data. Available online: https://www.webmineral.com/data/Quartz.shtml (accessed on 20 October 2022).
- Said, B.; Cacciaguerra, T.; Tancret, F.; Fajula, F.; Galarneau, A. Size control of self-supported LTA zeolite nanoparticles monoliths. Microporous Mesoporous Mater. 2016, 227, 176–190. [Google Scholar] [CrossRef]
- Zakri, T.; Laurent, J.-P.; Vauclin, M. Theoretical evidence for ‘Lichtenecker’s mixture formulae based on the effective medium theory. J. Phys. D: Appl. Phys. 1998, 31, 1589. [Google Scholar] [CrossRef]
- Goncharenko, A.V.; Lozovski, V.Z.; Venger, E.F. Lichtenecker’s equation: Applicability and limitations. Opt. Commun. 2000, 174, 19–32. [Google Scholar] [CrossRef]
- Sun, M.; Maichen, W.; Pophale, R.; Liu, Y.; Cai, R.; Lew, C.M.; Hunt, H.; Deem, M.W.; Davis, M.E.; Yan, Y. Dielectric constant measurement of zeolite powders by time-domain reflectometry. Microporous Mesoporous Mater. 2009, 123, 10–14. [Google Scholar] [CrossRef]
- Hunt, H.K.; Lew, C.M.; Sun, M.; Yan, Y.; Davis, M.E. Pure-silica LTA, CHA, STT, ITW, and -SVR thin films and powders for low-k applications. Microporous Mesoporous Mater. 2010, 130, 49–55. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 1962, 33, 3125. [Google Scholar] [CrossRef]
- Looyenga, H. Dielectric constants of hereogenous mixtures. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- Brouers, F.; Ramsamugh, A.; Dixit, V.V. A dielectric anomaly in electrolyte-saturated porous alumina ceramics. J. Mater. Sci. 1987, 22, 2759–2766. [Google Scholar] [CrossRef]
- Boughriet, A.; Poumaye, N.; Allahdin, O.; Revel, B.; Wartel, M. Experimental and theoretical study of acido-basic surface equilibria in zeolitized brick: Theoretical approach and magnetic behaviour of framework protons. Int. J. Sci. Res. Methodol. 2020, 15, 37–57. [Google Scholar]
- Huang, J.; Jiang, Y.; Reddy Marthala, V.R.; Wang, W.; Sulikowski, B.; Hunger, M. In situ 1H MAS NMR investigations of the H/D exchange of alkylaromatic hydrocarbons on zeolites H-Y, La, Na-Y, and H-ZSM-5. Microporous Mesoporous Mater. 2007, 99, 86–90. [Google Scholar] [CrossRef]
- Ma, D.; Han, X.; Xie, S.; Bao, X.; Hu, H.; Au-Yeung, S.C.F. An investigation of the roles of surface aluminum and acid sites in the zeolite MCM-22. Chem. Eur. J. 2002, 8, 162–170. Available online: http://wiley-vch.de/home/chemistry/ (accessed on 20 October 2022). [CrossRef]
- Kanellopoulos, J.; Gottert, C.; Schneider, D.; Knorr, B.; Prager, D.; Ernst, H.; Freude, D. NMR investigation of proton mobility in zeolites. J. Catal. 2008, 255, 68–78. [Google Scholar] [CrossRef]
- Gan, Z. 13C/14N heteronuclear multiple-quantum correlation with rotary resonance and REDOR dipolar recoupling. J. Magn. Reson. 2007, 184, 39–43. [Google Scholar] [CrossRef]
- Tricot, G.; Trébosc, J.; Pourpoint, F.; Gauvin, R.; Delevoye, L. The D-HMQC MAS-NMR Technique. In Annual Reports on NMR Spectroscopy; Webb, G.A., Ed.; Elsevier Ltd.: New York, NY, USA, 2014; Volume 81, pp. 145–184. [Google Scholar] [CrossRef]
- Chen, K.; Gan, Z.; Horstmeier, S.; White, J.L. Distribution of aluminum species in zeolite catalysts: 27Al NMR of framework, partially-coordinated framework, and non-framework moieties. J. Am. Chem. Soc. 2021, 143, 6669–6680. [Google Scholar] [CrossRef]

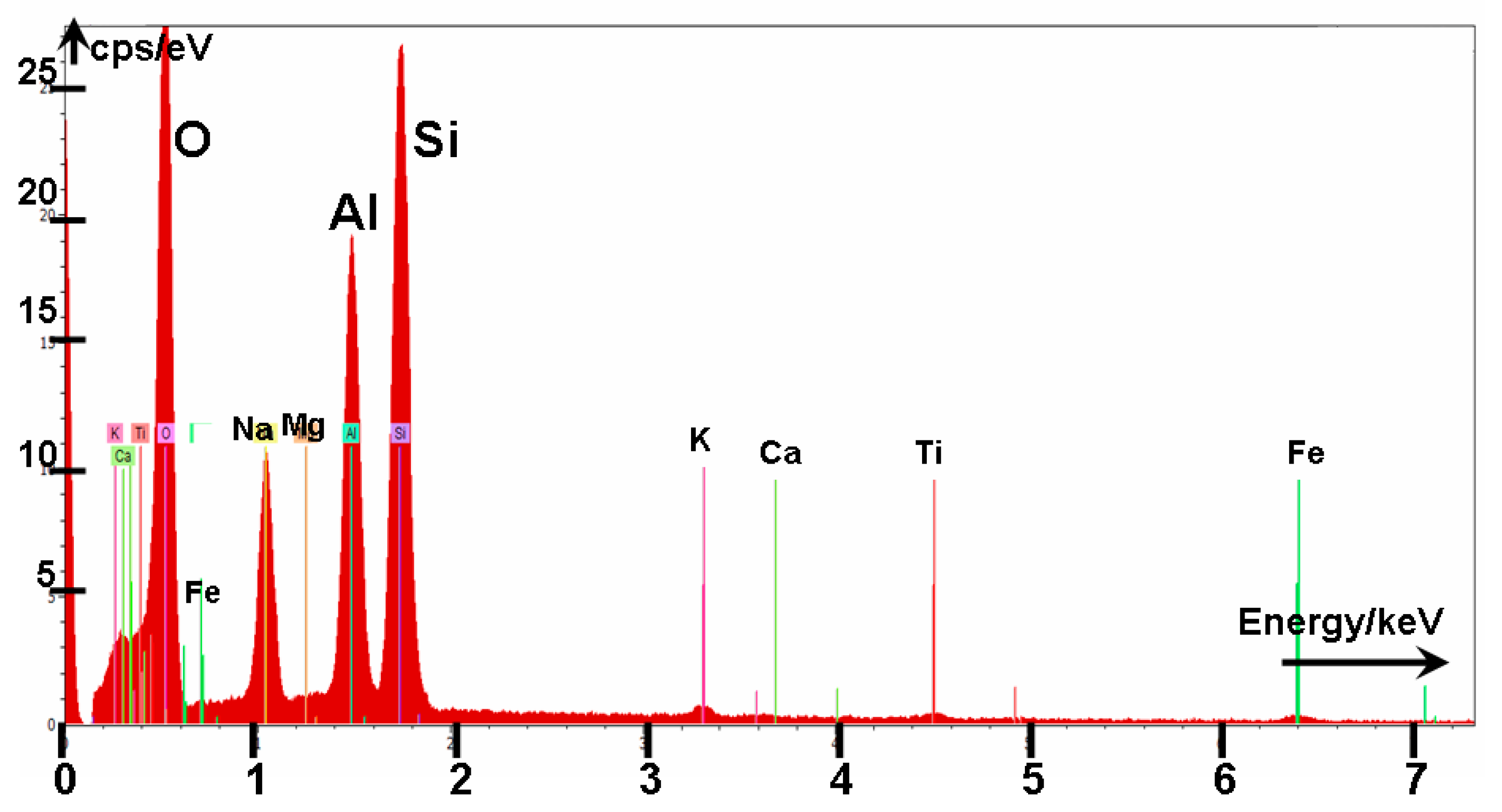



| NaA | Si−O(i) | Al−O(i) | rSi−O(i)H | rAl−O(i)H | rAl−(O(i)H)−Si | s/rSi−O(i)H | s/rAl−O(i)H | s/rAl−(O(i)H)−Si |
|---|---|---|---|---|---|---|---|---|
| O(1) | 1.5991 | 1.7189 | 2.6091 | 2.7289 | 2.6690 | 0.3833 | 0.2748 | 0.3290 |
| O(2) | 1.6100 | 1.7240 | 2.6200 | 2.7340 | 2.6770 | 0.3817 | 0.2743 | 0.3280 |
| O(3) | 1.6109 | 1.7371 | 2.6209 | 2.7471 | 2.6840 | 0.3816 | 0.2730 | 0.3273 |
| NaP | Si−O(i) | Al−O(i) | rSi−O(i)H | rAl−O(i)H | rAl−(O(i)H)−Si | s/rSi−O(i)H | s/rAl−O(i)H | s/rAl−(O(i)H)−Si |
| O(1) | 1.5920 | 1.7810 | 2.6020 | 2.7910 | 2.6965 | 0.3843 | 0.2687 | 0.3265 |
| O(2) | 1.6240 | 1.7390 | 2.6340 | 2.7490 | 2.6915 | 0.3796 | 0.2728 | 0.3262 |
| O(3) | 1.6620 | 1.6550 | 2.6720 | 2.6650 | 2.6685 | 0.3743 | 0.2814 | 0.3278 |
| O(4) | 1.5910 | 1.7490 | 2.6010 | 2.7590 | 2.6800 | 0.3845 | 0.2718 | 0.3282 |
| Volumic % of Zeolites on Alkali Brick | Dielectric Constant Measured at Alkali-Brick Surfaces (εalkali-brick) | ||||
|---|---|---|---|---|---|
| Bruggeman | Hashin-Shtrikman | Lichterecker | |||
| á = +1 | á = −1 | á = 0 | |||
| 36.71% (max.) | 3.272 | 3.150 | 3.492 | 2.741 | 3.126 |
| 30.72% (min.) | 3.473 | 3.346 | 3.669 | 2.933 | 3.327 |
| <εalkali-brick> | 3.373 | 3.248 | 3.581 | 2.837 | 3.227 |
| Average: 3.209 | |||||
| Thermodynamic Constant (pKPZC) for the Zero Point of Charge Equilibrium) [44]: S−OH2+↔>S−O− + 2H+(aq.) |
|---|
| CCM: pKPZC = 2pHPZC = 22.86(1/å) − 67.44(s/rM−OH) + 26.76 |
| DLM: pKPZC = 2pHPZC = 22.14(1/å) − 66.98(s/rM−OH) + 26.78 |
| TLM: pKPZC = 2pHPZC = 42.2316(1/å) − 85.8296(s/rM−OH) + 29.3732 |
| NaA | s/rSi−O(i)H | pHPZC (SiOH) | s/rAl−O(i)H | pHPZC (AlOH) | s/rAl−(O(i)H)−Si | pHPZC (AlOHSi) |
|---|---|---|---|---|---|---|
| O(1) | 0.38327 | 4.31 | 0.2748 | 7.94 | 0.3291 | 5.73 |
| O(2) | 0.38168 | 4.36 | 0.2743 | 7.96 | 0.3280 | 5.77 |
| O(3) | 0.38155 | 4.37 | 0.2730 | 8.00 | 0.3273 | 5.79 |
| NaP | s/rSi−O(i)H | pHPZC (SiOH) | s/rAl−O(i)H | pHPZC (AlOH) | s/rAl−(O(i)H)−Si | pHPZC (AlOHSi) |
| O(1) | 0.38432 | 4.27 | 0.2687 | 8.14 | 0.3265 | 5.82 |
| O(2) | 0.37965 | 4.43 | 0.2728 | 8.01 | 0.3262 | 5.83 |
| O(3) | 0.37425 | 4.61 | 0.2814 | 7.72 | 0.3278 | 5.77 |
| O(4) | 0.38447 | 4.27 | 0.2718 | 8.04 | 0.3282 | 5.76 |
| Dielectric Constant (εalkali brick) | pKPZC | pHPZC | |||||
|---|---|---|---|---|---|---|---|
| CCM | DLM | TLM | CCM | DLM | TLM | ||
| Bruggeman | 3.373 ± 0.100 | 11.78 ± 0.09 | 11.41 ± 0.09 | 13.79 ± 0.12 | 5.89 ± 0.05 | 5.70 ± 0.05 | 6.89 ± 0.06 |
| Hashin-Shtrikman | 3.248 ± 0.098 | 12.04 ± 0.09 | 11.66 ± 0.09 | 14.26 ± 0.12 | 6.02 ± 0.05 | 5.83 ± 0.05 | 7.13 ± 0.06 |
| Lichterecker (serial/parallel Form) | 3.581 ± 0.089 | 11.38 ± 0.09 | 11.02 ± 0.09 | 13.05 ± 0.12 | 5.69 ± 0.05 | 5.51 ± 0.05 | 6.53 ± 0.06 |
| Lichterecker (log. Form) | 3.227 ± 0.100 | 12.08 ± 0.09 | 11.70 ± 0.09 | 14.35 ± 0.12 | 6.04 ± 0.05 | 5.85 ± 0.05 | 7.18 ± 0.06 |
| Surface-Protonation Equilibrium Constants (Ká1 and Ká2) for Reactions (1) and (2) [44] |
|---|
| Constant capacitance model (CCM): pKá1(CCM) = ll.43(1/å) − [45.32 − 2.3 log I](s/rM−OH) + 14.18 pKá2(CCM) = ll.43(1/å) − [22.13 + 2(.3 log I](s/rM−OH) + 12.58 |
| Diffuse double layer model (DLM): pKá1(DLM) = ll.07(1/å) − 48.50(s/rM−OH) + 14.51 pKá2(DLM) = ll.07(1/å) − 18.49(s/rM−OH) + 12.27 |
| Triple layer model (TLM): pKá1(TLM) = 21.1158(1/å) − 49.2608(s/rM−OH) + 12.9181 pKá2(TLM) = 21.1158(1/å) 36.5688(s/rM−OH) + 16.4551 |
| Averaged pK (Alkali Brick) | Surface Equilibrium Constants | ||
|---|---|---|---|
| CCM | DLM | TLM | |
| <pKá1> | 2.28 ± 0.07 | 1.99 ± 0.07 | 3.20 ± 0.06 |
| <pKá2> | 9.33 ± 0.03 | 9.58 ± 0.03 | 10.89 ± 0.05 |
| <pKn> | 7.05 ± 0.10 | 7.58 ± 0.10 | 7.69 ± 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boughriet, A.; Allahdin, O.; Poumaye, N.; Tricot, G.; Revel, B.; Lesven, L.; Wartel, M. Micro-Analytical Study of a Zeolites/Geo-Polymers/Quartz Composite, Dielectric Behaviour and Contribution to Brønsted Sites Affinity. Ceramics 2022, 5, 908-927. https://doi.org/10.3390/ceramics5040066
Boughriet A, Allahdin O, Poumaye N, Tricot G, Revel B, Lesven L, Wartel M. Micro-Analytical Study of a Zeolites/Geo-Polymers/Quartz Composite, Dielectric Behaviour and Contribution to Brønsted Sites Affinity. Ceramics. 2022; 5(4):908-927. https://doi.org/10.3390/ceramics5040066
Chicago/Turabian StyleBoughriet, Abdel, Oscar Allahdin, Nicole Poumaye, Gregory Tricot, Bertrand Revel, Ludovic Lesven, and Michel Wartel. 2022. "Micro-Analytical Study of a Zeolites/Geo-Polymers/Quartz Composite, Dielectric Behaviour and Contribution to Brønsted Sites Affinity" Ceramics 5, no. 4: 908-927. https://doi.org/10.3390/ceramics5040066
APA StyleBoughriet, A., Allahdin, O., Poumaye, N., Tricot, G., Revel, B., Lesven, L., & Wartel, M. (2022). Micro-Analytical Study of a Zeolites/Geo-Polymers/Quartz Composite, Dielectric Behaviour and Contribution to Brønsted Sites Affinity. Ceramics, 5(4), 908-927. https://doi.org/10.3390/ceramics5040066







