A Physical Metric for Inertial Confinement Fusion Capsules
Abstract
:1. Introduction
2. Theory and Analysis
2.1. Metric
2.2. Ignition Criterion in Verious Forms
3. Discussions
3.1. Important Time Scales
3.2. Comparison of Ignition Metrics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kritcher, A.L.; Zylstra, A.B.; Callahan, D.A.; Hurricane, O.A.; Weber, C.R.; Clark, D.S.; Young, C.V.; Ralph, J.E.; Casey, D.T.; Pak, A.; et al. Design of an inertial fusion experiment exceeding the Lawson criterion for ignition. Phys. Rev. E 2022, 106, 025201. [Google Scholar] [CrossRef]
- Kritcher, A.L.; Young, C.V.; Robey, H.F.; Weber, C.R.; Zylstra, A.B.; Hurricane, O.A.; Callahan, D.A.; Ralph, J.E.; Ross, J.S.; Baker, K.L.; et al. Design of inertial fusion implosions reaching the burning plasma regime. Nat. Phys. 2022, 18, 251–258. [Google Scholar] [CrossRef]
- Zylstra, A.B.; Kritcher, A.L.; Hurricane, O.A.; Callahan, D.A.; Ralph, J.E.; Casey, D.T.; Pak, A.; Landen, O.L.; Bachmann, B.; Baker, K.L.; et al. Experimental achievement and signatures of ignition at the National Ignition Facility. Phys. Rev. E 2022, 106, 025202. [Google Scholar] [CrossRef]
- Kritcher, A.L.; Zylstra, A.B.; Callahan, D.A.; Hurricane, O.A.; Weber, C.; Ralph, J.; Casey, D.T.; Pak, A.; Baker, K.; Bachmann, B.; et al. Achieving record hot spot energies with large HDC implosions on NIF in HYBRID-E. Phys. Plasmas 2021, 28, 072706. [Google Scholar] [CrossRef]
- Zylstra, A.B.; Kritcher, A.L.; Hurricane, O.A.; Callahan, D.A.; Baker, K.; Braun, T.; Casey, D.T.; Clark, D.; Clark, K.; Döppner, T.; et al. Record Energetics for an Inertial Fusion Implosion at NIF. Phys. Rev. Lett. 2021, 126, 025001. [Google Scholar] [CrossRef]
- Abu-Shawared, H.; Acree, R.; Adams, P.; Adams, J.; Addis, B.; Aden, R.; Adrian, P.; Afeyan, B.B.; Aggleton, M.; Aghaian, L.; et al. (Indirect Drive ICF Collaboration), Lawson’s criteria for ignition exceeded in an inertial fusion experiment. Phys. Rev. Lett. 2022, 129, 075001. [Google Scholar] [CrossRef]
- Abu-Shawared, H.; Acree, R.; Adams, P.; Adams, J.; Addis, B.; Aden, R.; Adrian, P.; Afeyan, B.B.; Aggleton, M.; Aghaian, L.; et al. (Indirect Drive ICF Collaboration), Achievement of Target Gain Larger than Unity in an Inertial Fusion Experiment. Phys. Rev. Lett. 2024, 132, 065102. [Google Scholar] [CrossRef]
- Thomas, C.A.; Campbell, E.M.; Baker, K.L.; Casey, D.T.; Hohenberger, M.; Kritcher, A.L.; Spears, B.K.; Khan, S.F.; Nora, R.; Woods, D.T.; et al. Principal factors in performance of indirect-drive laser fusion experiments. Phys. Plasmas 2020, 27, 112712. [Google Scholar] [CrossRef]
- Hopkins, L.F.B.; Pape, S.L.; Pak, L.D.N.A.; Dewald, E.L.; Ho, D.D.; Bhandarkar, N.; Bhandarkar, S.; Bennedetti, L.R.; Bunn, T.; Biener, J.; et al. Toward a burning plasmas state using diamond ablator inertially conned 11 fusion (ICF) implosions on the National Ignition Facility. Plasma Phys. Control. Fusion 2019, 61, 014023. [Google Scholar] [CrossRef]
- Pape, S.L.; Hopkins, L.F.B.; Divol, L.; Pak, A.; Dewald, E.L.; Bhandarkar, S.; Bennedetti, L.R.; Bunn, T.; Biener, J.; Crippen, J.; et al. Fusion energy output greater than the kinetic energy of an imploding shell at the National Ignition Facility. Phys. Rev. Lett. 2018, 120, 245003. [Google Scholar] [CrossRef]
- Thomas, C.A.; Campbell, E.M.; Baker, K.L.; Casey, D.T.; Hohenberger, M.; Kritcher, A.L.; Spears, B.K.; Khan, S.F.; Nora, R.; Woods, D.T.; et al. Experiments to explore the influence of pulse shaping at the National Ignition Facility. Phys. Plasmas 2020, 27, 112708. [Google Scholar] [CrossRef]
- Dewald, E.L.; Tommasini, R.; Meezan, N.B.; Landen, O.L.; Khan, S.; Rygg, R.; Field, J.; Moore, A.S.; Sayre, D.; MacKinnon, A.J.; et al. First demonstration of improved capsule implosions by reducing radiation preheat in uranium versus gold hohlraums. Phys. Plasmas 2018, 25, 092702. [Google Scholar] [CrossRef]
- Casey, D.T.; Thomas, C.A.; Baker, K.L.; Spears, B.; Hohenberger, M.; Khan, S.F.; Nora, R.C.; Weber, C.R.; Woods, D.T.; Hurricane, O.; et al. The high velocity, high adiabat, bigfoot campaign and test of indirect-drive implosion scaling. Phys. Plasmas 2018, 25, 056308. [Google Scholar] [CrossRef]
- Baker, K.L.; Thomas, C.A.; Casey, D.; Khan, S.; Spears, B.K.; Nora, R.; Woods, T.; Milovich, J.; Berger, R.L.; Strozzi, D.; et al. High-performance indirect-drive cryogenic implosions at high adiabat on the National Ignition Facility. Phys. Rev. Lett. 2018, 121, 135001. [Google Scholar] [CrossRef] [PubMed]
- Patel, P.K.; Springer, P.T.; Weber, C.R.; Jarrott, L.C.; Hurricane, O.A.; Bachmann, B.; Baker, K.L.; Hopkins, L.F.B.; Callahan, D.A.; Casey, D.T.; et al. Hotspot conditions achieved in inertial confinement fusion experiments on the National Ignition Facility. Phys. Plasmas 2020, 27, 050901. [Google Scholar] [CrossRef]
- Landen, O.L.; Casey, D.T.; Nicola, J.M.D.; Doeppner, T.; Hartouni, E.P.; Hinkel, D.E.; Hopkins, L.F.B.; Hohenberger, M.; Kritcher, A.L.; Pape, S.L.; et al. Yield and compression trends and reproducibility at NIF. High Energy Density Phys. 2020, 36, 100755. [Google Scholar] [CrossRef]
- Clark, D.S.; Kritcher, A.L.; Yi, S.A.; Zylstra, A.B.; Haan, S.W.; Weber, C.R. Capsule physics comparison of National Ignition Facility implosion designs using plastic, high density carbon, and beryllium ablators. Phys. Plasmas 2018, 25, 032703. [Google Scholar] [CrossRef]
- Clark, D.S.; Weber, C.R.; Milovich, J.L.; Pak, A.E.; Casey, D.T.; Hammel, B.A.; Ho, D.D.; Jones, O.S.; Koning, J.M.; Kritcher, A.L.; et al. Three-dimensional modeling and hydrodynamic scaling of National Ignition Facility implosions. Phys. Plasmas 2019, 26, 050601. [Google Scholar] [CrossRef]
- Thomas, C.A.; Campbell, E.M.; Baker, K.L.; Casey, D.T.; Hohenberger, M.; Kritcher, A.L.; Spears, B.K.; Khan, S.F.; Nora, R.; Woods, D.T.; et al. Deficiencies in compression and yield in x-ray driven implosions. Phys. Plasmas 2020, 27, 112705. [Google Scholar] [CrossRef]
- Gaffney, J.A.; Brandon, S.T.; Humbird, K.D.; Kruse, M.K.G.; Nora, R.C.; Peterson, J.L.; Spears, B.K. Making inertial confinement fusion models more predictive. Phys. Plasmas 2019, 26, 082704. [Google Scholar] [CrossRef]
- Pak, A.; Divol, L.; Weber, C.R.; Hopkins, L.F.B.; Clark, D.S.; Dewald, E.L.; Fittinghoff, D.N.; Geppert-Kleinrath, V.; Hohenberger, M.; Pape, S.L.; et al. Impact of Localized Radiative Loss on Inertial Confinement Fusion Implosions. Phys. Rev. Lett. 2020, 124, 145001. [Google Scholar] [CrossRef]
- Park, H.-S.; Hurricane, O.A.; Callahan, D.A.; Casey, D.T.; Dewald, E.L.; Dittrich, T.R.; Doppner, T.; Hinkel, D.E.; Hopkins, L.F.B.; Pape, S.L.; et al. High-Adiabat High-Foot Inertial Confinement Fusion Experiments on the National Ignition Facility. Phys. Rev. Lett. 2014, 112, 055001. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.-M.; Batha, S.H. Scaling laws for ignition at the National Ignition Facility from first principles. Phys. Rev. E 2013, 88, 041101. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.M.; Yi, S.A.; Batha, S.H.; Wysocki, F.J. Ignition and pusher adiabat. Phys. Control. Fusion 2018, 60, 074011. [Google Scholar] [CrossRef]
- Cheng, B.; Bradley, P.A.; Finnagan, S.A.; Thomas, C.A. Fundamental factors affecting thermonuclear ignition. Nucl. Fusion 2020, 61, 096010. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.M.; Merrill, F.E.; Cerjan, C.J.; Batha, S.H. Analysis of NIF experiments with the minimal energy implosion model. Phys. Plasmas 2015, 22, 082704. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.M.; Yi, S.A.; Batha, S.H.; Wysocki, F.J. Effects of preheat and mix on the fuel adiabat of an imploding capsule. Phys. Plasmas 2016, 23, 120702. [Google Scholar] [CrossRef]
- Melvin, J.; Lim, H.; Rana, V.; Cheng, B.; Glimm, J.; Sharp, D.H.; Wilson, D.C. Sensitivity of inertial confinement fusion hot spot properties to the deuterium-tritium fuel adiabat. Phys. Plasmas 2015, 22, 022708. [Google Scholar] [CrossRef]
- Hurricane, O.A.; Callahan, D.A.; Casey, D.T.; Dewald, E.L.; Dittrich, T.R.; Döppner, T.; Haan, S.; Hinkel, D.E.; Hopkins, L.F.B.; Jones, O.; et al. Inertially confined fusion plasmas dominated by alpha-particle self-heating. Nat. Phys. 2016, 12, 800–806. [Google Scholar] [CrossRef]
- Callahan, D.A.; Hurricane, O.A.; Hinkel, D.E.; Döppner, T.; Ma, T.; Park, H.-S.; Garcia, M.A.B.; Hopkins, L.F.B.; Casey, D.T.; Cerjan, C.J.; et al. Higher velocity, high-foot implosions on the National Ignition Facility laser. Phys. Plasmas 2015, 22, 056314. [Google Scholar] [CrossRef]
- Haan, S.W.; Lindl, J.D.; Callahan, D.A.; Clark, D.S.; Salmonson, J.D.; Hammel, B.A.; Atherton, L.J.; Cook, R.C.; Edwards, M.J.; Glenzer, S.; et al. Point design targets, specifications, and requirements for the 2010 ignition campaign on the National Ignition Facility. Phys. Plasmas 2011, 18, 051001. [Google Scholar] [CrossRef]
- Hurricane, O.A.; Springer, P.T.; Patel, P.K.; Callahan, D.A.; Baker, K.; Casey, D.T.; Divol, L.; Doppner, T.; Hinkel, D.E.; Hohenberger, M.; et al. Approaching a burning plasma on the NIF. Phys. Plasmas 2019, 26, 052704. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Wang, Y.-M.; Batha, S.H. On Thermonuclear ignition criterion at the National Ignition Facility. Phys. Plasmas 2014, 21, 102707. [Google Scholar] [CrossRef]
- Ballabio, L.; Källne, J.; Gorini, G. Relativistic calculation of fusion product spectra for thermonuclear plasmas. Nucl. Fusion 1998, 38, 1723. [Google Scholar] [CrossRef]
- Murphy, T.J. The effect of turbulent kinetic energy on inferred ion temperature from neutron spectra. Phys. Plasmas 2014, 21, 072701. [Google Scholar] [CrossRef]
- Krokhin, O.N.; Rozanov, V.B. Escape of α particles from a laser-pulse-initiated thermonuclear reaction. Sov. J. Quantum Electron. 1973, 2, 393. [Google Scholar] [CrossRef]
- Cheng, B.; Kwan, T.J.T.; Yi, S.A.; Landen, O.L.; Wang, Y.M.; Cerjan, C.J.; Batha, S.H.; Wysocki, F.J. Effects of asymmetry and hot-spot shape on ignition capsules. Phys. Rev. E 2018, 98, 023203. [Google Scholar] [CrossRef]
- Zylstra, A.B.; Hurricane, O.A.; Callahan, D.A.; Kritcher, A.L.; Ralph, J.E.; Robey, H.F.; Ross, J.S.; Young, C.V.; Baker, K.L.; Casey, D.T.; et al. 2022 Burning plasma achieved in inertial fusion. Nature 2022, 601, 542–548. [Google Scholar] [CrossRef]
- Herrmann, M. Recent Inertial Confinement Fusion Results from the National Ignition Facility; NIF Press: Livermore, CA, USA, 2021. [Google Scholar]
- Hurricane, O.A.; Maclaren, S.A.; Rosen, M.D.; Hammer, J.H.; Springer, P.T.; Betti, R. A thermodynamic condition for ignition and burn-propagation in cryogenic layer inertially confined fusion implosions. Phys. Plasmas 2021, 28, 022704. [Google Scholar] [CrossRef]
- Kritcher, A.L.; Zylstra, A.B.; Weber, C.R.; Hurricane, O.A.; Callahan, D.A.; Clark, D.S.; Divol, L.; Hinkel, D.E.; Humbird, K.; Jones, O.; et al. Design of the first fusion experiment to achieve target energy gain G >1. Phys. Rev. E 2024, 109, 025204. [Google Scholar] [CrossRef]
- Lindl, J.D. Haan, S.W., Christopherson, A.R., Betti, R. Progress toward a self-consistent set of 1D ignition metrics in ICF. Phys. Plasmas 2018, 25, 122704. [Google Scholar] [CrossRef]
- Springer, P.T.; Hurricane, O.A.; Hammer, J.H.; Betti, R.; Callahan, D.A.; Campbell, E.M.; Casey, D.T.; Cerjan, C.J.; Cao, D.; Dewald, E.; et al. A 3D dynamic model to assess the impacts of low-mode asymmetry, aneurysms and mix-induced radiative loss on capsule performance across inertial confinement fusion platforms. Nucl. Fusion 2019, 59, 032009. [Google Scholar] [CrossRef]
- Hurricane, O.A.; Casey, D.T.; Landen, O.; Kritcher, A.L.; Nora, R.; Patel, P.K.; Gaffney, J.A.; Humbird, K.D.; Field, J.E.; Kruse, M.K.G.; et al. An analytic asymmetric-piston model for the impact of mode-1 shell asymmetry on ICF implosions. Phys. Plasmas 2020, 27, 062704. [Google Scholar] [CrossRef]
- Hurricane, O.A.; Callahan, D.A.; Springer, P.T.; Edwards, M.J.; Patel, P.; Baker, K.; Casey, D.T.; Divol, L.; Döppner, T.; Hinkel, D.E.; et al. Beyond alpha-heating: Driving inertially confined fusion implosions toward a burning-plasma state on the National Ignition Facility. Plasma Phys. Control. Fusion 2018, 61, 014033. [Google Scholar] [CrossRef]
- Christopherson, A.R.; Betti, R.; Miller, S.; Gopalaswamy, V.; Mannion, O.M.; Cao, D. Theory of ignition and burn propagation in inertial fusion implosions. Phys. Plasmas 2020, 27, 052708. [Google Scholar] [CrossRef]
- Atzeni, S.; Meyer-Ter-Vehn, J. The Physics of Inertial Fusion; Clarendon Pres: Oxford, UK, 2004. [Google Scholar]
- Tipton, R. Generalized Lawson Criteria for Inertial Confinement Fusion; LLNL Report No. LLNL-TR-67692 (2015), Private Communications and Preprint; Lawrence Livermore National Lab.: Livermore, CA, USA, 2015. [Google Scholar]
- Coutant, J. La Fusion Thermonucleaire Inertielle Par Laser; Dautray, R., Watteau, J.-P., Eds.; Eyrolles: Paris, France, 1993. [Google Scholar]
- Zhou, Y.; Williams, R.J.; Ramaprabhu, P.; Groom, M.; Thornber, B.; Hillier, A.; Mostert, W.; Rollin, B.; Balachandar, S.; Powell, P.D.; et al. Rayleigh–Taylor and Richtmyer–Meshkov instabilities: A journey through scales. Phys. D 2021, 423, 132838. [Google Scholar] [CrossRef]
- Zhou, Y.; Clark, T.T.; Clark, D.S.; Gail Glendinning, S.; Skinner, M.A.; Huntington, C.M.; Hurricane, O.A.; Dimits, A.M.; Remington, B.A. Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities. Phys. Plasmas 2019, 26, 080901. [Google Scholar] [CrossRef]
- Zhou, Y. Rayleigh-Taylor and Richtmyer-Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 2017, 720–722, 1–136. [Google Scholar] [CrossRef]
- Zhou, Y. Rayleigh-Taylor and Richtmyer-Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 2017, 723–725, 1–116. [Google Scholar] [CrossRef]
- Hicks, D.G.; Meezan, N.B.; Dewald, E.L.; Mackinnon, A.J.; Olson, R.E.; Callahan, D.A.; Döppner, T.; Benedetti, L.R.; Bradley, D.K.; Celliers, P.M.; et al. Implosion dynamics measurements at the National Ignition Facility. Phys. Plasmas 2012, 19, 122702. [Google Scholar] [CrossRef]
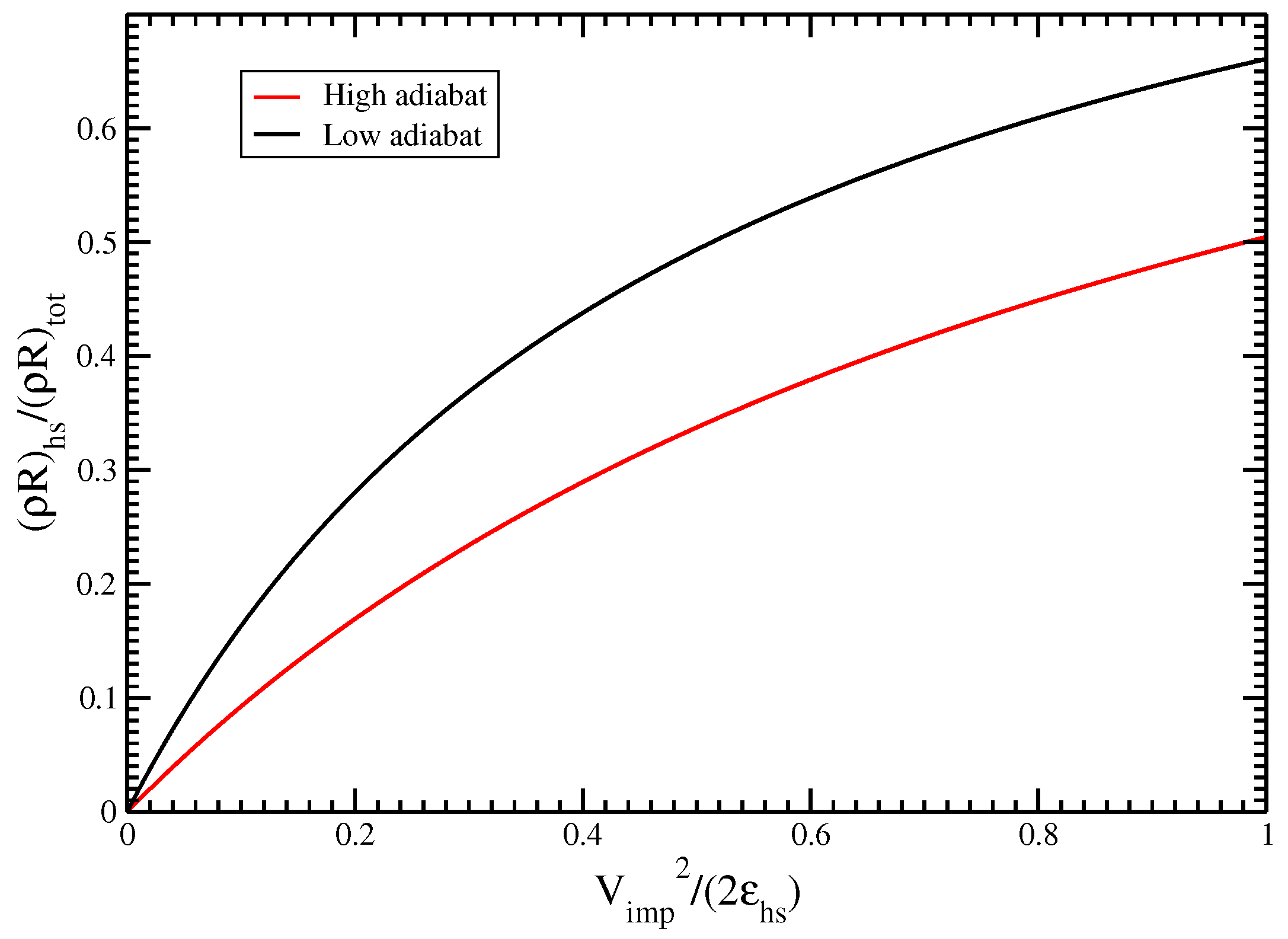
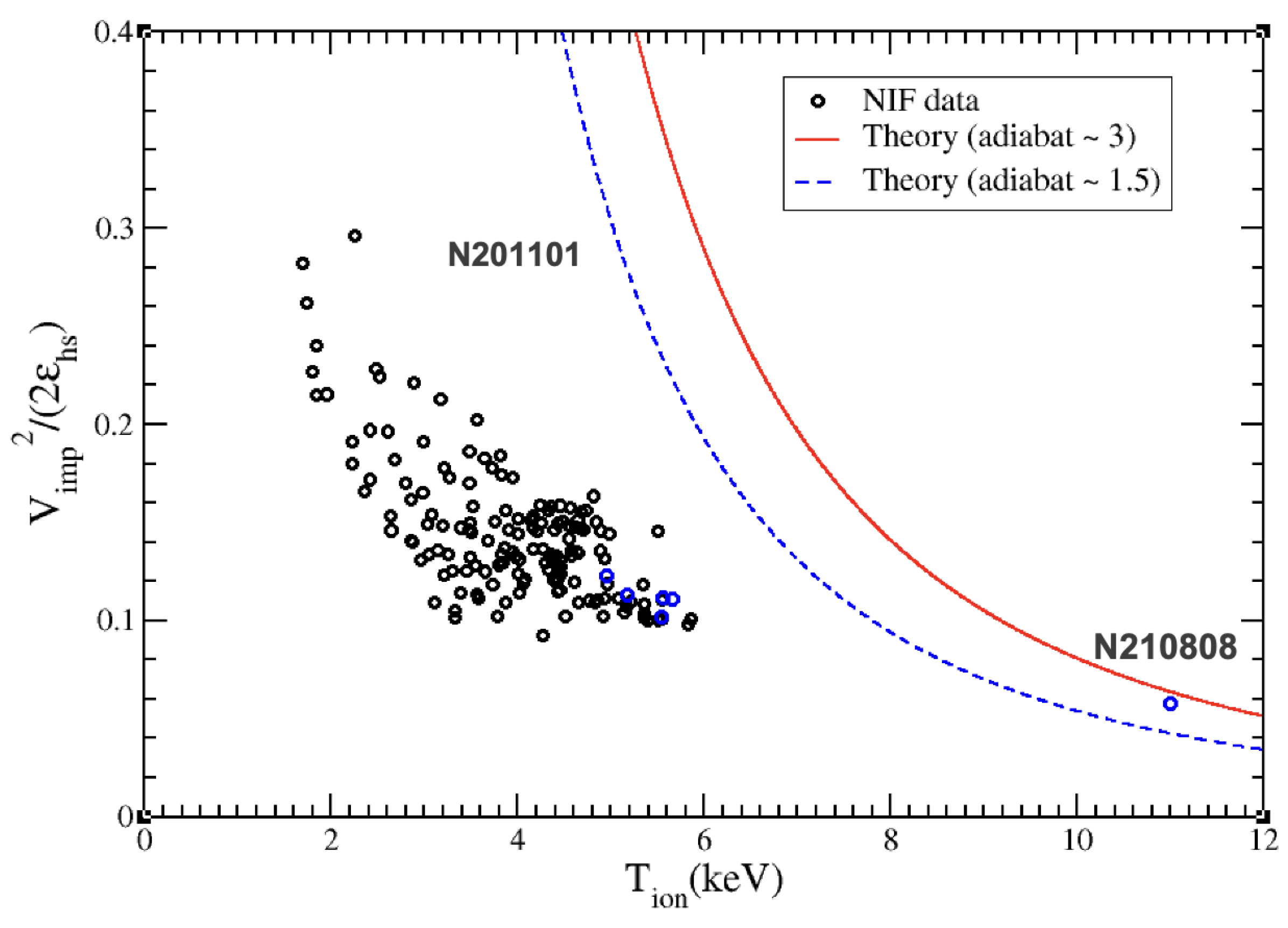
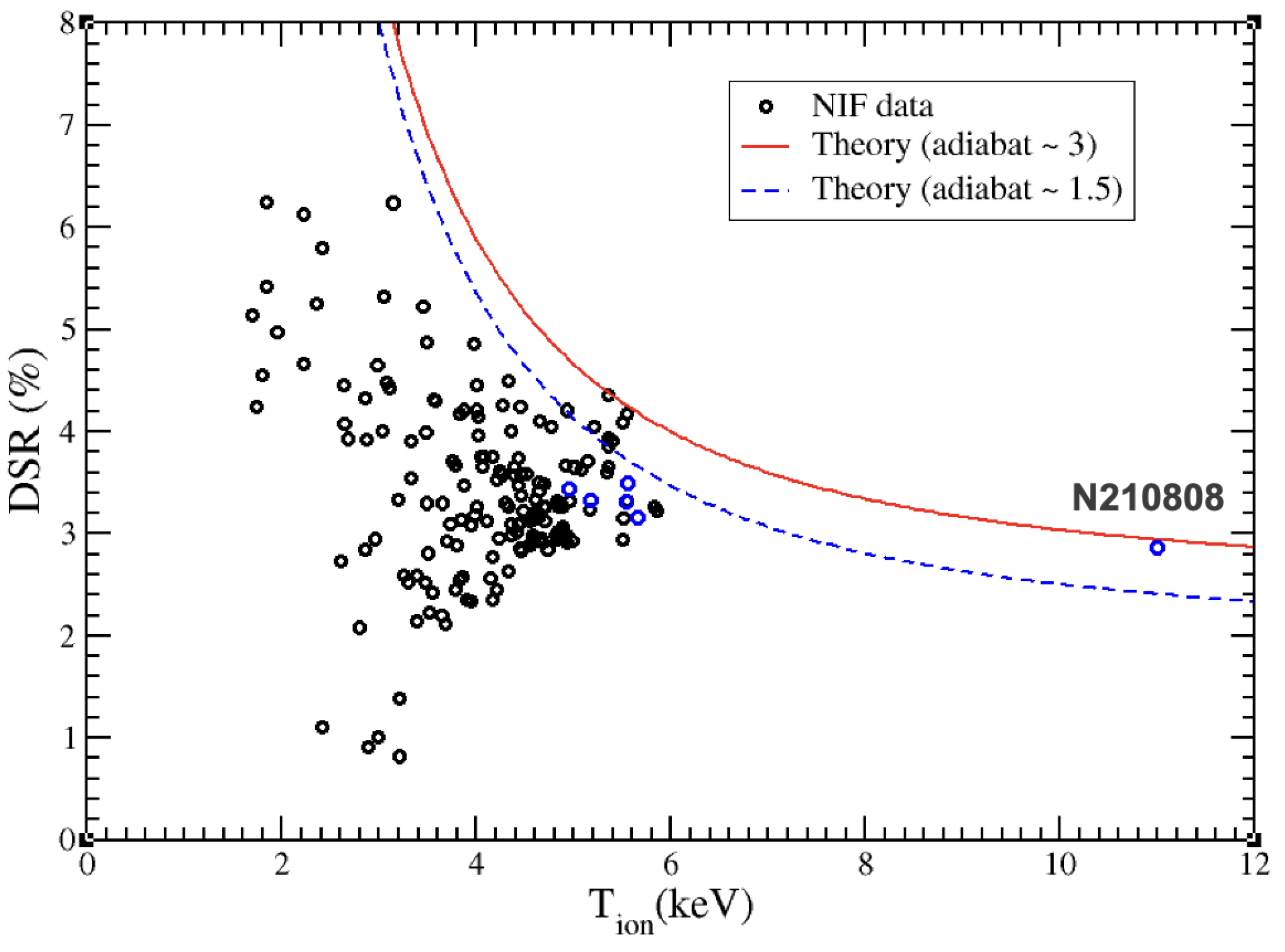
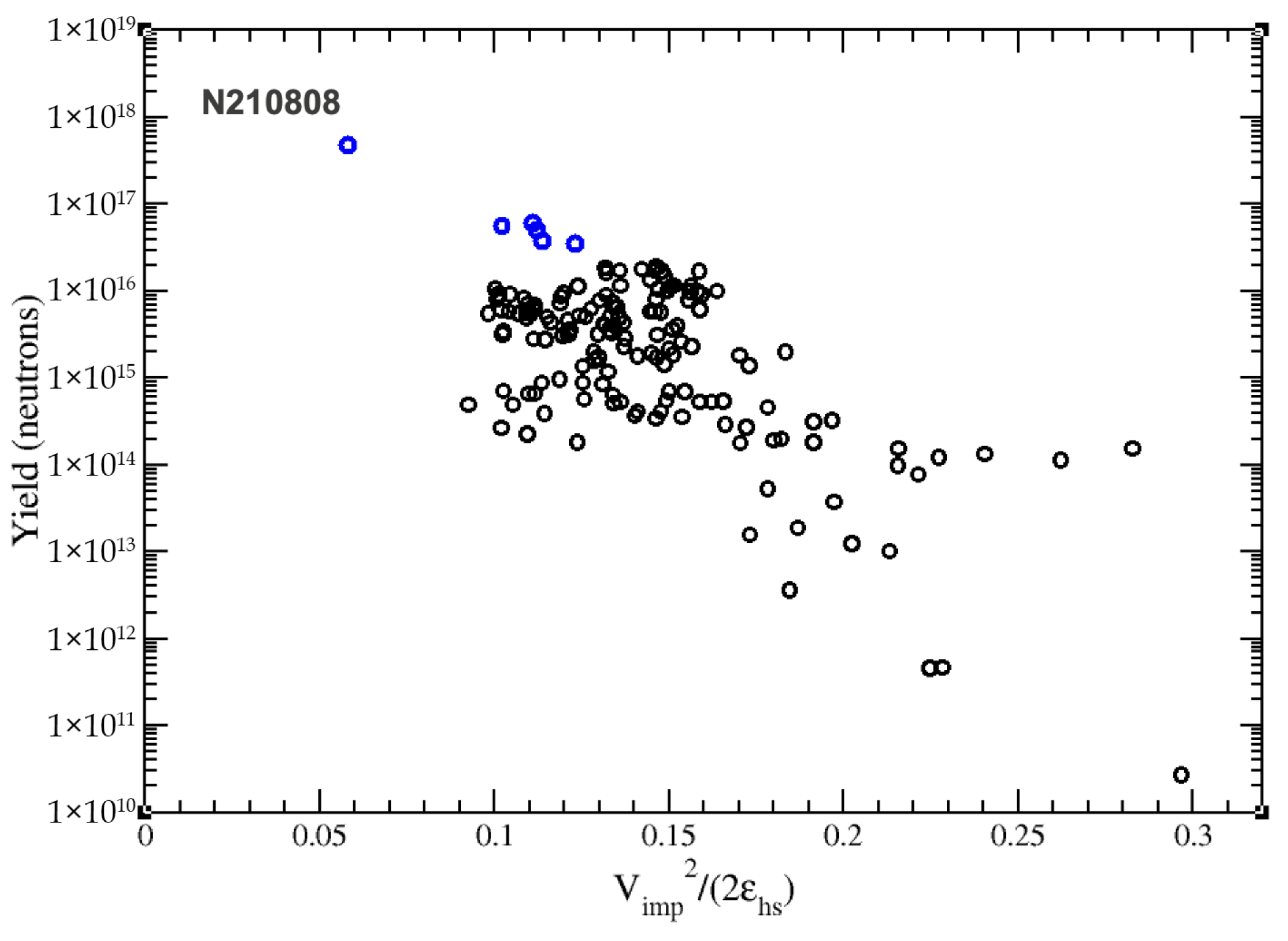
| Theory | |||
|---|---|---|---|
| Adiabat | |||
| 0.71 | 0.816 | 1.153 | |
| 1/8 | 1/5 | 1/3 | |
| 1/9 | 1/6 | 1/4 | |
| 1/4 | 1/5 | 1/9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, B.; Bradley, P.A. A Physical Metric for Inertial Confinement Fusion Capsules. Plasma 2024, 7, 146-159. https://doi.org/10.3390/plasma7010010
Cheng B, Bradley PA. A Physical Metric for Inertial Confinement Fusion Capsules. Plasma. 2024; 7(1):146-159. https://doi.org/10.3390/plasma7010010
Chicago/Turabian StyleCheng, Baolian, and Paul A. Bradley. 2024. "A Physical Metric for Inertial Confinement Fusion Capsules" Plasma 7, no. 1: 146-159. https://doi.org/10.3390/plasma7010010
APA StyleCheng, B., & Bradley, P. A. (2024). A Physical Metric for Inertial Confinement Fusion Capsules. Plasma, 7(1), 146-159. https://doi.org/10.3390/plasma7010010






