Influence of Voltage Rising Time on the Characteristics of a Pulsed Discharge in Air in Contact with Water: Experimental and 2D Fluid Simulation Study

Abstract

In the context of plasma–liquid interactions, the phase of discharge ignition is of great importance as it may influence the properties of the produced plasma. Herein, we investigated the influence of voltage rising time (${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$) on discharge ignition in air as well as on discharge propagation on the surface of water. Experimentally, ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was adjusted to 0.1, 0.4, 0.6, and 0.8 kV/ns using a nanosecond high-voltage pulser, and discharges were characterized using voltage/current probes and an ICCD camera. Faster ignition, higher breakdown voltage, and greater discharge current (peak value) were observed at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. ICCD images revealed that higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ also promoted the formation of more filaments, with increased radial propagation over the water surface. To further understand these discharges, a previously developed 2D fluid model was used to simulate discharge ignition and propagation under various ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ conditions. The simulation provided the spatiotemporal evolution of the E-field, electron density, and surface charge density. The trend of the simulated position of the ionization front is similar to that observed experimentally. Furthermore, rapid vertical propagation (<1 ns) of the discharge towards the liquid surface was observed. As ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ increased, the velocity of discharge propagation towards the liquid increased. Higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ values also led to more charges in the ionization front propagating at the water surface. The discharge ceased to propagate when the charge number in the ionization front reached 0.5 × ${10}^8$ charges, irrespective of the ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ value.

1. Introduction

When an electric field (E-field) is applied to a gaseous dielectric medium, the neutral molecules of the latter can become ionized by the impact of high-energy electrons, leading to the initiation and propagation of a discharge [1]. The separation of charges at the front of the ionization wave produces a high-magnitude space charge field [2,3]. If the magnitude of this field is comparable to that of the breakdown field (35 kV/cm for air at atmospheric pressure), the discharge transits to a streamer [4]. In general, a streamer is characterized by a non-equilibrium thermodynamic plasma channel [5] that propagates with high speed under the action of the space charge field at its head, with the assistance of photoionization to produce seed electrons ahead of its front [6]. Such unique properties promote the application of streamer discharges in various fields such as medicine [7], water depollution [5], and surface treatment [8]. Regardless of the application, better understanding of discharge ignition and plasma–surface interactions is needed to achieve the desired results [9,10].

Since the E-field is a primary factor influencing discharge dynamics, it is essential to understand the influence of voltage amplitude and application period on discharge ignition and propagation in a gap as well as on a surface. At a higher magnitude of the applied voltage, i.e., higher E-field, it is expected that the ionization of gas will occur earlier, and thus, a streamer will be established more quickly [11]. Li et al. [12] numerically demonstrated that by increasing the voltage magnitude from 92 to 112 kV, which corresponded to an increase of a field from 23 to 25 kV/cm, the discharge ignition time decreased from 8.50 to 3.75 ns. The propagation velocity of the discharge in the gap also increased from 0.25 to 0.40 mm/ns. Bourdon et al. [13] simulated discharge propagation in the gap between a pin and plane electrodes, and they observed that an increase in voltage rising time from 80 to 120 kV/ns led to earlier ignition, increased ignition voltage (from 14.5 to 17.4 kV), and faster propagation towards the plane; the times needed to reach the plane at 80 and 120 kV/ns were 5.83 and 2.03 ns, respectively.

In addition to discharge propagation in a gap, voltage characteristics influence propagation over the surface of a dielectric material, either solid or liquid. Konina et al. [14] simulated the propagation of an atmospheric plasma jet (Ar/${\mathrm{N}}_2$ = 90/10 with a nitrogen coflow) positioned at 0.8 mm above a ceramic tube, featuring a series of rectangular cross-sectional channels. They showed that by increasing the voltage magnitude from −20 to −25 kV, the surface ionization wave velocity and maximum electron density increased from 0.2 to 0.5 mm/ns and from $4\times {10}^{13}$ to $1\times {10}^{14}{\mathrm{c}\mathrm{m}}^{-3}$, respectively. Similarly, Höft et al. [15] highlighted that in a pin-to-liquid configuration with a pulsed applied voltage (9 kV of amplitude and 300 μs of pulse width), an increase in the discharge formation time from ~250 to 254 μs resulted in an increase in the generated charge from 2.8 to 5.2 nC. Yang et al. [16] investigated the impact of the voltage applied on an anode needle placed at 0.1 mm above a bismuth silicon oxide (BSO) crystal with a relative dielectric constant of 56. Using a high-voltage pulse with a rising time of 30 ns, they investigated the influence of the voltage plateau value on the discharge. Their results indicated that when the voltage plateau was increased from 4.0 to 5.5 kV, the propagation speed and maximum propagation distance over the surface increased from 0.1 to 0.4 mm/ns and from 5 to 9 mm, respectively.

When a discharge propagates over a dielectric surface, it tends to form filaments due to electron avalanche-triggered radial destabilization of the ionization wave at the discharge front. Therefore, changes in the voltage magnitude can also affect the filamentation process and the observed pattern. According to Yang et al. [16], the number of filaments increased from 6 to 9 as the voltage magnitude was increased from 4.0 to 5.5 kV. In a previous experimental study on discharge propagation over the surface of water [17], we found that with an increasing (breakdown) voltage from 6 to 10 kV, the number of filaments rose from 10 to 15.

In this paper, we aim to further investigate the impact of voltage rising time on the characteristics of a nanosecond discharge ignited in air and propagating over the surface of water, using both experiments and simulation. Experimentally, the rising period of the high voltage pulse was controlled between 0.1 and 0.8 kV/ns by adjusting its plateau value. The discharges were characterized electrically, by measuring voltage–current waveforms, and optically, by acquiring time-integrated and time-resolved ICCD images. As for the simulation, it was performed using a previously developed 2D fluid model, with some modifications. This simulation was used to capture the ignition of the discharge, the propagation in the gap, as well as the propagation on the water surface. The obtained simulation results allowed for the determination of different characteristics such as the spatiotemporal distribution of the E-field, density of charged species, and surface charge.

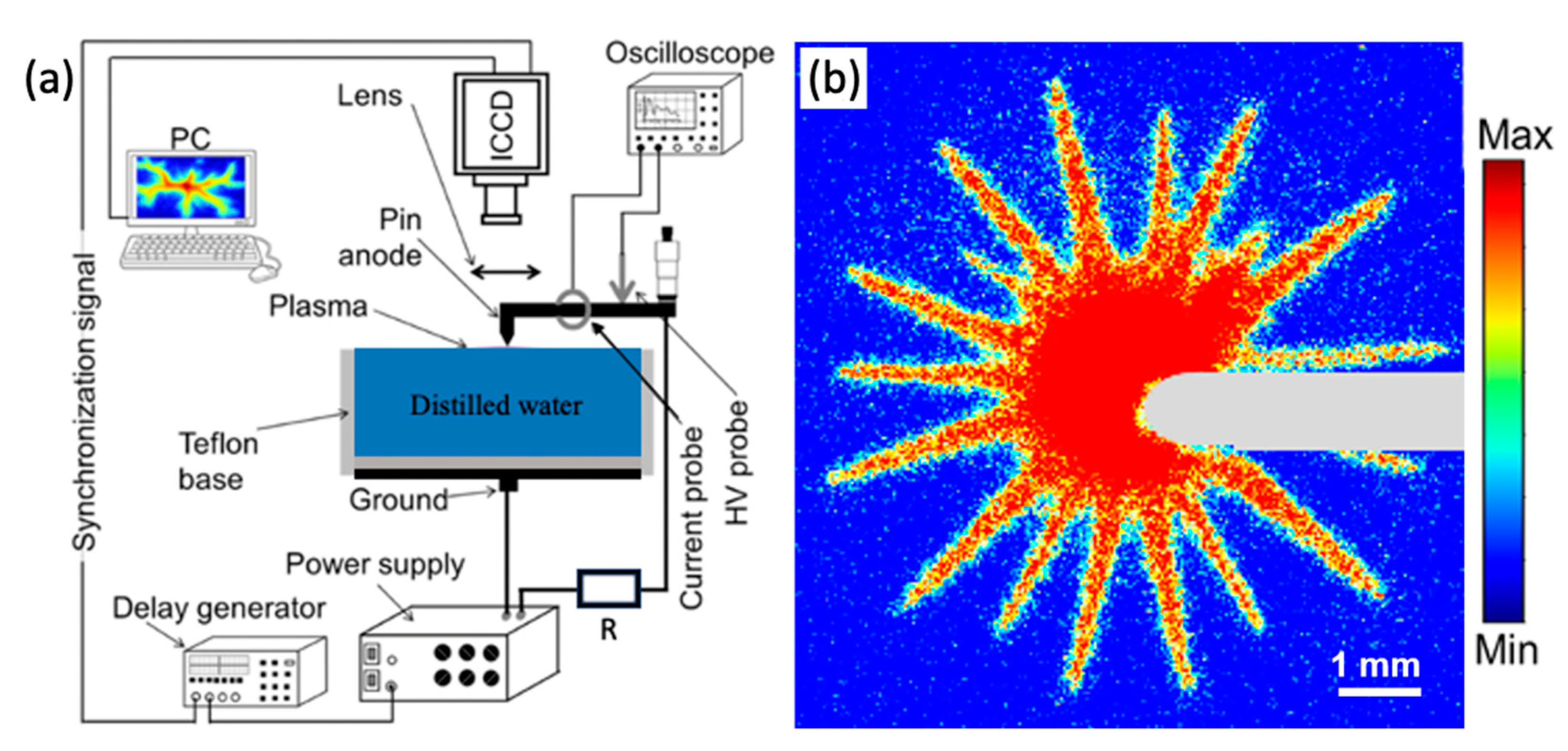
2. Experimental Conditions

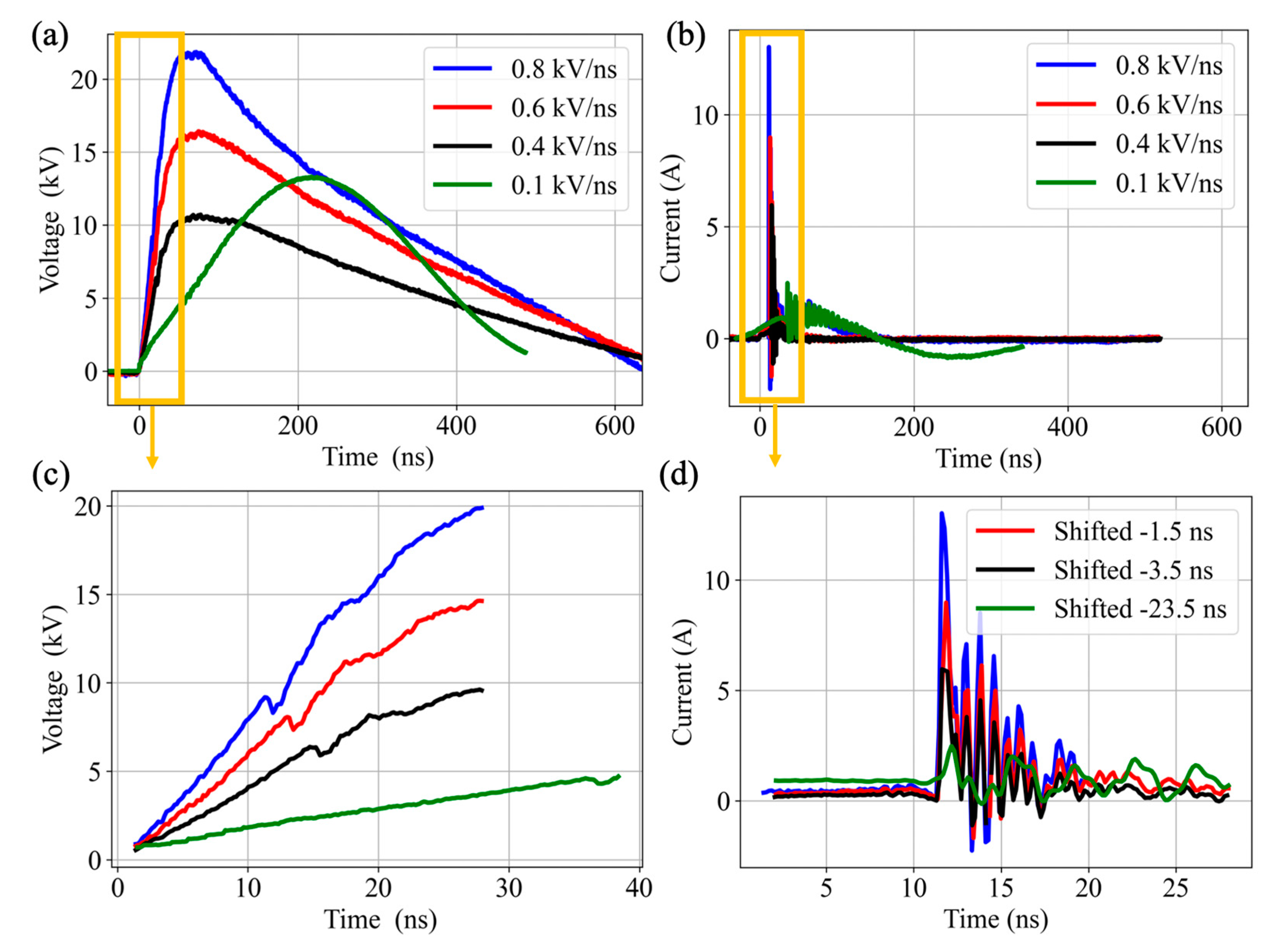
2.1. Electrical Characterization

As shown in Figure 1a, electrical discharges in air in contact with distilled water were ignited using a nanosecond positive pulsed power supply (NSP 120-20-P-500-TG-H; Eagle Harbor Technologies). The plateau duration of the pulse was fixed at $100 \mathrm{n}\mathrm{s}$, while its magnitude was adjusted between 10 and 20 kV to obtain different values of the rising time (${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = $0.4,0.6,\mathrm{a}\mathrm{n}\mathrm{d} 0.8$ k$\mathrm{V}/\mathrm{n}\mathrm{s}$). An external resistor of R = 250 $\mathsf{\Omega }$ was added to the circuit to further decrease ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ to 0.1 k$\mathrm{V}/\mathrm{n}\mathrm{s}$. A tungsten rod (diameter of $1 \mathrm{m}\mathrm{m}$) with a mechanically polished tip (pin angle of $~30°$) was used as the anode, whereas a stainless steel rod ($60 \mathrm{m}\mathrm{m}$ diameter) placed at the bottom of a cylindrical Teflon cell (diameter of $67 \mathrm{m}\mathrm{m}$ and height of $5.7 \mathrm{m}\mathrm{m}$) was used as the cathode. The cell was filled with $20 \mathrm{m}\mathrm{L}$ of distilled water with a dielectric permittivity of ε_r = 80 and an electrical conductivity of σ = 2 μS/cm, and the distance between the anode pin and water surface was fixed at $600 \mathrm{\mu }\mathrm{m}$. A vertically mounted ICCD camera (PIMAX-4: $1024$ EMB; Princeton Instruments) was used to monitor the behavior of the plasma emission at the solution surface. This camera is equipped with an RB-type intensifier that covers the wavelength range of $200–850 \mathrm{n}\mathrm{m}$ with a quantum efficiency between $2$ and $15\mathrm{\%}$, depending on the wavelength. The dimension of the captured zone was $10 \mathrm{m}\mathrm{m}\times 10 \mathrm{m}\mathrm{m}$. A delay generator (Quantum Composers Plus $9518$ Pulse Generator) was used to adjust the delay between the ICCD camera and the voltage pulse. Figure 1b presents the discharge emission (20 ns integrated ICCD image) at the water surface for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = $0.8$ k$\mathrm{V}/\mathrm{n}\mathrm{s}$, and it highlights the radial propagation of highly organized plasma filaments over the water surface.

The voltage and current characteristics of the discharges were measured using a high-voltage probe (P6015A; Tektronix) and a current monitor (6585; Pearson), respectively. These waveforms were visualized and recorded using an oscilloscope (MSO54, 2 GHz, 6.25 GS/s). Figure 2a,b depict typical voltage–current waveforms of discharges generated under the various conditions of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. Meanwhile, Figure 2c,d provide a closer examination of the region of interest when the discharge occurred at t = 36, 15, 13, and 11 ns for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.1, 0.4, 0.6, and 0.8 kV/ns, respectively. To present the results more clearly, the current waveforms in Figure 2d were all shifted to synchronize with the first peak. For each condition, breakdown occurred during the rising period of the pulse, enabling the investigation of the influence of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ on the discharges. For instance, for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$= 0.1, 0.4, 0.6, and 0.8 kV/ns, breakdown occurred at a voltage (${\mathrm{V}}_{\mathrm{b}\mathrm{d}}$) of ~4.5, 6.3, 7.8, and 9.1 kV, respectively (Figure 2c). The discharge current (peak value, ${\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$) also depended on ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. Indeed, ${\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increased from 2.2 to 12.9 A as ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ increased from 0.1 to 0.8 kV/ns. In our experimental setup, the maximal value of the displacement current during the rising time of the applied voltage was around 0.3 A, as highlighted by Hamdan et al. [18] in a previous study. Therefore, it was negligible compared to the current generated by the discharge.

To account for the stochastic nature of the discharge and accurately capture the typical dispersion of its electrical characteristics, 20 discharges were ignited under each condition. Figure 3a,b illustrate the statistical variation in the formation time (${\mathsf{\tau }}_{\mathrm{b}\mathrm{d}}$) and ${\mathrm{V}}_{\mathrm{b}\mathrm{d}}$ as a function of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. Evidently, ${\mathsf{\tau }}_{\mathrm{b}\mathrm{d}}$ decreased from ~35 ± 2 to 11 ± 1 ns and ${\mathrm{V}}_{\mathrm{b}\mathrm{d}}$ increased from ~4.5 ± 0.5 to 8.5 ± 2 kV as ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was raised from 0.1 to 0.8 kV/ns. This trend will be explained in Section 4.

The influence of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ on ${\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is depicted in Figure 4. Notably, the increase in ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ from 0.1 to 0.8 kV/ns produced an increase in ${\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ from ~2.5 ± 0.7 to 12.5 ± 1.3 A. Therefore, in addition to increased ${\mathrm{V}}_{\mathrm{b}\mathrm{d}}$, higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ values led to more intense discharges. This behavior provides insight into the charges generated during breakdown. In fact, Höft et al. [19] also measured that in a pin-to-pin configuration with a 1 mm gap in a gas containing 0.1% O₂ in N₂ at atmospheric pressure, an increase in τ_rise (with a plateau value of 10 kV) from 0.0075 to 0.2 kV/ns caused an increase in the maximal current value generated by the discharge from 125 to 175 mA, as well as an increase in the transferred charge from 1.5 to 3.5 nC.

2.2. ICCD Imaging

To elucidate the influence of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ on the dynamics of the discharge at the water surface, 20 ns integrated ICCD images of the discharge emission were recorded. Figure 5a shows images of typical discharges occurring at ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.1, 0.4, 0.6, and 0.8 kV/ns. Qualitatively, the images show that both the maximal propagation radius (${\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$) and the number of filaments (plasma dots, i.e., individual surface discharge channels) ${\mathrm{N}}_{\mathrm{d}\mathrm{o}\mathrm{t}\mathrm{s}}$ increased with increasing ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. Statistical analysis of numerous acquired ICCD images revealed that when ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was increased from 0.1 to 0.8 kV/ns, ${\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${\mathrm{N}}_{\mathrm{d}\mathrm{o}\mathrm{t}\mathrm{s}}$ increased from ~1.7 ± 0.3 to 4.0 ± 0.2 mm (Figure 5b) and from ~10 ± 1 to 20 ± 3 (Figure 5c), respectively. Such increases may be attributed to the increased discharge current at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$, which signifies a greater number of accumulated charges above the liquid surface. Note that since the ICCD images were integrated during 20 ns and the discharges were ignited only 10–50 ns after applying the voltage pulse, the timescale was too short to observe any Taylor cone formation such as the one described by Yoon et al. [20] as its formation time was on the order of microseconds. Moreover, the 20 consecutive discharges were run at low frequency (1 Hz), which made them not coupled in time and the liquid surface remained steady. The evaporation of the liquid can be neglected as the liquid was replaced after each experiment and the gap distance was adjusted after each set of 20 consecutive discharges.

Figure 6 shows the temporal evolution of the discharge emission over the water surface (1 ns integrated images) during the first $5 \mathrm{n}\mathrm{s}$ for all ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ conditions. In fact, the streamer discharge reached the liquid surface in less than $1 \mathrm{n}\mathrm{s}$ (i.e., unresolved here). Then, radial propagation took place over the liquid surface. During the first nanosecond, the emission was disc-like, while $1 \mathrm{n}\mathrm{s}$ later, it expanded radially and took the form of a ring-like structure. Then the ring continued to expand radially, and it broke into multiple single plasma dots at t = 3 ns for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.4, 0.6, and 0.8 kV/ns and at t = 4 ns for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.1 kV/ns. Finally, these plasma dots continued to expand radially until they faded away.

3. Numerical Simulation

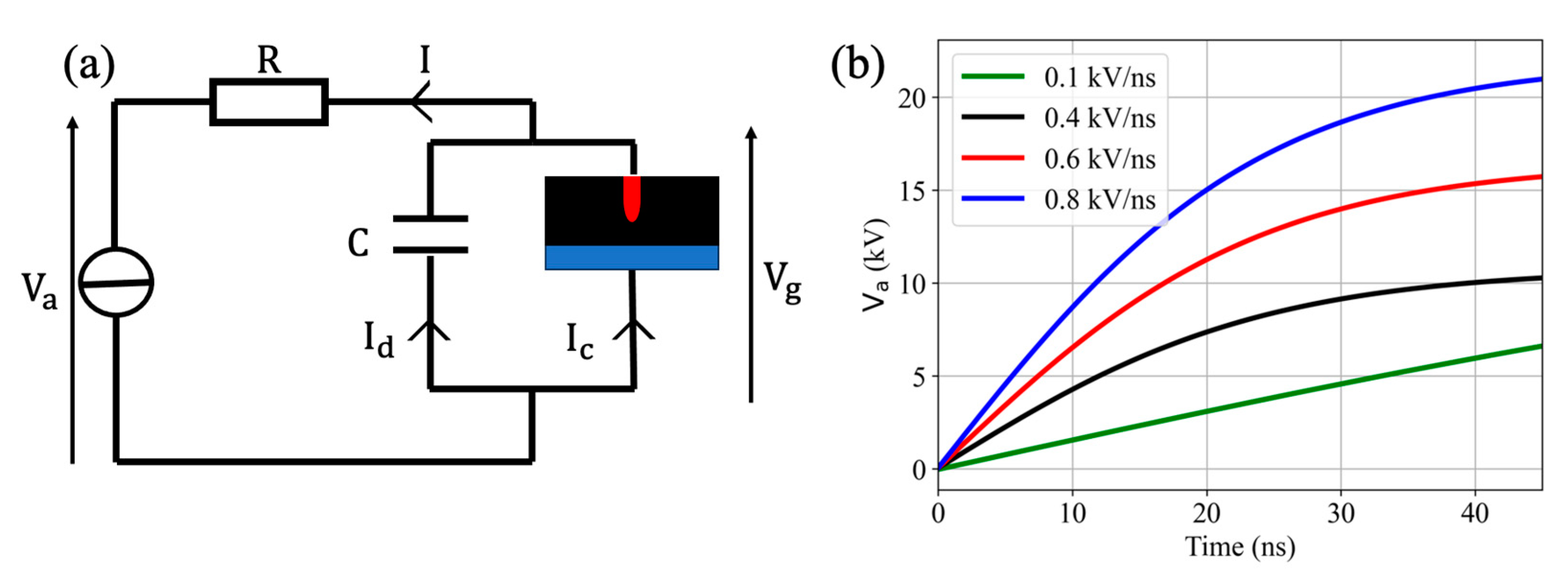
3.1. Discharge Model Equations, Boundary Conditions, and Computational Domain

Numerical simulations were conducted by employing a 2D axisymmetric cylindrical fluid model in air at atmospheric pressure. This model solves drift–diffusion equations, yielding the temporal evolution of electron (${\mathrm{n}}_{\mathrm{e}}$), positive ion (${\mathrm{n}}_{\mathrm{i}}$), and negative ion (${\mathrm{n}}_{\mathrm{n}}$) densities. All requisite coefficients, including the diffusion, mobility, gain terms (electron impact ionization, photoionization, and secondary electrons), and loss terms (electron attachment and recombination) were considered electric field-dependent. The liquid was treated as a solid dielectric because its corresponding free charge reorganization time (τ_r = ε_rε₀/σ = 3540 ns) was much longer than the typical timescale of discharge propagation (between 10 and 40 ns). Additionally, secondary electron emission was considered when positive ions hit the liquid surface. Dielectric surface charging was also incorporated in the model by including fluxes of charged species towards the liquid surface. The electric field distribution in the computational domain was determined by resolving Poisson’s equation. Meanwhile, photoionization was addressed by solving Helmholtz’s equations, according to the Finite Volume Method wherein charged species fluxes were computed based on the Scharfetter–Gummel scheme. Poisson’s and Helmholtz’s equations were solved using a direct solver in Python, and the Ghost Fluid Method was used to enhance the geometric accuracy in simulating the pin boundary. The 2nd order Runge–Kutta method was adopted for the integration of the fluid equations, and the time step was determined based on Courant–Friedrichs–Lewy (CFL) conditions. Moreover, an electron flux correction was implemented to circumvent the restriction of the dielectric relaxation time and optimize the computational efficiency. A comprehensive description of all transport coefficients and numerical methods employed herein can be found in [21].

Boundary conditions for ${\mathrm{n}}_{\mathrm{e}}$, ${\mathrm{n}}_{\mathrm{i}}$, ${\mathrm{n}}_{\mathrm{n}}$, and Helmholtz’s equations were the same as those described in [21]. Likewise, for Poisson’s equation, we employed the same boundary conditions as in [21], except for the Dirichlet boundary condition value at the anode. Herein, a dielectric (with a thickness of $500 \mathsf{\mu }\mathrm{m}$ and ε_r = $2$) was added between the ground and the water to reproduce the experimental setup.

The background density of electrons and ions (${\mathrm{n}}_{\mathrm{e},\mathrm{i}}$) was fixed at ${10}^9{\mathrm{m}}^{-3}$, and the initial density of ${\mathrm{n}}_{\mathrm{n}}$ was set to $0$. To optimize the computational time, a non-uniform grid was used, with high resolution near the regions of interest such as the liquid surface. As shown in Figure 7, the simulation was performed on a $10.4\times 6 {\mathrm{m}\mathrm{m}}^2$ rectangular domain with a grid size of $1082\times 1001$. Along the axial direction z, the dimensions used were the following:

• From $\mathrm{z}=0$ to $3.9 \mathrm{m}\mathrm{m}$, uniform grid with $∆\mathrm{z}=20 \mathsf{\mu }\mathrm{m}$;
• From $\mathrm{z}=3.9$ to $4.2 \mathrm{m}\mathrm{m}$, uniform grid with $∆\mathrm{z}=0.7 \mathsf{\mu }\mathrm{m}$;
• From $\mathrm{z}=4.2$ to $4.5 \mathrm{m}\mathrm{m}$, non-uniform grid with a geometric expansion ${∆\mathrm{z}}_{\mathrm{i}}=1.1{∆\mathrm{z}}_{\mathrm{i}-1}$ up to $∆\mathrm{z}=3.65 \mathsf{\mu }\mathrm{m}$;
• From $\mathrm{z}=4.5$ to $5.1 \mathrm{m}\mathrm{m}$, uniform grid with $∆\mathrm{z}=3.65 \mathsf{\mu }\mathrm{m}$;
• From $\mathrm{z}=5.1$ to $5.7 \mathrm{m}\mathrm{m}$, non-uniform grid with a geometric expansion ${∆\mathrm{z}}_{\mathrm{i}}=1.1{∆\mathrm{z}}_{\mathrm{i}-1}$ up to $∆\mathrm{z}=30 \mathsf{\mu }$m;
• From $\mathrm{z}=5.7$ to $10.4 \mathrm{m}\mathrm{m}$, non-uniform grid with a geometric expansion ${∆\mathrm{z}}_{\mathrm{i}}=1.1{∆\mathrm{z}}_{\mathrm{i}-1}$ up to $∆\mathrm{z}=60 \mathsf{\mu }\mathrm{m}$.

In the radial direction, a uniform grid with $∆\mathrm{r}=6 \mathsf{\mu }\mathrm{m}$ was used between $\mathrm{r}=0$ and $6\mathrm{m}\mathrm{m}$.

To replicate the experimental pulse, we assumed that the circuit depicted in Figure 8a was representative of the setup. The application of Kirchhoff’s voltage law on the circuit yielded the following equation:

$${\mathrm{V}}_{\mathrm{a}}=\mathrm{R}\mathrm{I}+{\mathrm{V}}_{\mathrm{g}}$$

(1)

where ${\mathrm{V}}_{\mathrm{a}}$ is the voltage applied by the pulser (depicted in Figure 8b), R = 1 kΩ is the pulser resistance [22], $\mathrm{I}$ is the total current, and ${\mathrm{V}}_{\mathrm{g}}$ is the voltage across the gap where the discharge occurs.

The circuit capacitance of $\mathrm{C}=0.1$ pF was estimated experimentally from the voltage–current measurements, based on the following formula, $C={\mathrm{I}}_{\mathrm{d}}/{\displaystyle \frac{\partial {\mathrm{V}}_{\mathrm{g}}}{\partial \mathrm{t}}}$, where ${\mathrm{I}}_{\mathrm{d}}$ is the displacement current. A more comprehensive equivalent circuit could be constructed, similar to the one developed in a previous study by Mericiris et al. [22]. However, for simplicity, computational efficiency, and due to the good agreement between the experimental and simulation results presented hereafter, we believe that this representation is satisfactory. Considering that I = I_d + ${\mathrm{I}}_{\mathrm{c}}$, where ${\mathrm{I}}_{\mathrm{c}}$ is the conduction current resulting from the discharge (calculated based on the extended Sato method [11]), Equation (1) was rearranged as

$$\mathrm{R}\mathrm{C}{\displaystyle \frac{\partial {\mathrm{V}}_{\mathrm{g}}}{\partial \mathrm{t}}}+{\mathrm{V}}_{\mathrm{g}}={\mathrm{V}}_{\mathrm{a}}-\mathrm{R}{\mathrm{I}}_{\mathrm{c}}$$

(2)

Knowing the values of R, C, V_a, and I_c, ${\mathrm{V}}_{\mathrm{g}}$ was determined by resolving Equation (2). To assess the effect of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ on discharge dynamics, four simulations were conducted at ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}=0.1, 0.4, 0.6, \mathrm{a}\mathrm{n}\mathrm{d} 0.8 \mathrm{k}\mathrm{V}/\mathrm{n}\mathrm{s}$. The value of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was varied by adjusting the waveform of ${\mathrm{V}}_{\mathrm{a}}$, as shown in Figure 8b.

3.2. Simulation Results

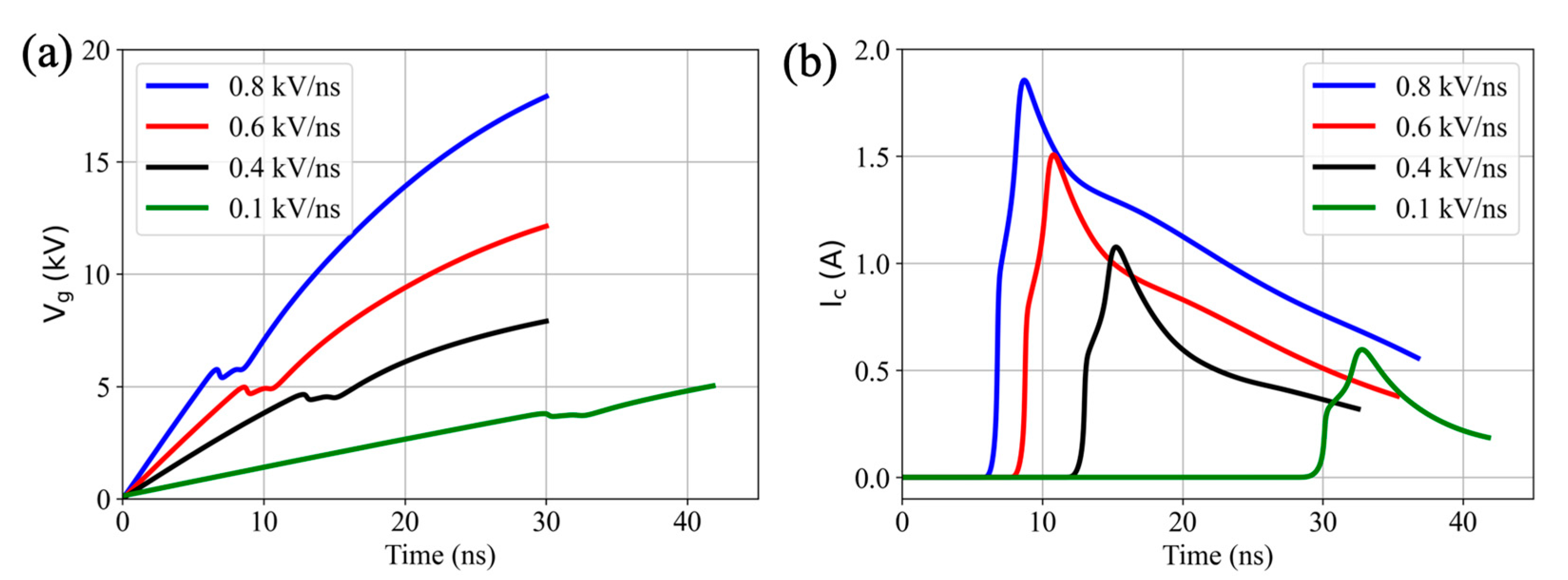
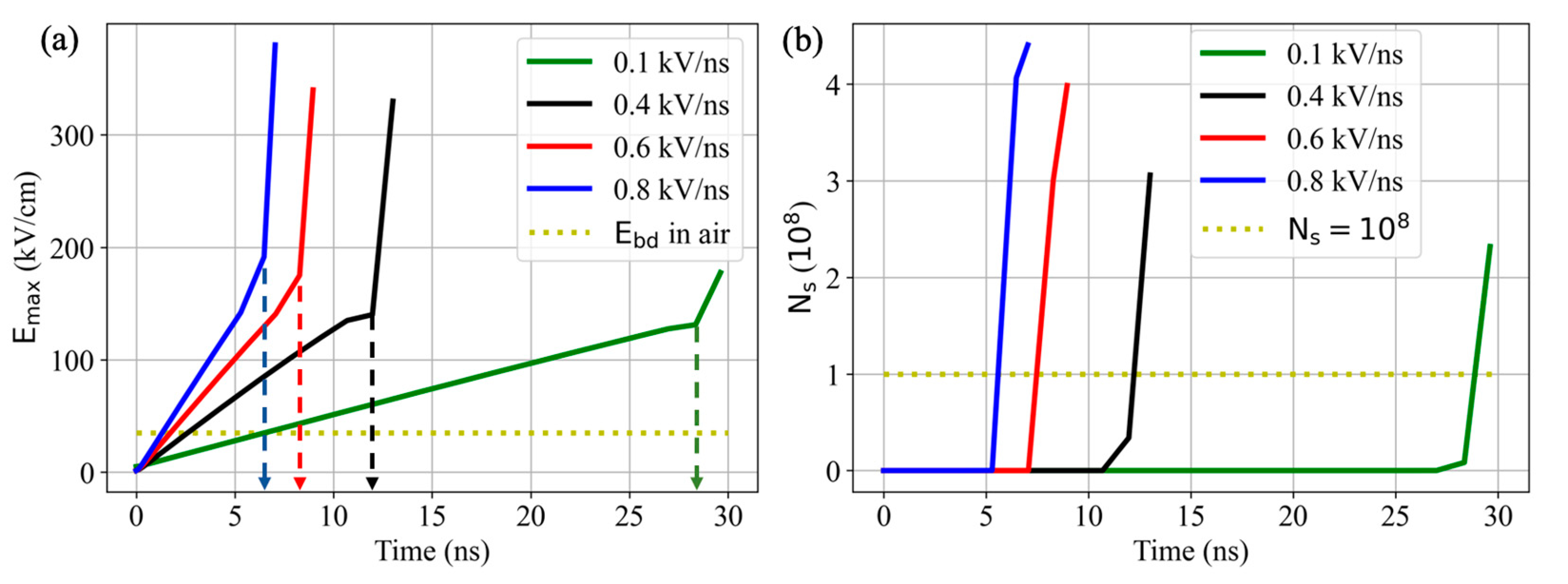
3.2.1. Electrical Results

Figure 9a,b display the temporal evolution of the simulated ${\mathrm{V}}_{\mathrm{g}}$ and ${\mathrm{I}}_{\mathrm{c}}$ values. Despite variations in the breakdown voltage and breakdown moment, the simulated voltage waveform is in excellent agreement with the experimental one (Figure 2c). Specifically, the simulated results show that the increase of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ from 0.1 to 0.8 kV/ns led to earlier breakdown (delay decreases from ~30 to 7 ns) and higher breakdown voltage (increases from ~3.7 to 5.9 kV)—a trend similar to the one observed experimentally. Moreover, the numerical model accurately captured the voltage drop caused by the intense current generation due to the ignition of the discharge, as observed experimentally in Figure 2c. Figure 8b shows the simulated discharge current, which is also similar to the experimental one. Indeed, ${\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increased from ~0.6 to 1.9 A as ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was raised from 0.1 to 0.8 kV/ns. Note that for all investigated conditions, the simulated ${\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ values are lower than the experimental ones, probably due to the lower breakdown voltage obtained numerically (approximately 1.5 times lower) compared to the experimental breakdown. The absence of oscillations from the simulated waveform was due to the fact that the voltage probe characteristics and RLC parasitic circuit were not considered in the simulation. Overall, the electrical characteristics simulated using the simplified circuit are comparable to those obtained experimentally, which indicates that the model is valid and can be used to analyze other plasma properties.

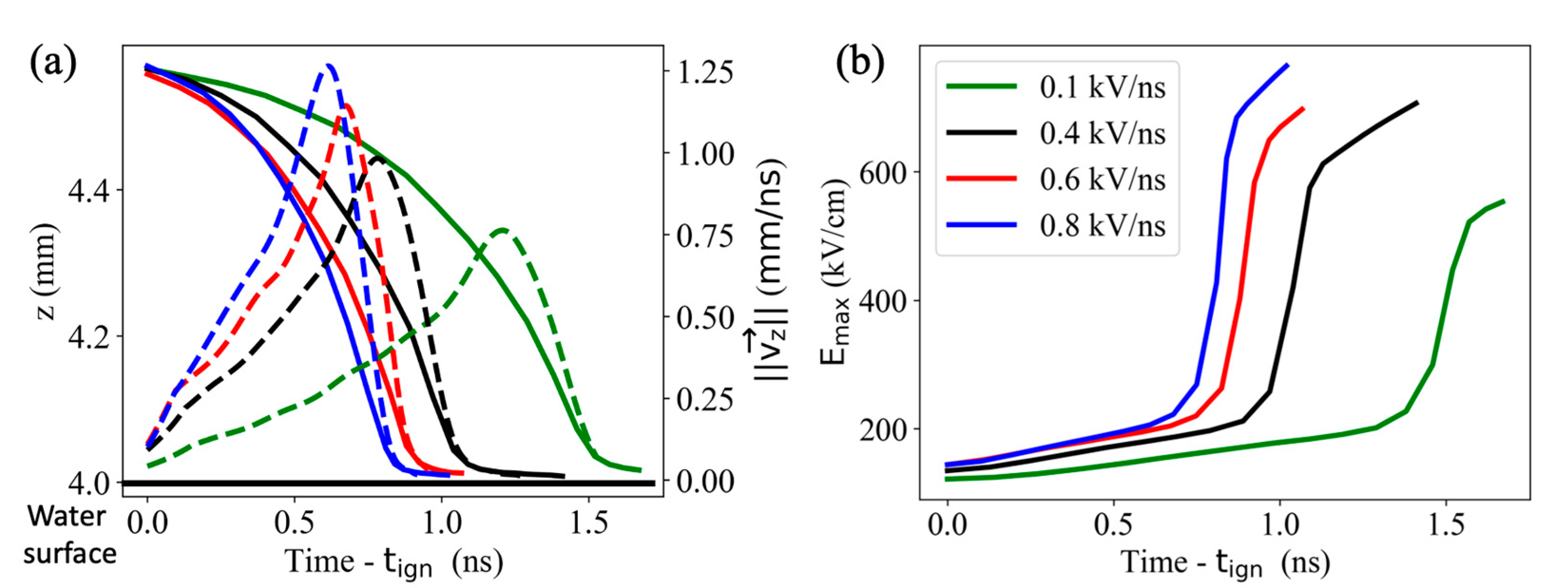
3.2.2. Vertical Propagation

Considering that ignition occurs at different times (${\mathrm{t}}_{\mathrm{i}\mathrm{g}\mathrm{n}}$) for different discharge events, the following results are presented with ${\mathrm{t}}_{\mathrm{i}\mathrm{g}\mathrm{n}}$ as a reference. Following ignition, an ionization wave (IW) propagated in the gap and reached the water surface in less than 1 ns. Since the vertical propagation of the discharge towards the liquid surface occurred in less than 1 ns, and given the stochastic nature of discharge ignition, even with an integration time as short as 1 ns, we were unable to accurately capture the vertical propagation of the discharge experimentally. Therefore, we decided to investigate it through simulation. Figure 10 depicts the temporal evolution of the E-field under various conditions of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. The propagation of the IW was mainly driven by the space charge field, and it was clearly affected by ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$, as the produced E-field was strongly dependent on this parameter. Indeed, for a comparable time and/or comparable position, the field was higher for higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. As the IW propagated in the gap, the E-field magnitude increased and reached a peak value when the IW touched the liquid surface; this was due to the accumulation of charges on the liquid surface. For instance, at ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.8 kV/ns, the IW reached the water surface at 0.8 ns after breakdown, and the peak value of the electric field was ~700 kV/cm.

Figure 11a displays the position of the IW as a function of time for different ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ conditions (solid lines). The magnitude of the axial propagation velocity ($‖\overrightarrow{{\mathrm{v}}_{\mathrm{z}}}‖$) of the IW is also shown in Figure 11a (dotted lines). Clearly, ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ had a significant effect on the propagation of the IW in the gap. At ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.1 kV/ns, the IW reached the liquid surface 1.5 ns after ignition, while at ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.8 kV/ns, it reached the surface 0.80 ns after ignition. As the IW traveled towards the liquid, $‖\overrightarrow{{\mathrm{v}}_{\mathrm{z}}}‖$ increased, reaching maximum just before approaching the liquid surface. Obviously, $‖\overrightarrow{{\mathrm{v}}_{\mathrm{z}}}‖$ tended to zero when it touched the liquid surface. The higher the ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$, the higher the ${‖\overrightarrow{{\mathrm{v}}_{\mathrm{z}}}‖}_{\mathrm{m}\mathrm{a}\mathrm{x}}$. For instance, ${‖\overrightarrow{{\mathrm{v}}_{\mathrm{z}}}‖}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increased from 0.75 to 1.25 mm/ns when ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ increased from 0.1 to 0.8 kV/ns. Figure 11b shows the evolution of ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ (at the IW head) as a function of time for different ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ conditions. The results also show that ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ was higher at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ values, not only during propagation in the air gap but also when reaching the water surface.

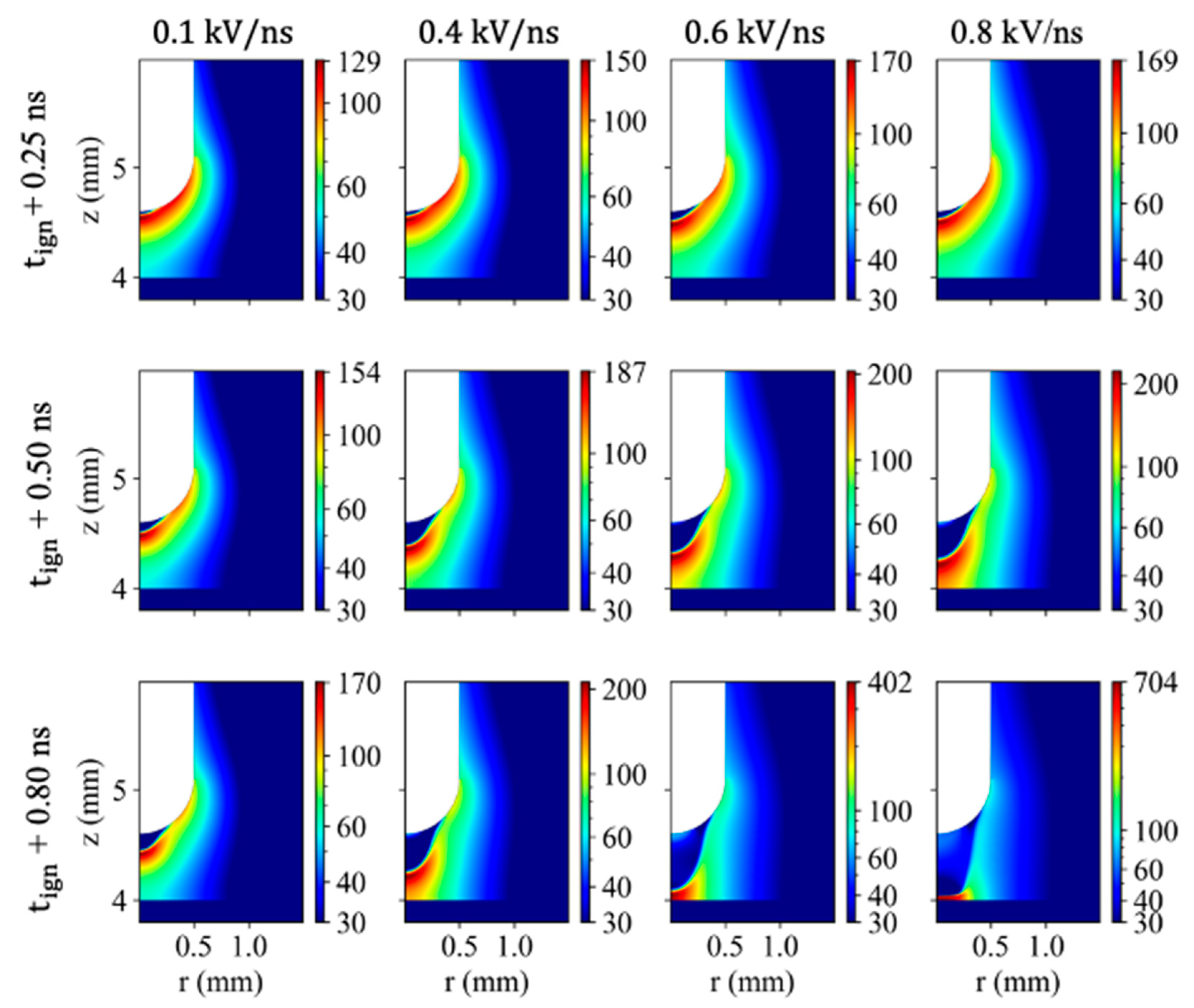
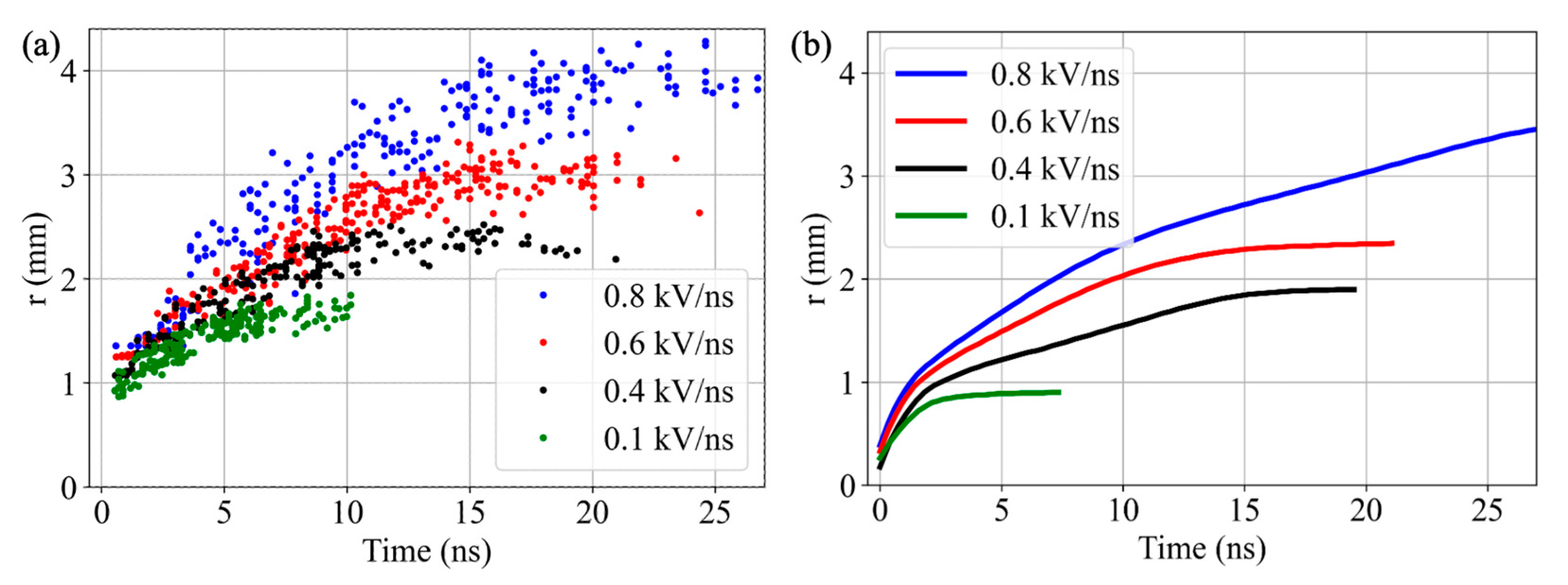
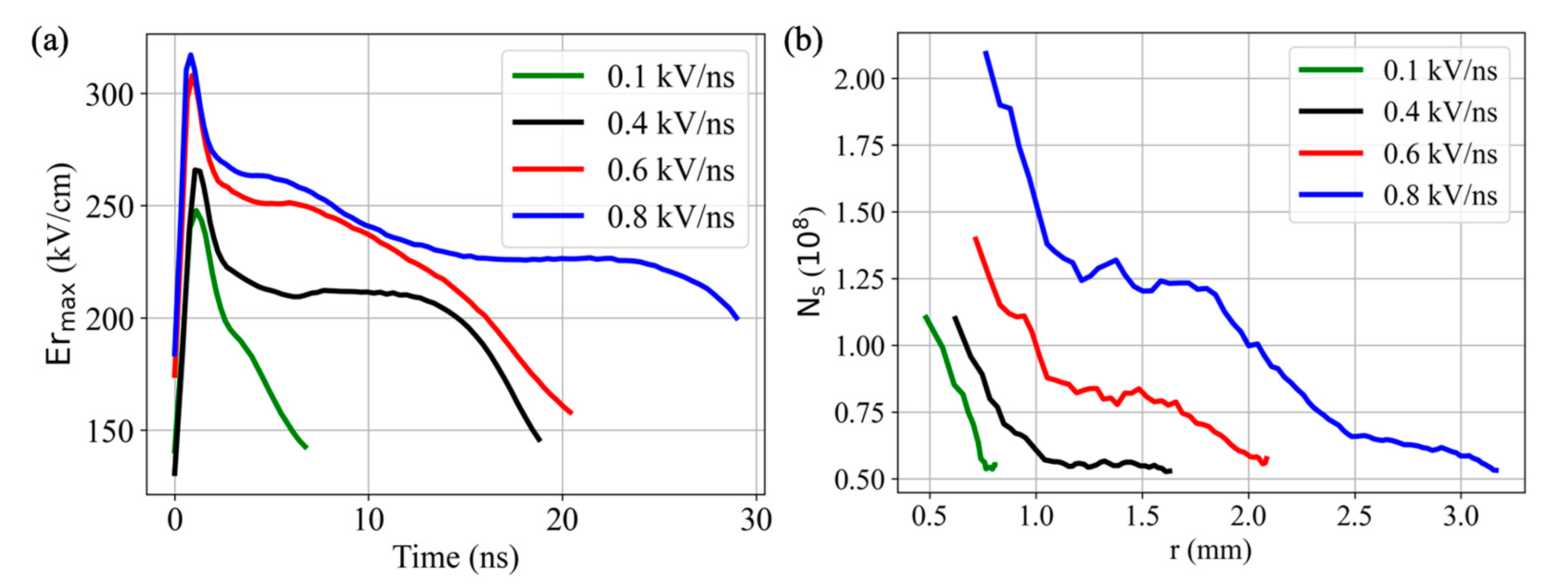
3.2.3. Radial Propagation

When the IW reaches a water surface, charges accumulate and produce a radial electric field that may ignite a surface discharge [23]. Herein, the propagation of the surface IW (SIW) was investigated under different conditions of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. Figure 12a,b show the spatiotemporal evolution of the E-field and ${\mathrm{n}}_{\mathrm{e}}$ for the different ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ values; ${\mathrm{t}}_{\mathrm{s}}$ is defined as the moment when the IW reaches the liquid surface. At ${\mathrm{t}}_{\mathrm{s}}$ + 1 ns, the SIW propagated relatively longer and the ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ was relatively higher at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. For instance, the values of r and ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ determined at ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.1 kV/ns were 0.4 mm and 650 kV/cm, compared to 0.75 mm and 1200 kV/cm at ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.8 kV/ns, respectively. Unlike r and ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$, ${\mathrm{n}}_{{\mathrm{e}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$ remained almost constant (~5–7 × ${10}^{20} {\mathrm{m}}^{-3}$), irrespective of the ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ condition. As the SIW propagated on the liquid surface, the radial position of the SIW changed significantly; for instance, at ${\mathrm{t}}_{\mathrm{s}}$ + 8 ns, we noted that r = 0.85 mm for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.1 kV/ns and r = 1.9 mm for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$= 0.8 kV/ns. However, the ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${\mathrm{n}}_{{\mathrm{e}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$ values remained within the same order for all conditions, with ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}~$860 kV/cm and ${\mathrm{n}}_{{\mathrm{e}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$ ~5 × ${10}^{20} {\mathrm{m}}^{-3}$. In our study, no back discharge on the pin surface was observed, contrary to what Höft et al. [15] observed in some cases. This difference can be attributed to our pin not being covered by a dielectric, thereby limiting surface propagation by preventing surface charging.

Figure 13 compares the simulation-derived and experimentally determined temporal evolution of the SIW position over the liquid surface. The experimental data were obtained by processing numerous 1 ns integrated ICCD images recorded at different times during SIW propagation (as illustrated on Figure 6) using a custom algorithm [17]. The simulated positions of the SIW were determined by identifying the maximal value of the ionization term at each moment, following the methodology outlined in [21]. As shown in Figure 13, the simulated temporal evolution profiles of the SIW position are in good agreement with the experimental profiles, irrespective of the ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ condition. However, the simulated ${\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ values are slightly lower than those determined experimentally. This difference is likely due to the numerical breakdown occurring at relatively lower ${\mathrm{V}}_{\mathrm{b}\mathrm{d}}$, which resulted in a lower background field in the air gap, thereby limiting the radial propagation in the simulations compared to the experimental results. Overall, the data indicate that both the propagation velocity and maximal radial position of the SIW increased at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$.

4. Discussion

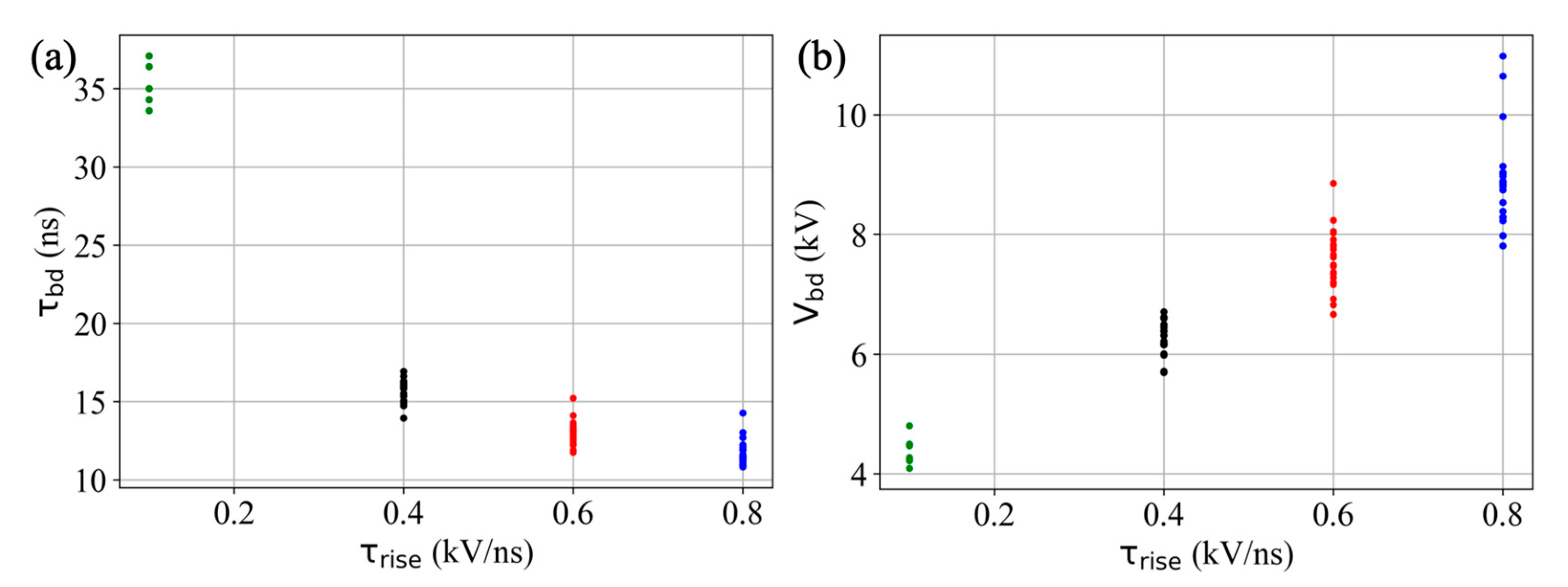
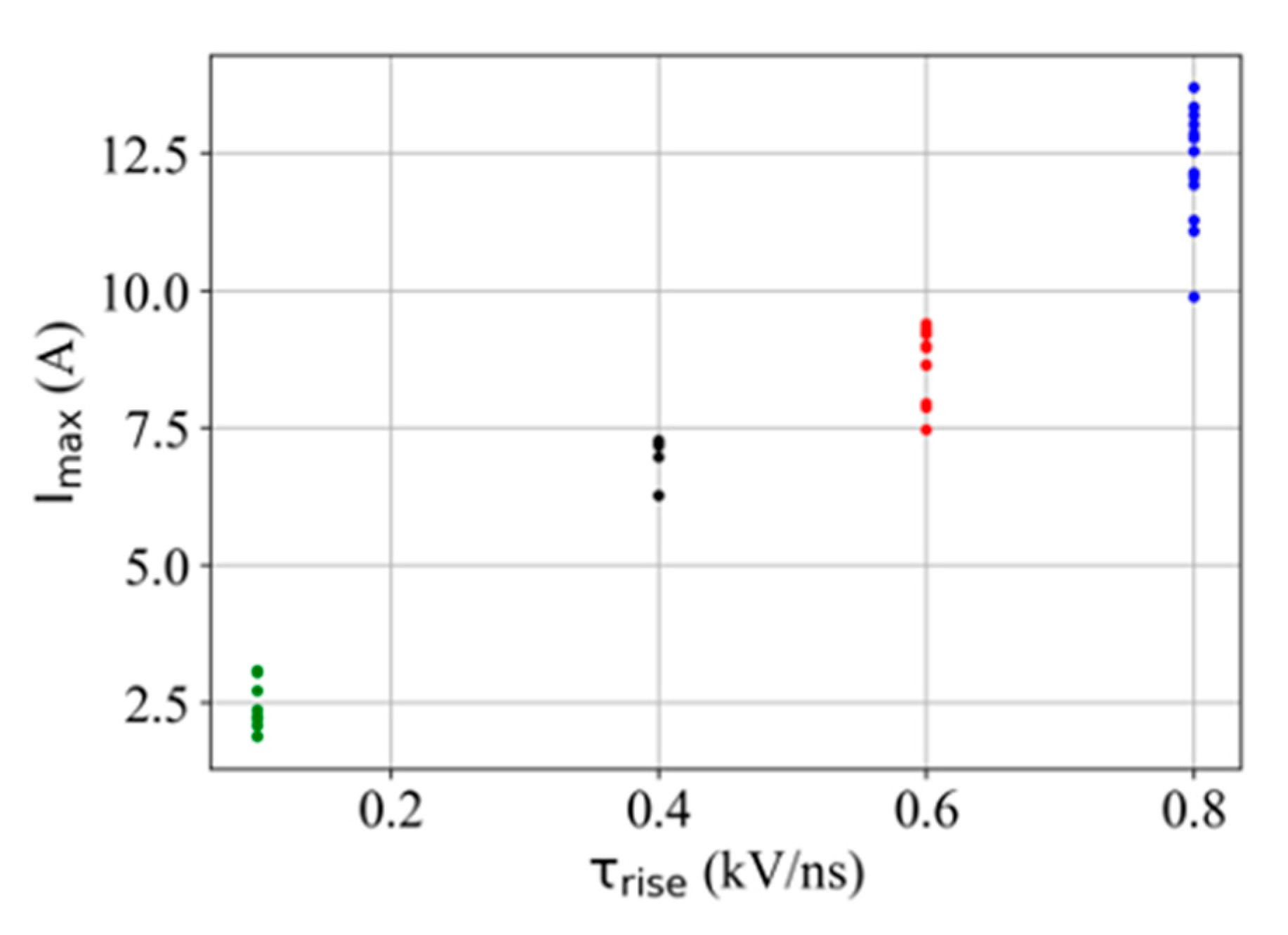
4.1. Impact of ${\tau }_{rise}$ on Discharge Ignition

It was feasible to estimate the ignition time of a streamer discharge under a given E-field using analytical formulas derived from the 1st Townsend coefficient. This coefficient offers an estimation of when a sufficient number of charged species are generated to initiate a streamer discharge [24]. However, in our case, breakdown occurred during the voltage rising period. As a result, the E-field was time-dependent and we could not estimate the formation time for a given E-field. Figure 14a illustrates the temporal evolution of the maximum E-field in the gap (from simulation) under various conditions of ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. The yellow dotted line represents the breakdown field in air (${\mathrm{E}}_{\mathrm{b}\mathrm{d}}$~35 kV/cm). Increasing ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ made reaching the breakdown field faster; for instance, ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ exceeded 35 kV/cm at t = 1.4 ns for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.8 kV/ns, while it was reached at t = 6.2 ns for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.1 kV/ns. The change in slopes for ${\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ across all conditions was attributed to discharge ignition, where the space charge field generated by the discharge surpassed the maximum Laplacian field measured before ignition (identified by the arrow for each condition on Figure 14a). Figure 14b depicts the temporal variation in the number of charged species (${\mathrm{N}}_{\mathrm{s}}$) generated at the anode tip. ${\mathrm{N}}_{\mathrm{s}}$ = ${10}^8$ represents Meek’s criterion, indicating the number of charged species needed to initiate a streamer discharge (marked by a yellow dotted line in the figure). Clearly, this criterion was met more rapidly at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$, which suggests that charged species were more easily produced at this condition. Indeed, Meek’s criterion was satisfied at t = 5.2 and 28 ns for ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ = 0.8 and 0.1 kV/ns, respectively.

4.2. Impact of ${\tau }_{rise}$ on the E-Field and $N_s$ during the Radial Propagation

The observed trend of SIW radial propagation can be understood by examining the radial electric field. Figure 15a shows that initially, i.e., once the SIW was ignited, the maximum radial field (${\mathrm{E}\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$) increased with increasing ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. Indeed, within the investigated ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ range of 0.1–0.8 kV/ns, the peak value of ${\mathrm{E}\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increased from ~245 to 346 kV/cm. This increase is attributed to a greater accumulation of charges induced by the increased initial electric field, as ${\mathrm{V}}_{\mathrm{b}\mathrm{d}}$ was higher at high ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. As the SIW propagated radially, ${\mathrm{E}\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ decreased after ignition for all conditions. However, at a given time, ${\mathrm{E}\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ remained higher for higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ values. For instance, at t = 6 ns, ${\mathrm{E}\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increased from 146 to 279 kV/cm when ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was raised from 0.1 to 0.8 kV/ns. The increase in the electric field further promoted the production of charged species, thereby contributing to the experimentally observed increase in ${\mathrm{I}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$, as highlighted in Figure 4.

Finally, Figure 15b shows the variation in ${\mathrm{N}}_{\mathrm{s}}$ during the radial propagation of the SIW over the liquid surface for all ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ conditions. The method used to determine ${\mathrm{N}}_{\mathrm{s}}$ was based on both the simulation and experimental results, and it is detailed elsewhere [21]. At a given radial position, we observed that ${\mathrm{N}}_{\mathrm{s}}$ increased with increasing ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. For example, when ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was increased from 0.1 to 0.8 kV/ns at r = 0.75 mm, ${\mathrm{N}}_{\mathrm{s}}$rose from 0.5 × ${10}^8$ to 2.1 × ${10}^8$. The relatively high values of ${\mathrm{N}}_{\mathrm{s}}$, i.e., verifying Meek’s criterion, indicated that the SIW may have been identified as a surface streamer discharge. For all the conditions, ${\mathrm{N}}_{\mathrm{s}}$ decreased as the SIW propagated radially, and notably, SIW ceased propagation at almost the same ${\mathrm{N}}_{\mathrm{s}}$ value of $~$0.5 × ${10}^8$.

5. Conclusions

In this study, experimental and numerical approaches were used to investigate the influence of voltage rising time (${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$) on discharges generated in air using a pin-to-water setup. Experimentally, it was observed that the discharge ignition time was reduced from 35 to 12 ns upon increasing ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ in the range of 0.1–0.8 kV/ns. Meanwhile, the breakdown voltage and maximal discharge current were increased from 4.5 to 8 kV and from 2.2 to 12.9 A, respectively. The simulation results showed similar trends, albeit with smaller values. These trends may be attributed to the rapid generation of an intense E-field at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$, which facilitated the attainment of Meek’s criterion (i.e., high number of charges) near the pin tip.

The simulation also captured the propagation of the discharge in the gap towards the liquid surface and showed that the maximal propagation velocity increased (from 0.75 to 1.25 mm/ns) at higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ (0.1–0.8 kV/ns), while the time needed for the ionization wave (IW) to reach the liquid surface decreased (from 1.5 to 0.8 ns).

Analysis of the propagation of the surface ionization wave (SIW) on the water surface revealed that when ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ was increased (from 0.1 to 0.8 kV/ns), a number of filaments formed over the surface and their maximal radial propagation increased (from 10 to 25 and from 1.7 to 4.1 mm, respectively). Such an increase may be attributed to the higher initial E-field generated by the filament at a higher ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$.

Based on the experimental and simulation findings, we determined that more charges accumulated in the discharge head upon increasing ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$. For all ${\mathsf{\tau }}_{\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}$ conditions, SIW propagation was arrested when the number of charges reached 0.5 × ${10}^8$.