Static and Dynamic Solutions of Functionally Graded Micro/Nanobeams under External Loads Using Non-Local Theory
Abstract
:1. Introduction
2. Modeling and Extraction of Governing Equation
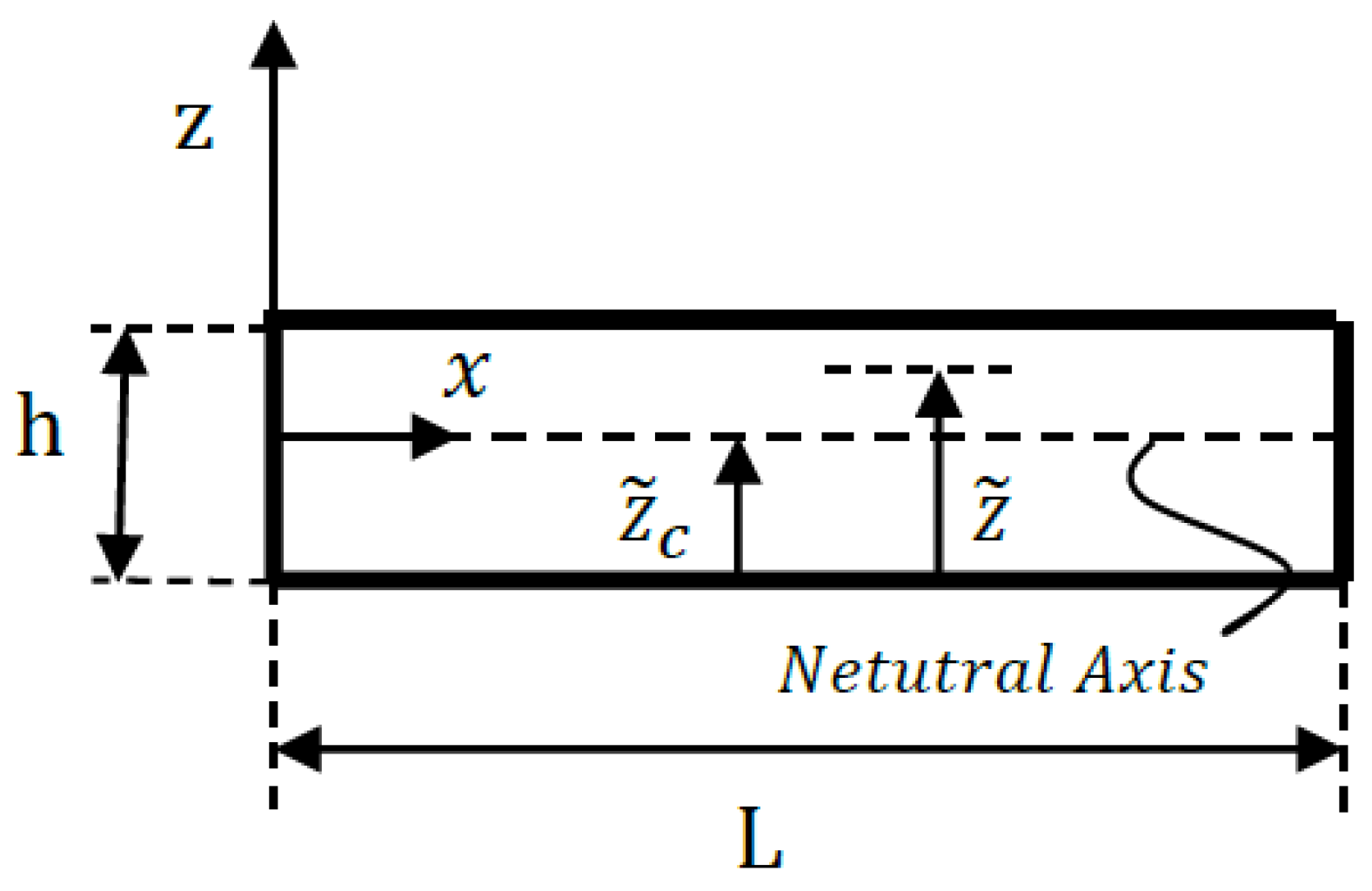
2.1. Formulation of the Problem
2.2. Governing Differential Equations for Functionally Graded (FG) Beam
2.3. Dimensionless Governing Equations in Different Boundary Conditions
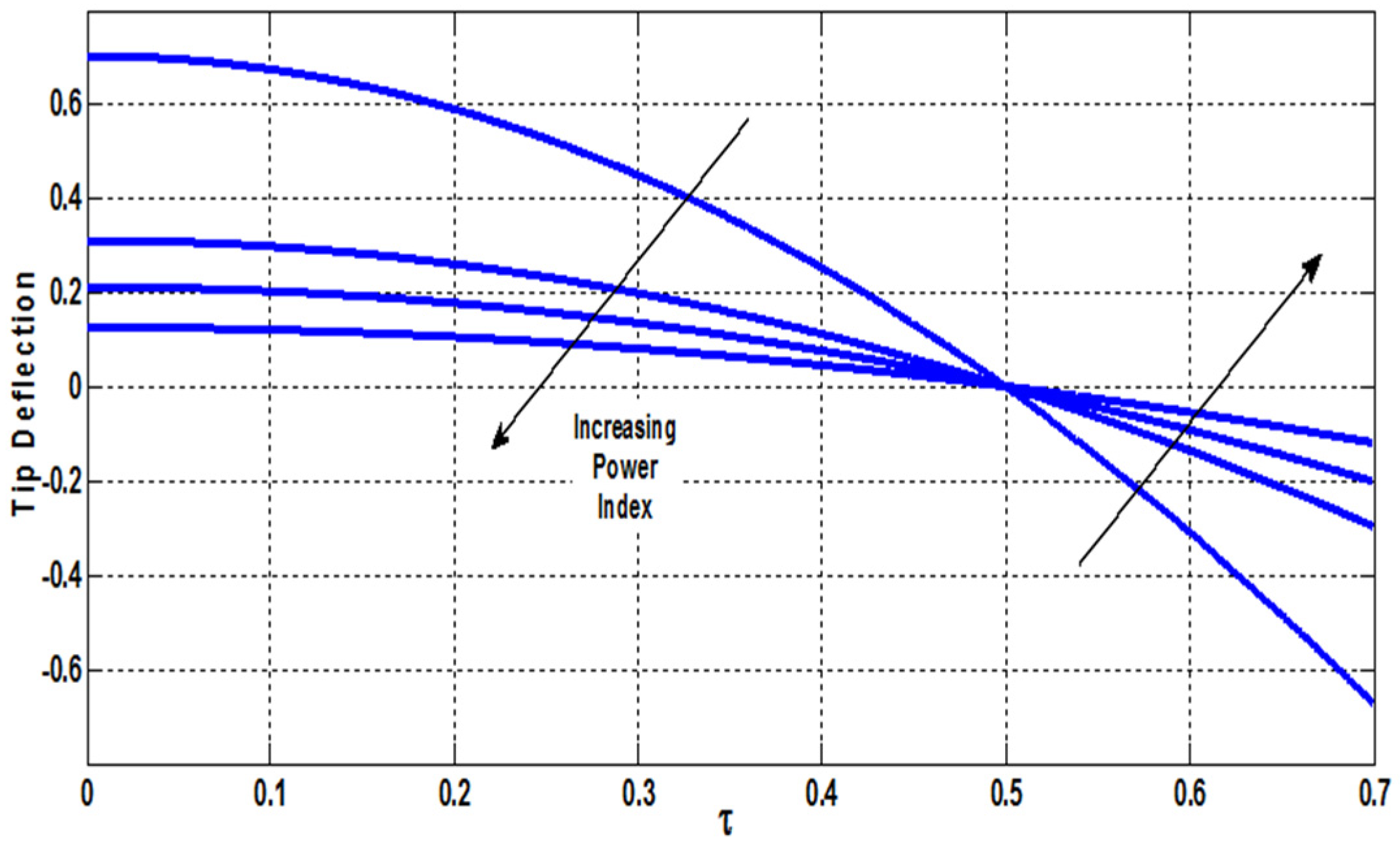
3. Static Analysis
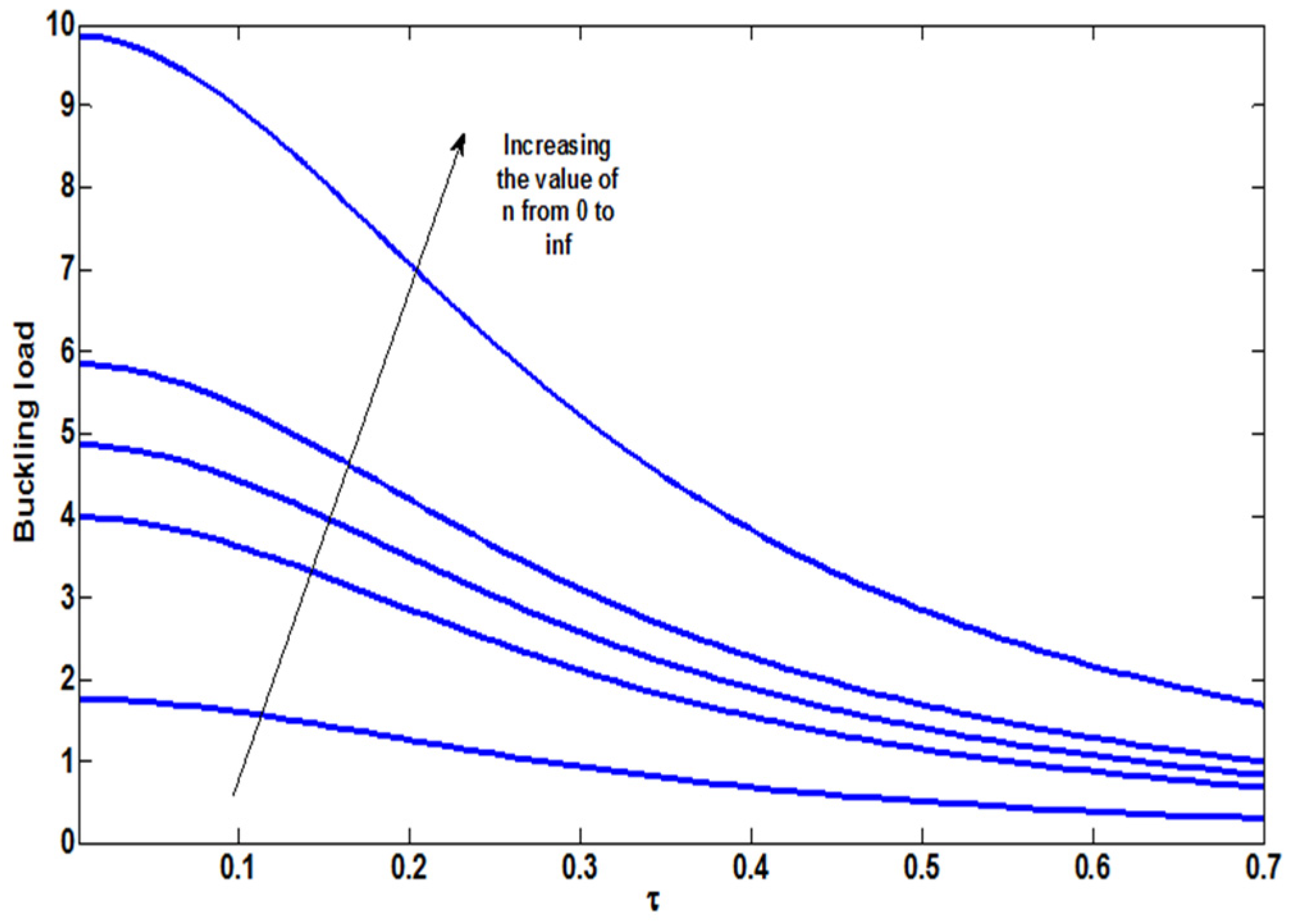
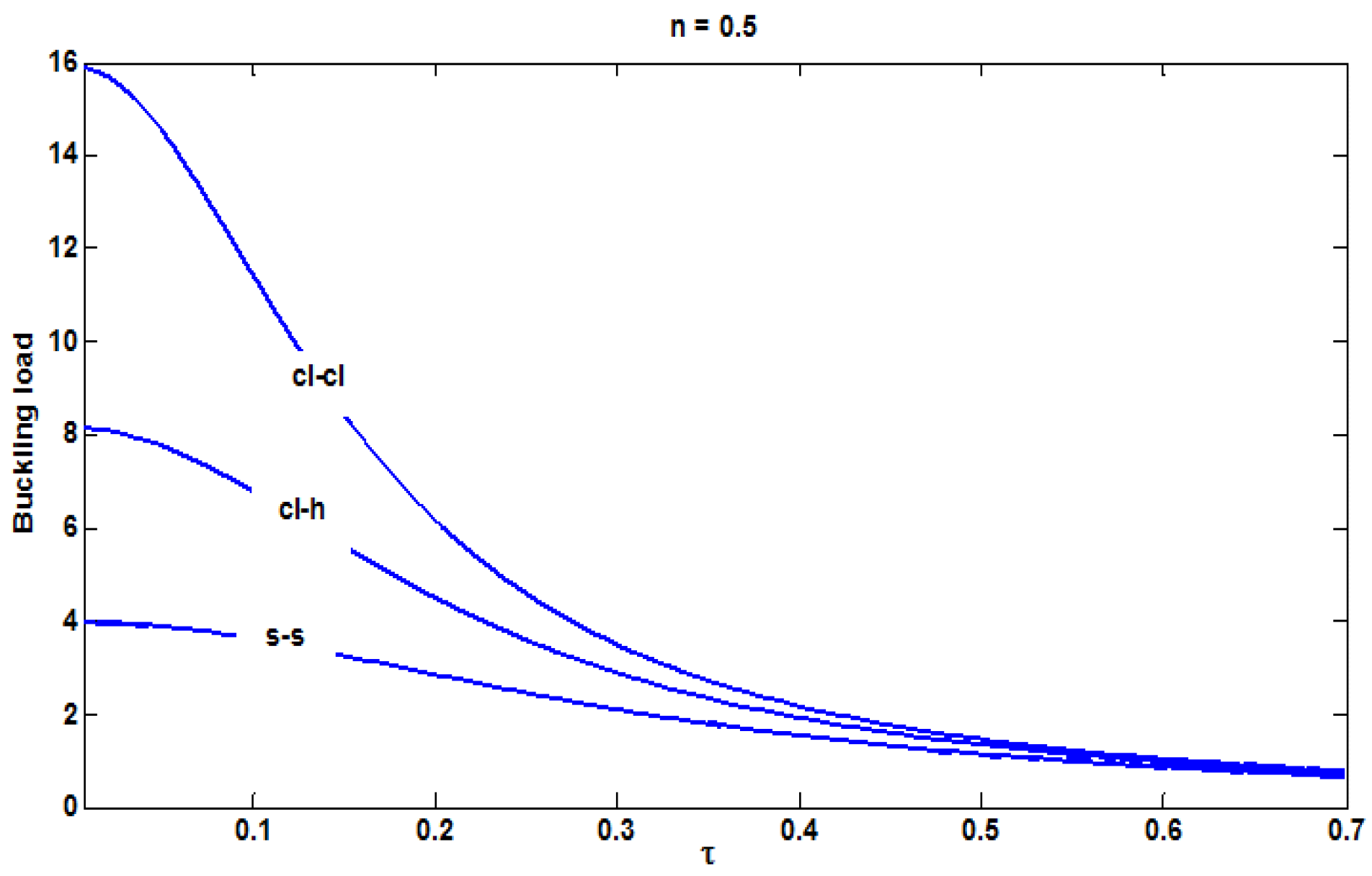
4. Buckling Analysis
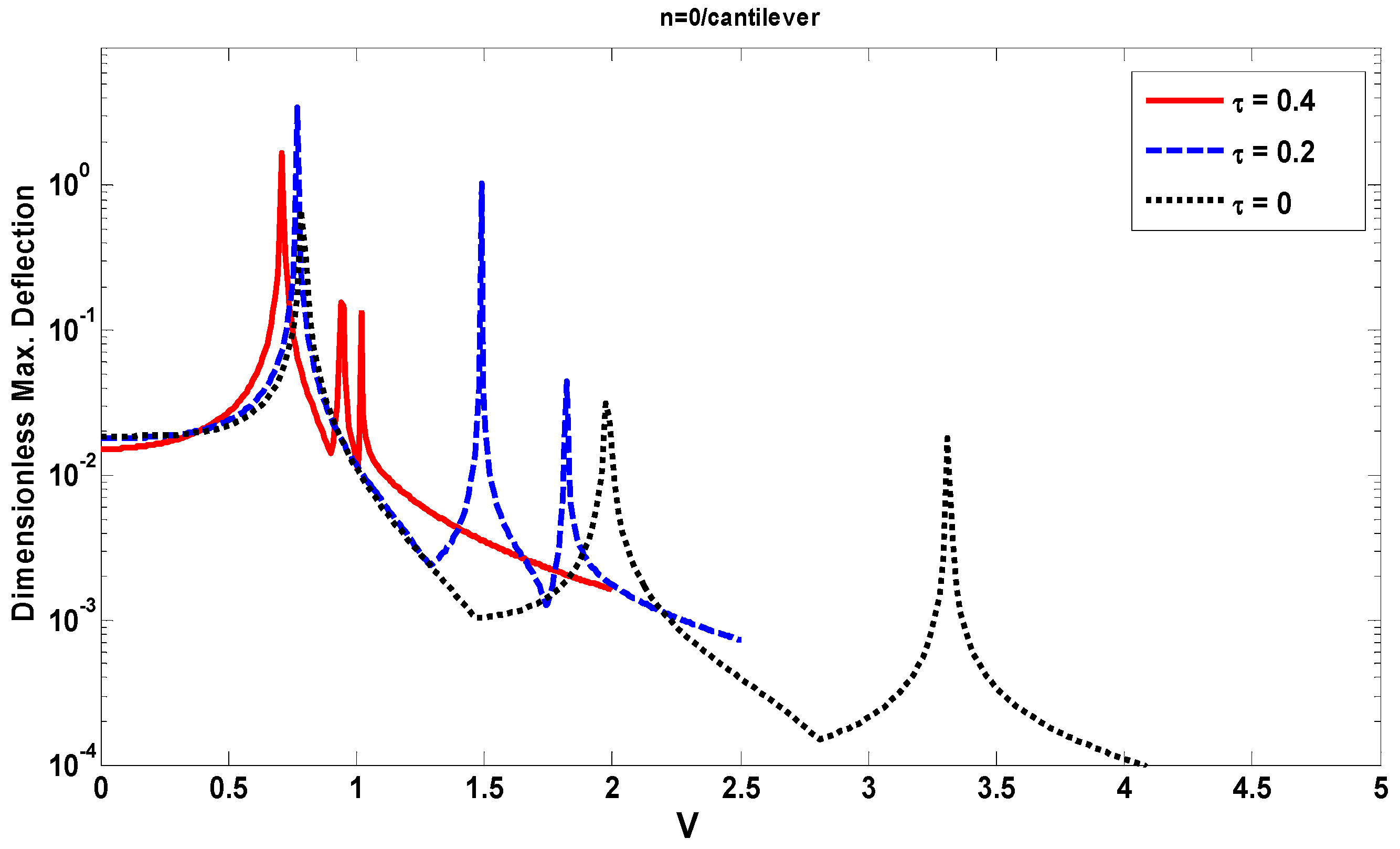
5. Dynamic Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.; Yao, L.; Chen, W.; Li, S. Comments on nonlocal effects in nano-cantilever beams. Int. J. Eng. Sci. 2015, 87, 47–57. [Google Scholar] [CrossRef]
- Fallah, A.; Firoozbakhsh, K.; Pasharavesh, A. Nonlinear Thermo-Mechanical Vibration Analysis of Functionally Graded Beams. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; pp. 787–792. [Google Scholar]
- Reddy, J. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Reddy, J. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Şimşek, M.; Yurtcu, H. Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos. Struct. 2013, 97, 378–386. [Google Scholar] [CrossRef]
- Thai, H.-T. A nonlocal beam theory for bending, buckling, and vibration of nanobeams. Int. J. Eng. Sci. 2012, 52, 56–64. [Google Scholar] [CrossRef]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Ruocco, E.; Zhang, H.; Wang, C. Buckling and vibration analysis of nonlocal axially functionally graded nanobeams based on Hencky-bar chain model. Appl. Math. Model. 2018, 63, 445–463. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.; Zhao, S.; Pang, X.; Safaei, B.; Chu, F. A unified solution for vibration analysis of laminated functionally graded shallow shells reinforced by graphene with general boundary conditions. Int. J. Mech. Sci. 2020, 170, 105341. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; De Sciarra, F.M. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphines. Comput. Mat. Sci. 2012, 51, 303–313. [Google Scholar] [CrossRef]
- Safaei, B.; Khoda, F.H.; Fattahi, A.M. Non-classical plate model for single-layered graphene sheet for axial buckling. Adv. Nano Res. 2019, 7, 265–275. [Google Scholar]
- Birman, V.; Byrd, L.W. Modeling and Analysis of Functionally Graded Materials and Structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Pasharavesh, A.; Zohoor, H.; Ahmadian, M.T. On the energy extraction from large amplitude vibrations of MEMS-based piezoelectric harvesters. Acta Mech. 2017, 228, 3445–3468. [Google Scholar] [CrossRef]
- Pasharavesh, A.; Zohoor, H.; Ahmadian, M.T. Electromechanical modeling and analytical investigation of nonlinearities in energy harvesting piezoelectric beams. Int. J. Mech. Mater. Des. 2016, 13, 499–514. [Google Scholar] [CrossRef]
- Pasharavesh, A.; Ahmadian, M.T. Analytical and numerical simulations of energy harvesting using MEMS devices operating in nonlinear regime. Eur. Phys. J. B 2018, 91, 241. [Google Scholar] [CrossRef]
- Arash, B.; Ansari, R. Evaluation of nonlocal parameter in the vibrations of single-walled carbon nanotubes with initial strain. Phys. E Low Dimens. Syst. Nanostruct. 2010, 42, 2058–2064. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Gan, Z.; Shen, L. Size-dependent functionally graded beam model based on an improved third-order shear deformation theory. Eur. J. Mech. A Solids 2014, 47, 211–230. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Eptaimeros, K.; Koutsoumaris, C.; Dernikas, I.; Zisis, T. Dynamical response of an embedded nanobeam by using nonlocal integral stress models. Compos. Part B Eng. 2018, 150, 255–268. [Google Scholar] [CrossRef]
- Simsek, M. Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach. Int. J. Eng. Sci. 2016, 105, 12–27. [Google Scholar] [CrossRef]
- Pasharavesh, A.; Ahmadian, M.T.; Zohoor, H. Coupled electromechanical analysis of MEMS-based energy harvesters integrated with nonlinear power extraction circuits. Microsyst. Technol. 2016, 23, 2403–2420. [Google Scholar] [CrossRef]
- Pasharavesh, A.; Moheimani, R.; Dalir, H. Performance Analysis of an Electromagnetically Coupled Piezoelectric Energy Scavenger. Energies 2020, 13, 845. [Google Scholar] [CrossRef] [Green Version]
- Pasharavesh, A.; Vaghasloo, Y.A.; Ahmadian, M.T.; Moheimani, R. Nonlinear Vibration Analysis of Nano to Micron Scale Beams Under Electric Force Using Nonlocal Theory. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; pp. 145–151. [Google Scholar]
- Sahmani, S.; Safaei, B. Nonlinear free vibrations of bi-directional functionally graded micro/nano-beams including nonlocal stress and microstructural strain gradient size effects. Thin Walled Struct. 2019, 140, 342–356. [Google Scholar] [CrossRef]
- Sahmani, S.; Safaei, B. Nonlocal strain gradient nonlinear resonance of bi-directional functionally graded composite micro/nano-beams under periodic soft excitation. Thin Walled Struct. 2019, 143, 106226. [Google Scholar] [CrossRef]
- Vaghasloo, Y.A.; Pasharavesh, A.; Ahmadian, M.T.; Fallah, A. Static Analysis of Electrically Actuated Nano to Micron Scale Beams Using Nonlocal Theory. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; pp. 391–396. [Google Scholar]
- Fattahi, A.M.; Safaei, B.; Ahmed, N.A. A comparison for the non-classical plate model based on axial buckling of single-layered graphene sheets. Eur. Phys. J. Plus 2019, 134, 555. [Google Scholar] [CrossRef]
- De Sciarra, F.M.; Barretta, R. A new nonlocal bending model for Euler–Bernoulli nanobeams. Mech. Res. Commun. 2014, 62, 25–30. [Google Scholar] [CrossRef]
- Wang, Q.; Liew, K.M. Application of nonlocal continuum mechanics to static analysis of micro- and nano-structures. Phys. Lett. A 2007, 363, 236–242. [Google Scholar] [CrossRef]
- Sahmani, S.; Safaei, B. Influence of homogenization models on size-dependent nonlinear bending and postbuckling of bi-directional functionally graded micro/nano-beams. Appl. Math. Model. 2020, 82, 336–358. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhao, K.; Sahmani, S.; Safaei, B. Size-dependent shear buckling response of FGM skew nanoplates modeled via different homogenization schemes. Appl. Math. Mech. 2020, 1–18. [Google Scholar] [CrossRef]
- Yang, X.; Sahmani, S.; Safaei, B. Postbuckling analysis of hydrostatic pressurized FGM microsized shells including strain gradient and stress-driven nonlocal effects. Eng. Comput. 2020, 119, 1–16. [Google Scholar] [CrossRef]
- Taati, E. Analytical solutions for the size dependent buckling and postbuckling behavior of functionally graded micro-plates. Int. J. Eng. Sci. 2016, 100, 45–60. [Google Scholar] [CrossRef]
- Eringen, A. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703. [Google Scholar] [CrossRef]
- Eringen, A.; Wegner, J. Nonlocal Continuum Field Theories. Appl. Mech. Rev. 2003, 56, B20–B22. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Ramesh, S.S.; Kitipornchai, S. Buckling analysis of micro- and nano-rods/tubes based on nonlocal Timoshenko beam theory. J. Phys. D Appl. Phys. 2006, 39, 3904–3909. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Hadi, A.; Rastgoo, A. Buckling analysis of arbitrary two-directional functionally graded Euler–Bernoulli nano-beams based on nonlocal elasticity theory. Int. J. Eng. Sci. 2016, 103, 1–10. [Google Scholar] [CrossRef]
- Chakraverty, S.; Behera, L. Buckling analysis of nanobeams with exponentially varying stiffness by differential quadrature method. Chin. Phys. B 2017, 26, 74602. [Google Scholar] [CrossRef]
- Rahmani, O.; Hosseini, S.A.; Parhizkari, M. Buckling of double functionally-graded nanobeam system under axial load based on nonlocal theory: An analytical approach. Microsyst. Technol. 2016, 23, 2739–2751. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Hu, Y.; Ding, Z.; Deng, W. Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos. Struct. 2017, 165, 250–265. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S. Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Phys. E Low Dimens. Syst. Nanostruct. 2009, 41, 1232–1239. [Google Scholar] [CrossRef]
- Ahmadian, M.T.; Pasharavesh, A.; Fallah, A. Application of Nonlocal Theory in Dynamic Pull-In Analysis of Electrostatically Actuated Micro and Nano Beams. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; pp. 255–261. [Google Scholar]
- Shahba, A.; Attarnejad, R.; Marvi, M.T.; Hajilar, S. Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions. Compos. Part B Eng. 2011, 42, 801–808. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, M.; Rong, H. Buckling Analysis of Axially Functionally Graded and Non-Uniform Beams Based on Timoshenko Theory. Acta Mech. Solida Sin. 2016, 29, 200–207. [Google Scholar] [CrossRef]
- Sahraee, S.; Saidi, A.R. Free vibration and buckling analysis of functionally graded deep beam-columns on two-parameter elastic foundations using the differential quadrature method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1273–1284. [Google Scholar] [CrossRef]
- Deng, H.; Chen, K.; Cheng, W.; Zhao, S. Vibration and buckling analysis of double-functionally graded Timoshenko beam system on Winkler-Pasternak elastic foundation. Compos. Struct. 2017, 160, 152–168. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar plates. Z. für Angew. Math. Phys. ZAMP 1967, 18, 12–30. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Weissmüller, J.; Larché, F. A general theory of curved deformable interfaces in solids at equilibrium. Philos. Mag. A 1998, 78, 1093–1109. [Google Scholar] [CrossRef]
- Pasharavesh, A.; Ahmadian, M.T. Toward Wideband Piezoelectric Harvesters Through Self-Powered Transitions to High-Energy Response. J. Vib. Acoust. 2019, 142, 1–28. [Google Scholar] [CrossRef]
- Fattahi, A.M.; Safaei, B.; Moaddab, E. The application of nonlocal elasticity to determine vibrational behavior of FG nanoplates. Steel Compos. Struct. 2019, 32, 281–292. [Google Scholar]
- El-Borgi, S.; Rajendran, P.; Friswell, M.; Trabelssi, M.; Reddy, J. Torsional vibration of size-dependent viscoelastic rods using nonlocal strain and velocity gradient theory. Compos. Struct. 2018, 186, 274–292. [Google Scholar] [CrossRef] [Green Version]
- Moheimani, R.; Pasharavesh, A.; Dalir, H. The effect of finite electrical conductivity of small-scale beam resonators on their vibrational response under electrostatic fields. Int. J. Mech. Mater. Des. 2020, 1–14. [Google Scholar] [CrossRef]
- Ma, L.; Ke, L.-L.; Reddy, J.; Yang, J.; Kitipornchai, S.; Wang, K. Wave propagation characteristics in magneto-electro-elastic nanoshells using nonlocal strain gradient theory. Compos. Struct. 2018, 199, 10–23. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; De Sciarra, F.M. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Moheimani, R.; Ahmadian, M.T. On Free Vibration of Functionally Graded Euler-Bernoulli Beam Models Based on the Non-Local Theory. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 169–173. [Google Scholar]
- Beer, F.P.; Johnston, E.R.; Dewoll, J.T. Mechanics of Materials, 3rd ed.; Prentice-Hall International: Upper Saddle River, NJ, USA, 2002. [Google Scholar]








| Materials | E (GPA) | ρ (kg/m3) |
|---|---|---|
| Metal (Aluminum) | 70 | 3960 |
| Ceramic (Aluminum oxide) | 390 | 2700 |
| BCs | k |
|---|---|
| Simply supported-Simply supported (S-S) | π |
| Simply supported-Clamped (S-C) | 4.4934 |
| Clamped-Clamped (C-C) | 6.2832 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moheimani, R.; Dalir, H. Static and Dynamic Solutions of Functionally Graded Micro/Nanobeams under External Loads Using Non-Local Theory. Vibration 2020, 3, 51-69. https://doi.org/10.3390/vibration3020006
Moheimani R, Dalir H. Static and Dynamic Solutions of Functionally Graded Micro/Nanobeams under External Loads Using Non-Local Theory. Vibration. 2020; 3(2):51-69. https://doi.org/10.3390/vibration3020006
Chicago/Turabian StyleMoheimani, Reza, and Hamid Dalir. 2020. "Static and Dynamic Solutions of Functionally Graded Micro/Nanobeams under External Loads Using Non-Local Theory" Vibration 3, no. 2: 51-69. https://doi.org/10.3390/vibration3020006
APA StyleMoheimani, R., & Dalir, H. (2020). Static and Dynamic Solutions of Functionally Graded Micro/Nanobeams under External Loads Using Non-Local Theory. Vibration, 3(2), 51-69. https://doi.org/10.3390/vibration3020006





