The Application of Micro-Vibratory Phenomena of a Shape-Memory Alloy Wire to a Novel Vibrator
Abstract
:1. Introduction
2. Materials and Methods
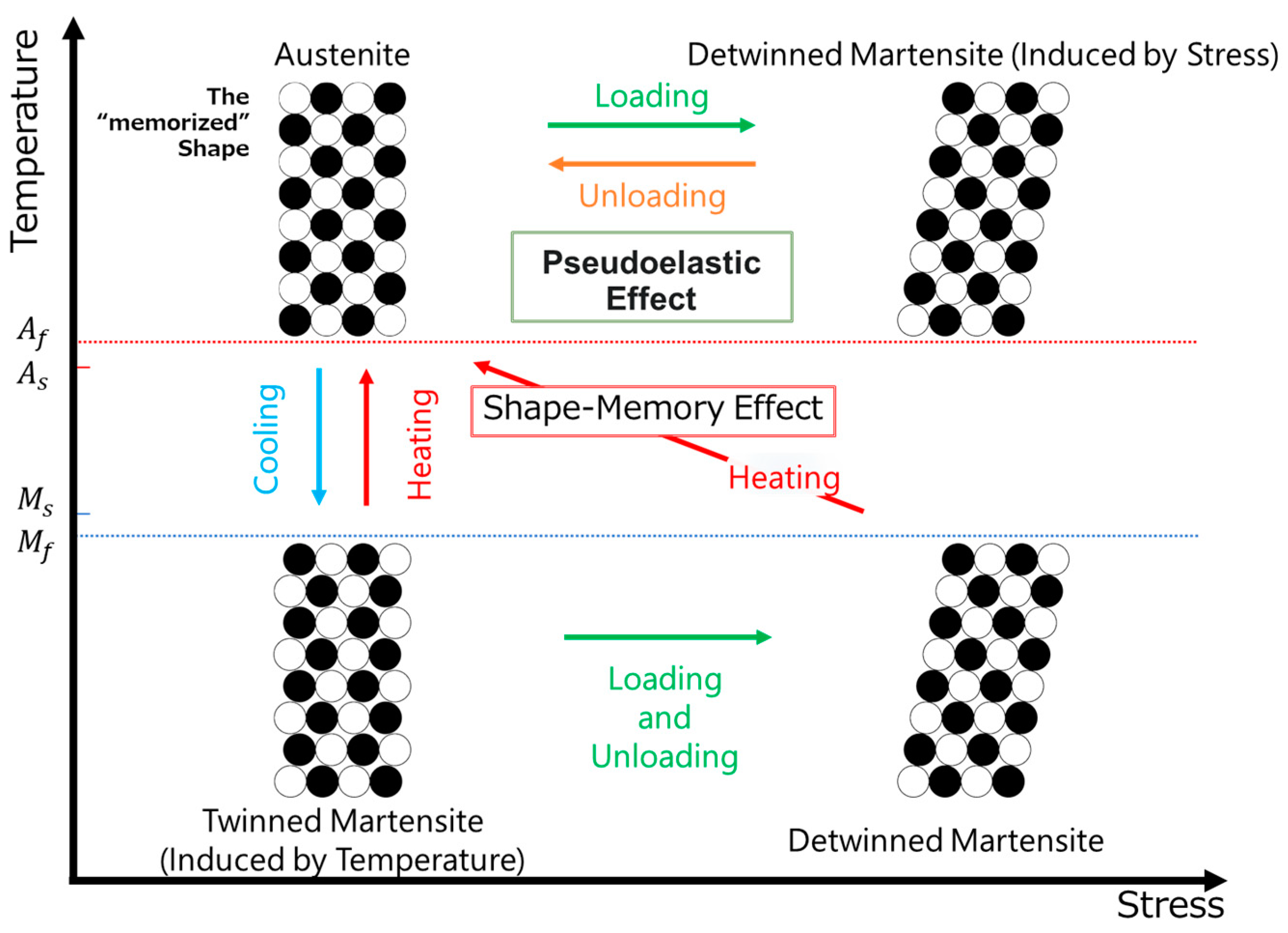
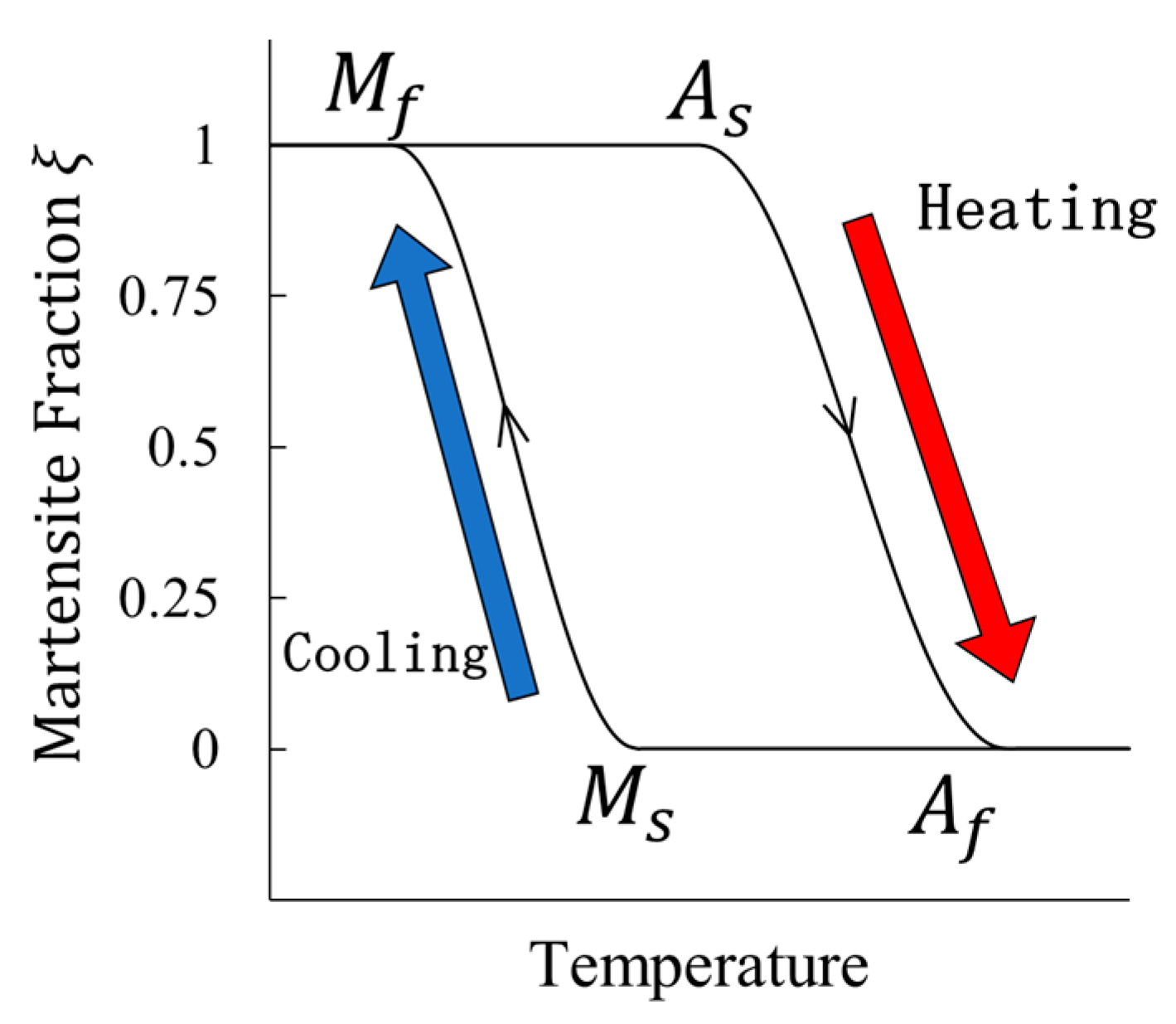
2.1. Shape-Memory Alloy and Its Physical Properties
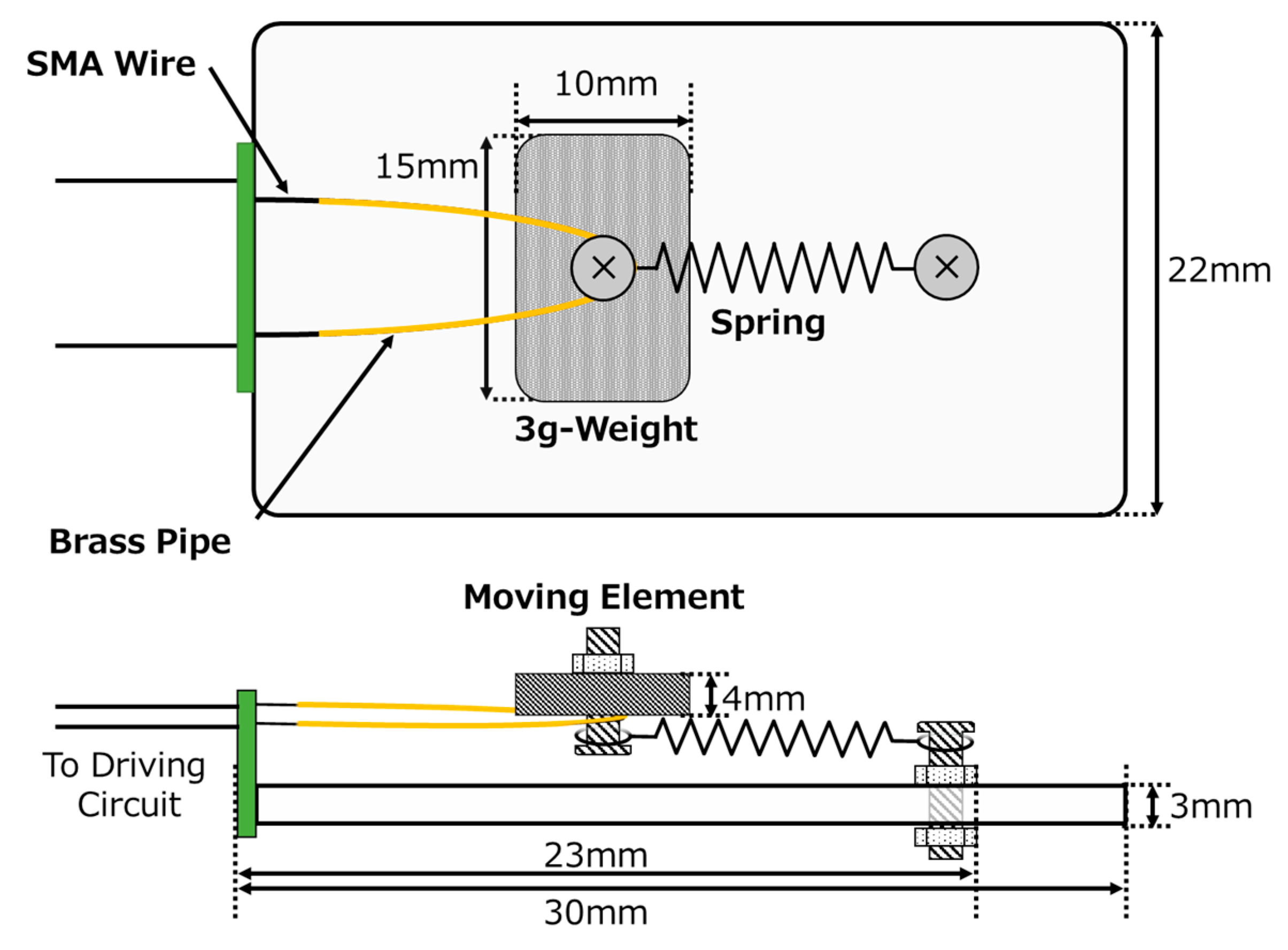
2.2. Micro-Vibration Actuator Using an SMA Wire
2.3. Novel Structure of a Vibrator Using an SMA Wire
3. Results
3.1. Evaluation of Vibration Performance
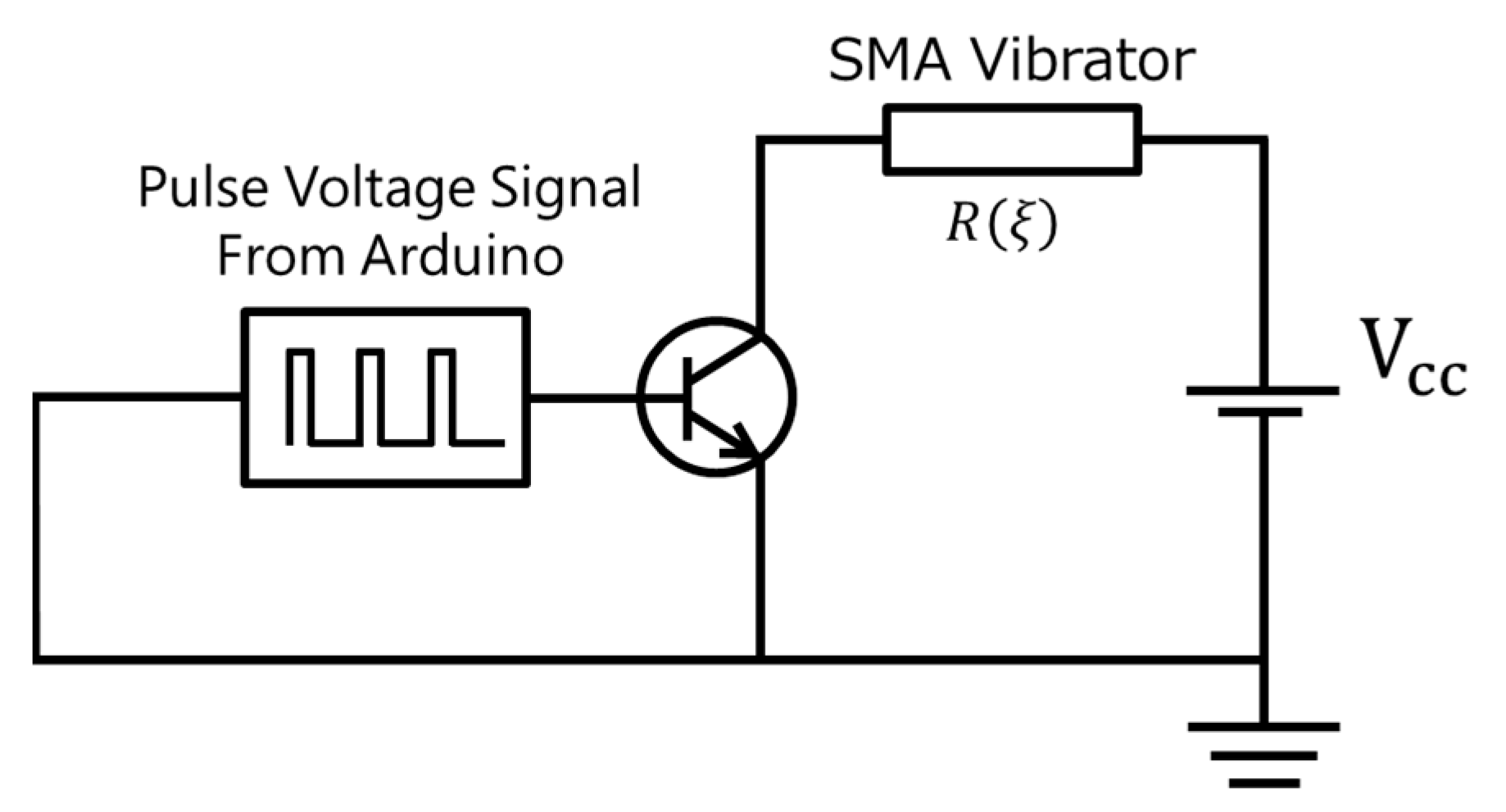
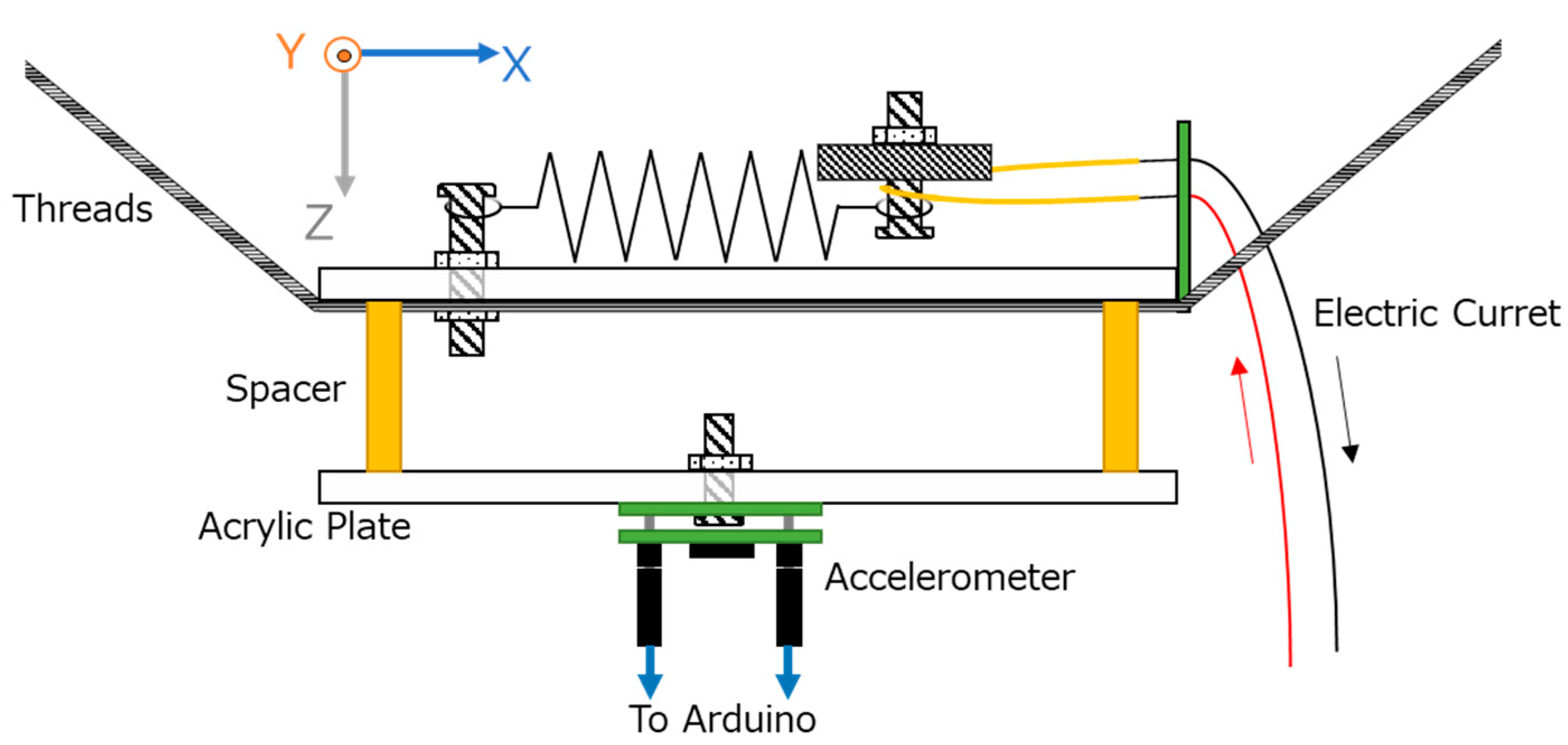
3.1.1. Experimental Setup for Measuring Applied Electrical Power and Generated Acceleration
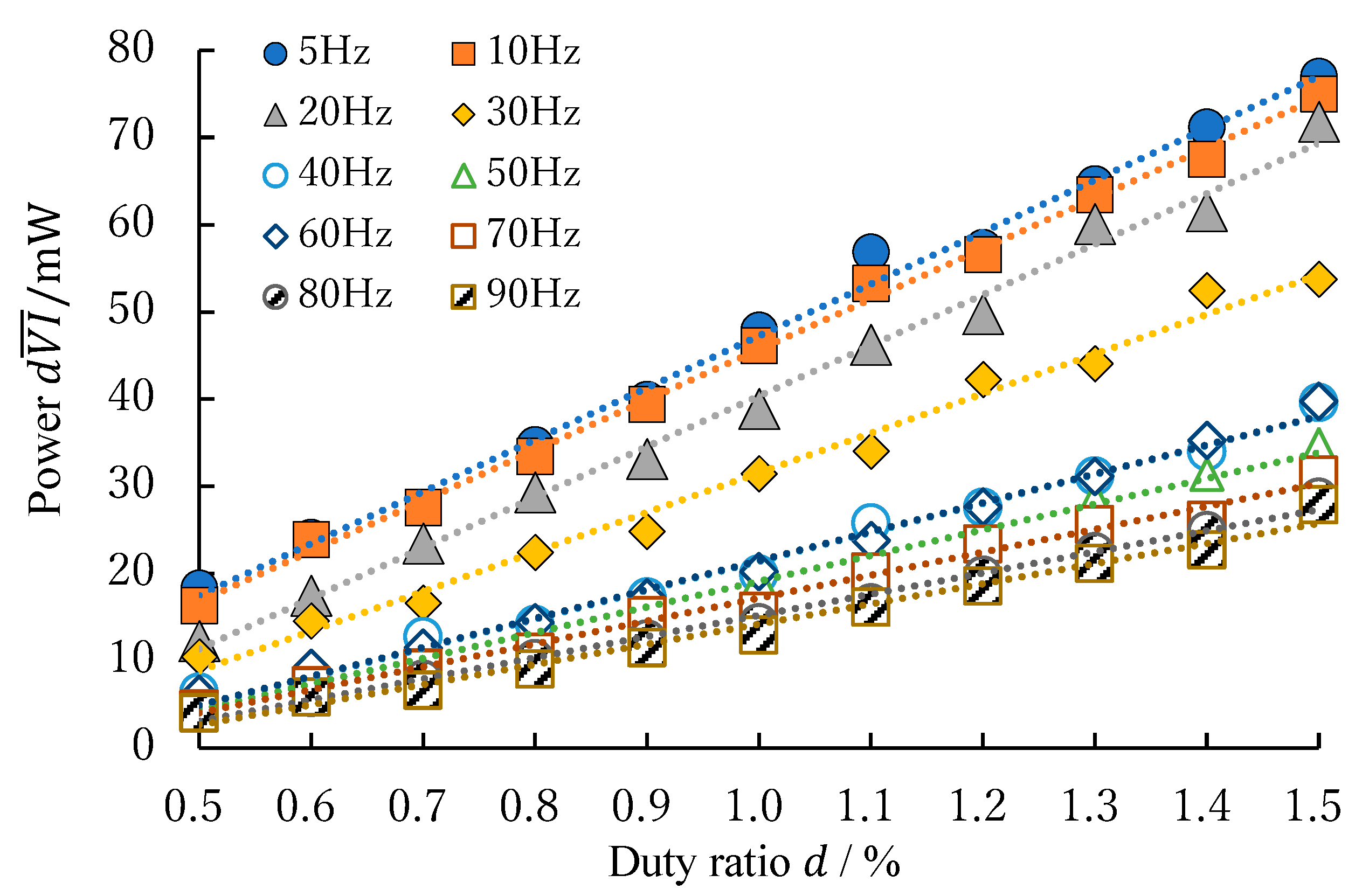
3.1.2. Power Consumption Measurement
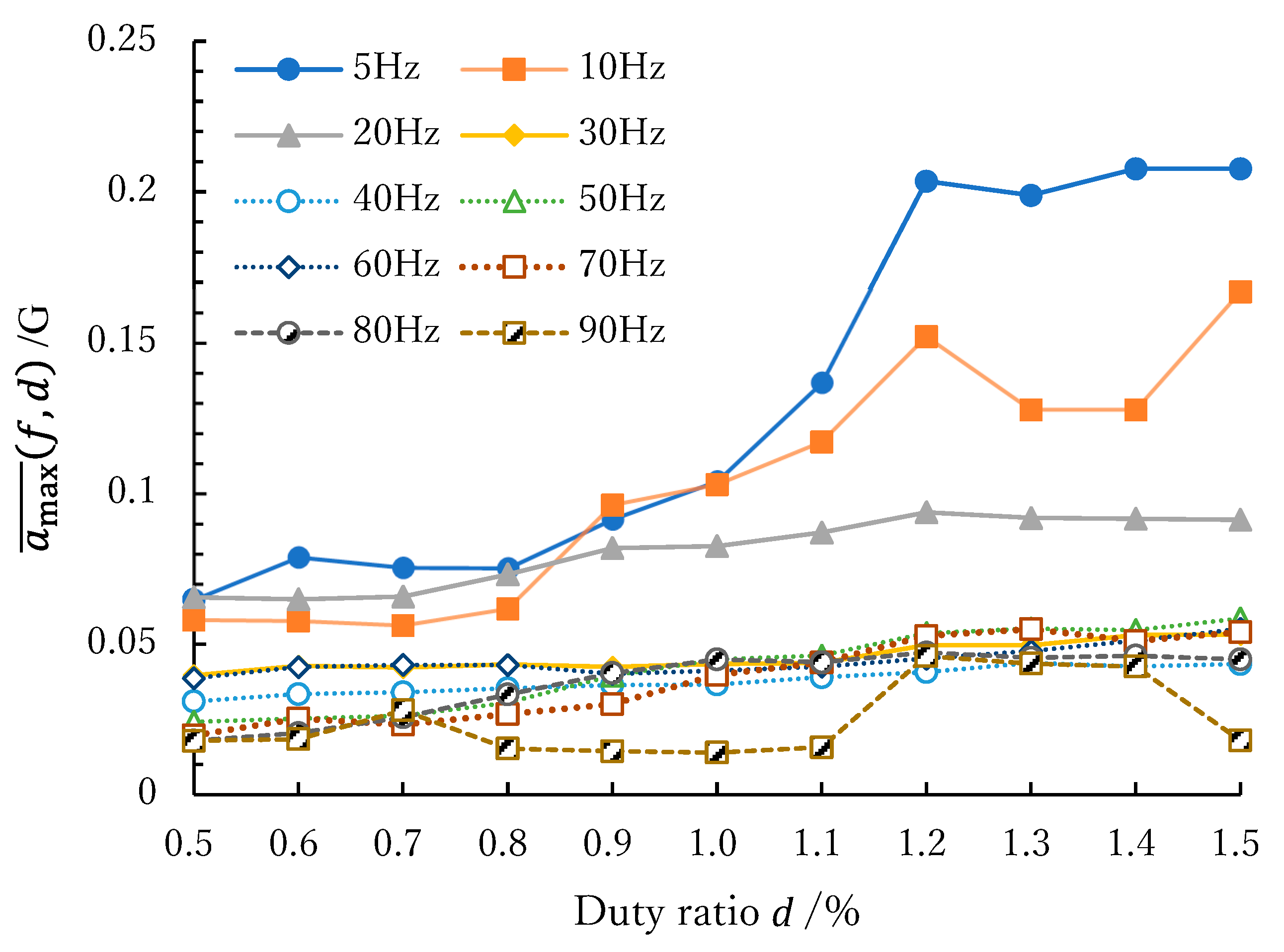
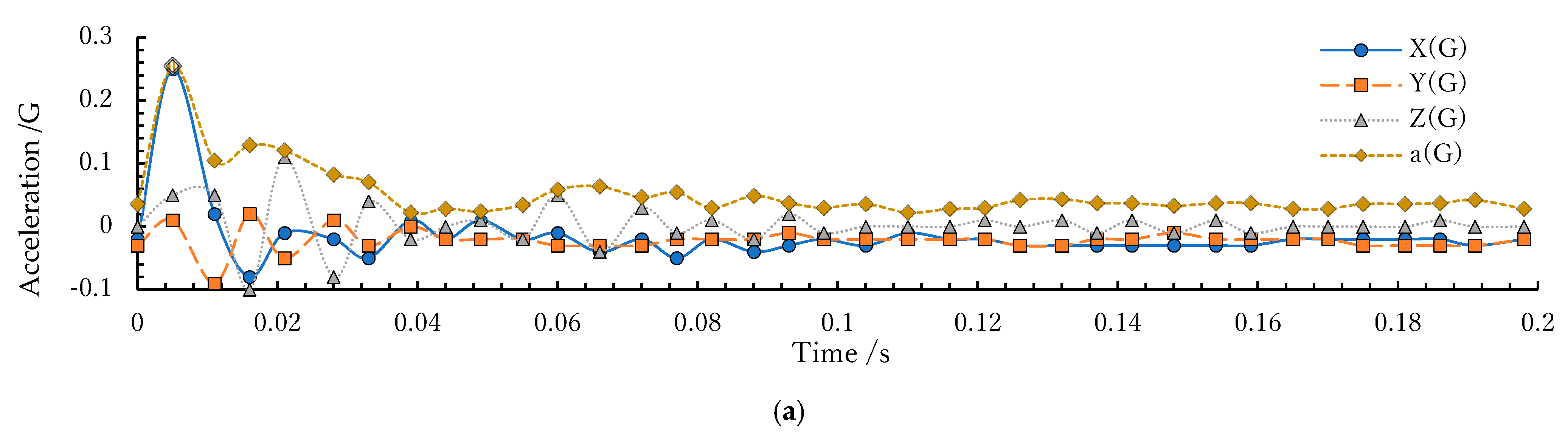
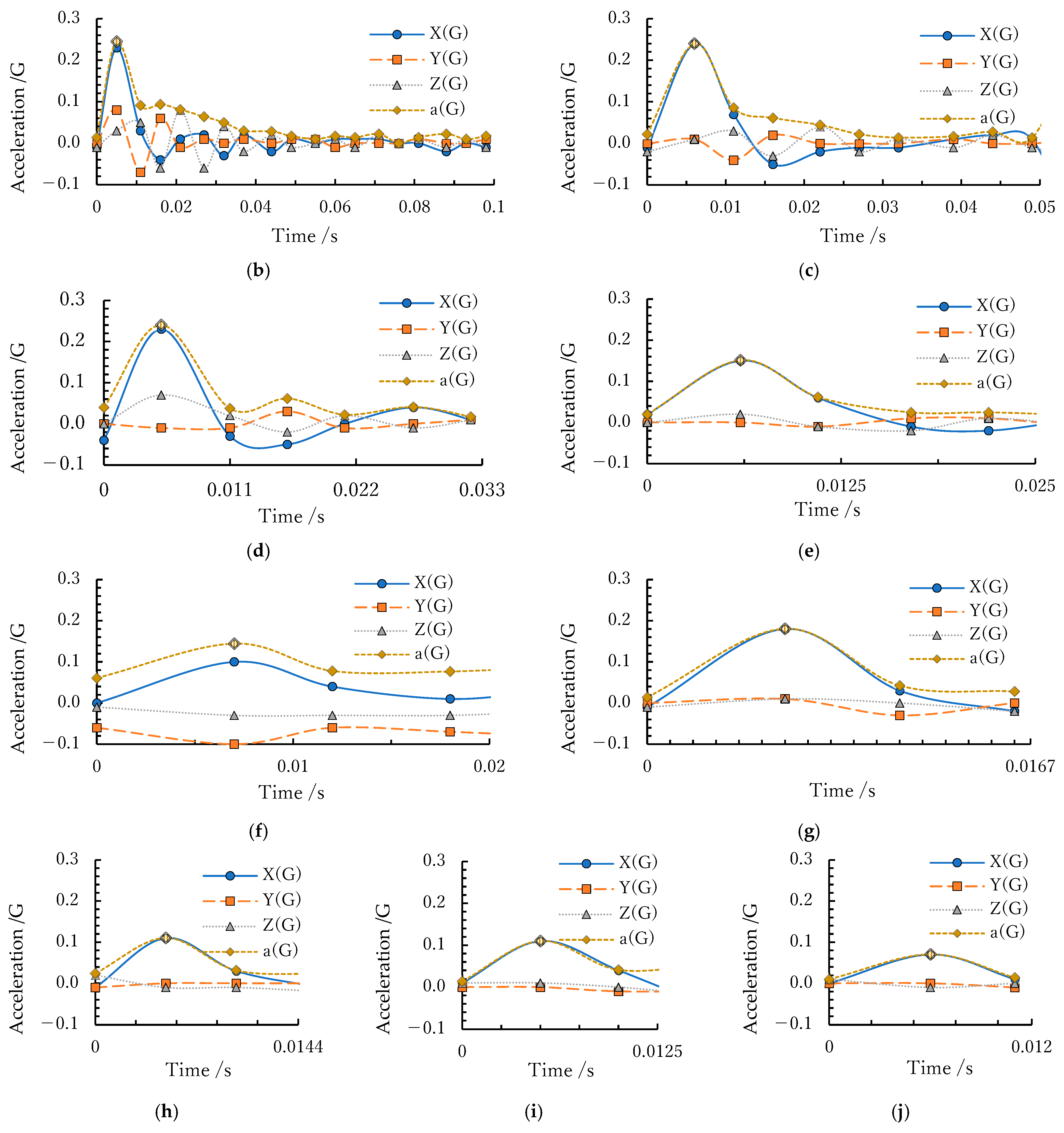
3.1.3. Acceleration Measurement
3.2. Vibration Evaluation by Users
3.2.1. Experimental Conditions for Vibration Evaluation
- Changing Duty Ratio Conditions
- B.
- Changing Frequency Conditions
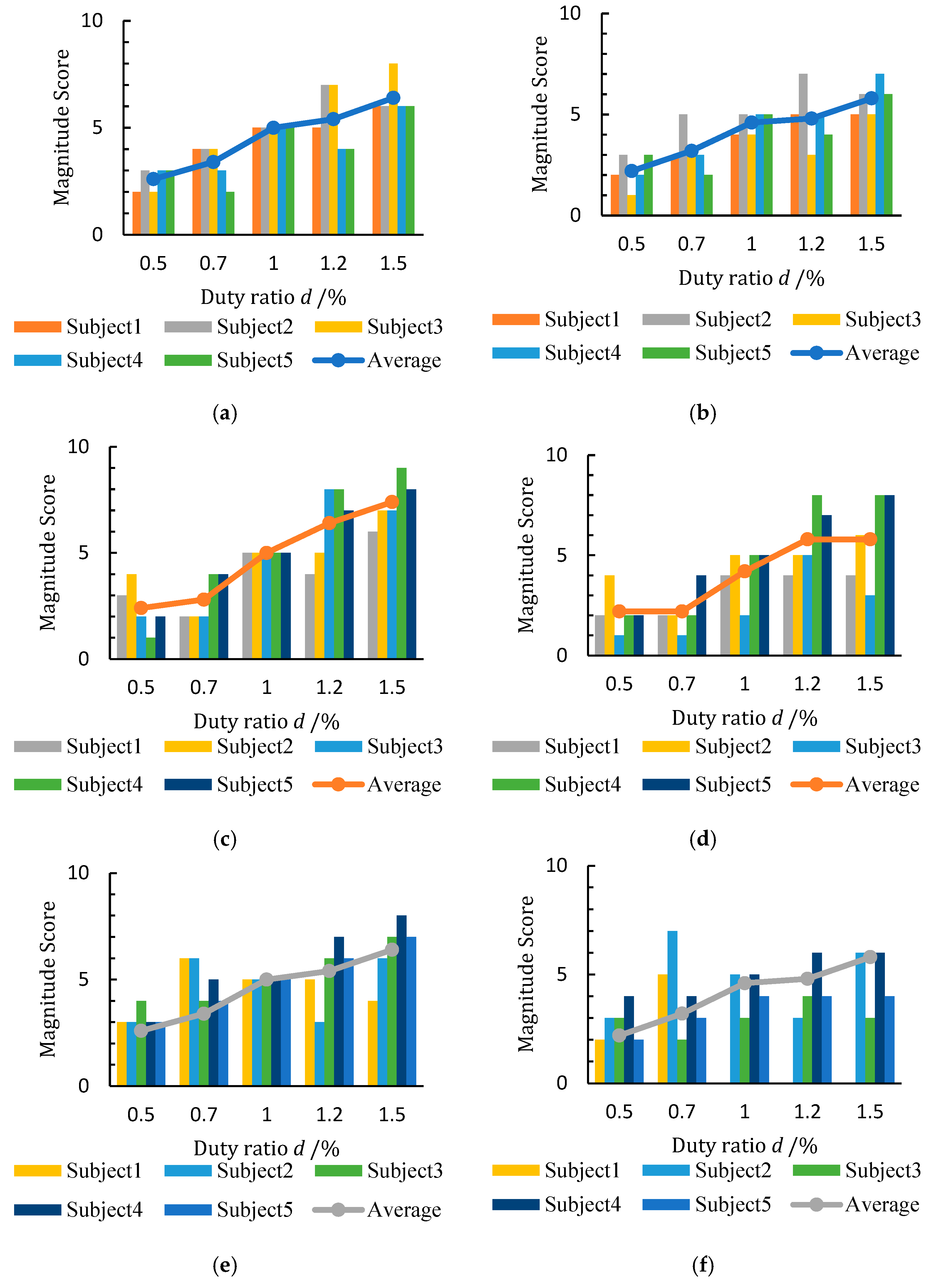
3.2.2. Evaluation Experiment and the Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, J.-W.; Yu, K.-H. Wearable Drone Controller: Machine Learning-Based Hand Gesture Recognition and Vibrotactile Feedback. Sensors 2023, 23, 2666. [Google Scholar] [CrossRef] [PubMed]
- Pyo, D.; Yang, T.-H.; Ryu, S.; Kwon, D.-S. Novel Linear Impact-Resonant Actuator for Mobile Applications. Sens. Actuators A Phys. 2015, 233, 460–471. [Google Scholar] [CrossRef]
- Kim, S.; Son, B.; Lee, Y.; Choi, H.; Lee, W.; Park, J. A Two-DOF impact actuator for haptic interaction. In Haptic Interaction: Perception, Devices and Algorithms 3; Kajimoto, H., Lee, D., Kim, S.-Y., Konyo, M., Kyung, K.-U., Eds.; Springer: Singapore, 2019; pp. 173–177. [Google Scholar]
- Jeon, I.; Nam, H.; Lee, H.; Ahn, Y.; Roh, J. An 80-V Integrated Boost Converter for Piezoelectric Actuators in Smartphones. Analog. Integr. Circ. Sig. Process. 2013, 75, 531–537. [Google Scholar] [CrossRef]
- Gu, H.; Bumke, L.; Chluba, C.; Quandt, E.; James, R.D. Phase Engineering and Supercompatibility of Shape Memory Alloys. Mater. Today 2018, 21, 265–277. [Google Scholar] [CrossRef]
- Gollerthan, S.; Young, M.L.; Baruj, A.; Frenzel, J.; Schmahl, W.W.; Eggeler, G. Fracture Mechanics and Microstructure in NiTi Shape Memory Alloys. Acta Mater. 2009, 57, 1015–1025. [Google Scholar] [CrossRef]
- Yi, J.; Xia, X.X.; Zhao, D.Q.; Pan, M.X.; Bai, H.Y.; Wang, W.H. Micro-and Nanoscale Metallic Glassy Fibers. Adv. Eng. Mater. 2010, 12, 1117–1122. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Wang, Q.; Wu, M.; Nan, D.; Shen, H.; Peng, H. Enhanced Tensile Properties and Fracture Reliability of Cu-Based Amorphous Wires via Pr-Doping. Adv. Eng. Mater. 2018, 20, 1700935. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, F.; Uchida, K.; Sawada, H. Research and Development on Portable Braille Display Using Shape Memory Alloy Wires. In Proceedings of the 2011 4th International Conference on Human System Interactions, HSI 2011, Yokohama, Japan, 9–21 May 2011; pp. 318–323. [Google Scholar]
- Song, C.; Shigemune, H.; Sawada, H. Information Display Around Eyes Using the Vibration of SMA Wires and Its Evaluation of Perceived Sensation. In Proceedings of the 2018 11th International Conference on Human System Interaction (HSI), Gdansk, Poland, 4–6 July 2018; pp. 398–403. [Google Scholar]
- Shen, J.; Chen, Y.; Sawada, H. A Wearable Assistive Device for Blind Pedestrians Using Real-Time Object Detection and Tactile Presentation. Sensors 2022, 22, 4537. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.M.; Ding, Z.; Wang, C.C.; Wei, J.; Zhao, Y.; Purnawali, H. Shape Memory Materials. Mater. Today 2010, 13, 54–61. [Google Scholar] [CrossRef]
- One-Dimensional Thermomechanical Constitutive Relations for Shape Memory Materials—C. Liang, C.A. Rogers. 1990. Available online: https://journals.sagepub.com/doi/10.1177/1045389×9000100205 (accessed on 7 May 2023).
- Toki Corporation. Artificial Metal-Based Muscle BioMetal Fiber BMF Series. Available online: https://www.toki.co.jp/biometal/download/downloadfiles/BMF_Catalog_20220425.pdf (accessed on 17 April 2023).
- Zhang, Z.; Luo, M.; Zhou, H.; Duan, J.-A. Design and Analysis of a Novel Two-Degree-of-Freedom Voice Coil Motor. IEEE/ASME Trans. Mechatron. 2019, 24, 2908–2918. [Google Scholar] [CrossRef]
- Heya, A.; Hirata, K. Three-Degree-of-Freedom Voice Coil Actuator Driven by a Four-Phase Current. Sensors 2022, 22, 6926. [Google Scholar] [CrossRef] [PubMed]





| Physical Property | Value |
|---|---|
| Standard diameter (µm) | 100 |
| Practical force produced (load) (gf) | 70 |
| Practical kinetic strain (%) | 4.0 |
| Standard drive current (mA) | 200 |
| Standard drive voltage (V/m) | 27 |
| Standard power (W/m) | 5.40 |
| Standard resistance (Ω/m) | 135 |
| Tensile strength (Kgf) | 0.8 |
| Weight (mg/m) | 50 |
| Frequency /Hz | / | Slope /mW/% | Standard Error /mW/% | Intercept /mW | Standard Error /mW |
|---|---|---|---|---|---|
| 5 | 0.994 | 59.5 | 1.56 | −12.3 | 1.63 |
| 10 | 0.998 | 57.8 | 0.96 | −12.1 | 1.01 |
| 20 | 0.993 | 58.0 | 1.63 | −17.6 | 1.71 |
| 30 | 0.989 | 45.4 | 1.62 | −13.8 | 1.70 |
| 40 | 0.989 | 33.2 | 1.16 | −11.8 | 1.22 |
| 50 | 0.990 | 29.5 | 0.98 | −10.3 | 1.02 |
| 60 | 0.992 | 33.2 | 0.99 | −11.7 | 1.04 |
| 70 | 0.989 | 26.3 | 0.93 | −9.1 | 0.98 |
| 80 | 0.992 | 24.3 | 0.71 | −9.0 | 0.74 |
| 90 | 0.983 | 23.1 | 1.02 | −8.9 | 1.07 |
| Frequency /Hz | / | Slope /G/% | Standard Error /G/% | Intercept /G | Standard Error /G |
|---|---|---|---|---|---|
| 5 | 0.883 | 0.17 | 0.021 | −0.04 | 0.022 |
| 10 | 0.879 | 0.11 | 0.014 | −0.01 | 0.015 |
| 20 | 0.887 | 0.03 | 0.004 | 0.05 | 0.004 |
| 30 | 0.856 | 0.01 | 0.002 | 0.03 | 0.002 |
| 40 | 0.960 | 0.01 | 0.001 | 0.02 | 0.001 |
| 50 | 0.955 | 0.04 | 0.003 | 0.00 | 0.003 |
| 60 | 0.708 | 0.01 | 0.003 | 0.03 | 0.003 |
| 70 | 0.922 | 0.04 | 0.004 | 0.00 | 0.004 |
| 80 | 0.802 | 0.03 | 0.005 | 0.01 | 0.005 |
| 90 | 0.234 | 0.02 | 0.011 | 0.01 | 0.012 |
| Number | Frequency/Hz | Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 |
|---|---|---|---|---|---|---|
| 1 | 5 | Heavy vibrations; poked or slapped sensation with a thin rod | Tap-tap, like a little fast pulsation | Like pulsating | Coarse and poke-like sensation | Like a heartbeat |
| 2 | 10 | Busy poking; like weak machine-gun stimulation | To-to-to-to, like a very fast pulse | Felt like really getting out of breath | Fine sensation compared with No.1 | Felt like pouring liquid |
| 3 | 20 | Colicky sensations | Raspy | Just barely coarse | A sensation of trembling in small increments | Felt like holding an insect |
| 4 | 40 | Rough feeling; most stimulating | Susurrus, like a numb feeling | Fast | A sensation of numbing rather than poking; harder to distinguish each pulse than Nos. 1 to 3 | Felt like the wings of a cicada vibrating |
| 5 | 80 | Fine vibrations; like a fluffy sensation | Vroom Zzzz | Fine, but felt the “grain” of vibration | Numbing sensation | Felt slightly ticklish |
| 6 | 120 | Finer or fluffier vibration than No.5; like grabbing something soft | Voom | Very fine | Little or no sensation of vibration | Fine vibrations |
| 7 | 240 | Very fine vibration; did not feel much | The sensation of tracing things at a distance that may or may not touch | Smooth | Did not feel as if it was vibrating | Did not feel the vibration |
| 8 | 480 | No vibration was felt, but a sound was heard | Felt nothing | Little vibration felt | Unable to perceive the vibrations | Did not feel the vibration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chujo, T.; Sawada, H. The Application of Micro-Vibratory Phenomena of a Shape-Memory Alloy Wire to a Novel Vibrator. Vibration 2023, 6, 584-598. https://doi.org/10.3390/vibration6030036
Chujo T, Sawada H. The Application of Micro-Vibratory Phenomena of a Shape-Memory Alloy Wire to a Novel Vibrator. Vibration. 2023; 6(3):584-598. https://doi.org/10.3390/vibration6030036
Chicago/Turabian StyleChujo, Takashi, and Hideyuki Sawada. 2023. "The Application of Micro-Vibratory Phenomena of a Shape-Memory Alloy Wire to a Novel Vibrator" Vibration 6, no. 3: 584-598. https://doi.org/10.3390/vibration6030036
APA StyleChujo, T., & Sawada, H. (2023). The Application of Micro-Vibratory Phenomena of a Shape-Memory Alloy Wire to a Novel Vibrator. Vibration, 6(3), 584-598. https://doi.org/10.3390/vibration6030036






