Abstract
Self-mixing interferometry (SMI) is suitable to sense and measure vibrations of amplitudes ranging from picometers to millimeters at frequencies from sub-Hz to MHz’s. As an optical probe, SMI has the advantage of being non-invasive with the ability to measure without any treatment of the target surface and operate from a substantial standoff distance from the target. As an additional advantage, the SMI configuration is much simpler than that of conventional interferometers as it does not require any optical part external to the laser source. After a short introduction to the basics of SMI, we review the development of configurations of SMI instruments for vibration measurements, based on both analog and digital processing, with record performance to cover the range of vibration amplitudes from 0.1 nm to 1 mm, frequencies up to MHz, and stand-off distances up to 100 m. These performances set a benchmark that is unequaled by other approaches reported so far in the literature. The configurations we describe are (i) a simple MEMS-response testing instrument based on fringe counting, (ii) a half-fringe locking vibrometer for mechanical mode analysis and transfer function measurements, with a wide linear response on six decades of amplitude, (iii) a vibrometer with analog switching cancellation for μm-to-mm amplitude of vibrations, and (iv) a long standoff distance vibrometer for testing large structures at distances up to 100 m and with nm sensitivity. Lastly, as the vibrometer will almost invariably operate on untreated, diffusing surfaces, we provide an evaluation of phase-induced speckle pattern errors affecting the SMI measurement.
1. Introduction
Optical techniques are attractive for vibration measurements because they are non-invasive, fast, and accurate [1,2]. A straightforward optical technique like triangulation [3] supplies an appreciable sensitivity in the measurement of small vibrations—for example, resolving 15 μm for a parallax resolution of Δα = 0.3 mr and a base D and standoff distance L both of 5 cm [3,4]. However, coherent techniques like interferometry outperform this result of decades, offering sub-nm resolution, a dynamic range up to mm, standoff distances up to hundreds of meters, MHz bandwidth, and, last but not least, a compact and inexpensive setup.
In this introduction, we briefly recall the principle of laser interferometry and the most recent version of it, self-mixing interferometry (SMI). Among the several applications of SMI that have been demonstrated, in this paper, we focus exclusively on the measurement of vibrations, that is, periodic (and most frequently) sinusoidal small movement of the target. We will not treat other self-mixing measurements or applications like, for example, displacement [5,6,7,8], distance [9,10], velocity and flow rate [11,12], planarity [3], angle [13,14,15], physical quantities (thickness and index of refraction [16,17], linewidth [18], and alpha-factor [19]), the use of self-mix as a detector of optical echoes [20,21], or consumer applications like scroll [22] and gesture AR/VR [23] sensors. The interested reader may also consult general reviews [24] and tutorials like those provided by Refs. [25,26].
1.1. The Laser Interferometer
The first experiments using interferometry date back to 150 years ago. However, only with the advent of the laser, and thanks to its exceptional coherence, has it been exploited in a number of scientific and industrial applications.
As interferometry uses the interference of superposed beams and generates a signal modulated with the wavelength period, its resolution allows the measurement of very minute displacements down to a small fraction of wavelength.
The concept was implemented into a very successful industrial product called the “Laser Interferometer” (LI), the famous HP5525 model introduced in 1967 by Hewlett Packard for the calibration of machine tools, an instrument is capable of resolving displacements in steps of λ/8 = 79 nm with a counting speed of 5 MHz on a distance range of a few meters [3,27].
Following a number of variants from several manufacturers, like the one reported in Figure 1 (top), the LI was then basically made around a λ-stabilized He-Ne laser and an external optical interferometer—typically, a Fabry–Perot configuration. The two beams propagated to the target being measured at distance s and to the fixed reference path sr were superposed at a detector, generating a signal I = I0 cos 2k(s − sr), where k = 2π/λ is the wavenumber [28].
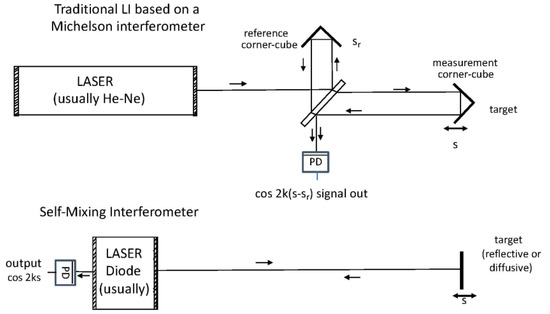
Figure 1.
(top) Schematic showing a traditional LI based on an external optical Michelson interferometer, which is used to split the laser output into reference and measurement beams and then recombine them after propagation on the photodetector PD, which generates a beating in the form of the cos 2ks signal. (bottom) The self-mixing interferometer mixes the optical field returning from the target with the in-cavity field to generate an amplitude modulation, again of the form cos 2ks, which is detected with the photodetector PD placed on the rear mirror of the laser diode.
Counting the zero-crossing of signal I, variations Δs of a quarter wavelength could be easily measured. Eventually, after adding a second signal I* = I0 sin 2k(sm − sr) obtained with polarization splitting of the interferometer [28], the number of zero-crossings was doubled, thus bringing the resolution to λ/8, which is the performance available in commercial products.
It is worth noting that the LI works in the digital mode, with up/down counting of λ/8 displacement variations Δsm and requires a corner cube as the target for operation. The corner cube ensures the angular alignment of reference and measurement beams, relieving the user from painstaking alignment operations, and, importantly, it prevents retroreflection from the target (which is seen to disturb its λ-stabilization) from entering the laser cavity. When the retroreflection process is well controlled, we obtain the self-mixing interferometer (SMI) configuration shown in Figure 1 (bottom), and analyzing this configuration, we find that the perturbed cavity field carries both amplitude (AM) and frequency (FM) modulations in the form of two orthogonal signals, cos 2ks and sin 2ks (at weak feedback). The AM component is detected using the monitor photodiode PD, usually mounted in the laser package by the manufacturer for the purpose of controlling the emitted power.
For a vibration measurement, we shall modify the basic configuration of the SMI with a lens in place of the measurement corner cube, as shown in Figure 2, to allow the incoming and outgoing beams to be superposed correctly at the beamsplitter. With this modification, we obtain a laser vibrometer that reads the vibration amplitude digitally, in steps of λ/8 (=79 nm for the 633 nm He-Ne laser) and has a dynamic range (or maximum measurable amplitude) limited by a fraction of the lens focal length (and with typical values of 5–20 mm in practice).
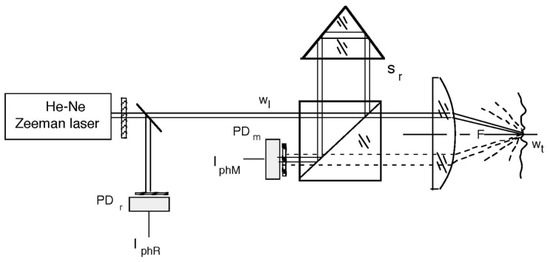
Figure 2.
To modify the LI so that it works as a vibrometer, we shall use a focusing lens to replace the measure corner cube, so as to create the necessary transversal displacement of the returning beam.
It is worth noting that the configuration can work with a considerable stand-off distance (typically, meters) just by increasing the distance of the lens from the beamsplitter.
1.2. The Self-Mixing Interferometer (SMI)
The SMI has several advantages with respect to the LI because (i) it has a minimum part count (no optical interferometer necessary), so it is potentially low-cost; (ii) it is self-aligned, as it takes the measurement where the spot falls; (iii) it requires no filter to remove ambient light, as the laser cavity performs this function; (iv) the vibration signal is available everywhere on the beam and also at the target side; and (v) it has good performance for small signals (close to the quantum limit, typically 10 pm) and bandwidths (up to MHz) and a wide dynamic range (depending on coherence length) [24,25].
On the other hand, the metrological precision of the λ-stabilized LI (typically six decimal places) is not usually required in vibration measurements and prompts the use of a cheap and compact laser diode (that also includes the photodiode), offering a precision of two to three decimal places (three to four in thermally controlled units).
To explain the working principle of the SMI, many approaches have been devised at increasing levels of coverage [24,25]; yet, the simplest one based on rotating-vector modeling (Figure 3) already explains the mechanism of operation. Indeed, we represent the unperturbed cavity field with a rotating vector E (which rotates at the optical frequency) so that the returning rotating field received by the laser cavity is aE exp iϕ, where a is the attenuation and ϕ = 2ks the optical phase shift accumulated along the go-and-return path to the target.
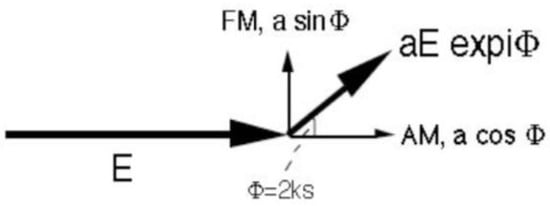
Figure 3.
Model explaining the AM and FM of the SMI field with the rotating field addition of the unperturbed field E and of the returning field aE exp iϕ fed back into the laser cavity by the target.
Now, the summation of rotating vectors E and aE exp iϕ, which take place in the cavity, generates amplitude (AM) and frequency (FM) modulations of the resulting field ER.
The in-phase component of the returning field is aE cos ϕ and produces the increase (decrease) in the resultant field according to the positive (negative) sign of cos ϕ. Thus, an AM of perturbed field is generated, with a modulation index mAM = a cos ϕ.
Similarly, the in-quadrature component aE sin ϕ either accelerates or decelerates the rotating field according to the sign of sin ϕ. Thus, it is responsible for an FM with a modulation index mFM = a sin ϕ.
In addition, by considering the time-dependent evolution of the rotating vector addition, it is found that when a is large enough, the trajectory of the resulting field makes a loop—or there is a switching both in amplitude and frequency [24,25].
In Figure 4, we can see the evolution of the amplitude waveform ER. The evolution is governed by the feedback parameter C, which is proportional to the distance times the fraction of returning field [29]. At small C (say, ≤0.05), the waveform of the SMI field ER is sinusoidal, and the output signal detected by the photodiode PD follows the dependence I = I0 cos 2ks of a normal interferometer (Figure 4, bottom traces). At increasing feedback, we first notice a distortion in the cosine waveform, with the leading edge becoming slower than the trailing edge (C = 0.1 to 0.8 in Figure 4). Then, we obtain switching from top to bottom at increasing phase shifts (C ≥ 1), which will become a bottom-to-top when phase shift ϕ = 2ks decreases [24,25].
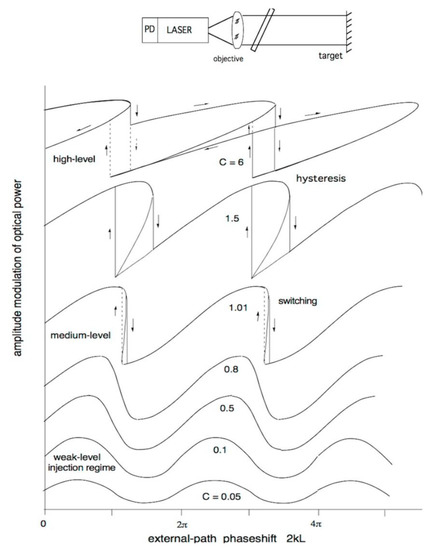
Figure 4.
The SMI signal out of the detecting photodiode (PD in Figure 1, bottom) is the cosine of optical pathlength, like in a normal LI for weak feedback (C = 0.05). Then, it becomes distorted at C = 0.1 to 0.9 and finally exhibits a switching, starting from C = 1.
In the experiment, we change the feedback level using a variable attenuator, drive the target with a sine wave, and observe the waveforms exactly as predicted by theory.
It is very important to note that the periodicity of the SMI waveform is always λ/2 at any C, and in each period of the SMI signal, the upgoing switching is for increasing and the down-going switching is for decreasing distance, thus supplying the sign of the λ/2 variations Δs of target distance. This circumstance was used to build a single-channel SMI displacement measuring instrument [8,24] around an 850 nm laser diode, capable of following the displacement of a diffusive target with a digital readout in steps of λ/2 = 425 nm, with a bandpass of 1 MHz (or a target speed up to 0.42 m/s), and a 1 to 2 m distance range.
When the C factor is increased above C = 4.6, we enter a strong regime of feedback, with two switchings per period, at C = 7.85 and above three per period. At still larger values, the switching becomes erratic [30], and the laser exhibits a regime of chaotic oscillations. But, staying at 1 < C < 4.6, the moderate feedback regime, the laser works in a stable and reliable way that is totally suitable for measurements applications.
2. Classification of SMI Instruments and Their Typical Performance
From an application point of view, it is fundamental to classify interferometric instruments into two categories, as shown in Figure 5 (top): (i) displacement-measuring instruments, when the s(t) measurand is aperiodic and the time-dependence is arbitrary—this is the case of the machine-tool turret positioning—and (ii) vibration-measuring instrument, when the s(t) waveform is periodic—this is the case of a mechanical transfer response study.
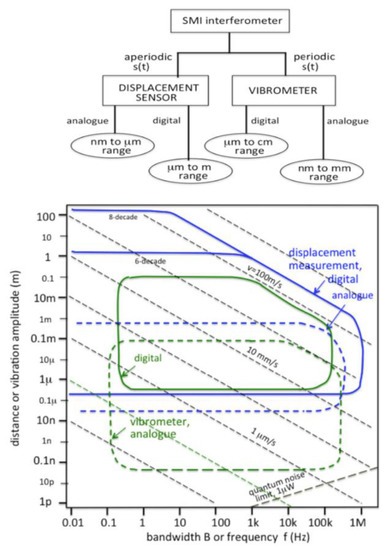
Figure 5.
(top) Classes of interferometric measurements: displacement sensors are for aperiodic signals s(t) and vibrometer sensors are for small periodic signals s(t). In both cases, processing can be either analog or digital, with corresponding different working ranges of amplitudes. (bottom) Diagram showing performance, with the amplitude of measurable displacement plotted versus the bandwidth of measurement or frequency of vibration. The operation of state-of-the-art design is inside the perimeters of the curves. Typical performances are indicated, for both analog (dotted lines) and digital (full lines) processing. In the bottom right corner, the quantum noise limit for 1 μW of received power is indicated.
Note that a displacement measurement is incremental, usually based on up/down counting of fringes or fraction thereof, and thus requires an initial zeroing operation. We can also develop (iii) an absolute distance meter, typically using sweeping wavelength [9,10,25] but with lower resolution.
A further classification for interferometric and SMI instruments is according to the type of signal processing used in the instrument, either analog or digital.
The performance of SMI displacement and the vibration SMI instrument with respect to the measurable amplitude and bandwidth of s(t) is summarized in the chart shown in Figure 5 (bottom).
Analog processing is best suited to approach minimum detectable signal set by quantum noise, whereas digital processing has a wider dynamic range of measurement.
For each class of instrument, we find a minimum and maximum measurable signal amplitude as well as a low- and high-frequency cutoff, to which we shall add the Doppler limit due to the target speed v = ds(t)/dt, which increases the bandwidth content of the interferometric signal as v/λ and thus introduces a boundary at −45 degrees, as shown in Figure 5.
Regarding vibrometers, in the following, we review preferred design schematics to implement vibrometers that offer full coverage of the range of performance reported in Figure 5 as well as a range of standoff distances for operation. Then, we briefly discuss the applications for which these vibrometers have been developed.
These case studies represent benchmarks of vibrometer performance that should be borne in mind when developing new solutions because of their proven performance, particularly simple and cheap structure, and minimal requirement for processing the detected signals.
Other than measuring displacements in λ/2 steps, the SMI basic configuration can obviously be used as a vibrometer giving a digital readout with an amplitude resolution of about Δs = λ/2 = 0.4 μm, a dynamic range of counting up to s0 = 1 m with a counting speed of f2 = 1 MHz, and coverage of frequency of oscillation given by f2 Δs/s0. The digital readout is adequate for measuring vibration amplitudes of say, 50 μm at a frequency f = 10 kHz but suffers from the inverse s0 dependence of bandwidth at a large dynamic range.
3. Transfer Function Measured Using a Digital Readout (DR) SMI Vibrometer
To illustrate the performance of an SMI interferometer used as a digital readout vibrometer, we now describe its application to the measurement of the mechanical transfer frequency response of a miniature device, a MEMS (micro-electro-mechanical system) [31,32]. The device is a MEMS gyroscope, with a suspended test mass and 2-D comb structure to actuate and read the Coriolis’ force developed by inertial rotation.
As we can see in Figure 6, the SMI is in the basic setup, and we read the signal at the output of the photodiode. A lens focuses the 850 nm laser beam on the 100 × 100 μm2 test mass at a slant angle of 20 degrees to develop a measurable component when the mass vibrates in plane. The gyroscope is kept under vacuum to eliminate the damping due to the air. By exciting the device with the operating square wave (Figure 7, left), we obtain an SMI signal containing fringes that are easily measured (or even simpler, counted by sight). By repeating the measurement at several excitation frequencies, we can easily build up the frequency response of the MEMS, as shown in Figure 7 on the right.
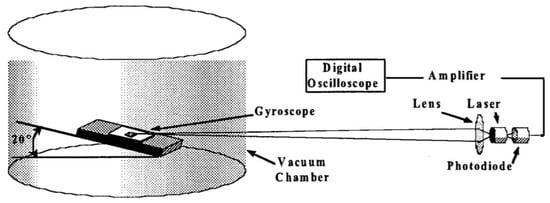
Figure 6.
Sensing the in-plane vibration of a MEMS gyroscope using an SMI vibrometer (from Ref. [32], with permission from the IEEE).
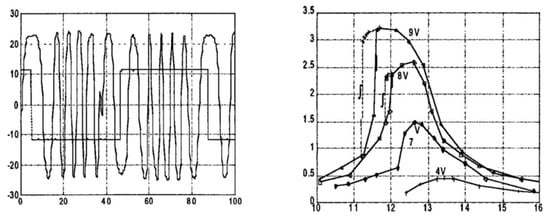
Figure 7.
(left) A 7 V, 12.5 Hz square wave exciting the oscillation of the MEMS test mass, and the resulting SMI signal at the photodiode output. (right) The frequency response of the device, at several drive voltage amplitudes (from Ref. [32], with permission from the IEEE).
Several details in Figure 7 are worth noting. First of all, we are able to measure the resonance frequency fres of the device and its linewidth Δfres (due to damping). Also, we can measure the dependence of fres from the drive voltage and find that it decreases with the increasing amplitude of the drive. Last and quite important, performing the measurement at increasing and then decreasing frequency, we may detect a hysteresis of the response curve, which is a premonitory of mechanical creep known to eventually lead to soft failure of the device.
Of course, if we wish to avoid hysteresis, we shall work at a safe drive voltage, as we can read from Figure 7 on the right. Similarly, hysteresis is also found in the response vs. residual air pressure inside the MEMS package. Thus, the SMI in its simplicity is a powerful diagnostic tool for assessing the appropriate working conditions (voltage, pressure, etc.) of the device.
4. Half-Fringe-Stabilized (HFS) Analog Readout SMI Vibrometer
Stabilization of the LI working point at half-fringe is a well-known technique that is useful to read vibrations much smaller than the λ/2 fringe amplitude. The scheme is depicted in Figure 8, where the reference arm of the conventional LI based on a Michelson interferometer is used to adjust the pathlength difference to λ/4 using a piezo actuator fed by the detected signal, properly filtered to pass the low-frequency components.
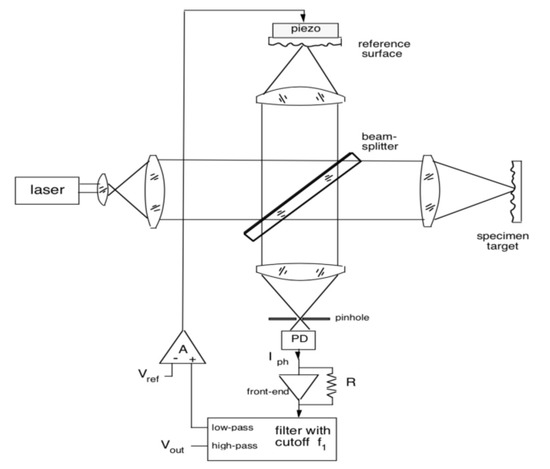
Figure 8.
The half-fringe-stabilized LI has a reference arm driven with a piezoceramic actuator that keeps the pathlength difference with respect to the measurement arm dynamically locked at λ/4 (or 90 degrees in phase).
Then, if the measurement arm pathlength is sm = s0 + Δs, where s0 is the standoff distance and Δs is the small vibration to be measured, and the reference arm pathlength is sR = s0 + λ/4, then the SMI signal reads I = I0 cos 2k(sm − sr) = I0 cos 2k(Δs + λ/4) = I0 sin 2kΔs ≈ I0 2kΔs.
Thus, the phase is linearly converted into an amplitude, and we can read it as an analog signal of the SMI at the high pass output of the filter (Figure 8). The advantage of the scheme is its immunity to ambient-related vibrations (microphonic effect), which are canceled by the feedback loop ending on the piezo, while the disadvantage is the λ/2 limit to large signals (or dynamic range).
With the HFS scheme, small vibrations of SAW (surface acoustic wave) devices can be measured down to a fraction of Angstrom (=0.1 nm) amplitude (see Figure 9 [33]).
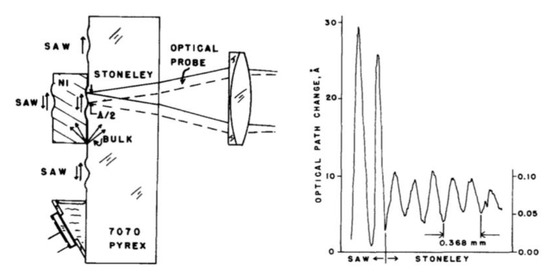
Figure 9.
Detection of sub-nm (1 Å = 0.1 nm) vibrations in a SAW device using the HFS interferometer. Stoneley and ordinary surface waves are observed at the oscillation frequency of 8 MHz (from [33], ©American Institute of Physics; reprinted with permission).
Refurbishing the HFS interferometer with the SMI concept is not straightforward because the SMI has just one arm, i.e., no reference arm is available to be actuated. However, the use of a laser diode as the source of the SMI brings about the advantage (in this case) of wavelength λ being dependent on bias current Ibias through a coefficient αλ = dλ/dIbias.
Then, the optical phaseshift variation Δϕ = Δ(2ks) = 2(sΔk + kΔs) can be dynamically kept equal to zero by making sΔk = −kΔs, where Δk = −2πΔλ/λ2 and Δλ is obtained using the change in bias current as Δλ = αλΔIbias [34,35]. To complete the feedback loop, we have a voltage-to-current drive of bias current, Ibias = GmVout, and the amplified signal of the photodiode, from which the level Vhf of the half-fringe is subtracted.
A scheme showing the feedback loop of such an HFS SMI is presented in Figure 10. It has two ‘virtual ground nodes’ with functionality similar to the virtual ground of an operational amplifier: the phase node, where ϕ = sΔk + kΔs ≈ 0, and the difference amplifier inputs, where Vin − Vhf ≈ 0 (where Vhf is the level of half-fringe). With the notation ≈0, we indicate that the signals are kept dynamically very small, at a level just enough to be amplified and generate the desired amplitudes along the loop.
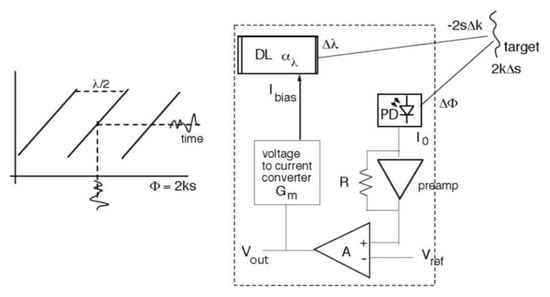
Figure 10.
Working at half-fringe with an SMI under the moderate feedback regime (1 < C < 4.6) gives a quasi-linear response (left panel), which is useful to convert the phaseshift Φ into an amplitude signal. As the feedback loop (right panel) keeps sΔk = −kΔs at the target and the DL and Gm blocks provide a linear constant response, the vibration signal Δs is available at the amplifier output Vout.
From the condition sΔk + kΔs = 0, where k = 2π/λ, we obtain Δs/s = Δλ/λ. After inspection of the feedback loop in Figure 10, we can write Δλ = Ibiasαλ = VoutαλGm, and substituting in Δs, the signal voltage is found as Vout = (s/λαλGm)Δs.
An important consequence is that the response factor s/λαλGm is independent of the optical power carrying the signal—provided the loop gain Gloop is large enough.
Indeed, the loop gain of the scheme in Figure 10 is easily seen to be Gloop = 2ks I0 RAGm (αλ/λ), and its value can be made Gloop ≈ 103 in practice.
Thus, as it is well known from the general properties of feedback, all sources of disturbances and deviation from linearity are reduced by a factor given by the loop gain plus one, or ≈103. In particular, unexpectedly, speckle pattern fluctuations of the signal amplitude are washed out and absorbed by the loop gain.
The nonlinearity is also very important due to the λ/2 fringe amplitude being affected. The resulting dynamic range is no longer λ/2 of the plain interferometer, but it is now (1 + Gloop)λ/2, or a fraction of an mm instead of a fraction of a μm.
Qualitatively, this result is explained considering that as the Δs signal increases and tends to escape out of the λ/2 width of the fringe, the feedback action pulls it back to the middle of the fringe—so a much larger amplitude (1 + Gloop)λ/2 is necessary to finally reach the boundary of the dynamic range.
Because of the same mechanism, the linearity error is reduced by (1 + Gloop), and for a signal amplitude of half the dynamic range ΔΦ = ±2kΔs = ±45 degrees (or Δs = ±(π/4)/2k = λ/16≈ ±50 nm for λ = 800 nm, which becomes (1 + Gloop)λ/16 ≈ ±50 μm with feedback, that is, 100 μm peak-to-peak), we have a linearity error el = (π/4 − sin π/4)/2k = 0.078λ/12.56 = 0.0062 800 nm = 4.96 nm, a record result (=0.005%) for such a large 100 μm signal.
Regarding the minimum measurable displacement or NED (noise-equivalent displacement), this is due to the quantum noise in of the beam carrying the phase signal 2kΔs and is given [34,35] by NED = (λ/4π)(I0/in) = (λ/4π) (2eB/I0)1/2, where I0 is the detected current and B is the measurement bandwidth, with typical values of 20 to 100 pm/√Hz in practice [34].
A totally different method to linearize the response of the SMI has been recently introduced [36], and the method is based on working under the strong feedback (or high C) regime. Indeed, at large C (say, 10 … 20) the amplitude of fringes is found to decrease while increasing intervals of the SMI waveform are dragged by the target displacement s(t), until at a certain Cmin, the fringes disappear and the SMI signal is just a replica of Δs(t). At still larger C = Cmax, however, the system enters the bifurcation regime, and period-1 chaotic oscillations are generated [30]. Thus, we shall adjust the feedback parameter C to stay in the interval Cmin < C < Cmax, typically 10 to 30. The drawback of the method is that the C-interval depends on the amplitude of the phase signal kΔs, on the stand-off distance s and on the drive current Ibias [36], so it is difficult to accommodate a large dynamic range of signals kΔs.
4.1. Measuring Vibration Modes with the HFS SMI
Thanks to the wide dynamic range extending for several decades, e.g., from ≈50 pm to ≥500 μm, the good linearity in the response, and the substantial bandwidth (typically several hundred kHz), the HFS SMI can easily supply the spectrum of modes of a mechanical structure. An example is provided in Figure 11, where we report the frequency spectrum of the SMI signal (Vout of Figure 10) obtained when pointing the device at the door of a car with the motor engine running. A complicated set of vibration modes of the structure is unveiled by the SMI measurement.
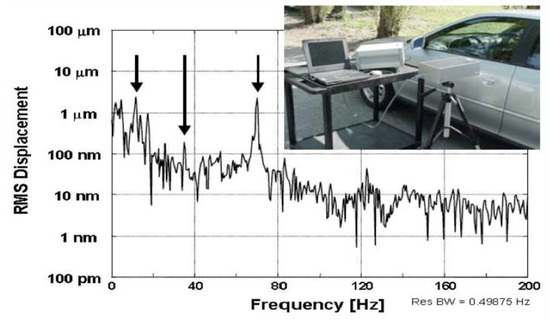
Figure 11.
Vibration modes of a car structure are obtained by aiming the device at a door of a car. The motor rotates at 35 Hz, and two other major peaks are seen, due to spikes at 70 Hz and to the suspension resonance at 13 Hz. Many other (unidentified) peaks are found in the structure because their intensity is well above the 100 pm noise floor of the instrument (from Ref. [34], ©IoP; reprinted with permission).
4.2. Measuring Mechanical Hysteresis with a Differential HFS SMI
The SMI can be made quasi-differential by pairing two HFS units and making the difference be their output signals [34].
The difference Vout1 − Vout2 is not exactly the same as the difference of phases ϕ1 − ϕ2 = 2k(s1 − s2) made by the superposition of measurement and reference beams in a normal LI. However, it closely approaches it inasmuch as Vout is linearly related to Δs, like in an HFS interferometer.
For best results, the noise and dynamic range of two HFS SMIs shall be matched within 5%, and then a weighted subtraction Vout1 − ηVout2 is made, adjusting the weight η so that when the two units are aimed just to the same point, the difference in the outputs is <10−3 of the single component output.
Then, the differential SMI can be applied to the measurement of a small sample, for example, a bead of a motor damper, subjected to a vibratory stress (one unit) and to the base holding the object (the other unit). In this way, we have (i) a common mode signal, proportional to the applied stress (or force per unit area) and (ii) a differential signal proportional to the strain (or relative deformation) imparted to the sample.
The result is shown in Figure 12. Note that the measurement of the hysteresis cycle supplies an important design tool because it allows for selecting the right level of stress to maximize the power dissipated by the damper (given by the area of the cycle times the frequency of operation) while keeping a safe margin to avoid breakdown of the sample.
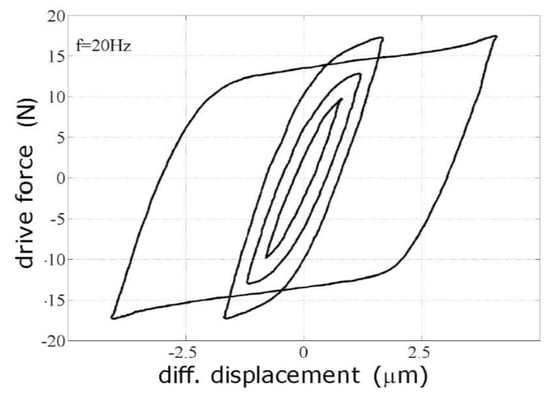
Figure 12.
Mechanical hysteresis cycle of a bead sample measured with the HFS SMI. Up to a force F = ±5 N, the regime is Newtonian, and then the sample enters the plastic regime and the hysteresis area (and dissipated power) increases until about F = ±18 N, where the sample breaks down.
For more information on the HFS method, the reader may consult Refs. [34,35,37], and Ref. [38] that reports the complete performances of a commercial vibrometer inspired by the research described in this Section.
4.3. Measuring Acoustic Emission with the High-C Linearized SMI
The high-C linearized SMI has been successfully used to measure the AE (acoustic emission) from an aluminum rectangular plate excited with a small piezo placed on the edge of the plate, where the SMI sensor was a fiber-pigtailed DFB laser [36]. The sensing length of the fiber, glued to the Al plate, was 15 cm, and the total (standoff) fiber length was 1.50 m. At f = 40 kHz of excitation, the SMI vibration sensor was able to detect 14 με of strain (where ε = Δl/l is the strain unit), corresponding to an amplitude of 2.12 μm, and it had a noise-limited sensitivity of 0.25 nε/√Hz [36].
5. Switching Cancellation (SC) Analog Readout SMI Vibrometer
A simple yet effective method for reconstructing the SMI waveform under the moderate feedback regime (1 < C < 4.6) was introduced in Ref. [39], which was developed for the measurement of vibrations and oscillation mode of medium-size structures (say, a few meters in size) in Ref. [40]. It starts from the observation that, if we remove the switching steps in the SMI signal I = I0 cos 2ks(t), after sliding the waveform to restore its continuity, the result is practically coincident with the drive waveform s(t) (see Figure 5 in Ref. [39]).
To implement this concept, called switching cancellation (SC), we first time-differentiate the SMI signal to obtain a sequence of positive and negative pulses in correspondence with the upgoing and down-going switching, then separate the positive and negative pulses and send them to a stretcher circuit supplying a step waveform slowly decaying in time (to avoid a pile-up of tails), and then subtract the steps to the SMI signal, thus removing the switching.
Theoretically, this procedure is difficult to analyze and justify. However, heuristically, it proves to be robust and fairly accurate in the moderate feedback range because the error of reconstruction is just a little fast ripple easily filtered out using a low-pass operation.
An example of waveforms obtained using the SC circuit is shown in Figure 13. Here, a loudspeaker with a cone covered with untreated white paper was used as the diffusive target. It was driven with a sine wave, yielding a peak-to-peak signal amplitude of 5 μm at 20 Hz; the wavelength of the laser was 780 nm, and the feedback factor was estimated to be C ≈ 3. Similar waveforms were also observed for peak-to-peak signal amplitudes from 400 nm to 20 μm, in a range of frequency going from 0.1 Hz to 100 Hz [40].
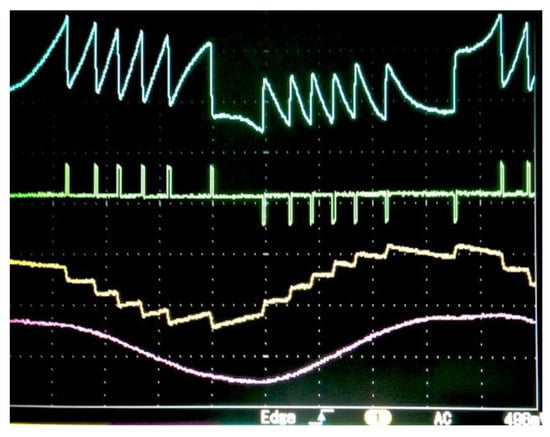
Figure 13.
Waveforms obtained using SC processing. Traces from top to bottom: the SMI signal; the differentiated pulses; the switching removed; and the final reconstructed (low pass filtered) signal (from Ref. [40], ©SPIE; reprinted with permission).
Observing the SMI reconstructed signal at the (electrical) spectrum analyzer reveals the ambient-related vibrations collected using the setup and, adding an excitation, the vibration modes of the structure. As an example, by pointing the beam of the SC-SMI at the floor when placed on an anti-vibration table at 1.2 m height, we were able to measure the spectrum of the vibrations collected by the floor, as reported in Figure 14.
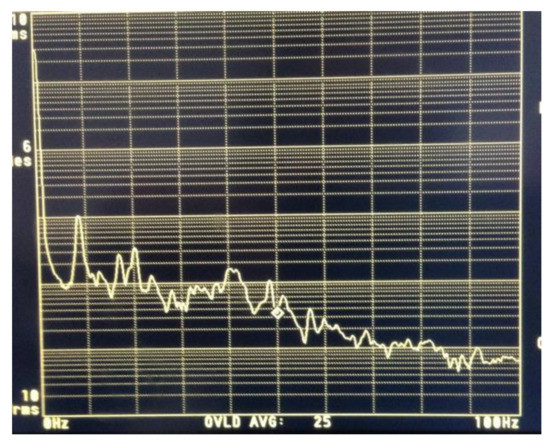
Figure 14.
Frequency spectrum of the SC-SMI vibrometer signal in calm environmental conditions. The vertical scale is log and covers six decades; the horizontal scale is linear and spans 0 to 100 Hz (or 10 Hz per division). The peak at ≈9 Hz is identified as the resonance of the anti-vibration table. When the environment is perturbed by people walking nearby, the signal is seen to increase on the 10–50 Hz band (from Ref. [40], ©SPIE; reprinted with permission).
The SC-SMI vibrometer is simple and easy to use and works well on untreated target surfaces. Its performance is limited by the circuits handling the SMI signal and covering the middle-to-high range of amplitudes, that is, from ≈0.5 μm to ≈50 μm, and the frequency components from 0.1 to 100 Hz.
A potential application of this version SC-SMI of the vibration analyzer is the low-cost intrusion detector for approaching persons.
6. Frequency-Shifted (FS) Long Standoff Distance Vibrometer (LI and SMI)
Testing large structures using a laser vibrometer is an application that was developed soon after the advent of the laser. Since the 1980s, He-Ne-based instruments have been extensively used in the field [41,42,43] for the remote (standoff distance of ≈100 m) monitoring of structures like dams and towers [44].
The most viable and commonly accepted approach to build a single-channel (i.e., yielding a cos 2ks signal) laser interferometer yielding a long standoff distance and nm-capability is the frequency-shifted (FS) approach, in connection with a frequency stabilized laser (to attain a long coherence length).
The shift is obtained by a Bragg acousto-optic cell, which allows the signal 2ks(t) to be impressed on a carrier frequency of 20–50 MHz so that by demodulating the received signal, we can trace back the small vibration s(t) [45]. This operation is carried out using the arrangement shown in Figure 15.
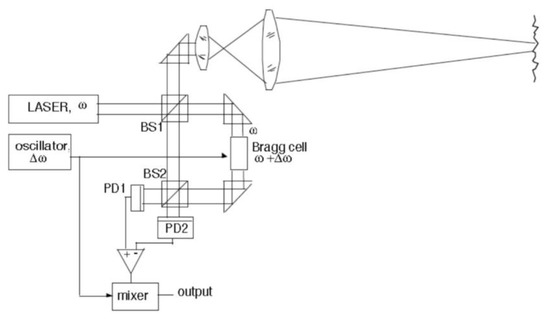
Figure 15.
Scheme showing a long standoff distance LI using a Bragg cell to shift the interferometric signal from the baseband to a carrier frequency Δω. At the receiver, mixing the signal with the frequency-shifted oscillation returns the s(t) vibration signal.
The source is a laser stabilized in frequency so that the linewidth (typ. Δν = 100 kHz) is narrow enough to give interference after the long (2 s = 200 m, typically) propagation path to the remote target and back, and the wavelength is chosen in correspondence with atmospheric minima of absorption [45]. The He-Ne is a good choice along with the CO2 laser at λ = 10.6 μm for better transmission through haze.
Recently, the GaAlAs diode laser (grating stabilized for low Δν) was used in connection with the SMI version of the vibrometer. This is obtained simply by placing the Bragg cell of Figure 15 along the propagation path to the target.
Regarding the minimum detectable displacement (or NED), this is determined by the quantum noise of the detected return and eventually by the limited coherence length, with a usually substantial contribution of the 1/f component. As we can see from Figure 16, the NED for a CO2 laser is better than that of a He-Ne, and both are comparable to the GaAlAs laser diode in the SMI configuration.
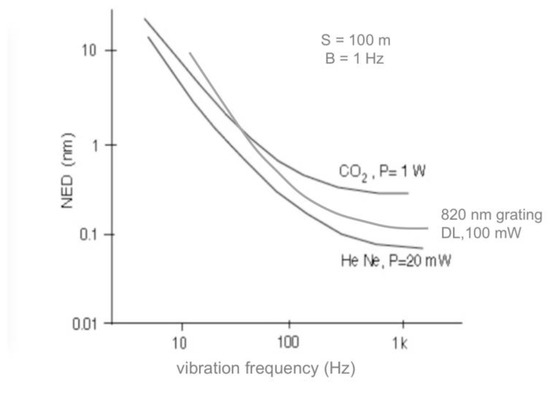
Figure 16.
Typical NED vs. frequency for long standoff distance vibrometers using He-Ne and CO2 lasers in a LI configuration and a GaAlAs diode laser in an SMI configuration.
The long-distance vibrometer is useful for detecting the vibration mode and frequency response of a large structure, for example, a tower, as shown in Figure 17.
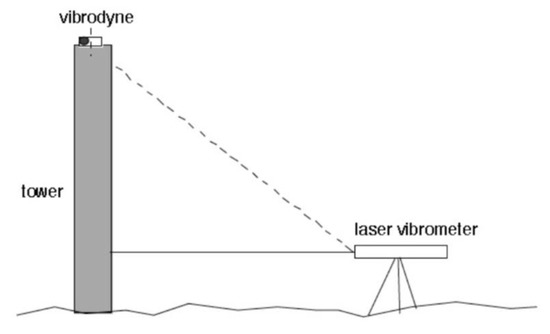
Figure 17.
Setup for testing the integrity of a tower with a laser vibrometer, taking advantage of the minute (few nm) vibration imparted to the structure by the vibrodyne. The laser is aimed at different heights to create a map showing the frequency response.
Here, a vibrodyne—a rotating motor with an eccentric-mounted mass—is mounted atop the tower and scanned in frequency to measure the frequency response, as shown in Figure 18.
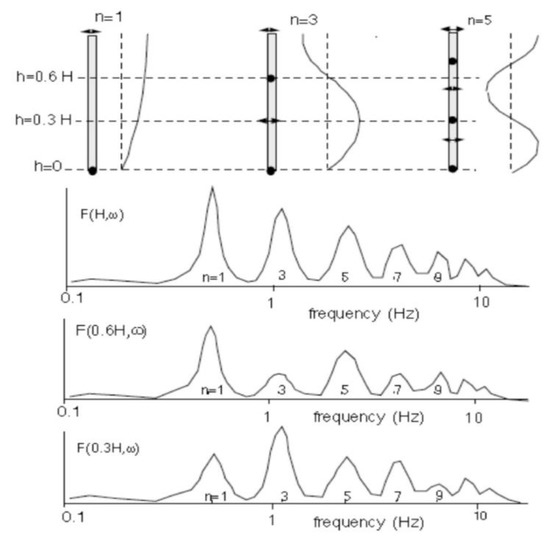
Figure 18.
A tower has bending vibration modes with nodes (dots) and antinodes (arrows) at integer fractions of height H, which are revealed by the frequency response measured with the vibrometer.
The laser vibrometer scans spots at selected heights of the tower, and the result is a chart showing responses that the structural engineer can interpret to diagnose the integrity of the structure.
7. Speckle Pattern Errors
As native targets are usually diffusive surfaces, the field returning to the measuring port (either the beamsplitter of the LI or the DL of the SMI) is subject to well-known speckle pattern statistics [46,47,48,49,50,51].
Speckle statistics bring about measurement error, and we can consider circumventing it using a mirror as the target. However, this option is to be absolutely avoided because it is invasive and requires a clumsy alignment operation. Using a corner cube [52] eliminates the alignment but aggravates the invasiveness, so it is never used in practice, except in displacement measurements with tool machines because it can be fastened to the moving turret. A retroreflector tape (or varnish) over the native surface can be used to obtain an increase in the retroreflected power by a factor of 20 to 50, together with the mitigation of speckle errors and the alignment requisite. Yet, the retroreflector tape is also invasive, and we should possibly avoid it when working on the native, diffusive surface of the target.
On a diffusive surface, speckle statistics [46,47,48] are generated by the randomness, at the λ-scale, of the height of individual elemental areas illuminated with the incoming laser spot. As a result, both the amplitude and phase of the field returning to the measuring port fluctuate (or have an error) because of the speckle noise, both in LI and SMI.
The statistics of speckle intensity is a negative exponential with a decay constant equal to the average value: that of amplitude is a Rayleigh distribution, and that of phase is a uniform distribution over 0–2π [46,47,48].
Given the point-wise nature of the vibration measurement, amplitude fluctuation is easily cured. If we unfortunately fall on a dark speckle giving back a signal amplitude much less than the average, we simply move the aim of the beam away and find another spot nearby where the amplitude is larger and sufficient.
An SMI with BST (bright speckle tracking) was developed [49] to cure amplitude fading. Also, remarkably, the HFS SMI can bear a substantial attenuation of speckle amplitude thanks to the feedback loop gain, but all the other LI and SMI schemes are subject to full speckle amplitude fading.
On the other hand, the phase error entirely impacts the measurement because theoretically, we cannot distinguish it from the useful phase signal ϕ = 2ks.
An analysis of the phenomenon shows that the phase error can be reduced by making the spot size as small as possible because the phase-induced error (or NED, noise equivalent displacement) is given by [46,47,48,49,50] NED = (C/4√2)Δ(D/2z)2, where Δ is the amplitude of the vibration, D is the spot diameter, z is the target distance, and C/4√2 is a multiplicative factor not much different from one. In Figure 19, we plot the NED as a function of normalized distance z/(D/2). As we can see, the nose contribution can become even smaller than the quantum noise of the beam (for a detected current of 1 μA) for z > (≈200) (D/2), that is, for z = 100 mm when D = 1 mm.
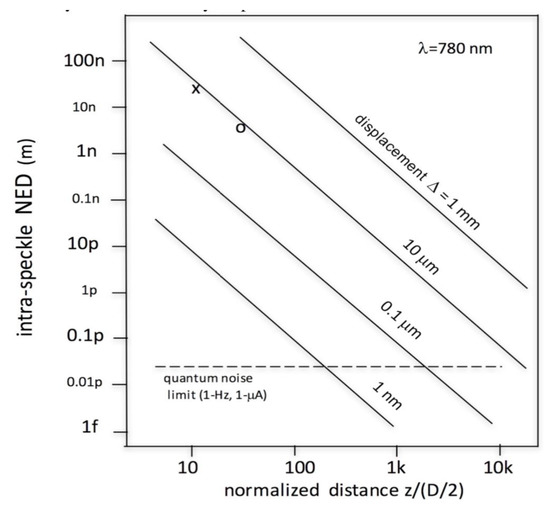
Figure 19.
NED of speckle pattern phase noise plotted vs. distance z to spot size D/2 ratio and with the amplitude of vibration Δ as a parameter. For a peak amplitude Δ = 10 μm, two experimental points are shown (from Ref. [50], ©IEEE; reprinted with permission).
8. Discussion and Conclusions
In Figure 20, we summarize the typical performances of SMI vibrometers described in the previous Sections with regard to the covered measurement range and standoff distance.
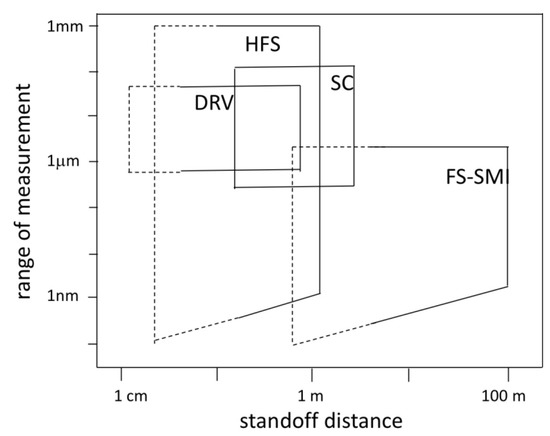
Figure 20.
The measurement range achieved with the SMI vibrometers described in this paper vs. the standoff distance of operation. Full lines represent the normally used regions and the dotted lines represent the possible extension at short distances. DRV: digital readout vibrometer; HFS: half-fringe-stabilized; SC: switching cancellation; FS-SMI: frequency-modulated.
These results demonstrate the suitability of SMI techniques for non-invasive, contactless measurement of vibrations and for assessing the parameters of a mechanical system, all with the fine spatial resolution determined by the laser spot size.
The reported approaches offer case studies and guidelines to develop vibration measurements spanning from tens of picometer to millimeters in amplitude and sub-Hz to MHz in frequency, with a variety of standoff distances. Thus, they provide a benchmark and a guide for anyone entering the field of vibration measurement of kinematic quantities.
Vibrations are also called for in several other fields of science and technology, for example, in biomedical sensing, structural testing, and seismology, where they are still in their infancy but may lead soon to important breakthroughs, an important event for all researchers interested in the field. In all the techniques described, the SMI configuration demonstrates itself as particularly simple and low-cost, while supplying a high sensitivity of detection and fast response.
Regarding the development of new ideas in SMI, a crucial caveat to bear in mind is that, given the advantages of the simple starting configuration, one with low cost and minimum part count, any added expensive component should be carefully avoided, as well as avoiding heavy computer resources. In other words, adding components to the SMI destroys the inherent simplicity of the configuration and is not at all advisable.
Also, the operation should be on diffusive targets (not mirrors or other components attached to the target or part of the setup) to maintain the non-invasiveness and non-contact remote mode of operation.
Funding
This research received no external funding.
Data Availability Statement
Data supporting the reported results are found in the papers cited in the References.
Conflicts of Interest
The author declares no conflict of interest.
References
- Piersol, A.G.; Paez, T.L. Harris’ Shock and Vibration Handbook, 6th ed.; McGraw Hill: New York, NY, USA, 2010; pp. 10.32–10.34. [Google Scholar]
- Ver, I.L.; Beranek, L.L. Noise and Vibration Control Engineering, 2nd ed.; J. Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Donati, S. Electrooptical Instrumentation; Prentice Hall: Upper Saddle River, NJ, USA, 2004; pp. 40–43, 94–107 and 109–110. [Google Scholar]
- Dorsch, R.G.; Hausler, G.; Hermann, J.M. Laser Triangulation: Fundamental Uncertainty in Distance Measurements. Appl. Opt. 1994, 33, 1306–1314. [Google Scholar] [CrossRef] [PubMed]
- Bes, C.; Plantier, G.; Bosch, T. Displacement measurements using a self-mixing laser diode under moderate feedback. IEEE Trans. Instrum. Meas. 2006, 55, 1101–1105. [Google Scholar] [CrossRef]
- Donati, S.; Gotti, R.; Agnesi, A.; Pirzio, F. Self-Mixing Displacement Measured by a Two-Color Laser in 66-nm steps. IEEE Trans. Instrum. Meas. 2023, 72, 7000607. [Google Scholar] [CrossRef]
- Wang, H.; Ruan, Y.; Yu, Y.; Guo, Q.; Xi, J. A New Algorithm for Displacement Measurements Using Self-Mix Interferometry with Modulated Injection Current. IEEE Access 2020, 8, 123253–123261. [Google Scholar] [CrossRef]
- Donati, S.; Giuliani, G.; Merlo, S. Laser Diode Feedback Interferometer for Measurement of Displacement without Ambiguity. IEEE J. Quant. Electr. 1995, 31, 113–119. [Google Scholar] [CrossRef]
- Gouaux, F.; Bosch, F.S.T. Absolute Distance Measurement with a Feedback Interferometer. Appl. Opt. 1998, 37, 6684–6689. [Google Scholar] [CrossRef]
- Norgia, M.; Giuliani, G.; Donati, S. Absolute Distance Measurement with Improved Accuracy Using Laser Diode Self-Mixing Interferometry in a Closed Loop. IEEE Trans. Instrum. Meas. 2007, 56, 1894–1900. [Google Scholar] [CrossRef]
- Scalise, L.; Yu, Y.; Giuliani, G.; Plantier, G.; Bosch, T. Self-mixing laser diode velocimetry: Application to vibration and velocity measurement. IEEE Trans. Instrum. Meas. 2004, 53, 223–232. [Google Scholar] [CrossRef]
- Norgia, M.; Pesatori, A.; Donati, S. Compact Laser Diode Instrument for Flow Rate Measurement. IEEE Trans. Instrum. Meas. 2016, 64, 1478–1483. [Google Scholar] [CrossRef]
- Giuliani, G.; Donati, S.; Passerini, M.; Bosch, T. Angle Measurement by Injection Detection Interferometry in a Laser Diode. Opt. Engin. 2001, 40, 95–99. [Google Scholar] [CrossRef]
- Jingya, Q.; Zhao, W.; Huang, J.H.; Yu, B.; Jianmin, G.; Donati, S. Enhancing the Sensitivity of Roll-Angle Measurement with a Novel Interferometric Configuration based on Waveplates and Folding Mirror. Rev. Sci. Instr. 2016, 87, 036106. [Google Scholar]
- Chen, W.; Zhang, S.; Long, X. Angle measurement with laser feedback instrument. Opt. Expr. 2013, 21, 2277–2289. [Google Scholar] [CrossRef]
- Fathi, M.; Donati, S. Simultaneous Measurement of Thickness and Refractive Index by a Single-Channel Self-Mixing Interferometer. IET Optoelectron. 2012, 6, 7–12. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Y.; Wang, X.; Wang, X. Refractive Index Measurement with High Precision by a Laser Diode Self-Mixing Interferometer. IEEE Photonics J. 2015, 7, 2600506. [Google Scholar] [CrossRef]
- Giuliani, G.; Norgia, M. Laser Diode Linewidth Measurement by Means of Selfmix Interferometry. IEEE Photonics Technol. Lett. 2000, 12, 1028–1030. [Google Scholar] [CrossRef]
- Yu, Y.; Giuliani, G.; Donati, S. Measurement of the Linewidth Enhancement Factor of Semiconductor Lasers based on the Optical Feedback Self-Mixing Effect. IEEE Photonic Technol. Lett. 2004, 14, 900–902. [Google Scholar] [CrossRef]
- Donati, S.; Sorel, M. A Phase-Modulated Feedback Method for Testing Optical Isolators Assembled into the Laser Package. IEEE Photonics Technol. Lett. 1996, 8, 405–407. [Google Scholar] [CrossRef]
- Dean, P.; Lim, Y.L.; Valavanis, A.; Kliese, R.; Nikolić, M.; Khanna, S.P.; Lachab, M.; Indjin, D.; Ikonić, Z.; Harrison, P.; et al. Terahertz Imaging through Self-Mixing in a Quantum Cascade Laser. Opt. Lett. 2011, 36, 2587–2589. [Google Scholar] [CrossRef]
- Grabherr, M.; Moench, H.; Pruijmboom, A. VCSELs for optical mice and sensing. In VCSELs; Springer Series in Optical Sciences; Springer: Berlin, Germany, 2013; Volume 166, pp. 521–532. [Google Scholar]
- Mutlu, M.; Cihan, A.F.; Winkler, M.; Chen, T. Self-Mixing Interferometry-Based Gesture Input System Including a Wearable or Handheld Device. U.S. Patent US20210072833A1, 21 July 2020. [Google Scholar]
- Donati, S. Chapter 5: ‘Self-Mixing Interferometry’. In Photonic Instrumentation; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2023; pp. 173–232. [Google Scholar]
- Donati, S. Developing Self-Mixing Interferometry for Instrumentation and Measurements. Laser Photonics Rev. 2012, 6, 393–417. [Google Scholar] [CrossRef]
- Taimre, T.; Nikolic, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakic, A.D. Laser feedback interferometry: A tutorial on the self-mixing effect for coherent sensing. Adv. Opt. Photonics 2015, 7, 570–631. [Google Scholar] [CrossRef]
- Wuerz, L.J.; Quenelle, R.C. Laser interferometer system for metrology and machine tool applications. Precis. Eng. 1983, 5, 111–114. [Google Scholar] [CrossRef]
- Chapter 4: ‘Laser Interferometry’. In Photonic Instrumentation; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2023; pp. 101–172.
- Acket, G.A.; Lenstra, D.; DenBoef, A.J.; Verbek, B.H. The influence of feedback intensity on longitudinal mode properties and optical noise in index-guided semiconductor lasers. IEEE J. Quantum Electron. 1984, 20, 1163–1169. [Google Scholar] [CrossRef]
- Donati, S.; Hwang, S.-K. Chaos and High-Level Dynamics in Coupled Lasers and their Applications. Prog. Quantum Electron. 2012, 36, 293–341. [Google Scholar] [CrossRef]
- Annovazzi-Lodi, V.; Merlo, S.; Norgia, M. Measurements on a Micromachined Silicon Gyroscope by Feedback Interferometry. IEEE/ASME Trans. Mechatron. 2001, 6, 1–6. [Google Scholar] [CrossRef]
- Donati, S.; Annovazzi-Lodi, V.; Merlo, S.; Norgia, M. Measurements of ME\S Mechanical Parameters by Injection Interferometry. In Proceedings of the IEEE/LEOS International Conference on Optical MEMS, Kawai, HI, USA, 21–24 August 2000; pp. 89–90. [Google Scholar]
- Claus, R.O.; Palmer, C.H. Direct Measurement of Ultrasonic Stoneley Waves. Appl. Phys. Lett. 1977, 31, 547–548. [Google Scholar] [CrossRef]
- Giuliani, G.; Bozzi-Pietra, S.; Donati, S. Self-Mixing Laser Diode Vibrometer. Meas. Sci. Technol. 2003, 14, 24–32. [Google Scholar] [CrossRef]
- Donati, S.; Norgia, M.; Giuliani, G. Self-mixing differential vibrometer based on electronic channel subtraction. Appl. Opt. 2006, 45, 7264–7268. [Google Scholar] [CrossRef]
- Liu, B.; Ruan, Y.; Yu, Y. All-Fiber Laser-Self-Mixing Sensor for Acoustic Emission Measurement. IEEE J. Lightw. Technol. 2021, 39, 4062–4068. [Google Scholar] [CrossRef]
- Chapter 5.4.2: ‘Differential Vibrometer for Measuring Mechanical Hysteresis’. In Photonic Instrumentation; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2023; pp. 199–201.
- Julight. Available online: https://lnx.julight.it/web/product/laser-vibrometers/ (accessed on 16 February 2019).
- Norgia, M.; Pesatori, A. A Fully Analog Self-Mix Laser Vibrometer. In Proceedings of the 2011 IEEE International Instrumentation and Measurement Technology Conference, Hangzhou, China, 10–12 May 2011. [Google Scholar] [CrossRef]
- Donati, S.; Martini, G.; Hwang, S.-K. Measurement of ambient vibration by self-mixing interferometry and its application to intrusion detection. Opt. Eng. 2018, 57, 051508. [Google Scholar] [CrossRef]
- Corti, M.; Parmigiani, F.; Botcherby, T. Description of a Coherent Light Technique to Detect Vibration of an Arch Dam. J. Sound Vib. 1981, 84, 35–45. [Google Scholar] [CrossRef]
- Macchi, G.; Pavese, A. Diagnosis of Masonry Towers Using Interferometry. In Proc. ODIMAP III; Donati, S., Ed.; AEIT (Milano): Pavia, Italy, 2002; pp. 20–22 and 51–56. [Google Scholar]
- Miks, A.; Novak, J. Non-contact Measurements in Civil Engineering. In Proc. ODIMAP III; Donati, S., Ed.; AEIT (Milano): Pavia, Italy, 2002; pp. 57–62. [Google Scholar]
- Yue, K.D.; Zhou, X.; Gao, J. Automatic Laser Monitoring for Dam Safety. Key Eng. Mater. 2005, 295, 239–244. [Google Scholar] [CrossRef]
- Chapter 4.5.2: ‘Long Stand-off Vibrometry’. In Photonic Instrumentation; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2023; pp. 145–151.
- Goodman, J.W. Statistical Properties of Laser Speckle Pattern. In Laser Speckle and Related Phenomena, 2nd ed.; Dainty, J.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 9–74. [Google Scholar]
- Donati, S.; Martini, G. Speckle-Pattern Intensity and Phase Second-Order Conditional Statistics. J. Opt. Soc. Am. 1979, 69, 1690–1694. [Google Scholar] [CrossRef]
- Chapter 6: ‘Speckle Pattern and Applications’. In Photonic Instrumentation; CRC Press Taylor & Francis: Boca Raton, FL, USA, 2023; pp. 233–274.
- Norgia, M.; Donati, S.; d’Alessandro, D. Interferometric Measurements of Displacement on a Diffusing Target by a Speckle-Tracking Technique. IEEE J. Quantum Electron. 2001, 37, 800–806. [Google Scholar] [CrossRef]
- Donati, S.; Martini, G.; Tambosso, T. Speckle Pattern Errors in Self-Mixing Interferometry. IEEE J. Quantum Electron. 2013, 49, 798–806. [Google Scholar] [CrossRef]
- Atashkhooei, R.; Royo, S.; Azcona, F.J. Dealing with Speckle Effects in Self-Mixing Interferometry Measurements. IEEE Sens. J. 2013, 13, 1641–1647. [Google Scholar] [CrossRef]
- Donati, S. Photodetectors, 2nd ed.; IEEE Press Wiley: Piscataway, NJ, USA, 2022; p. 269. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).