Effect of Viscous Dampers with Variable Capacity on the Response of Steel Buildings
Abstract
1. Introduction
2. Description of the Structures
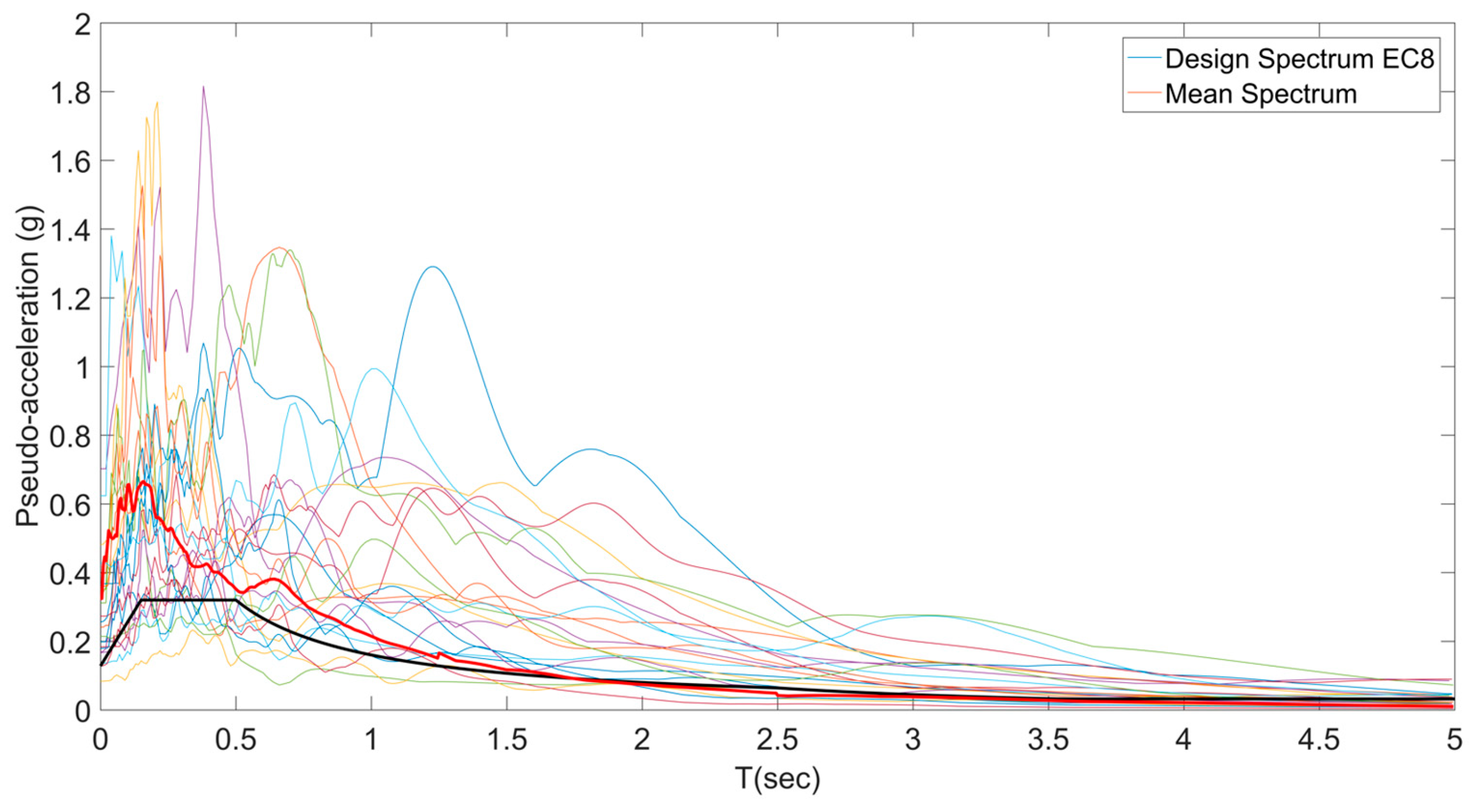
3. Modeling Assumptions and Seismic Motions
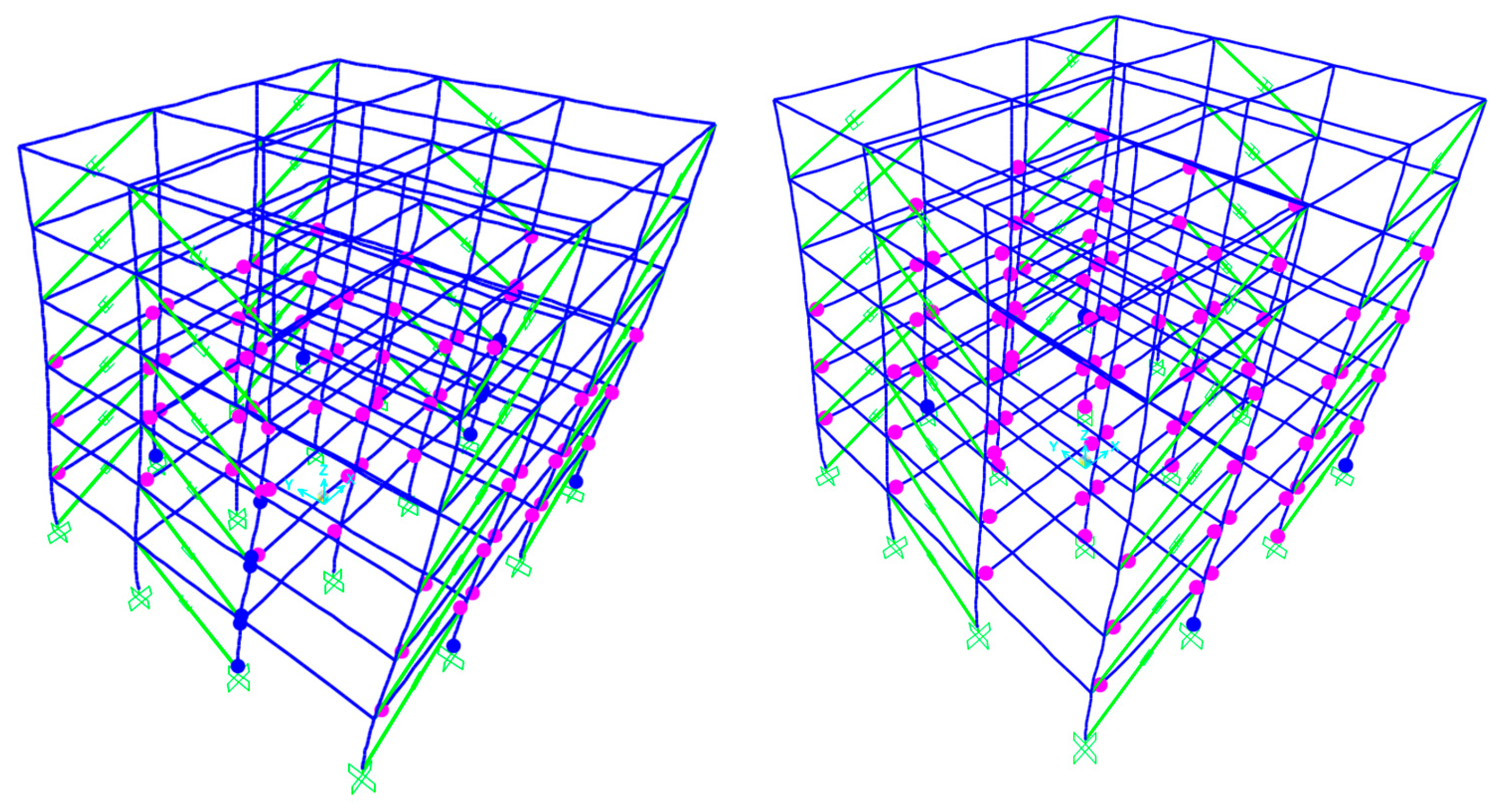
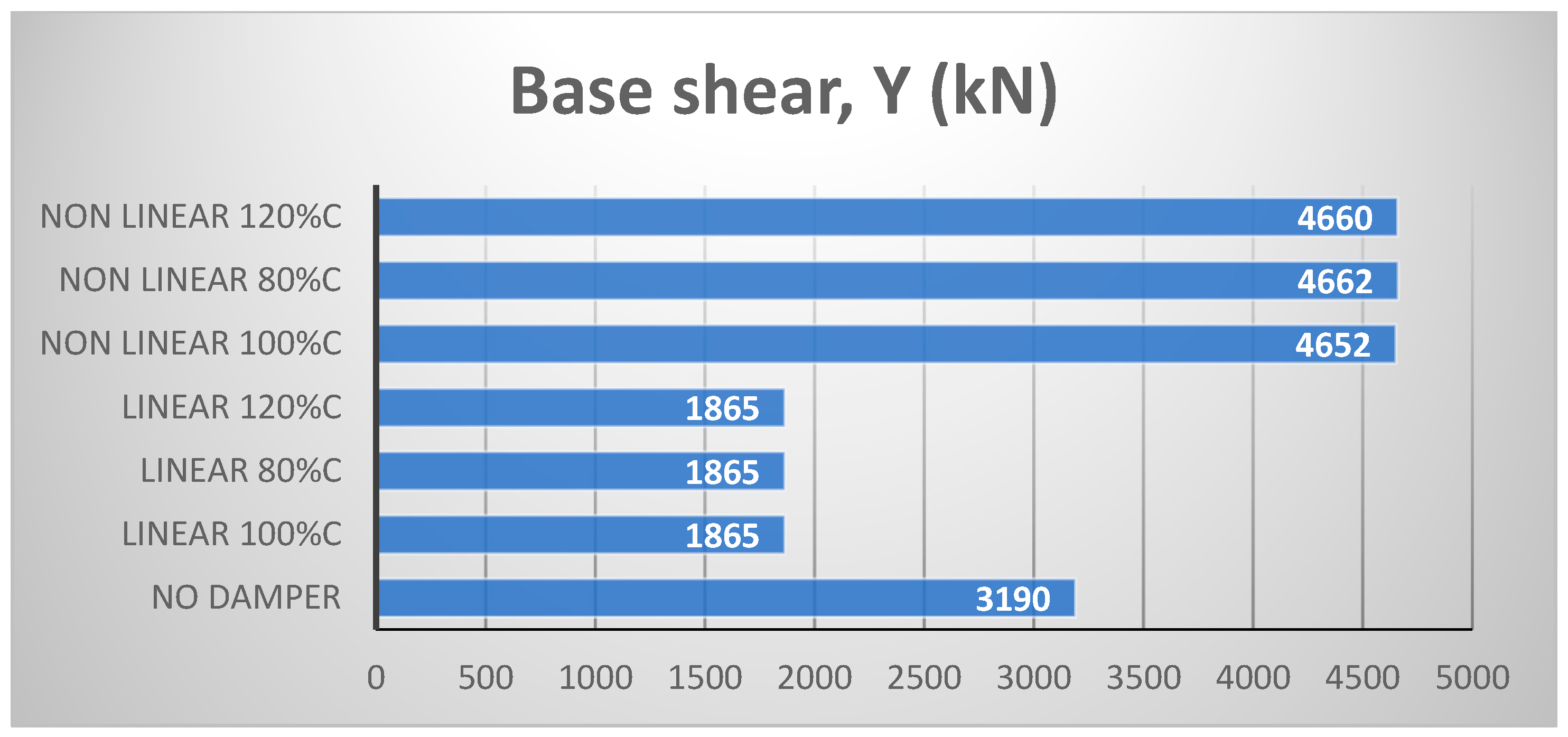
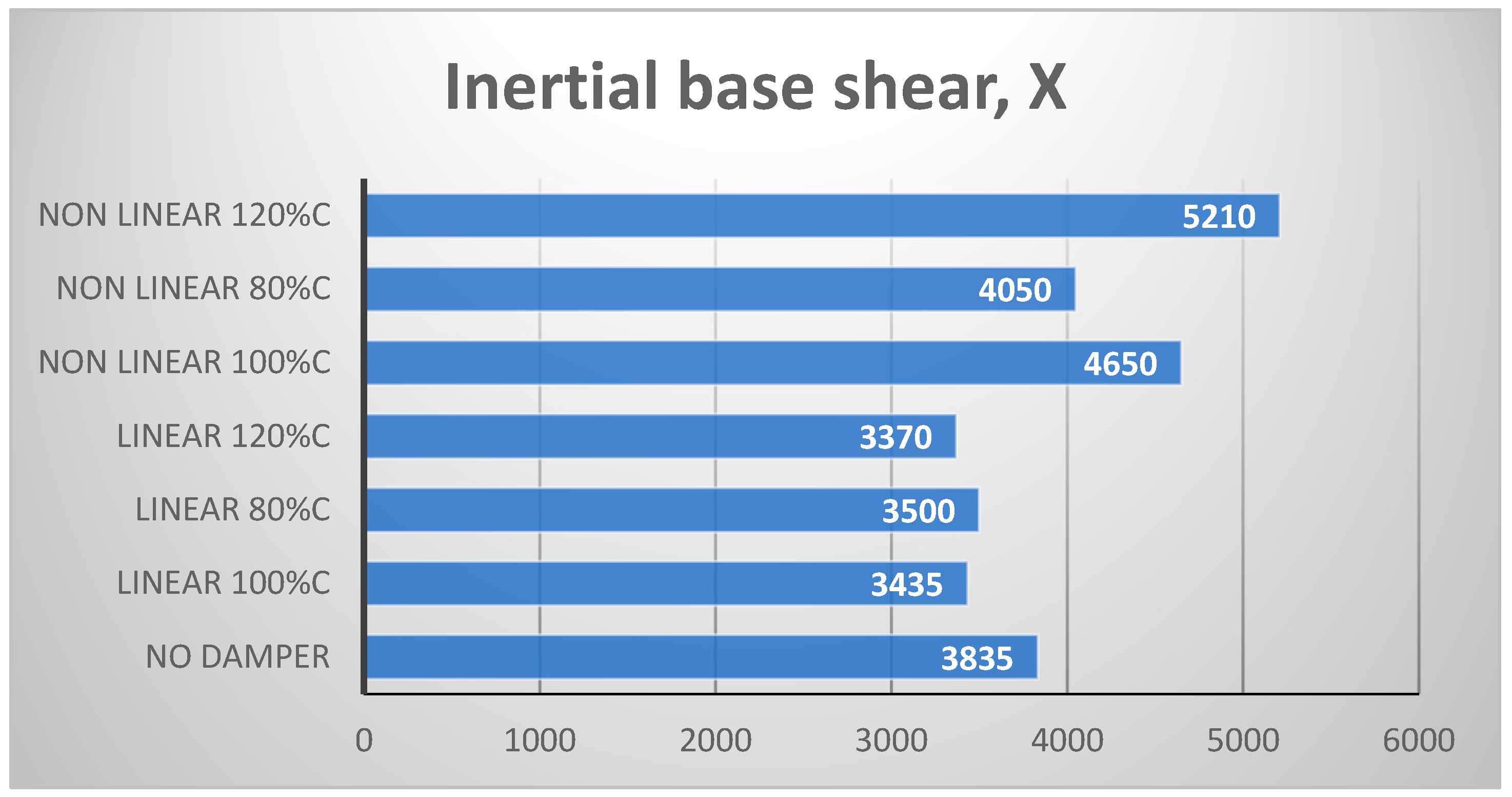
4. Seismic Response Results
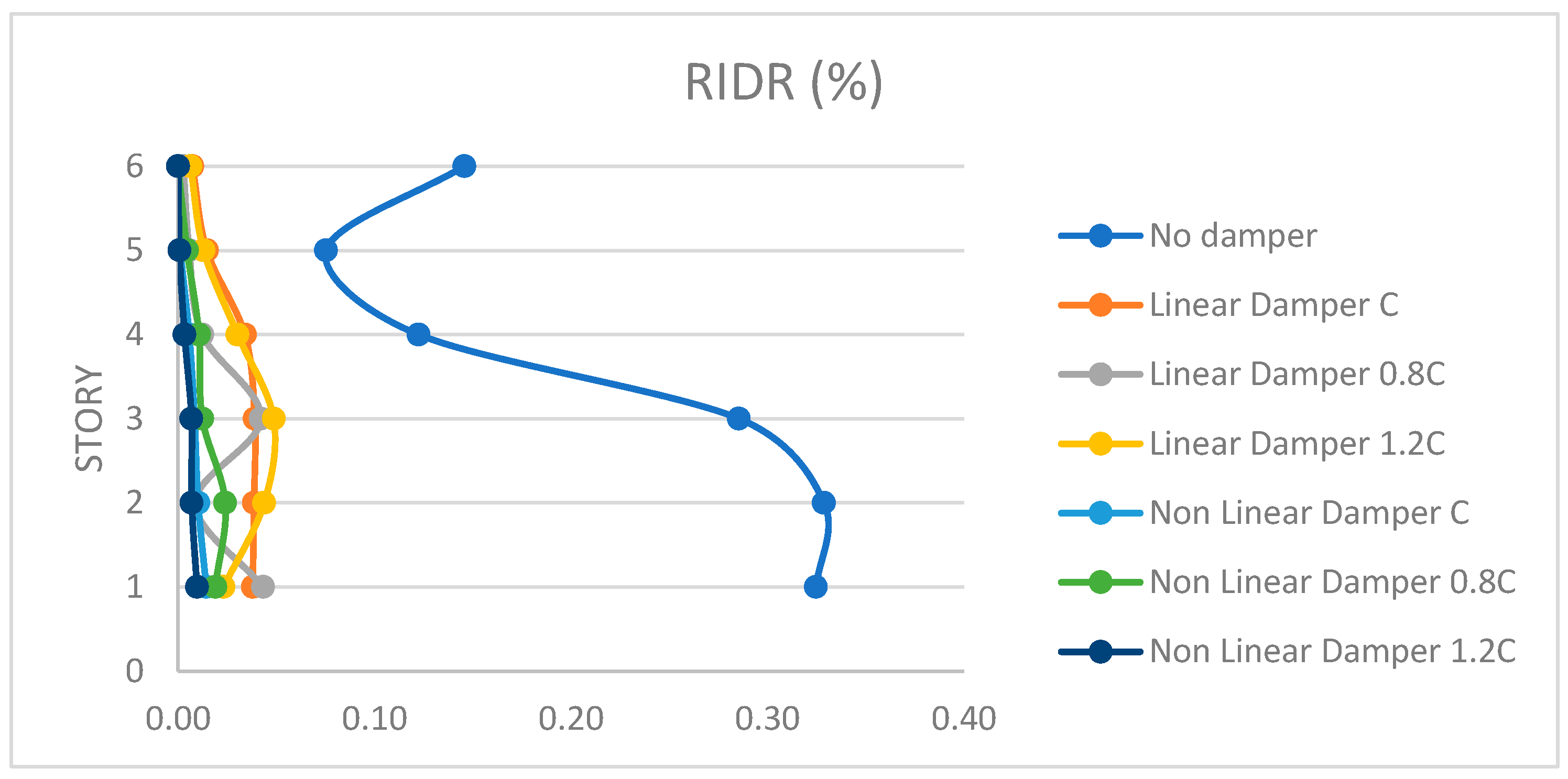
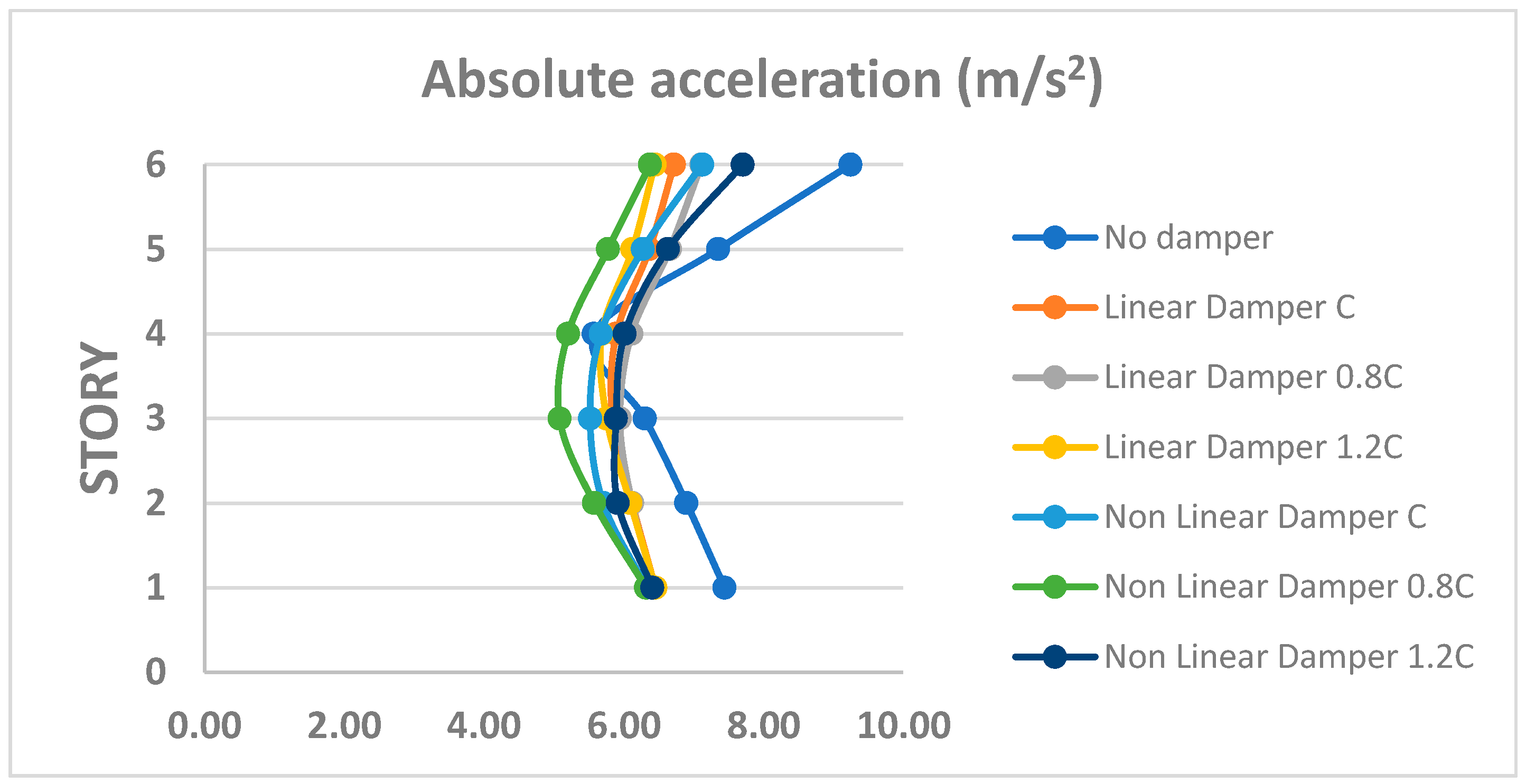
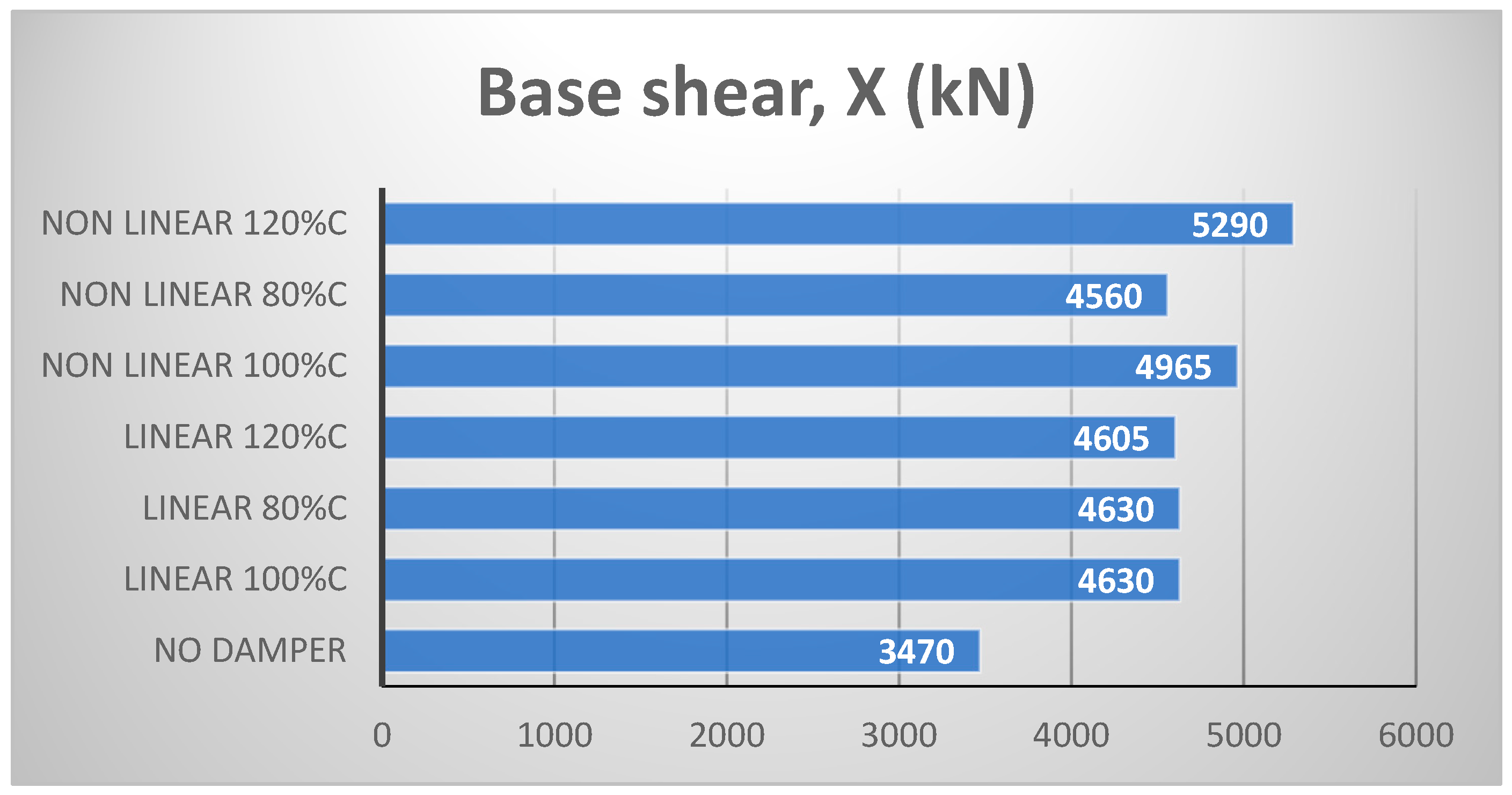
4.1. Six-Story Structure
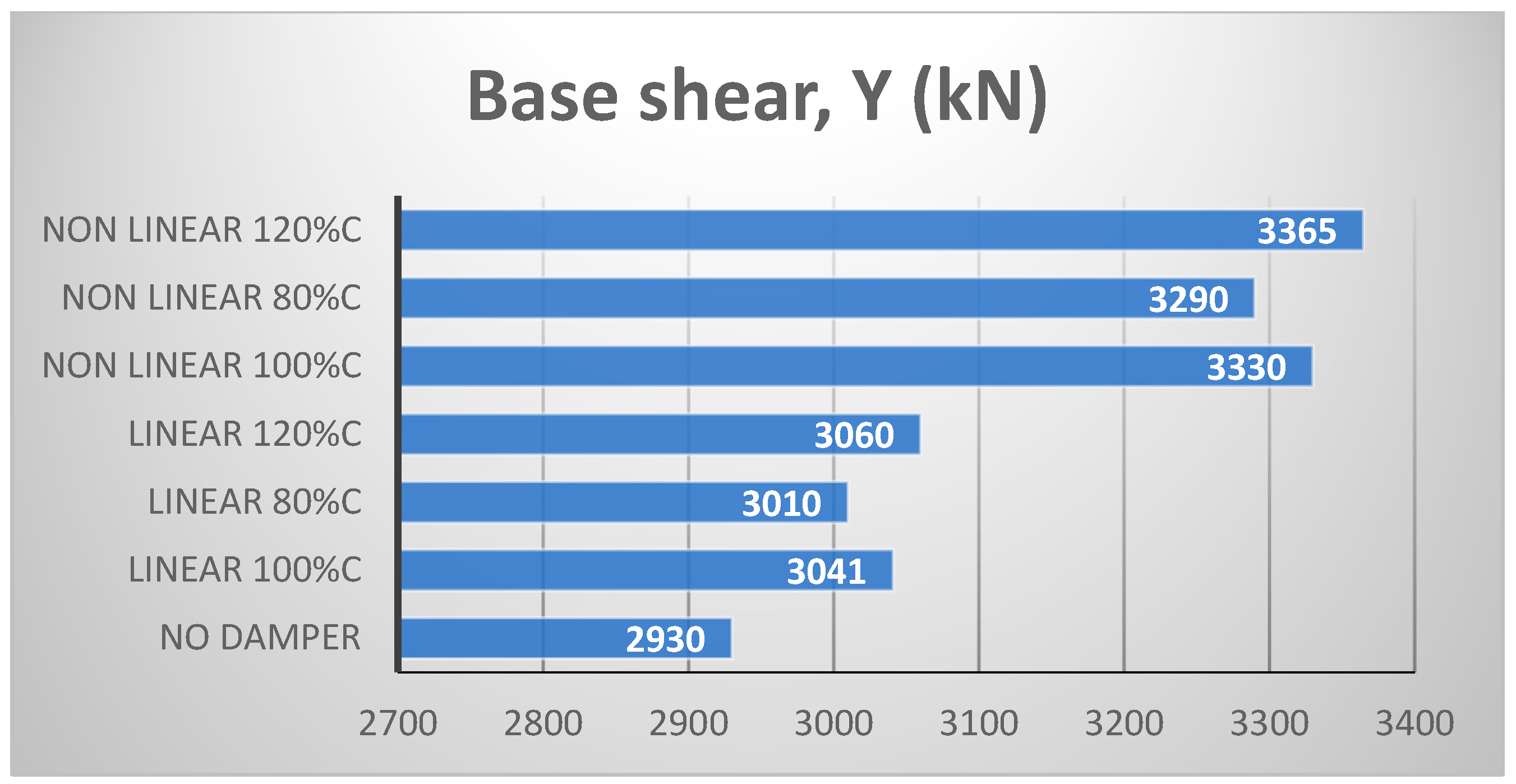
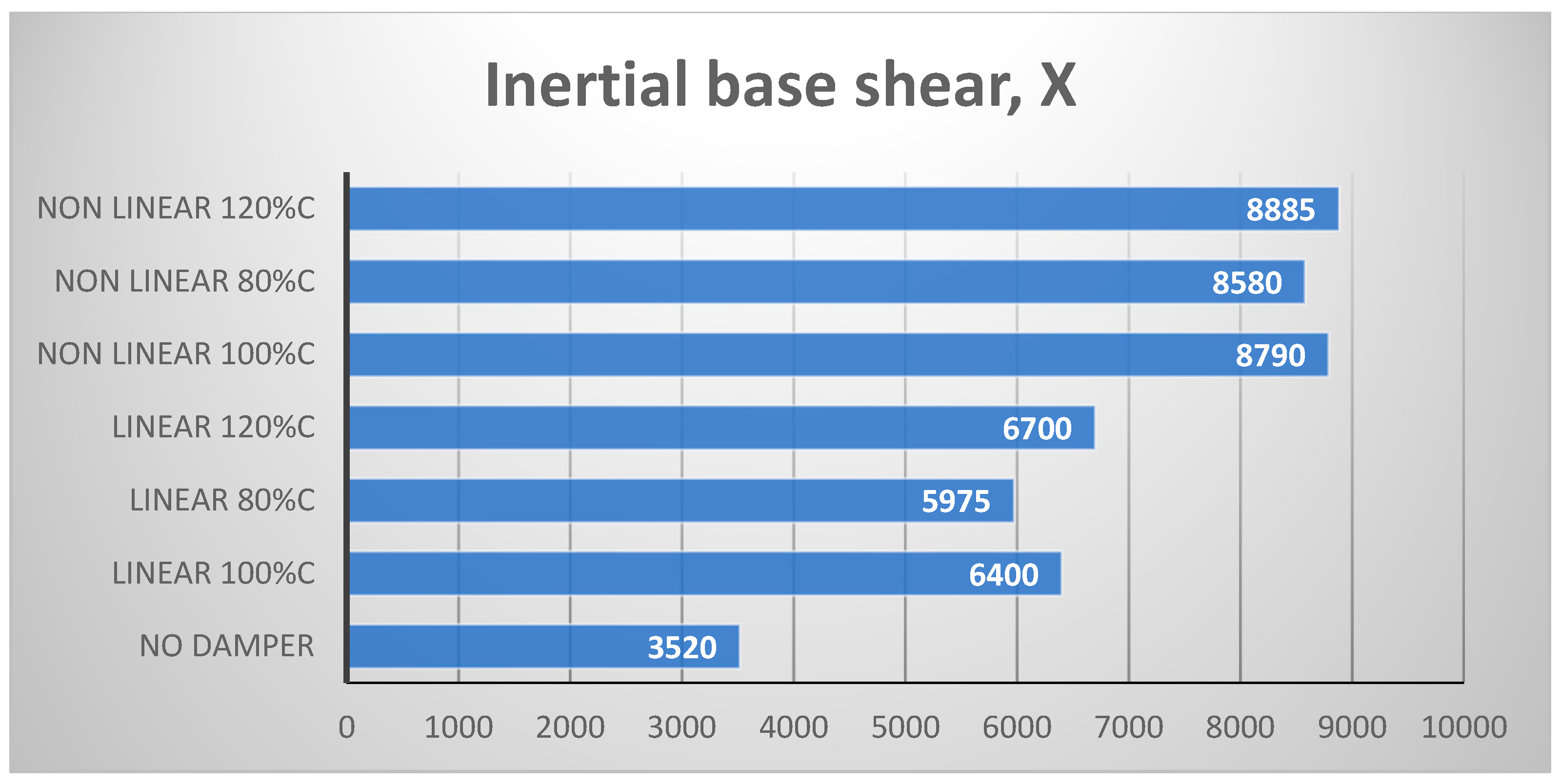
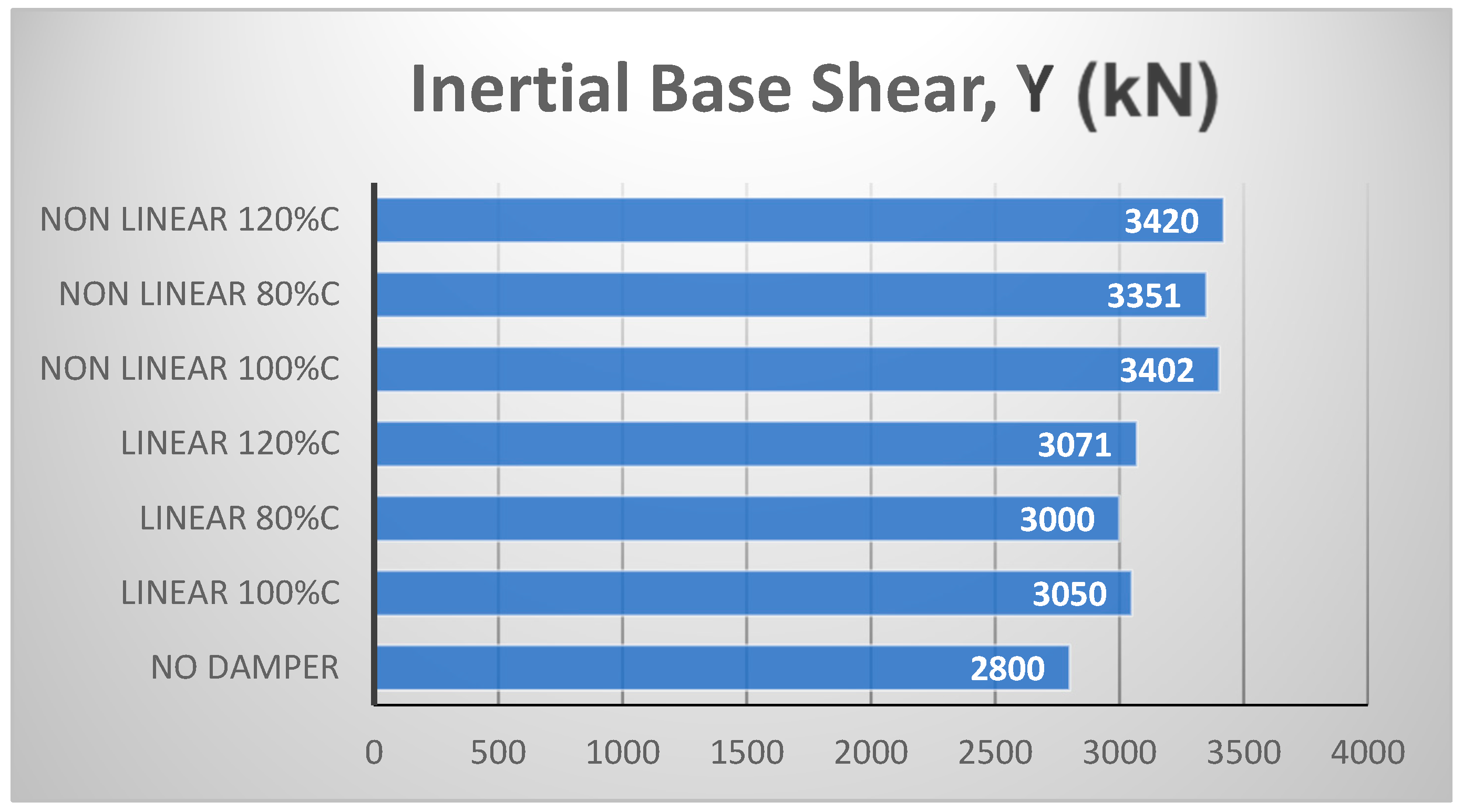
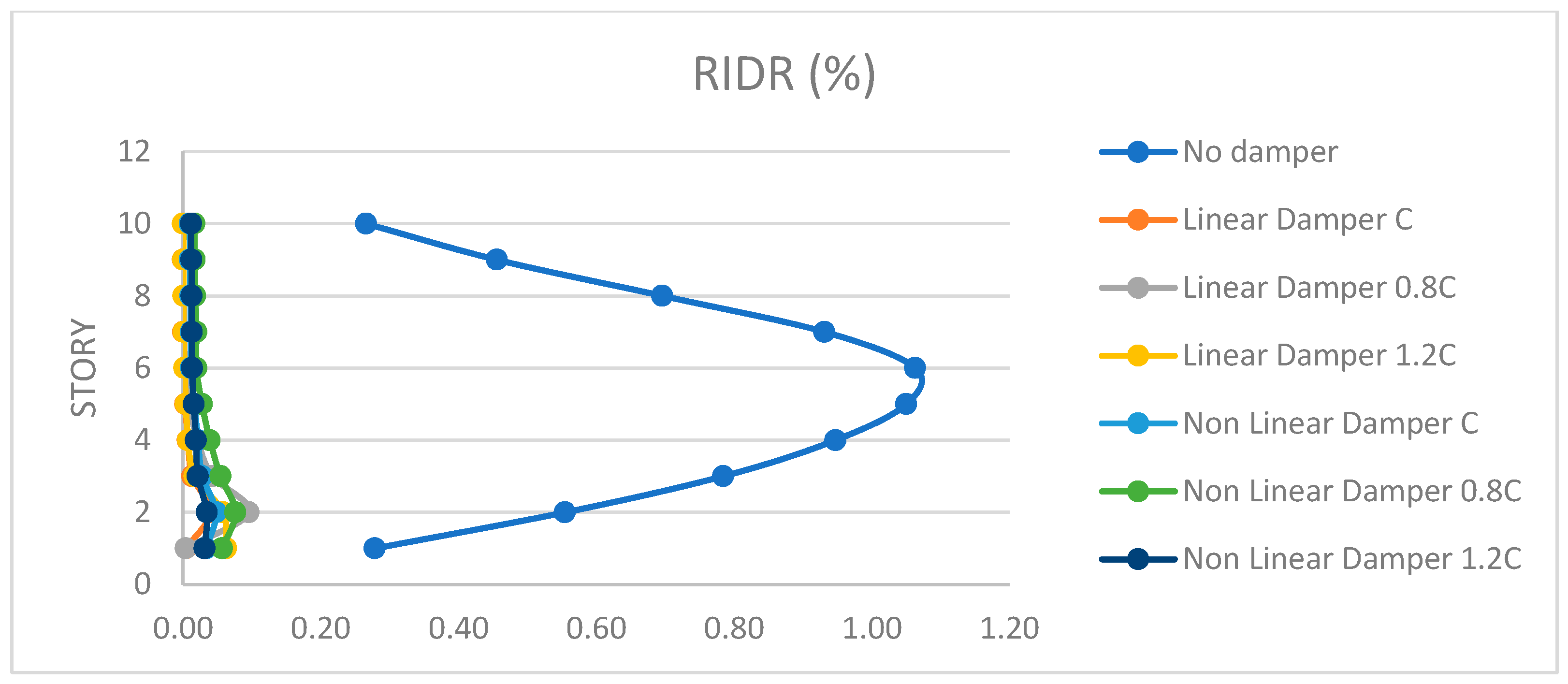
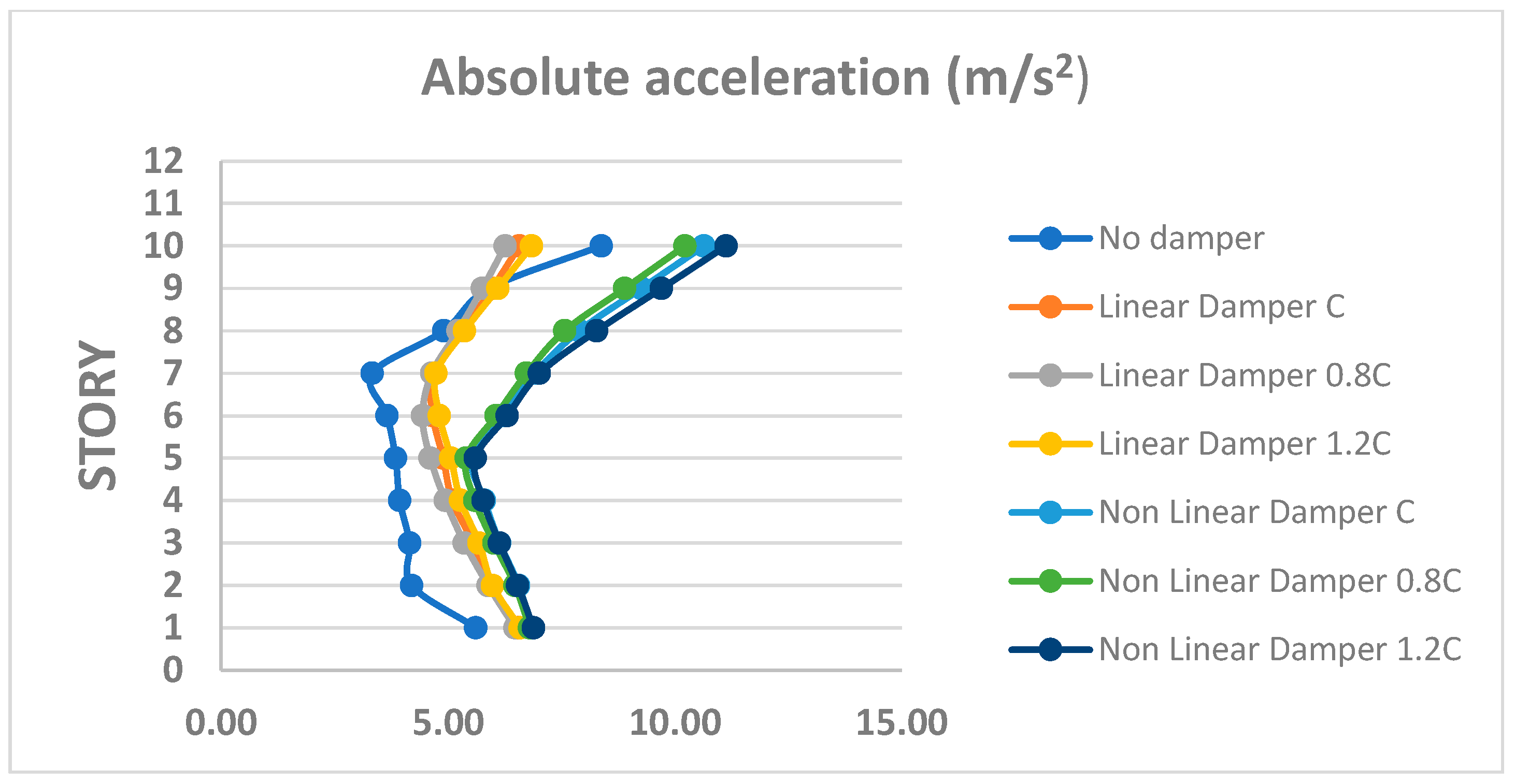
4.2. Ten-Story Structure
5. Conclusions
- In general, the incorporation of both linear and nonlinear viscous dampers significantly improved the seismic performance of the buildings without viscous dampers.
- The effectiveness of viscous dampers was contingent upon the height of the building, with the taller building (10-story) benefiting more than the shorter one (6-story).
- A higher damping coefficient (1.2∙C) consistently resulted in enhanced performance across all the assessed parameters.
- Even with lower damping coefficients (0.8∙C), there were notable improvements compared to the scenarios without damping.
- Linear dampers contributed to a more uniform distribution of plastic hinges throughout the building.
- The use of both types of dampers led to a significant reduction in both the inter-story drift ratio (IDR) and the relative inter-story drift ratio (RIDR).
- Higher damping coefficients (1.2∙C) were particularly effective in controlling drift.
- Floor accelerations were markedly reduced, especially in the upper levels of the structures.
- Both linear and nonlinear dampers proved effective in decreasing acceleration demands.
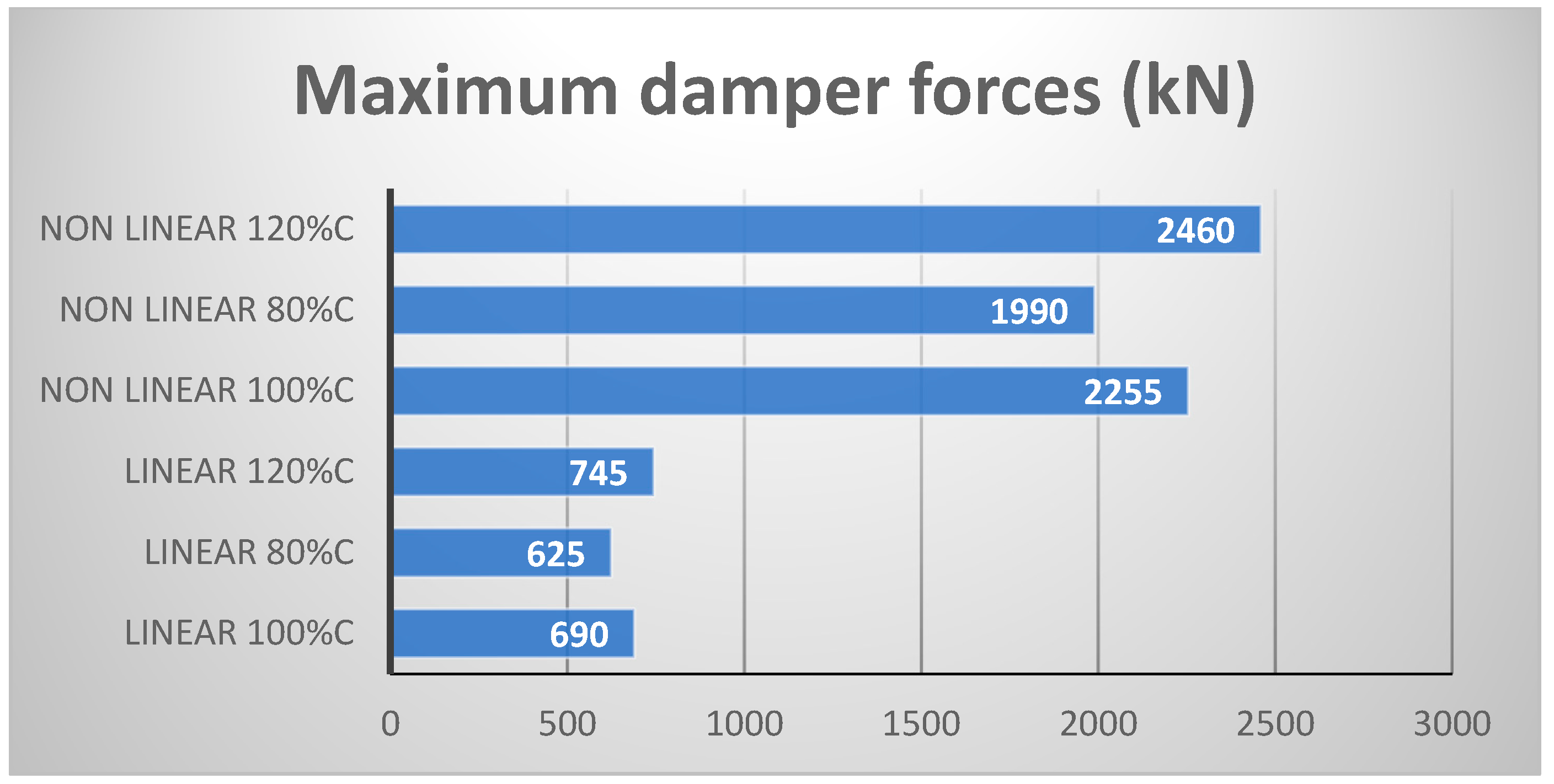
- Both types of dampers led to increased values of the structural base shear.
- The computation of both structural and inertial base shear was necessary regardless of whether the viscous dampers were linear or nonlinear.
6. Limitations, Future Research, and Physical Interpretation
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Christopoulos, C.; Filiatrault, A. Principles of Passive Supplemental Damping and Seismic Isolation; IUSS Press: Pavia, Italy, 2006. [Google Scholar]
- Cheng, F.Y.; Jiang, H.; Lou, K. Smart Structures: Innovative Systems for Seismic Response Control; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. ASCE 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Connor, J.; Laflamme, L. Structural Motion Engineering; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Mahjoubi, S.; Maleki, S. Seismic performance evaluation and design of steel structures equipped with dual-pipe dampers. J. Constr. Steel Res. 2016, 122, 25–39. [Google Scholar] [CrossRef]
- Hsu, H.L.; Halim, H. Improving seismic performance of framed structures with steel curved dampers. Eng. Struct. 2017, 130, 99–111. [Google Scholar] [CrossRef]
- Katsimpini, P.S.; Papagiannopoulos, G.A.; Askouni, P.K.; Karabalis, D.L. Seismic response of low-rise 3-D steel structures equipped with the seesaw system. Soil Dyn. Earthq. Eng. 2020, 128, 105877. [Google Scholar] [CrossRef]
- Javidan, M.M.; Kim, J. A rotational friction damper-brace for seismic design of resilient framed structures. J. Build. Eng. 2022, 51, 104248. [Google Scholar] [CrossRef]
- Mao, H.; Yan, X.; Wei, X.; Liu, X. Seismic analysis of a frame structure equipped with displacement-amplified torsional dampers. Structures 2022, 41, 190–202. [Google Scholar] [CrossRef]
- Ellsa Sarassantika, I.P.; Hsu, H.L. Upgrading framed structure seismic performance using steel lever-armed dampers in braces. Eng. Struct. 2023, 280, 115683. [Google Scholar] [CrossRef]
- Available online: https://www.taylordevices.com/projects/ (accessed on 29 December 2024).
- Constantinou, M.C.; Tadjbakhsh, I.G. Optimum design of a first story damping system. Comput. Struct. 1983, 17, 305–310. [Google Scholar] [CrossRef]
- Uetani, K.; Tsuji, M.; Takewaki, I. Application of an optimum design method to practical building frames with viscous dampers and hysteretic dampers. Eng. Struct. 2003, 25, 579–592. [Google Scholar] [CrossRef]
- Takewaki, I. Optimal damper placement for minimum transfer functions. Earthq. Eng. Struct. Dynam. 1997, 26, 1113–1124. [Google Scholar] [CrossRef]
- Akehashi, H.; Takewaki, I. Frequency-domain optimal viscous damper placement using lower-bound transfer function and multimodal adaptability. Struct. Control Health Monit. 2022, 29, e2951. [Google Scholar] [CrossRef]
- Lopez-Garcia, D. A simple method for the design of optimal damper configurations in MDOF structures. Earthq. Spectra 2001, 17, 387–398. [Google Scholar] [CrossRef]
- Lavan, O. Optimal design of viscous dampers and their supporting members for the seismic retrofitting of 3D irregular frame structures. J. Struct. Eng. 2015, 141, 04015026. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Kookalani, S.; Shen, D.; Zhu, L.L.; Lindsey, M. An overview of optimal damper placement methods in structures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 1–20. [Google Scholar] [CrossRef]
- Del Gobbo, G.M.; Williams, M.S.; Blakeborough, A. Comparing fluid viscous damper placement methods considering total-building seismic performance. Earthq. Eng. Struct. Dyn. 2018, 47, 2864–2886. [Google Scholar] [CrossRef]
- CEN/TC 340—EN 15129; Anti-Seismic Devices. European Committee for Standardization (CEN): Brussels, Belgium, 2018.
- Wang, S.; Mahin, S.A. Seismic retrofit of a high-rise steel moment-resisting frame using fluid viscous dampers. Struct. Des. Tall Spec. Build. 2017, 26, e1367. [Google Scholar] [CrossRef]
- ASCE/SEI 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2017.
- ASCE/SEI 7-22; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2022.
- Kitayama, S.; Constantinou, M.C. Seismic Performance of Buildings with Viscous Damping Systems Designed by the Procedures of ASCE/SEI 7-16. J. Struct. Eng. 2018, 144, 4018050. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D.; Pnevmatikos, N.G. Maximum damping forces for structures with viscous dampers under near-source earthquakes. Eng. Struct. 2014, 68, 1–13. [Google Scholar] [CrossRef]
- Logotheti, V.E.; Kafetzi, T.C.; Papagiannopoulos, G.A.; Karabalis, D.L. On the use of interstorey velocity for the seismic retrofit of steel frames with viscous dampers. Soil Dyn. Earthq. Eng. 2020, 129, 105312. [Google Scholar] [CrossRef]
- Banazadeh, M.; Ghanbari, A. Seismic performance assessment of steel moment-resisting frames equipped with linear and nonlinear fluid viscous dampers with the same damping ratio. J. Constr. Steel Res. 2017, 136, 215–228. [Google Scholar] [CrossRef]
- Hwang, J.S.; Huang, Y.N.; Yi, S.L.; Ho, S.Y. Design formulations for supplemental viscous dampers to building structures. J. Struct. Eng. ASCE 2008, 134, 22–31. [Google Scholar] [CrossRef]
- EN 1993-1; Eurocode 3. Design of Steel Structures—Part 1.1: General Rules and Rules for Buildings. Committee for Standardization (CEN): Brussels, Belgium, 2009.
- Eurocode 8. Design of Structures for Earthquake Resistance, Part 1–1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization (CEN): Brussels, Belgium, 2005. [Google Scholar]
- SAP 2000. Static and Dynamic Finite Element Analysis of Structures: Version 25.0; Computers and Structures: Berkeley, CA, USA, 2022. [Google Scholar]
- ASCE 41-13. Seismic Evaluation and Retrofit of Existing Buildings; American Society of Civil Engineers: Reston, VA, USA, 2017. [Google Scholar]
- Seleemah, A.; Constantinou, M.C. Investigation of Seismic Response of Buildings with Linear and Nonlinear Fluid Viscous Dampers; Report No. NCEER 97-0004; National Center for Earthquake Engineering Research, State University of New York: Buffalo, NY, USA, 1997. [Google Scholar]
- Rodriguez, M.E.; Restrepo, J.I.; Carr, A.J. Earthquake-induced floor horizontal accelerations in buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 693–718. [Google Scholar] [CrossRef]
- Goel, R.K. Comparison of base shears estimated from floor accelerations and column shears. Earthq. Spectra 2011, 27, 939. [Google Scholar] [CrossRef]
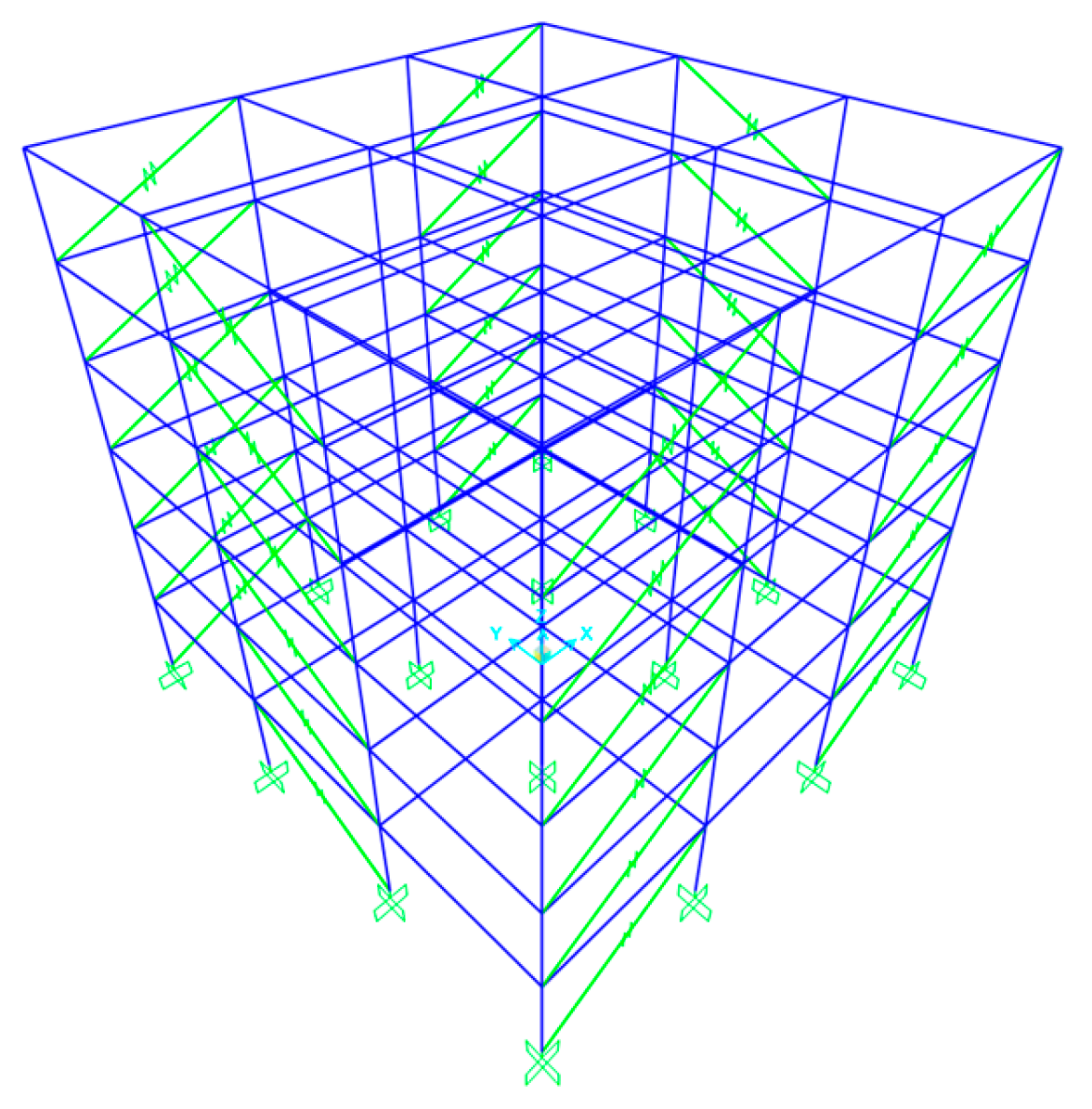
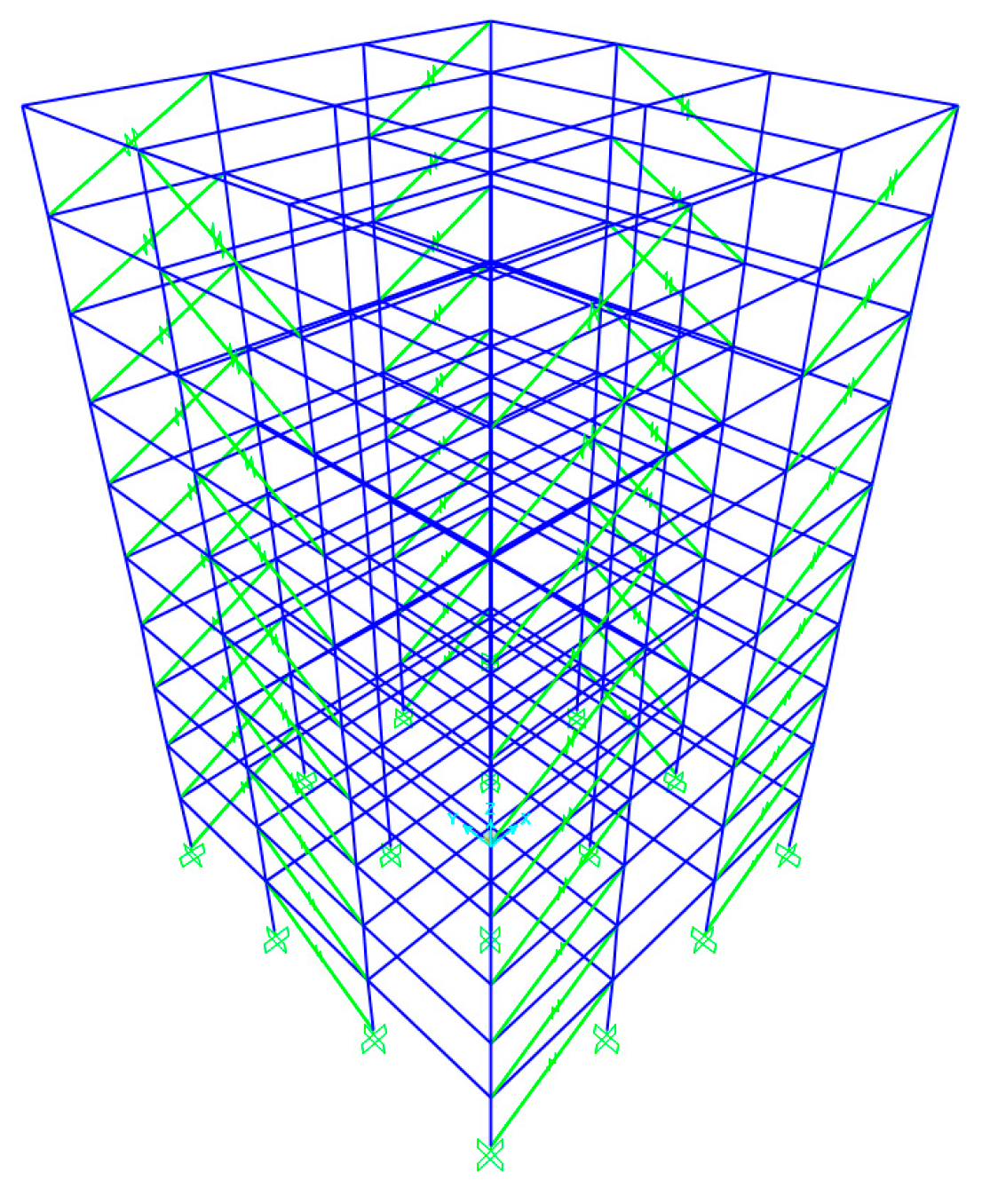

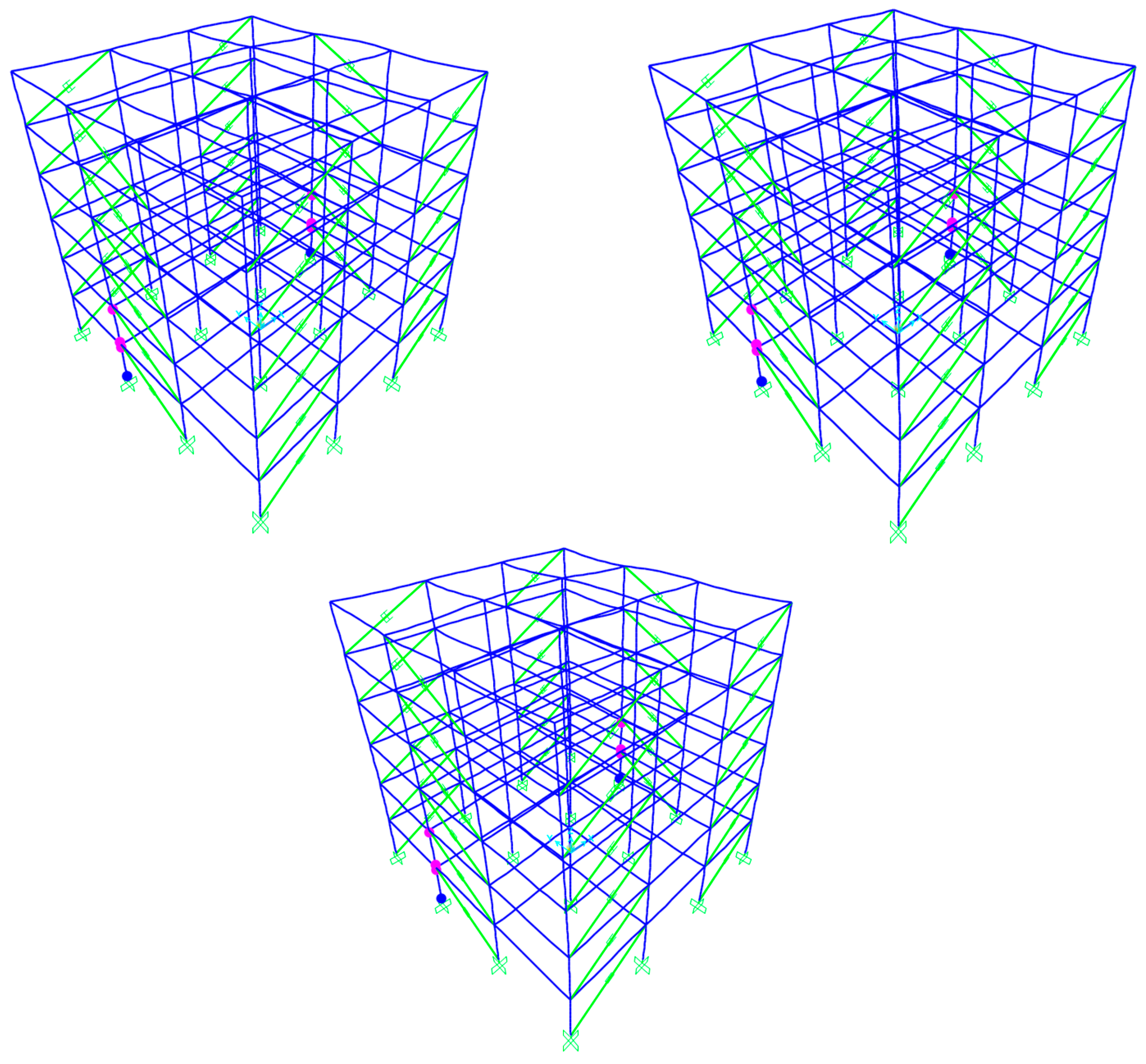






| Story | Column | Beam |
|---|---|---|
| 1st | HEB400 | IPE300 |
| 2nd | HEB400 | IPE300 |
| 3nd | HEB400 | IPE300 |
| 4nd | HEB400 | IPE300 |
| 5nd | HEB400 | IPE300 |
| 6nd | HEB400 | IPE300 |
| Story | Column | Beam |
|---|---|---|
| 1st | HEB450 | IPE360 |
| 2nd | HEB450 | IPE360 |
| 3rd | HEB450 | IPE360 |
| 4th | HEB450 | IPE360 |
| 5th | HEB450 | IPE360 |
| 6th | HEB450 | IPE360 |
| 7th | HEB400 | IPE300 |
| 8th | HEB400 | IPE300 |
| 9th | HEB400 | IPE300 |
| 10th | HEB400 | IPE300 |
| No. | Earthquake | Date | Station | Mw |
|---|---|---|---|---|
| 1 | Bam, Iran | 26 December 2003 | Bam | 6.5 |
| 2 | Cape Mendocino, U.S.A. | 25 April 1992 | Cape Mendocino | 6.9 |
| 3 | Darfield, New Zealand | 3 September 2010 | Greendale | 7.0 |
| 4 | Superstition Hills, U.S.A. | 24 November 1987 | Parachute Test Site | 6.5 |
| 5 | Kobe, Japan | 17 January 1995 | Takatori | 6.9 |
| 6 | Loma Prieta, U.S.A. | 17 October 1989 | Los Gatos | 7.0 |
| 7 | San Fernando, U.S.A. | 9 February 1971 | Pacoima Dam | 6.6 |
| 8 | Cape Mendocino, U.S.A. | 25 April 1992 | Petrolia | 6.9 |
| 9 | Vrancea, Romania | 30 August 1986 | INCERC | 7.3 |
| 10 | El Salvador, El Salvador | 13 January 2001 | Observatorio | 7.6 |
| 11 | El Salvador, El Salvador | 13 January 2001 | Observatorio | 7.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mavroeidakos, P.; Katsimpini, P.; Papagiannopoulos, G. Effect of Viscous Dampers with Variable Capacity on the Response of Steel Buildings. Vibration 2025, 8, 11. https://doi.org/10.3390/vibration8010011
Mavroeidakos P, Katsimpini P, Papagiannopoulos G. Effect of Viscous Dampers with Variable Capacity on the Response of Steel Buildings. Vibration. 2025; 8(1):11. https://doi.org/10.3390/vibration8010011
Chicago/Turabian StyleMavroeidakos, Panagiotis, Panagiota Katsimpini, and George Papagiannopoulos. 2025. "Effect of Viscous Dampers with Variable Capacity on the Response of Steel Buildings" Vibration 8, no. 1: 11. https://doi.org/10.3390/vibration8010011
APA StyleMavroeidakos, P., Katsimpini, P., & Papagiannopoulos, G. (2025). Effect of Viscous Dampers with Variable Capacity on the Response of Steel Buildings. Vibration, 8(1), 11. https://doi.org/10.3390/vibration8010011









