Rhythmic Analysis in Animal Communication, Speech, and Music: The Normalized Pairwise Variability Index Is a Summary Statistic of Rhythm Ratios
Abstract
:1. Introduction
1.1. Rhythm in Speech, Music, and Bioacoustics
1.2. Describing Rhythm Across Disciplines
1.3. Measuring Rhythm
1.4. The Normalized Pairwise Variability Index
1.5. Rhythm Ratios
2. Results and Discussion
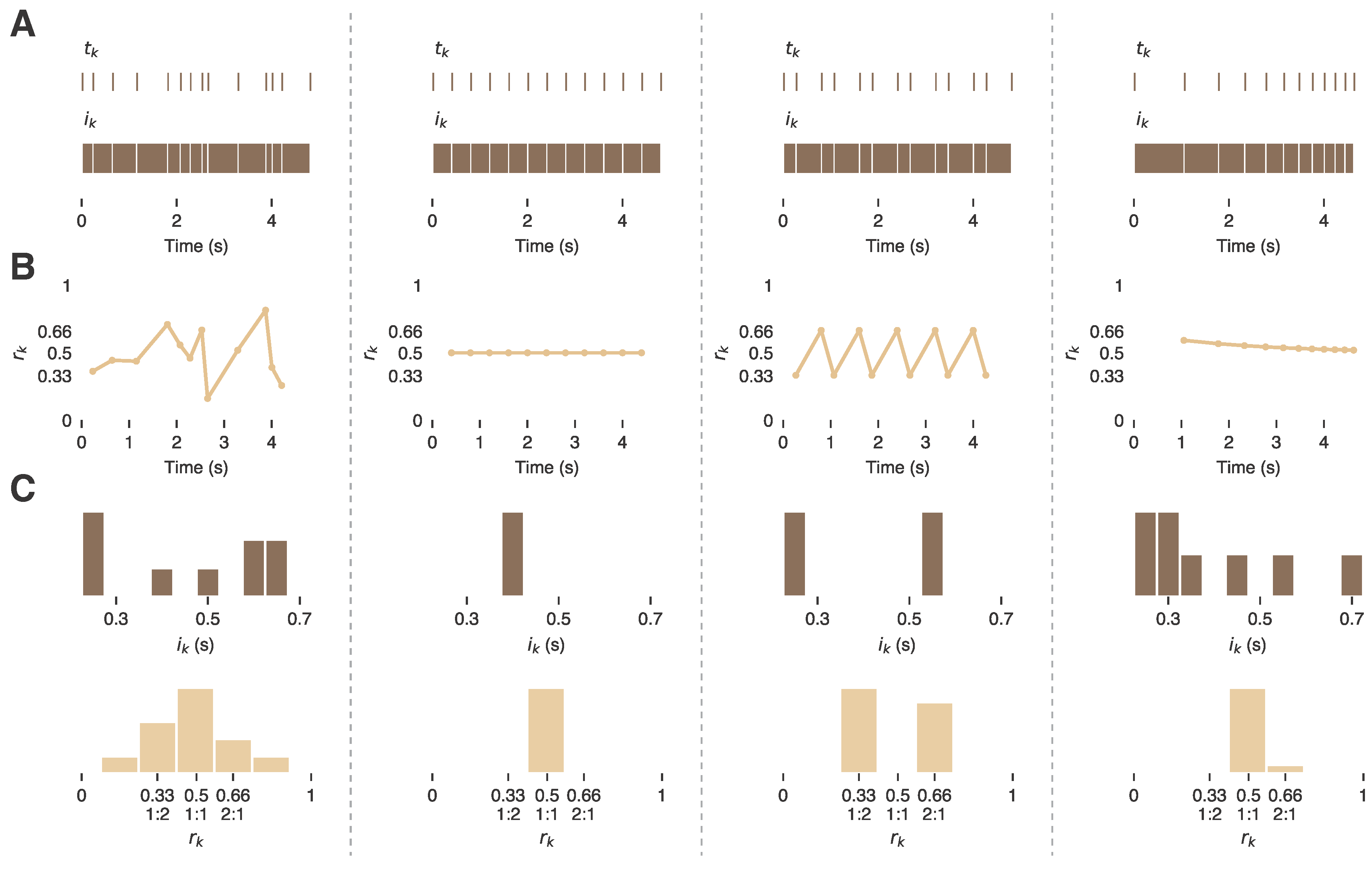
2.1. The Relationship Between the nPVI and Rhythm Ratios
2.2. Interpretation of the nPVI and Rhythm Ratios
2.3. Alternative and Complementary Summary Statistics of rk
2.4. nPVI and rk Are Inherently Local Measures
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Larsson, M. Self-Generated Sounds of Locomotion and Ventilation and the Evolution of Human Rhythmic Abilities. Anim. Cogn. 2014, 17, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Myers, B.R.; Lense, M.D.; Gordon, R.L. Pushing the Envelope: Developments in Neural Entrainment to Speech and the Biological Underpinnings of Prosody Perception. Brain Sci. 2019, 9, 70. [Google Scholar] [CrossRef] [PubMed]
- Bolton, T.L. Rhythm. Am. J. Psychol. 1894, 6, 145–238. [Google Scholar] [CrossRef]
- Nolan, F.; Jeon, H.-S. Speech Rhythm: A Metaphor? Phil. Trans. R. Soc. B 2014, 369, 20130396. [Google Scholar] [CrossRef]
- Goldbeter, A. Computational Approaches to Cellular Rhythms. Nature 2002, 420, 238–245. [Google Scholar] [CrossRef]
- Dotov, D.; Trainor, L.J. Cross-Frequency Coupling Explains the Preference for Simple Ratios in Rhythmic Behaviour and the Relative Stability across Non-Synchronous Patterns. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2021, 376, 20200333. [Google Scholar] [CrossRef]
- Bigand, F.; Bianco, R.; Abalde, S.F.; Novembre, G. The Geometry of Interpersonal Synchrony in Human Dance. Curr. Biol. 2024, 34, 3011–3019.e4. [Google Scholar] [CrossRef]
- Kadar, E.E.; Schmidt, R.C.; Turvey, M.T. Constants Underlying Frequency Changes in Biological Rhythmic Movements. Biol. Cybern. 1993, 68, 421–430. [Google Scholar] [CrossRef]
- Smith, R.; Rathcke, T.; Cummins, F.; Overy, K.; Scott, S. Communicative Rhythms in Brain and Behaviour. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369, 20130389. [Google Scholar] [CrossRef]
- Chay, T.R. Bifurcations in Heart Rhythms. Int. J. Bifurc. Chaos 1995, 5, 1439–1486. [Google Scholar] [CrossRef]
- Katz, P.S. Evolution of Central Pattern Generators and Rhythmic Behaviours. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2016, 371, 20150057. [Google Scholar] [CrossRef] [PubMed]
- Greenfield, M.D.; Aihara, I.; Amichay, G.; Anichini, M.; Nityananda, V. Rhythm Interaction in Animal Groups: Selective Attention in Communication Networks. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2021, 376, 20200338. [Google Scholar] [CrossRef] [PubMed]
- Kello, C.T.; Bella, S.D.; Médé, B.; Balasubramaniam, R. Hierarchical Temporal Structure in Music, Speech and Animal Vocalizations: Jazz Is like a Conversation, Humpbacks Sing like Hermit Thrushes. J. R. Soc. Interface 2017, 14, 20170231. [Google Scholar] [CrossRef] [PubMed]
- Hersh, T.A.; Ravignani, A.; Burchardt, L.S. Robust Rhythm Reporting Will Advance Ecological and Evolutionary Research. Methods Ecol. Evol. 2023, 14, 1398–1407. [Google Scholar] [CrossRef]
- Toussaint, G.T. The Geometry of Musical Rhythm: What Makes a “Good” Rhythm Good? 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2019; ISBN 978-1-351-24777-1. [Google Scholar]
- McAuley, J.D. Tempo and Rhythm. In Music Perception; Handbook of Auditory Research; Riess Jones, M., Fay, R.R., Popper, A.N., Eds.; Springer: New York, NY, USA, 2010; Volume 36, pp. 165–199. ISBN 978-1-4419-6113-6. [Google Scholar]
- Honing, H.; Bouwer, F.L. Rhythm. In Foundations in Music Psychology: Theory and Research; The MIT Press: Cambridge, MA, USA, 2019; pp. 33–69. ISBN 978-0-262-03927-7. [Google Scholar]
- Leow, L.-A.; Grahn, J. Neural Mechanisms of Rhythm Perception: Present Findings and Future Directions. Adv. Exp. Med. Biol. 2014, 829, 325–338. [Google Scholar] [CrossRef]
- Rohrmeier, M.; Zuidema, W.; Wiggins, G.A.; Scharff, C. Principles of Structure Building in Music, Language and Animal Song. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140097. [Google Scholar] [CrossRef]
- Fitch, W.T. The Biology and Evolution of Rhythm: Unravelling a Paradox. In Language and Music as Cognitive Systems; Oxford University Press: New York, NY, USA, 2012; pp. 73–95. ISBN 978-0-19-955342-6. [Google Scholar]
- Fitch, W.T. The Biology and Evolution of Music: A Comparative Perspective. Cognition 2006, 100, 173–215. [Google Scholar] [CrossRef]
- Honing, H.; Ten Cate, C.; Peretz, I.; Trehub, S.E. Without It No Music: Cognition, Biology and Evolution of Musicality. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140088. [Google Scholar] [CrossRef]
- Ravignani, A.; Norton, P. Measuring Rhythmic Complexity: A Primer to Quantify and Compare Temporal Structure in Speech, Movement, and Animal Vocalizations. J. Lang. Evol. 2017, 2, 4–19. [Google Scholar] [CrossRef]
- Burchardt, L.; Briefer, E.; Knörnschild, M. Novel Ideas to Further Expand the Applicability of Rhythm Analysis. Ecol. Evol. 2021, 11, 1–9. [Google Scholar] [CrossRef]
- Burchardt, L.S.; Knörnschild, M. Comparison of Methods for Rhythm Analysis of Complex Animals’ Acoustic Signals. PLoS Comput. Biol. 2020, 16, e1007755. [Google Scholar] [CrossRef] [PubMed]
- Burchardt, L.S.; Picciulin, M.; Parmentier, E.; Bolgan, M. A Primer on Rhythm Quantification for Fish Sounds: A Mediterranean Case Study. R. Soc. Open Sci. 2021, 8, 210494. [Google Scholar] [CrossRef] [PubMed]
- Schneider, J.N.; Mercado III, E. Characterizing the Rhythm and Tempo of Sound Production by Singing Whales. Bioacoustics 2019, 28, 239–256. [Google Scholar] [CrossRef]
- Le Bot, O.; Bonnel, J.; Mars, J.I.; Gervaise, C. Odontocete Click Train Deinterleaving Using a Single Hydrophone and Rhythm Analysis. In Proceedings of the ICA 2013 Proceedings—Volume 19 of POMA (Proceedings of Meetings on Acoustics), Montreal, QC, Canada, 2–7 June 2013; Volume 19. [Google Scholar]
- Malige, F.; Djokic, D.; Patris, J.; Sousa-Lima, R.; Glotin, H. Use of Recurrence Plots for Identification and Extraction of Patterns in Humpback Whale Song Recordings. Bioacoustics 2020, 680–695. [Google Scholar] [CrossRef]
- Heinsohn, R.; Zdenek, C.N.; Cunningham, R.B.; Endler, J.A.; Langmore, N.E. Tool-Assisted Rhythmic Drumming in Palm Cockatoos Shares Key Elements of Human Instrumental Music. Sci. Adv. 2017, 3, e1602399. [Google Scholar] [CrossRef]
- Kershenbaum, A.; Bowles, A.E.; Freeberg, T.M.; Jin, D.Z.; Lameira, A.R.; Bohn, K. Animal Vocal Sequences: Not the Markov Chains We Thought They Were. Proc. Biol. Sci. 2014, 281, 20141370. [Google Scholar] [CrossRef]
- Kershenbaum, A.; Blumstein, D.T.; Roch, M.A.; Akçay, Ç.; Backus, G.; Bee, M.A.; Bohn, K.; Cao, Y.; Carter, G.; Cäsar, C.; et al. Acoustic Sequences in Non-Human Animals: A Tutorial Review and Prospectus. Biol. Rev. Camb. Philos. Soc. 2016, 91, 13–52. [Google Scholar] [CrossRef]
- Arnaud, V.; Pellegrino, F.; Keenan, S.; St-Gelais, X.; Mathevon, N.; Levréro, F.; Coupé, C. Improving the Workflow to Crack Small, Unbalanced, Noisy, but Genuine (SUNG) Datasets in Bioacoustics: The Case of Bonobo Calls. PLoS Comput. Biol. 2023, 19, e1010325. [Google Scholar] [CrossRef]
- Kvsn, R.R.; Montgomery, J.; Garg, S.; Charleston, M. Bioacoustics Data Analysis—A Taxonomy, Survey and Open Challenges. IEEE Access 2020, 8, 57684–57708. [Google Scholar] [CrossRef]
- Oswald, J.N.; Van Cise, A.M.; Dassow, A.; Elliott, T.; Johnson, M.T.; Ravignani, A.; Podos, J. A Collection of Best Practices for the Collection and Analysis of Bioacoustic Data. Appl. Sci. 2022, 12, 12046. [Google Scholar] [CrossRef]
- Sousa-Lima, R.S.; Norris, T.F.; Oswald, J.N.; Fernandes, D.P. A review and inventory of fixed autonomous recorders for passive acoustic monitoring of marine mammals. Aquat. Mamm. 2013, 39, 23–53. [Google Scholar] [CrossRef]
- Dalla Bella, S.; Farrugia, N.; Benoit, C.E.; Begel, V.; Verga, L.; Harding, E.; Kotz, S.A. BAASTA: Battery for the assessment of auditory sensorimotor and timing abilities. Behav. Res. Methods 2017, 49, 1128–1145. [Google Scholar] [CrossRef] [PubMed]
- Fiveash, A.; Bella, S.D.; Bigand, E.; Gordon, R.L.; Tillmann, B. You got rhythm, or more: The multidimensionality of rhythmic abilities. Atten. Percept. Psychophys. 2022, 84, 1370–1392. [Google Scholar] [CrossRef]
- Tavano, A.; Maess, B.; Poeppel, D.; Schröger, E. Neural entrainment via perceptual inferences. Eur. J. Neurosci. 2022, 55, 3277–3287. [Google Scholar] [CrossRef]
- Grabe, E.; Low, E.L. Durational Variability in Speech and the Rhythm Class Hypothesis. Pap. Lab. Phonol. 2002, 7, 515–546. [Google Scholar]
- Roeske, T.C.; Tchernichovski, O.; Poeppel, D.; Jacoby, N. Categorical Rhythms Are Shared between Songbirds and Humans. Curr. Biol. 2020, 30, 3544–3555.e6. [Google Scholar] [CrossRef]
- Pike, K.L. The Intonation of American English; Greenwood Press: Westport, CT, USA, 1979; ISBN 978-0-313-20910-9. [Google Scholar]
- Abercrombie, D. Studies in Phonetics and Linguistics; Oxford University Press: Oxford, UK, 1965; ISBN 978-0-19-437023-3. [Google Scholar]
- Ozaki, Y.; Tierney, A.; Pfordresher, P.Q.; McBride, J.M.; Benetos, E.; Proutskova, P.; Chiba, G.; Liu, F.; Jacoby, N.; Purdy, S.C.; et al. Globally, Songs and Instrumental Melodies Are Slower and Higher and Use More Stable Pitches than Speech: A Registered Report. Sci. Adv. 2024, 10, eadm9797. [Google Scholar] [CrossRef]
- Patel, A.D.; Daniele, J.R. An Empirical Comparison of Rhythm in Language and Music. Cognition 2003, 87, B35–B45. [Google Scholar] [CrossRef]
- London, J.; Jones, K. Rhythmic Refinements to the nPVI Measure: A Reanalysis of Patel & Daniele (2003a). Music Percept. 2011, 29, 115–121. [Google Scholar] [CrossRef]
- Daniele, J.R. A Tool for the Quantitative Anthropology of Music: Use of the nPVI Equation to Analyze Rhythmic Variability within Long-Term Historical Patterns in Music. Empir. Musicol. Rev. 2017, 11, 228–233. [Google Scholar] [CrossRef]
- Daniele, J.R.; Patel, A.D. An Empirical Study of Historical Patterns in Musical Rhythm. Music Percept. 2013, 31, 10–18. [Google Scholar] [CrossRef]
- Vukovics, K.; Shanahan, D. Rhythmic Variability, Language, and Style: A Replication and Extension of nPVI Findings with the RISM Dataset. J. New Music Res. 2020, 49, 285–297. [Google Scholar] [CrossRef]
- Temperley, D. Rhythmic Variability in European Vocal Music. Music Percept. 2017, 35, 193–199. [Google Scholar] [CrossRef]
- VanHandel, L. The War of the Romantics: An Alternate Hypothesis Using nPVI for the Quantitative Anthropology of Music. Empir. Musicol. Rev. 2017, 11, 234. [Google Scholar] [CrossRef]
- VanHandel, L.; Song, T. The Role of Meter in Compositional Style in 19th Century French and German Art Song. J. New Music Res. 2010, 39, 1–11. [Google Scholar] [CrossRef]
- Kocsis, K.; Duengen, D.; Jadoul, Y.; Ravignani, A. Harbour Seals Use Rhythmic Percussive Signalling in Interaction and Display. Anim. Behav. 2024, 207, 223–234. [Google Scholar] [CrossRef]
- Condit-Schultz, N. Deconstructing the nPVI. Music Percept. 2019, 36, 300–313. [Google Scholar] [CrossRef]
- Rossi, M.; Smit, E.A.; van der Werff, J.; Ravignani, A.; Rathcke, T. Testing Rhythmic Abilities in Developmental Dyslexia: Is Internal Rhythm Generation Intact? Music Percept. 2024, 42, 135–148. [Google Scholar] [CrossRef]
- Jacoby, N.; McDermott, J.H. Integer Ratio Priors on Musical Rhythm Revealed Cross-Culturally by Iterated Reproduction. Curr. Biol. 2017, 27, 359–370. [Google Scholar] [CrossRef]
- Savage, P.E.; Brown, S.; Sakai, E.; Currie, T.E. Statistical Universals Reveal the Structures and Functions of Human Music. Proc. Natl. Acad. Sci. USA 2015, 112, 8987–8992. [Google Scholar] [CrossRef]
- Daikoku, T. Temporal dynamics of uncertainty and prediction error in musical improvisation across different periods. Sci. Rep. 2024, 14, 22297. [Google Scholar] [CrossRef] [PubMed]
- Nave, K.; Carrillo, C.; Jacoby, N.; Trainor, L.; Hannon, E. The development of rhythmic categories as revealed through an iterative production task. Cognition 2024, 242, 105634. [Google Scholar] [PubMed]
- De Gregorio, C.; Valente, D.; Raimondi, T.; Torti, V.; Miaretsoa, L.; Friard, O.; Giacoma, C.; Ravignani, A.; Gamba, M. Categorical Rhythms in a Singing Primate. Curr. Biol. 2021, 31, R1379–R1380. [Google Scholar] [CrossRef] [PubMed]
- De Gregorio, C.D.; Raimondi, T.; Bevilacqua, V.; Pertosa, C.; Valente, D.; Carugati, F.; Bandoli, F.; Favaro, L.; Lefaux, B.; Ravignani, A.; et al. Isochronous Singing in 3 Crested Gibbon Species (Nomascus spp.). Curr. Zool. 2024, 70, 291–297. [Google Scholar]
- Ma, H.; Wang, Z.; Han, P.; Fan, P.; Chapman, C.A.; Garber, P.A.; Fan, P. Small Apes Adjust Rhythms to Facilitate Song Coordination. Curr. Biol. 2024, 34, 935–945.e3. [Google Scholar] [CrossRef]
- Raimondi, T.; Di Panfilo, G.; Pasquali, M.; Zarantonello, M.; Favaro, L.; Savini, T.; Gamba, M.; Ravignani, A. Isochrony and Rhythmic Interaction in Ape Duetting. Proc. R. Soc. B Biol. Sci. 2023, 290, 20222244. [Google Scholar] [CrossRef]
- Lameira, A.R.; Hardus, M.E.; Ravignani, A.; Raimondi, T.; Gamba, M. Recursive Self-Embedded Vocal Motifs in Wild Orangutans. eLife 2024, 12, RP88348. [Google Scholar] [CrossRef]
- van der Vleuten, B.J.R.; Hovenkamp, V.A.; Varkevisser, J.M.; Spierings, M.J. Context-dependent rhythmicity in chimpanzee displays. Proc. B 2024, 291, 20242200. [Google Scholar]
- De Gregorio, C.; Maiolini, M.; Raimondi, T.; Carugati, F.; Miaretsoa, L.; Valente, D.; Torti, V.; Giacoma, C.; Ravignani, A.; Gamba, M. Isochrony as Ancestral Condition to Call and Song in a Primate. Ann. N. Y. Acad. Sci. 2024, 1537, 41–50. [Google Scholar] [CrossRef]
- Demartsev, V.; Haddas-Sasson, M.; Ilany, A.; Koren, L.; Geffen, E. Male Rock Hyraxes That Maintain an Isochronous Song Rhythm Achieve Higher Reproductive Success. J. Anim. Ecol. 2023, 92, 1520–1531. [Google Scholar] [CrossRef]
- Xing, J.; Sainburg, T.; Taylor, H.; Gentner, T.Q. Syntactic Modulation of Rhythm in Australian Pied Butcherbird Song. R. Soc. Open Sci. 2022, 9, 220704. [Google Scholar] [CrossRef] [PubMed]
- Eleuteri, V.; van der Werff, J.; Wilhelm, W.; Soldati, A.; Crockford, C.; Desai, N.; Fedurek, P.; Fitzgerald, M.; Graham, K.E.; Koops, K.; et al. Chimpanzee Drumming Shows Rhythmicity and Subspecies Variation; University of St Andrews: Scotland, UK, 2024; submitted. [Google Scholar]
- Laffi, L.; Raimondi, T.; Ferrante, C.; Pagliara, E.; Bertuglia, A.; Briefer, E.F.; Gamba, M.; Ravignani, A. The Rhythm of Horse Gaits. Ann. N. Y. Acad. Sci. 2024, 1543, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Laffi, L.; Bigand, F.; Peham, C.; Novembre, G.; Gamba, M.; Ravignani, A. Rhythmic Categories in Horse Gait Kinematics. J. Anat. 2025, 246, 456–465. [Google Scholar] [CrossRef] [PubMed]
- Jadoul, Y.; Tufarelli, T.; Coissac, C.; Gamba, M.; Ravignani, A. Hidden Assumptions of Integer Ratio Analyses in Bioacoustics and Music. arXiv 2025, arXiv:2502.04464. [Google Scholar] [CrossRef]
- Feutrill, A.; Roughan, M. A Review of Shannon and Differential Entropy Rate Estimation. Entropy 2021, 23, 1046. [Google Scholar] [CrossRef]
- Picciulin, M.; Bolgan, M.; Burchardt, L.S. Rhythmic Properties of Sciaena Umbra Calls across Space and Time in the Mediterranean Sea. PLoS ONE 2024, 19, e0295589. [Google Scholar] [CrossRef]
- Osiecka, A.N.; Fearey, J.; Ravignani, A.; Burchardt, L.S. Isochrony in Barks of Cape Fur Seal (Arctocephalus pusillus pusillus ) Pups and Adults. Ecol. Evol. 2024, 14, e11085. [Google Scholar] [CrossRef]

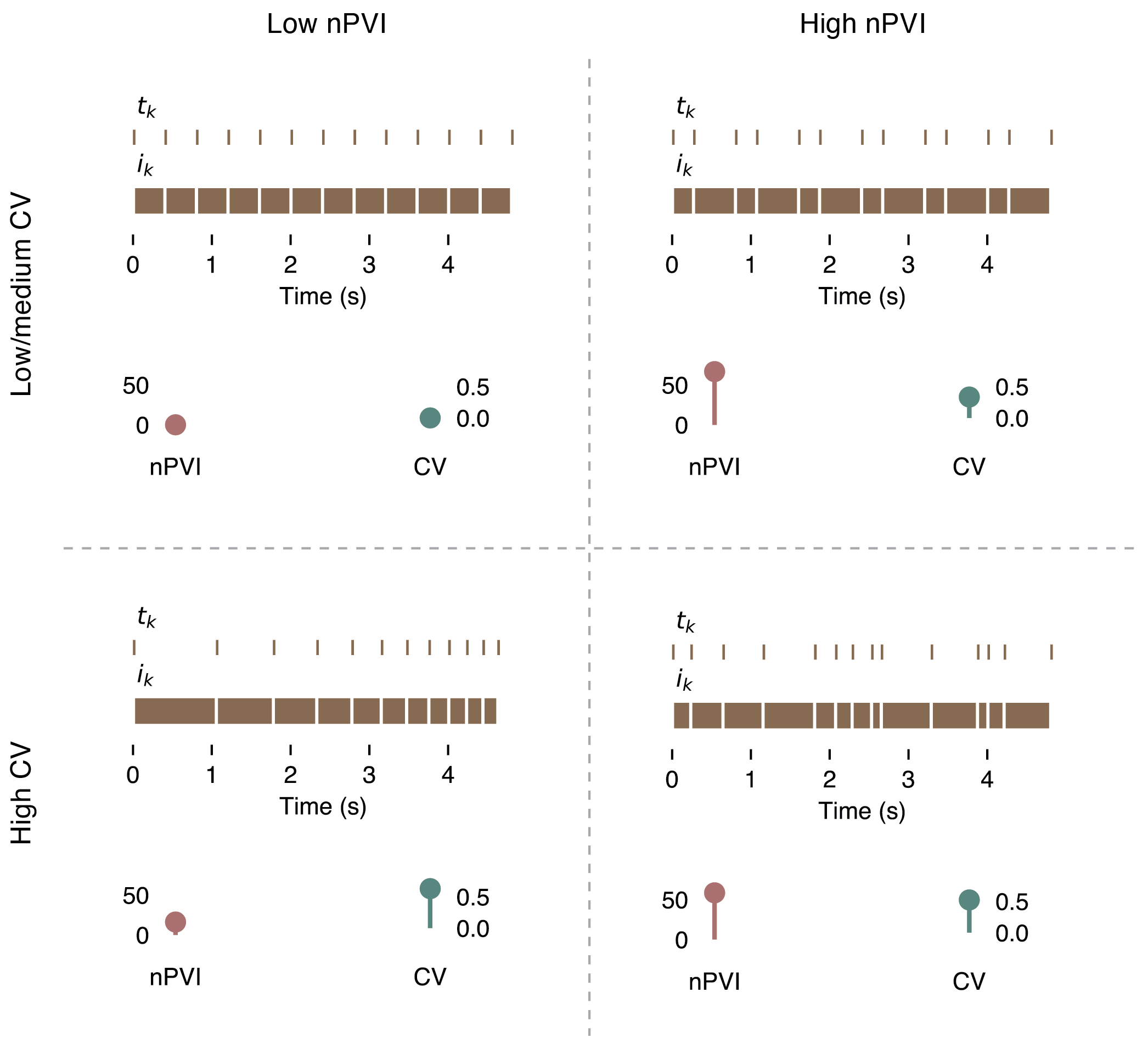
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jadoul, Y.; D’Orazio, F.; Eleuteri, V.; van der Werff, J.; Tufarelli, T.; Gamba, M.; Raimondi, T.; Ravignani, A. Rhythmic Analysis in Animal Communication, Speech, and Music: The Normalized Pairwise Variability Index Is a Summary Statistic of Rhythm Ratios. Vibration 2025, 8, 12. https://doi.org/10.3390/vibration8020012
Jadoul Y, D’Orazio F, Eleuteri V, van der Werff J, Tufarelli T, Gamba M, Raimondi T, Ravignani A. Rhythmic Analysis in Animal Communication, Speech, and Music: The Normalized Pairwise Variability Index Is a Summary Statistic of Rhythm Ratios. Vibration. 2025; 8(2):12. https://doi.org/10.3390/vibration8020012
Chicago/Turabian StyleJadoul, Yannick, Francesca D’Orazio, Vesta Eleuteri, Jelle van der Werff, Tommaso Tufarelli, Marco Gamba, Teresa Raimondi, and Andrea Ravignani. 2025. "Rhythmic Analysis in Animal Communication, Speech, and Music: The Normalized Pairwise Variability Index Is a Summary Statistic of Rhythm Ratios" Vibration 8, no. 2: 12. https://doi.org/10.3390/vibration8020012
APA StyleJadoul, Y., D’Orazio, F., Eleuteri, V., van der Werff, J., Tufarelli, T., Gamba, M., Raimondi, T., & Ravignani, A. (2025). Rhythmic Analysis in Animal Communication, Speech, and Music: The Normalized Pairwise Variability Index Is a Summary Statistic of Rhythm Ratios. Vibration, 8(2), 12. https://doi.org/10.3390/vibration8020012







