Instability of a Moving Bogie: Analysis of Vibrations and Possibility of Instability in Subcritical Velocity Range
Abstract
1. Introduction
2. Description of the Model and Governing Equations
3. Results
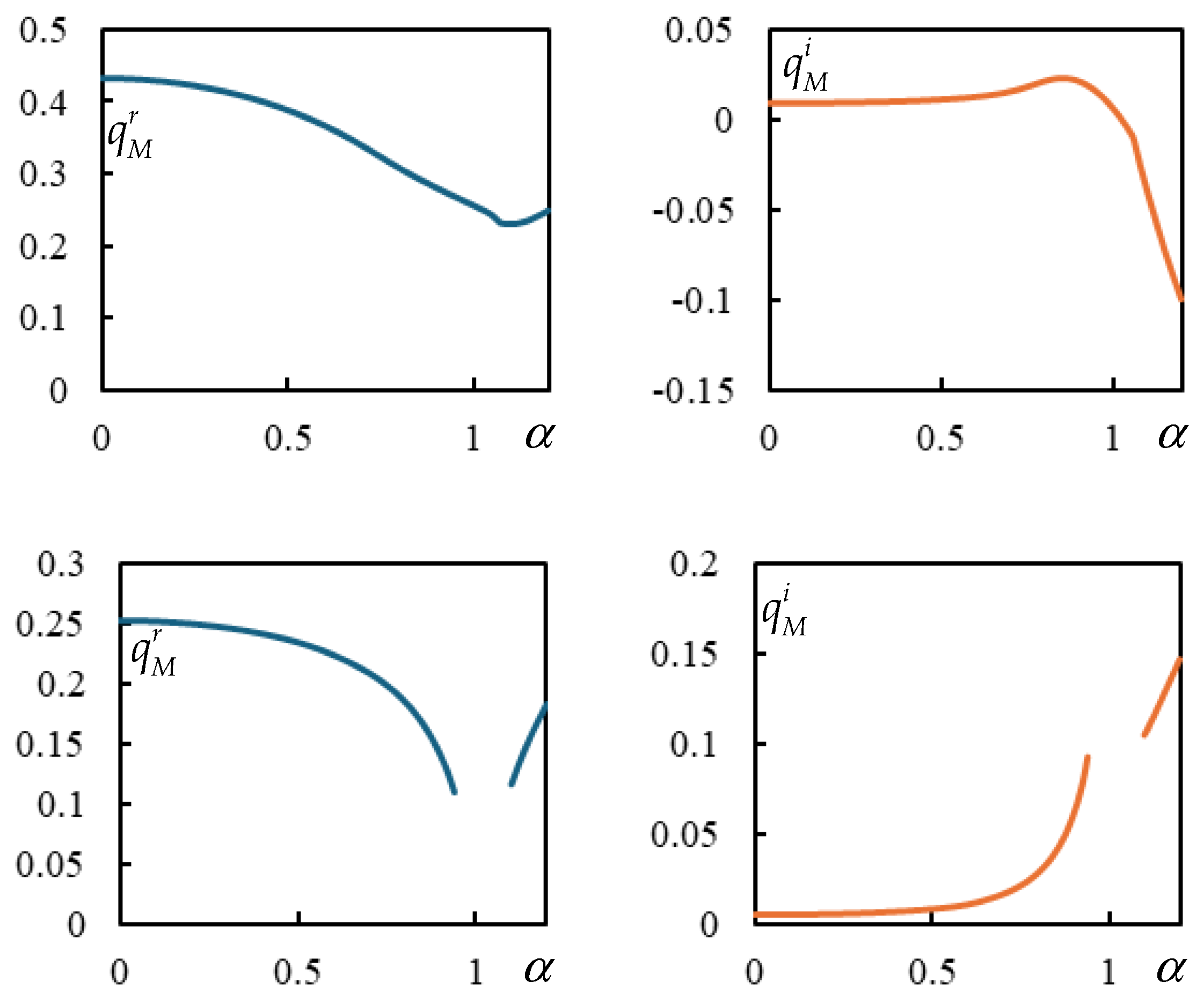
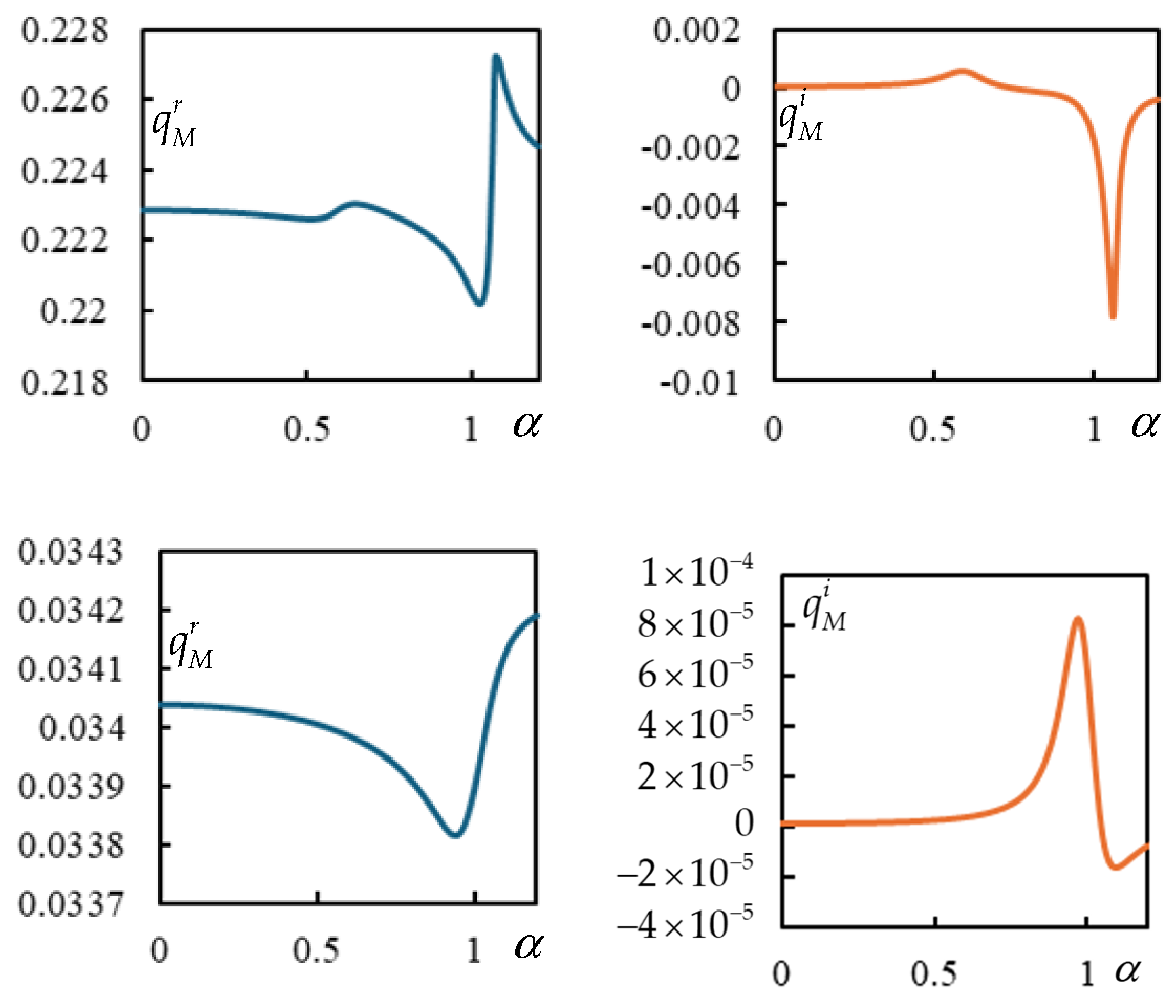
3.1. Induced Frequencies
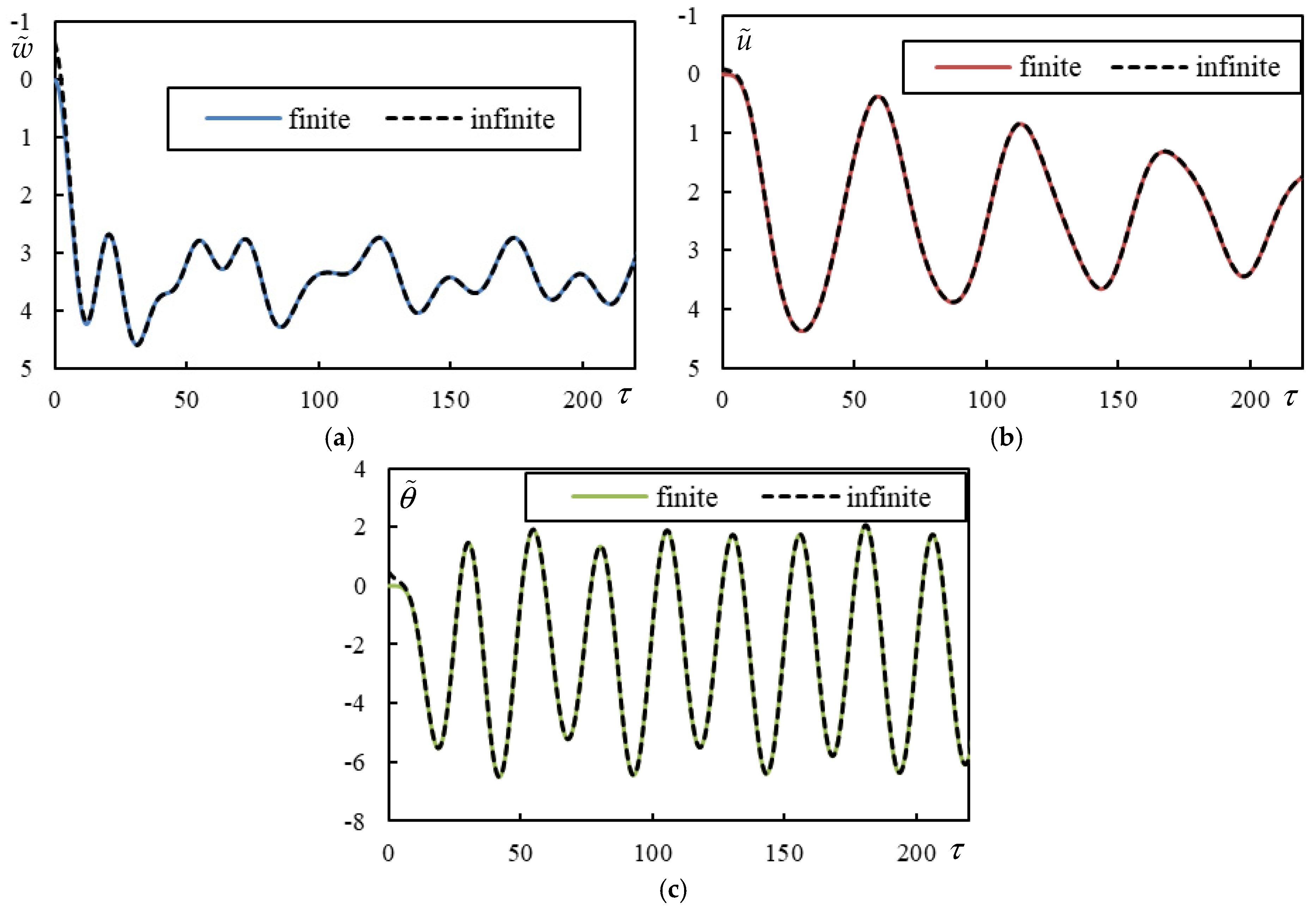
3.2. Validation on Finite Beams
3.3. Timoshenko-Rayleigh Beam
3.4. Tested Cases
3.5. Comparison with Moving Masses
3.6. Effect of Suspension Damping
3.7. Impact of Beam Theory on the Results
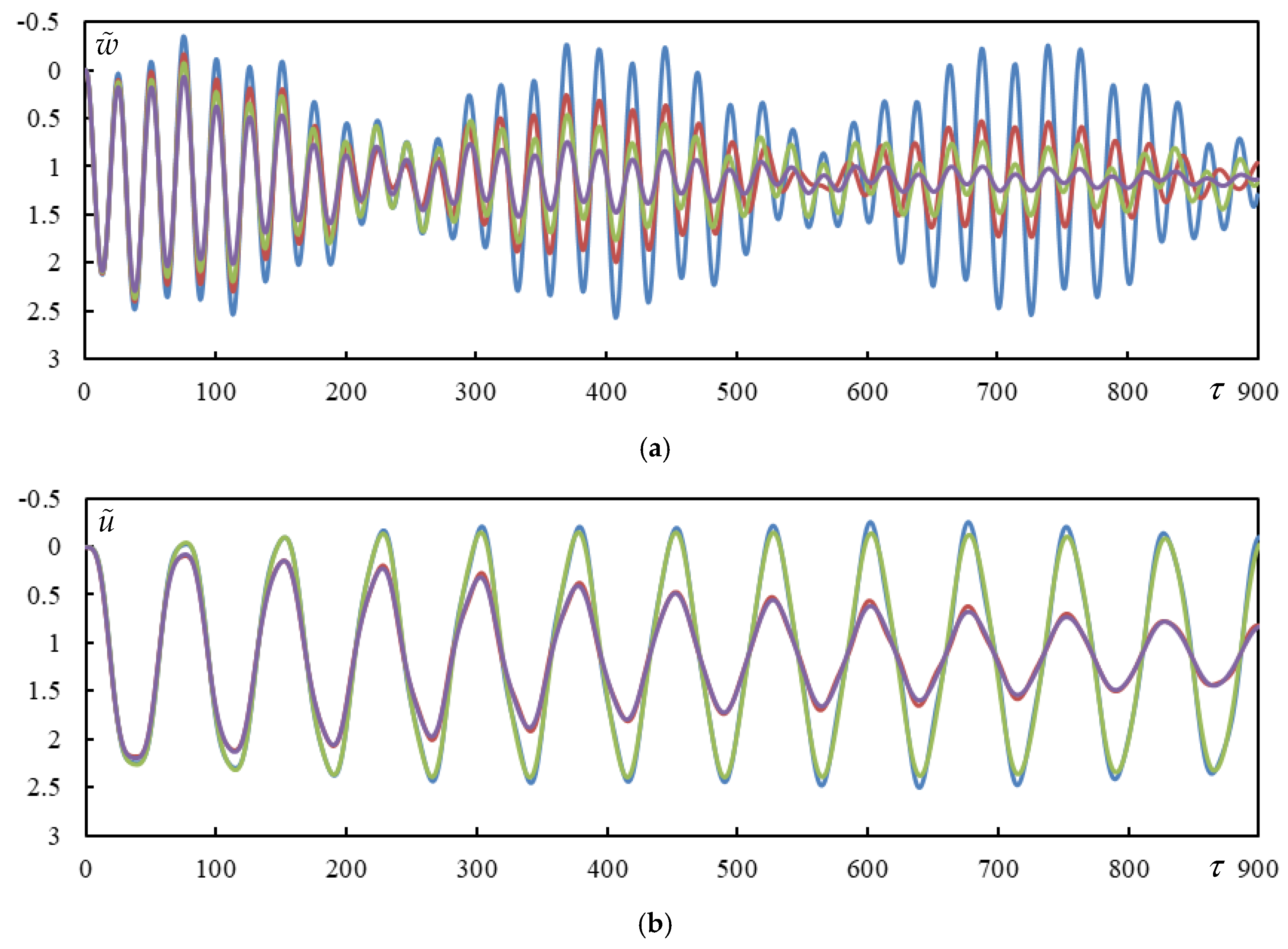
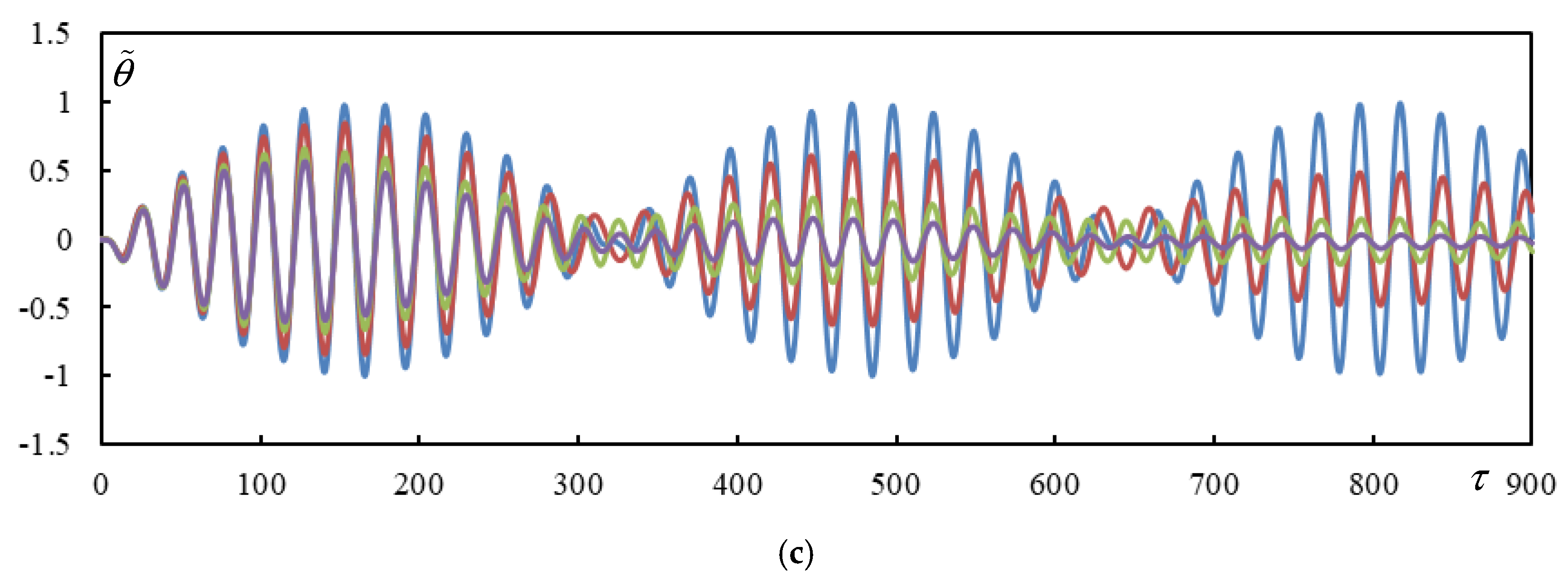
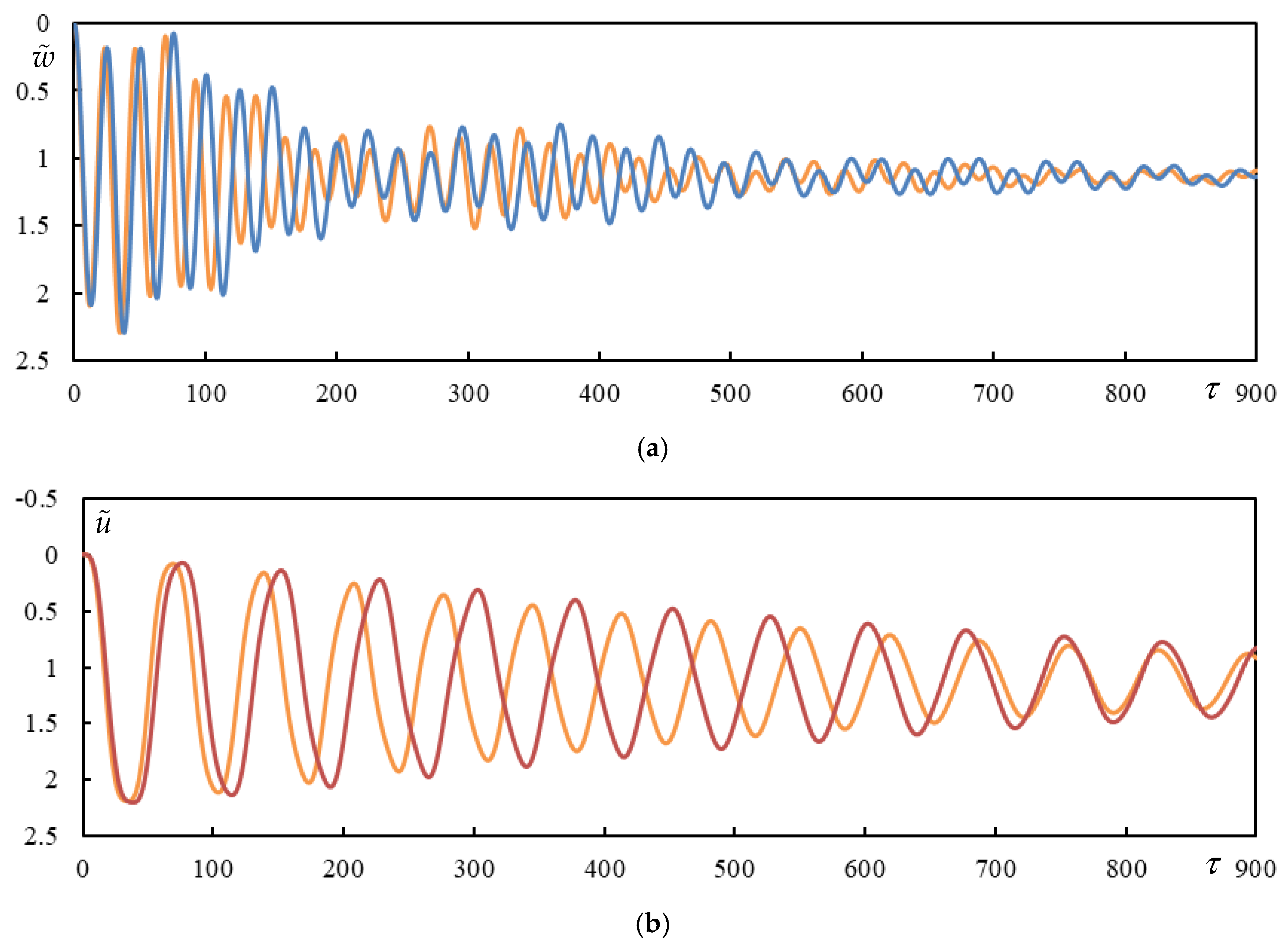
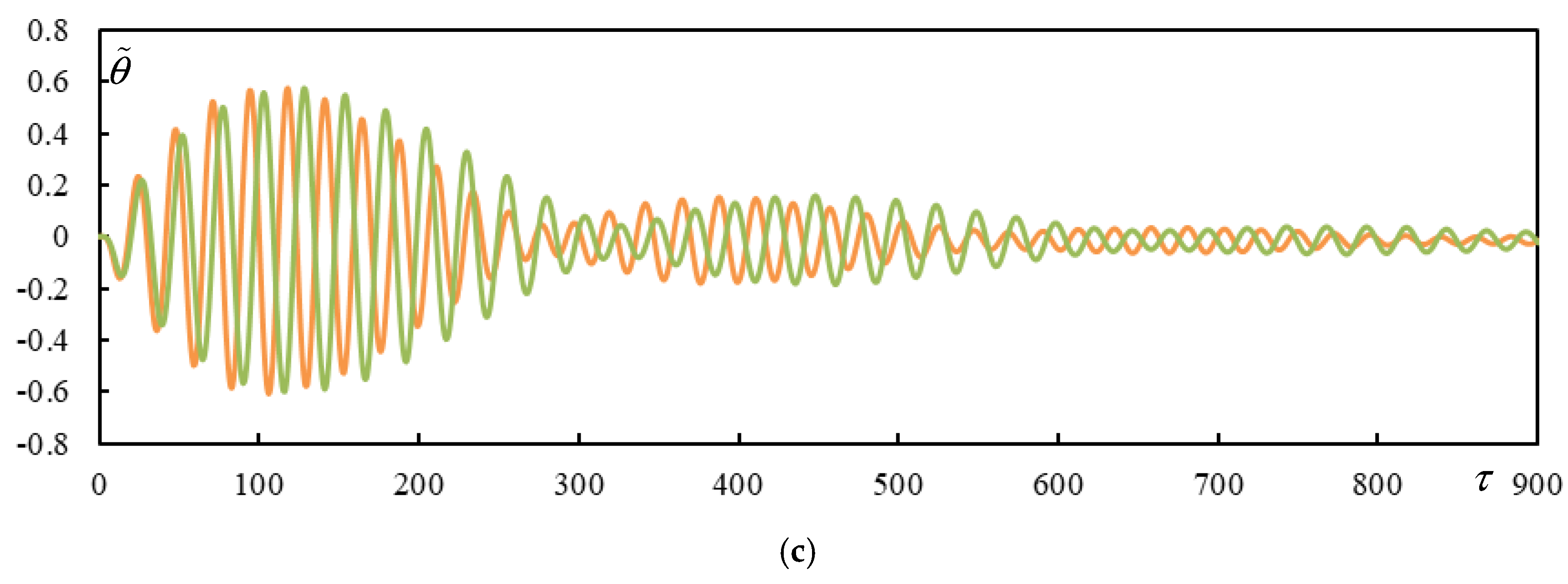
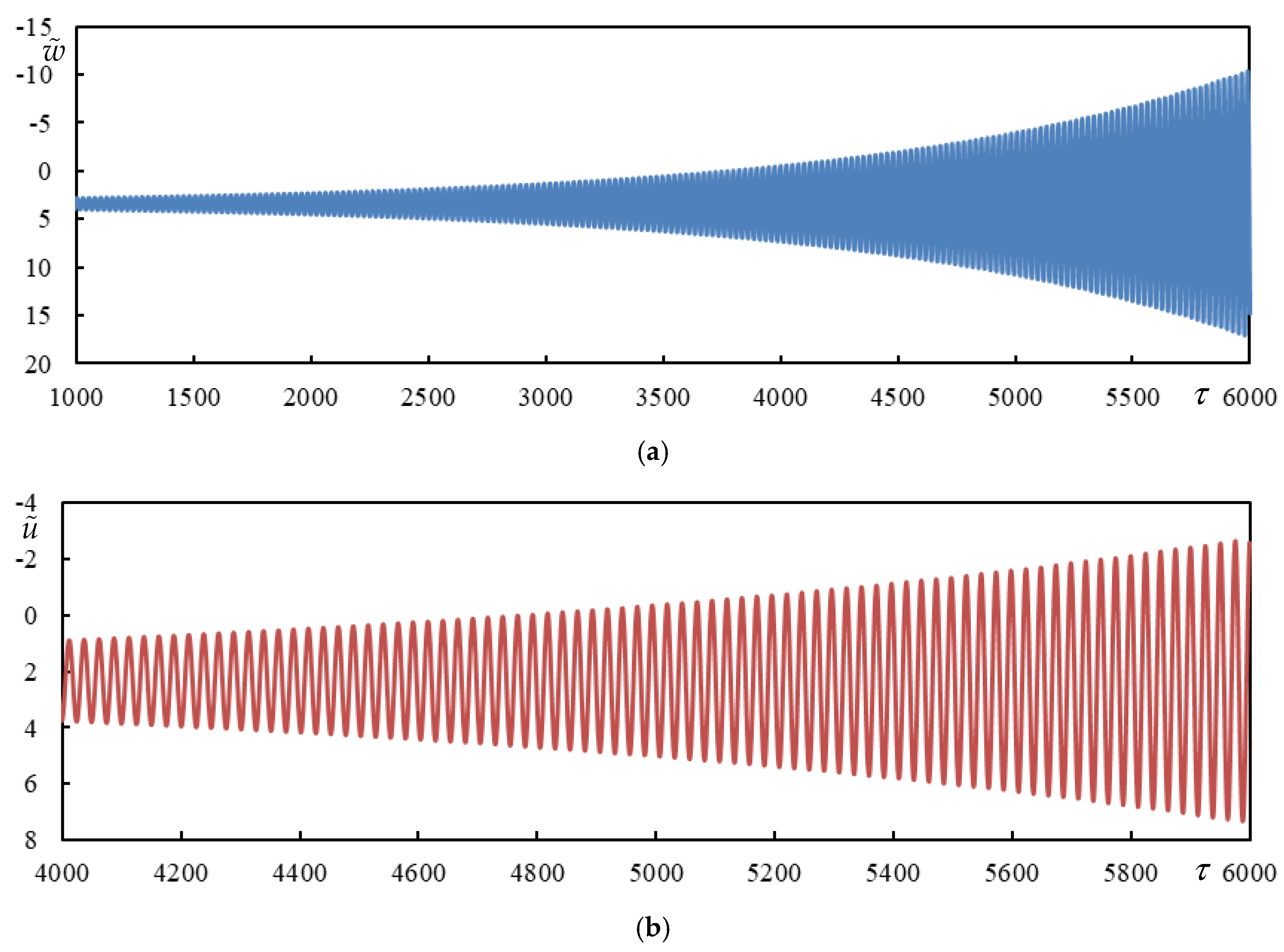
3.8. Time Series of Other Cases from Table 1
3.9. Comparison with Other Published Works
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Rodrigues, A.S.F.; Dimitrovová, Z. Applicability of a three-layer model for the dynamic analysis of ballasted railway tracks. Vibration 2021, 4, 151–174. [Google Scholar] [CrossRef]
- Dimitrovová, Z. On the critical velocity of moving force and instability of moving mass in layered railway track models by semianalytical approaches. Vibration 2023, 6, 113–146. [Google Scholar] [CrossRef]
- Grassie, S.L.; Gregory, R.W.; Harrison, D.; Johnson, K.L. The dynamic response of railway track to high frequency vertical excitation. J. Mech. Eng. Sci. 1982, 24, 77–90. [Google Scholar] [CrossRef]
- Knothe, K.L.; Grassie, S.L. Modelling of railway track and vehicle-track interaction at high frequencies. Veh. Syst. Dyn. 1993, 22, 209–262. [Google Scholar] [CrossRef]
- Dahlberg, T. Vertical dynamic train/track interaction—Verifying a theoretical model by full-scale experiments. Veh. Syst. Dyn. 1995, 24, 45–57. [Google Scholar] [CrossRef]
- Zhai, W.; Cai, Z. Dynamic interaction between a lumped mass vehicle and a discretely supported continuous rail track. Comput. Struct. 1997, 63, 987–997. [Google Scholar] [CrossRef]
- Oscarsson, J.; Dahlberg, T. Dynamic train/track/ballast interaction—Computer models and full-scale experiments. Veh. Syst. Dyn. 1998, 29, 73–84. [Google Scholar] [CrossRef]
- Oscarsson, J. Dynamic train-track interaction: Variability attributable to scatter in the track properties. Veh. Syst. Dyn. 2002, 37, 59–79. [Google Scholar] [CrossRef]
- Oscarsson, J. Simulation of train-track interaction with stochastic track properties. Veh. Syst. Dyn. 2002, 37, 449–469. [Google Scholar] [CrossRef]
- Bureika, G.; Subačius, R. Mathematical model of dynamic interaction between wheel-set and rail track. Transport 2002, 17, 46–51. [Google Scholar] [CrossRef]
- Lei, X.; Noda, N.A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile. J. Sound Vib. 2002, 258, 147–165. [Google Scholar] [CrossRef]
- Kouroussis, G.; Gazetas, G.; Anastasopoulos, I.; Conti, C.; Verlinden, O. Discrete modelling of vertical track-soil coupling for vehicle-track dynamics. Soil Dyn. Earthq. Eng. 2011, 31, 1711–1723. [Google Scholar] [CrossRef]
- Nguyen, K.; Goicolea, J.M.; Galbadon, F. Comparison of dynamic effects of high-speed traffic load on ballasted track using a simplified two-dimensional and full three-dimensional model. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 228, 128–142. [Google Scholar] [CrossRef]
- Zhai, M.W.; Wang, K.Y.; Lin, J.H. Modelling and experiment of railway ballast vibrations. J. Sound Vib. 2004, 270, 673–683. [Google Scholar] [CrossRef]
- Ahlbeck, D.R.; Meacham, H.C.; Prause, R.H. The development of analytical models for railroad track dynamics. In Railroad Track Mechanics and Technology; Pergamon Press: Oxford, UK, 1975. [Google Scholar] [CrossRef]
- Doyle, N.F. Railway Track Design: A Review of Current Practice. Bureau of Transport Economics (BTE), 1980. Available online: https://www.bitre.gov.au/sites/default/files/op_035.pdf (accessed on 13 March 2025).
- Kerr, D. On the determination of the rail support modulus k. Int. J. Solids Struct. 2000, 37, 4335–4351. [Google Scholar] [CrossRef]
- Zhai, W.M.; Sun, X. A detailed model for investigating vertical interaction between railway vehicle and track. Veh. Syst. Dyn. 1994, 23, 603–615. [Google Scholar] [CrossRef]
- Beskou, N.D.; Muho, E.V. Review on dynamic response of road pavements to moving vehicle loads; part 1: Rigid pavements. Soil. Dyn. Earthq. Eng. 2023, 175, 108249. [Google Scholar] [CrossRef]
- Muho, E.V.; Beskou, N.D. Review on dynamic analysis of road pavements under moving vehicles and plane strain conditions. J. Road Eng. 2024, 4, 54–68. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Semi-analytical analysis of vibrations induced by a mass traversing a beam supported by a finite depth foundation with simplified shear resistance. Meccanica 2020, 55, 2353–2389. [Google Scholar] [CrossRef]
- Ouyang, L.; Xiang, Z.; Zhen, B.; Yuan, W. Analytical Study on the Impact of Nonlinear Foundation Stiffness on Pavement Dynamic Response under Vehicle Action. Appl. Sci. 2024, 14, 8705. [Google Scholar] [CrossRef]
- Hua, X.; Zatar, W.; Cheng, X.; Chen, G.S.; She, Y.; Xu, X.; Liao, Z. Modeling and Characterization of Complex Dynamical Properties of Railway Ballast. Appl. Sci. 2024, 14, 11224. [Google Scholar] [CrossRef]
- Yang, J.; He, X.; Jing, H.; Wang, H.; Tinmitonde, S. Dynamics of Double-Beam System with Various Symmetric Boundary Conditions Traversed by a Moving Force: Analytical Analyses. Appl. Sci. 2019, 9, 1218. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, S.-L. Analytical determination of critical velocity and frequencies of beam with moving mass under different supporting conditions. J. Vibroeng. 2024, 26, 1014–1026. [Google Scholar] [CrossRef]
- Al-Ashtari, W. A new approach for modelling the vibration of beams under moving load effect. ARPN J. Eng. Appl. Sci. 2023, 18, 1195–1206. [Google Scholar]
- Ghannadiasl, A.; Mofid, M. Sensitivity analysis of vibration response of timoshenko beam to mass ratio and velocity of moving mass and boundary conditions: Semi-analytical approach. Forces Mech. 2023, 11, 100205. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, P.; Li, Y.; Tao, Y.G.; Xu, J.; Zhu, Z. Interfacial properties of double-block ballastless track under various environmental conditions. Int. J. Mech. Sci. 2024, 266, 108954. [Google Scholar] [CrossRef]
- Dumitriu, M. Fault detection of damper in railway vehicle suspension based on the cross-correlation analysis of bogie accelerations. Mech. Ind. 2019, 20, 102. [Google Scholar] [CrossRef]
- Heydari, H. Evaluating the dynamic behavior of railway-bridge transition zone: Numerical and field measurements. Can. J. Civil Eng. 2024, 51, 399–408. [Google Scholar] [CrossRef]
- Jain, A.; Metrikine, A.V.; Steenbergen, M.J.M.M.; van Dalen, K.N. Railway Transition Zones: Energy Evaluation of a Novel Transition Structure for Critical Loading Conditions. J. Vib. Eng. Technol. 2025, 13, 15. [Google Scholar] [CrossRef]
- Uranjek, M.; Imamović, D.; Peruš, I. Mathematical Modeling of the Floating Sleeper Phenomenon Supported by Field Measurements. Mathematics 2024, 12, 3142. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Zhang, P.; Núñez, A.; Dollevoet, R. Mechanism of short pitch rail corrugation: Initial excitation and frequency selection for consistent initiation and growth. Int. J. Rail Transp. 2024, 12, 13150. [Google Scholar] [CrossRef]
- Zhang, P.; He, C.; Shen, C.; Dollevoet, R.; Li, Z. Comprehensive validation of three-dimensional finite element modelling of wheel-rail high-frequency interaction via the V-Track test rig. Veh. Syst. Dyn. 2024, 62, 2785–2809. [Google Scholar] [CrossRef]
- Fărăgău, A.B.; Metrikine, A.V.; van Dalen, K.N. Transition radiation in a piecewise-linear and infinite one-dimensional structure–a Laplace transform method. Nonlinear Dyn. 2019, 98, 2435–2461. [Google Scholar] [CrossRef]
- Fărăgău, A.B.; Keijdener, C.; de Oliveira Barbosa, J.M.; Metrikine, A.V.; van Dalen, K.N. Transition radiation in a nonlinear and infinite one-dimensional structure: A comparison of solution methods. Nonlinear Dyn. 2021, 103, 1365–1391. [Google Scholar] [CrossRef]
- Fărăgău, A.B.; Mazilu, T.; Metrikine, A.V.; Tao, L.; van Dalen, K.N. Transition radiation in an infinite one-dimensional structure interacting with a moving oscillator—The Green’s function method. J. Sound Vib. 2021, 492, 115804. [Google Scholar] [CrossRef]
- Gao, L.; Shi, S.; Zhong, Y.; Xu, M.; Xiao, Y. Real-time evaluation of mechanical qualities of ballast bed in railway tamping maintenance. Int. J. Mech. Sci. 2023, 248, 108192. [Google Scholar] [CrossRef]
- Yang, Y.B.; Gao, S.Y.; Shi, K.; Mo, X.Q.; Yuan, P.; Wang, H.Y. Selection of the Span Length of an Analogic Finite Beam to Simulate the Infinite Beam Resting on Viscoelastic Foundation Under a Harmonic Moving Load. Int. J. Struct. Stab. Dyn. 2025, 2540001. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Semi-analytical solution for a problem of a uniformly moving oscillator on an infinite beam on a two-parameter visco-elastic foundation. J. Sound Vib. 2019, 438, 257–290. [Google Scholar] [CrossRef]
- Dimitrovová, Z. A General Procedure for the Dynamic Analysis of Finite and Infinite Beams on Piece-Wise Homogeneous Foundation under Moving Loads. J. Sound Vib. 2010, 329, 2635–2653. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Two-layer model of the railway track: Analysis of the critical velocity and instability of two moving proximate masses. Int. J. Mech. Sci. 2022, 217, 107042. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Complete semi-analytical solution for a uniformly moving mass on a beam on a two-parameter visco-elastic foundation with non-homogeneous initial conditions. Int. J. Mech. Sci. 2018, 144, 283–311. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, W.; Yang, C. Semi-analytical solution to the steady-state periodic dynamic response of an infinite beam carrying a moving vehicle. Int. J. Mech. Sci. 2022, 226, 107409. [Google Scholar] [CrossRef]
- Mazilu, T.; Răcănel, I.R.; Gheți, M.A. Vertical interaction between a driving wheelset and track in the presence of the rolling surfaces harmonic irregularities. Rom. J. Transp. Infrastruct. 2020, 9, 38–52. [Google Scholar] [CrossRef]
- Kiani, K.; Nikkhoo, A. On the limitations of linear beams for the problems of moving mass-beam interaction using a meshfree method. Acta Mech. Sin. 2011, 28, 164–179. [Google Scholar] [CrossRef]
- Kiani, K.; Nikkhoo, A.; Mehri, B. Prediction capabilities of classical and shear deformable beam models excited by a moving mass. J. Sound Vib. 2009, 320, 632–648. [Google Scholar] [CrossRef]
- Kiani, K.; Nikkhoo, A.; Mehri, B. Assessing dynamic response of multispan viscoelastic thin beams under a moving mass via generalized moving least square method. Acta Mech. Sin. 2010, 26, 721–733. [Google Scholar] [CrossRef]
- Jahangiri, A.; Attari, N.K.A.; Nikkhoo, A.; Waezi, Z. Nonlinear dynamic response of an Euler–Bernoulli beam under a moving mass–spring with large oscillations. Arch. Appl. Mech. 2020, 90, 1135–1156. [Google Scholar] [CrossRef]
- Tran, M.T.; Ang, K.K.; Luong, V.H. Vertical dynamic response of non-uniform motion of high-speed rails. J. Sound Vib. 2014, 333, 5427–5442. [Google Scholar] [CrossRef]
- Dai, J.; Lim, J.G.Y.; Ang, K.K. Dynamic response analysis of high-speed maglev-guideway system. J. Vib. Eng. Technol. 2023, 11, 2647–2658. [Google Scholar] [CrossRef]
- Stojanović, V.; Kozić, P.; Petković, M.D. Dynamic instability and critical velocity of a mass moving uniformly along a stabilized infinity beam. Int. J. Solids Struct. 2017, 108, 164–174. [Google Scholar] [CrossRef]
- Dimitrovová, Z. New semi-analytical solution for a uniformly moving mass on a beam on a two-parameter visco-elastic foundation. Int. J. Mech. Sci. 2017, 127, 142–162. [Google Scholar] [CrossRef]
- Metrikine, A.V.; Verichev, S.N.; Blaauwendraad, J. Stability of a two-mass oscillator moving on a beam supported by a visco-elastic half-space. Int. J. Solids Struct. 2005, 42, 1187–1207. [Google Scholar]
- Mazilu, T.; Dumitriu, M.; Tudorache, C. Instability of an oscillator moving along a Timoshenko beam on viscoelastic foundation. Nonlinear Dyn. 2012, 67, 1273–1293. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Dynamic interaction and instability of two moving proximate masses on a beam on a Pasternak viscoelastic foundation. Appl. Math. Modell. 2021, 100, 192–217. [Google Scholar] [CrossRef]
- Mazilu, T. Instability of a train of oscillators moving along a beam on a viscoelastic foundation. J. Sound Vib. 2013, 332, 4597–4619. [Google Scholar] [CrossRef]
- Yang, B.; Gao, H.; Liu, S. Vibrations of a Multi-Span Beam Structure Carrying Many Moving Oscillators. Int. J. Struct. Stab. Dyn. 2018, 18, 1850125. [Google Scholar] [CrossRef]
- Stojanović, V.; Petković, M.D.; Deng, J. Stability and vibrations of an overcritical speed moving multiple discrete oscillators along an infinite continuous structure. Eur. J. Mech. A/Solids 2019, 75, 367–380. [Google Scholar] [CrossRef]
- Nassef, A.S.E.; Nassar, M.M.; EL-Refaee, M.M. Dynamic response of Timoshenko beam resting on nonlinear Pasternak foundation carrying sprung masses. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 419–426. [Google Scholar] [CrossRef]
- Stojanović, V.; Petković, M.; Deng, J. Instability of vehicle systems moving along an infinite beam on a viscoelastic foundation. Eur. J. Mech. A. Solids 2018, 69, 238–254. [Google Scholar] [CrossRef]
- Dimitrovová, Z. Instability of vibrations of mass(es) moving uniformly on a two-layer track model: Parameters leading to irregular cases and associated implications for railway design. Appl. Sci. 2023, 13, 12356. [Google Scholar] [CrossRef]
- Yang, C.J.; Xu, Y.; Zhu, W.D.; Fan, W.; Zhang, W.H.; Mei, G.M. A three-dimensional modal theory-based Timoshenko finite length beam model for train-track dynamic analysis. J. Sound Vib. 2020, 479, 115363. [Google Scholar] [CrossRef]
- Abea, K.; Chidaa, Y.; Quinay, P.E.B.; Koroa, K. Dynamic instability of a wheel moving on a discretely supported infinite rail. J. Sound Vib. 2014, 333, 3413–3427. [Google Scholar] [CrossRef]
- Gasch, R.; Hauschild, W.; Kik, W.; Knothe, K.; Steinborn, H. Stability and Forced Vibrations of a 4-axled Railway Vehicle with Elastic Car Body. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 1977, 6, 191–195. [Google Scholar] [CrossRef]
- Fujimoto, H.; Tanifuji, K.; Miyamoto, M. Influence of track gauge variation on rail vehicle dynamics (an examination based on comparison between data from a test train running on track with irregularity artificially set and numerical simulation). Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2000, 214, 223–230. [Google Scholar] [CrossRef]
- Verichev, S.N.; Metrikine, A.V. Instability of a bogie moving on a flexibly supported Timoshenko beam. J. Sound Vib. 2002, 253, 653–668. [Google Scholar] [CrossRef]
- Stojanović, V.; Deng, J.; Petković, M.; Milić, D. Non-stability of a bogie moving along a specific infinite complex flexibly beam-layer structure. Eng. Struct. 2023, 295, 116788. [Google Scholar] [CrossRef]
- Stojanović, V.; Deng, J.; Milić, D.; Petković, M.D. Dynamics of moving coupled objects with stabilizers and unconventional couplings. J. Sound Vib. 2024, 570, 118020. [Google Scholar] [CrossRef]
- Dimitrovová, Z.; Mazilu, T. Semi-Analytical Approach and Green’s Function Method: A Comparison in the Analysis of the Interaction of a Moving Mass on an Infinite Beam on a Three-Layer Viscoelastic Foundation at the Stability Limit—The Effect of Damping of Foundation Materials. Materials 2024, 17, 279. [Google Scholar] [CrossRef]
- Dimitrovová, Z.; Rodrigues, A.F.S. Critical Velocity of a Uniformly Moving Load. Adv. Eng. Softw. 2012, 50, 44–56. [Google Scholar] [CrossRef]



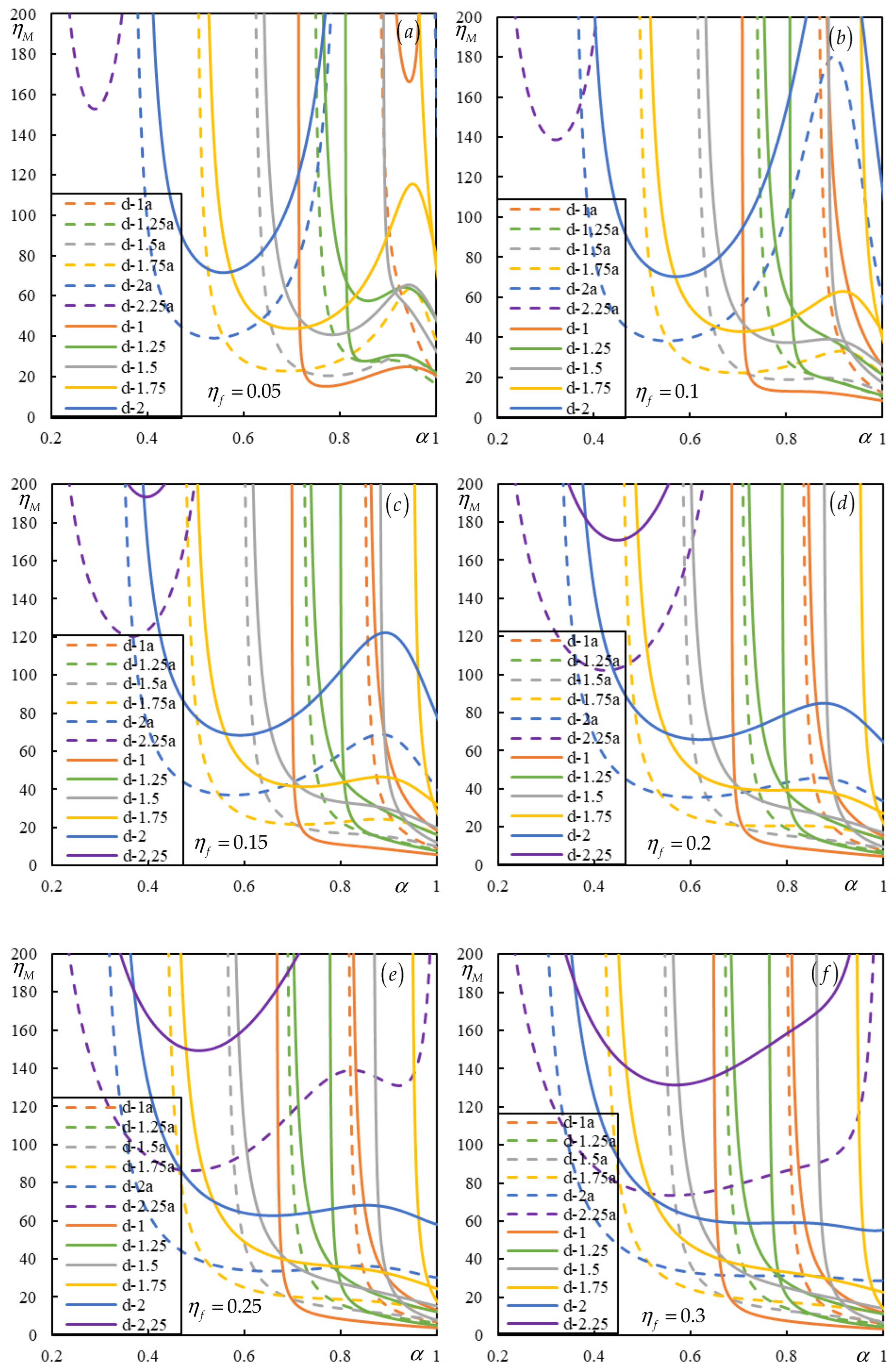

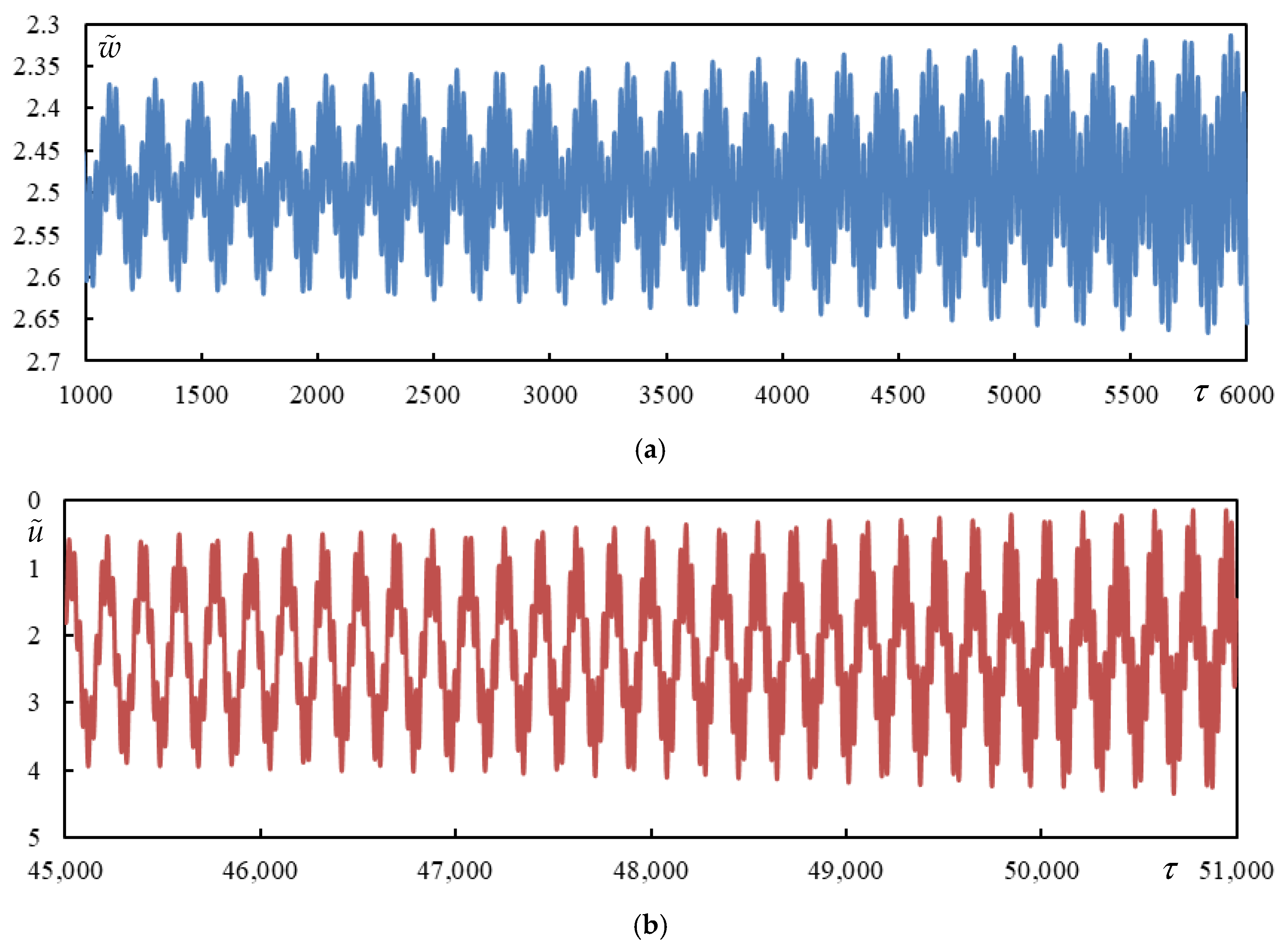
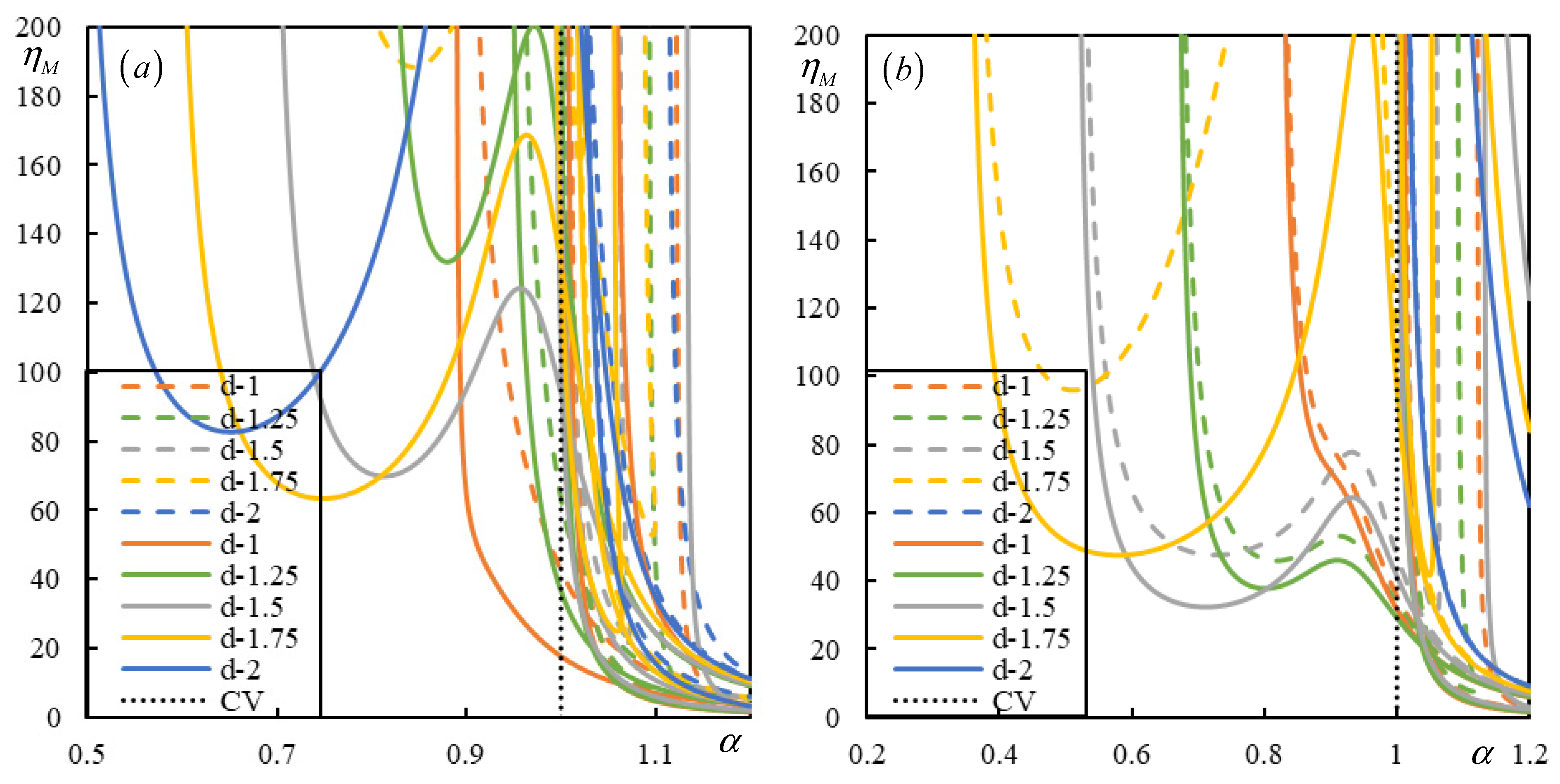
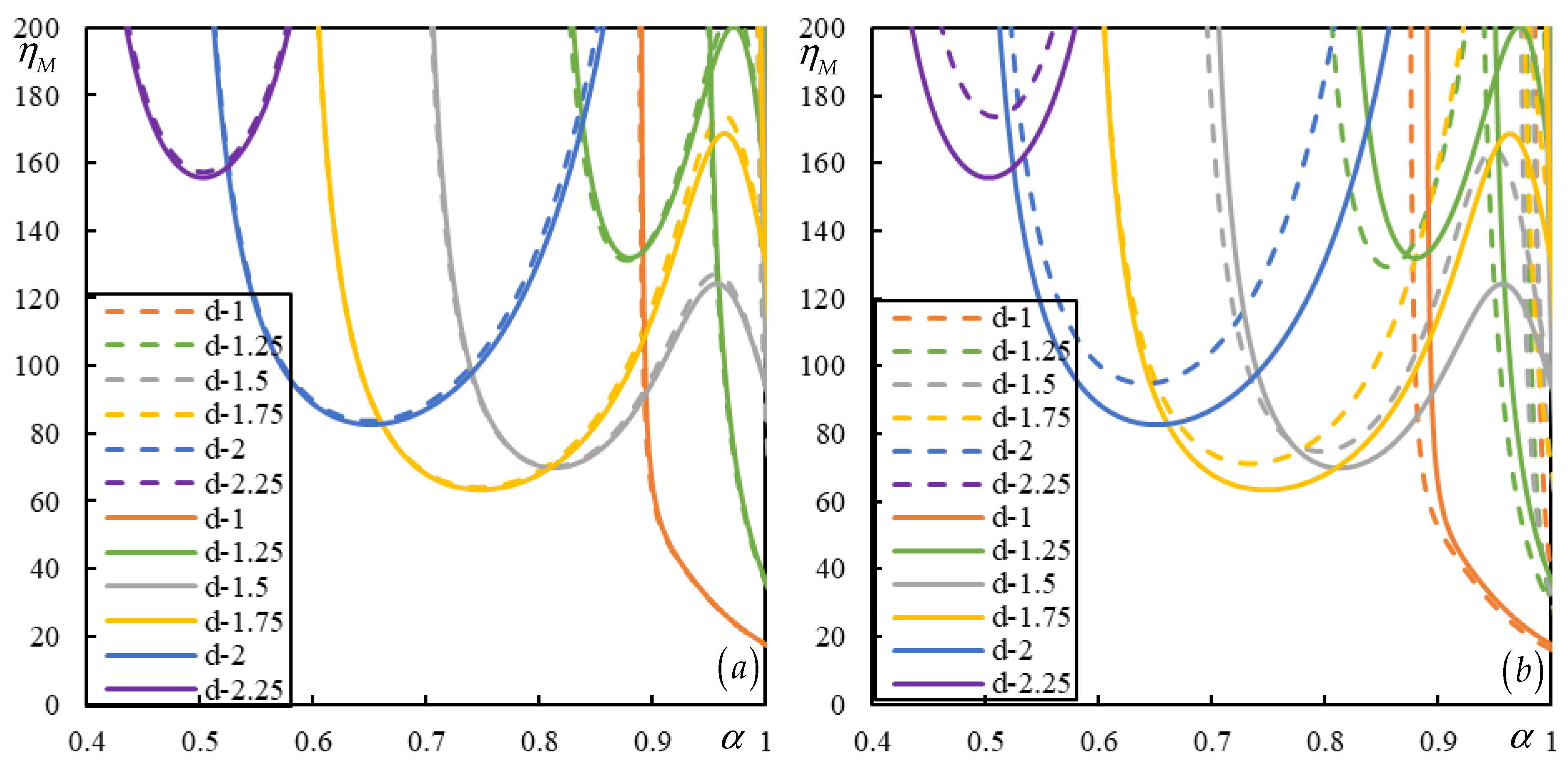
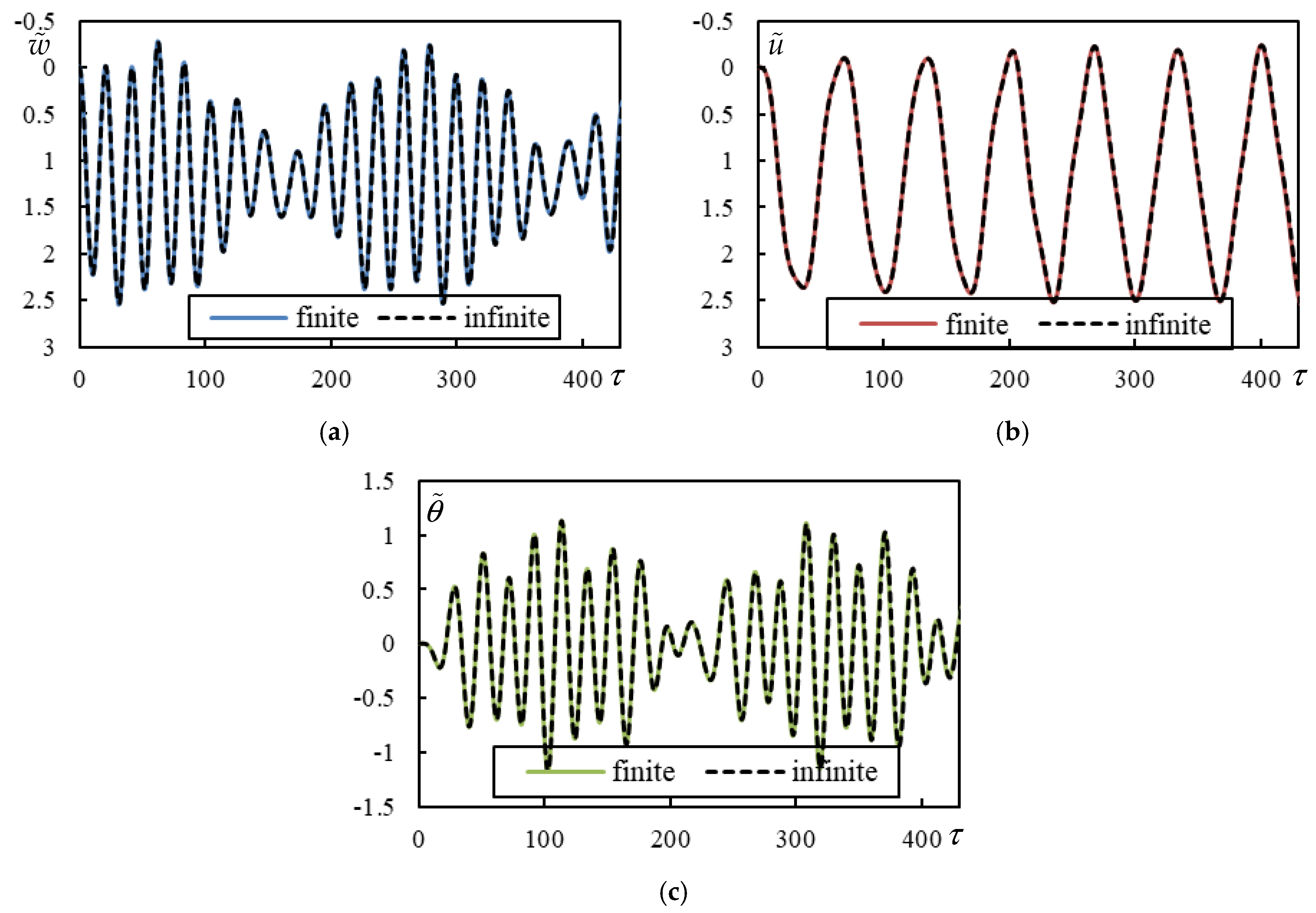
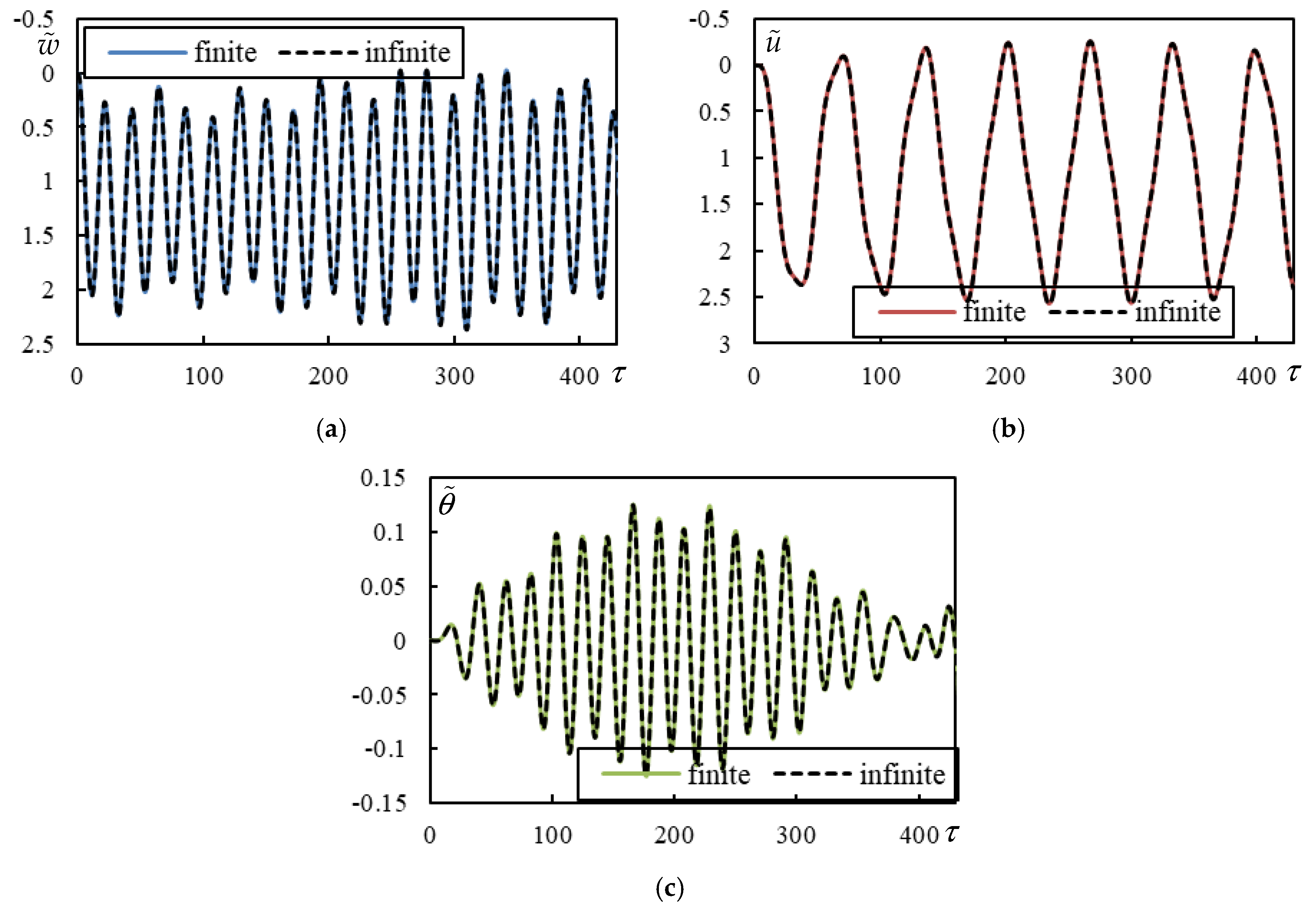

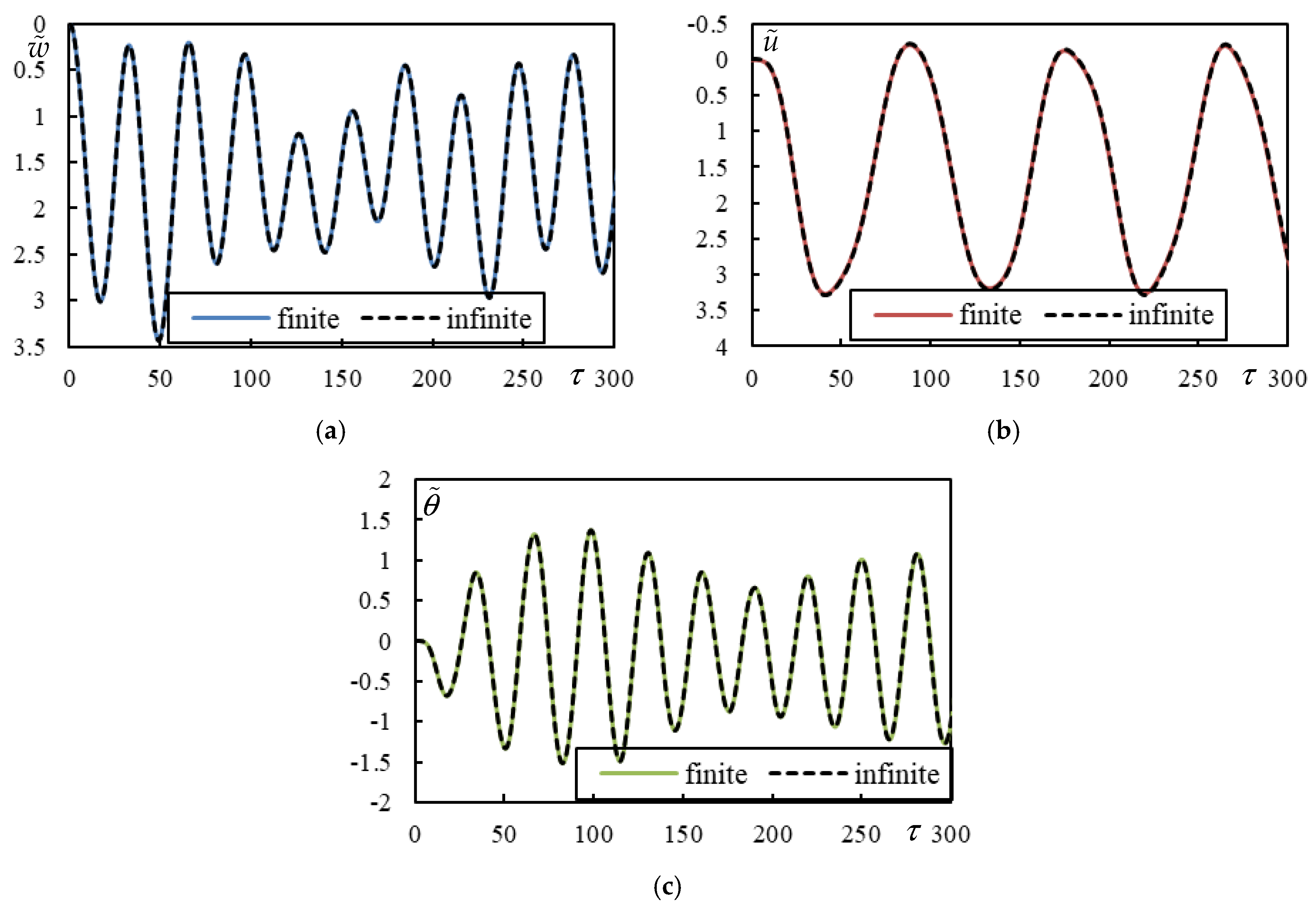

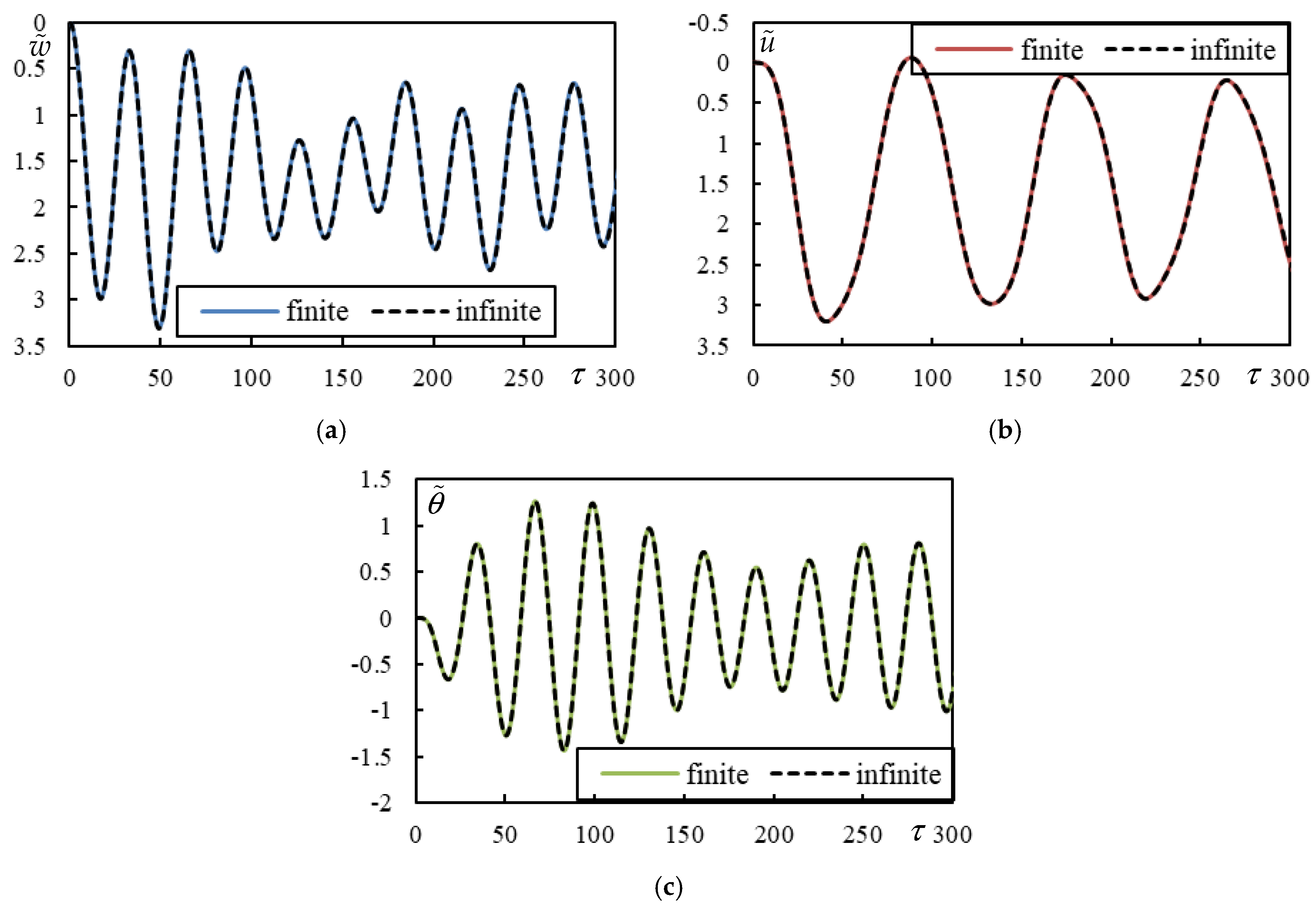
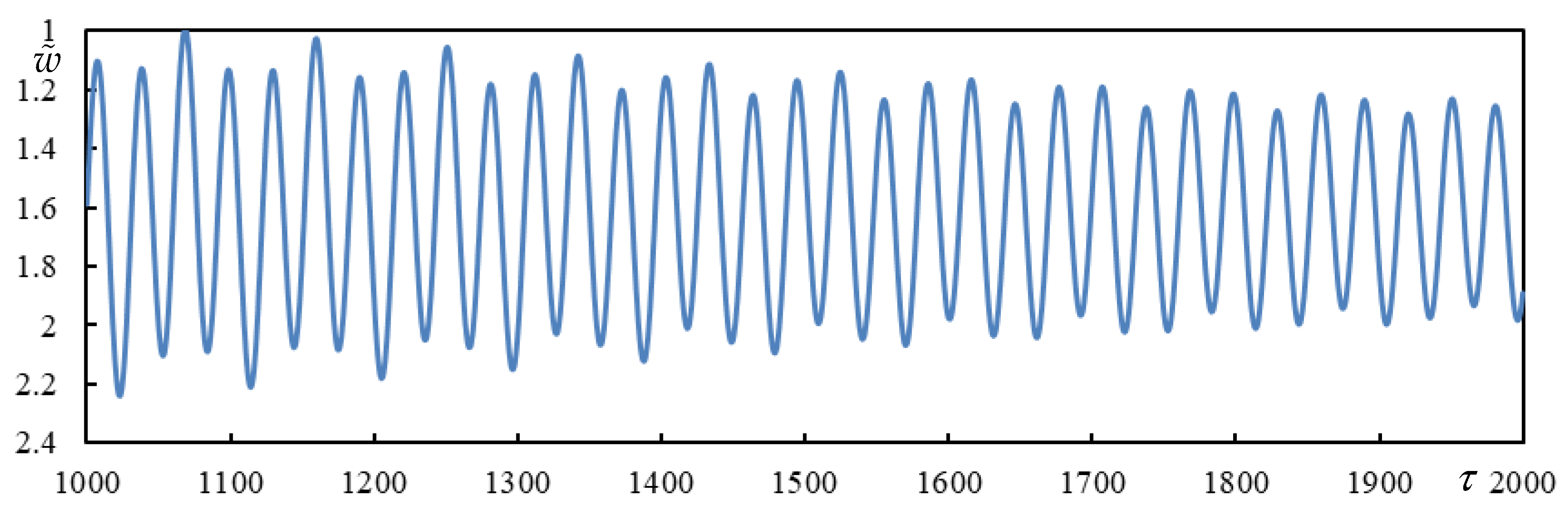
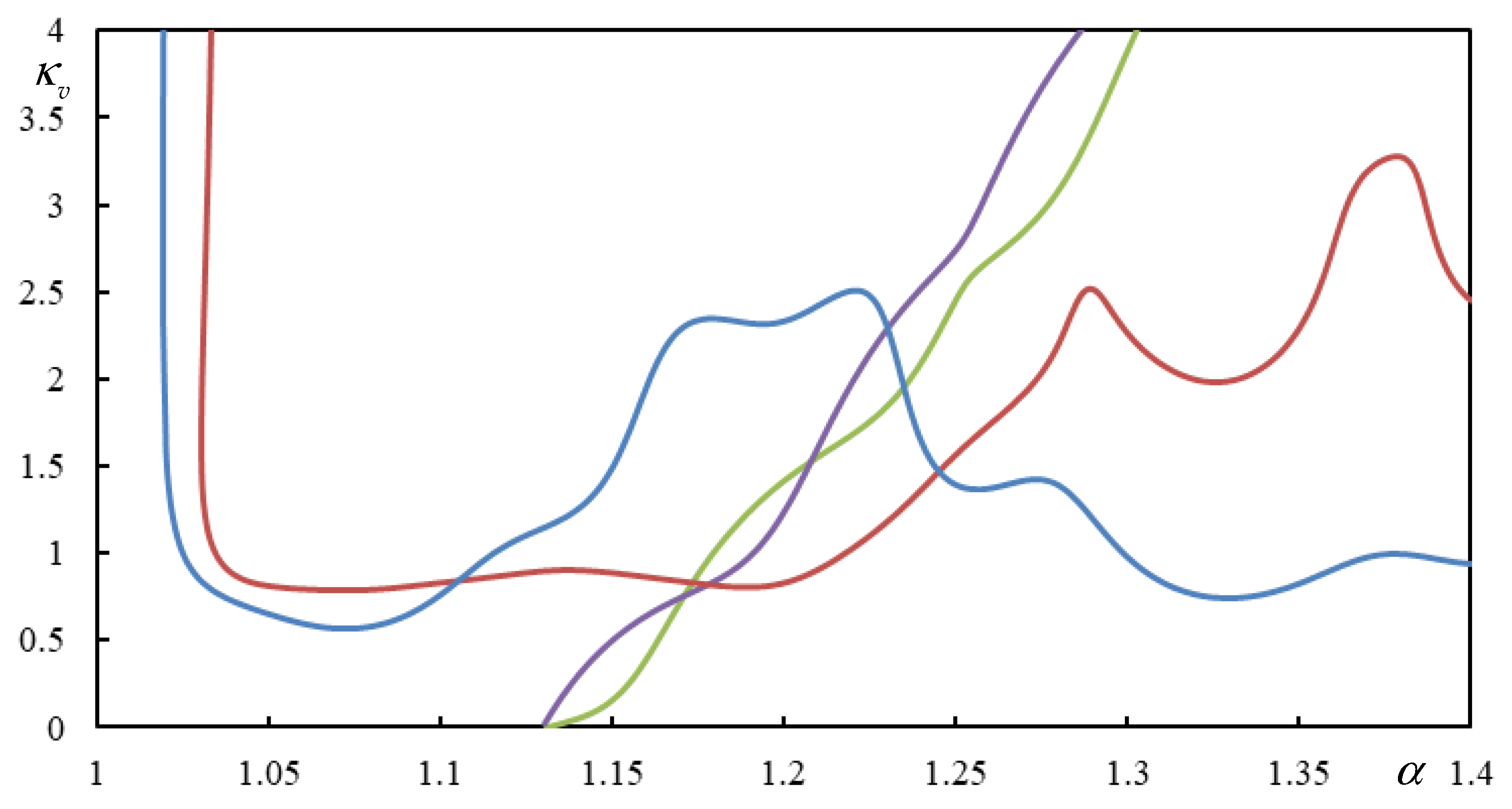
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Case 1 | 0.1 | 20 | 1 | 1.7 | 0.01 | 0.02 | 0 | 0.8 |
| Case 2 | 0 | 20 | 2 | 2 | 0.1 | 0.2 | 0 | 0.5 |
| Case 3 | 0 | 20 | 5 | 2 | 0.1 | 0.2 | 0 | 0.5 |
| Case 4 | 0 | 20 | 5 | 1.7 | 0.1 | 0.2 | 0 | 0.5 |
| Case 5 | 0.05 | 40 | 1.5 | 1.7 | 0.01 | 0.2 | 0 | 0.7 |
| Case 6 | 0.05 | 40 | 1.5 | 1.7 | 0.01 | 0.2 | 0.05 | 0.7 |
| Case 7 | 0.05 | 30 | 2 | 1.7 | 0.01 | 0.2 | 0.05 | 0.4 |
| Case 8 | 0.05 | 30 | 2 | 1.7 | 0.01 | 0.2 | 0 | 0.4 |
| Case 9 | 0 | 30 | 2 | 1.7 | 0.01 | 0.2 | 0.05 | 0.4 |
| Case 10 | 0 | 30 | 2 | 1.7 | 0.01 | 0.2 | 0 | 0.4 |
| Case 11 | 0.05 | 25 | 2 | 1.7 | 0.01 | 0.2 | 0.05 | 0.4 |
| Case 12 | 0.15 | 50 | 1.5 | 1.7 | 0.1 | 0.2 | 0 | 0.85 |
| Case 13 | 0.15 | 15 | 1 | 1.7 | 0.1 | 0.2 | 0 | 0.95 |
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Case 1 | ±0.307227 | 0.021025 | ±0.222538 | −0.000130 | ±0.184817 | 0.028535 | ±0.033910 | 0.000014 |
| Case 2 | ±0.319059 | 0 | ±0.290698 | 0 | ±0.200435 | 0 | ±0.094072 | 0 |
| Case 3 | ±0.310632 | 0 | ±0.294334 | 0 | ±0.200910 | 0 | ±0.094035 | 0 |
| Case 4 | ±0.310639 | 0 | ±0.294718 | 0 | ±0.200910 | 0 | ±0.101860 | 0 |
| Case 5 | ±0.505305 | 0.000454 | ±0.206528 | −0.000472 | ±0.174711 | 0.007546 | ±0.070460 | 0.000121 |
| Case 6 | ±0.501188 | 0.063327 | ±0.206521 | 0.000448 | ±0.174683 | 0.008301 | ±0.070451 | 0.001137 |
| Case 7 | ±0.577601 | 0.084896 | ±0.255723 | 0.003197 | ±0.236572 | 0.004611 | ±0.083388 | 0.001565 |
| Case 8 | ±0.583823 | 0.000110 | ±0.255859 | 0.001562 | ±0.236478 | 0.004163 | ±0.083397 | 0.000047 |
| Case 9 | ±0.577617 | 0.084792 | ±0.255809 | 0.001646 | ±0.236376 | 0.000436 | ±0.083390 | 0.001518 |
| Case 10 | ±0.583817 | 0 | ±0.255864 | 0 | ±0.236346 | 0 | ±0.083394 | 0 |
| Case 11 | ±0.631225 | 0.101825 | ±0.279230 | 0.003868 | ±0.257027 | 0.005435 | ±0.091336 | 0.001877 |
| Case 12 | ±0.186008 | −0.000482 | ±0.148407 | 0.016963 | ±0.122981 | 0.013168 | ±0.062675 | 0.000636 |
| Case 13 | ±0.354144 | 0.025958 | ±0.249576 | −0.000631 | ±0.167778 | 0.148504 | ±0.113114 | 0.004749 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitrovová, Z. Instability of a Moving Bogie: Analysis of Vibrations and Possibility of Instability in Subcritical Velocity Range. Vibration 2025, 8, 13. https://doi.org/10.3390/vibration8020013
Dimitrovová Z. Instability of a Moving Bogie: Analysis of Vibrations and Possibility of Instability in Subcritical Velocity Range. Vibration. 2025; 8(2):13. https://doi.org/10.3390/vibration8020013
Chicago/Turabian StyleDimitrovová, Zuzana. 2025. "Instability of a Moving Bogie: Analysis of Vibrations and Possibility of Instability in Subcritical Velocity Range" Vibration 8, no. 2: 13. https://doi.org/10.3390/vibration8020013
APA StyleDimitrovová, Z. (2025). Instability of a Moving Bogie: Analysis of Vibrations and Possibility of Instability in Subcritical Velocity Range. Vibration, 8(2), 13. https://doi.org/10.3390/vibration8020013








