Crack Location in Wind Turbine Blades Using Vibration Signal and Support Vector Machine
Abstract
1. Introduction
| Technique | Description | Advantages | Limitations |
|---|---|---|---|
| Ultrasonic Testing [11]. | High-frequency sound waves are introduced into the material. Reflections from cracks provide information about their size and location. | Highly sensitive to internal flaws. | Requires skilled operators and can be time-consuming. |
| Thermographic Inspection [12,13]. | Infrared cameras detect temperature variations on the surface, indicating structural changes. | Non-destructive and covers large areas quickly. | Requires a heat source. |
| Acoustic Emission Testing [14,15]. | Detects sound waves emitted from materials under stress, identifying crack formation in real-time. | Effective for continuous monitoring. | Requires specialized equipment. |
| X-ray Computed Tomography [16,17]. | Provides 3D images of the internal structure, allowing detailed visualization of cracks. | High-resolution imaging of internal flaws. | Expensive and requires specialized facilities. |
| Fiber Bragg Grating Sensors [18]. | Optical sensors embedded in the blade material monitor strain and detect cracks. | Real-time monitoring and high sensitivity. | Initial installation can be complex. |
| Robotic and Drone Inspection [19]. | Drones equipped with cameras can perform visual inspections and advanced imaging techniques. | Access to hard-to-reach areas. | Do not detect all internal defects. |
| Image Processing [20]. | Involves the use of various techniques to analyze visual data captured from cameras or sensors | Non-destructive and high sensitivity. | Environmental sensitivity, data overload, and complexity of implementation |
| Vibration Monitoring [21]. | Piezoelectric sensors can be embedded in or attached to turbine blades to continuously monitor vibration signals, providing real-time data for crack detection. | Direct measurement of stress and strain can lead to early detection of cracks. | Sensor placement and calibration can be challenging. |
| Approach | Description | Advantages | Limitations |
|---|---|---|---|
| Experimental Modal Analysis [22,23]. | This technique involves measuring the natural frequencies and mode shapes of the WTBs. Changes in these parameters can indicate the presence of cracks or structural alterations. | Sensitive to small changes in structural integrity; can be performed in situ. | Requires baseline data for comparison and can be influenced by environmental factors |
| Vibration Signal Processing [24]. | Advanced signal processing techniques, such as fast Fourier transform (FFT) and wavelet transform, analyze the frequency content of vibration signals to detect anomalies indicative of cracks. | Effective in identifying specific frequency changes associated with crack formation. | Requires sophisticated data analysis tools and expertise. |
| Operational Modal Analysis [25,26]. | OMA is a method that captures the dynamic response of the structure during operation, allowing for the identification of changes in modal parameters due to crack initiation. | Non-invasive and suitable for structures under operational conditions. | Can be less accurate than laboratory-based modal analysis. |
| Machine Learning Approaches [27,28,29]. | Machine learning algorithms can analyze vibration data to identify patterns and predict the presence of cracks based on historical data. | Capable of processing large datasets and improving detection accuracy. | Requires substantial training data and may face challenges with generalization. |
| Time-Frequency Analysis [30]. | This technique combines time and frequency domain analyses to capture transient events associated with crack propagation, providing more detailed information on crack dynamics. | Effective in detecting non-stationary signals related to crack growth. | Computationally intensive and complex to interpret. |
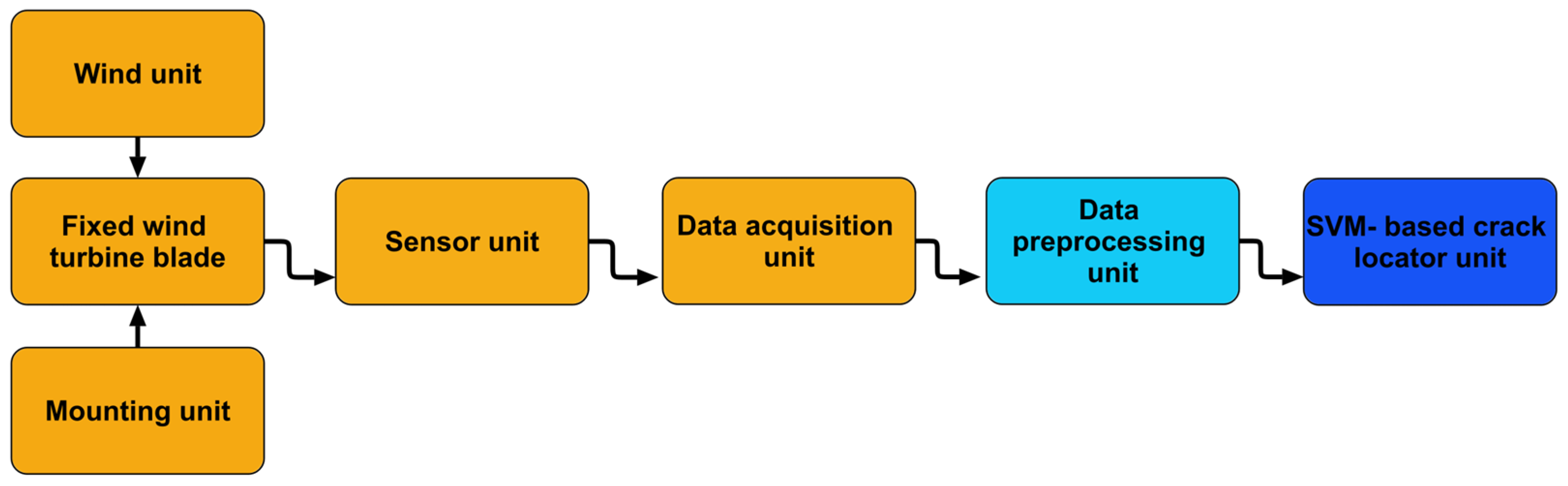
2. Crack Location Method
2.1. Data Acquisition
2.2. Data Preprocessing
2.3. Training the SVM Model
2.4. Evaluating the SVM Model
3. Experimental Validation
3.1. SVM Model
- Import the relevant modules from Scikit-learn for SVM and data handling.
- Import and preprocess the dataset. The min–max scaling method was applied during the data normalization process. Relevant features were extracted from the previously mentioned dataset using the Pandas library. Pandas is a Python 3.11.5 package that calculates many time series characteristics or features. The selected characteristics included mean, standard deviation, maximum frequency, skewness, and kurtosis. The preprocessed data dimension is 300 × 5 × 4 (signal samplings × features × WTB).
- Split the preprocessed dataset into training and test subsets. The test subset was randomly split into 20% of the extracted feature data, and the training subset was split randomly into 80%. The train–test split function was used to split the data.
- Initialize the SVM model. The SVM used for classification was the SVC (support vector classifier), a linear kernel. Tune the hyperparameters using GridSearchCV. Apply the cross-validation technique.
- Fit the SVM classifier model using the fit() method on the training dataset.
- Predict using the predict() function on the test dataset.
- Evaluate the SVM’s model performance using metrics. The , , , and were computed using sklean metrics. Meanwhile, the multiclass confusion matrix was plotted using sklearn metrics and the matplotlib.pyplot module. Matplotlib displays the results in a more intuitive visual format using colors and bold type.
3.2. KNN Model
- Execute steps 1 to 3 outlined in Section 3.1.
- Choose the value for K (the number of nearest neighbors). The initial value of K is set at 3.
- Fit the KNN model to the training dataset. The libraries used were sklearn.neighbors.KNeighborsClassifier.
- Predict using the predict() function on the test dataset.
- Evaluate the KNN’s model performance using metrics. The , , , and Recall were computed using sklean metrics.
- Test different values of K to determine the best value of K for the classifier. The best value of K was 5.
3.3. DT Model
- Execute steps 1 to 3 outlined in Section 3.1.
- Initialize the DT model using the DecisionTreeClassifier from sklearn.tree. The best combination of hyperparameter values was found using Scikit-Learn’s GridSearchCV.
- Fit the DT classifier model using the fit() method on the training dataset.
- Predict using the predict() function on the test dataset.
- Evaluate the DT’s model performance using metrics. The , , , and Recall were computed using sklean metrics.
4. Results and Discussions
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WTB | Wind turbine blade |
| FFT | Fast Fourier transform |
| ML | Machine learning |
| KNN | K-nearest neighbors |
| SVM | Support vector machine |
| UAV | Unmanned aerial vehicles |
| DT | Decision tree |
| AI | Artificial intelligence |
| TP | True positive |
| TN | True negative |
| FP | False positive |
| FN | False negative |
| H | Healthy |
| CR | Crack in root |
| CM | Crack in midsection |
| CT | Crack in tip |
References
- Li, J.; Wu, Z.; Tan, X.; Chen, B. Review of wind power generation and relative technology development. Electr. Power Constr. 2011, 32, 64–72. [Google Scholar]
- Jensen, F.M.; Braner, K. Introduction to Wind Turbine Blade Design. In Advances in Wind Turbine Blade Design and Materials, 2nd ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2023; pp. 3–53. ISBN 9780081030073. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, S.; Jing, X.; Peng, Y.; Wu, H.; Kwok, N. Damage Detection Techniques for Wind Turbine Blades: A Review. Mech. Syst. Signal Process. 2020, 141, 106445. [Google Scholar] [CrossRef]
- Katsaprakakis, D.A.; Papadakis, N.; Ntintakis, I.A. Comprehensive Analysis of Wind Turbine Blade Damage. Energies 2021, 14, 5974. [Google Scholar] [CrossRef]
- Kaewniam, P.; Cao, M.; Alkayem, N.F. Recent Advances in Damage Detection of Wind Turbine Blades: A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2023, 167, 112723. [Google Scholar] [CrossRef]
- Kong, K.; Dyer, K.; Payne, C.; Hamerton, I.; Weaver, P.M. Progress and Trends in Damage Detection Methods, Maintenance, and Data-Driven Monitoring of Wind Turbine Blades—A Review. Renew. Energy Focus 2023, 44, 390–412. [Google Scholar] [CrossRef]
- Reddy, S.S.P.; Suresh, R.; M.B., H.; Shivakumar, B.P. Use of Composite Materials and Hybrid Composites in Wind Turbine Blades. Mater. Today Proc. 2021, 46, 2827–2830. [Google Scholar] [CrossRef]
- Madhav, P.; Matavkar, D.; Mayekar, N.; Parsekar, M. A Review on Crack Detection in Wind Turbine Blade. Int. J. Res. Appl. Sci. Eng. Technol. 2024, 12, 3129–3140. [Google Scholar] [CrossRef]
- Benaissa, B.; Hocine, N.A.; Khatir, S.; Riahi, M.K.; Mirjalili, S. YUKI Algorithm and POD-RBF for Elastostatic and dynamic crack identification. J. Comput. Sci. 2021, 55, 101451. [Google Scholar] [CrossRef]
- Amoura, N.; Benaissa, B.; Al Ali, M.; Khatir, S. Deep Neural Network and YUKI Algorithm for Inner Damage Characterization Based on Elastic Boundary Displacement. In Proceedings of the International Conference of Steel and Composite for Engineering Structures. ICSCES 2022, Barcelona, Spain, 15–17 September 2022; Lecture Notes in Civil Engineering, 317. Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, Z.; Zhou, Q.; Zhu, C.; Liu, T.; Wang, B. Damage Identification of Wind Turbine Blades Based on Deep Learning and Ultrasonic Testing. Nondestruct. Test. Eval. 2024, 1, 1–26. [Google Scholar] [CrossRef]
- Hwang, S.; An, Y.-K.; Sohn, H. Continuous-Wave Line Laser Thermography for Monitoring of Rotating Wind Turbine Blades. Struct. Health Monit. 2019, 18, 1010–1021. [Google Scholar] [CrossRef]
- Jaeger, B.E.; Schmid, S.; Grosse, C.U.; Gögelein, A.; Elischberger, F. Infrared Thermal Imaging-Based Turbine Blade Crack Classification Using Deep Learning. J. Nondestruct. Eval. 2022, 41, 74. [Google Scholar] [CrossRef]
- Bo, Z.; Zhan, Y.; Changzheng, C. Acoustic Emission Detection of Fatigue Cracks in Wind Turbine Blades Based on Blind Deconvolution Separation. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 959–970. [Google Scholar] [CrossRef]
- Ding, S.; Yang, C.; Zhang, S. Acoustic-Signal-Based Damage Detection of Wind Turbine Blades—A Review. Sensors 2023, 23, 4987. [Google Scholar] [CrossRef]
- Fantidis, J.G.; Potolias, C.; Bandekas, D.V. Wind Turbine Blade Nondestructive Testing with a Transportable Radiography System. Sci. Technol. Nucl. Install. 2011, 2011, 347320. [Google Scholar] [CrossRef]
- Lee, H.; Hwang, Y.M.; Lee, J.; Kim, N.; Ko, S.-K. A Drone-Driven X-Ray Image-Based Diagnosis of Wind Turbine Blades for Reliable Operation of Wind Turbine. IEEE Access 2024, 12, 56141–56158. [Google Scholar] [CrossRef]
- Yan, Q.; Che, X.; Li, S.; Wang, G.; Liu, X. π-FBG Fiber Optic Acoustic Emission Sensor for the Crack Detection of Wind Turbine Blades. Sensors 2023, 23, 7821. [Google Scholar] [CrossRef]
- Memari, M.; Shakya, P.; Shekaramiz, M.; Seibi, A.C.; Masoum, M.A.S. Review on the Advancements in Wind Turbine Blade Inspection: Integrating Drone and Deep Learning Technologies for Enhanced Defect Detection. IEEE Access 2024, 12, 33236–33282. [Google Scholar] [CrossRef]
- Hang, X.; Zhu, X.; Gao, X.; Wang, Y.; Liu, L. Study on Crack Monitoring Method of Wind Turbine Blade Based on AI Model: Integration of Classification, Detection, Segmentation and Fault Level Evaluation. Renew. Energy 2024, 224, 120152. [Google Scholar] [CrossRef]
- Movsessian, A.; García Cava, D.; Tcherniak, D. An Artificial Neural Network Methodology for Damage Detection: Demonstration on an Operating Wind Turbine Blade. Mech. Syst. Signal Process. 2021, 159, 107766. [Google Scholar] [CrossRef]
- Ganeriwala, S.; Jun, Y.; Richardson, M. Using Modal Analysis for Detecting Cracks in Wind Turbine Blades. Sound Vib. 2011, 45, 10–13. [Google Scholar]
- Ulriksen, M.D.; Skov, J.F.; Dickow, K.A.; Kirkegaard, P.H.; Damkilde, L. Modal Analysis for Crack Detection in Small Wind Turbine Blades. In Key Engineering Materials; Trans Tech Publications, Ltd.: Stafa-Zurich, Switzerland, 2013; Volumes 569–570, pp. 603–610. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Arrigan, J.; Basu, B. Damage Detection in Wind Turbine Blades Using Time-Frequency Analysis of Vibration Signals. In Proceedings of the International Joint Conference on Neural Networks, Barcelona, Spain, 18–23 July 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Lorenzo, E.D.; Petrone, G.; Manzato, S.; Peeters, B.; Desmet, W.; Marulo, F. Damage Detection in Wind Turbine Blades by Using Operational Modal Analysis. Struct. Health Monit. 2016, 15, 289–301. [Google Scholar] [CrossRef]
- Pacheco-Chérrez, J.; Cárdenas, D.; Delgado-Gutiérrez, A.; Probst, O. Operational Modal Analysis for Damage Detection in a Rotating Wind Turbine Blade in the Presence of Measurement Noise. Compos. Struct. 2023, 321, 117298. [Google Scholar] [CrossRef]
- Rangel-Rodriguez, A.H.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P.; Bueno-Lopez, M.; Valtierra-Rodriguez, M. Analysis of Vibration Signals Based on Machine Learning for Crack Detection in a Low-Power Wind Turbine. Entropy 2023, 25, 1188. [Google Scholar] [CrossRef] [PubMed]
- Joshuva, A.; Sugumaran, V. Crack Detection and Localization on Wind Turbine Blade Using Machine Learning Algorithms: A Data Mining Approach. Struct. Durab. Health Monit. 2019, 13, 181–203. [Google Scholar] [CrossRef]
- Ogaili, A.A.F.; Jaber, A.A.; Hamzah, M.N. A Methodological Approach for Detecting Multiple Faults in Wind Turbine Blades Based on Vibration Signals and Machine Learning. Curved Layer. Struct. 2023, 10, 20220214. [Google Scholar] [CrossRef]
- Zabihi, A.; Aghdasi, F.; Ellouzi, C.; Singh, N.K.; Jha, R.; Shen, C. Non-Contact Wind Turbine Blade Crack Detection Using Laser Doppler Vibrometers. Energies 2024, 17, 2165. [Google Scholar] [CrossRef]
- Carrattieri, L.; Cravero, C.; Marsano, D.; Valenti, E.; Sishtla, V.; Halbe, C. The Development of Machine Learning Models for Radial Compressor Monitoring With Instability Detection. J. Turbomach. 2025, 147, 051004. [Google Scholar] [CrossRef]
- Saito, H.; Kanzaki, D.; Yonekura, K. Applications of machine learning in surge prediction for vehicle turbochargers. Mach. Learn. Appl. 2024, 16, 100560. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, X.; Xiong, Y.; Dai, F.; Zhang, Y. Intelligent Fault Diagnosis of Turbine Blade Cracks via Multiscale Sparse Filtering and Multi-Kernel Support Vector Machine for Information Fusion. Adv. Eng. Inf. 2023, 56, 101979. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z. Automatic Detection of Wind Turbine Blade Surface Cracks Based on UAV-Taken Images. IEEE Trans. Ind. Electron. 2017, 64, 7293–7303. [Google Scholar] [CrossRef]
- Ashkarkalaei, M.; Ghiasi, R.; Pakrashi, V.; Malekjafarian, A. An Unsupervised Damage Detection Method for an Operating Wind Turbine Blade. In Proceedings of the 11th European Workshop on Structural Health Monitoring (EWSHM 2024), Potsdam, Germany, 10–13 June 2024. [Google Scholar]
- Zhu, X.; Hang, X.; Gao, X.; Yang, X.; Xu, Z.; Wang, Y.; Liu, H. Research on Crack Detection Method of Wind Turbine Blade Based on a Deep Learning Method. Appl. Energy 2022, 328, 120241. [Google Scholar] [CrossRef]
- Xu, D.; Wen, C.; Liu, J. Wind Turbine Blade Surface Inspection Based on Deep Learning and UAV-Taken Images. J. Renew. Sustain. Energy 2019, 11, 053305. [Google Scholar] [CrossRef]
- Lee, N.; Woo, J.; Kim, S. A Deep Reinforcement Learning Ensemble for Maintenance Scheduling in Offshore Wind Farms. Appl. Energy 2025, 377, 124431. [Google Scholar] [CrossRef]
- Dervilis, N.; Choi, M.; Taylor, S.G.; Barthorpe, R.J.; Park, G.; Farrar, C.R.; Worden, K. On Damage Diagnosis for a Wind Turbine Blade Using Pattern Recognition. J. Sound Vib. 2014, 333, 1833–1850. [Google Scholar] [CrossRef]
- Calderano, P.; De Marins, D.B.; Ayala, H. A Comparison of Feature Extraction Methods for Crack and Ice Monitoring in Wind Turbine Blades: System Identification and Matrix Decomposition. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Vouliagmeni, Greece, 28 June–1 July 2022; pp. 779–784. [Google Scholar] [CrossRef]
- Rizos, P.; Aspragathos, N.; Dimarogonas, A. Identification of crack location and magnitude in a cantilever beam from the vibration modes. J. Sound Vib. 1990, 138, 381–388. [Google Scholar] [CrossRef]
- Saurabh, U.S.; Santosh, J.C.; Nilaj, N.D. Effect of crack on natural frequency for beam type of structures. AIP Conf. Proc. 2017, 1859, 020056. [Google Scholar] [CrossRef]
- Pooja, D.M.; Aditya, A.Y.; Anamika, M.P.; Venkatesh, A.K. Comparative analysis of natural frequency for cantilever beam through analytical and software approach. Int. Res. J. Eng. Technol. 2018, 5, 656–671. [Google Scholar]
- De Felice, A.; Sorrentino, S. Effects of anisotropic supports on the stability of parametrically excited slender rotors. Nonlinear Dyn. 2022, 109, 793–813. [Google Scholar] [CrossRef]
- Nyquist, H. Certain Topics in Telegraph Transmission Theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]





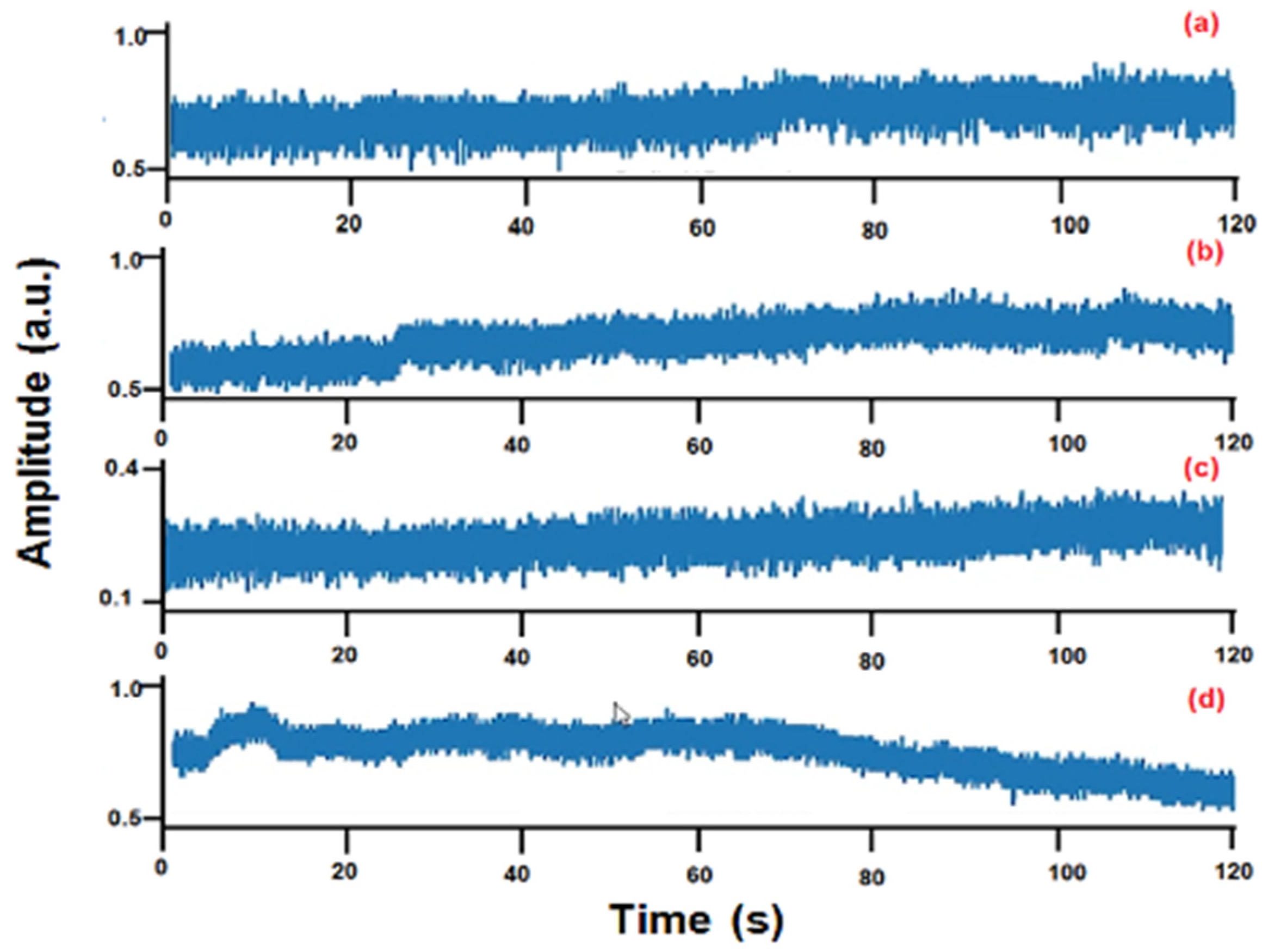

| WTB Condition | Class Label |
|---|---|
| Healthy | H |
| Crack in tip | CT |
| Crack in midsection | CM |
| Crack in root | CR |
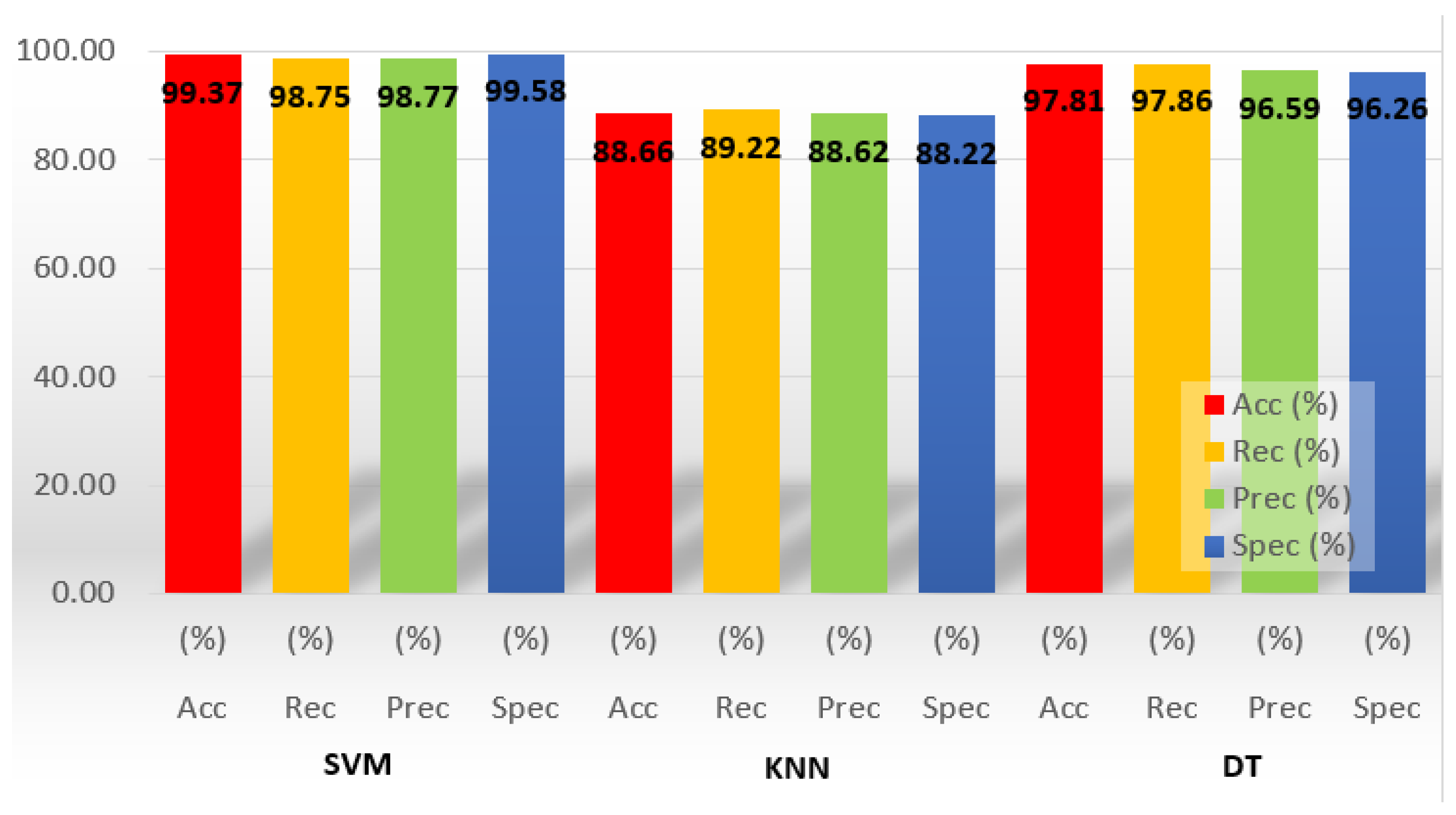
| WTB Condition | SVM | KNN | DT | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc (%) | Rec (%) | F1 (%) | Prec (%) | Spec (%) | Acc (%) | Rec (%) | F1 (%) | Prec (%) | Spec (%) | Acc (%) | Rec (%) | F1 (%) | Prec (%) | Spec (%) | |
| CR | 100 | 100 | 100 | 100 | 100 | 88.71 | 88.65 | 87.44 | 87.76 | 88.98 | 98.57 | 98.66 | 98.91 | 97.34 | 96.43 |
| CM | 98.75 | 96.66 | 97.47 | 98.30 | 99.44 | 87.67 | 88.54 | 86.63 | 87.90 | 86.30 | 95.42 | 96.66 | 95.37 | 96.78 | 95.24 |
| CT | 99.58 | 98.33 | 99.15 | 100 | 100 | 88.76 | 89.66 | 89.56 | 88.80 | 89.05 | 98.53 | 97.23 | 96.77 | 95.45 | 96.45 |
| H | 99.16 | 100 | 98.35 | 96.77 | 98.88 | 89.50 | 90.01 | 91.45 | 90.00 | 88.56 | 98.73 | 98.88 | 96.56 | 96.79 | 96.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sevilla-Camacho, P.Y.; Robles-Ocampo, J.B.; Rodríguez-Resendíz, J.; De la Cruz-Arreola, S.; Zuñiga-Reyes, M.A.; Hernández-Estrada, E.N. Crack Location in Wind Turbine Blades Using Vibration Signal and Support Vector Machine. Vibration 2025, 8, 20. https://doi.org/10.3390/vibration8020020
Sevilla-Camacho PY, Robles-Ocampo JB, Rodríguez-Resendíz J, De la Cruz-Arreola S, Zuñiga-Reyes MA, Hernández-Estrada EN. Crack Location in Wind Turbine Blades Using Vibration Signal and Support Vector Machine. Vibration. 2025; 8(2):20. https://doi.org/10.3390/vibration8020020
Chicago/Turabian StyleSevilla-Camacho, Perla Y., José B. Robles-Ocampo, Juvenal Rodríguez-Resendíz, Sergio De la Cruz-Arreola, Marco A. Zuñiga-Reyes, and Edwin N. Hernández-Estrada. 2025. "Crack Location in Wind Turbine Blades Using Vibration Signal and Support Vector Machine" Vibration 8, no. 2: 20. https://doi.org/10.3390/vibration8020020
APA StyleSevilla-Camacho, P. Y., Robles-Ocampo, J. B., Rodríguez-Resendíz, J., De la Cruz-Arreola, S., Zuñiga-Reyes, M. A., & Hernández-Estrada, E. N. (2025). Crack Location in Wind Turbine Blades Using Vibration Signal and Support Vector Machine. Vibration, 8(2), 20. https://doi.org/10.3390/vibration8020020








