Investigation of Bunch Compressor and Compressed Electron Beam Characteristics by Coherent Transition Radiation
Abstract
:1. Introduction
2. Magnetic Chicane Bunch Compressor
3. Coherent Transition Radiation
4. Measurement Set-Up
4.1. Spatial Distribution of the CTR
4.2. CTR Intensity
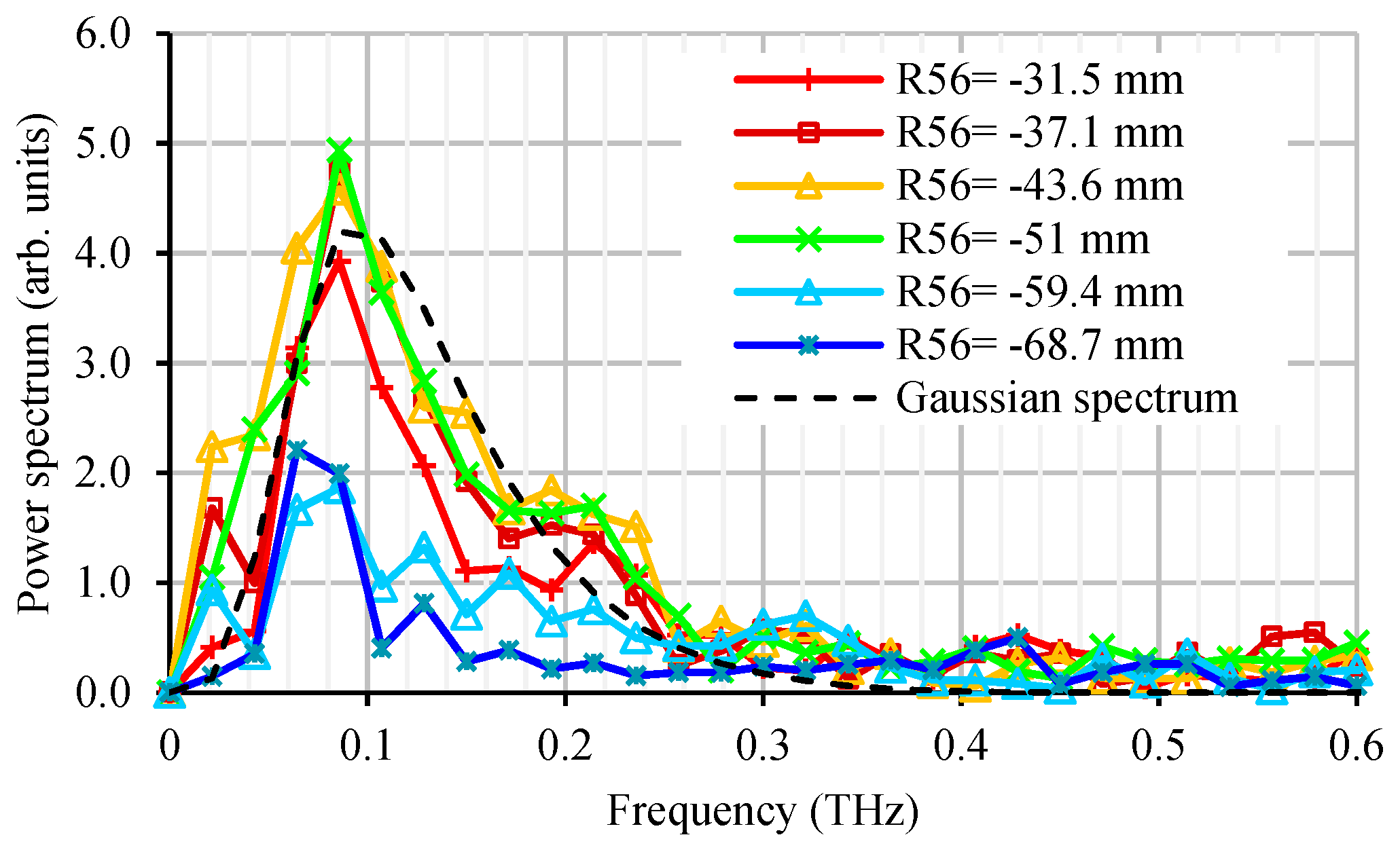
4.3. CTR Spectrum
5. Results and Analysis
5.1. Spatial Distributions of the CTR
5.2. Bunch Compression Characteristics
5.3. Maximum Bunch Compression Condition
5.4. Bunch Length Estimation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tonouchi, M. Cutting-edge Terahertz Technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Doria, A.; Gallerano, G.P.; Giovenale, E.; Messina, G.; Spassovsky, I. Enhanced coherent emission of terahertz radiation by energy-phase correlation in a bunched electron beam. Phys. Rev. Lett. 2004, 93, 264801. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Huang, S.; Lin, L.; Wang, F.; Zhu, F.; Feng, L.; Yang, L.; Wang, Z.; Fan, P.; Hao, J.; et al. Superradiant THz undulator radiation source based on a superconducting photo-injector. Nucl. Instrum. Methods Phys. Res. A 2016, 820, 75–79. [Google Scholar] [CrossRef]
- Suphakul, S.; Tsugamura, Y.; Zen, H.; Kii, T.; Ohgaki, H. Development of compact THZ-FEL system at Kyoto university. In Proceedings of the 36th Free Electron Laser Conference, Basel, Switzerland, 25–29 August 2014; pp. 501–504. [Google Scholar]
- Terunuma, N.; Murata, A.; Fukuda, M.; Hirano, K. Improvement of an S-band RF gun with a Cs2Te photocathode. Nucl. Instrum. Methods Phys. Res. A 2010, 613, 1–8. [Google Scholar] [CrossRef]
- Damminsek, K.; Rimjaem, S.; Suphakul, S.; Thongbai, C. Electron Beam Properties from a Compact Seeded Terahertz FEL Amplifier at Kyoto University. In Proceedings of the 37th Free Electron Laser Conference, Daejeon, Korea, 23–28 August 2015; pp. 85–88. [Google Scholar]
- Zen, H.; Suphakul, S.; Kii, T.; Masuda, K.; Ohgaki, H. Present status and Perspectives of Long wavelength Free electron Laser at Kyoto University. Phys. Procedia 2016, 84, 47–53. [Google Scholar] [CrossRef]
- Zen, H.; Suphakul, S.; Kii, T.; Ohgaki, H. Development of Photocathode Drive Laser System for RF Guns in KU-FEL. In Proceedings of the 36th Free Electron Laser Conference, Basel, Switzerland, 25–29 August 2014. [Google Scholar]
- Van der Geer, S.B.; de Loos, M.J. General Particle Tracer: A 3D code for accelerator and beamline design. In Proceedings of the 6th European Particle Accelerator Conference, Stockholm, Sweden, 22–26 June 1998; p. 1245. [Google Scholar]
- Barry, W. An autocorrelation technique for measuring sub-picosecond bunch length using coherent transition radiation. In Proceedings of the Workshop on Advanced Beam Instrumentation, Tsukuba, Japan, 22–24 April 1991; pp. 224–235. [Google Scholar]
- Lihn, H.C.; Kung, P.; Settakorn, C.; Wiedemann, H.; Bocek, D. Measurment of subpicosecond electron pulses. Phys. Rev. E 1996, 53, 6413. [Google Scholar] [CrossRef]
- Settakorn, C. Generation and Use of Coherent Transition Radiation from Short Electron Bunches. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2001. [Google Scholar] [Green Version]
- Zen, H.; Okumura, J.; Tagiri, S.; Krainara, S.; Suphakul, S.; Torgasin, K.; Kii, T.; Masuda, K.; Ohagaki, H. Present Status of Infrared FEL Facility at Kyoto University. In Proceedings of the 38th Free Electron Laser Conference, Santa Fe, NM, USA, 20–25 August 2017. [Google Scholar]
- General Purpose Detector. Available online: http://www.millitech.com/MMW-MixerDetector-DET.htm (accessed on 31 October 2018).
- Instrument for THz-Wave. Available online: http://phluxi.com/en/product/thz_peripheral/ (accessed on 31 October 2018).
- Sei, N.; Naional Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Ibaraki, Japan. Personal communication, 2016.
- Yang, Y.; Shutler, A.; Grischkowsky, D. Measurement of the transmission of atmosphere from 0.2 to 2 THz. Opt. Express 2011, 19, 8830–8838. [Google Scholar] [CrossRef] [PubMed]














| Parameters | Value |
|---|---|
| Beam energy | 4.6 MeV |
| RF power for the RF-gun | 9 MW |
| RF frequency/RF pulse duration Number of RF micropulses per macropulse | 2856 MHz/2 μs 5700 |
| 1st-order momentum compaction factor (R56) | min−68.7 mm |
| Solenoid magnetic field | 194 mT |
| Laser repetition rate of electron micropulse | 89.25 MHz |
| Laser pulse duration (FWHM) | ~6 ps |
| Laser temporal/spatial distribution | Gaussian/Gaussian |
| Laser size at cathode (horizontal/vertical) | 0.4/0.5 mm (rms) |
| Number of laser pulses per macropulse | 1 to 4 pulses |
| Laser pulse energy per macropulse | 133 to 300 μJ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suphakul, S.; Zen, H.; Kii, T.; Ohgaki, H. Investigation of Bunch Compressor and Compressed Electron Beam Characteristics by Coherent Transition Radiation. Particles 2019, 2, 32-43. https://doi.org/10.3390/particles2010003
Suphakul S, Zen H, Kii T, Ohgaki H. Investigation of Bunch Compressor and Compressed Electron Beam Characteristics by Coherent Transition Radiation. Particles. 2019; 2(1):32-43. https://doi.org/10.3390/particles2010003
Chicago/Turabian StyleSuphakul, Sikharin, Heishun Zen, Toshiteru Kii, and Hideaki Ohgaki. 2019. "Investigation of Bunch Compressor and Compressed Electron Beam Characteristics by Coherent Transition Radiation" Particles 2, no. 1: 32-43. https://doi.org/10.3390/particles2010003
APA StyleSuphakul, S., Zen, H., Kii, T., & Ohgaki, H. (2019). Investigation of Bunch Compressor and Compressed Electron Beam Characteristics by Coherent Transition Radiation. Particles, 2(1), 32-43. https://doi.org/10.3390/particles2010003






