Status and Perspectives of 2ϵ, ϵβ+ and 2β+ Decays
Abstract
:1. Introduction
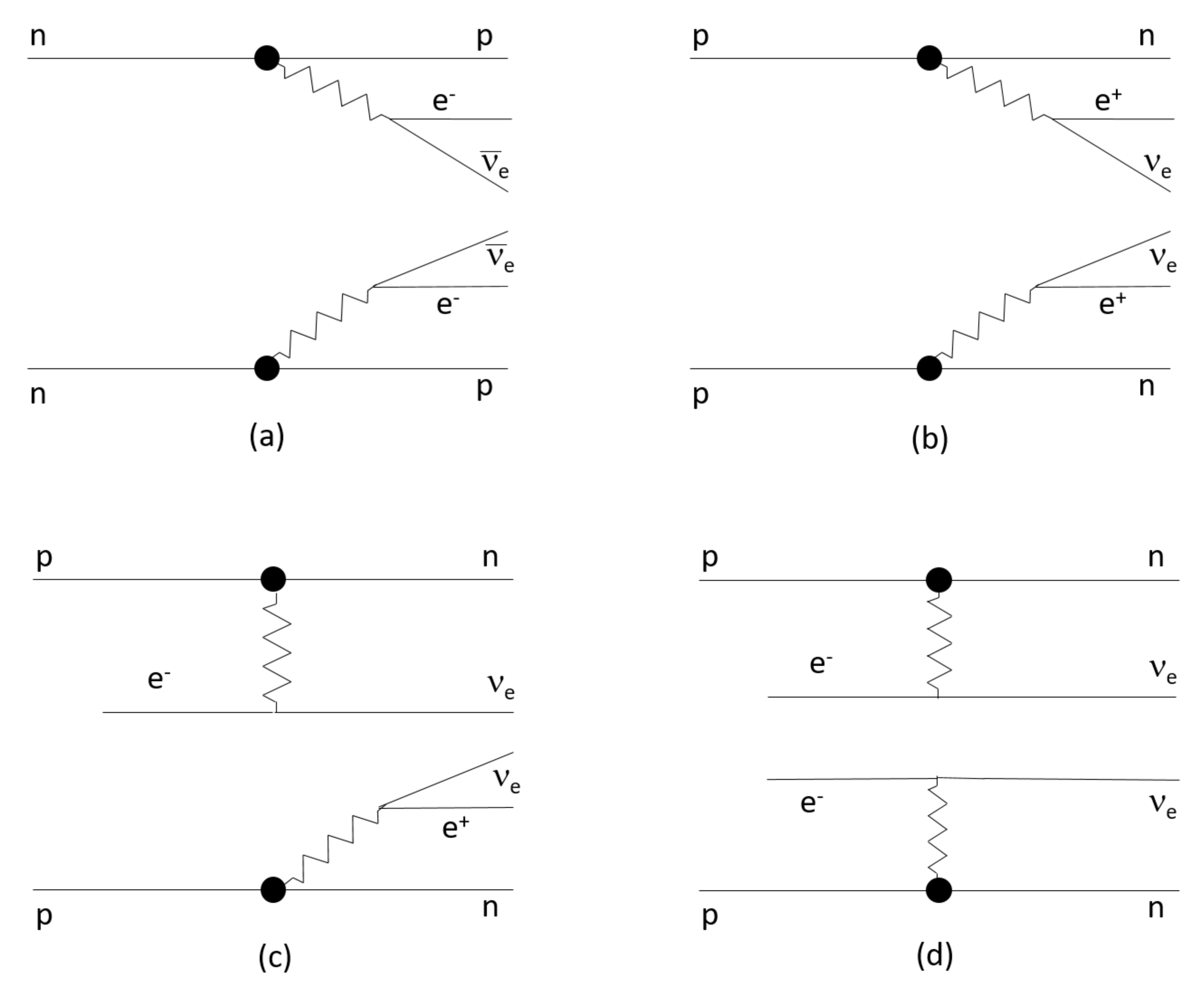
2. Experimental Techniques to Study the Double Beta Decay in Positive Modes
- cosmic rays: this implies installing the experiment deep underground;
- neutrons that are induced by muons and neutrinos in the rock or by (,n) reactions: a suitable dedicated shield has to be implemented when necessary;
- natural radioactivity due to the U/Th chains, K isotope, Pb, etc.;
- anthropogenic activities, in particular for Cs;
- cosmogenic activation: radio-isotopes that are induced by spallation in the material during their storage at sea level or during transportation; and,
- radio-isotopic activation that is induced by neutron calibration procedures when applied.
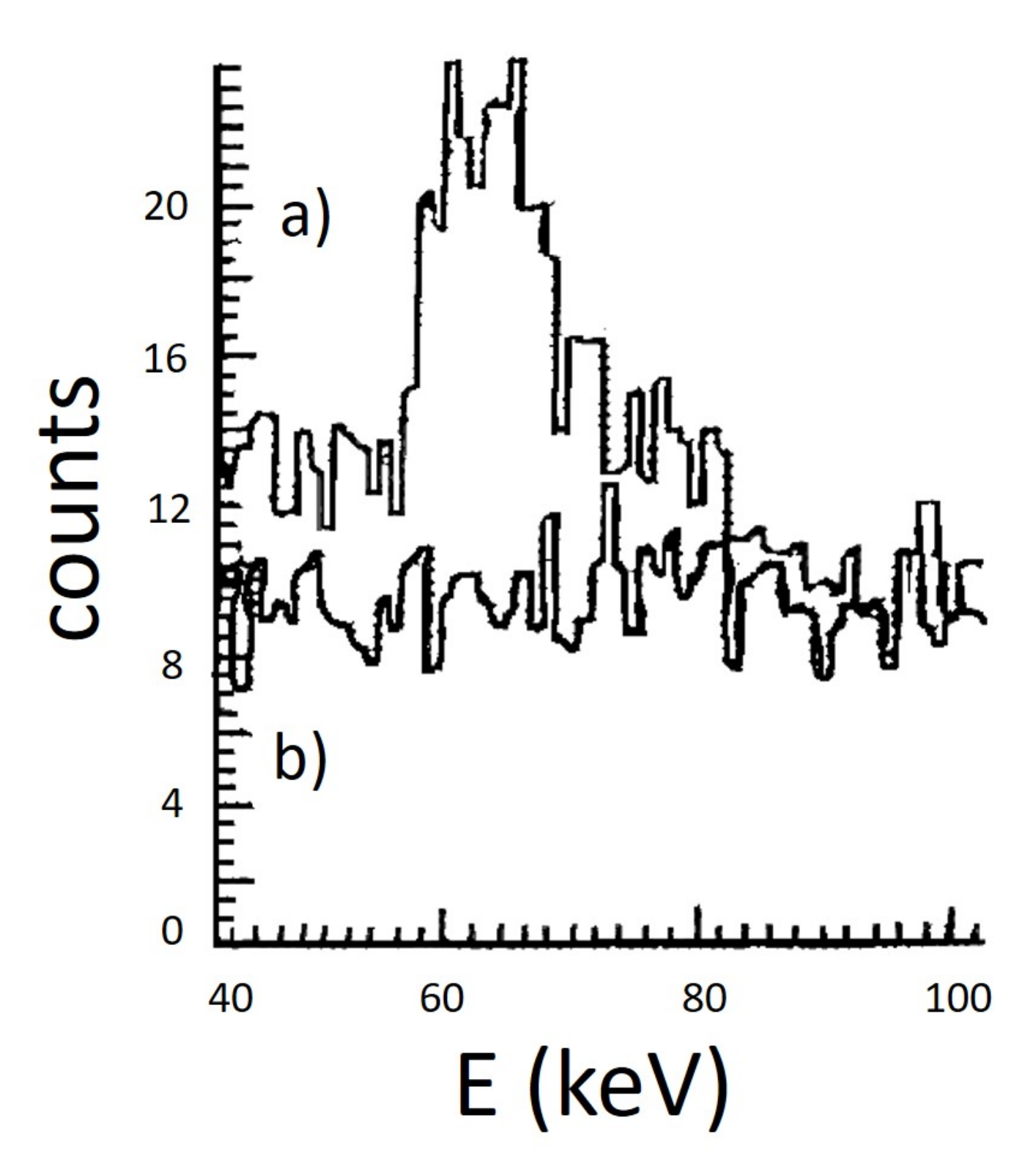
2.1. Examples of Energy Distributions in Case of an Experiment of DBD+ with “Source = Detector”
3. Status of Experimental Sensitivities
3.1. Positive Claims for Some DBD+ Modes
3.2. Experiments Using Solid Detectors as “Source = Detector”
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Ca →Ar | 193.51(2) | 96.941(156) | ≥ [CaWO (SB)] [200] | – | |
| ≥ [CaF(Eu) (S)] [208] | ≥ [CaWO (SB)] [200] | ||||
| Zn →Ni | 1094.9(7) | 49.17(75) | 2K | ≥ [ZnWO (S)] [100] | – |
| – | ≥ [HPGe] [209] | ||||
| ≥ (a) [ZnWO (S)] [100] | ≥ [ZnSe (SB)] [210] | ||||
| ≥ (b) [HPGe] [209] | |||||
| Te →Sn | 1730(3) | 0.09(1) | ≥ [CdTe, CdZnTe (SC)] [211] | – | |
| KK/KL/LL | – | ≥ [HPGe] [212] | |||
| ( 1171.3) | ≥ (b) [HPGe] [212] | ≥ [CdZnTe (SC)] [213] | |||
| ≥ [TeO (B)] [214] | ≥ [TeO (B)] [203] | ||||
| W →Hf | 143.23(28) | 0.12(1) | KK | ≥ [CaWO (SB)] [200] | – |
| – | ≥ [CaWO (SB)] [200] | ||||
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Ce →Ba | 2378.55(27) | 0.186(2) | KK/KL/LL | ≥ [CeCl (S)] [86] | ≥ [HPGe] [224] |
| ( 818.5) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 1551.0) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 1579.0) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2080.1) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2128.9) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2141.4) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2222.7) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2315.3) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ≥ (a) [HPGe] [224] | ≥ [HPGe] [224] | ||||
| ( 818.5) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ≥ [HPGe] [224] | ≥ [HPGe] [224] | ||||
| Sm →Nd | 1782.4(8) | 3.08(4) | KK/KL/LL | – | ≥ [HPGe] [56] |
| KK ( 696.6) | ≥ [HPGe] [56] | ≥ [HPGe] [56] | |||
| KK ( 1560.9) | ≥ [HPGe] [56] | ≥ [HPGe] [56] | |||
| ≥ [HPGe] [56] | ≥ [HPGe] [56] | ||||
| ( 696.6) | ≥ [HPGe] [56] | ≥ [HPGe] [56] | |||
| Gd →Sm | 55.69(18) | 0.20(3) | ≥ (b,c) [GEO] [229] | ||
| Dy →Gd | 2005.95(10) | 0.056(3) | KK/KL/LL | ≥ [HPGe] [230] | ≥ [HPGe] [230] |
| ( 89.0) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1049.5) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1129.4) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1154.2) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1168.2) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (0 1715.2) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (2 1771.1) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (2 1827.8) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (0 1851.3) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| KK ( 1914.8) (d) | ≥ (c) [HPGe] [230] | ||||
| KL ( 1946.4) (d) | ≥ (c) [HPGe] [230] | ≥ [HPGe] [231] | |||
| KL ( 1952.4) (d) | ≥ (c) [HPGe] [230] | ≥ [HPGe] [231] | |||
| 2L ( 1988.5) (d) | ≥ (c) [HPGe] [230] | ≥ [HPGe] [231] | |||
| 2L ( 2003.7) (d) | ≥ [HPGe] [230] | ≥ [HPGe] [231] | |||
| ≥ (c) [HPGe] [230] | |||||
| ( 89.0) | ≥ (c) [HPGe] [230] | ||||
3.3. Experiments Based on the “Source ≠ Detector” Approach
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Ar →Se | 432.58(19) | 0.3336(210) | – | ≥ [HPGe] [233] | |
| Cr →Ti | 1169.6(5) | 4.345(13) | ≥ (68%)(a) [HPGe] [234] | ||
| ≥ (95%)(a) [HPGe] [235] | |||||
| Fe →Cr | 680.3(4) | 5.845(105) | KK/KL/LL | – | ≥ (68%) [HPGe] [236] |
| Ni →Fe | 1926.4(3) | 68.0769(100) | – | ≥(b) [HPGe] [237] | |
| (, 810.8) | ≥ [HPGe] [237] | – | |||
| (, 1674.7) | ≥ [HPGe] [237] | – | |||
| ≥ [HPGe] [237] | – | ||||
| (, 810.8) | ≥ [HPGe] [237] | – | |||
| Se →Ge | 1209.24(1) | 0.86(3) | 2 | ≥ (a) [HPGe] [238] | |
| KK/KL/LL | – | ≥ [HPGe] [239] | |||
| KK/KL/LL (, 595.9) | ≥ [HPGe] [239] | ≥ [HPGe] [239] | |||
| (, 1204.2) | ≥ (a,c) [HPGe] [240] | ≥ [HPGe] [239] | |||
| ≥ (a) [HPGe] [239] | |||||
| Ru →Mo | 2714.50(12) | 5.54(14) | KK/KL/LL | – | ≥ [HPGe] [241] |
| KL (b)/LL (b) | – | ≥ [HPGe] [241] | |||
| ( 778.2) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1148.1) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1497.8) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1625.9) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 2095.7) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 2426.1) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 2622.5) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ≥ [HPGe] [241] | ≥ [HPGe] [241] | ||||
| ( 778.2) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1148.1) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1497.8) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1625.9) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ≥ [HPGe] [241] | ≥ [HPGe] [241] | ||||
| Pd →Ru | 1203.3(4) | 1.02(1) | – | – | |
| (, 475.1) | ≥(a) [HPGe] [242] | ||||
| (, 943.7) | ≥(a) [HPGe] [242] | ||||
| (, 1103.0) | ≥(a) [HPGe] [242] | ||||
| – | – | ||||
| (, 475.1) | ≥(a) [HPGe] [242] | ||||
| Sn →Cd | 1919.80(16) | 0.97(1) | KK/KL/LL | – | ≥ [HPGe] [243] |
| ( 617.5) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1224.3) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1312.4) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1415.5) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1433.3) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1468.8) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1870.7) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1871.0) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ≥ (a) [HPGe] [243] | |||||
| ( 617.5) | ≥ (a) [HPGe] [243] | ||||
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Dy →Gd | 282.2(24) | 0.095(3) | KK | ≥ [HPGe] [230] | ≥ [HPGe] [230] |
| ( 79.5) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| 2L ( 261.5) (a) | ≥ (b) [HPGe] [230] | ||||
| Er →Dy | 1846.96(30) | 0.139(5) | KK/KL/LL | ≥ [HPGe] [62] | ≥ [HPGe] [62] |
| ( 80.7) | ≥ [HPGe] [62] | – | |||
| ( 888.2) | ≥ [HPGe] [62] | – | |||
| ( 1400.3) | ≥ [HPGe] [62] | – | |||
| ( 1453.5) | ≥ [HPGe] [62] | – | |||
| ( 1666.3) | ≥ [HPGe] [62] | – | |||
| ( 1728.3) | ≥ [HPGe] [62] | – | |||
| KL ( 1782.7) | ≥ [HPGe] [62] | – | |||
| KK ( 80.7) | – | ≥ [HPGe] [62] | |||
| KK ( 888.2) | – | ≥ [HPGe] [62] | |||
| KK ( 1400.3) | – | ≥ [HPGe] [62] | |||
| KK ( 1453.5) | – | ≥ [HPGe] [62] | |||
| KK ( 1666.3) | – | ≥ [HPGe] [62] | |||
| KK ( 1728.3) | – | ≥ [HPGe] [62] | |||
| KL (a) ( 1782.7) | – | ≥ [HPGe] [62] | |||
| ≥ [HPGe] [62] | ≥ [HPGe] [62] | ||||
| ( 80.7) | ≥ [HPGe] [62] | ≥ [HPGe] [62] | |||
| Er →Dy | 25.08(11) | 1.601(3) | ≥(b,c) [GEO] [229] | ||
| Yb →Er | 1409.27(25) | 0.123(3) | KK/KL/LL | ≥ [HPGe] [57] | ≥ [HPGe] [57] |
| ( 78.8) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| ( 821.2) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| ( 1217.2) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| ( 1276.3) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| MM ( 1403.7) (a) | – | ≥ [HPGe] [57] | |||
| ≥ [HPGe] [57] | ≥ [HPGe] [57] | ||||
| ( 78.8) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| Hf →Yb | 1100.0(23) | 0.16(12) | KK/KL/LL | ≥ [HPGe] [250] | ≥ [HPGe] [250] |
| KK/KL/LL ( 76.5) | ≥ [HPGe] [250] | ≥ [HPGe] [250] | |||
| K | ≥(b) [HPGe] [250] | ||||
| L | ≥(b) [HPGe] [250] | ||||
| Os →W | 1452.8(7) | 0.02(2) | KK/KL/LL | ≥ [HPGe] [251] | ≥ [HPGe] [252] |
| KK/KL/2 ( 112.2) | ≥ [HPGe] [251] | ≥ [HPGe] [251,252] | |||
| ( 903.3) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| ( 1002.5) | ≥ [HPGe] [252] | ≥ [HPGe] [252] | |||
| ( 1121.5) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| KK ( 1322.2) | ≥ [HPGe] [251] | ≥ (a) [HPGe] [251] | |||
| KL ( 1386.3) | ≥ [HPGe] [251] | ≥ (a) [HPGe] [252] | |||
| LL ( 1425.0) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| LL ( 1431.0) | ≥ [HPGe] [251] | ≥ (a) [HPGe] [252] | |||
| ( 112.2) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| ( 112.2) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| Pt →Os | 1401.3(4) | 0.012(2) | KK/KL/LL | ≥ [HPGe] [253] | ≥ [HPGe] [253] |
| KK ( 186.7) | ≥ [HPGe] [253] | – | |||
| KK ( 558.0) | ≥ [HPGe] [253] | – | |||
| KK ( 911.8) | ≥ [HPGe] [253] | – | |||
| KK ( 1114.7) | ≥ [HPGe] [253] | – | |||
| ( 186.7) | – | ≥ [HPGe] [253] | |||
| ( 558.0) | – | ≥ [HPGe] [253] | |||
| ( 911.8) | – | ≥ [HPGe] [253] | |||
| ( 1114.7) | – | ≥ [HPGe] [253] | |||
| MM/MN/NN (0, 1, 2 1382.4) (a) | ≥(b) [HPGe] [253] | ||||
| ≥ [HPGe] [253] | ≥ [HPGe] [253] | ||||
| ( 186.7) | ≥(b) [HPGe] [253] | ||||
| Hg →Pt | 818.6(30) | 0.15(1) | KK | – | ≥ [HPGe] [254] |
| KK ( 355.7) | ≥(b) [HPGe)] [254] | ||||
4. Perspectives and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weizsäcker, C.F. Zur Theorie der Kernmassen. Z. Phys. 1935, 96, 431. [Google Scholar] [CrossRef]
- Goeppert-Mayer, M. Double Beta-Disintegration. Phys. Rev. 1935, 48, 512. [Google Scholar] [CrossRef]
- Suhonen, J.; Civitarese, O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys. Rep. 1998, 300, 123–214. [Google Scholar] [CrossRef]
- Mohapatra, R.N. New contributions to neutrinoless double-beta decay in supersymmetric theories. Phys. Rev. D 1986, 34, 3457–3461. [Google Scholar] [CrossRef]
- Babu, K.S.; Mohapatra, R.N. New Vector-Scalar contributions to neutrinoless double beta decay and constraints on R-parity violation. Phys. Rev. Lett. 1995, 75, 2276–2279. [Google Scholar] [CrossRef] [Green Version]
- Faessler, A.; Gutsche, T.; Kovalenko, S.; Šimkovic, F. Pion dominance in R-parity violating supersymmetry induced neutrinoless double beta decay. Phys. Rev. D 2008, 77, 113012. [Google Scholar] [CrossRef] [Green Version]
- Vergados, J.D. Pion-double-charge-exchange contribution to neutrinoless double-decay. Phys. Rev. D 1982, 25, 914–917. [Google Scholar] [CrossRef]
- Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Kovalenko, S.G. New contributions to supersymmetric mechanism of neutrinoless double beta decay. Phys. Lett. B 1995, 352, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Frank, M.; Majumdar, C.; Poulose, P.; Senapati, S.; Yajnik, U.A. Exploring 0νββ and leptogenesis in the alternative left-right model. Phys. Rev. D 2020, 102, 075020. [Google Scholar] [CrossRef]
- Mitra, M.; Senjanović, G.; Vissani, F. Neutrinoless double beta decay and heavy sterile neutrinos. Nucl. Phys. B 2012, 856, 26–73. [Google Scholar] [CrossRef] [Green Version]
- Masaru Doi, M.; Kotani, T.; Takasugi, E. Double beta decay and Majorana neutrino. Prog. Theo. Phys. Supp. 1985, 83, 1–175. [Google Scholar]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 8, 083C01. [Google Scholar]
- Hirsch, H. Calculation of double beta plus decay matrix elements. Nulc. Phys. A 1994, 557, 411c–414c. [Google Scholar] [CrossRef]
- Tretyak, V.I.; Zdesenko, Y.G. Tables of double beta decay data: An update. Atom. Data Nucl. Data Tabl. 2020, 80, 83–116. [Google Scholar] [CrossRef]
- Maalampi, J.; Suhonen, J. Neutrinoless Double β+/EC Decays. Adv. High Energy Phys. 2013, 2013, 505874. [Google Scholar] [CrossRef]
- Winter, R.G. Double K capture and single K capture with positron emission. Phys. Rev. 1955, 100, 142–144. [Google Scholar] [CrossRef]
- Voloshin, M.B.; Mitselmakher, G.V.; Eramzhyan, R.A. Conversion of an atomic electron into a positron and double β+ decay. JETP Lett. 1982, 35, 656–659. [Google Scholar]
- Bernabeu, J.; De Rujula, A.; Jarlskog, C. Neutrinoless double electron capture as a tool to measure the electron neutrino mass. Nucl. Phys. B 1983, 223, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless double-electron capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar] [CrossRef]
- Krivoruchenko, M.I.; Šimkovic, F.; Frekers, D.; Faessler, D. Resonance enhancement of neutrinoless double electron capture. Nucl. Phys. A 2011, 859, 140. [Google Scholar] [CrossRef] [Green Version]
- Georgi, H.M.; Glashow, S.L.; Nussinov, S. Unconventional model of neutrino masses. Nucl. Phys. B 1981, 193, 297–316. [Google Scholar] [CrossRef]
- Eliseev, S.A.; Novikov, Y.N.; Blaum, K. Search for resonant enhancement of neutrinoless double-electron capture by high-precision Penning-trap mass spectrometry. J. Phys. G 2012, 39, 124003. [Google Scholar] [CrossRef]
- Klapdor-Kleingrothaus, H.V.; Krivosheina, I.V. Nuclear Double Beta Decay, Fundamental Particle Physics, Hot Dark Matter, And Dark Energy. In Proceedings of the 7th International Heidelberg Conference: Dark Matter in Astrophysics and Particle Physics, Christchurch, New Zealand, 18–24 January 2009; pp. 137–169. [Google Scholar]
- Kuzmin, V.A.; Rubakov, V.A.; Shaposhnikov, M.E. On anomalous electroweak baryon-number non-conservation in the early universe. Phys. Lett. B 1985, 155, 36–42. [Google Scholar] [CrossRef]
- Barabash, A.S. Possibilities of future double beta decay experiments to investigate inverted and normal ordering region of neutrino mass. Front. Phys. 2019, 6, 160. [Google Scholar] [CrossRef] [Green Version]
- Gando, A.; Gando, Y.; Hachiya, T.; Hayashi, A.; Hayashida, S.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; Karino, Y.; Koga, M.; et al. Search for Majorana Neutrinos Near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys. Rev. Lett. 2016, 117, 082503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adams, D.Q.; Alduino, C.; Alfonso, K.; Avignone, F.T.; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Biassoni, M.; Branca, A.; et al. Improved Limit on Neutrinoless Double-Beta Decay in 130Te with CUORE. Phys. Rev. Lett. 2020, 124, 122501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agostini, M.; Araujo, G.R.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; et al. Final Results of GERDA on the Search for Neutrinoless Double–β Decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Baker, J.D.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Brudanin, V.; Busto, J.; et al. Results of the search for neutrinoless double-β decay in 100Mo with the NEMO-3 experiment. Phys. Rev. D 2015, 92, 072011. [Google Scholar] [CrossRef] [Green Version]
- Tretyak, V.I.; Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Aurora experiment: Final results of studies of 116Cd 2β decay with enriched 116CdWO4 crystal scintillators. AIP Conf. Proc. 2019, 2165, 020029. [Google Scholar]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; et al. Final results of the Aurora experiment to study 2β decay of 116Cd with enriched 116CdWO4 crystal scintillators. Phys. Rev. D 2018, 98, 092007. [Google Scholar] [CrossRef] [Green Version]
- Abada, A.; Bhattacharyya, G. Impact of CP phases on neutrinoless double beta decay. Phys. Rev. D 2003, 68, 033004. [Google Scholar] [CrossRef] [Green Version]
- Cremonesi, O.; Pavan, M. Challenges in Double Beta Decay. Adv. High Energy Phys. 2014, 2014, 951432. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Giunti, C. Neutrinoless double-beta decay: A probe of physics beyond the Standard Model. Int. J. Mod. Phys. A 2015, 30, 1530001. [Google Scholar] [CrossRef] [Green Version]
- Suhonen, J.T. Value of the axial-vector coupling strength in β and ββ decays: A review. Front. Phys. 2017, 5, 55. [Google Scholar] [CrossRef]
- Beringer, J.; Arguin, J.F.; Barnett, R.M.; Copic, K.; Dahl, O.; Groom, D.E.; Lin, C.J.; Lys, J.; Murayama, H.; Wohl, C.G.; et al. Review of particle physics. Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef] [Green Version]
- Engel, J.; Menendez, J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: A review. Rep. Prog. Phys. 2017, 80, 046301. [Google Scholar] [CrossRef] [PubMed]
- Suhonen, J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys. Rev. C 2017, 96, 055501. [Google Scholar] [CrossRef] [Green Version]
- Suhonen, J.; Kostensalo, J. Double β decay and the axial strength. Front. Phys. 2019, 7, 00029. [Google Scholar] [CrossRef]
- Ejiri, H. Axial-vector weak coupling at medium momentum for astro neutrinos and double beta decays. J. Phys. G Nucl. Part. Phys. 2019, 46, 125202. [Google Scholar] [CrossRef] [Green Version]
- Ejiri, H.; Suhonen, J.; Zuber, K. Neutrino–nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys. Rep. 2019, 797, 1–102. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Incicchitti, A.; Merlo, V. Double beta decay to excited states of daughter nuclei. Universe 2020, 6, 239. [Google Scholar] [CrossRef]
- Ejiri, H.; Elliott, S.R. Charged current neutrino cross section for solar neutrinos, and background to ββ(0ν) experiments. Phys. Rev. C 2014, 89, 055501. [Google Scholar] [CrossRef] [Green Version]
- Ianni, A. Considerations on Underground Laboratories. J. Phys. Conf. Ser. 2020, 1342, 012003. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Di Nicolantonio, W.; Ignesti, G.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Ding, L.K.; Kuang, H.H.; et al. Performances of the ≃100 kg NaI(Tl) set-up of the DAMA experiment at Gran Sasso. Nuovo Cimento A 1999, 112, 6. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; De Pascale, M.P.; Paoluzi, L.; Santonico, R.; Taborgna, R.; Iucci, N.; Villoresi, G. Deep Underground Neutron Flux Measurement With Large BF3 Counters. Nuovo Cimento A 1998, 101, 959–966. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Borovlev, Y.A.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kobychev, V.V.; et al. Improvement of radiopurity level of enriched 116CdWO4 and ZnWO4 crystal scintillators by recrystallization. Nucl. Instrum. Methods 2016, 883, 77–81. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Klavdiinienko, V.R.; et al. Search for Double Beta Decay of 106Cd with an Enriched 106CdWO4 Crystal Scintillator in Coincidence with CdWO4 Scintillation Counters. Universe 2020, 6, 182. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Kobychev, V.V.; Kovtun, G.P.; et al. Search for α decay of naturally occurring osmium nuclides accompanied by γ quanta. Phys. Rev. C 2020, 102, 024605. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Kasperovych, D.V.; et al. Low background scintillators to investigate rare processes. JINST 2020, 15, C07037. [Google Scholar] [CrossRef]
- Caracciolo, V.; Nagorny, S.S.; Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Incicchitti, A.; Laubenstein, M.; Merlo, V.; Nisi, S.; et al. Search for α decay of naturally occurring Hf-nuclides using a Cs2HfCl6 scintillator. Nucl. Phys. A 2002, 1002, 121941. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Cherubini, N.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Merlo, V.; et al. Developments and improvements of radiopure ZnWO4 anisotropic scintillators. JINST 2020, 15, C05055. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.; Incicchitti, A.; Kasperovych, D.; Merlo, V.; Polischuk, O.; et al. The Future Role of Inorganic Crystal Scintillators in Dark Matter Investigations. Instruments 2021, 5, 16. [Google Scholar] [CrossRef]
- Polischuk, O.G.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; et al. New limit on two neutrino electron capture with positron emission in 106Cd. AIP Conf. Proc. 2019, 2165, 020020. [Google Scholar]
- Kasperovych, D.V.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; et al. Study of double-β decay of 150Nd to the first 0+ excited level of 150Sm. AIP Conf. Proc. 2019, 2165, 020014. [Google Scholar]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Kropivyansky, B.N.; et al. First direct search for 2ϵ and ϵβ+ decay of 144Sm and 2β− decay of 154Sm. Eur. Phys. J. A 2019, 55, 201. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; di Vacri, M.L.; Incicchitti, A.; Kropivyansky, B.N.; et al. First search for 2ϵ and ϵβ+ processes in 168Yb. Nucl. Phys. A 2019, 990, 64–78. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Borovlev, Y.A.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Polischuk, O.G.; et al. New development of radiopure ZnWO4 crystal scintillators. Nucl. Instrum. Methods A 2019, 935, 89–94. [Google Scholar] [CrossRef]
- Di Marco, A.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; et al. Recent Developments and Results on Double Beta Decays with Crystal Scintillators and HPGe Spectrometry. Universe 2018, 4, 147. [Google Scholar] [CrossRef] [Green Version]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Dai, C.J.; et al. Search for rare processes with DAMA experimental set-ups. EPJ Web Conf. 2018, 182, 02027. [Google Scholar] [CrossRef] [Green Version]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; et al. Double beta decay of 150Nd to the first excited 0+ level of 150Sm: Preliminary results. Nucl. Phys. Atom. Energy 2018, 19, 95–102. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kropivyansky, B.N.; Laubenstein, M.; et al. First search for 2ϵ and ϵβ+ decay of 162Er and new limit on 2β− decay of 170Er to the first excited level of 170Yb. J. Phys. G 2018, 45, 095101. [Google Scholar] [CrossRef] [Green Version]
- Barabash, A.S.; Basharina-Freshville, A.; Blot, S.; Bongrand, M.; Bourgeois, C.; Breton, D.; Brudanin, V.; Burešovà, H.; Busto, J.; Caffrey, A.J.; et al. Calorimeter development for the SuperNEMO double beta decay experiment. Nucl. Instrum. Methods A 2017, 868, 98–108. [Google Scholar] [CrossRef]
- Ejiri, H.; Higa, K.; Kamada, T.; Kobiki, H.; Matsuoka, K.; Okada, K.; Sano, H.; Shibata, T.; Shima, T.; Tanabe, N.; et al. The high sensitivity beta-gamma spectrometer ELEGANTS V for rare β(e) and ββ(ee) decays. Nucl. Instrum. Methods A 1991, 302, 304–314. [Google Scholar] [CrossRef]
- Zuber, K. COBRA-double beta decay searches using CdTe detectors. Phys. Lett. B 2001, 519, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Ebert, J.; Fritts, M.; Gehre, D.; Gößling, C.; Göpfert, T.; Hagner, C.; Heidrich, N.; Klingenberg, R.; Köttig, T.; Kröninger, C.; et al. The COBRA demonstrator at the LNGS underground laboratory. Nucl. Instrum. Methods A 2016, 807, 114–120. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cerulli, R.; Danevich, F.A.; d’Angelo, A.; Goriletsky, V.I.; Grinyov, B.V.; Incicchitti, A.; Kobychev, V.V.; Laubenstein, M.; et al. 7Li solar axions: Preliminary results and feasibility studies. Nucl. Phys. A 2008, 806, 388. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Cappella, F.; Incicchitti, A.; Prosperi, D.; Castellano, S.; Cerulli, R.; et al. Search for possible charge non-conserving decay of 139La into 139Ce with LaCl3(Ce) scintillator. Ukr. J. Phys. 2006, 51, 1037. [Google Scholar]
- Belli, P.; Bernabei, R.; Dai, C.J.; He, H.L.; Ignesti, G.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; Montecchia, F.; Ponkratenko, O.A.; et al. New experimental limit on the electron stability and non-paulian transitions in iodine atoms. Phys. Lett. B 1999, 460, 236. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; He, H.L.; Ignesti, G.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; Montecchia, F.; Ponkratenko, O.A.; et al. New limits on the nuclear levels excitation of 127I and 23Na during charge nonconservation. Phys. Rev. C 1999, 60, 065501. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cerulli, R.; Montecchia, F.; Nozzoli, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; He, H.L.; Kuang, H.H.; et al. Search for solar axions by Primakoff effect in NaI crystals. Phys. Lett. B 2001, 515, 6. [Google Scholar] [CrossRef]
- Cappella, F.; Cerulli, R.; Incicchitti, A. A preliminary search for Q-balls by delayed coincidences in NaI(Tl). Eur. Phys. J. C 2002, 14, 1. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Incicchitti, A.; Prosperi, D.; Cerulli, R.; Dai, C.J.; et al. Search for spontaneous transition of nuclei to a superdense stat. Eur. Phys. J. A 2005, 23, 7. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Incicchitti, A.; Prosperi, D.; Cerulli, R.; Dai, C.J.; et al. A search for spontaneous emission of heavy clusters in the 127I nuclide. Eur. Phys. J. A 2005, 24, 51. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Dai, C.J.; d’Angelo, A.; He, H.L.; Incicchitti, A.; Kuang, H.H.; Ma, X.H.; et al. New search for processes violating the Pauli-Exclusion-Principle in Sodium and in Iodine. Eur. Phys. J. C 2009, 62, 327. [Google Scholar] [CrossRef] [Green Version]
- Bernabei, R.; Belli, P.; Montecchia, F.; De Sanctis, M.; Di Nicolantonio, W.; Incicchitti, A.; Prosperi, D.; Bacci, C.; Dai, C.J.; Ding, L.K.; et al. Search for non-paulian transitions in 23Na and 127I. Phys. Lett. B 1997, 408, 439. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cerulli, R.; Montecchia, F.; Amato, M.; Ignesti, G.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; He, H.L.; et al. Extended limits on neutral strongly interacting massive particles and nuclearites from NaI(Tl) scintillators. Phys. Rev. Lett. 1999, 83, 4918. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Danevich, F.A.; Incicchitti, A.; Tretyak, V.I. Experimental searches for rare alpha and beta decays. Eur. Phys. J. A 2019, 55, 140. [Google Scholar] [CrossRef] [Green Version]
- Barabash, A.S. Average and recommended half-life values for two-neutrino double beta decay: Upgrade-2019. AIP Conf. Proc. 2019, 2165, 020002. [Google Scholar]
- Belli, P.; Bernabei, R.; Boiko, R.A.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Search for double-β decay processes in 106Cd with the help of a 106CdWO4 crystal scintillator. Phys. Rev. C 2012, 85, 044610. [Google Scholar] [CrossRef] [Green Version]
- Polischuk, O.G.; Belli, P.; Bernabei, R.; Brudanin, V.D.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Search for 2β processes in 106Cd with 106CdWO4 crystal scintillator. Funct. Mater. 2005, 22, 135. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.A.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, V.D.; Klavdiienko, V.R.; et al. Search for double-β decay in 106Cd with an enriched 106CdWO4 crystal scintillator in coincidence with four HPGe detectors. Phys. Rev. C 2016, 93, 045502. [Google Scholar] [CrossRef] [Green Version]
- Polischuk, O.G. Enriched Crystal Scintillators for 2β Experiments. Physics 2021, 3, 103–119. [Google Scholar] [CrossRef]
- Cappella, F.; Incicchitti, A. Techniques for background identification in the search for rare processes with crystal scintillators. Physics 2021, 3, 187–206. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; Incicchitti, A.; Kobychev, V.V.; Ponkratenko, O.A.; Prosperi, D.; Tretyak, V.I.; et al. Performances of a CeF3 crystal scintillator and its application to the search for rare processes. Nucl. Instrum. Methods A 2003, 498, 352. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, A.; Di Marco, A.; Incicchitti, A.; Nozzoli, F.; Tretyak, V.I. Search for 2β decay of cerium isotopes with CeCl3 scintillator. J. Phys. G Nucl. Part. Phys. 2011, 38, 015103. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Cappella, F.; Cerulli, R.; Incicchitti, A.; Laubenstein, M.; Prosperi, D.; Tretyak, V.I. First limits on neutrinoless resonant 2ϵ captures in 136Ce and new limits for other 2β processes in 136Ce and 138Ce isotopes. Nucl. Phys. A 2009, 824, 101. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Incicchitti, A.; Prosperi, D.; Bacci, C.; De Notaristefani, F.; Davies, G.J.; Dai, C.J. Feasibility of 2β decay searches with Ce isotopes using CeF3 scintillators. Nuovo Cimento A 1997, 110, 189. [Google Scholar]
- Belli, P.; Bernabei, R.; Cerulli, R.; Danevich, F.A.; Galenin, E.; Gektin, A.; Incicchitti, A.; Isaienko, V.; Kobychev, V.V.; Laubenstein, D.; et al. Radioactive contamination of SrI2(Eu) crystal scintillator. Nucl. Instrum. Methods A 2012, 670, 10. [Google Scholar] [CrossRef] [Green Version]
- Danevich, F.A.; Chernyak, D.M.; Dubovik, A.M.; Grinyov, B.V.; Henry, S.; Kraus, H.; Kudovbenko, V.M.; Mikhailik, V.B.; Nagornay, L.L.; Podviyanuk, R.B.; et al. MgWO4 a new crystal scintillator. Nucl. Instrum. Methods A 2009, 608, 107. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Bukilic, N.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; Degoda, V.Y.; et al. Development of enriched 106CdWO4 crystal scintillators to search for double beta decay processes in 106Cd. Nucl. Instrum. Methods A 2010, 615, 301. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Nagorny, S.S.; Nozzoli, F.; et al. Search for double beta decay processes in 108Cd and 114Cd with the help of low background CdWO4 crystal scintillator. Eur. Phys. J. A 2008, 36, 167. [Google Scholar] [CrossRef]
- Cerulli, R.; Belli, P.; Bernabei, R.; Cappella, F.; Nozzoli, F.; Montecchia, F.; d’Angelo, A.; Incicchitti, A.; Prosperi, D.; Dai, C.J. Performances of a BaF2 detector and its application to the search for 2β decay modes in 130Ba. Nucl. Instrum. Methods A 2004, 525, 535. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Poda, D.V.; Polischuk, O.G.; et al. Investigation of rare nuclear decays with BaF2 crystal scintillator contaminated by radium. Eur. Phys. J. A 2014, 50, 134. [Google Scholar] [CrossRef] [Green Version]
- Caracciolo, V.; Cappella, F.; Cerulli, R.; Di Marco, A.; Laubenstein, M.; Nagorny, S.S.; Safonova, O.E.; Shlegel, V.N. Limits and Performances of a BaWO4 Single Crystal. Nucl. Instrum. Methods A 2018, 901, 150. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Dubovik, A.M.; d’Angelo, S.; Galashov, E.N.; Grinyov, B.V.; Incicchitti, A.; et al. Radioactive contamination of ZnWO4 crystal scintillators. Nucl. Instrum. Methods A 2011, 626, 31. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Dubovik, A.M.; d’Angelo, S.; Galashov, E.N.; Grinyov, B.V.; Incicchitti, A.; et al. Radiopurity of ZnWO4 crystal scintillators. Acta Phys. Polonica A 2010, 117, 139. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Grinyov, B.V.; Incicchitti, A.; Kobychev, V.V.; Mokina, V.M.; Nagorny, S.S.; et al. Search for double beta decay of zinc and tungsten with low background ZnWO4 crystal scintillators. Nucl. Phys. A 2009, 826, 256. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Grinyov, B.V.; Incicchitti, A.; Kobychev, V.V.; Nagornaya, L.L.; Nagorny, S.S.; et al. Search for 2β processes in 64Zn with the help of ZnWO4 crystal scintillator. Phys. Lett. B 2008, 658, 193. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Poda, D.V.; et al. Final results of experiment to search for 2β processes in zinc and tungsten with the help of radiopure ZnWO4 crystal scintillators. J. Phys. G Nucl. Part. Phys. 2011, 38, 115107. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Danevich, F.A.; Denisov, V.Y.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Poda, D.V.; Polischuk, O.G.; et al. Search for long-lived superheavy eka-tungsten with radiopure ZnWO4 crystal scintillator. Phys. Scr. 2015, 90, 085301. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Cherubini, N.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Piccinelli, E.; et al. Measurements of ZnWO4 anisotropic response to nuclear recoils for the ADAMO project. Eur. Phys. J. A 2020, 56, 83. [Google Scholar] [CrossRef]
- Danevich, F.A.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; et al. Development of radiopure cadmium tungstate crystal scintillators from enriched 106Cd and 116Cd to search for double beta decay. AIP Conf. Proc. 2013, 1549, 201. [Google Scholar]
- Ejiri, H. Double Beta Decays and Neutrino Masses. J. Phys. Soc. Jpn. 2005, 74, 2101–2127. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Bukilic, N.; Cappella, F.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; de Laeter, J.R.; Incicchitti, A.; Kobychev, V.V.; et al. Investigation of beta decay of 113Cd. Phys. Rev. C 2007, 76, 064603. [Google Scholar]
- Danevich, F.A.; Georgadze, A.S.; Kobychev, V.V.; Nagorny, S.S.; Nikolaiko, A.S.; Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, S.Y.; Zdesenko, Y.G.; Bizzeti, P.G.; et al. Alpha activity of natural tungsten isotopes. Phys. Rev. C 2003, 67, 014310. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; d’Angelo, A.; Incicchitti, A.; Kobychev, V.V.; Nagorny, S.S.; et al. Search for alpha decay of natural Europium. Nucl. Phys. A 2007, 789, 15. [Google Scholar] [CrossRef]
- Zdesenko, Y.G.; Avignone, F.T.; Brudanin, V.B.; Danevich, F.A.; Nagorny, S.S.; Solsky, I.M.; Tretyak, V.I. Scintillation properties and radioactive contamination of CaWO4 crystal scintillators. Nucl. Instrum. Methods A 2005, 538, 657. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Kropivyansky, B.N.; et al. New observation of 2β2ν decay of 100Mo to the 01+ level of 100Ru in the ARMONIA experiment. Nucl. Phys. A 2010, 846, 143–156. [Google Scholar] [CrossRef]
- Polischuk, O.G.; Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Investigation of 2β decay of 116Cd with the help of enriched 116CdWO4 crystal scintillators. AIP Conf. Proc. 2017, 1894, 020018. [Google Scholar]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Montecchia, F.; Nozzoli, F.; Incicchitti, A.; Prosperi, D.; Tretyak, V.I.; Zdesenko, Y.G.; et al. Search for β and ββ decays in 48Ca. Nucl. Phys. A 2002, 705, 29–39. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, A.; Incicchitti, A.; Kobychev, V.V.; Laubenstein, M.; Polischuk, O.G.; et al. Search for 7Li solar axions using resonant absorption in LiF crystal: Final results. Phys. Lett. B 2012, 711, 41–45. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Cappella, F.; Incicchitti, A.; Prosperi, D.; Castellano, S.; Cerulli, R.; et al. Performances and potentialities of a LaCl3:Ce scintillator. Nucl. Instrum. Methods A 2005, 555, 270–281. [Google Scholar] [CrossRef]
- Elwell, D.; Scheel, H.J. Crystal Growth from High-Temperature Solutions; Academic Press: London, UK, 2003. [Google Scholar]
- Scheel, H.J. Historical Introduction, Chapter 1 in Handbook of Crystal Growth; Hurle, D.T.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1993; Volume 1. [Google Scholar]
- Scheel, H.J.; Fukuda, T. Crystal Growth Technology; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Feigelson, R.S. 50 Years Progress in Crystal Growth; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Lecoq, P.; Gektin, A.; Korzhik, M. Inorganic Scintillators for Detector Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Dhanaraj, G.; Byrappa, K.; Prasad, V.; Dudley, M. Handbook of Crystal Growth; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kubota, S.; Hishida, M.; Suzuki, M.; Ruan, J.Z. Dynamical behavior of free electrons in the recombination process in liquid argon, krypton, and xenon. Phys. Rev. B 1979, 20, 3486. [Google Scholar] [CrossRef]
- Barabanov, I.R.; Gavrin, V.N.; Pshukov, A.M. Liquid xenon scintillation spectrometer. Nucl. Instrum. Methods A 1987, 254, 355–360. [Google Scholar] [CrossRef]
- Incicchitti, A.; Belli, P.; Scafi, M. Liquid Xenon as a detector medium. Nucl. Instrum. Methods A 1990, 289, 236–242. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Andreanelli, L.; Bronzini, F.; Buccheri, A.; Incicchitti, A.; Prosperi, D. Liquid Xenon detectors and their applications. Nucl. Instrum. Methods A 1990, 299, 191–194. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Incicchitti, A.; Prosperi, D. Detecting ’dark matter’ using a liquid xenon scintillation detector. Nuovo Cimento A 1990, 103, 767–771. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Incicchitti, A.; Prosperi, D. Liquid xenon scintillators. Nucl. Instrum. Methods A 1991, 310, 150–153. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Bacci, C.; Incicchitti, A.; Marcovaldi, R.; Prosperi, D. Liquid xenon detectors for dark matter experiments. Nucl. Instrum. Methods A 1992, 316, 55–57. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Di Nicolantonio, W.; Landoni, V.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Bacci, C.; Besida, O.; Dai, C.J. Search for WIMPs with enriched xenon at Gran Sasso. Nuovo Cimento C 1996, 19, 537–544. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Di Nicolantonio, W.; Landoni, V.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Bacci, C. Charge conservation and electron lifetime: Limits from a liquid xenon scintillator. Astropart. Phys. 1996, 5, 217–219. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Di Nicolantonio, W.; Landoni, V.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Bacci, C.; Dai, C.J. Limits on WIMP–129Xe inelastic scattering. Phys. Lett. B 1996, 387, 222–226. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Angelone, M.; Batistoni, P.; Pillon, M. New limits on particle dark matter search with a liquid Xenon target-scintillator. Phys. Lett. B 1998, 436, 379–388. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; Ignesti, G.; Incicchitti, A.; Montecchia, F.; Ponkratenko, O.A.; Prosperi, D.; Tretyak, V.I.; Zdesenko, Y.G. Charge non–conservation restrictions from the nuclear levels excitation of Xe–129 induced by the electron’s decay on the atomic shell. Phys. Lett. B 1999, 465, 315–322. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; Ignesti, G.; Incicchitti, A.; Montecchia, F.; Ponkratenko, O.A.; Prosperi, D.; Tretyak, V.I.; Zdesenko, Y.G. Quest for electron decay e−→νeγ with a liquid xenon scintillator. Phys. Rev. D 2000, 61, 117301. [Google Scholar] [CrossRef]
- Bernabei, R.; Amato, M.; Belli, P.; Cerulli, R.; Dai, C.J.; Denisov, V.Y.; He, H.L.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; et al. Search for the nucleon and di-nucleon decay into invisible channels. Phys. Lett. B 2000, 493, 12–18. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cerulli, R.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Angelone, M.; Batistoni, P.; Pillon, M. Light response of a pure liquid xenon scintillator irradiated with 2.5 MeV neutrons. Eur. Phys. J. 2001, 3, 1–11. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J. Search for neutrinoless beta beta decay in 134Xe. Phys. Lett. B 2002, 527, 182–186. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J. Investigation of beta beta decay modes in 134Xe and 136Xe. Phys. Lett. B 2002, 546, 23–28. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Bussolotti, A.; Cappella, F.; Cerulli, R.; Montecchia, F.; Dai, C.J.; Incicchitti, A.; Mattei, A.; Prosperi, D. The liquid xenon set-up of the DAMA experiment. Nucl. Instrum. Methods A 2002, 482, 728–743. [Google Scholar] [CrossRef]
- Collar, J.I. A Realistic Assessment of the Sensitivity of XENON10 and XENON100 to Light-Mass WIMPs. arXiv 2011, arXiv:1106.0653. [Google Scholar]
- Doke, T. Fundamental properties of liquid argon, krypton and xenon as radiation detector media. Port. Phys. 1981, 12, 9. [Google Scholar]
- Brassard, C. Liquid ionization detectors. Nucl. Instrum. Methods 1979, 162, 29. [Google Scholar] [CrossRef]
- Feltesse, J. Liquid noble gas and warm liquid detectors. Nucl. Instrum. Methods A 1989, 283, 375. [Google Scholar] [CrossRef]
- Davies, G.J.; Davies, J.D.; Lewin, J.D.; Smith, P.F.; Jones, W.G. Liquid xenon as a dark matter detector. Prospects for nuclear recoil discrimination by photon timing. Phys. Lett. B 1994, 320, 395. [Google Scholar] [CrossRef]
- Asakura, K.; Gando, A.; Gando, Y.; Hachiya, T.; Hayashida, S.; Ikeda, H.; Inouea, K.; Ishidoshiro, K.; Ishikawa, T.; Ishio, S.; et al. Search for double-beta decay of 136Xe to excited states of 136Ba with the KamLAND-Zen experiment. Nucl. Phys. A 2016, 946, 171–181. [Google Scholar] [CrossRef] [Green Version]
- Galan, J. Microbulk MicrOMEGAs for the search of 0νββ of 136Xe in the PandaX-III experiment. JINST 2016, 11, P04024. [Google Scholar] [CrossRef] [Green Version]
- Albert, J.B.; Auger, M.; Auty, D.J.; Barbeau, P.S.; Beauchamp, E.; Beck, D.; Belov, V.; Benitez-Medina, C.; Bonatt, J.; Breidenbach, M.; et al. Improved measurement of the 2νββ half-life of 136Xe with the EXO-200 detector. Phys. Rev. C 2014, 89, 015502. [Google Scholar] [CrossRef] [Green Version]
- Agostini, F.; Ahmed Maouloud, S.E.M.; Althueser, L.; Amaro, F.; Antunovic, B.; Aprile, E.; Baudis, L.; Baur, D.; Biondi, Y.; Bismark, A.; et al. Sensitivity of the DARWIN observatory to the neutrinoless double beta decay of 136Xe. Eur. Phys. J. C 2020, 80, 808. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Incicchitti, A.; Prosperi, D. Liquid Noble Gases for Dark Matter Searches: A Synoptic Survey; Exorma: Rome, Italy, 2009; ISBN 978-88-95688-12-1. [Google Scholar]
- Bernabei, R.; Belli, P.; Incicchitti, A.; Cappella, F.; Cerulli, R. Liquid Noble gases for Dark Matter searches: An updated survey. Int. J. Mod. Phys. A 2015, 30, 1530053. [Google Scholar] [CrossRef]
- Doke, T.; Hitachi, A.; Kikuchi, J.; Masuda, K.; Okada, H.; Shibamura, E. Absolute Scintillation Yields in Liquid Argon and Xenon for Various Particles. Jpn. J. Appl. Phys. 2002, 41, 1538. [Google Scholar] [CrossRef]
- Shutt, T.; Dahl, C.E.; Kwong, J.; Bolozdynya, A.; Brusov, P. Performance and fundamental processes at low energy in a two-phase liquid xenon dark matter detector. Nucl. Phys. B 2007, 173, 160. [Google Scholar] [CrossRef] [Green Version]
- Chepel, V.; Araújo, H. Liquid noble gas detectors for low energy particle physics. JINST 2013, 8, R04001. [Google Scholar] [CrossRef] [Green Version]
- Fiorini, E.; Niinikoski, T.O. Low-temperature calorimetry for rare decays. Nucl. Instrum. Methods A 1984, 224, 83. [Google Scholar] [CrossRef] [Green Version]
- Goulding, F.S.; Landis, D.A. Semiconductor Detector Spectrometer Electronics. Pure Appl. Phys. 1974, 40, 413–481. [Google Scholar]
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Pirro, S. Further developments in mechanical decoupling of large thermal detectors. Nucl. Instrum. Methods A 2009, 559, 672–674. [Google Scholar] [CrossRef]
- Barucci, M.; Beeman, J.W.; Caracciolo, V.; Pagnanini, L.; Pattavina, L.; Pessina, G.; Pirro, S.; Rusconi, C.; Schäffner, K. Cryogenic light detectors with enhanced performance for rare event physics. Nucl. Instrum. Methods A 2019, 935, 150–155. [Google Scholar] [CrossRef] [Green Version]
- Razeti, M. Distillation and separation of some rare isotopes and their applications. Nuovo Cimento C 2017, 41, 84. [Google Scholar]
- Agnes, P.; Albergo, S.; Albuquerque, I.F.M.; Alexander, T.; Alici, A.; Alton, A.K.; Amaudruz, P.; Arba, M.; Arpaia, P.; Arcelli, S. Separating 39Ar from 40Ar by cryogenic distillation with Aria for dark matter searches. arXiv 2021, arXiv:2101.08686. [Google Scholar]
- Dell’Oro, S.; Marcocci, S.; Vissani, F. New expectations and uncertainties on neutrinoless double beta decay. Phys. Rev. D 2014, 90, 033005. [Google Scholar] [CrossRef] [Green Version]
- Caracciolo, V. Feasibility Study of an Experiment to Investigate the Double Beta Decay Modes in 106Cd. Ph.D. Thesis, University of L’Aquila, L’Aquila, Italy, 2012. [Google Scholar]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, L.; Araujoa, H.; Arce, P.; Asaiga, M.; Axeni, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods A 2003, 506, 250. [Google Scholar] [CrossRef] [Green Version]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce Dubois, P.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270. [Google Scholar] [CrossRef] [Green Version]
- Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, Y.G. Event generator DECAY4 for simulating double-beta processes and decays of radioactive nuclei. Phys. At. Nucl. 2000, 63, 1282. [Google Scholar] [CrossRef] [Green Version]
- Tretyak, V.I.; (Institute for Nuclear Research of NASU, Kyiv, Ukraine). Private communication, 2007.
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The Ame2016 atomic mass evaluation. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Beck, M.; Bockholt, J.; Echternach, J.; Heusse, G.; Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Piepke, A.; Strecker, H.; Zuber, K.; Bakalyarov, A.; et al. New half life limits for the ββ2ν+0ν decay of 76Ge to the excited states of 76Se from the Heidelberg-Moscow ββ experiment. Z. Phys. A 1992, 343, 397. [Google Scholar] [CrossRef]
- Meija, J.; Coplen, T.B.; Berglund, M.; Brand, A.; De Biévre, P.; Gröning, M.; Holden, N.E.; Irrgeher, J.; Loss, R.D.; Walczyk, T.; et al. Isotopic compositions of the elements 2013 (IUPAC Technical Report). Pure Appl. Chem. 2016, 88, 293. [Google Scholar] [CrossRef] [Green Version]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S. Indications of 2ν2K capture in 78Kr. Phys. Rev. C 2013, 87, 035501. [Google Scholar] [CrossRef]
- Ratkevich, S.S.; Gangapshev, A.M.; Gavrilyuk, Y.M.; Karpeshin, F.F.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Trzhaskovskaya, M.B.; Yakimenko, S.P. Comparative study of the double-K-shell-vacancy production in single- and double-electron-capture decay. Phys. Rev. C 2017, 96, 065502. [Google Scholar] [CrossRef] [Green Version]
- Sáenz, C.; Cerezo, E.; García, E.; Morales, A.; Morales, J.; Núñez-Lagos, R.; Ortiz de Solórzano, A.; Puimedón, J.; Salinas, A.; Sarsa, M.L.; et al. Results of a search for double positron decay and electron-positron conversion of 78Kr. Phys. Rev. C 1994, 50, 1170. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Antochi, V.C.; Arneodo, F.; Baudis, L.; et al. Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 2019, 568, 532–535. [Google Scholar]
- Abe, K.; Hiraide, K.; Ichimura, K.; Kishimoto, Y.; Kobayashi, K.; Kobayashi, M.; Moriyama, S.; Nakahata, M.; Norita, T.; Ogawa, H.; et al. Improved search for two-neutrino double electron capture on 124Xe and 126Xe using particle identification in XMASS-I. Prog. Theor. Exp. Phys. 2018, 5, 053D03. [Google Scholar]
- Barabash, A.S.; Kuzminov, V.V.; Lobashev, V.M.; Movikov, V.M.; Ovchinnikov, B.M.; Pomansky, A.A. Results of the experiment on the search for double beta decay of 136Xe, 134Xe and 124Xe. Phys. Lett. B 1989, 223, 273–276. [Google Scholar] [CrossRef]
- Meshik, A.P.; Hohenberg, C.M.; Pravdivtseva, O.V.; Kapusta, Y.S. Weak decay of 130Ba and 132Ba: Geochemical measurements. Phys. Rev. C 2001, 64, 035205. [Google Scholar] [CrossRef] [Green Version]
- Pujol, M.; Marty, B.; Burnard, P.; Philippot, P. Xenon in Archean barite: Weak decay of 130Ba, mass-dependent isotopic fractionation and implication for barite formation. Geochim. Cosmochim. Acta 2009, 73, 6834–6846. [Google Scholar] [CrossRef]
- Barabash, A.S.; Saakyan, R.R. Experimental limits on 2β+, Kβ+, and 2K processes for 130Ba and on 2K capture for 132Ba. Phys. At. Nucl. 1996, 59, 179–184. [Google Scholar]
- Srinivasan, B. Barite: Anomalous xenon from spallation and neutron-induced reactions. Earth Planet. Sci. Lett. 1976, 31, 129–141. [Google Scholar] [CrossRef]
- Aunola, M.; Suhonen, J. Systematic study of beta and double beta decay to excited final states. Nucl. Phys. A 1996, 602, 133. [Google Scholar] [CrossRef]
- Rumyantsev, O.A.; Urin, M.H. The strength of the analog and Gamow-Teller giant resonances and hindrance of the 2νβ+β+ decay rate. Phys. Lett. B 1998, 51, 443. [Google Scholar]
- Staudt, A.; Muto, K.; Klapdor-Kleingrothaus, H.V. Nuclear matrix elements for double positron emission. Phys. Let. B 1991, 268, 312–316. [Google Scholar] [CrossRef]
- Mishra, S.; Shukla, A.; Sahu, R.; Kota, V.K.B. Deformed shell model calculations of half lives for β+/EC decay and 2ν β+β+/β+EC/ECEC decay in medium-heavy NZ nuclei. Phys. Rev. C 2008, 78, 024307. [Google Scholar] [CrossRef]
- Domir, P.; Kovalenko, S.; Šimkovic, F.; Semeno, S.V. Neutrino accompanied βpmβpm, β+/EC and EC/EC processes within single state dominance hypothesis. Nucl. Phys. A 2005, 753, 337–363. [Google Scholar]
- Sahu, R.; Kota, V.K.B. Deformed shell model studies of spectroscopic properties of 64Zn and 64Ni and the positron double beta decay of 64Zn. Pramana 2014, 82, 757. [Google Scholar] [CrossRef]
- Gavriljuk, J.M.; Kuzminov, V.V.; Osetrova, N.Y.; Ratkevich, S.S. New limit on the half-life of 78Kr with respect to the 2K(2ν)-capture decay mode. Phys. At. Nucl. 2000, 63, 2201–2204. [Google Scholar] [CrossRef] [Green Version]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S.; Yakimenko, S.P. Investigating 2K capture in 78Kr with a large-volume copper proportional counter. Bull. Russ. Ac. Sci. Phys. 2011, 75, 526. [Google Scholar] [CrossRef]
- Ameenah, R.F.; Balraj, S. Nuclear Data Sheets for A = 78. Nucl. Data Sheets 2009, 110, 1917–2080. [Google Scholar]
- Hirsch, M.; Muto, K.; Oda, T.; Klapdor-Kleingrothaus, H.V. Nuclear structure calculation of β+β+, β+/EC and EC/EC decay matrix elements. Z. Phys. A 1994, 347, 151. [Google Scholar] [CrossRef]
- Suhonen, J. Double beta decays of 124Xe investigated in the QRPA framework. J. Phys. G 2013, 40, 075102. [Google Scholar] [CrossRef]
- Singh, S.; Chandra, R.; Rath, P.K.; Raina, P.K.; Hirsch, J.G. Nuclear deformation and the two-neutrino double-β decay in 124,126Xe, 128,130Te, 130,132Ba and 150Nd isotopes. Eur. Phys. J. A 2007, 33, 375. [Google Scholar] [CrossRef] [Green Version]
- Shukla, A.; Raina, P.K.; Rath, P.K. Study of two neutrino β+β+/β+EC/ECEC decay of 124,126Xe and 130,132Ba for 0+→0+ transition in PHFB model. J. Phys. G Nucl. Part. Phys. 2007, 34, 549. [Google Scholar] [CrossRef]
- Nesterenko, D.A.; Blaum, K.; Block, M.; Droese, C.; Eliseev, S.; Herfurth, F.; Minaya Ramirez, E.; Novikov, Y.N.; Schweikhard, L.; Shabaev, V.M.; et al. Double-β transformations in isobaric triplets with mass numbers A = 124, 130 and 136. Phys. Rev. C 2012, 86, 044313. [Google Scholar] [CrossRef]
- Barabash, A. Precise Half-Life Values for Two-Neutrino Double-β Decay: 2020 review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S.; Tekueva, D.A.; Yakimenko, S.P. Search for 2K(2ν)-capture of 124Xe. Phys. Part. Nucl. 2017, 48, 38. [Google Scholar] [CrossRef]
- Abe, K.; Hiraide, K.; Ichimura, K.; Kishimoto, Y.; Kobayashi, K.; Kobayashi, M.; Moriyama, S.; Nakagawa, K.; Nakahata, M.; Norita, T. Search for two-neutrino double electron capture on 124Xe with the XMASS-I detector. Phys. Lett. B 2016, 759, 64. [Google Scholar] [CrossRef] [Green Version]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Amaro, F.D.; Anthony, M.; Arneodo, F.; Barrow, P.; Baudis, L.; Bauermeister, B. Search for two-neutrino double electron capture of 124Xe with XENON100. Phys. Rev. C 2017, 95, 024605. [Google Scholar] [CrossRef] [Green Version]
- Katakura, J.; Wu, Z.D. Nuclear Data Sheets for A = 124. Nucl. Data Sheets 2008, 109, 1655–1877. [Google Scholar] [CrossRef]
- Barabash, A.S. How to detect two-neutrino double K capture in a direct (counter) experiment. JETP Lett. 1994, 59, 644. [Google Scholar]
- Meshik, A.; Pravdivtseva, O. Weak Decay of Tellurium and Barium Isotopes in Geological Samples: Current Status. JPS Conf. Proc. 2017, 14, 020702. [Google Scholar]
- Balraj, S. Nuclear Data Sheets for A = 130. Nucl. Data Sheets 2001, 93, 33–242. [Google Scholar]
- Angloher, G.; Bauer, M.; Bauer, P.; Bavykina, I.; Bento, A.; Bucci, C.; Canonica, L.; Ciemniak, C.; Defay, X.; Deuter, G.; et al. New limits on double electron capture of 40Ca and 180W. Nucl. Phys. G 2016, 43, 095202. [Google Scholar] [CrossRef] [Green Version]
- Latest COBRA Annual Report. Available online: https://www.cobra-experiment.org/ (accessed on 1 January 2021).
- Joachim, E.; Fritts, M.; Gehre, D.; Gößling, C.; Hagner, C.; Heidrich, N.; Klingenberg, R.; Kröninger, K.; Nitsch, K.; Oldorf, C.; et al. Results of a search for neutrinoless double-β decay using the COBRA demonstrator. Phys. Rev. C 2016, 94, 024603. [Google Scholar]
- Alduino, C.; Alfonso, K.; Artusa, D.R.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Bersani, A.; Biassoni, M.; et al. Search for neutrinoless β+EC decay of 120Te with CUORE-0. Phys. Rev. C 2018, 97, 055502. [Google Scholar] [CrossRef] [Green Version]
- Alduino, C.; Alfonso, K.; Artusa, D.R.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Bersani, A.; Biassoni, M.; et al. CUORE-0 detector: Design, construction and operation. J. Instrum. 2016, 11, P07009. [Google Scholar] [CrossRef] [Green Version]
- Alfonso, K.; Artusa, D.R.; Avignone, F.T., III; Azzolini, O.; Balata, M.; Banks, T.I.; Bari, G.; Beeman, J.W.; Bellini, F.; Bersani, A.; et al. Search for Neutrinoless Double-Beta Decay of 130Te with CUORE-0. Phys. Rev. Lett. 2015, 115, 102502. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, W.R.; Chang, C.; Hafidi, K.; Lisovenko, M.; Novosad, V.; Pearson, J.; Polakovic, T.; Wang, G.; Yefremenko, V.; Zhang, J.; et al. CUPID pre-CDR. arXiv 2019, arXiv:1907.09376. [Google Scholar]
- Ching, C.; Ho, T.; Zhao, W. Is 40Ca A Stable Isotope? Commun. Theor. Phys. 1984, 3, 517–520. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; Grianti, F.; He, H.L.; Ignesti, G.; Incicchitti, A.; .Kuang, H.H.; Ma, J.M.; Montecchia, F.; et al. New limits on spin-dependent coupled WIMPs and on 2β processes in 40Ca and 46Ca by using low radioactive CaF2(Eu) crystal scintillators. Nucl. Phys. B 1999, 563, 97–106. [Google Scholar] [CrossRef]
- Bellini, F.; Beretta, M.; Cardani, L.; Carniti, P.; Casali, N.; Celi, E.; Chiesa, D.; Clemenza, M.; Dafinei, I.; Di Domizio, S.; et al. Search for double β-decay modes of 64Zn using purified zinc. Eur. Phys. J. C 2021, 81, 106. [Google Scholar] [CrossRef]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Cardani, L.; Celi, C. Search for neutrinoless double beta decay of 64Zn and 70Zn with CUPID-0. Eur. Phys. J. C 2020, 80, 702. [Google Scholar] [CrossRef]
- Kiel, H.; Münstermann, D.; Zuber, K. A search for various double beta decay modes of Cd, Te, and Zn isotopes. Nucl. Phys. A 2003, 723, 499–514. [Google Scholar] [CrossRef] [Green Version]
- Barabash, A.S.; Hubert, F.; Hubert, P.; Umatov, V. New limits on the β+EC and ECEC processes in 120Te. J. Phys. G 2007, 34, 1721–1728. [Google Scholar] [CrossRef] [Green Version]
- Dawson, J.V.; Goessling, C.; Janutta, B.; Junker, M.; Koettig, M.; Muenstermann, D.; Rajek, S.; Reeve, C.; Schulz, O.; Wilson, J.R.; et al. Experimental study of double-β decay modes using a CdZnTe detector array. Phys. Rev. C 2009, 80, 025502. [Google Scholar] [CrossRef] [Green Version]
- Andreotti, E.; Arnaboldi, C.; Avignone, F.T., III; Balata, M.; Bandac, I.; Barucci, M.; Beeman, J.W.; Bellini, F.; Broferio, C.; Bryant, A.; et al. Search for β+/EC double beta decay of 120Te. Astropart. Phys. 2011, 34, 643–648. [Google Scholar] [CrossRef] [Green Version]
- Bikit, I.; Slivka, J.; Anicin, I.; Veskovic, M.; Conkic, L. Electron-positron conversion decay of 64Zn. Appl. Radiat. Isot. 1995, 46, 455. [Google Scholar] [CrossRef]
- Pirinen, P.; Suhonen, J. Systematic approach to β and 2νββ decays of mass A=100-136 nuclei. Phys. Rev. C 2015, 91, 054309. [Google Scholar] [CrossRef] [Green Version]
- Danevich, F.A.; Georgadze, A.S.; Kobychev, V.V.; Nikolaiko, A.S.; Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, S.Y.; Zdesenko, Y.G.; Bizzeti, P.G.; Fazzini, T.F.; et al. Two-neutrino 2βdecay of 116Cd and new half-lifelimits on 2β decay of 180W and 186W. Nucl. Phys. A 2003, 717, 129–145. [Google Scholar] [CrossRef]
- Kang, W.G.; Choi, J.H.; Jeon, E.J.; Lee, J.I.; Kim, H.J.; Kim, S.K.; Kim, Y.D.; Lee, J.H.; Maa, K.J.; Myung, S.S.; et al. Ultra-low gamma-ray measurement system for neutrinoless double beta decay. Appl. Rad. Isot. 2013, 81, 290–293. [Google Scholar] [CrossRef] [PubMed]
- Barabash, A.S.; Gurrianin, R.; Hubert, F.; Hubert, P.; Umatov, V.I. Improved limits on double beta processes in 92Mo. Z. Phys. A 1997, 357, 351–352. [Google Scholar] [CrossRef]
- Bellotti, E.; Fiorini, E.; Liguori, C.; Pullia, A.; Sarbacino, A.; Zanotti, L. An experimental investigation on lepton number conservation in double-beta processes. Lett. Nuovo Cimento 1982, 33, 273. [Google Scholar] [CrossRef]
- Lee, J.I.; Bhang, H.C.; Choi, J.H.; Jeon, E.J.; Kang, W.G.; Kim, H.J.; Kim, S.C.; Kim, S.K.; Kim, Y.D.; Leeet, J.H.; et al. Experimental study on neutrinoless double beta decay of 92Mo. Nucl. Instrum. Met. A 2011, 654, 157–161. [Google Scholar] [CrossRef]
- Rukhadze, N.I.; Briancon, C.; Brudanin, B.B.; Egorov, V.G.; Klimenko, A.A.; Kovalik, A.; Timkin, V.V.; Čhermák, P.; Shitov, Y.A.; Šimkovic, F.; et al. Search for double-β decay of 106Cd. Bull. Russ. Acad. Sci. Phys. 2011, 75, 879. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, R.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kropivyansky, B.N.; Laubenstein, M.; Poda, D.V.; et al. Search for double beta decay of 136Ce and 138Ce with HPGe gamma detector. Nulc. Phys. A 2014, 930, 195–208. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kropivyansky, B.N.; Laubenstein, M.; Mokina, V.M.; et al. New limits on 2ϵ, ϵβ+ and 2ϵ decay of 136Ce and 138Ce with deeply purified cerium sample. Eur. Phys. J. A 2017, 53, 172. [Google Scholar] [CrossRef]
- De Frenne, D.; Negret, A. Nuclear data sheets for A = 106. Nucl. Data Sheets 2008, 109, 943–1102. [Google Scholar] [CrossRef]
- Tretyak, V.I.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, D.F.; d’Angelo, S.; et al. First results of the experiment to search for 2β decay of 106Cd with 106CdWO4 crystal scintillator in coincidence with four crystals HPGe detector. EPJ Web Conf. 2014, 65, 01003. [Google Scholar] [CrossRef] [Green Version]
- Danevich, F.A.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; d’Angelo, S.; Incicchitti, A.; et al. Search for double beta processes in 106Cd with enriched 106CdWO4 crystal scintillator in coincidence with four crystals HPGe detector. AIP Conf. Proc. 2015, 1686, 020006. [Google Scholar]
- Tretyak, V.I.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, D.F.; d’Angelo, S.; et al. New limits on 2β processes in 106Cd. J. Phys. Conf. Ser. 2016, 718, 062062. [Google Scholar] [CrossRef]
- Nozzoli, F. 146Nd, 144Sm, and other unexplored 2β-decay isotopes. Phys. Rev. C 2018, 97, 015501. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Di Vacri, M.L.; Incicchitti, A.; Laubenstein, M.; Nagaorny, S.S. First search for double β decay of dysprosium. Nucl. Phys. A 2011, 859, 126–139. [Google Scholar] [CrossRef] [Green Version]
- Finch, S.W.; Tornow, W. Search for neutrinoless double-electron capture of 156Dy. Phys. Rev. C 2015, 92, 065503. [Google Scholar] [CrossRef] [Green Version]
- Laubenstein, M. Screening of materials with high purity germanium detectors at the Laboratori Nazionali del Gran Sasso. Int. J. Mod. Phys. A 2017, 32, 1743002. [Google Scholar] [CrossRef]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barros, N.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; et al. Limit on the radiative neutrinoless double electron capture of 36Ar from GERDA Phase I. Eur. Phys. J. C 2016, 76, 652. [Google Scholar] [CrossRef] [Green Version]
- Bikit, I.; Zikić-Todorović, N.; Slivka, J.; Vesković, M.; Krmar, M.; Čonkić, L.J.; Puzović, J.; Aničin, I.V. Double β decay of 50 Cr. Phys. Rev. C 2003, 67, 065801. [Google Scholar] [CrossRef]
- Norman, E.B. Improved limits on the double beta decay half-lives of 50Cr, 64Zn, 92Mo and 96Ru. Phys. Rev. C 1973, 31, 1937. [Google Scholar] [CrossRef] [Green Version]
- Bikit, I.; Krmat, M.; Slivka, J.; Vesković, M.; Čonkić, L.J.; Aničin, I.V. New results on the double β decay of Iron. Phys. Rev. C 1998, 58, 2566. [Google Scholar] [CrossRef]
- Rukhadze, N.I.; Brudanin, V.B.; Klimenko, A.A.; Piquemal, F.; Rukhadze, E.N.; Shitov, Y.A.; Štekl, I.; Warot, G. Investigating the Double Beta Decay of 58Ni. Bull. Rus. Ac. Sci. Phys. 2018, 82, 708–711. [Google Scholar] [CrossRef]
- Jeskovsky, M.; Frekers, D.; Kovacik, A.; Povinec, P.P.; Puppe, P.; Stanicek, J.; Sykora, I.; Simkovic, F.; Thies, J.H. A search for double-electron capture in 74Se using coincidence/anticoincidence gamma-ray spectrometry. arXiv 2015, arXiv:1507.02200. [Google Scholar]
- Barabash, A.S.; Brudanin, V.B.; Klimenko, A.A.; Konovalov, S.I.; Rakhimov, A.V.; Rukhadze, E.N.; Rukhadze, N.I.; Shitov, Y.A.; Stekl, I.; Warot, G.; et al. Improved limits on β+EC and ECEC processes in 74Se. Nucl. Phys. A 2020, 996, 121697. [Google Scholar] [CrossRef] [Green Version]
- Frekers, D.; Puppe, P.; Thies, J.H.; Povinec, P.P.; Šimkovic, F.; Staniček, J.; Sýkora, I. Double-electron capture of 74Se and the search for neutrinoless decay. Nucl. Phys. A 2011, 860, 1–7. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kovtun, G.P.; Kovtun, N.G.; Laubenstein, M.; et al. Search for 2β decays of 96Ru and 104Ru by ultralow-background HPGe γ spectrometry at LNGS: Final results. Phys. Rev. C 2013, 87, 034607. [Google Scholar] [CrossRef] [Green Version]
- Lehnert, B.; Andreotti, E.; Degering, D.; Hult, M.; Laubenstein, M.; Wester, T.; Zuber, K. Double beta decays into excited states in 110Pd and 102Pd. J. Phys. G 2016, 43, 115201. [Google Scholar] [CrossRef] [Green Version]
- Barabash, A.S.; Hubert, P.; Nachab, A.; Konovalov, S.I.; Umatov, V. Improved limits on β+EC and ECEC processes in 112Sn. Phys. Rev. C 2011, 83, 045503. [Google Scholar] [CrossRef]
- Ješkovský, M.D.; Fekers, D.; Kováčik, A.; Povinec, P.P.; Puppe, P.; Staníček, J.; Sýcora, I.; Šimkovic, F.; Thies, J.H. A search for double-electron capture of 74Se to excited levels using coincidence/anticoincidence gamma-ray spectrometry. Nucl. Instrum. Methods A 2015, 795, 268–275. [Google Scholar] [CrossRef] [Green Version]
- Lehnert, B.; Wester, T.; Degering, D.; Somme, D.; Wagner, L.; Zuber, K. Double electron capture searches in 74Se. J. Phys. G 2016, 43, 085201. [Google Scholar] [CrossRef] [Green Version]
- Boiko, R.S. Chemical purification of lanthanides for low-background experiments. Int. J. Mod. Phys. A 2017, 32, 1743005. [Google Scholar] [CrossRef]
- Marchegiani, F.; Ferella, F.; Nisi, S. Material screening with mass spectrometry. Physics 2021, 3, 71–84. [Google Scholar] [CrossRef]
- Polischuk, O.G.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Laubenstein, M.; et al. Purification of Lanthanides for Double Beta Decay Experiments. AIP Conf. Proc. 2013, 1549, 124. [Google Scholar]
- Boiko, R.S.; Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Laubenstein, M.; Mokina, V.M.; et al. Purification of cerium, neodymium and gadolinium for low background experiments. EPJ Web Conf. 2014, 65, 04001. [Google Scholar] [CrossRef]
- Danevich, F.A.; Hult, M.; Kasperovych, D.V.; Kovtunc, G.P.; Kovtun, K.V.; Lutter, G.; Marissens, G.; Polischuk, O.G.; Stetsenko, S.P.; Tretyak, V.I. First search for 2ϵ and ϵβ+ decay of 174Hf. Nucl. Phys. A 2020, 996, 121703. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Kobychev, V.V.; Kovtun, G.G.; et al. New experimental limits on double-beta decay of osmium. J. Phys. G Nucl. Part. Phys. 2021. accepted for publication. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Di Marco, A.; Incicchitti, A.; Kovtun, G.P.; Kovtun, N.G.; et al. First search for double-β decay of 184Os and 192Os. Eur. Phys. J. A 2013, 49, 24. [Google Scholar] [CrossRef] [Green Version]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Laubenstein, M.; Nagorny, S.S.; Nisi, S. First search for double-β decay of platinum by ultra-low background HPGe γ spectrometry. Eur. Phys. J. A 2011, 47, 91. [Google Scholar] [CrossRef] [Green Version]
- Bukhner, E.; Vishnevskij, I.N.; Danevich, F.A. Rare decays of mercury nuclei. Sov. J. Nucl. Phys. 1990, 52, 193–197. [Google Scholar]
- Kawrakow, I.; Rogers, D.W.O. The EGSnrc Code System: Monte Carlo Simulation of Electron and Photon Transport; NRCC Rep. (National Research Council Canada) Report PIRS-701; NRCC: Ottawa, ON, Canada, 2003. [Google Scholar]










| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Kr →Se | 2847.67(26) | 0.355(3) | KK | [LPC] [168] | ≥ [LPC] [168] |
| [LPC] [169] | |||||
| KK (, 1498.6) | ≥ [LPC] [168] | – | |||
| KK (, 2838.5) (a) | – | ≥ [LPC] [168] | |||
| K | ≥ (68%) [LPC] [170] | ≥ (68%) [LPC] [170] | |||
| ≥(b) (68%) [LPC] [170] | |||||
| Xe →Te | 2863.9(22) | 0.095(5) | [LXe (TPC)] [171] | – | |
| KK | ≥ [LXe (S)] [172] | – | |||
| K | ≥ (68%) [Xe (HPIC)] [173] | ≥ (68%) [Xe (HPIC)] [173] | |||
| K ( 602.7) | ≥ (68%) [Xe (HPIC)] [173] | – | |||
| ≥ (68%) [Xe (HPIC)] [173] | ≥ (68%) [Xe (HPIC)] [173] | ||||
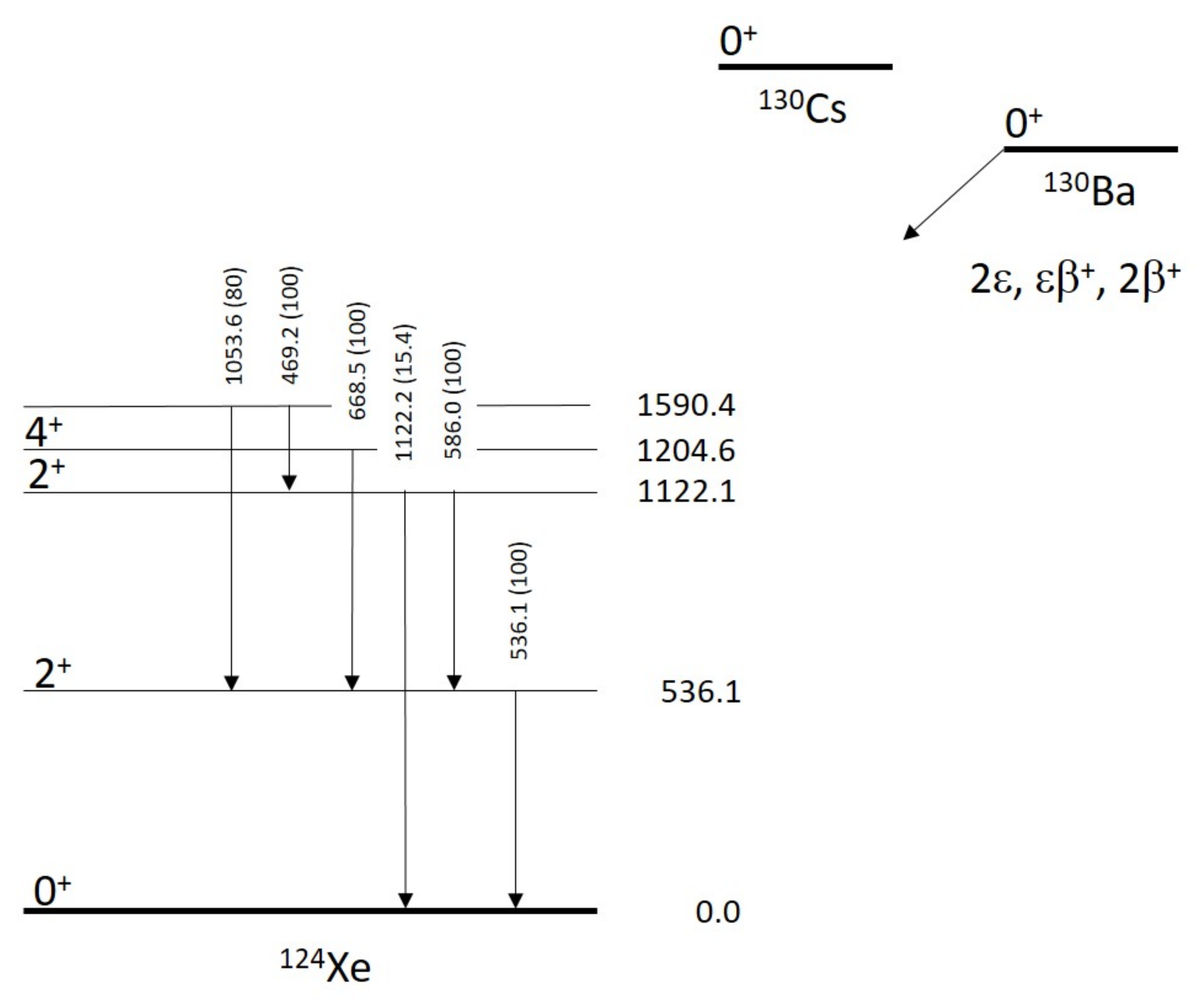
| Ba →Xe | 2618.9(26) | 0.11(1) | (b) [GEO] [174] | ||
| (b) [GEO] [175] | |||||
| (b,c) [GEO] [176] | |||||
| ≥ (68%) (b,c) [GEO] [176] | |||||
| – | – | ||||
| – | ≥ [BaF (S)] [93] | ||||
| ( 536.1) | – | ≥ [BaF (S)] [93] | |||
| ( 1122.1) | – | ≥ [BaF (S)] [93] | |||
| ( 1204.6) | – | ≥ [BaF (S)] [93] | |||
| – | ≥ [BaF (S)] [93] | ||||
| ( 536.1) | – | ≥ [BaF (S)] [93] | |||
| Ba →Xe | 843.9(11) | 0.10(1) | (b,d) [GEO] [174] | ||
| ≥ (68%) (b) [GEO] [174] | |||||
| ≥(68%) (b,c) [GEO] [176] | |||||
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Sr →Kr | 1789.8(12) | 0.355(3) | KK/KL/LL | – | ≥ [SrI (S)] [89] |
| ( 881.6) | ≥ [SrI (S)] [89] | ≥ [SrI (S)] [89] | |||
| ≥ [SrI (S)] [89] | ≥ [SrI (S)] [89] | ||||
| Mo →Zr | 1650.45(19) | 14.649(2) | – | ≥ [HPGe + CaMoO (S)] [218] | |
| (, 934.5) | ≥ (a) [HPGe] [219] | ≥ [HPGe + CaMoO (S)] [218] | |||
| (, 1382.7) | ≥ (a) [HPGe] [219] | ≥ [HPGe + CaMoO (S)] [218] | |||
| (, 1495.5) | ≥ (a) [Ge(Li)] [220] | ||||
| ≥ (a) [HPGe] [219] | ≥ [CsI(Tl) (S) + CaMoO (S)] [221] | ||||
| Cd →Pd | 2775.39(10) | 1.245(22) | ≥ [HPGe] [222] | ≥ [CdwO (S)] [80] | |
| ( 511.9) | ≥ [CdwO (S) + HPGe] [82] | ≥ [CdWO (S)] [80] | |||
| ( 1128.0) | ≥ [CdWO (S)] [48] | ≥ [CdWO (S) + HPGe] [82] | |||
| ( 1133.8) | ≥ [CdWO (S) + HPGe] [82] | ≥ [CdWO (S) + HPGe] [82] | |||
| ( 1562.3) | ≥ [CdWO (S)] [48] | ≥ [CdWO (S)] [48] | |||
| ( 1706.4) | ≥ [CdWO (S) + HPGe] [82] | ≥ [CdWO (S)] [48] | |||
| ( 2001.5) | ≥ [CdWO (S)] [48] | ≥ [CdWO (S) + HPGe] [82] | |||
| ( 2278.1) | ≥ [CdWO (S)] [48] | ≥ [CdWO (S)] [48] | |||
| KK (2718) (b) | – | ≥ [CdWO (S)] [48,80] | |||
| KL ( 2741) (b) | – | ≥ [CdWO (S)] [48,80] | |||
| KL (2, 2748) (b) | – | ≥ [CdWO (S)] [48,80] | |||
| ≥ [CdWO (S)] [48] | ≥ [CdWO (S)] [80] | ||||
| ( 511.9) | ≥ [CdWO (S)] [48] | ≥ [CdWO (S)] [48] | |||
| ( 1128.0) | ≥ [CdWO (S)] [48] | ≥ [CdWO (S)] [48] | |||
| ( 1133.8) | ≥ [CdWO (S)] [48] | ≥ [CdWO (S) + HPGe] [82] | |||
| ≥ [CdWO (S) + HPGe] [82] | ≥ [CdWO (S)] [48] | ||||
| ( 511.9) | ≥ [CdWO (S) + HPGe] [82] | ≥ [CdWO (S)] [48] | |||
| Cd →Pd | 271.8(8) | 0.888(11) | 2K | ≥ [CdWO (S)] [92] | – |
| 2 | – | ≥ [CdWO (S)] [92] | |||
| Xe →Te | 918(4) | 0.089(3) | KK | ≥ [LXe] [172] | – |
| Ce →Ba | 691(5) | 0.251(2) | KK/KL/LL | ≥ [CeCl (S)] [86] | ≥ [HPGe] [223,224] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belli, P.; Bernabei, R.; Caracciolo, V. Status and Perspectives of 2ϵ, ϵβ+ and 2β+ Decays. Particles 2021, 4, 241-274. https://doi.org/10.3390/particles4020023
Belli P, Bernabei R, Caracciolo V. Status and Perspectives of 2ϵ, ϵβ+ and 2β+ Decays. Particles. 2021; 4(2):241-274. https://doi.org/10.3390/particles4020023
Chicago/Turabian StyleBelli, Pierluigi, Rita Bernabei, and Vincenzo Caracciolo. 2021. "Status and Perspectives of 2ϵ, ϵβ+ and 2β+ Decays" Particles 4, no. 2: 241-274. https://doi.org/10.3390/particles4020023
APA StyleBelli, P., Bernabei, R., & Caracciolo, V. (2021). Status and Perspectives of 2ϵ, ϵβ+ and 2β+ Decays. Particles, 4(2), 241-274. https://doi.org/10.3390/particles4020023








