Abstract
Unruh effect entropy is estimated for a spherically symmetric source with an exponential energy distribution; angular degrees of freedom are suggested to be equally likely to contribute. Calculations are performed with an assumption about finite energy and multiplicity ranges. The result is represented in the units of Schwarzschild black hole entropy, with the analytical ratio being expressed analytically and generalized to homogeneous distribution over other degrees of freedom.
1. Introduction
It is well known that all inertial observers are expected to agree upon measurements after the appropriate Lorentz transforms. The situation changes dramatically in case in which curved space-time is involved. Relativity, together with the properties of Hilbert space, makes the definition of quantum vacuum depend on the chosen reference frame. Specifically, an accelerated observer will detect particles even if an inertial one registers a quantum vacuum. This is known as the Fulling–Davies–Unruh effect, or the Unruh effect for brevity [1,2,3]. The emitted particles exhibit thermal behavior, with the emission spectrum being the same as for a thermal source at a temperature of
in Planck units where a stands for acceleration of the non-inertial observer. It was shown [4,5] that Equation (1) holds true not only for spinless particles but also for both bosons and fermions with different spin values.
Such non-invariant thermodynamics seems to be a strange phenomenon. To formalize this, one may consider particle detection within the context of its interaction with some real two-level system. This allows us to quantify the effect in terms of detector excitation probability as a function of its acceleration [6]. But the impact is expected to be very small outside the Planck scale. So one needs to use sophisticated techniques [7,8,9,10] or powerful energy sources [11] to make the effect noticeable. Alternatively, high-momentum exchange rates during QCD scattering should contribute to the color string fragmentation [12,13,14].
Unruh radiation is a well-defined phenomenon for a constantly accelerating observer and is obtained for space-time. Any additional spatial dimensions participate via the tensor product and, therefore, can be excluded with no consequences. On the other hand, its spectrum tends to change the statistics for odd dimensions [15], thus leaving room for debate as to the reality of the effect. However, a rigorous analysis of various switching conditions [16,17] and different trajectories [18,19,20,21,22] reveals that the radiation cannot vanish for realistic scenarios.
This feature inspired the search for the interpretation of the effect that is so heavily susceptible to the reference frame. The study [23] shows that the quantity T from Equation (1) stands for the lowest temperature possible, thus inducing the vacuum thermalization of an accelerated system [24,25]. In addition, it was revealed that the Unruh temperature may serve as an indicator for the critical point in a fermion system [26]. On the other hand, the recent finding [27] claims that it is possible to distinguish between a thermal bath and the effect.
Emerging at the intersection of relativity, quantum physics, and thermodynamics, the Unruh effect has inspired a search for its possible applications in particle production and quantum physics in curved space-times [28].
Schwarzschild black hole radiation looks like a prominent example of the effect; this can be seen in, e.g., [29] on p. 282. Extrapolating further, one may try to justify other black hole thermodynamic quantities in terms of the Unruh mechanism.
Black hole entropy is one of the challenges. As is well known, black holes emit radiation [30]. Such behavior implies some kind of equilibrium with its surroundings and, therefore, should be governed by thermodynamics. It was shown [31,32] that black holes do exhibit the properties typical of any thermodynamic system. However, the entropy of a Schwarzschild black hole turned out to be equal to a quarter of its event horizon area in Planck units. Since it is well known as the area law, such a dependency seems to contradict a common thermodynamic entropy exhibiting extensive properties. The other most prominent challenges are the information loss problem [33] and the magnitude of .
To solve these challenges, plenty of approaches have been suggested. These include counting configurations [34,35,36,37,38,39,40], spectrum quantization [41], holography [42,43,44], boundary approaches [45,46,47,48], and entanglement [49,50,51]. For comprehensive reviews, we refer to [52,53,54].
The Unruh effect is one of the approaches from the above list. However, although the effect has much in common with the black hole radiation, these phenomena can be distinguishable, as discussed in, e.g., [55,56].
The present study considers the Unruh effect from the perspective of information theory. It is dedicated to the analysis of correlations among different degrees of freedom and how they contribute to the effect. We begin with a Minkowski vacuum state, which is an entangled state of Rindler modes for an accelerated observer. We estimate the entropy of Unruh radiation from a source with a spherical symmetry assuming an exponential energy spectrum for the emitted quanta and arbitrary multiplicity. In addition, Unruh radiation is -dimensional. For a space-time, one should take into account additional spatial dimensions; we do so via the angular degrees of freedom. For comparison reasons, the obtained quantity is expressed in the units of the entropy of a Schwarzschild black hole, with the temperature being equal to the Unruh temperature. The black hole’s radius is suggested to be the same as the size of the source of Unruh radiation.
Section 2 describes some necessary basics of probability and information entropy. Section 3 is devoted to model features and the assumptions made. One can find results and their analysis in Section 4. Discussion and final conclusions are drawn in Section 5. Essential technical details and exact analytical expressions can be found in the Appendix B.
2. Information Entropy
Let us have some distribution , with a (non-normalized) probability , for an outcome . If is a discrete one, is the Shannon entropy [57] and is expressed as
where .
Dealing with the distribution implies a lack of data about a physical system, and serves as a measure for that. In other words, it tells us how much we do not know about the system.
The same applies for a joint distribution , for which a naive extrapolation gives
However, Equation (3) requires taking into account the total phase space of our system. To reduce memory costs, it is more convenient to estimate in terms of conditional entropies
given that
Here and onwards, stands for an average estimate of f with respect to .
As one can deduce from Equation (5), the entropy becomes additive if the joint probability factorizes, . In such a situation, distributions over different degrees of freedom become independent of each other and the total entropy exhibits bulk properties, which is typical for thermodynamics.
For a continuous distribution , in order to avoid problems with the Shannon entropy dimension, one needs to use the Jaynes’ entropy [58,59], which reads
Here, the term is known as the limiting density of discrete points. It estimates information being lost under the discrete–continuum transition. In practice, it estimates the entropy of bin width distribution during the discretization process.
3. Model
Throughout the paper, we will use Planck units, . As mentioned in the introduction, the vacuum state is non-invariant with respect to the frame of reference. This can be explained simply as follows. As is well known, the Hilbert space is a linear space, so any observer may choose any arbitrarily complete basis. The transition among bases can be carried out with the relevant transform. This means that the same quantum state can be represented in different ways. For example, the Minkowski vacuum state reads [4,5]
where E is the energy of quanta, stands for the relevant Rindler mode with n quanta, and N is the number of basis vectors for the Hilbert space. The subscripts determine the modes with respect to the event horizon emerging due to relativity restrictions. Therefore, the reasons for the Unruh effect are solely geometrical.
Having no access to the degrees of freedom under the horizon, the accelerated observer is forced to trace out the subspace beneath, thus resulting in a state
where we have omitted the subscript for brevity. This is a mixed state describing the Rindler modes outside the horizon, for which the von Neumann entropy reads
where
Relevant details of its derivation can be found in the Appendix A; see (A1). Therefore, the accelerated observer detects some thermal radiation with non-zero entropy instead of the vacuum as observed by the inertial one.
If the emitted quanta have some other degrees of freedom governed by additional quantum number , one needs to re-define the entropy of emitted particles as
where the averaged over Q term is governed by Equation (9).
The density matrix describing the Unruh radiation is defined for a space-time. Additional spatial dimensions are introduced via the tensor product to the total Hilbert space of the system. Therefore, one can trace them out while deriving with no consequences. However, for a space-time, one should take into account the contribution of all possible Unruh horizons.
Additional spatial dimensions should contribute to the total entropy of Unruh radiation as a sum over all possible directions of emitted particles. The sum can be treated as a number of dimensions of the relevant Hilbert subspace governed by the angular momentum operator and its projection , namely , where and are eigenvalues of the operators, correspondingly. The largest angular momentum value possible is defined as , where r is the radius of the source, which we suggest is equal to the radius of the black hole with a temperature of , and is the particle’s momentum; m is the rest mass of produced particles. For such geometrical reasons of emitting any particle at energy E, the operator spectrum is restricted as
thus giving
Here, we assume that the source size is restricted by , i.e., by the Schwarzschild radius of a black hole with the same temperature.
The applied approximation has much in common with a mapping of a 3D ball by a set of rings of different radii ( in the expression above) and orientation ().
For any source with a spherical symmetry, emission probability does not depend on angular degrees of freedom. This means that the source can emit particles at all possible values of l and independently. All such processes are expected to compensate for each other to ensure the zeroth total angular momentum of radiation. Considering them as a set of independent identical emitters, we take into account the contribution of additional spatial dimensions to the Unruh entropy as a effect via multiplying the entropy by from Equation (13).
Such a situation has much in common with the Boltzmann entropy: thermal equilibrium implies that all the particles contribute as independent sources to the total entropy, thus resulting in its bulk properties.
The eigenvalues of determine the probability of emitting n particles at given temperature T and energy E, with the maximum multiplicity being equal to . In other terms, this is the conditional distribution , and from Equation (9) represents its entropy.
Now, we are ready to take into account the energy distribution . To do this, one needs information about the emission probability of a particle at a given energy. Any such data require knowledge from the domain behind the horizon, which is prohibited due to relativity. It seems impossible to define even the Hamiltonian governing the intrinsic state of matter and degrees of freedom unless one has a consistent and complete quantum gravity theory.
To describe particle emission spectra, various approaches can be applied. They are mostly based on general laws, such as energy conservation. Such restrictions on possible quantum states make the outgoing quanta correlated with the environment, thus heralding the importance of quantum entanglement for black hole physics [60]. For example, one can interpret particle emission as some tunneling process and use the WKB approximation [61] to obtain . Together with the energy conservation, this reproduces the area law as shown in [62]. However, the emerging probability distribution does not obey a typical thermal behavior.
Here, we use the same technique as in [63]. Specifically, from Equation (8), one can see that the probability emitting any particle at a given temperature T always contains an exponential function of E reading
where D is a function which is responsible for any deviations from the exponential distribution. In order to determine it, one needs access to all matter interactions, which are hidden behind the horizon.
In what follows, we assume D to be constant. Normalizing , one then obtains
where m stands for the rest mass of emitted quanta and M is the maximum energy.
In what follows, we also assume that any additional quantum numbers do not affect the Unruh radiation. Then, from Equation (11) becomes additive, i.e., , as discussed below Equation (5).
In addition, we assume to be independent of energy. Note that in general, the distribution is governed by conservation laws and can be influenced by a particle’s energy E, thus complicating the entropy estimates. Moreover, the conservation laws might affect the background metric of space-time itself, especially if an emitting particle at some violates the spherical symmetry of the source.
Finally, taking into account all of the above about angular degrees of freedom, one obtains the total entropy of a spherical source of Unruh radiation; see (5),
where is the entropy of the energy distribution at given temperature T, and the term
describes the contribution of both the Unruh effect and averaged over the energy spectrum. Note that the contribution of additional space-like dimensions is taken into account via . The multiplier is the entropy of a Schwarzschild black hole with temperature T. It is introduced for scaling reasons.
The first term from Equation (16) is a common entropy of the exponential energy distribution given by Equation (14) but expressed in the units of . Quantity describes the contribution of any other quantum numbers, and is responsible for the Unruh effect at given temperature T. Exact analytical expressions for all three terms can be found in the Appendix B.
4. Results
The total entropy —see Equation (16)—depends on various parameters, such as maximum multiplicity at given energy E and temperature T, the rest mass of emitted particles m, their maximal energy M, and any additional quantum numbers governed by .
Noting that for any particles known to date
one can set with a high accuracy in what follows.
The energy contribution to the total entropy is presented by (A3). Its key dependence on and is governed by
which is depicted in Figure 1. Note that it is measured in arbitrary units, due do the unknown value of ; see Equations (A3) and (6) for details. The quantity takes negative values, which is just a logarithmic artifact of the firt term: there is no entropy if , so a common treatment in such a case is to set it to 0.
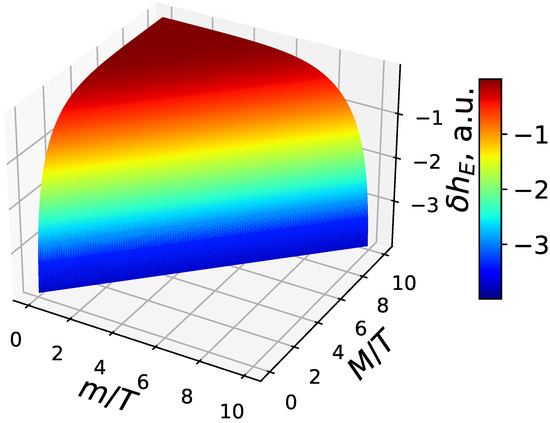
Figure 1.
Quantity as a function of and .
The plot shows gradual increase in with increasing; the quantity decreases with rising. Here, we have left the rest mass m untouched because it is present as the ratio and can be large even though Equation (17) is valid.
The ratio as a function of M and T at is depicted in Figure 2, see (A6). One can see that additional quantum numbers’ contribution to the total entropy exhibits an uprising trend with the increasing temperature, as expected. A similar tendency is observed for the maximum energy M, but at a much slower pace.
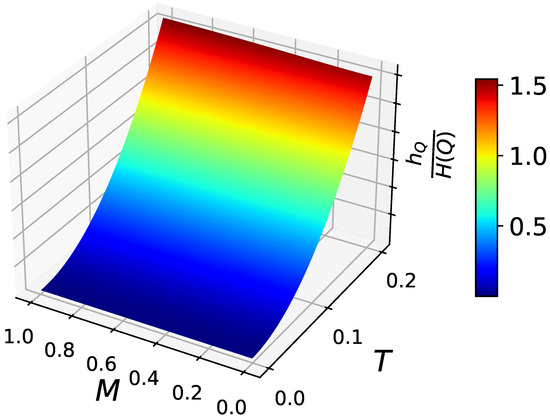
Figure 2.
Scaled term as a function of M and T for .
It should be mentioned that the model seems to fail in the case any of the scaled terms from Equation (16) or their sum is approaching 1. This implies the entropy from Equation (16) exceeds , which is highly unlikely. Therefore, combining this with the plotted data in Figure 2 allows us to specify model restrictions: the approach is valid only for temperatures .
Finally, the term from Equation (A10) as a function of M and T at is depicted in Figure 3 for and in Figure 4 for . Note that the case describes the emission of the particles with spin .
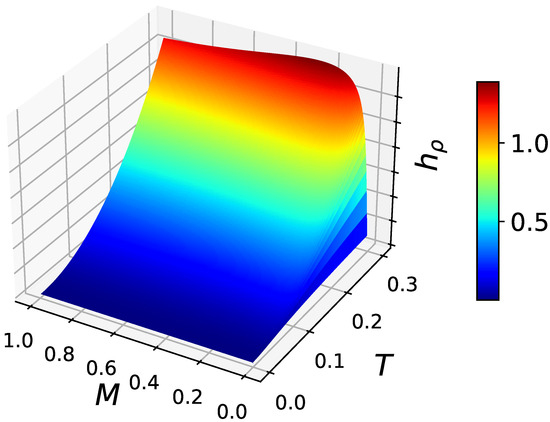
Figure 3.
Scaled term as a function of M and T for and .
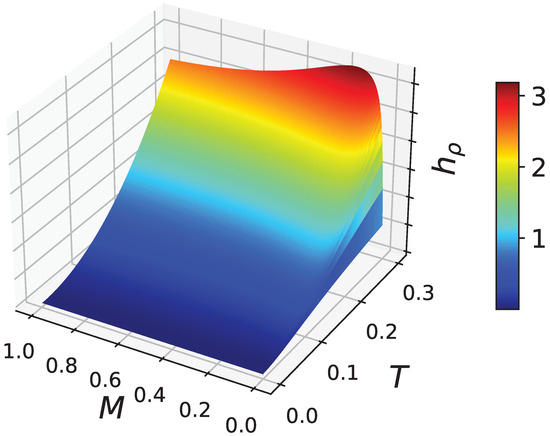
Figure 4.
Scaled term as a function of M and T for and .
Both cases demonstrate an increase in with temperature rising. The plots have a more significant role of the Unruh term for larger N, thus claiming the contribution of multiplicity to the phase space volume occupied by radiation.
Both plots for exhibit a maximum with respect to maximal emission energy M, which becomes more pronounced for larger N. One might have expected the entropy to increase gradually for a wider energy range. However, is the conditional Unruh entropy being averaged over the energy spectrum, and its dependence on M might be highly non-trivial.
Also note that for , the mass of a Schwarzschild black hole equals . On the other hand, any energies close to might affect the background metric, thus making all the analysis not valid, because the Unruh effect implies that emitted particles cannot disturb the horizon. Exceeding the threshold requires taking into account the appropriate corrections to the space-time in the total Hamiltonian. So the presented model implies , where both Figure 3 and Figure 4 demonstrate a gradual increase with respect to M.
For hot horizons, when , both and diverge as expected for any source with increasing temperature. In such a case, for [63], i.e., it becomes constant and reproduces a typical behavior of ; see (A6).
From Equation (7), it follows that the total state factorizes for . Tracing out the domain under the horizon results in a pure state. This means that at low temperatures, and the term gives no contribution to the total entropy. However, the term for too, in contrast to what was obtained in [64]. Such a discrepancy can be explained by different model assumptions. In [64] entropy is additive with respect to the energy E of emitted particles, while here, an exponential dependence has been imposed.
5. Discussion
We calculated the Unruh entropy for a spherically symmetric source with an exponential energy spectrum in the analytical form and compared it to the entropy of a Schwarzschild black hole. Generalization to arbitrary multiplicity, which is introduced via the parameter N, allows us to estimate the contribution of fermions and bosons separately.
Within the model, we assumed entanglement among Rindler modes to be the crucial source for the entropy of Unruh radiation. The presented approach relies on the von Neumann entropy and, therefore, may differ from other interpretations [65] for the effect.
We would like to emphasize that our model does not identify the Unruh effect and Hawking radiation. Even a naive dimensional analysis indicates discrepancies: the effect can be considered as a -dimensional one, while any spherical source is embedded into a space-time. Despite that, they turned out to have something in common, thus stimulating ongoing interest in the issue [66,67,68,69,70].
For reasons of symmetry, the model assumes that angular degrees of freedom contribute independently in the form of an additional multiplier over the spectra of the angular momentum operator and its projection.
Exponential energy dependence for the probability emission has allowed us to estimate the total entropy of Unruh radiation analytically for an arbitrary energy range. However, the semi-classical approach used in the Unruh effect limits the applicability of the model.
Within the approach, the contribution of any other degrees of freedom is assumed to be independent of both angular momentum and energy.
It may be argued that (7) interconnects different reference frames that cannot be extended to the whole space-time in the general case. On the other hand, the mixed state (8) increases the entropy of the accelerated observer while being detected. From a quantum perspective, this contribution cannot be eradicated at zero cost and, therefore, should increase the total entropy of the whole space-time.
One may mention that the Unruh effect neglects any effects of particle emission on the background metric. Then, there is no sense in studying the contribution of correlations among different quantum numbers to the emitted entropy. For example, the previous study [64], utilizing a similar approach except for the exponential energy distribution, recovered the area law for ; this allowed to consider the Unruh effect contribution to the black hole entropy as a significant one. Alternatively, the area law is reproducible within other approaches, e.g., non-thermal energy spectra [62] or a thermal equilibrium at different spin quantum numbers [71], or via the analysis of a thin shell in the vicinity of the horizon [72].
As shown in [24], the entropy is susceptible to a certain form of the stress–energy tensor governing the contribution of any degrees of freedom and correlations among them. This implies strong entropy dependence on both the energy spectra and the subsequent metric back-reaction, thus indicating a significant role of conditional distributions. In this context, the presented approach can be extended to any additional degrees of freedom of emitted quanta that can be beneficial even for far-from-equilibrium cases.
Author Contributions
Conceptualization, M.T., E.Z. and L.B.; methodology, M.T.; software, M.T.; investigation, M.T.; resources, L.B.; writing—original draft preparation, M.T.; writing—review and editing, M.T., E.Z. and L.B.; visualization, M.T.; supervision, L.B.; project administration, L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. The Von Neumann Entropy for Rindler Modes
The density matrix , as shown in (8), describes a mixed state and is represented in its eigenbasis. The von Neumann entropy for the state reads
where the expression
has been used.
Appendix B. Analytical Expressions for h(E), hQ, and hρ
To proceed further, we need a lower incomplete gamma function
and generalized binomial coefficients , which we determine via the series
References
- Fulling, S.A. Nonuniqueness of Canonical Field Quantization in Riemannian Space-Time. Phys. Rev. D 1973, 7, 2850–2862. [Google Scholar] [CrossRef]
- Davies, P.C.W. Scalar production in Schwarzschild and Rindler metrics. J. Phys. A Math. Gen. 1975, 8, 609. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870–892. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R. Hawking black body spectrum from tunneling mechanism. Phys. Lett. B 2009, 675, 243–245. [Google Scholar] [CrossRef]
- Roy, D. The Unruh thermal spectrum through scalar and fermion tunneling. Phys. Lett. B 2009, 681, 185–189. [Google Scholar] [CrossRef]
- Svaiter, B.F.; Svaiter, N.F. Inertial and noninertial particle detectors and vacuum fluctuations. Phys. Rev. D 1992, 46, 5267–5277. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.S.; Leinaas, J.M. Electrons as accelerated thermometers. Nucl. Phys. B 1983, 212, 131–150. [Google Scholar] [CrossRef]
- Gooding, C.; Biermann, S.; Erne, S.; Louko, J.; Unruh, W.G.; Schmiedmayer, J.; Weinfurtner, S. Interferometric Unruh Detectors for Bose-Einstein Condensates. Phys. Rev. Lett. 2020, 125, 213603. [Google Scholar] [CrossRef] [PubMed]
- Vriend, S.; Grimmer, D.; Martín-Martínez, E. The Unruh Effect in Slow Motion. Symmetry 2021, 13, 1977. [Google Scholar] [CrossRef]
- Bunney, C.R.D.; Biermann, S.; Barroso, V.S.; Geelmuyden, A.; Gooding, C.; Ithier, G.; Rojas, X.; Louko, J.; Weinfurtner, S. Third sound detectors in accelerated motion. arXiv 2023, arXiv:2302.12023. [Google Scholar] [CrossRef]
- Chen, P.; Tajima, T. Testing Unruh Radiation with Ultraintense Lasers. Phys. Rev. Lett. 1999, 83, 256–259. [Google Scholar] [CrossRef]
- Kharzeev, D.; Tuchin, K. From Color Glass Condensate to Quark Gluon Plasma through the event horizon. Nucl. Phys. A 2005, 753, 316–334. [Google Scholar] [CrossRef]
- Castorina, P.; Kharzeev, D.; Satz, H. Thermal hadronization and Hawking–Unruh radiation in QCD. Eur. Phys. J. C 2007, 52, 187–201. [Google Scholar] [CrossRef]
- Satz, H. Thermal Hadron Production by QCD Hawking Radiation. Prog. Theor. Phys. Suppl. 2007, 168, 338–346. [Google Scholar] [CrossRef][Green Version]
- Takagi, S. Vacuum Noise and Stress Induced by Uniform Acceleration: Hawking-Unruh Effect in Rindler Manifold of Arbitrary Dimension. Prog. Theor. Phys. Suppl. 1986, 88, 1–142. [Google Scholar] [CrossRef]
- Higuchi, A.; Matsas, G.E.A.; Peres, C.B. Uniformly accelerated finite-time detectors. Phys. Rev. D 1993, 48, 3731–3734. [Google Scholar] [CrossRef] [PubMed]
- Louko, J.; Satz, A. Transition rate of the Unruh–DeWitt detector in curved space-time. Class. Quantum Gravity 2008, 25, 055012. [Google Scholar] [CrossRef]
- Obadia, N.; Milgrom, M. Unruh effect for general trajectories. Phys. Rev. D 2007, 75, 065006. [Google Scholar] [CrossRef]
- Barbado, L.C.; Visser, M. Unruh-DeWitt detector event rate for trajectories with time-dependent acceleration. Phys. Rev. D 2012, 86, 084011. [Google Scholar] [CrossRef]
- Ostapchuk, D.C.M.; Lin, S.Y.; Mann, R.B.; Hu, B.L. Entanglement dynamics between inertial and non-uniformly accelerated detectors. J. High Energy Phys. 2012, 2012, 72. [Google Scholar] [CrossRef]
- Lin, S.Y. Quantum radiation by an Unruh-DeWitt detector in oscillatory motion. J. High Energy Phys. 2017, 2017, 102. [Google Scholar] [CrossRef][Green Version]
- Ahmadzadegan, A.; Kempf, A. On the Unruh effect, trajectories and information. Class. Quantum Gravity 2018, 35, 184002. [Google Scholar] [CrossRef]
- Becattini, F. Thermodynamic equilibrium with acceleration and the Unruh effect. Phys. Rev. D 2018, 97, 085013. [Google Scholar] [CrossRef]
- Becattini, F.; Rindori, D. Extensivity, entropy current, area law, and Unruh effect. Phys. Rev. D 2019, 99, 125011. [Google Scholar] [CrossRef]
- Lima, C.A.U.; Brito, F.; Hoyos, J.A.; Vanzella, D.A.T. Probing the Unruh effect with an accelerated extended system. Nat. Commun. 2019, 10, 3030. [Google Scholar] [CrossRef] [PubMed]
- Prokhorov, G.Y.; Teryaev, O.V.; Zakharov, V.I. Novel phase transition at the Unruh temperature. arXiv 2023, arXiv:2304.13151. [Google Scholar] [CrossRef]
- Bunney, C.R.; Parry, L.; Perche, T.R.; Louko, J. Ambient temperature versus ambient acceleration in the circular motion Unruh effect. Phys. Rev. D 2024, 109, 065001. [Google Scholar] [CrossRef]
- Crispino, L.C.B.; Higuchi, A.; Matsas, G.E.A. The Unruh effect and its applications. Rev. Mod. Phys. 2008, 80, 787–838. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Ashtekar, A.; Baez, J.; Corichi, A.; Krasnov, K. Quantum Geometry and Black Hole Entropy. Phys. Rev. Lett. 1998, 80, 904–907. [Google Scholar] [CrossRef]
- Khriplovich, I.B. Entropy and area of black holes in loop quantum gravity. Phys. Lett. B 2002, 537, 125–129. [Google Scholar] [CrossRef]
- Bianchi, E. Black hole entropy, loop gravity, and polymer physics. Class. Quantum Gravity 2011, 28, 114006. [Google Scholar] [CrossRef]
- Livine, E.R.; Terno, D.R. Entropy in the classical and quantum polymer black hole models. Class. Quantum Gravity 2012, 29, 224012. [Google Scholar] [CrossRef]
- Strominger, A.; Vafa, C. Microscopic Origin of the Bekenstein-Hawking Entropy. Phys. Lett. B 1996, 379, 99–104. [Google Scholar] [CrossRef]
- Emparan, R.; Horowitz, G.T. Microstates of a Neutral Black Hole in M Theory. Phys. Rev. Lett. 2006, 97, 141601. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Lawrence, A.; Magán, J.M.; Sasieta, M. Microscopic Origin of the Entropy of Black Holes in General Relativity. Phys. Rev. X 2024, 14, 011024. [Google Scholar] [CrossRef]
- Silva, C.A.S.; Landim, R.R. A note on black-hole entropy, area spectrum, and evaporation. Europhys. Lett. 2011, 96, 10007. [Google Scholar] [CrossRef]
- Susskind, L. The World as a Hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Ryu, S.; Takayanagi, T. Holographic Derivation of Entanglement Entropy from the anti–de Sitter Space/Conformal Field Theory Correspondence. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Ryu, S.; Takayanagi, T. Aspects of holographic entanglement entropy. J. High Energy Phys. 2006, 2006, 045. [Google Scholar] [CrossRef]
- ’t Hooft, G. On the quantum structure of a black hole. Nucl. Phys. B 1985, 256, 727–745. [Google Scholar] [CrossRef]
- Brustein, R.; Kupferman, J. Black hole entropy divergence and the uncertainty principle. Phys. Rev. D 2011, 83, 124014. [Google Scholar] [CrossRef]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black holes: Complementarity or firewalls? J. High Energy Phys. 2013, 2013, 62. [Google Scholar] [CrossRef]
- ’t Hooft, G. The Firewall Transformation for Black Holes and Some of Its Implications. Found. Phys. 2017, 47, 1503–1542. [Google Scholar] [CrossRef]
- Srednicki, M. Entropy and area. Phys. Rev. Lett. 1993, 71, 666–669. [Google Scholar] [CrossRef]
- Das, S.; Shankaranarayanan, S. Where are the black-hole entropy degrees of freedom? Class. Quantum Gravity 2007, 24, 5299. [Google Scholar] [CrossRef]
- Das, S.; Shankaranarayanan, S.; Sur, S. Black hole entropy from entanglement: A review. arXiv 2008, arXiv:0806.0402. [Google Scholar]
- Polchinski, J. The Black Hole Information Problem. In New Frontiers in Fields and Strings; World Scientific: London, UK, 2016; pp. 353–397. [Google Scholar] [CrossRef]
- Unruh, W.G.; Wald, R.M. Information loss. Rep. Prog. Phys. 2017, 80, 092002. [Google Scholar] [CrossRef] [PubMed]
- Stoica, O.C. Revisiting the Black Hole Entropy and the Information Paradox. Adv. High Energy Phys. 2018, 2018, 4130417. [Google Scholar] [CrossRef]
- Singleton, D.; Wilburn, S. Hawking Radiation, Unruh Radiation, and the Equivalence Principle. Phys. Rev. Lett. 2011, 107, 081102. [Google Scholar] [CrossRef] [PubMed]
- Barbado, L.C.; Barceló, C.; Garay, L.J.; Jannes, G. Hawking versus Unruh effects, or the difficulty of slowly crossing a black hole horizon. J. High Energy Phys. 2016, 2016, 161. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. In Lecture in Theoretical Physics: Statistical Physics; Ford, K.W., Ed.; W. A. Benjamin, Inc.: Los Angeles, CA, USA, 1963; Volume 3, pp. 181–218. [Google Scholar]
- Jaynes, E.T. Prior Probabilities. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 227–241. [Google Scholar] [CrossRef]
- Solodukhin, S.N. Entanglement Entropy of Black Holes. Living Rev. Relativ. 2011, 14, 8. [Google Scholar] [CrossRef] [PubMed]
- Parikh, M.K.; Wilczek, F. Hawking Radiation As Tunneling. Phys. Rev. Lett. 2000, 85, 5042–5045. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Cai, Q.y.; You, L.; Zhan, M.s. Hidden messenger revealed in Hawking radiation: A resolution to the paradox of black hole information loss. Phys. Lett. B 2009, 675, 98–101. [Google Scholar] [CrossRef]
- Teslyk, M.; Bravina, L.; Zabrodin, E. Unruh Effect and Information Entropy Approach. Particles 2022, 5, 157–170. [Google Scholar] [CrossRef]
- Teslyk, M.; Teslyk, O.; Bravina, L.; Zabrodin, E. Unruh Entropy of a Schwarzschild Black Hole. Particles 2023, 6, 864–875. [Google Scholar] [CrossRef]
- Rovelli, C.; Smerlak, M. Unruh effect without trans-horizon entanglement. Phys. Rev. D 2012, 85, 124055. [Google Scholar] [CrossRef]
- Chung, W.S.; Hassanabadi, H. Black hole temperature and Unruh effect from the extended uncertainty principle. Phys. Lett. B 2019, 793, 451–456. [Google Scholar] [CrossRef]
- Scully, M.O.; Svidzinsky, A.; Unruh, W. Entanglement in Unruh, Hawking, and Cherenkov radiation from a quantum optical perspective. Phys. Rev. Res. 2022, 4, 033010. [Google Scholar] [CrossRef]
- Ramakrishna, S. An observer’s perspective of the Unruh and Hawking effects—Using coherent signals to extract information from a black hole. Europhys. Lett. 2023, 144, 49003. [Google Scholar] [CrossRef]
- Chen, A. Generalized Unruh effect: A potential resolution to the black hole information paradox. Phys. Rev. D 2023, 107, 056014. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; Roberts, C.D.; Terzić, B. Poincaré invariance, the Unruh effect, and black hole evaporation. arXiv 2024, arXiv:2405.06002. [Google Scholar] [CrossRef]
- Dowker, J.S. Remarks on geometric entropy. Class. Quantum Gravity 1994, 11, L55. [Google Scholar] [CrossRef]
- Iorio, A.; Lambiase, G.; Vitiello, G. Entangled quantum fields near the event horizon and entropy. Ann. Phys. 2004, 309, 151–165. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).