Theoretical WIMP–Nucleus Scattering Rates for Isomeric Nuclei

Abstract

The direct detection of dark matter constituents, particularly weakly interacting massive particles (WIMPs), is central to particle physics and cosmology. In this paper, we develop the formalism for WIMP–nucleus-induced transitions from isomeric nuclear states, with particular focus on the experimentally interesting target ¹⁸⁰Ta.

1. Introduction

At present, there is plenty of evidence of the existence of dark matter in the form of cosmological observations, DASI [1], COBE/DMR Cosmic Microwave Background (CMB), observations [2] as well as the recent WMAP [3] and Planck [4] data. It is, however, essential to directly detect such matter in order to unravel the nature of its constituents.

At present, there are many such candidates, which are known as weakly interacting massive particles (WIMPs).

WIMP direct searches have been performed by exploiting WIMP–nucleus elastic scattering; see, e.g., the collaborations PandaX-II [5], XENONIT [6,7] and CDMSLite [8]. No WIMPs have been directly detected, but quite stringent exclusion limits have been extracted for the WIMP–nucleon scattering cross section vs. dark matter mass; see, e.g., the recent review [9].

Spin-dependent WIMP–nucleon interactions can lead to inelastic WIMP–nucleus scattering with a non-negligible probability, provided that the energy of the excited state is sufficiently low. So, for sufficiently heavy WIMPs, the available energy via the high-velocity tail of the M-B distribution maybe adequate to allow scattering to low-lying excited states of certain targets, e.g., of $57.7$ keV for the $7/2^{+}$ excited state of ¹²⁷I, 39.6 keV for the first excited $3/2^{+}$ of ¹²⁹Xe, 35.48 keV for the first excited $3/2^{+}$ state of ¹²⁵Te, and 9.4 keV for the first excited $7/2^{+}$ state of ⁸³Kr. In fact, calculations of the event rates for the inelastic WIMP–nucleus transitions involving the above systems have been performed [10].

The interest in inelastic WIMP–nucleus scattering has recently been revived by a new proposal of searching for the collisional de-excitation of metastable nuclear isomers [11]. The longevity of these isomers is related to a strong suppression of $\gamma$ and $\beta$-transitions, typically inhibited by a large difference in the angular momentum for the nuclear transition. Collisional de-excitation by dark matter is possible since heavy dark matter particles can have a momentum exchange with the nucleus comparable to the inverse nuclear size [12]. In this reference, the mathematical and physical formulation of the method employed for the present calculations has been elaborated on. The reader is referred to this reference for experimental issues that are not discussed in the present work. We only mention that the transition can lead to the ground state or a lower state of excitation. In the latter case, one may detect the $\gamma$ ray following the de-excitation of the final state, providing an extra signature against the background.

2. Expressions for the Cross Section

The evaluation of the differential rate for a WIMP-induced transition $A_{iso}^i\left(E_x\right)$ for an isomeric nuclear state at excitation energy $E_x$ to another one $A_{iso}^f\left(E_x^{\prime }\right)$ (or to the ground state) proceeds in a fashion similar to that of the standard inelastic WIMP-induced transition, except that the kinematics are different. We will make a judicious choice of the final nuclear state so that it can decay in a standard manner to the ground state or to another less excited state:

$$A_{iso}^i\left(E_x\right)+\chi \to A_{iso}^f\left(E_x^{\prime }\right)+\chi$$

(1)

with $\chi$ for the dark matter particle (WIMP). Assuming that all particles involved are non-relativistic, we obtain the following:

$${\displaystyle \frac{{\mathbf{p}}_{\chi }^2}{2m_{\chi }}}+E_x={\displaystyle \frac{{\mathbf{p}}_{\chi }^{\prime 2}}{2m_{\chi }}}+E_x^{\prime }+{\displaystyle \frac{{\mathbf{q}}^2}{2m_A}}$$

(2)

where $\mathbf{q}$ is the momentum transfer to the nucleus $\mathbf{q}={\mathbf{p}}_{\chi }-{\mathbf{p}}_{\chi }^{\prime }$. So the above equation becomes

$${\displaystyle \frac{-{\mathbf{q}}^2}{2{\mu }_r}}+\upsilon \xi q-\Delta =0,\Delta =E_x-E^{\prime }x\iff -{\displaystyle \frac{m_A}{{\mu }_r}}{E}_R+\upsilon \xi \sqrt{2m_A{E}_R}+\Delta =0,\Delta >0$$

(3)

where $\xi$ is the cosine of the angle between the incident WIMP and the recoiling nucleus, $\upsilon$ is the oncoming WIMP velocity, $E_R$ is the nuclear recoil energy, and ${\mu }_r$ is the reduced mass of the WIMP–nucleus system, i.e.,

$${\displaystyle \frac{1}{{\mu }_r}}={\displaystyle \frac{1}{m_{\chi }}}+{\displaystyle \frac{1}{m_A}}.$$

(4)

The differential cross section is given by

$$d\sigma ={\displaystyle \frac{1}{\upsilon }}{\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{d}^3\mathbf{q}\delta \left({\displaystyle \frac{q^2}{2{\mu }_r}}-q\upsilon \xi -\Delta \right){\left({\displaystyle \frac{G_F}{\sqrt{2}}}\right)}^2{\left|ME\left(q^2\right)\right|}^2$$

(5)

where ${\left|ME\left(q\right)\right|}^2$ is the nuclear matrix element of the WIMP–nucleus interaction in dimensionless units and $G_F$ is the standard weak interaction strength.

We find it convenient to express this in terms of the nucleon cross section so that our results are independent of the scale parameters $f_V$ and $f_A$. The total WIMP–nucleon cross section can easily be obtained (see Appendix I of ref. [12]). Thus, Equation (5) can be cast in the following form:

$$d\sigma =\mathrm{\Lambda }{\displaystyle \frac{{\sigma }_N}{m_N^2}}{\displaystyle \frac{1}{\upsilon }}{\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{d}^3\mathbf{q}\delta \left({\displaystyle \frac{q^2}{2{\mu }_r}}-q\upsilon \xi -\Delta \right){\displaystyle \frac{|ME\left(q^2\right){|}^2|}{f_V^2+3f_A^2}},\mathrm{\Lambda }={\displaystyle \frac{2\pi }{4}}$$

(6)

Folding Equation (6) with the velocity distribution, we find (the factor ${\displaystyle \frac{1}{{\upsilon }_0}}$, with a dimension of inverse velocity, was introduced for convenience. A compensating factor ${\upsilon }_0$ will be used to multiply the particle density to obtain the flux. Thus, we obtain the traditional formulas, flux = particle density × velocity and rate = flux × cross section).

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\upsilon }_0}}{\displaystyle \frac{1}{{\sigma }_N}}\langle \upsilon {\displaystyle \frac{d\sigma }{d{E}_R}}\rangle =& \mathrm{\Lambda }{\displaystyle \frac{m_A}{m_N^2}}{\displaystyle \frac{1}{{\upsilon }_0}}{\displaystyle \frac{1}{2\pi }}{\displaystyle \frac{|ME\left(q^2\right){|}^2}{f_V^2+3f_A^2}}\hfill \\ \hfill & \left[\left(\mathrm{\Theta }\left(\Delta -{\displaystyle \frac{M_A{E}_R}{{\mu }_r}}\right)\right){\int }_{{\upsilon }_1}^{{\upsilon }_{esc}}K\left(\upsilon \right)d\upsilon +\left(\mathrm{\Theta }\left(-\Delta +{\displaystyle \frac{M_A{E}_R}{{\mu }_r}}\right)\right){\int }_{{\upsilon }_2}^{{\upsilon }_{esc}}K\left(\upsilon \right)d\upsilon \right]\hfill \end{array}$$

(7)

where $E_R$ is the nuclear recoil energy, $\mathrm{\Theta }$ is the step function, and $K\left(\upsilon \right)$ is given by the velocity distribution

$$K\left(\upsilon \right)=\int d\mathrm{\Omega }\left(\widehat{\upsilon }\right)\upsilon f_{distr}\left(\mathit{v}\right)$$

(8)

Furthermore,

$${\upsilon }_1={\displaystyle \frac{1}{q}}(\Delta -{\displaystyle \frac{q^2}{2{\mu }_r}}),{\upsilon }_2={\displaystyle \frac{1}{q}}({\displaystyle \frac{q^2}{2{\mu }_r}}-\Delta )$$

(9)

Note that the dependence of the cross section on the recoil energy occurs in two ways: (i) it results the nuclear form factor and (ii) it also results from the minimum required velocities ${\upsilon }_1$ and ${\upsilon }_2$ in the folding with the velocity distribution.

We will specialize our results in the commonly used Maxwell–Boltzmann (MB) distribution in the local frame [12]. The integrals involved can by computed analytically

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\upsilon }_0}}{\displaystyle \frac{1}{{\sigma }_N}}\langle \upsilon {\displaystyle \frac{d\sigma }{d{E}_R}}\rangle =& \mathrm{\Lambda }{\displaystyle \frac{m_A}{m_N^2}}{\displaystyle \frac{1}{{\upsilon }_0^2}}{\displaystyle \frac{1}{2\pi }}{\displaystyle \frac{|ME\left(q^2\right){|}^2}{f_V^2+3f_A^2}}\hfill \\ \hfill & \left[\left(\mathrm{\Theta }\left(\Delta -{\displaystyle \frac{M_A{E}_R}{{\mu }_r}}\right)\right){\psi }_1(y_1,y_{esc})+\left(\mathrm{\Theta }\left(-\Delta +{\displaystyle \frac{M_A{E}_R}{{\mu }_r}}\right)\right){\psi }_2(y_2,y_{esc})\right]\hfill \end{array}$$

(10)

where

$$\begin{array}{cc}\hfill {\psi }_1(y_1,y_{esc})=& {\displaystyle \frac{1}{4}}\sqrt{\pi }\left(\mathrm{erf}\left(1-y_1\right)+\mathrm{erf}\left(y_1+1\right)\right)-{\displaystyle \frac{1}{4}}\sqrt{\pi }\left(\mathrm{erf}\left(1-y_{esc}\right)+\mathrm{erf}\left(y_{esc}+1\right)\right),\hfill \\ \hfill {\psi }_2(y_2,y_{esc})=& {\displaystyle \frac{1}{4}}\sqrt{\pi }\left(\mathrm{erf}\left(1-y_2\right)+\mathrm{erf}\left(y_2+1\right)\right)-{\displaystyle \frac{1}{4}}\sqrt{\pi }\left(\mathrm{erf}\left(1-y_{esc}\right)+\mathrm{erf}\left(y_{esc}+1\right)\right)\hfill \end{array}$$

(11)

where

$$erf\left(z\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^z{E}^{-t^2}dt(\mathrm{error} \mathrm{function})$$

The functions ${\psi }_i(y_i,y_{esc})$ depend on the momentum transfer. This depends on the specific nuclear target and will be discussed below.

3. Nuclear Structure

The isomeric nuclei are deformed and have complicated structures, so the usual techniques employed in obtaining the structure of atomic nuclei terms of the spherical shell model do not apply. We find it simple and appropriate to use the Nilsson model, in which a cylindrical harmonic oscillator is used instead of a spherical one. It is characterized by a deformation $ϵ$, reflecting the departure of the cylindrical shape from sphericity. The single-particle orbitals in the Nilsson model are labeled by $\mathrm{\Omega }\left[N{n}_z\mathrm{\Lambda }\right]$, where N is the total number of the oscillator quanta, $n_z$ is the number of quanta along the z-axis of cylindrical symmetry, while $\mathrm{\Lambda }$ ($\mathrm{\Omega }$) is the projection of the orbital (total) angular momentum on the z-axis.

In what follows, it will be of interest to consider the expansions of the Nilsson orbitals on the spherical shell model basis $|Nlj\mathrm{\Omega }\rangle$, where N is the principal quantum number, l (j) is the orbital (total) angular momentum, and $\mathrm{\Omega }$ is the projection of the total angular momentum on the z-axis. The necessary expansions have been obtained as described in Ref. [13] and are found in Appendix IV of ref. [12] for three different values of the deformation $ϵ$.

4. The Nucleus ¹⁸⁰Ta

This nucleus is preferred for experimental reasons. The even core of ${}_{73}{}^{180}\mathrm{Ta}_{107}$ is ${}_{72}{}^{178}\mathrm{Hf}_{106}$, for which the experimental value of the collective deformation variable $\beta$ is 0.2779 [14]; thus, the Nilsson deformation $ϵ=0.95\beta$ [15] is 0.2640.

Several different theoretical calculations, including covariant density functional theory using the DDME2 functional [16,17], Skyrmre–Hartree–Fock–BCS [18] (see also the private communication by N. Minkov), as well as a two-quasiparticle plus rotor model in the mean field represented by a deformed Woods–Saxon potential [19] agree that the first neutron orbital lying above the Fermi surface of the core nucleus ${}_{72}{}^{178}\mathrm{Hf}_{106}$ is the 9/2[624] orbital, while the first proton orbital lying above the Fermi surface of the core nucleus ${}_{72}{}^{178}\mathrm{Hf}_{106}$ is the 9/2[514] orbital. Therefore, it is safe to assume that these two orbitals will play a major role in the formation of the $9^{-}$ isomer state of ${}_{73}{}^{180}\mathrm{Ta}$.

It is instructive to consider the formation of the abovementioned states in light of the expansions of the Nilsson orbitals in terms of spherical shell model orbitals, found in Appendix IV of ref. [12].

The orbitals participating in the formation of the $9^{-}$ isomer, proton 9/2[514] and neutron 9/2[624], are both intruder orbitals; thus, the main contribution comes from the $|5511/29/2\rangle$ component of the former and the $|6613/29/2\rangle$ component of the latter.

The orbitals participating in the formation of the $2^{+}$ excited state are the proton 9/2[514] (intruder) and neutron 5/2[512] (normal parity) orbitals, from which the leading contribution will come from the $|5511/29/2\rangle$ and $|537/25/2\rangle$ vectors, respectively.

5. Some Features Regarding the Target ¹⁸⁰Ta

We begin by considering the transition of the isomeric $9^{-}$ state to the $2^{+}$ state. The momentum dependence of the cross section arising from the velocity distribution for a transition energy is $\Delta =37$ keV, which is given in Figure 1.

To proceed further, we need to determine the structure of the target ¹⁸⁰Ta. As explained in Section 4, in the context of the Nilsson model, we can consider the proton orbital ${\displaystyle \frac{9}{2}}$[514] both in the initial state $9^{-}$ and the final $2^{+}$. Furthermore, for the neutrons, we use ${\displaystyle \frac{9}{2}}$[624] for the $9^{-}$ and the ${\displaystyle \frac{5}{2}}$[512] for the $2^{+}$. To proceed further, we use the expansion of the Nilsson orbitals into shell model states, as shown in Appendix IV of [12] for a deformation parameter of 0.30. Note that in this case, only the neutrons can undergo transitions, while the protons are just spectators.

5.1. Shell Model Form Factors

The vector and axial vector reduced nuclear matrix elements can be obtained using the standard techniques, as described in Appendix II and Appendix III of [12] with the quantities of subscript 1 indicating neutrons while those for 2 are associated with protons. Thus, we find

$$\begin{array}{cc}\hfill RM{E}_V=& {\displaystyle \frac{f_V}{f_A}}(0.0644445F(4,3,7,u)+1.01419F(4,5,7,u)+1.01419F(4,5,9,u)+1.52946F(6,3,7,u)\hfill \\ \hfill & +1.52946F(6,3,9,u)+1.52946F(6,5,7,u)+1.79799F(6,5,9,u)+2.19718F(6,5,11,u)\hfill \end{array}$$

$$\begin{array}{cc}\hfill RM{E}_A=& 0.321503F(4,3,7,u)+2.05117F(4,5,7,u)+2.16715F(4,5,9,u)+2.04512F(6,3,7,u)\hfill \\ \hfill & +3.3217F(6,3,9,u)+2.04512F(6,5,7,u)+2.31181F(6,5,9,u)+3.58938F(6,5,11,u)\hfill \end{array}$$

In the above expressions, $F(\ell ,{\ell }^{\prime },\lambda )$ are the single-particle form factors. The first two integers indicate orbital angular momentum quantum numbers $\ell ,{\ell }^{\prime }$, while the last integer $\lambda$ gives the multipolarity of the transition. The quantity u corresponds to $b_{N}q$, where $b_N$ is the harmonic oscillator length parameter. The relevant form factors are exhibited in Figure 2a.

The relevant nuclear ME is given by

$$R_{ME}^2\left(q^2\right)={\displaystyle \frac{1}{19}}\left(RM{E}_V^2+RM{E}_A^2\right)$$

(12)

Its momentum dependence is exhibited in Figure 3a. We should note that the large value of the matrix element in the case of large $f_V$ is due to the normalization adopted to make the matrix element independent of the scale. Recall that a combination factor appear in the cross section. In the present work, we will adopt $f_V=f_A$.

5.2. Phenomenological Form Factors

It is generally believed that the shell model single particle factors lead to large suppression. So some phenomenological form factors. One example is the the Helm like single particle form factors:

$$F_{\lambda }\left(q\right)=(2\lambda +1)e^{-{\displaystyle \frac{1}{2}}{a}^2{q}^2}{\displaystyle \frac{j_{\lambda }\left(qR\right)}{qR}}$$

(13)

Our treatment means that the radial integrals are independent of the angular momentum quantum numbers $\ell ,{\ell }^{\prime }$. The obtained results are exhibited in Figure 2b. (Odd (parity-changing) transitions are relevant). The reduced matrix elements for the vector and the axial vector are

$$\begin{array}{cc}\hfill RME{H}_A=& 3.58938F_{11}(a,q,R)+6.46292F_7+7.80066F_9(a,q,R)\hfill \\ \hfill RME{H}_V=& {\displaystyle \frac{f_V}{f_A}}(2.19718F_{11}(a,q,R)+4.13756F_7(a,q,R)+4.34165F_9(a,q,R))\hfill \end{array}$$

(14)

where $F_{\lambda }$ are the Helm single-particle form factors. The nuclear matrix element is

$$R_{MEH}^2\left(q^2\right)={\displaystyle \frac{1}{19}}\left(RME{H}_V^2+RME{H}_A^2\right)$$

(15)

The momentum dependence of this ME is exhibited in Figure 3b.

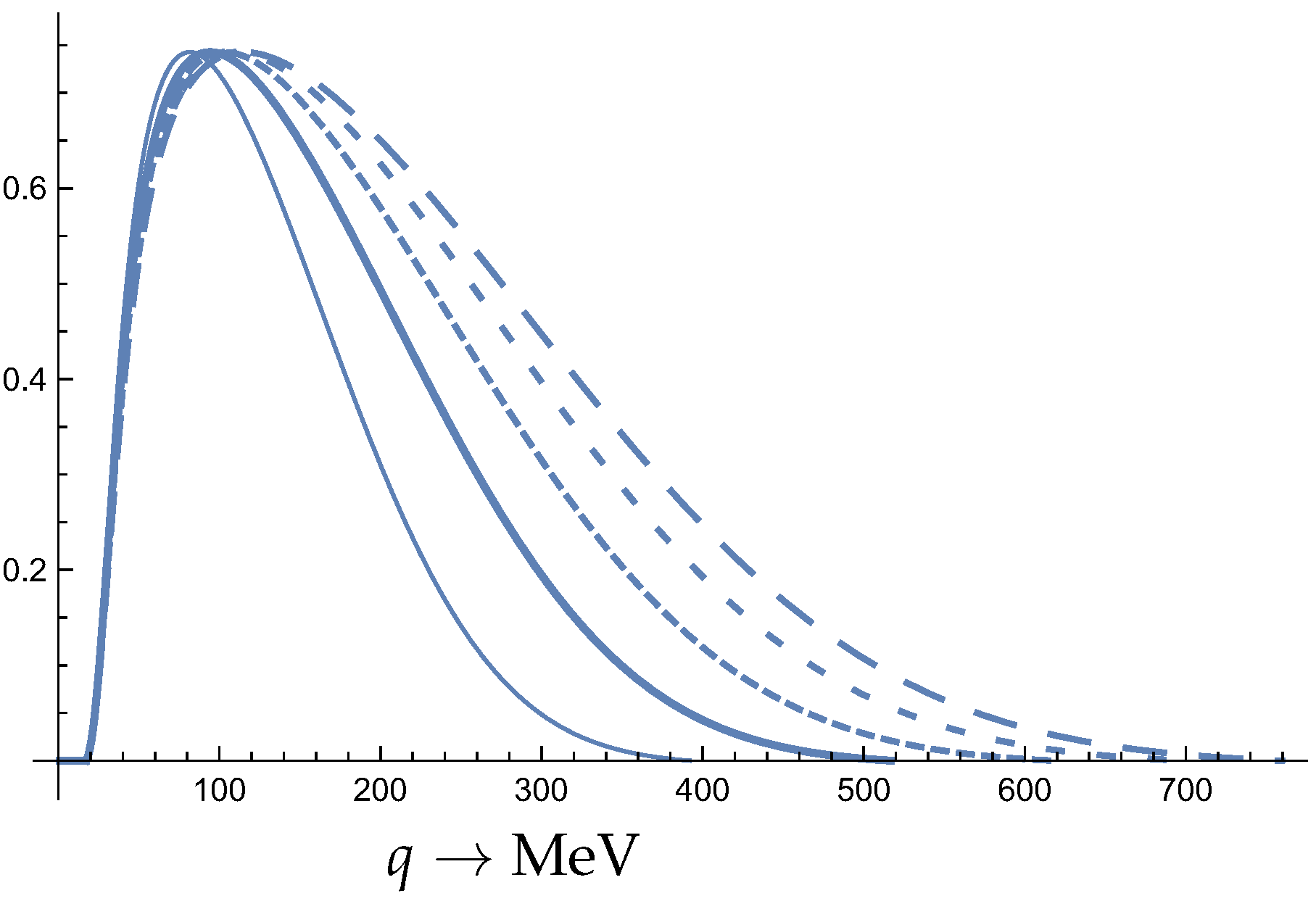
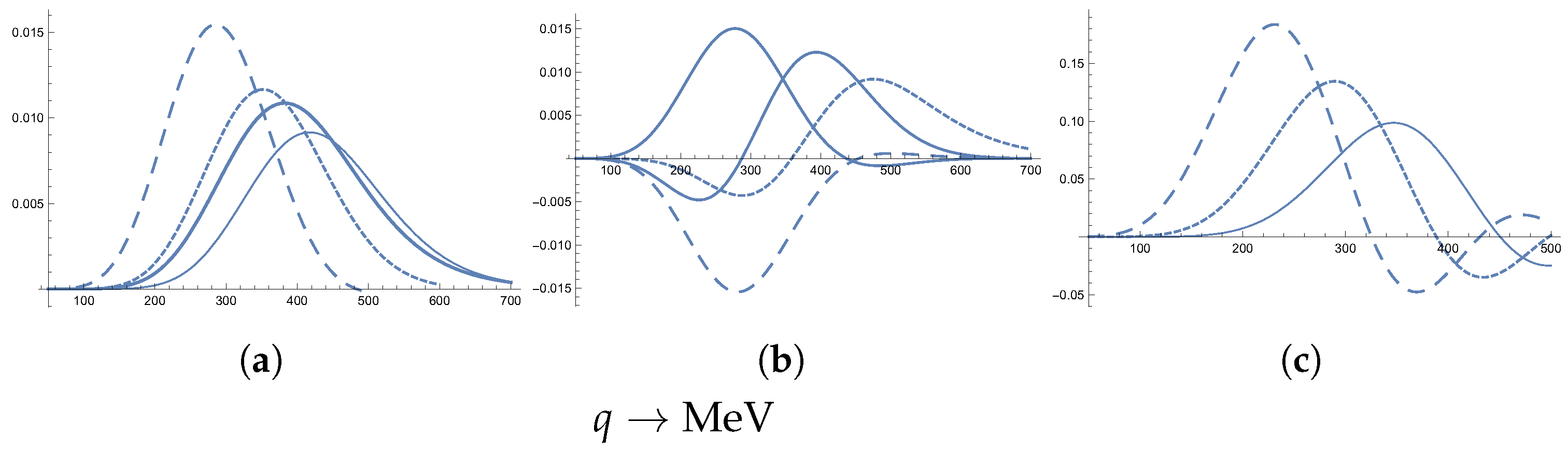
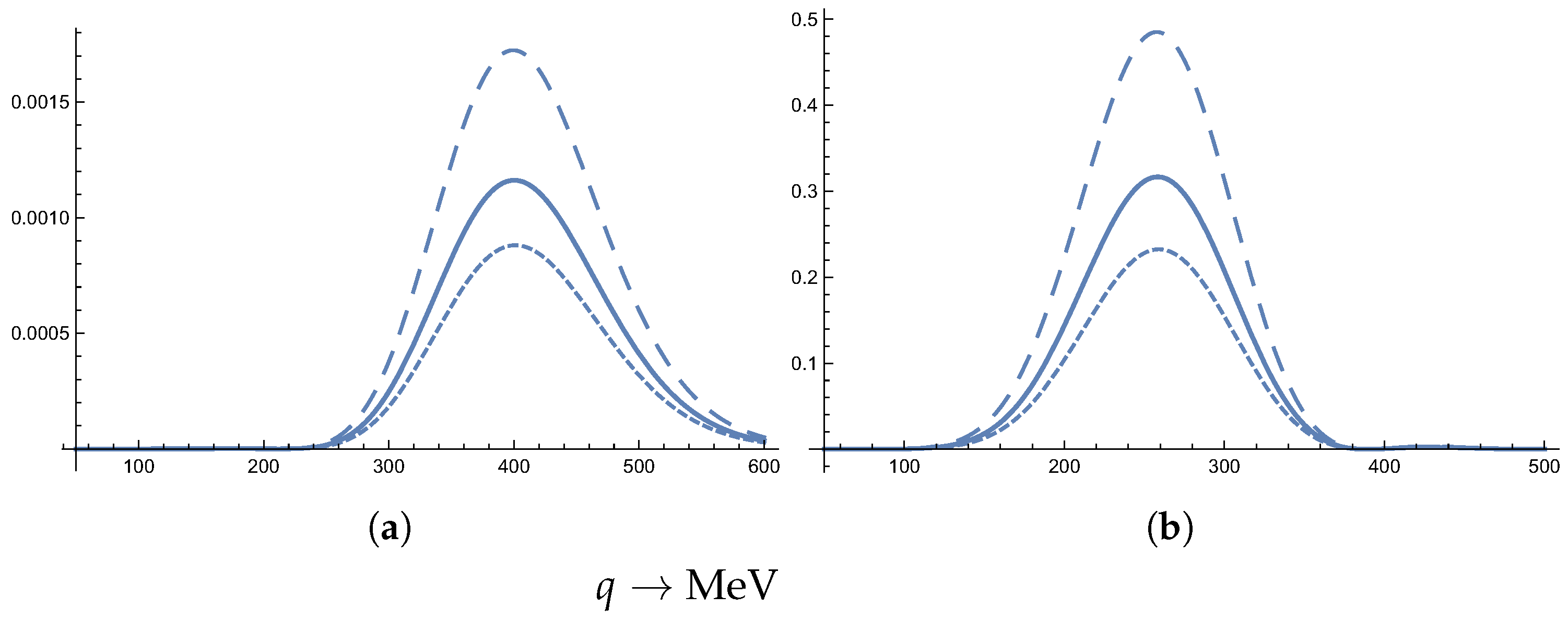
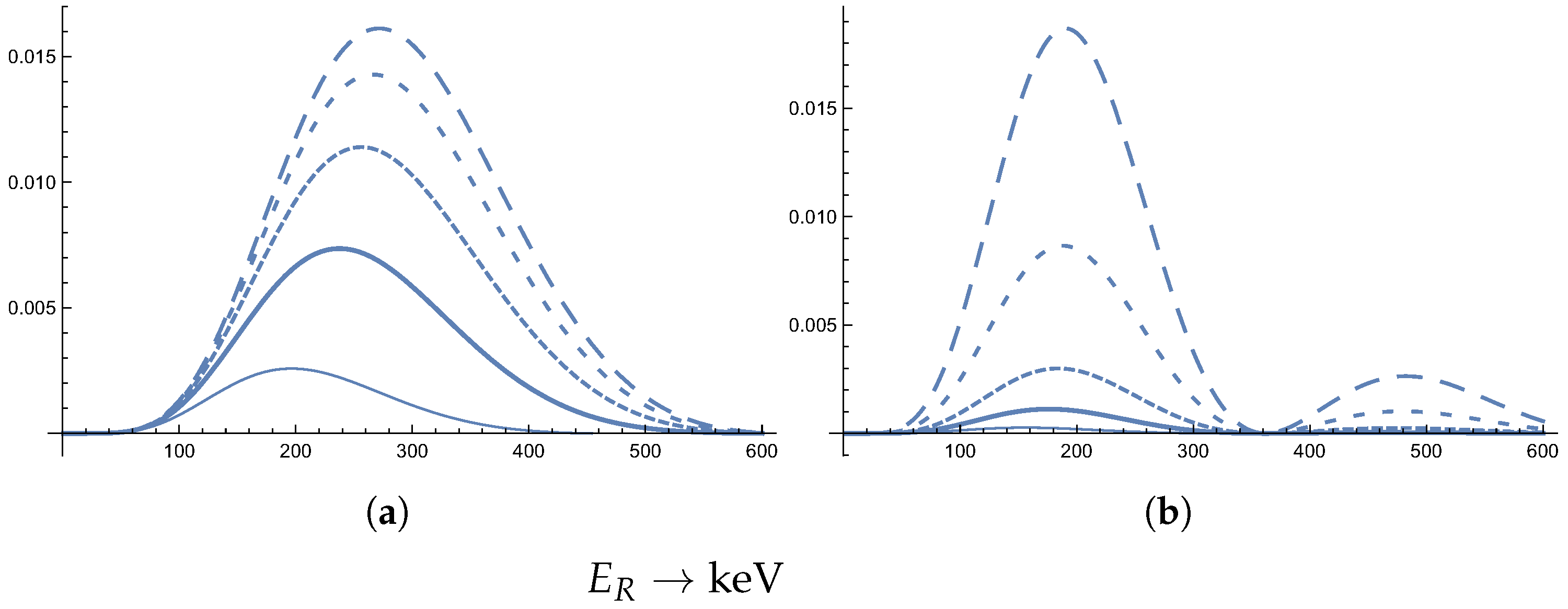
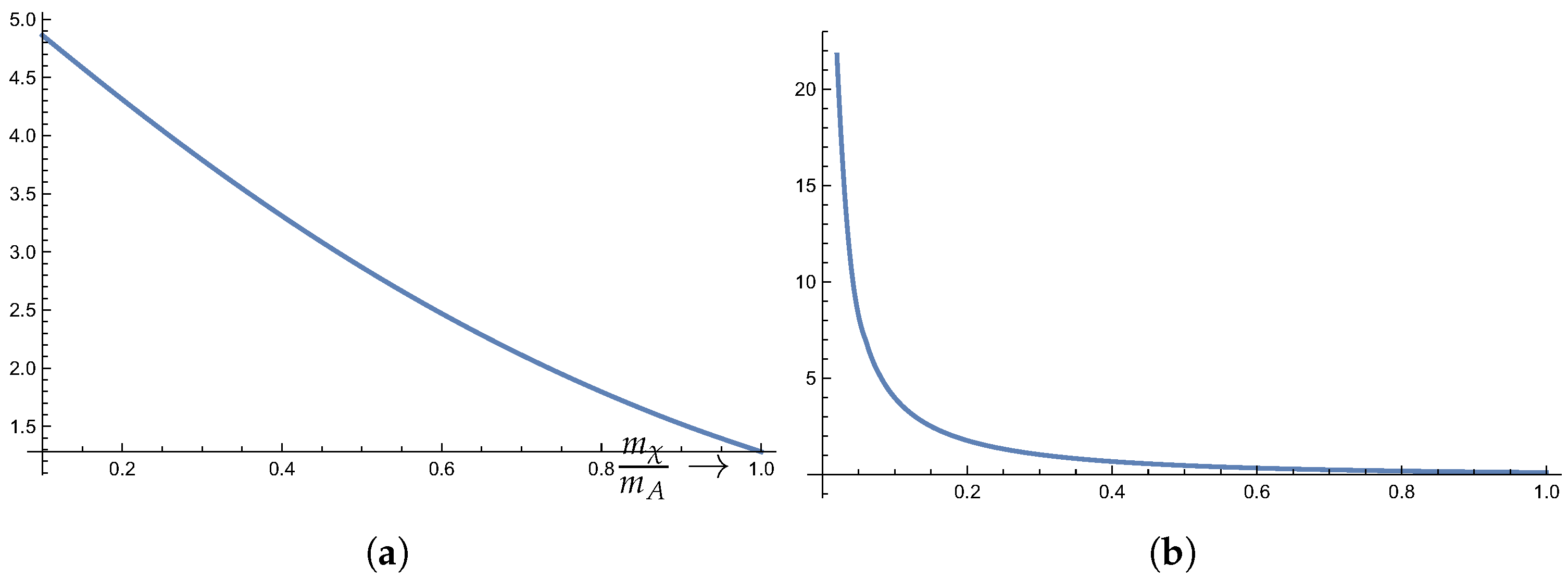
5.3. Some Results for ¹⁸⁰Ta

The numerical value of $\mathrm{\Lambda }{\displaystyle \frac{m_A}{m_N^2}}{\displaystyle \frac{1}{{\upsilon }_0^2}}{\displaystyle \frac{1}{2\pi }}$ in Equation (7 for $f_A/f_V=1$, is 0.068 for A = 180, expressed in units of keV⁻¹. The plot of ${\displaystyle \frac{1}{{\upsilon }_0}}{\displaystyle \frac{1}{{\sigma }_N}}\langle \upsilon {\displaystyle \frac{d\sigma >}{d{E}_R}}\rangle$ vs. the previous ones are multiplied with 0.063. We prefer to express this as a function of $E_R$ in units of keV, as shown in Figure 4a. It can be shown that a similar expression holds for the rate ${\displaystyle \frac{1}{R_N}}{\displaystyle \frac{dR}{d{E}_R}}$; see Figure 4b.

The expressions for $\sigma$ and R for ¹⁸⁰Ta can be obtained using the relevant values for the nucleon (see Appendix I of ref. [12]):

$${\sigma }_N=8.8\times {10}^{-40}{cm}^2(f_V^2+3f_A^2)$$

$f_R=2.1\times {10}^{38}$ cm⁻²y⁻¹${\displaystyle \frac{m_N}{m_{\chi }}}$ (kinematics factor), yielding. This leads to the total rate:

$$R_N=f_R{\sigma }_N=0.72y^{-1}(f_V^2+3f_A^2)$$

For orientation purposes, here, we employ $f_V=f_A=1$.

One can integrate the differential cross section over the recoil energy $E_R$ and multiply it with the total nucleon to obtain the WIMP–nucleus cross section as a function of the wimp mass $m_{\chi }$; this is exhibited in Figure 5a.

In the same fashion, one can obtain differential rate

$${\displaystyle \frac{1}{R_N\left(m_{\chi }\right)}}{\displaystyle \frac{dR}{d{E}_R}}$$

since the WIMP density used to obtain the densities is the same. The situation is, however, changed if one is comparing the obtained differential rate relative to the total rate for the nucleon at some fixed value of the WIMP mass. We note that the overall momentum dependence is obtained by combining the effect of the velocity distribution—see Figure 1—and the momentum dependence of the nuclear matrix element as shown in Figure 3b. The exhibited differential rate contains, of course, the WIMP mass dependence arising from the WIMP density in our galaxy. The thus obtained differential rate in units total rate of the nucleon for $m_N/m_{\chi }=1$ is exhibited in Figure 4b.

One can integrate the differential rate over the recoil energy $E_R$ and multiply with the total nucleon rate to obtain the total WIMP–nucleus rate section as a function of the WIMP mass $m_{\chi }$; this is exhibited in Figure 5b.

6. Discussion

We have seen that, not unexpectedly, the nuclear ME encountered in the inelastic WIMP–nucleus scattering involving isomeric nuclei is much smaller than that involved in the elastic process considered in the standard WIMP searches. This occurs for two reasons: (a) the form factor in the elastic is favorable and (b) in the elastic case, the cross section is proportional to the mass number $A^2$. In the present case, the nuclear matrix element for ¹⁸⁰Ta, as indicated by the coefficients appearing in Equation (14), is not unusually small compared to other typical inelastic processes. The Nilsson model is expected to work well in the case of ¹⁸⁰Ta, but the obtained event rate is quite small. It seems that the mechanism of suppression encountered in the standard decay of the isomeric state may somewhat persist in the WIMP–nucleus cross section as well.

The expected events in this work have been obtained with an unrealistic target mass ${10}^{24}$ particles, compared to more realistic ${10}^{19}$ [12]. On the other hand, an estimated half-life time limit is $4.5\times {10}^{16}$ years (90% 350 C.L.) [20]. Further improvement can be achieved by using an isomer with larger mass combined with a better detection efficiency in the experiments. Furthermore, the experiments can exploit the signal provided by the subsequent standard decay of the $2^{+}$ state to the ground state. This is an advantage that is not available in conventional WIMP searches.