Photoproduction of Heavy Meson and Photon Pairs
Abstract
1. Introduction
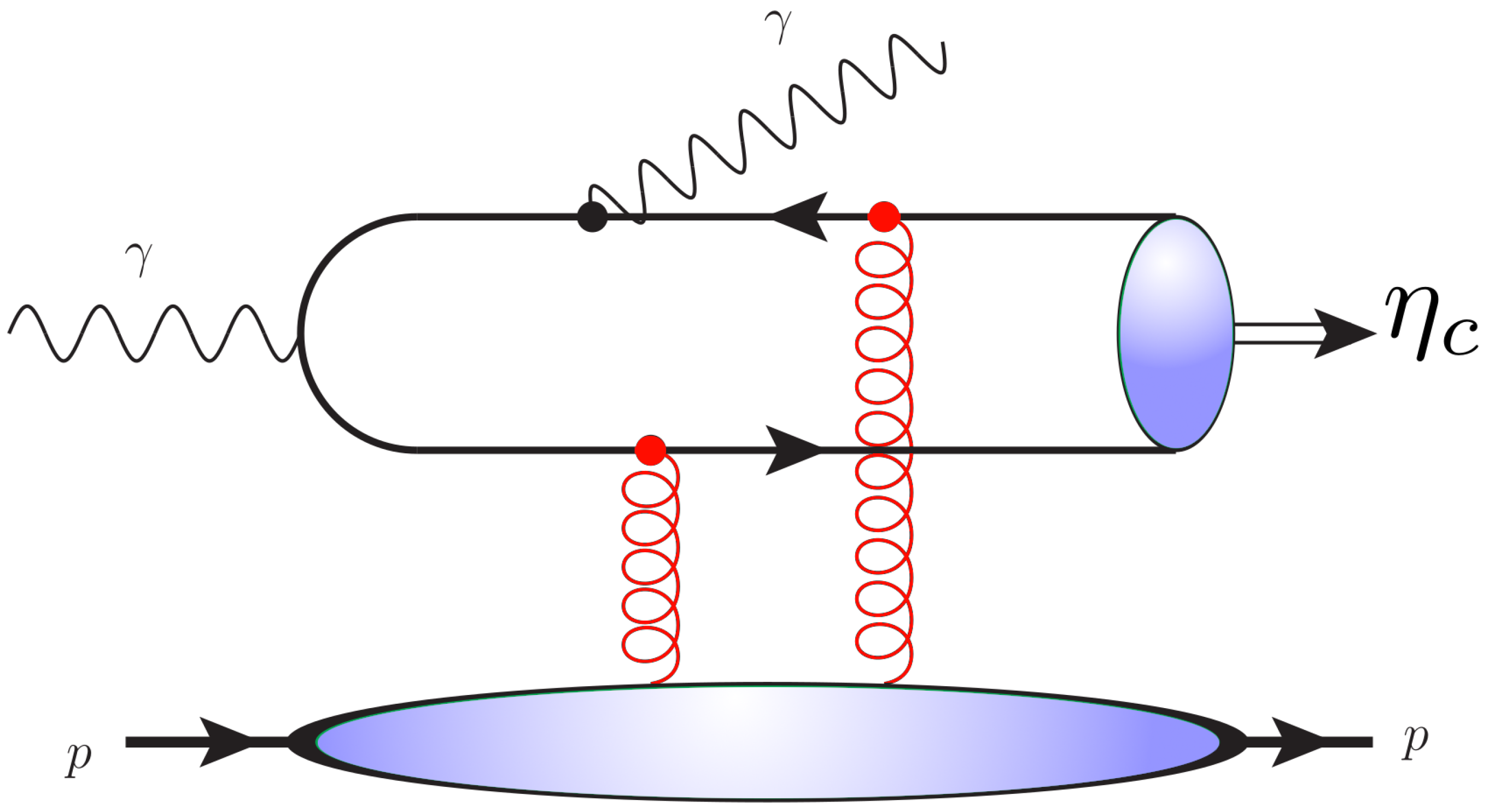
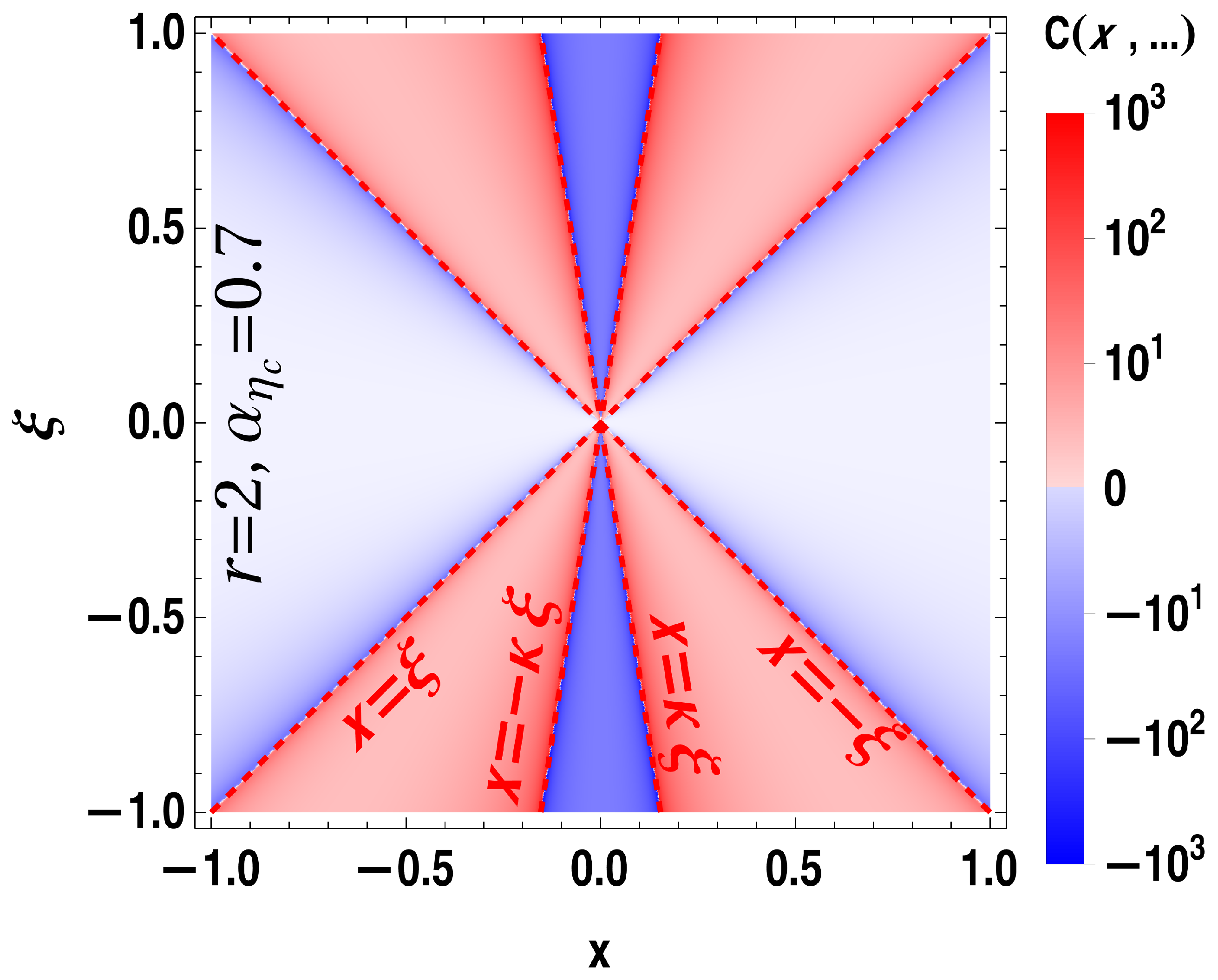
2. Amplitude of the Process in the Collinear Factorization Framework
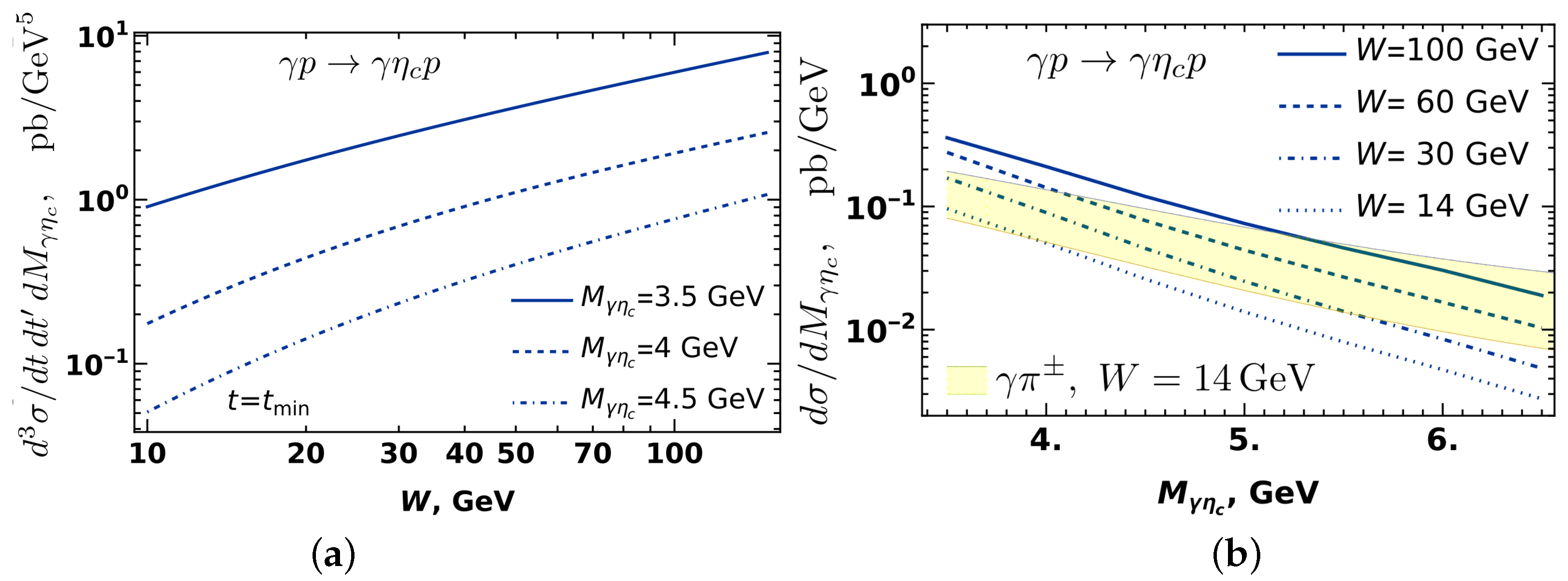
3. Results
4. Discussion and Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Goeke, K.; Polyakov, M.V.; Vanderhaeghen, M. Hard exclusive reactions and the structure of hadrons. Prog. Part. Nucl. Phys. 2001, 47, 401. [Google Scholar] [CrossRef]
- Diehl, M. Generalized parton distributions. Phys. Rept. 2003, 388, 41. [Google Scholar] [CrossRef]
- Guidal, M.; Moutarde, H.; Vanderhaeghen, M. Generalized Parton Distributions in the valence region from Deeply Virtual Compton Scattering. Rept. Prog. Phys. 2013, 76, 066202. [Google Scholar] [CrossRef] [PubMed]
- Dutrieux, H.; Lorcé, C.; Moutarde, H.; Sznajder, P.; Trawinski, A.; Wagner, J. Phenomenological assessment of proton mechanical properties from deeply virtual Compton scattering. Eur. Phys. J. C 2021, 81, 300. [Google Scholar] [CrossRef]
- Burkert, V.; Elouadrhiri, L.; Afanasev, A.; Arrington, J.; Contalbrigo, M.; Cosyn, W.; Deshpande, A.; Glazier, D.; Ji, X.; Liuti, S.; et al. Precision Studies of QCD in the Low Energy Domain of the EIC. arXiv 2002, arXiv:2211.15746. [Google Scholar] [CrossRef]
- Khalek, R.A.; Accardi, A.; Adam, J.; Adamiak, D.; Akers, W.; Albaladejo, M.; Al-Bataineh, A.; Alexeev, M.G.; Ameli, F.; Antonioli, P.; et al. Science Requirements and Detector Concepts for the Electron-Ion Collider: EIC Yellow Report. arXiv 2021, arXiv:2103.05419. [Google Scholar]
- Kumericki, K.; Liuti, S.; Moutarde, H. GPD phenomenology and DVCS fitting: Entering the high-precision era. Eur. Phys. J. A 2016, 52, 157. [Google Scholar] [CrossRef]
- Bertone, V.; Dutrieux, H.; Mezrag, C.; Moutarde, H.; Sznajder, P. Deconvolution problem of deeply virtual Compton scattering. Phys. Rev. D 2021, 103, 114019. [Google Scholar] [CrossRef]
- Moffat, E.; Freese, A.; Cloët, I.; Donohoe, T.; Gamberg, L.; Melnitchouk, W.; Metz, A.; Prokudin, A.; Sato, N. Shedding light on shadow generalized parton distributions. Phys. Rev. D 2023, 108, 036027. [Google Scholar] [CrossRef]
- Duplančić, G.; Nabeebaccus, S.; Passek-Kumerički, K.; Pire, B.; Szymanowski, L.; Wallon, S. Accessing chiral-even quark generalised parton distributions in the exclusive photoproduction of a γπ± pair with large invariant mass in both fixed-target and collider experiments. J. High Energy Phys. 2023, 03, 241. [Google Scholar] [CrossRef]
- Duplančić, G.; Passek-Kumerički, K.; Pire, B.; Szymanowski, L.; Wallon, S. Probing axial quark generalized parton distributions through exclusive photoproduction of a γπ± pair with a large invariant mass. J. High Energy Phys. 2018, 11, 179. [Google Scholar] [CrossRef]
- Siddikov, M. Exclusive photoproduction of ηcγ pairs with large invariant mass. Phys. Rev. D 2024, 110, 056043. [Google Scholar] [CrossRef]
- Boussarie, R.; Pire, B.; Szymanowski, L.; Wallon, S. Exclusive photoproduction of a γρ pair with a large invariant mass. J. High Energy Phys. 2017, 2, 54, Erratum in J. High Energy Phys. 2018, 10, 29. [Google Scholar]
- Cosyn, W.; Pire, B. Diffractive rho plus lepton pair production at an electron-ion collider. Phys. Rev. D 2021, 103, 114002. [Google Scholar] [CrossRef]
- Pedrak, A.; Pire, B.; Szymanowski, L.; Wagner, J. Electroproduction of a large invariant mass photon pair. Phys. Rev. D 2020, 101, 114027. [Google Scholar] [CrossRef]
- Pire, B.; Szymanowski, L.; Wallon, S. Diffractive deeply virtual Compton scattering. Phys. Rev. D 2020, 101, 074005. [Google Scholar] [CrossRef]
- Pedrak, A.; Pire, B.; Szymanowski, L.; Wagner, J. Hard photoproduction of a diphoton with a large invariant mass. Phys. Rev. D 2017, 96, 074008. [Google Scholar] [CrossRef]
- Beiyad, M.E.; Pire, B.; Segond, M.; Szymanowski, L.; Wallon, S. Photoproduction of a πρT pair with a large invariant mass and transversity generalized parton distribution. Phys. Lett. B 2010, 688, 154. [Google Scholar] [CrossRef]
- Ivanov, D.Y.; Pire, B.; Szymanowski, L.; Teryaev, O.V. Probing chiral-odd GPDs in diffractive electroproduction of two vector mesons. Phys. Lett. B 2002, 550, 65. [Google Scholar] [CrossRef]
- Duplančić, G.; Nabeebaccus, S.; Passek-Kumerički, K.; Pire, B.; Szymanowski, L.; Wallon, S. Accessing GPDs through the exclusive photoproduction of a photon-meson pair with a large invariant mass. arXiv 2022, arXiv:2212.01034. [Google Scholar]
- Qiu, J.W.; Yu, Z. Extracting transition generalized parton distributions from hard exclusive pion-nucleon scattering. Phys. Rev. D 2024, 109, 074023. [Google Scholar] [CrossRef]
- Qiu, J.W.; Yu, Z. Extraction of the Parton Momentum-Fraction Dependence of Generalized Parton Distributions from Exclusive Photoproduction. Phys. Rev. Lett. 2023, 131, 161902. [Google Scholar] [CrossRef] [PubMed]
- Deja, K.; Martinez-Fernandez, V.; Pire, B.; Sznajder, P.; Wagner, J. Phenomenology of double deeply virtual Compton scattering in the era of new experiments. Phys. Rev. D 2023, 107, 094035. [Google Scholar] [CrossRef]
- Siddikov, M.; Schmidt, I. Exclusive production of quarkonia pairs in collinear factorization framework. Phys. Rev. D 2023, 107, 034037. [Google Scholar] [CrossRef]
- Siddikov, M.; Schmidt, I. Exclusive photoproduction of D-meson pairs with large invariant mass. Phys. Rev. D 2023, 108, 096031. [Google Scholar] [CrossRef]
- Bodwin, G.T.; Braaten, E.; Lepage, G.P. Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D 1995, 51, 1125, Erratum in Phys. Rev. D 1997, 55, 5853. [Google Scholar] [CrossRef]
- Maltoni, F.; Mangano, M.L.; Petrelli, A. Quarkonium photoproduction at next-to-leading order. Nucl. Phys. B 1998, 519, 361. [Google Scholar] [CrossRef]
- Brambilla, N.; Eidelman, S.; Heltsley, B.K.; Vogt, R.; Bodwin, G.T.; Eichten, E.; Frawley, A.D.; Meyer, A.B.; Mitchell, R.E.; Papadimitriou, V.; et al. Heavy quarkonium: Progress, puzzles, and opportunities. Eur. Phys. J. C 2011, 71, 1534. [Google Scholar]
- Diehl, M.; Feldmann, T.; Jakob, R.; Kroll, P. The overlap representation of skewed quark and gluon distributions. Nucl. Phys. B 2001, 596, 33, Erratum in Nucl. Phys. B 2001, 605, 647. [Google Scholar] [CrossRef]
- Boer, D.; Diehl, M.; Milner, R.; Venugopalan, R.; Vogelsang, W.; Accardi, A.; Aschenauer, E.; Burkardt, M.; Ent, R.; Guzey, V.; et al. Gluons and the quark sea at high energies: Distributions, polarization, tomography. arXiv 2011, arXiv:1108.1713. [Google Scholar]
- Belitsky, A.V.; Mueller, D.; Kirchner, A. Theory of deeply virtual Compton scattering on the nucleon. Nucl. Phys. B 2002, 629, 323. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Radyushkin, A.V. Unraveling hadron structure with generalized parton distributions. Phys. Rept. 2005, 418, 1–387. [Google Scholar] [CrossRef]
- Goloskokov, S.V.; Kroll, P. The Longitudinal cross-section of vector meson electroproduction. Eur. Phys. J. C 2007, 50, 829. [Google Scholar] [CrossRef]
- Goloskokov, S.V.; Kroll, P. The Role of the quark and gluon GPDs in hard vector-meson electroproduction. Eur. Phys. J. C 2008, 53, 367. [Google Scholar] [CrossRef]
- Goloskokov, S.V.; Kroll, P. The target asymmetry in hard vector-meson electroproduction and parton angular momenta. Eur. Phys. J. C 2009, 59, 809. [Google Scholar] [CrossRef]
- Goloskokov, S.V.; Kroll, P. An attempt to understand exclusive π+ electroproduction. Eur. Phys. J. C 2010, 65, 137. [Google Scholar] [CrossRef]
- Goloskokov, S.V.; Kroll, P. Transversity in hard exclusive electroproduction of pseudoscalar mesons. Eur. Phys. J. A 2011, 47, 112. [Google Scholar] [CrossRef]
- Accardi, A.; Albacete, J.L.; Anselmino, M.; Armesto, N.; Aschenauer, E.C.; Bacchetta, A.; Boer, D.; Brooks, W.K.; Burton, T.; Chang, N.B.; et al. Electron-Ion Collider: The next QCD frontier: Understanding the glue that binds us all. Eur. Phys. J. A 2016, 52, 268. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C.; et al. Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Ahmed, S.; Albrecht, M.; Alekseev, M.; Amoroso, A.; An, F.F.; An, Q.; Bai, Y.; Bakina, O.; et al. Measurements of the branching fractions of ηc→K+K−π0, K±π∓,2(π+π−π0), and pp. Phys. Rev. D 2019, 100, 012003. [Google Scholar] [CrossRef]
- Accardi, A.; Achenbach, P.; Adhikari, D.; Afanasev, A.; Akondi, C.S.; Akopov, N.; Albaladejo, M.; Albataineh, H.; Albrecht, M.; Almeida-Zamora, B.; et al. Strong Interaction Physics at the Luminosity Frontier with 22 GeV Electrons at Jefferson Lab. Eur. Phys. J. A 2024, 60, 173. [Google Scholar] [CrossRef]

| Production Rates | Counting Rates | ||||
|---|---|---|---|---|---|
| 49 | 127 | 32/month | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddikov, M. Photoproduction of Heavy Meson and Photon Pairs. Particles 2025, 8, 23. https://doi.org/10.3390/particles8010023
Siddikov M. Photoproduction of Heavy Meson and Photon Pairs. Particles. 2025; 8(1):23. https://doi.org/10.3390/particles8010023
Chicago/Turabian StyleSiddikov, Marat. 2025. "Photoproduction of Heavy Meson and Photon Pairs" Particles 8, no. 1: 23. https://doi.org/10.3390/particles8010023
APA StyleSiddikov, M. (2025). Photoproduction of Heavy Meson and Photon Pairs. Particles, 8(1), 23. https://doi.org/10.3390/particles8010023








