Higgs Physics at the Muon Collider †
Abstract
1. Introduction
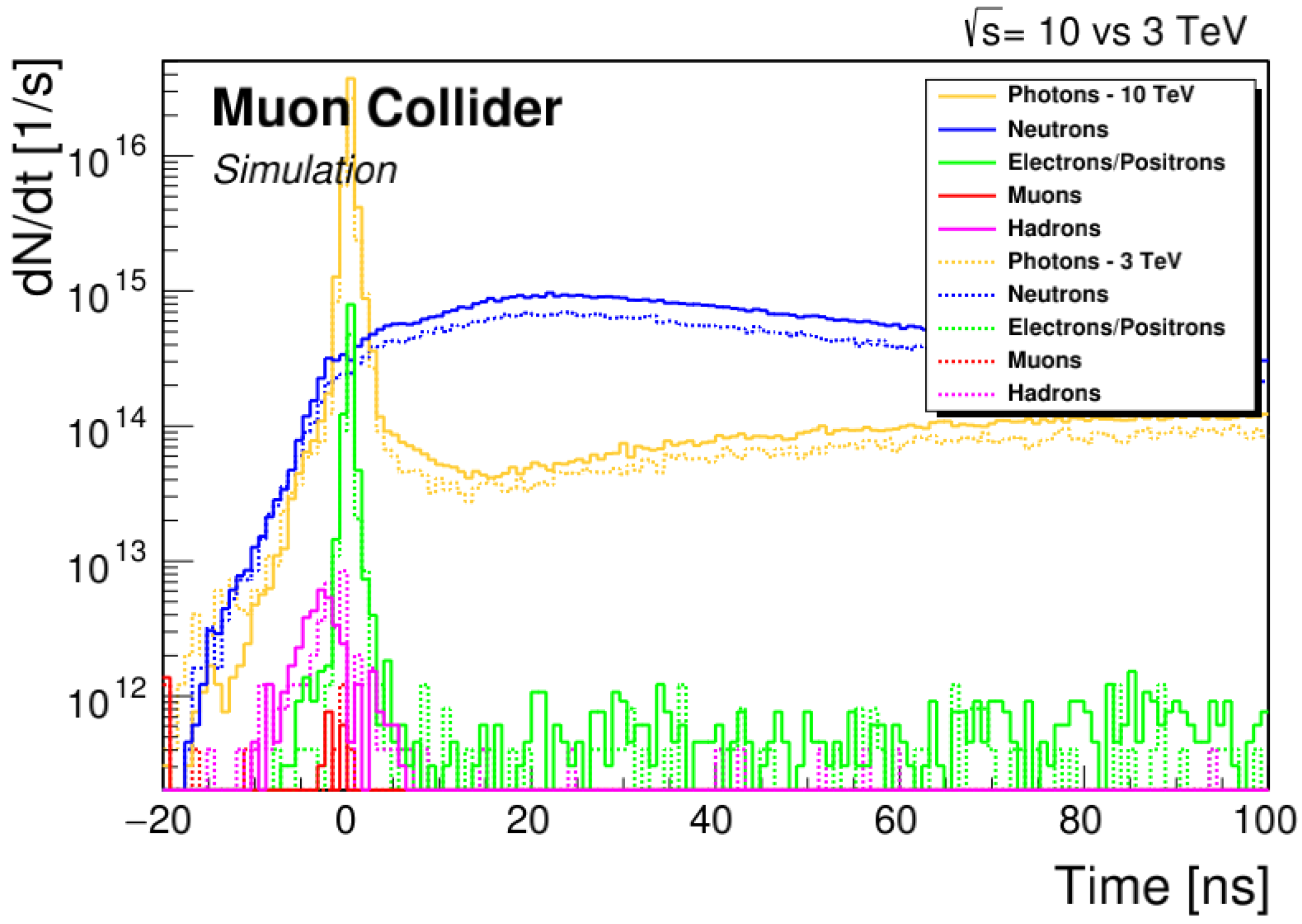
2. Beam-Induced Background (BIB)
3. Higgs Cross-Section
- Monte Carlo Event Generation: The Higgs decay modes considered in this study include the following:
- –
- ;
- –
- ;
- –
- ;
- –
- ;
- –
- .
Signal events were generated in leading order using the Monte Carlo event generators MadGraph5_aMC@NLO [8] (referred to hereafter as MadGraph) and WHIZARD2 [9]. Particle showering and hadronization were handled with PYTHIA version 8.200. The Higgs boson was produced via W boson fusion () and Z boson fusion (). For each decay mode, the corresponding background processes were also simulated. The complete list of generated samples is provided in Appendix A. - Detector Simulation: A detailed detector simulation was carried out using GEANT4 [10]. The detector incorporates advanced silicon-based tracking systems, electromagnetic and hadronic calorimeters, and operates within a 3.57 T magnetic field. Beam-Induced Background (BIB) was overlaid at the hit level, and digitization was applied to simulate sensor responses with realistic timing and spatial resolutions. The detector model is shown in Figure 2.
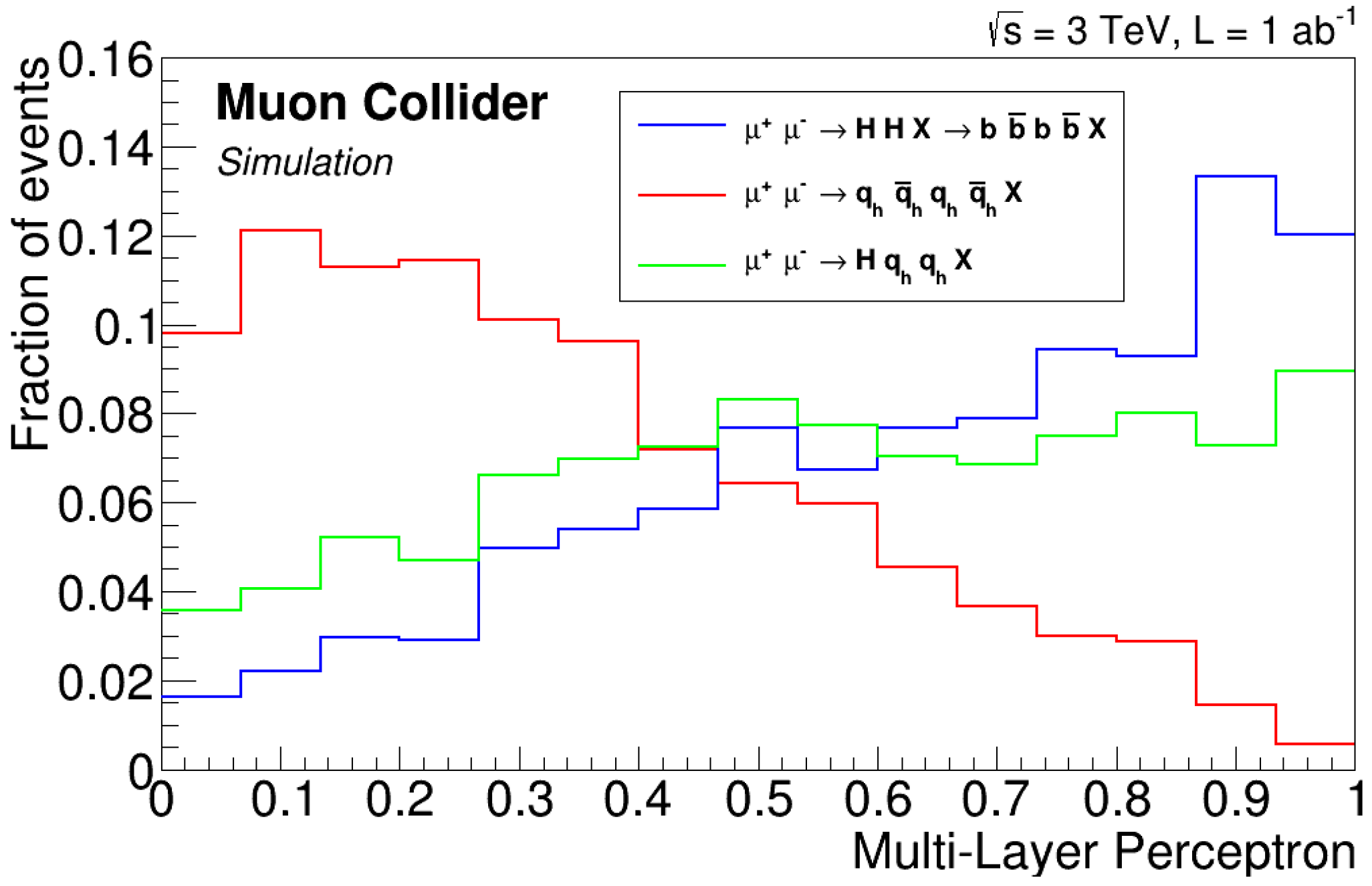
- Determination of the Sensitivity: The sensitivity on the cross-section for each Higgs decay mode was derived from the sensitivity on the number of events using the relation below:where is the luminosity, is the efficiency, and is the cross-section. The sensitivity on was determined by propagating the sensitivity on the number of events, assuming negligible uncertainties on the luminosity and efficiency.For , the cross-section was determined by fitting the di-jet invariant mass distributions of signal and background using double-Gaussian functions to model the signal and background. A detailed description is reported in [13]. A likelihood function was constructed with these models, and an unbinned maximum-likelihood fit was performed on pseudo-data. The signal and background yields were allowed to float to extract the yield and its uncertainty. The uncertainty on the cross-section was estimated by averaging over several pseudo-experiments. The result is shown in Table 2.For the other signals considered in this study, the statistical sensitivity on the cross-section was determined using a counting experiment. Assuming negligible uncertainties on the efficiency and integrated luminosity, the relative error on is given bywhere S and B are the expected numbers of signal and background events, respectively. To maximize the signal-to-background ratio, machine learning algorithms such as Boosted Decision Trees (BDTs) [14] and Multi-Layer Perceptrons (MLPs) [15] were trained on physical observables specific to each signal process and used as discriminators. The results are presented in Table 2. The table also includes results obtained with fast simulation performed with Delphes cards [16] without incorporating BIB [17]. The two estimates are in very good agreement, indicating that BIB effects on physics performance are manageable.
4. Double Higgs Cross-Section
- The invariant masses of the two jet pairs;
- The magnitude of the vector sum of the four jet momenta;
- The total energy of the four jets;
- The angle between the two jet pairs relative to the leading candidate;
- The maximum separation angle between jets in the event;
- The angles between the highest- jet in the pair and the leading and sub-leading candidates with respect to the z-axis;
- The transverse momenta of the four jets.
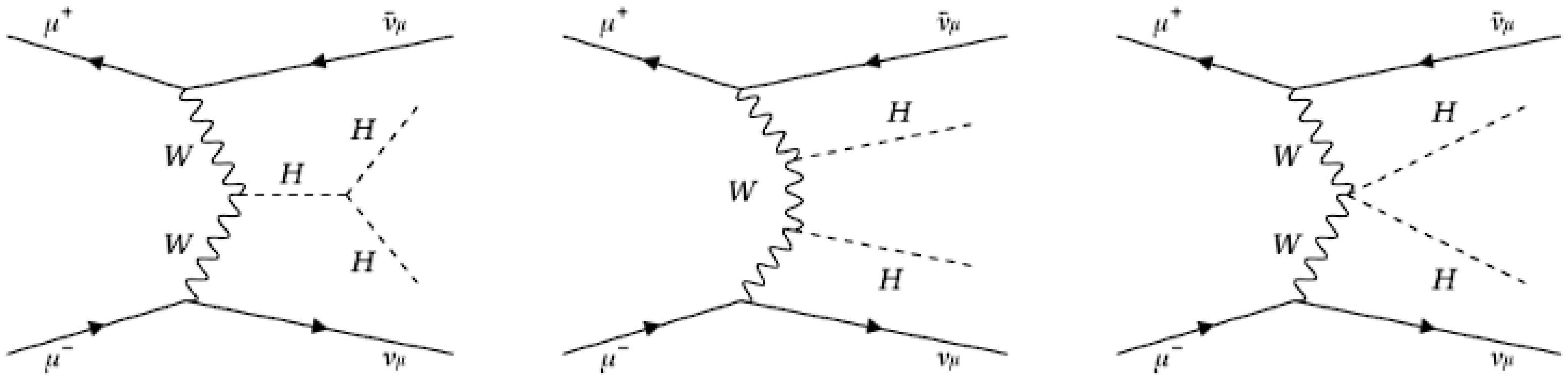
5. Trilinear Higgs Coupling
- A different set of double Higgs events has been generated with WHIZARD, varying from 0.2 to 1.8 with 0.2 steps.
- The same MLP used in Section 4 has been exploited to separate the SM signal, corresponding to , from the physical background.
- A second MLP has been trained to separate the double Higgs processes via from the other two. The observables considered to perform the discrimination were the angle between the two Higgs boson momenta in the laboratory frame, the angle between the highest- jet momenta of each pair with respect to the z-axis, and the helicity angle of the two Higgs boson candidates.
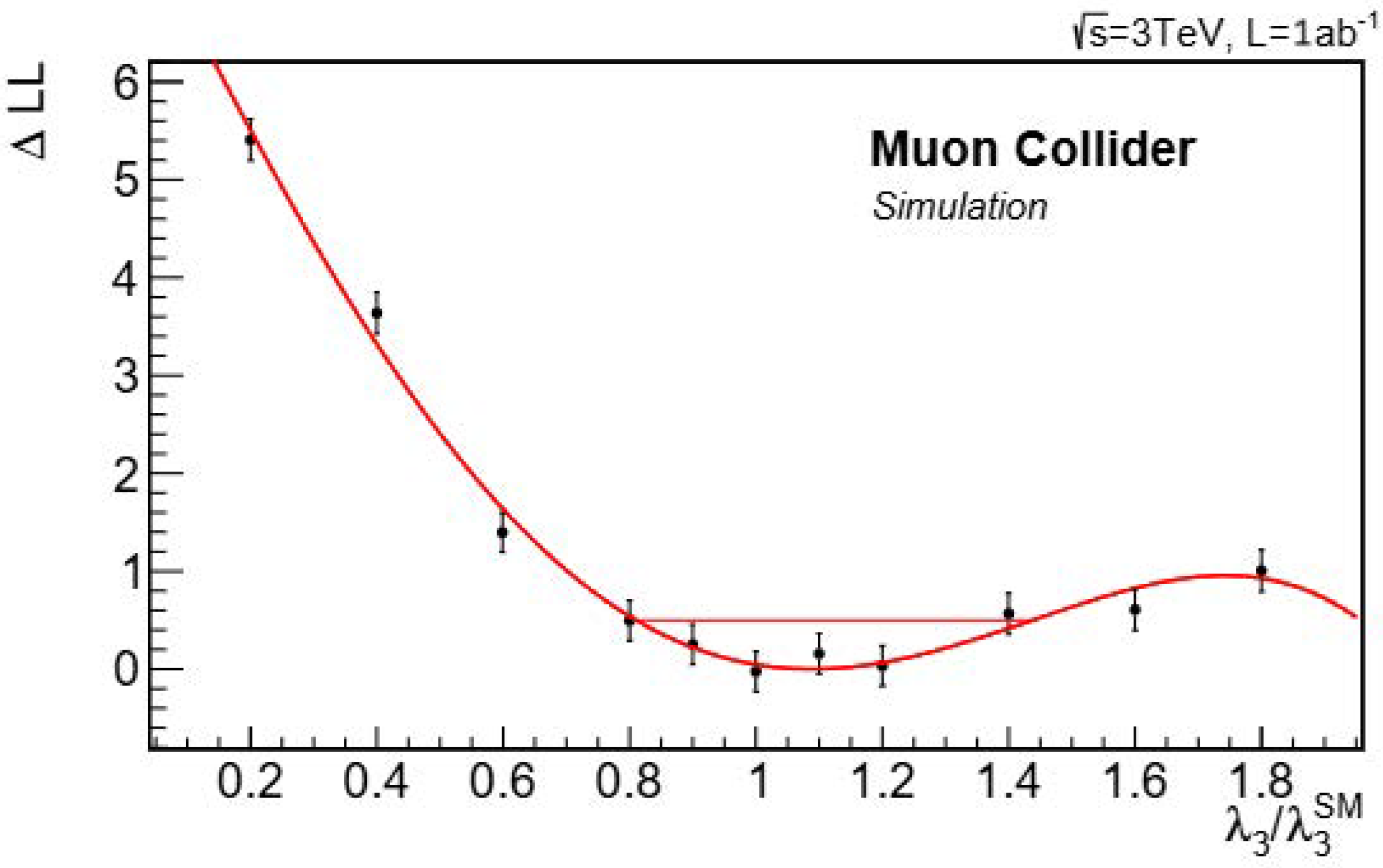
- The scores of the two MLPs for the considered samples have been arranged in 2-dimensional histograms. To obtain the expected data distribution, 2-dimensional templates of the signal and background components are built for each hypothesis.
- Pseudo-datasets are generated with the total 2D template for the hypothesis. For each pseudo-experiment, the likelihood difference is calculated as a function of by comparing the pseudo-data distribution to the templates.
- The log-likelihood profile has been fitted with a polynomial function of fourth degree. The uncertainty on at 68% Confidence Level (C.L.) is estimated as the interval around where the fitted polynomial has a value below 0.5.
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Process | Generator | Kinematical Requirements |
|---|---|---|
| WHIZARD | - | |
| WHIZARD | - | |
| WHIZARD | - | |
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| WHIZARD | - | |
| MadGraph | - | |
| WHIZARD | - | |
| WHIZARD | GeV | |
| MadGraph | GeV | |
| MadGraph | GeV, | |
| MadGraph | > 1 GeV, < 3 | |
| > 5 GeV, < 3 | ||
| > 0.2, | ||
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| MadGraph | > 1 GeV, < 3 | |
| > 5 GeV, < 3 | ||
| > 0.2, | ||
| MadGraph | > 10 GeV | |
| > 5 GeV, < 3 | ||
| > 0.2, | ||
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| WHIZARD | GeV | |
| WHIZARD | 10 GeV < < 150 GeV | |
| < 2.5, < 2.5 | ||
| > 5 GeV, > 5 GeV | ||
| > 0.3 | ||
| MadGraph | GeV, | |
| MadGraph | GeV, | |
| MadGraph | GeV | |
| Madgraph | GeV, | |
| Madgraph | GeV, | |
| Madgraph | GeV, | |
| Madgraph | GeV, |
References
- de Blas, J.; Cepeda, M.; D’Hondt, J.; Ellis, R.; Grojean, C.; Heinemann, B.; Maltoni, F.; Nisati, A.; Petit, E.; Rattazzi, R.; et al. Higgs Boson studies at future particle colliders. J. High Energy Phys. 2020, 2020, 139. [Google Scholar] [CrossRef]
- Dainese, A.; Mangano, M.; Meyer, A.B.; Nisati, A.; Salam, G.; Vesterinen, M.A. Report on the Physics at the HL-LHC and Perspectives for the HE-LHC. arXiv 2019, arXiv:1902.10229. [Google Scholar]
- Chiesa, M.; Maltoni, F.; Mantani, L.; Mele, B.; Piccinini, F.; Zhao, X. Measuring the quartic Higgs self-coupling at a multi-TeV muon collider. J. High Energy Phys. 2020, 2020, 98. [Google Scholar] [CrossRef]
- Lucchesi, D.; Bartosik, N.; Calzolari, D.; Castelli, L.; Lechner, A. Machine-Detector interface for multi-TeV Muon Collider. PoS 2024, EPS-HEP2023, 630. [Google Scholar] [CrossRef]
- Bartosik, N.; Bertolin, A.; Buonincontri, L.; Casarsa, M.; Collamati, F.; Ferrari, A.; Ferrari, A.; Gianelle, A.; Lucchesi, D.; Mokhov, N.; et al. Detector and Physics Performance at a Muon Collider. J. Instrum. 2020, 15, P05001. [Google Scholar] [CrossRef]
- Bartosik, N.; Krizka, K.; Griso, S.P.; Aimè, C.; Apyan, A.; Mahmoud, M.A.; Bertolin, A.; Braghieri, A.; Buonincontri, L.; Calzaferri, S.; et al. Simulated Detector Performance at the Muon Collider. arXiv 2022, arXiv:2203.07964. [Google Scholar]
- Casarsa, M. Detector Performance for Low- and High-Momentum Particles in = 10 TeV Muon Collisions. In Proceedings of the 42nd International Conference on High Energy Physics (ICHEP2024), Prague, Czech Republic, 18–24 July 2024. [Google Scholar]
- Alwall, J.; Frederix, R.; Frixione, S.; Hirschi, V.; Maltoni, F.; Mattelaer, O.; Shao, H.S.; Stelzer, T.; Torrielli, P.; Zaro, M. The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. J. High Energy Phys. 2014, 7, 79. [Google Scholar] [CrossRef]
- Bredt, P.M.; Kilian, W.; Reuter, J.; Stienemeier, P. NLO electroweak corrections to multi-boson processes at a muon collider. J. High Energy Phys. 2022, 12, 138. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.A.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Gaede, F. Marlin and LCCD—Software tools for the ILC. Nucl. Instrum. Methods A 2006, 559, 177–180. [Google Scholar] [CrossRef]
- Thomson, M. Particle flow calorimetry and the PandoraPFA algorithm. Nucl. Instrum. Methods A 2009, 611, 25–40. [Google Scholar] [CrossRef]
- Andreetto, P.; Bartosik, N.; Buonincontri, L.; Calzolari, D.; Candelise, V.; Casarsa, M.; Castelli, L.; Chiesa, M.; Colaleo, A.; Molin, G.D.; et al. Higgs Physics at a TeV Muon Collider with detailed detector simulation. arXiv 2024, arXiv:2405.19314. [Google Scholar]
- Roe, B.P.; Yang, H.J.; Zhu, J.; Liu, Y.; Stancu, I.; McGregor, G. Boosted decision trees as an alternative to artificial neural networks for particle identification. Nucl. Instrum. Methods A 2005, 543, 577–584. [Google Scholar] [CrossRef]
- Hoecker, A.; Speckmayer, P.; Stelzer, J.; Therhaag, J.; von Toerne, E.; Voss, H.; Backes, M.; Carli, T.; Cohen, O.; Christov, A.; et al. TMVA—Toolkit for Multivariate Data Analysis. arXiv 2009, arXiv:physics/0703039. [Google Scholar]
- de Favereau, J.; Delaere, C.; Demin, P.; Giammanco, A.; Lemaitre, V.; Mertens, A.; Selvaggi, M. DELPHES 3: A modular framework for fast simulation of a generic collider experiment. J. High Energy Phys. 2014, 2, 57. [Google Scholar] [CrossRef]
- Forslund, M.; Meade, P. Precision Higgs Width and Couplings with a High Energy Muon Collider. arXiv 2024, arXiv:2308.02633. [Google Scholar] [CrossRef]
- Buonincontri, L. Study of Mitigation Strategies of Beam-Induced Background and Higgs Boson Couplings Measurements at a Muon Collider. Master’s Thesis, University of Padua, Padua, Italy, 2020. [Google Scholar]
- Buonincontri, L. Search for Heavy Flavour Higgs Boson Decays at Hadron and Future Muon Collider. Ph.D. Thesis, University of Padua, Padua, Italy, 2023. [Google Scholar]
- Accettura, C.; Adams, D.; Agarwal, R.; Ahdida, C.; Aimè, C.; Amapane, N.; Amorim, D.; Andreetto, P.; Anulli, F.; Appleby, R.; et al. Towards a Muon Collider. Eur. Phys. J. C 2023, 83, 864. [Google Scholar] [CrossRef]
- Li, P.; Liu, Z.; Lyu, K.F. Higgs Width and Couplings at High Energy Muon Colliders with Forward Muon Detection. arXiv 2024, arXiv:2401.08756. [Google Scholar] [CrossRef]
- Ruhdorfer, M.; Salvioni, E.; Wulzer, A. Invisible Higgs boson decay from forward muons at a muon collider. Phys. Rev. D 2023, 107, 095038. [Google Scholar] [CrossRef]
- Ruhdorfer, M.; Salvioni, E.; Wulzer, A. Why detect forward muons at a muon collider. arXiv 2024, arXiv:2411.00096. [Google Scholar]
- Castelli, L.; Collamati, F.; Calzolari, D.; Lucchesi, D. Status of 3 TeV MDI Studies. Available online: https://agenda.infn.it/event/44387/contributions/250843/attachments/129104/191446/rd_mucoll24.pdf (accessed on 17 January 2025).

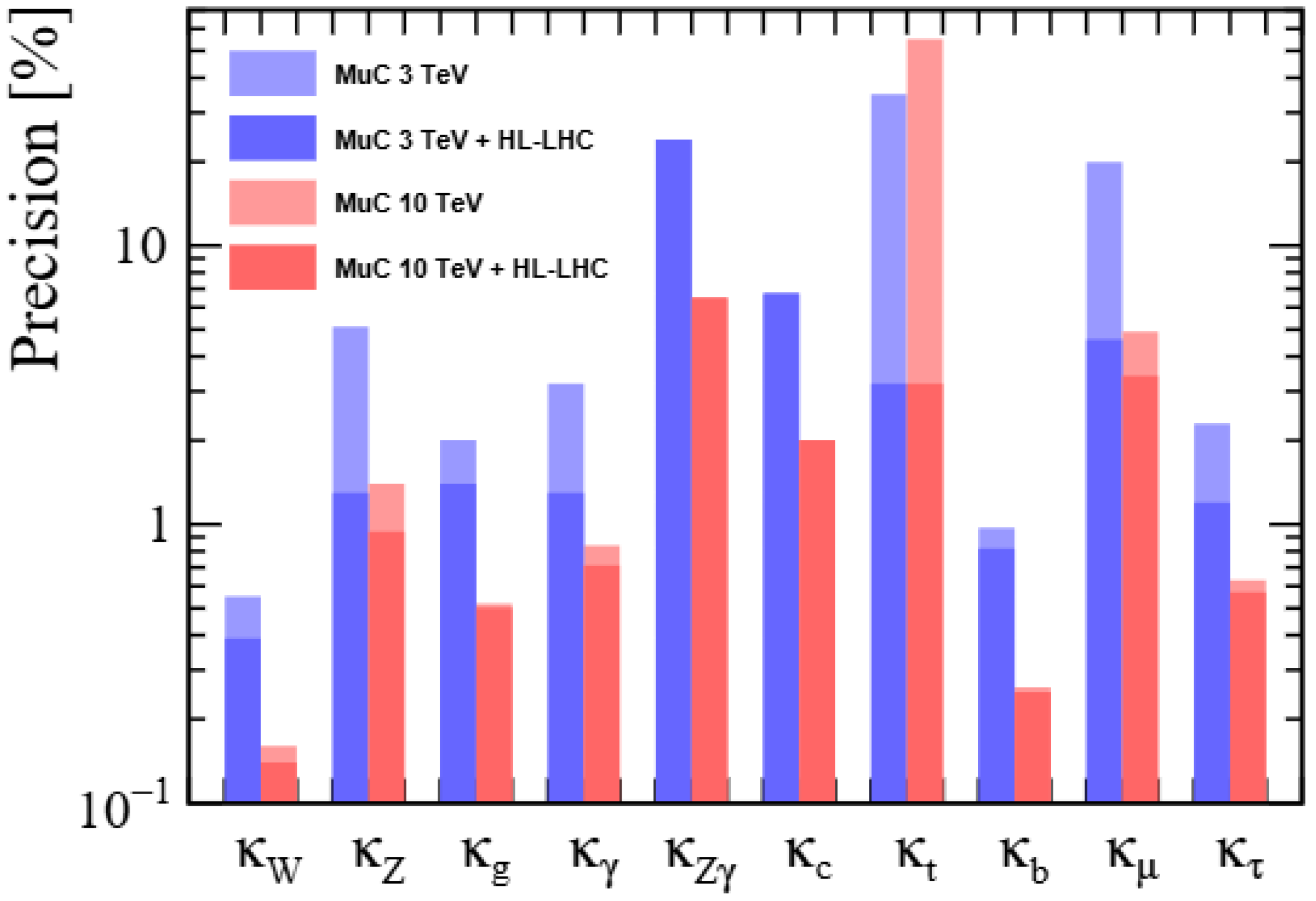
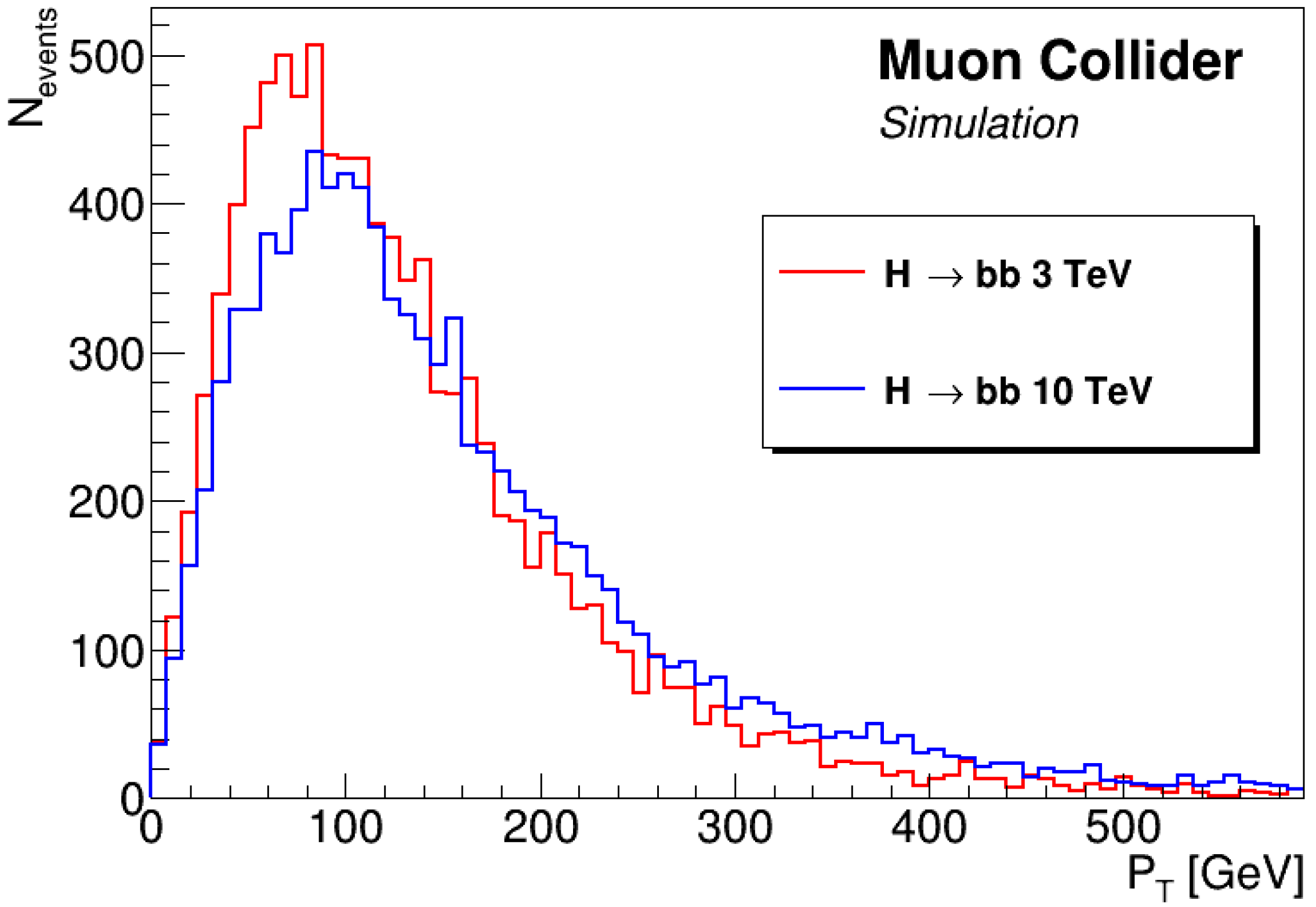
| C.o.M Energy [TeV] | Luminosity [] | Higgs Events |
|---|---|---|
| 3 | 1 | |
| 10 | 10 | |
| 14 | 20 | |
| 30 | 90 |
| Channel | Full Sim. | Fast Sim. |
|---|---|---|
| 17 | 11 | |
| 39 | 40 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castelli, L., on behalf of the International Muon Collider Collaboration. Higgs Physics at the Muon Collider. Particles 2025, 8, 28. https://doi.org/10.3390/particles8010028
Castelli L on behalf of the International Muon Collider Collaboration. Higgs Physics at the Muon Collider. Particles. 2025; 8(1):28. https://doi.org/10.3390/particles8010028
Chicago/Turabian StyleCastelli, Luca on behalf of the International Muon Collider Collaboration. 2025. "Higgs Physics at the Muon Collider" Particles 8, no. 1: 28. https://doi.org/10.3390/particles8010028
APA StyleCastelli, L., on behalf of the International Muon Collider Collaboration. (2025). Higgs Physics at the Muon Collider. Particles, 8(1), 28. https://doi.org/10.3390/particles8010028








