Examining Factors That Affect Movie Gross Using Gaussian Copula Marginal Regression
Abstract
:1. Introduction
2. Data Description
- rating: categorical variable with the levels of G, PG, PG-13, R, NC-17, TV-PG, TV-14, TV-MA, Not Rated, Unrated, X, and Approved
- genre: categorical variable with levels of drama, adventure, action, comedy, horror, biography, crime, fantasy, family, sci-fi, animation, romance, music, western, thriller, history, mystery, sport, and musical
- year: numerical variable with values ranging from 1980 to 2020
- released: character variable formatted as “Month Day, Year”
- budget: numerical variable measured in United States dollar
- gross: numerical variable measured in United States dollar. Additionally, this refers to U.S. gross only
- rating: levels of G, PG, PG-13, R, and Other
- genre: levels of action, adventure, biography, comedy, crime, drama, fantasy, horror, mystery and other
- season: levels of fall, winter, spring, and summer
- adjustedBudget: measured in United States dollars
- adjustedGross: measured in United States dollars
- year: ranges from 1980 to 2020.
3. Statistical Methods
3.1. Multiple Linear Regression
3.2. Gaussian Copula Marginal Regression and Vine Copula
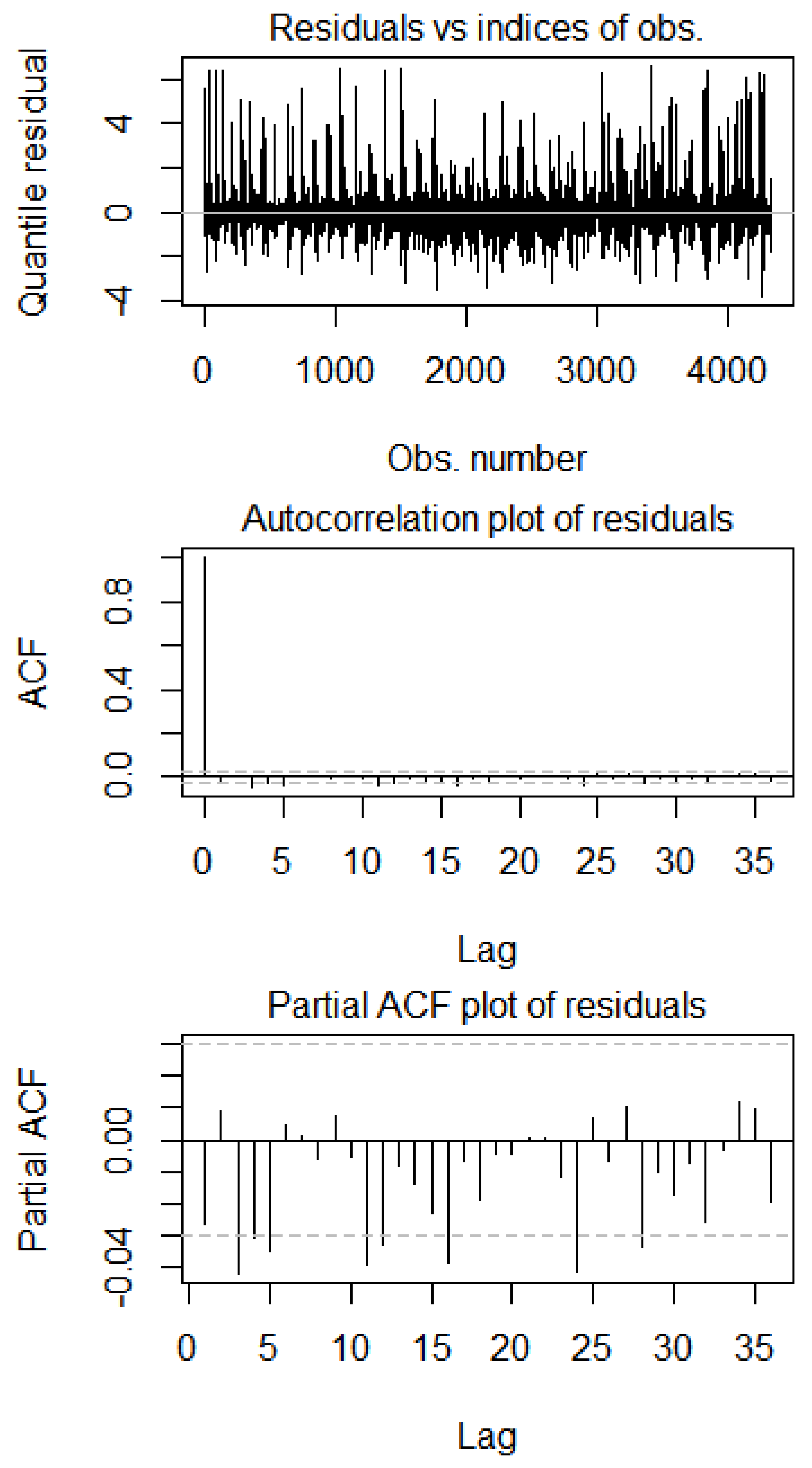
4. Copula Data Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Childress, E.; Staff, R.T. The 50 Highest-Grossing Movies of All Time: Your Top Box Office Earners Ever Worldwide. Rotten Tomatoes. 24 February 2022. Available online: https://editorial.rottentomatoes.com/article/highest-grossing-movies-all-time/ (accessed on 3 March 2022).
- McClintock, P. Global Box Office Revenue Hits Record $41B in 2018, Fueled by Diverse U.S. Audiences. The Hollywood Reporter. 21 March 2019. Available online: https://www.hollywoodreporter.com/news/general-news/global-box-office-revenue-hits-record-41b-2018-fueled-by-diverse-us-audiences-1196010/ (accessed on 3 March 2022).
- Chang, B.-H.; Ki, E.-J. Devising a practical model for predicting theatrical movie success: Focusing on the experience good property. J. Media Econ. 2005, 18, 247–269. [Google Scholar] [CrossRef]
- Lash, M.T.; Zhao, K. Early Predictions of Movie Success: The Who, What, and When of Profitability. J. Manag. Inf. Syst. 2016, 33, 874–903. [Google Scholar] [CrossRef] [Green Version]
- Ho, J.Y.C.; Krider, R.E.; Chang, J. Mere newness: Decline of movie preference over time. Can. J. Adm. Sci. 2017, 34, 33–46. [Google Scholar] [CrossRef]
- Du, J.; Xu, H.; Huang, X. Box office prediction based on microblog. Expert Syst. Appl. 2014, 41, 1680–1689. [Google Scholar] [CrossRef]
- Lee, K.; Park, J.; Kim, I.; Choi, Y. Predicting movie success with machine learning techniques: Ways to improve accuracy. Inf. Syst. Front. 2018, 20, 577–588. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Xie, T. Machine learning versus econometrics: Prediction of box office. Appl. Econ. Lett. 2019, 26, 124–130. [Google Scholar] [CrossRef]
- Xiao, X.; Cheng, Y.; Kim, J.-M. Movie Title Keywords: A Text Mining and Exploratory Factor Analysis of Popular Movies in the United States and China. J. Risk Financ. 2021, 14, 68. [Google Scholar] [CrossRef]
- Kim, J.-M.; Xia, L.; Kim, I.-S.; Lee, S.-J.; Lee, K.-H. Finding Nemo: Predicting Movie Performances by Machine Learning Methods. J. Risk Financ. Manag. 2020, 13, 93. [Google Scholar] [CrossRef]
- Kim, J.-M.; Xiao, X.; Kim, I.-S. Hollywood Movie Analysis by Social Network Analysis and Text Mining. Int. Electron. Commer. Stud. 2020, 11, 75–92. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sklar, A. Fonctions de Repartition á n Dimensions et Leurs Marges; Publications de l’Institut de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Masarotto, G.; Varin, C. Gaussian copula marginal regression. Electron. J. Stat. 2020, 6, 1517–1549. [Google Scholar] [CrossRef]
- Cherubini, U.; Luciano, E.; Vecchiato, W. Copula Methods in Finance; John Wiley: Chichester, UK, 2004. [Google Scholar]
- Kim, J.-M. A Review of Copula Methods for Measuring Uncertainty in Finance and Economics. Quant. Bio-Sci. 2020, 39, 81–90. [Google Scholar]
- Kim, J.M.; Jung, H. Relationship between Oil Price and Exchange Rate by FDA and Copula. Appl. Econ. 2018, 50, 2486–2499. [Google Scholar] [CrossRef]
- Kim, J.-M.; Kim, D.H.; Jung, H. Modeling Non-normal Corporate Bond Yield Spreads by Copula. N. Am. Econ. Financ. 2020, 53, 101210. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models; Chapman and Hall: New York, NY, USA, 1989. [Google Scholar]
- Joe, H. Families of m-variate distributions with given margins and m(m − 1)/2 bivariate dependence parameters. In Distributions with Fixed Marginals and Related Topics; Rüschendorf, L., Schweizer, B., Taylor, M.D., Eds.; Institute of Mathematical Statistics: Washington, DC, USA, 1996; pp. 120–141. [Google Scholar]
- Bedford, T.; Cooke, R.M. Vines—A new graphical model for dependent random variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Aas, K.; Berg, D. Models for construction of multivariate dependence: A comparison study. Eur. Financ. 2009, 15, 639–659. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef] [Green Version]
- Kurowicka, D.; Cooke, R.M. Distribution—Free continuous bayesian belief nets. In Proceedings of the Fourth International Conference on Mathematical Methods in Reliability Methodology and Practice, Santa Fe, NM, USA, 21–25 June 2004. [Google Scholar]
- Bauer, A.; Czado, C.; Klein, T. Pair-copula constructions for non-Gaussian DAG models. Can. J. Stat. 2012, 40, 86–109. [Google Scholar] [CrossRef] [Green Version]
- Brechmann, E.; Czado, C.; Aas, K. Truncated and simplified regular vines in high dimensions with application to financial data. Can. J. Stat. 2012, 40, 68–85. [Google Scholar] [CrossRef]
- Hobæk Haff, I.; Aas, K.; Frigessi, A. On the simplified pair-copula construction—Simply useful or too simplistic? J. Multivar. Anal. 2010, 101, 1296–1310. [Google Scholar] [CrossRef] [Green Version]
- Panagiotelis, A.; Czado, C.; Joe, H. Pair Copula Constructions for Multivariate Discrete Data. J. Am. Stat. Assoc. 2012, 107, 1063–1072. [Google Scholar] [CrossRef]
- Smith, M.; Min, A.; Almeida, C.; Czado, C. Modelling longitudinal data using a pair-copula decomposition of serial dependence. J. Am. Stat. 2010, 105, 1467–1479. [Google Scholar] [CrossRef]
- Kim, D.; Kim, J.-M.; Liao, S.-M.; Jung, Y. Mixture of D-vine Copula Approach for Modeling Dependence. Comput. Data Anal. 2013, 64, 1–19. [Google Scholar] [CrossRef]
- Pourkhanali, A.; Kim, J.-M.; Tafakori, L.; Fard, F.A. Measuring Systemic Risk Using VineCopula. Econ. Model. 2016, 53, 63–74. [Google Scholar] [CrossRef]
- Jang, H.; Kim, J.-M.; Noh, H. Vine Copula Granger Causality in Mean. Econ. Model. 2022, 109, 105798. [Google Scholar] [CrossRef]
- Brechmann, E.C.; Schepsmeier, U. Modeling Dependence with C- and D-Vine Copulas: The R Package CDVine. J. Stat. Softw. 2013, 52, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Kraus, D.; Czado, C. D-vine copula based quantile regression. Comput. Stat. Data Anal. 2017, 110, 1–18. [Google Scholar] [CrossRef] [Green Version]
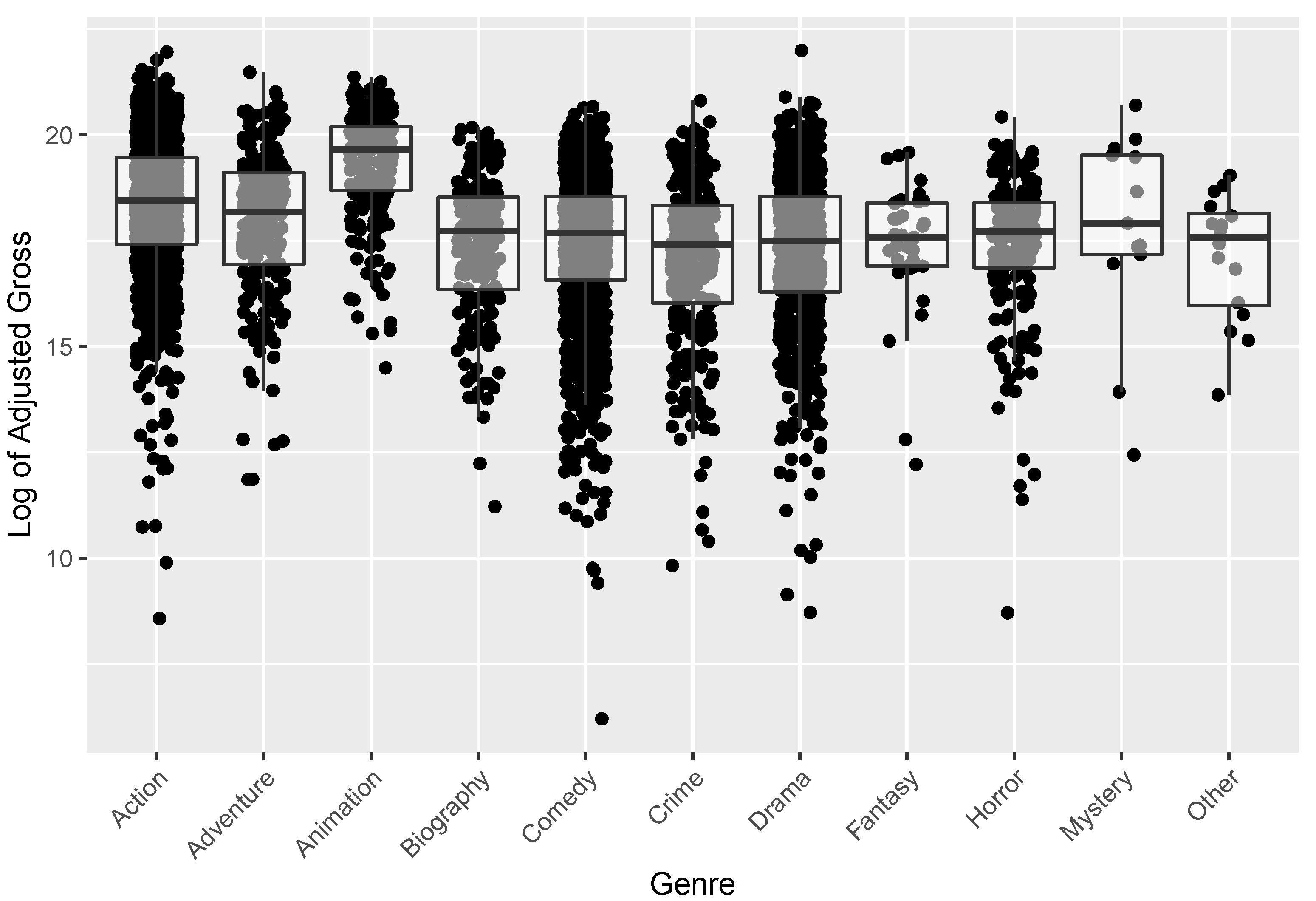


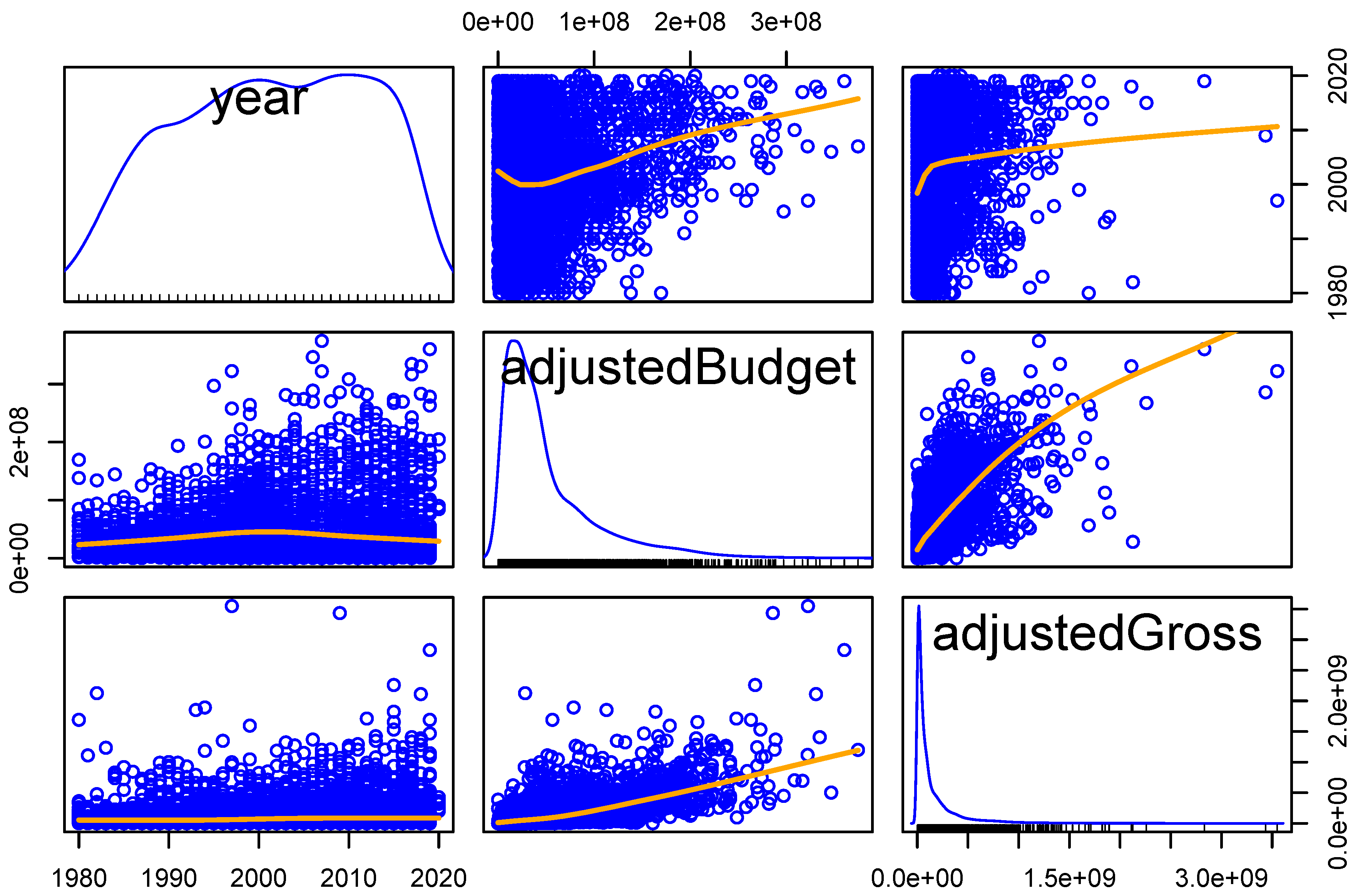

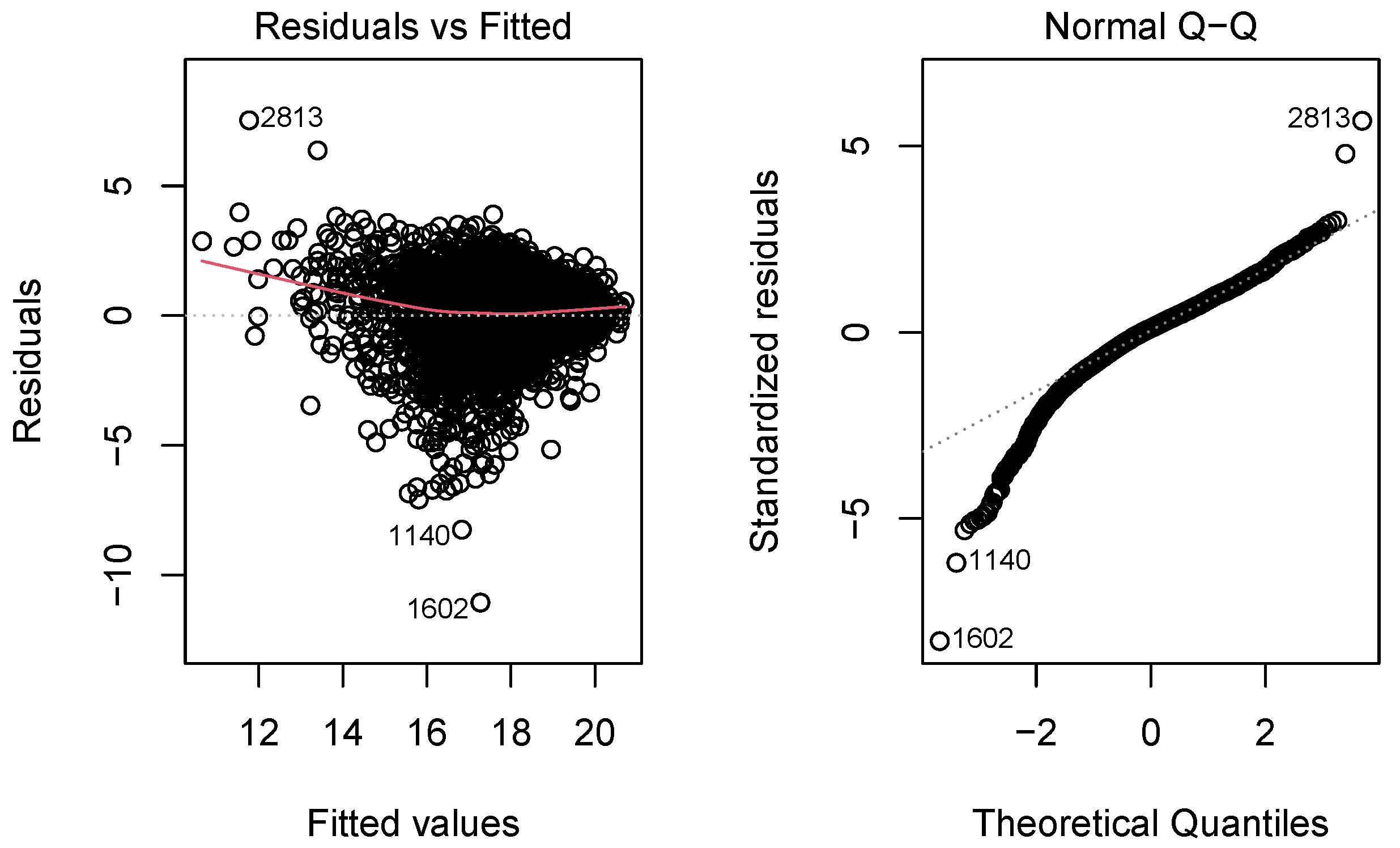

| Variable | Mean Adjusted Gross | Median Adjusted Gross | Count |
|---|---|---|---|
| G | 332,980,911 | 217,551,764 | 80 |
| Rating PG | 201,944,372 | 92,265,952 | 730 |
| Rating PG-13 | 196,379,106 | 90,102,607 | 1448 |
| Rating R | 86,180,464 | 37,829,074 | 2036 |
| Rating Other | 4,734,253 | 1,935,220 | 28 |
| Summer | 183,515,782 | 86,822,241 | 1162 |
| Winter | 136,243,168 | 68,325,093 | 1017 |
| Spring | 154,837,912 | 52,443,968 | 1018 |
| Fall | 110,738,808 | 43,177,273 | 1125 |
| Model | AIC |
|---|---|
| modGCMR | 176,322.1 |
| modGCMR2 | 175,865.9 |
| modGCMR3 | 176,161.2 |
| modGCMR4 | 176,211.5 |
| Estimate | Std. Error | p-Value | |
|---|---|---|---|
| (Intercept) | −1,878,000,000 | 0.00000000005 | 0.000 |
| year | 932,800 | 0.00000010700 | 0.000 |
| ratingOther | −14,460,000 | 0.00000000001 | 0.000 |
| ratingPG | −8,075,000 | 0.00000000007 | 0.000 |
| ratingPG-13 | −16,860,000 | 0.00000000010 | 0.000 |
| ratingR | −27,640,000 | 0.00000000013 | 0.000 |
| genreAdventure | 6,948,000 | 0.00000000001 | 0.000 |
| genreAnimation | 83,410,000 | 0.00000000006 | 0.000 |
| genreBiography | −7,783,000 | 0.00000000001 | 0.000 |
| genreComedy | −63,970 | 0.00000000006 | 0.000 |
| genreCrime | −3,041,000 | 0.00000000002 | 0.000 |
| genreDrama | 10,320,000 | 0.00000000003 | 0.000 |
| genreFantasy | 2,675,000 | 0.00000000000 | 0.000 |
| genreHorror | 42,060,000 | 0.00000000003 | 0.000 |
| genreMystery | 70,180,000 | 0.00000000000 | 0.000 |
| genreOther | −37,120,000 | 0.00000000000 | 0.000 |
| seasonSpring | 21,200,000 | 0.00000000003 | 0.000 |
| seasonSummer | 29,630,000 | 0.00000000004 | 0.000 |
| seasonWinter | 13,280,000 | 0.00000000000 | 0.000 |
| adjustedBudget | 3 | 0.04797000000 | 0.000 |
| sigma | 174,000,000 | 0.00000000025 | 0.000 |
| AR(1) | 0.957043 | 0.007122 | 0.000 |
| MA(1) | −0.79955 | 0.016851 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eklund, J.; Kim, J.-M. Examining Factors That Affect Movie Gross Using Gaussian Copula Marginal Regression. Forecasting 2022, 4, 685-698. https://doi.org/10.3390/forecast4030037
Eklund J, Kim J-M. Examining Factors That Affect Movie Gross Using Gaussian Copula Marginal Regression. Forecasting. 2022; 4(3):685-698. https://doi.org/10.3390/forecast4030037
Chicago/Turabian StyleEklund, Joshua, and Jong-Min Kim. 2022. "Examining Factors That Affect Movie Gross Using Gaussian Copula Marginal Regression" Forecasting 4, no. 3: 685-698. https://doi.org/10.3390/forecast4030037
APA StyleEklund, J., & Kim, J.-M. (2022). Examining Factors That Affect Movie Gross Using Gaussian Copula Marginal Regression. Forecasting, 4(3), 685-698. https://doi.org/10.3390/forecast4030037