Granger Causality-Based Forecasting Model for Rainfall at Ratnapura Area, Sri Lanka: A Deep Learning Approach
Abstract
1. Introduction
Background
2. Materials and Methods
2.1. Data and Data Pre-Processing
2.2. Feature Selection and Model Building
2.2.1. Random Forest Regression
2.2.2. Granger Causality Test
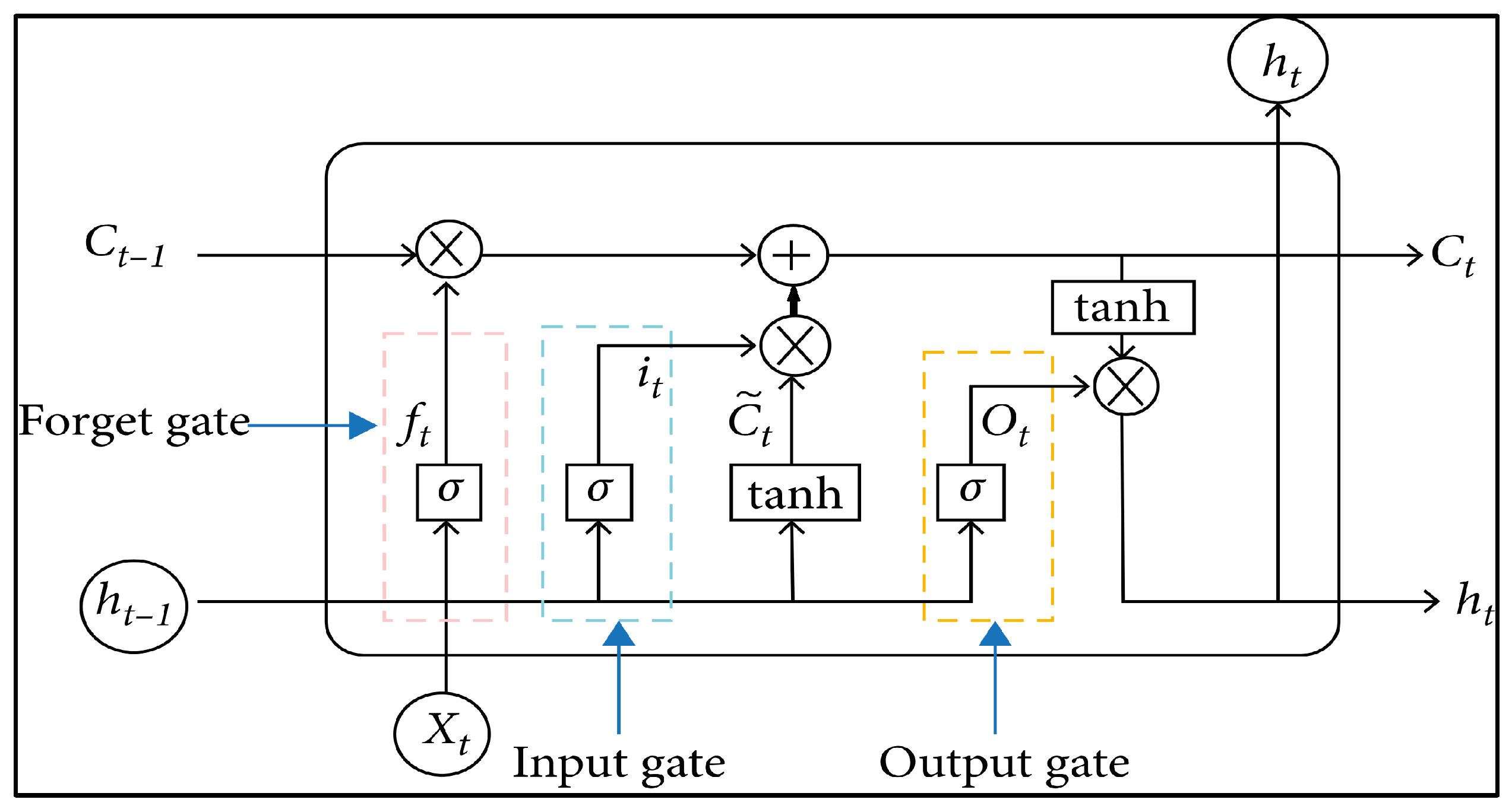
2.2.3. Long Short-Term Memory (LSTM)
2.2.4. Model Evaluation
3. Results and Discussion
3.1. Feature Selection
3.1.1. Modeling with Random Forest Regression
3.1.2. Granger Causality Test Results
3.2. Rainfall Modeling with LSTM Models
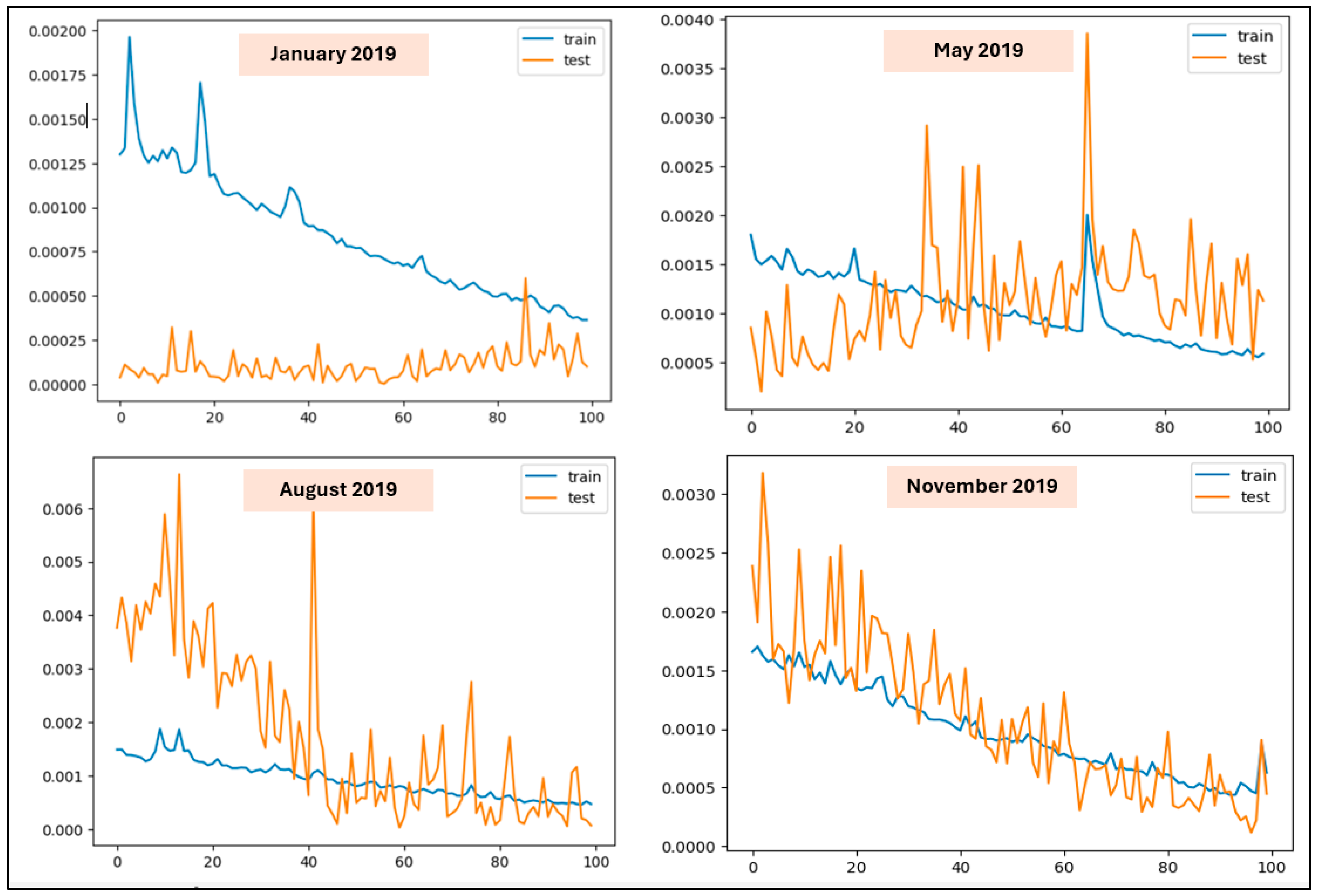
3.3. Residual Analysis
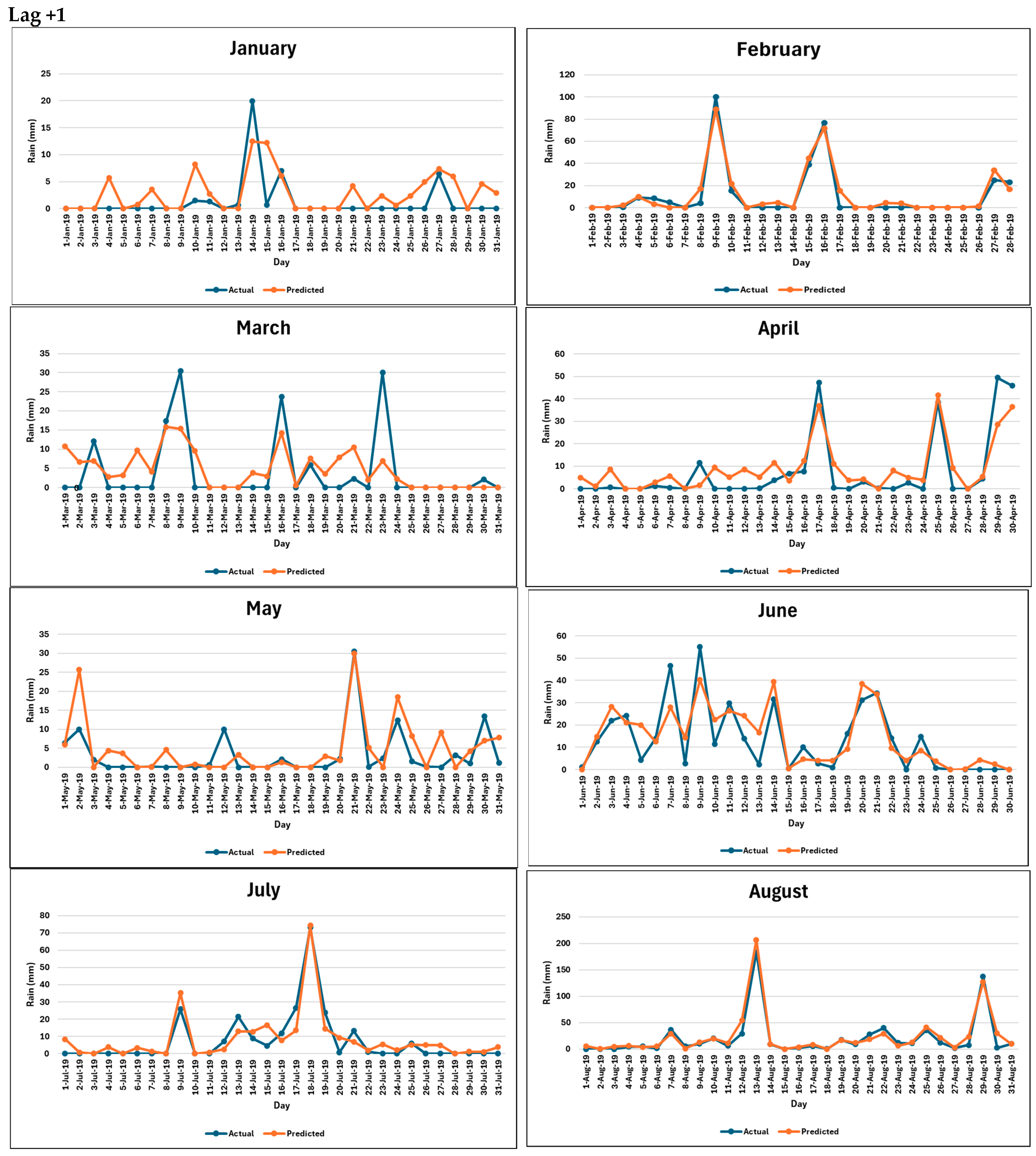
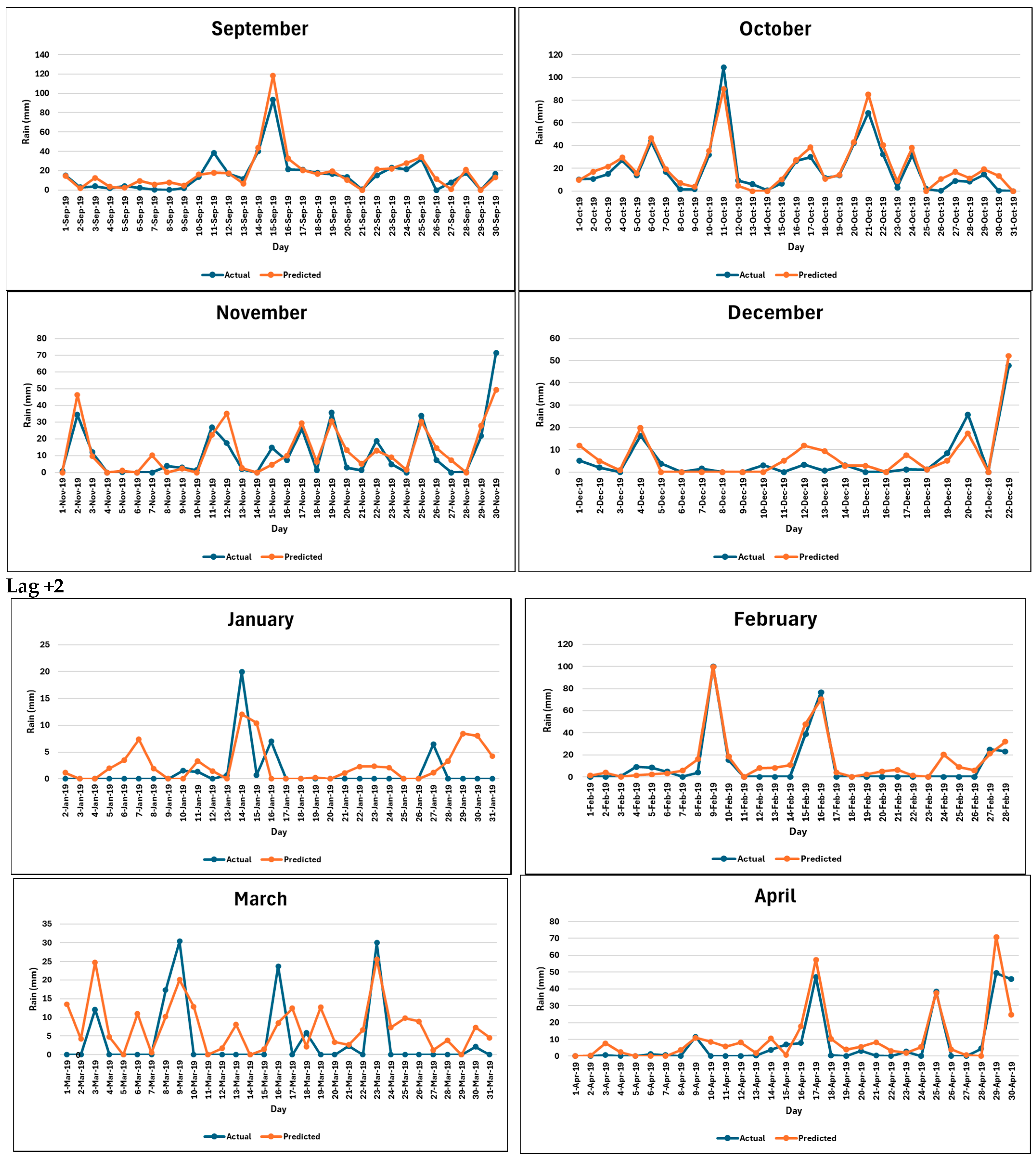
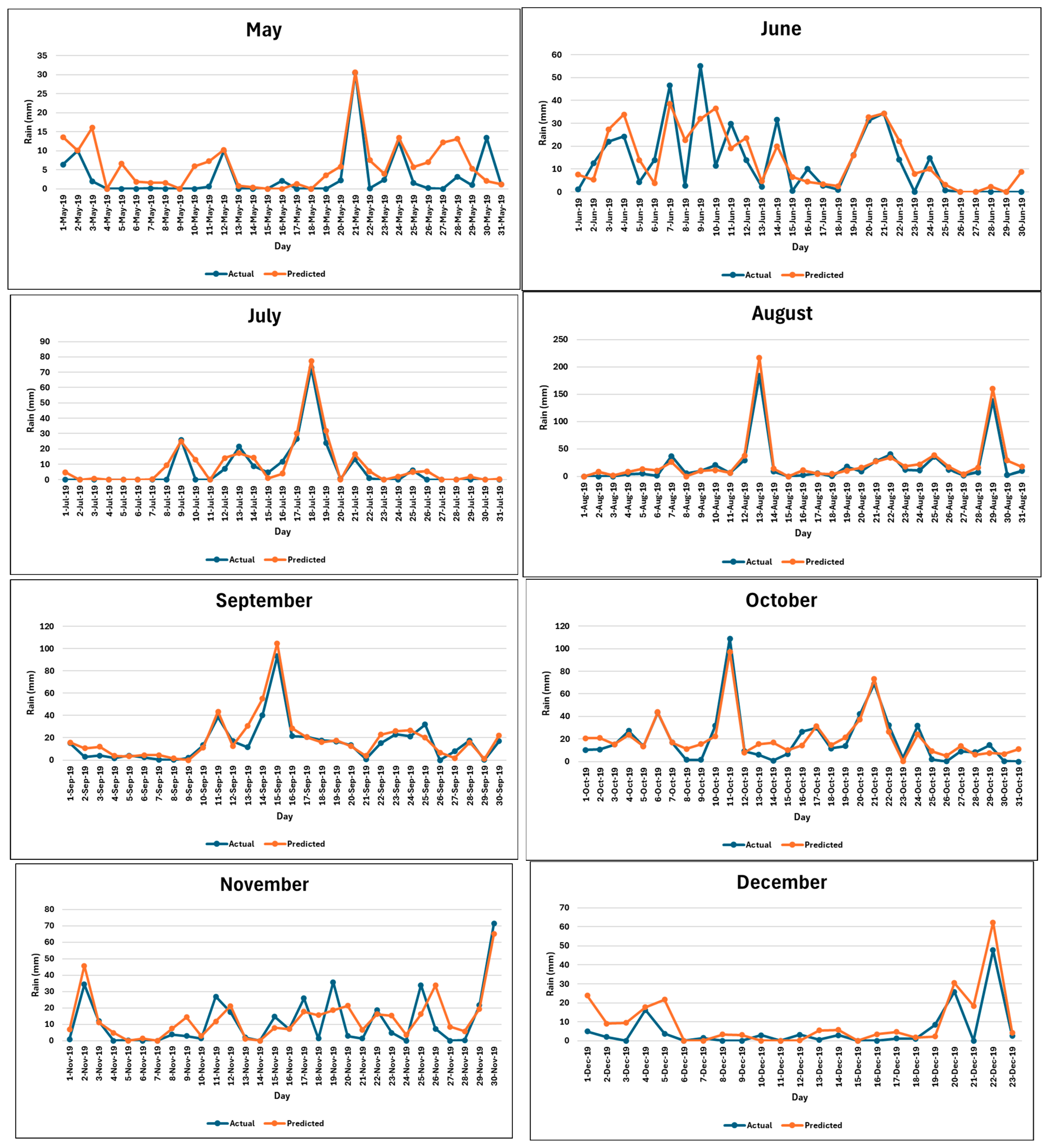
3.4. Verification of Capacity of the Bidirectional LSTM Model in Forecasting Extreme Rainfall Events
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| X | Score | Rank | X | Score | Rank | X | Score | Rank |
|---|---|---|---|---|---|---|---|---|
| arain-1 | 0.064382 | 1 | Tmax-2 | 0.014435 | 25 | WsM-2 | 0.008733 | 49 |
| krig-1 | 0.055808 | 2 | RhN-1 | 0.013962 | 26 | ClM-2 | 0.00819 | 50 |
| MslpM-3 | 0.042258 | 3 | WdM-1 | 0.013813 | 27 | SOI-3 | 0.007514 | 51 |
| DwE-2 | 0.033979 | 4 | DwE-3 | 0.013768 | 28 | SOI-2 | 0.007351 | 52 |
| krig-3 | 0.033791 | 5 | MslpE-2 | 0.013196 | 29 | WdM-2 | 0.007021 | 53 |
| Evp-3 | 0.03149 | 6 | arain-2 | 0.013001 | 30 | ClM-1 | 0.006932 | 54 |
| DwM-1 | 0.030326 | 7 | Evp-2 | 0.012845 | 31 | Con_rainD-1 | 0.006644 | 55 |
| SunS-3 | 0.026023 | 8 | Tmax-1 | 0.012527 | 32 | SOI-1 | 0.006516 | 56 |
| Evp-1 | 0.024442 | 9 | Tmin-1 | 0.012433 | 33 | Con_rainD-3 | 0.0062 | 57 |
| MslpE-1 | 0.023756 | 10 | RhN-2 | 0.012348 | 34 | ClE-2 | 0.005406 | 58 |
| RhD-1 | 0.022631 | 11 | WsE-1 | 0.011952 | 35 | ClE-3 | 0.005384 | 59 |
| Tmin-3 | 0.021286 | 12 | arain-3 | 0.011473 | 36 | Con_rainD-2 | 0.004991 | 60 |
| MslpE-3 | 0.021097 | 13 | RhD-2 | 0.011363 | 37 | ClE-1 | 0.004071 | 61 |
| krig-2 | 0.019664 | 14 | WdE-2 | 0.011105 | 38 | satellite-3 | 0.003898 | 62 |
| SunS-1 | 0.019503 | 15 | DwM-2 | 0.010978 | 39 | Con_dryD-2 | 0.003573 | 63 |
| DwM-3 | 0.018093 | 16 | WsM-1 | 0.01076 | 40 | Con_dryD-3 | 0.00233 | 64 |
| MslpM-1 | 0.017396 | 17 | rain-1 | 0.01069 | 41 | nino-2 | 0.001527 | 65 |
| WsE-2 | 0.016956 | 18 | WsE-3 | 0.010488 | 42 | satellite-1 | 0.001499 | 66 |
| DwE-1 | 0.016285 | 19 | WdE-3 | 0.010026 | 43 | nino-1 | 0.001373 | 67 |
| Tmax-3 | 0.016263 | 20 | RhN-3 | 0.010019 | 44 | nino-3 | 0.001285 | 68 |
| SunS-2 | 0.015948 | 21 | WdE-1 | 0.009944 | 45 | satellite-2 | 0.001259 | 69 |
| RhD-3 | 0.015594 | 22 | WdM-3 | 0.009841 | 46 | Con_dryD-1 | 0.001116 | 70 |
| WsM-3 | 0.014633 | 23 | Tmin-2 | 0.009725 | 47 | rain-3 | 0.000839 | 71 |
| MslpM-2 | 0.014511 | 24 | ClM-3 | 0.008754 | 48 | rain-2 | 0.000787 | 72 |
| Training | Testing | |||||
|---|---|---|---|---|---|---|
| Number of Features | R2 | RMSE | MAE | R2 | RMSE | MAE |
| 1 | −0.1795 | 21.1003 | 11.7105 | −0.1219 | 16.0250 | 10.24466 |
| 2 | −0.03761 | 19.8320 | 11.1934 | −0.07725 | 15.7029 | 10.3040 |
| 3 | 0.021505 | 19.3014 | 11.3090 | −0.02741 | 15.3353 | 10.4247 |
| 4 | 0.005957 | 19.5047 | 11.3620 | 0.032873 | 14.8786 | 10.2054 |
| 5 | −0.00268 | 19.4815 | 11.3543 | 0.080018 | 14.5114 | 10.0594 |
| 6 | 0.013278 | 19.3550 | 11.2862 | 0.042413 | 14.8051 | 10.4354 |
| 7 | 0.009207 | 19.3524 | 11.2642 | 0.02596 | 14.9317 | 10.3643 |
| 8 | 0.001962 | 19.3912 | 11.3569 | 0.051679 | 14.7332 | 10.2129 |
| 9 | −0.0084 | 19.4972 | 11.4726 | 0.0247 | 14.9411 | 10.4089 |
| 10 | −0.0073 | 19.4222 | 11.4170 | 0.0129 | 15.0312 | 10.4358 |
| 11 | 0.0158 | 19.3157 | 11.3796 | 0.0056 | 15.0867 | 10.4711 |
| 12 | 0.0101 | 19.3121 | 11.4324 | −0.0040 | 15.1594 | 10.4680 |
| 13 | 0.0092 | 19.3161 | 11.4465 | −0.0136 | 15.2319 | 10.5142 |
| 14 | 0.0049 | 19.3632 | 11.4963 | −0.0046 | 15.1638 | 10.5279 |
| 15 | 0.0120 | 19.3231 | 11.4601 | −0.0291 | 15.3481 | 10.5831 |
| 16 | −0.0002 | 19.3797 | 11.4916 | −0.0321 | 15.3705 | 10.5693 |
| 17 | −0.0049 | 19.4316 | 11.5121 | −0.0406 | 15.4334 | 10.6077 |
| 18 | −0.0079 | 19.4679 | 11.5468 | −0.0436 | 15.4558 | 10.6201 |
| 19 | −0.0105 | 19.4733 | 11.5540 | −0.0383 | 15.4161 | 10.6424 |
| 20 | −0.0123 | 19.5170 | 11.6042 | −0.0317 | 15.3672 | 10.6127 |
| 21 | −0.0084 | 19.5156 | 11.5922 | −0.0280 | 15.3400 | 10.6164 |
| 22 | −0.0056 | 19.4805 | 11.5965 | −0.0335 | 15.3809 | 10.6181 |
| 23 | 0.0001 | 19.4661 | 11.5491 | −0.0298 | 15.3535 | 10.5880 |
| 24 | −0.0105 | 19.4853 | 11.5909 | −0.0263 | 15.3267 | 10.5838 |
| 25 | −0.0126 | 19.4970 | 11.5897 | −0.0176 | 15.2617 | 10.5336 |
| 26 | −0.0102 | 19.4973 | 11.5775 | −0.0156 | 15.2472 | 10.5101 |
| 27 | −0.0049 | 19.4477 | 11.5785 | −0.0229 | 15.3015 | 10.5633 |
| 28 | −0.0069 | 19.4922 | 11.5962 | −0.0200 | 15.2802 | 10.5384 |
| 29 | −0.0087 | 19.4707 | 11.6265 | −0.0268 | 15.3308 | 10.5958 |
| 30 | −0.0055 | 19.4675 | 11.6042 | −0.0089 | 15.1965 | 10.5306 |
| 31 | −0.0079 | 19.4874 | 11.6298 | −0.0223 | 15.2970 | 10.5888 |
| 32 | −0.0094 | 19.4916 | 11.6369 | −0.0247 | 15.3153 | 10.5707 |
| 33 | −0.0115 | 19.5196 | 11.6441 | −0.0358 | 15.3975 | 10.6290 |
| 34 | −0.0125 | 19.5078 | 11.6534 | −0.0306 | 15.3589 | 10.6261 |
| 35 | −0.0123 | 19.5417 | 11.6789 | −0.0375 | 15.4106 | 10.67682 |
| 36 | −0.0163 | 19.5666 | 11.6731 | −0.0350 | 15.3919 | 10.6520 |
| 37 | −0.0150 | 19.5494 | 11.6880 | −0.0348 | 15.3907 | 10.6676 |
| 38 | −0.0165 | 19.5748 | 11.7174 | −0.0394 | 15.4244 | 10.7113 |
| 39 | −0.0165 | 19.5883 | 11.7245 | −0.0358 | 15.3976 | 10.7152 |
| 40 | −0.0227 | 19.5843 | 11.7440 | −0.0275 | 15.3356 | 10.6883 |
| 41 | −0.0201 | 19.6020 | 11.7252 | −0.0336 | 15.3814 | 10.6883 |
| 42 | −0.0241 | 19.6019 | 11.7253 | −0.0329 | 15.3761 | 10.6903 |
| 43 | −0.0187 | 19.6067 | 11.7185 | −0.0333 | 15.3794 | 10.7274 |
| 44 | −0.0175 | 19.5922 | 11.7277 | −0.0361 | 15.3998 | 10.7273 |
| 45 | −0.0205 | 19.5951 | 11.7326 | −0.0356 | 15.3967 | 10.7319 |
| 46 | −0.0210 | 19.6070 | 11.7214 | −0.0316 | 15.3668 | 10.7050 |
| 47 | −0.0209 | 19.5930 | 11.7347 | −0.0356 | 15.3964 | 10.7023 |
| 48 | 0.0187 | 19.5874 | 11.7058 | −0.0304 | 15.3580 | 10.6828 |
| 49 | −0.0195 | 19.5836 | 11.7230 | −0.0282 | 15.3411 | 10.6673 |
| 50 | −0.0206 | 19.5985 | 11.7161 | −0.0266 | 15.3294 | 10.6545 |
| 51 | −0.0238 | 19.5840 | 11.7407 | −0.0400 | 15.4293 | 10.7135 |
| 52 | −0.0237 | 19.6094 | 11.7457 | −0.0375 | 15.4107 | 10.7151 |
| 53 | −0.0213 | 19.6192 | 11.7448 | −0.0214 | 15.2903 | 10.6330 |
| 54 | −0.0231 | 19.6211 | 11.7492 | −0.0286 | 15.3443 | 10.6539 |
| 55 | −0.0190 | 19.6044 | 11.7468 | −0.0284 | 15.3427 | 10.6515 |
| 56 | −0.0169 | 19.6136 | 11.7476 | −0.0270 | 15.3326 | 10.6323 |
| 57 | −0.0235 | 19.6045 | 11.7517 | −0.0323 | 15.3715 | 10.6643 |
| 58 | −0.0236 | 19.6022 | 11.7543 | −0.0271 | 15.3329 | 10.6479 |
| 59 | −0.0228 | 19.6005 | 11.7327 | −0.0306 | 15.3595 | 10.6586 |
| 60 | −0.0226 | 19.5983 | 11.7545 | −0.0301 | 15.3557 | 10.6597 |
| 61 | −0.0219 | 19.5983 | 11.7519 | −0.0230 | 15.3022 | 10.6315 |
| 62 | −0.0218 | 19.6041 | 11.7305 | −0.0298 | 15.3530 | 10.6674 |
| 63 | −0.0189 | 19.5895 | 11.7310 | −0.0281 | 15.3408 | 10.6527 |
| 64 | −0.0243 | 19.6274 | 11.7374 | −0.0239 | 15.3089 | 10.6453 |
| 65 | −0.0218 | 19.6204 | 11.7403 | −0.0258 | 15.3234 | 10.6613 |
| 66 | −0.0220 | 19.6035 | 11.7437 | −0.0285 | 15.3431 | 10.6806 |
| 67 | −0.0204 | 19.5975 | 11.7346 | −0.0262 | 15.3261 | 10.6556 |
| 68 | −0.0234 | 19.6060 | 11.7363 | −0.0260 | 15.3246 | 10.6438 |
| 69 | −0.0233 | 19.6104 | 11.7214 | −0.0263 | 15.3274 | 10.6439 |
| 70 | −0.0206 | 19.6176 | 11.7527 | −0.0273 | 15.3342 | 10.6593 |
| 71 | −0.0227 | 19.6305 | 11.7416 | −0.0275 | 15.3362 | 10.6570 |
| 72 | −0.0219 | 19.6040 | 11.7263 | −0.0290 | 15.3474 | 10.6818 |
Appendix B
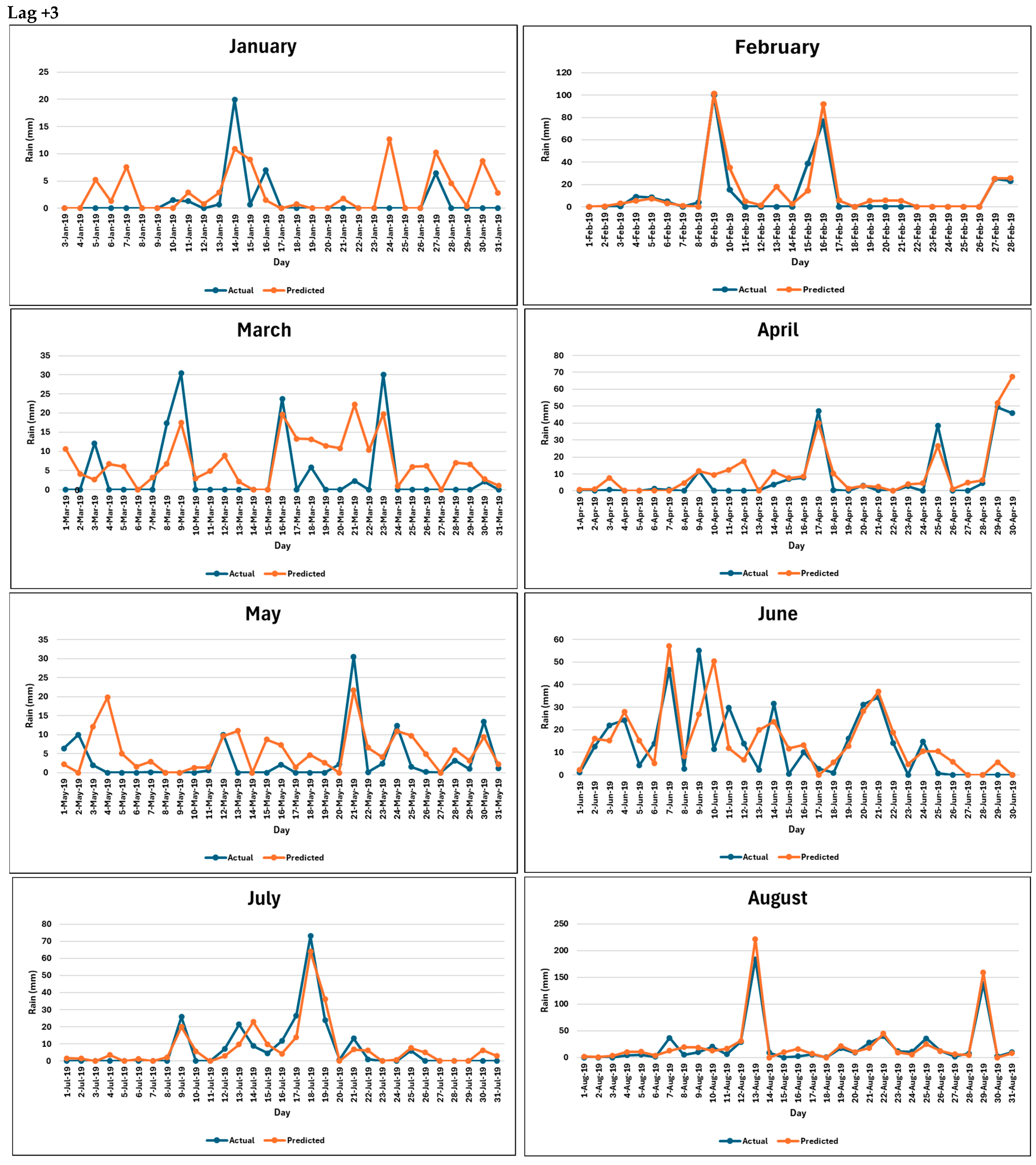
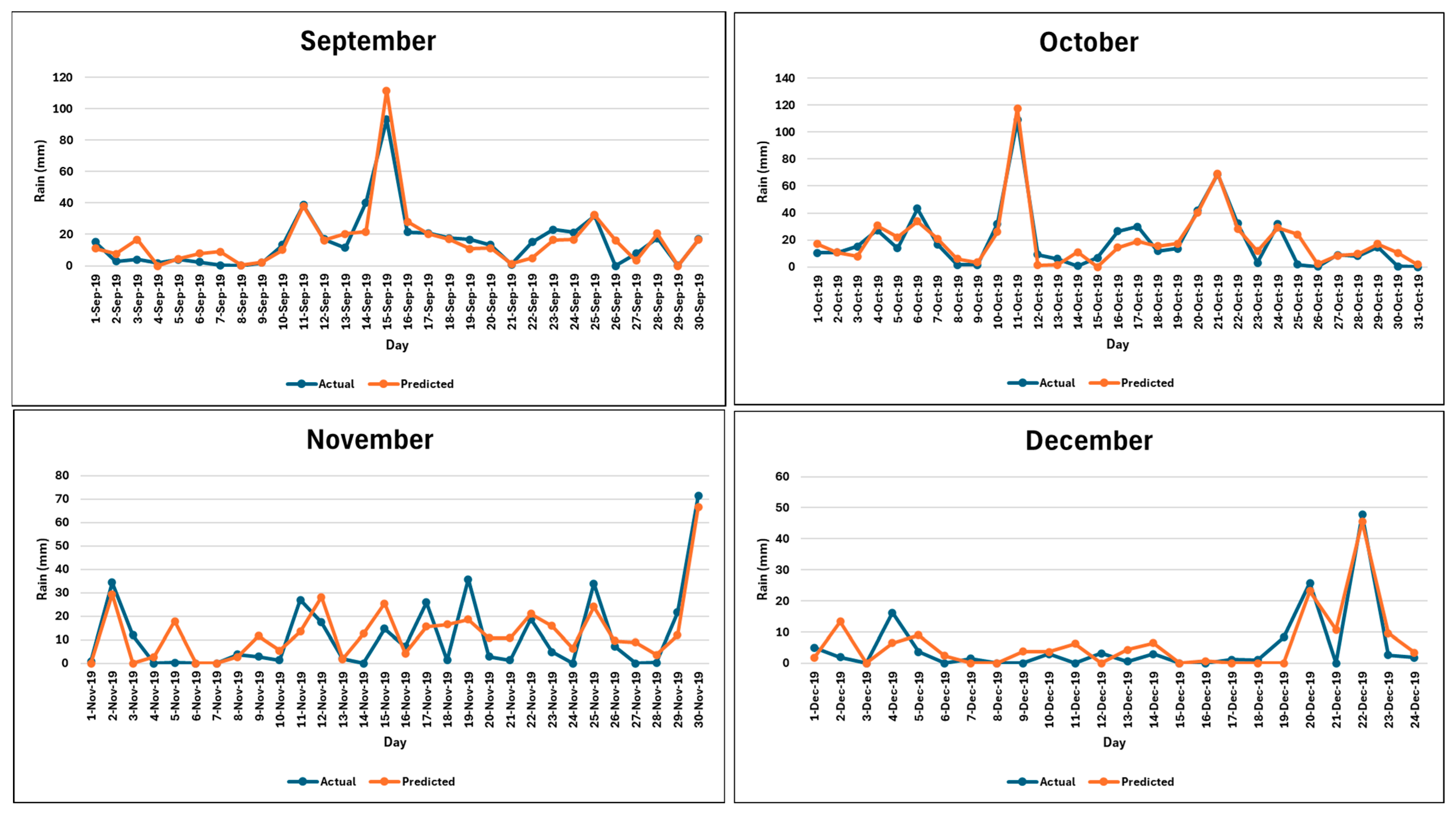
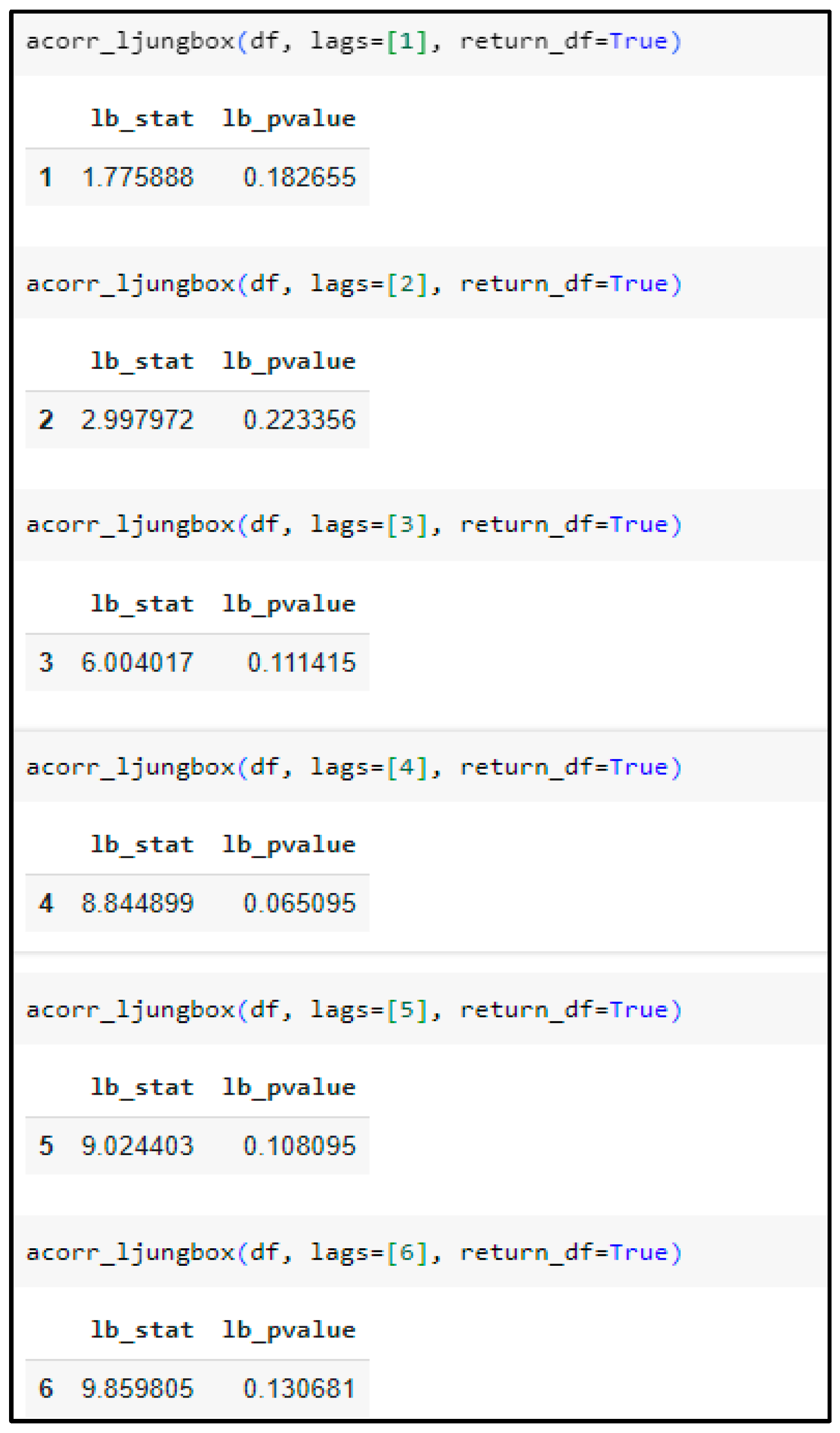
References
- Nagahamulla, H.R.K.; Ratnayake, U.R.; Ratnaweera, A. Monsoon rainfall forecasting in Sri Lanka using artificial neural networks. In Proceedings of the 2011 6th International Conference on Industrial and Information Systems, Kandy, Sri Lanka, 16–19 August 2011; pp. 305–309. [Google Scholar] [CrossRef]
- Perera, H.; Sonnadara, D.; Jayewardene, D. Forecasting the Occurrence of Rainfall in Selected Weather Stations in the Wet and Dry Zones of Sri Lanka. Sri Lankan J. Phys. 2002, 3, 39–52. [Google Scholar] [CrossRef]
- Haq, D.Z.; Novitasari, D.C.R.; Hamid, A.; Ulinnuha, N.; Arnita; Farida, Y.; Nugraheni, R.D.; Nariswari, R.; Ilham; Rohayani, H.; et al. Long Short-Term Memory Algorithm for Rainfall Prediction Based on El-Nino and IOD Data. Procedia Comput. Sci. 2021, 179, 829–837. [Google Scholar] [CrossRef]
- Kundu, S.; Biswas, S.K.; Tripathi, D.; Karmakar, R.; Majumdar, S.; Mandal, S. A Review on Rainfall Forecasting using Ensemble Learning Techniques. e-Prim. Adv. Electr. Eng. Electron. Energy 2023, 6, 100296. [Google Scholar] [CrossRef]
- Chang, C.B. A case study of excessive rainfall forecasting. Meteorol. Atmos. Phys. 1998, 66, 215–227. [Google Scholar] [CrossRef]
- Ridwan, W.M.; Sapitang, M.; Aziz, A.; Kushiar, K.F.; Ahmed, A.N.; El-Shafie, A. Rainfall forecasting model using machine learning methods: Case study Terengganu, Malaysia. Ain Shams Eng. J. 2020, 12, 1651–1663. [Google Scholar] [CrossRef]
- Yang, B.; Chen, L.; Singh, V.P.; Yi, B.; Leng, Z.; Zheng, J.; Song, Q. A Method for Monthly Extreme Precipitation Forecasting with Physical Explanations. Water 2023, 15, 1545. [Google Scholar] [CrossRef]
- Singhal, A.; Raman, A.; Jha, S.K. Potential Use of Extreme Rainfall Forecast and Socio-Economic Data for Impact-Based Forecasting at the District Level in Northern India. Front. Earth Sci. 2022, 10, 846113. [Google Scholar] [CrossRef]
- Saubhagya, S.; Tilakaratne, C.; Mammadov, M.; Lakraj, P. An Application of Ensemble Spatiotemporal Data Mining Techniques for Rainfall Forecasting. Eng. Proc. 2023, 39, 6. [Google Scholar] [CrossRef]
- Hong, W.C. Rainfall forecasting by technological machine learning models. Appl. Math. Comput. 2008, 200, 41–57. [Google Scholar] [CrossRef]
- Hand, W.H.; Fox, N.I.; Collier, C.G. A study of twentieth—Century extreme rainfall events in the United Kingdom with implications for forecasting. Meteorol. Appl. 2004, 11, 15–31. [Google Scholar] [CrossRef]
- Sangiorgio, M.; Barindelli, S.; Biondi, R.; Solazzo, E.; Realini, E.; Venuti, G.; Guariso, G. Improved Extreme Rainfall Events Forecasting Using Neural Networks and Water Vapor Measures. In Proceedings of the ITISE 2019 (6th International Conference on Time Series and Forecasting), Granada, Spain, 25–27 September 2019. [Google Scholar]
- Araújo, A.d.S.; Silva, A.R.; Zárate, L.E. Extreme Precipitation Prediction Based on Neural Network Model—A Case Study for Southeastern Brazil. J. Hydrol. 2022, 606, 127454. [Google Scholar] [CrossRef]
- Gouda, K.; Nahak, S.; Goswami, P. Evaluation of a GCM in seasonal forecasting of extreme rainfall events over continental India. Weather Clim. Extrem. 2018, 21, 10–16. [Google Scholar] [CrossRef]
- Samantray, P.; Gouda, K.C. A review on the extreme rainfall studies in India. Nat. Hazards Res. 2023, 4, 347–356. [Google Scholar] [CrossRef]
- Luk, K.C.; Ball, J.E.; Sharma, A. An application of artificial neural networks for rainfall forecasting. Math. Comput. Model. 2001, 33, 683–693. [Google Scholar] [CrossRef]
- Rathnayake, V.; Premaratne, H.; Sonnadara, D. Performance of neural networks in forecasting short range occurrence of rainfall. J. Natl. Sci. Found. Sri Lanka 2011, 39, 251–260. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Nagahamulla, H.R.K.; Ratnayake, U.R.; Ratnaweera, A. Artificial neural network ensembles in time series forecasting: An application of rainfall forecasting in Sri Lanka. Int. J. Adv. ICT Emerg. Reg. (ICTer) 2014, 6, 1–11. [Google Scholar] [CrossRef]
- Bushara, N.; Abraham, A. Novel ensemble method for long term rainfall prediction. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2015, 7, 116–130. [Google Scholar]
- Mohd, R.; Butt, M.A.; Baba, M.Z. Comparative study of rainfall prediction modeling techniques (A case study on Srinagar, J&K, India). Asian J. Comput. Sci. Technol. 2018, 7, 13–19. [Google Scholar]
- Anwar, M.T.; Winarno, E.; Hadikurniawati, W.; Novita, M. Rainfall prediction using extreme gradient boosting. J. Phys. Conf. Ser. 2021, 1869, 012078. [Google Scholar] [CrossRef]
- Liyew, C.M.; Melese, H.A. Machine learning techniques to predict daily rainfall amount. J. Big Data 2021, 8, 1–11. [Google Scholar] [CrossRef]
- Chowdhary, M.; Anabarasi, M. Enhanced rainfall predictions using stacking technique. Int. J. Emerg. Technol. Innov. Res. 2020, 7, 750–755. [Google Scholar]
- Singh, G.; Kumar, D. Hybrid prediction models for rainfall forecasting. In Proceedings of the 9th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 10–11 January 2019; IEEE: New York, NY, USA, 2019; pp. 392–396. [Google Scholar]
- Osman, A.I.A.; Ahmed, A.N.; Chow, M.F.; Huang, Y.F.; El-Shafie, A. Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Wanless, A.C.; Riley, R.E. Examining Extreme Rainfall Forecast and Communication Processes in the South-Central United States. Weather Clim. Soc. 2023, 15, 787–800. [Google Scholar] [CrossRef]
- Gope, S.; Sarkar, S.; Mitra, P.; Ghosh, S. Early Prediction of Extreme Rainfall Events: A Deep Learning Approach. In Advances in Data Mining. Applications and Theoretical Aspects; Springer: Cham, Switzerland, 2016; Volume 9728, pp. 154–167. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. The All Relevant Feature Selection using Random Forest. arXiv 2011, arXiv:1106.5112. [Google Scholar]
- Pudjihartono, N.; Fadason, T.; Kempa-Liehr, A.W.; O’Sullivan, J.M. A Review of Feature Selection Methods for Machine Learning-Based Disease Risk Prediction. Front. Bioinform. 2022, 2, 927312. [Google Scholar] [CrossRef]
- Brownlee, J. How to Choose a Feature Selection Method For Machine Learning. 2020. Available online: https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/ (accessed on 1 June 2024).
- Nguyen, C.; Wang, Y.; Nguyen, H.N. Random forest classifier combined with feature selection for breast cancer diagnosis and prognostic. J. Biomed. Sci. Eng. 2013, 6, 551–560. [Google Scholar] [CrossRef]
- Niu, D.; Wang, K.; Sun, L.; Wu, J.; Xu, X. Short-term photovoltaic power generation forecasting based on random forest feature selection and CEEMD: A case study. Appl. Soft Comput. 2020, 93, 106389. [Google Scholar] [CrossRef]
- Niu, D.; Wang, K.; Sun, L.; Wu, J.; Xu, X. LSTM integrated with Boruta-random forest optimiser for soil moisture estimation under RCP4.5 and RCP8.5 global warming scenarios. Stoch. Environ. Res. Risk Assess. 2021, 35, 1851–1881. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Zhang, Q.; Wu, L. Building Auto-Encoder Intrusion Detection System Based on Random Forest Feature Selection. Comput. Secur. 2020, 95, 101851. [Google Scholar] [CrossRef]
- Sylvester, E.V.A.; Bentzen, P.; Bradbury, I.R.; Clément, M.; Pearce, J.; Horne, J.; Beiko, R.G. Applications of random forest feature selection for fine-scale genetic population assignment. Evol. Appl. 2017, 11, 153–165. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Mu, Y.; Chen, K.; Li, Y.; Guo, J. Daily Activity Feature Selection in Smart Homes Based on Pearson Correlation Coefficient. Neural Process. Lett. 2020, 51, 1771–1787. [Google Scholar] [CrossRef]
- Nasir, I.M.; Khan, M.A.; Yasmin, M.; Shah, J.H.; Gabryel, M.; Scherer, R.; Damaševičius, R. Pearson Correlation-Based Feature Selection for Document Classification Using Balanced Training. Sensors 2020, 20, 6793. [Google Scholar] [CrossRef]
- Saidi, R.; Bouaguel, W.; Essoussi, N. Hybrid Feature Selection Method Based on the Genetic Algorithm and Pearson Correlation Coefficient. In Machine Learning Paradigms: Theory and Application; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Chen, P.; Li, F.; Wu, C. Research on Intrusion Detection Method Based on Pearson Correlation Coefficient Feature Selection Algorithm. J. Phys. Conf. Ser. 2021, 1757, 012054. [Google Scholar] [CrossRef]
- Risqiwati, D.; Wibawa, A.D.; Pane, E.S.; Islamiyah, W.R.; Tyas, A.E.; Purnomo, M.H. Feature Selection for EEG-Based Fatigue Analysis Using Pearson Correlation. In Proceedings of the 2020 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 22–23 July 2020; pp. 164–169. [Google Scholar] [CrossRef]
- Saikhu, A.; Nopember, I.T.S.; Arifin, A.; Fatichah, C. Correlation and Symmetrical Uncertainty-Based Feature Selection for Multivariate Time Series Classification. Int. J. Intell. Eng. Syst. 2019, 12, 129–137. [Google Scholar] [CrossRef]
- Attanasio, A.; Pasini, A.; Triacca, U. Granger Causality Analyses for Climatic Attribution. Atmos. Clim. Sci. 2013, 3, 515–522. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Li, M. Modeling of Precipitation Prediction Based on Causal Analysis and Machine Learning. Atmosphere 2023, 14, 1396. [Google Scholar] [CrossRef]
- McGraw, M.C.; Barnes, E.A. Memory Matters: A Case for Granger Causality in Climate Variability Studies. J. Clim. 2018, 31, 3289–3300. [Google Scholar] [CrossRef]
- He, Y.; Lee, E. Empirical Relationships of Sea Surface Temperature and Vegetation Activity with Summer Rainfall Variability over the Sahel. Earth Interact. 2015, 20, 1–18. [Google Scholar] [CrossRef]
- Silva, F.N.; Vega-Oliveros, D.A.; Yan, X.; Flammini, A.; Menczer, F.; Radicchi, F.; Kravitz, B.; Fortunato, S. Detecting climate teleconnections with Granger causality. Geophys. Res. Lett. 2020, 48, e2021GL094707. [Google Scholar] [CrossRef]
- Xu, F.; Sun, S.; Zhao, P.; Jia, S. Granger causal weather time series forecasting simulation combined with mutual information. J. Phys. Conf. Ser. 2021, 1861, 012061. [Google Scholar] [CrossRef]
- Greeshma, K.; Pramod, N.; Nair, M.S. Deep Learning Approach to Rainfall Prediction. Master’s Thesis, Amrita School of Physical Sciences, Coimbatore, India, 2023. [Google Scholar] [CrossRef]
- Amir, G.; Sanandaji, B.M.; Ghaderi, F. Deep forecast: Deep learning-based spatio-temporal forecasting. arXiv 2017, arXiv:1707.08110. [Google Scholar]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef]
- Basha, C.Z.; Bhavana, N.; Bhavya, P.; Sowmya, V. Rainfall prediction using machine learning & deep learning techniques. In Proceedings of the 2020 International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; IEEE: New York, NY, USA; pp. 92–97. [Google Scholar]
- Yen, M.H.; Liu, D.W.; Hsin, Y.C.; Lin, C.E.; Chen, C.C. Application of the deep learning for the prediction of rainfall in Southern Taiwan. Sci. Rep. 2019, 9, 12774. [Google Scholar] [CrossRef]
- Hernández, E.; Sanchez-Anguix, V.; Julian, V.; Palanca, J.; Duque, N. Rainfall prediction: A deep learning approach. In Hybrid Artificial Intelligent Systems, Proceedings of the 11th International Conference, HAIS 2016, Seville, Spain, 18–20 April 2016, Proceedings 11; Springer International Publishing: Cham, Switzerland, 2016; pp. 151–162. [Google Scholar]
- Narejo, S.; Jawaid, M.M.; Talpur, S.; Baloch, R.; Pasero, E.G.A. Multi-step rainfall forecasting using deep learning approach. PeerJ Comput. Sci. 2021, 7, e514. [Google Scholar] [CrossRef]
- Barrera-Animas, A.Y.; Oyedele, L.O.; Bilal, M.; Akinosho, T.D.; Delgado, J.M.D.; Akanbi, L.A. Rainfall prediction: A comparative analysis of modern machine learning algorithms for time-series forecasting. Mach. Learn. Appl. 2022, 7, 100204. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM based sequence to sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Hou, G.H.; Li, J.N.; Huang, X.S.; Ban, J.R.; Wang, Y.B.; Zhou, Y. Research on rainfall prediction based on LSTM, RF and SVM models. In Proceedings of the 2nd International Conference on Computer Vision, Image, and Deep Learning, Liuzhou, China, 25–27 June 2021; SPIE: Bellingham, WA, USA, 2021; Volume 11911, pp. 225–231. [Google Scholar]
- Aderyani, F.R.; Mousavi, S.J.; Jafari, F. Short-term rainfall forecasting using machine learning-based approaches of PSO-SVR, LSTM and CNN. J. Hydrol. 2022, 614, 128463. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Prediction of rainfall using intensified LSTM based recurrent neural network with weighted linear units. Atmosphere 2019, 10, 668. [Google Scholar] [CrossRef]
- Ponnoprat, D. Short-term daily precipitation forecasting with seasonally-integrated autoencoder. Appl. Soft Comput. 2021, 102, 107083. [Google Scholar] [CrossRef]
- Gu, N.; Wan, D. Trend analysis of extreme rainfall based on BP neural network. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 4, pp. 1925–1928. [Google Scholar] [CrossRef]
- Perera, V.A.P.C.; Peiris, K.G.H.S. An Improved Statistical Method for Rainfall Forecasting in Sri Lanka using the WRF Model. In Proceedings of the 2020 International Conference and Utility Exhibition on Energy, Environment and Climate Change (ICUE), Pattaya, Thailand, 20–22 October 2020; IEEE: New York, NY, USA, 2020; pp. 1–7. [Google Scholar]
- Saparamadu, S.; Bandara, S.; Hewawasam, C.; Abeysinghe, U. Mathematical Models to Forecast Rainfall for Disaster Conditions in Sri Lanka. EPH-Int. J. Math. Stat. 2018, 4, 16–22. [Google Scholar] [CrossRef]
- Punyawardena, B.; Cherry, N.J. Assessment of the predictability of the seasonal rainfall in Ratnapura using Southern Oscillation and its two extremes. J. Natl. Sci. Found. Sri Lanka 1999, 27, 187–195. [Google Scholar] [CrossRef]
- Hemachandra, E.M.G.P.; Dayawansa, N.D.K.; De Silva, R. Developing a Composite Map of Vulnerability to Rainfall Extremes in Sri Lanka. In Water, Flood Management and Water Security Under a Changing Climate; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Darji, M.P.; Dabhi, V.K.; Prajapati, H.B. Rainfall forecasting using neural network: A survey. In Proceedings of the 2015 International Conference on Advances in Computer Engineering and Applications, Ghaziabad, India, 19–20 March 2015. [Google Scholar] [CrossRef]
- Ratnayake, U.; Sachindra, D.; Nandalal, K.D.W. Rainfall forecasting for flood prediction in the Nilwala Basin. In Proceedings of the International Conference on Sustainable Built Environments 2010, Kandy, Sri Lanka, 13–14 December 2010. [Google Scholar]
- Fawagreh, K.; Gaber, M.M.; Elyan, E. Random Forests: From Early Developments to Recent Advancements. Syst. Sci. Control. Eng. 2014, 2, 602–609. [Google Scholar] [CrossRef]
- Goehry, B.; Yan, H.; Goude, Y.; Massart, P.; Poggi, J.-M. Random Forests for Time Series. REVSTAT-Stat. J. 2023, 21, 283–302. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by Random Forest. Forest 2001, 23, 19–22. [Google Scholar]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. In Essays in Econometrics: Collected Papers of Clive W. J. Granger; Ghysels, E., Swanson, N.R., Watson, M.W., Eds.; Econometric Society Monographs; Cambridge University Press: Cambridge, UK, 2001; pp. 31–47. [Google Scholar]
- Understanding LSTM Networks. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 13 July 2024).
- Brownlee, J. Stacked Long Short-Term Memory Networks. 2019. Available online: https://machinelearningmastery.com/stacked-long-short-term-memory-networks/ (accessed on 10 June 2024).
- Sahar, A.; Han, D. An LSTM-based Indoor Positioning Method Using Wi-Fi Signals. In Proceedings of the ICVISP 2018: The 2nd International Conference on Vision, Image and Signal Processing, Las Vegas, NV, USA, 27–29 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Brownlee, J. How to Develop LSTM Models for Time Series Forecasting. 2020. Available online: https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/ (accessed on 10 June 2024).
- Saubhagya, S.; Tilakaratne, C.; Lakraj, P.; Mammadov, M. A Novel Hybrid Spatiotemporal Missing Value Imputation Approach for Rainfall Data: An Application to the Ratnapura Area, Sri Lanka. Appl. Sci. 2024, 14, 999. [Google Scholar] [CrossRef]
- Fan, H.; Wu, S.; Chen, N.; Gao, B.; Xu, Y. A New Approach for Short-term Time Series Forecasting. IOP Conf. Ser. Mater. Sci. Eng. 2019, 646, 012015. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; 2018; Available online: https://otexts.com/fpp2/long-short-ts.html (accessed on 10 June 2024).
- Xu, D.-M.; Hu, X.-X.; Wang, W.-C.; Chau, K.-W.; Zang, H.-F.; Wang, J. A new hybrid model for monthly runoff prediction using ELMAN neural network based on decomposition-integration structure with local error correction method. Expert Syst. Appl. 2023, 238, 121719. [Google Scholar] [CrossRef]
- Broersen, P.M.T. Error Correction of Rainfall-Runoff Models With the ARMAsel Program. IEEE Trans. Instrum. Meas. 2007, 56, 2212–2219. [Google Scholar] [CrossRef]
- Mondal, P.; Shit, L.; Goswami, S. Study of Effectiveness of Time Series Modeling (Arima) in Forecasting Stock Prices. Int. J. Comput. Sci. Eng. Appl. 2014, 4, 13–29. [Google Scholar] [CrossRef]
- Moffat, I.U.; Akpan, E.A. White Noise Analysis: A Measure of Time Series Model Adequacy. Appl. Math. 2019, 10, 989–1003. [Google Scholar] [CrossRef]
- Hassani, H.; Yeganegi, M.R. Selecting optimal lag order in Ljung–Box test. Phys. A Stat. Mech. Appl. 2019, 541, 123700. [Google Scholar] [CrossRef]
- Lee, T. Wild bootstrap Ljung–Box test for cross correlations of multivariate time series. Econ. Lett. 2016, 147, 59–62. [Google Scholar] [CrossRef]
- How to Perform a Ljung-Box Test in Python. 2021. Available online: https://koalatea.io/python-ljung-box-test/ (accessed on 10 June 2024).


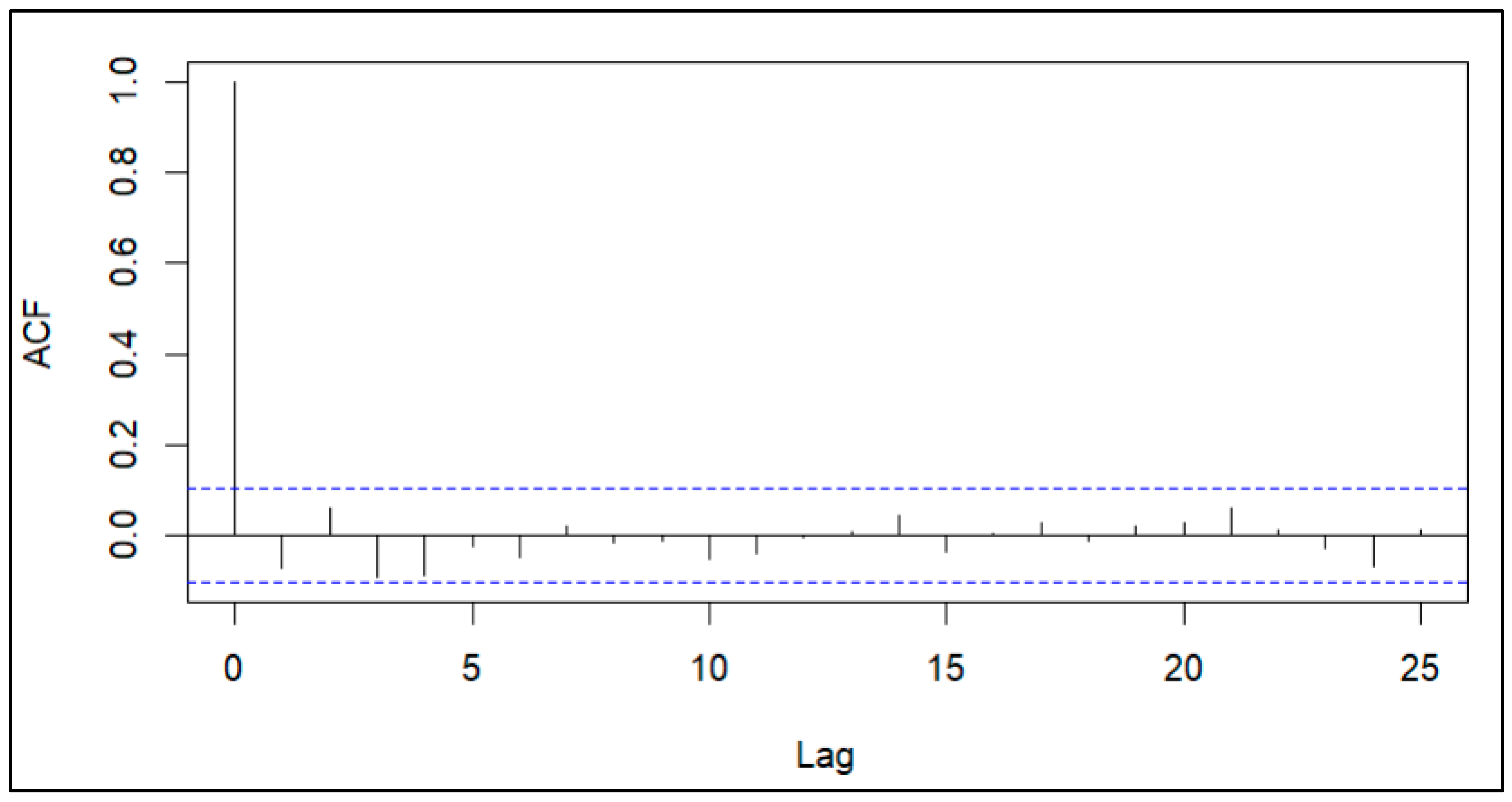
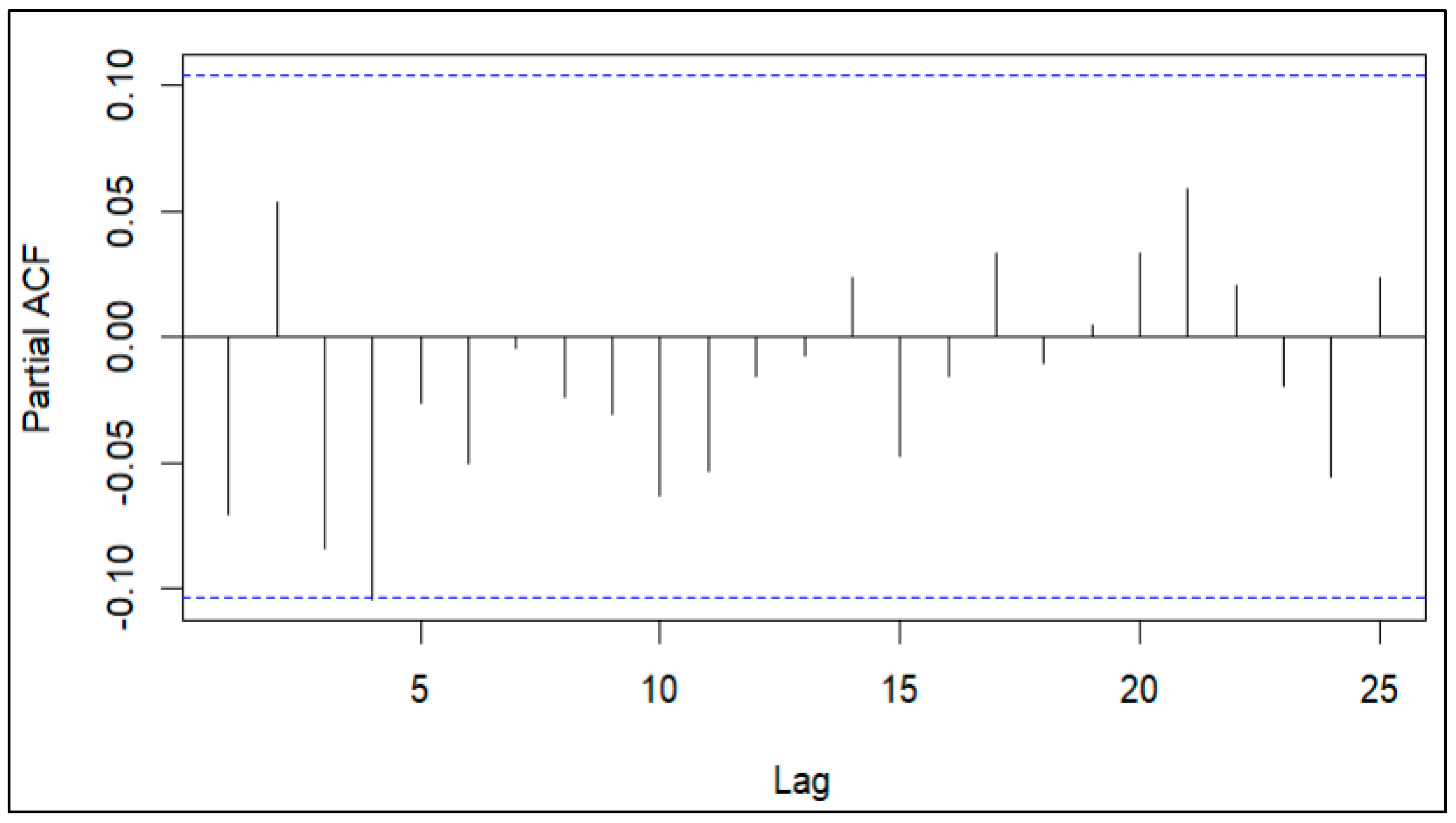

| Parameters | Value |
|---|---|
| n_estimator | 100 |
| n_samples | 60% |
| max_features | n_features |
| k (in k-fold cross-validation) | 5 |
| Predictor Variable | Significant Past Lag Range (at 5% Significance Level) | Minimum of p Values Within 14 Lags |
|---|---|---|
| accumulated rain | 1–2 | 0.0007 |
| kriging interpolation | 1–9 | 0.0009 |
| dew point (evening) | more than 14 | <1 × 10−12 |
| evaporation | more than 14 | 0.0001 |
| dew point (morning) | more than 14 | <1 × 10−12 |
| sunshine hours | more than 14 | <1 × 10−12 |
| relative humidity (day) | more than 14 | <1 × 10−12 |
| temperature (minimum) | 1–5 | 0.0001 |
| relative humidity (night) | more than 14 | <1 × 10−12 |
| temperature (maximum) | 1–2 | 0.0055 |
| cloud amount (morning) | 1 | 0.0127 |
| cloud amount (evening) | more than 14 | <1 × 10−12 |
| continuous dry days | 1–12 | <1 × 10−12 |
| continuous wet days | 1–2 | 0.0014 |
| Model | Stacked LSTM | Bidirectional LSTM | Encoder-Decoder LSTM | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Forecasted Day-Ahead | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| January | RMSE | 4.34 | 4.81 | 4.94 | 3.59 | 4.06 | 4.40 | 4.02 | 4.57 | 5.49 |
| MAE | 3.43 | 3.69 | 2.97 | 2.18 | 2.77 | 2.71 | 2.99 | 3.26 | 3.57 | |
| May | RMSE | 11.10 | 10.10 | 9.99 | 4.83 | 5.40 | 5.97 | 8.07 | 7.13 | 7.47 |
| MAE | 8.14 | 7.70 | 8.12 | 2.85 | 3.76 | 4.09 | 6.68 | 5.66 | 5.92 | |
| August | RMSE | 26.80 | 20.60 | 42.00 | 9.50 | 10.60 | 11.20 | 30.70 | 28.90 | 38.10 |
| MAE | 16.70 | 14.50 | 23.70 | 6.38 | 7.60 | 7.85 | 18.00 | 16.50 | 19.10 | |
| November | RMSE | 16.20 | 15.90 | 18.50 | 7.28 | 9.86 | 9.24 | 15.70 | 16.10 | 16.70 |
| MAE | 11.90 | 11.60 | 14.00 | 5.19 | 7.06 | 7.69 | 12.60 | 11.50 | 12.10 | |
| Rainfall Event/Class | Number of Days Forecasted Ahead | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||
| Stacked LSTM | Actual Count | Accurately Forecasted Count | Actual Count | Accurately Forecasted Count | Actual Count | Accurately Forecasted Count | |
| No/Mild Rain | 30 | 30 (100) | 29 | 29 (100) | 28 | 28 (100) | |
| January | Moderate Rain | 1 | 0 (0) | 1 | 0 (0) | 1 | 0 (0) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| No/Mild Rain | 29 | 22 (76) | 28 | 24 (86) | 27 | 23 (85) | |
| May | Moderate Rain | 2 | 0 (0) | 2 | 0 (0) | 2 | 0 (0) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| No/Mild Rain | 22 | 12 (55) | 21 | 10 (48) | 20 | 9 (45) | |
| August | Moderate Rain | 7 | 4 (57) | 7 | 4 (57) | 7 | 4 (57) |
| Extreme Rain | 2 | 1 (50) | 2 | 1 (50) | 2 | 0 (0) | |
| No/Mild Rain | 20 | 10 (50) | 19 | 9 (47) | 19 | 10 (53) | |
| November | Moderate Rain | 10 | 8 (80) | 10 | 8 (80) | 9 | 4 (44) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| Bidirectional LSTM | |||||||
| No/Mild Rain | 30 | 30 (100) | 29 | 29 (100) | 28 | 27 (96) | |
| January | Moderate Rain | 1 | 0 (0) | 1 | 0 (0) | 1 | 0 (0) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| No/Mild Rain | 29 | 27 (93) | 28 | 25 (89) | 27 | 26 (96) | |
| May | Moderate Rain | 2 | 1 (50) | 2 | 1 (50) | 2 | 1 (50) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| No/Mild Rain | 22 | 17 (77) | 21 | 12 (57) | 20 | 16 (80) | |
| August | Moderate Rain | 7 | 7 (100) | 7 | 5 (71) | 7 | 6 (86) |
| Extreme Rain | 2 | 2 (100) | 2 | 2 (100) | 2 | 2 (100) | |
| No/Mild Rain | 20 | 18 (90) | 19 | 14 (74) | 19 | 15 (79) | |
| November | Moderate Rain | 10 | 9 (90) | 10 | 8 (80) | 9 | 8 (89) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| Encoder-decoder LSTM | |||||||
| No/Mild Rain | 30 | 30 (100) | 29 | 28 (97) | 28 | 27 (96) | |
| January | Moderate Rain | 1 | 0 (0) | 1 | 0 (0) | 1 | 0 (0) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| No/Mild Rain | 29 | 24 (83) | 28 | 26 (93) | 27 | 25 (93) | |
| May | Moderate Rain | 2 | 0 (0) | 2 | 1 (50) | 2 | 0 (0) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| No/Mild Rain | 22 | 10 (45) | 21 | 10 (48) | 20 | 10 (50) | |
| August | Moderate Rain | 7 | 3 (43) | 7 | 3 (43) | 7 | 3 (43) |
| Extreme Rain | 2 | 1 (50) | 2 | 1 (50) | 2 | 0 (0) | |
| No/Mild Rain | 20 | 8 (40) | 19 | 13 (68) | 19 | 9 (47) | |
| November | Moderate Rain | 10 | 6 (60) | 10 | 8 (80) | 9 | 6 (67) |
| Extreme Rain | 0 | 0 | 0 | 0 | 0 | 0 | |
| Parameters | Value |
|---|---|
| Activation function | ReLU |
| Epochs | 100 |
| Number of hidden layers | 1 |
| Number of neurons in hidden layer | 100 |
| Batch size | 72 |
| Learning rate | 0.01 |
| Optimizer | Adam |
| Loss function | MAE |
| n_steps_in/historical window | 14 |
| n_step_out/forecast step | 3 |
| Rainfall Event/Class | Number of Days Forecasted Ahead | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| Actual Count | Accurately Forecasted Count | Actual Count | Accurately Forecasted Count | Actual Count | Accurately Forecasted Count | |
| No/Mild Rain | 266 | 244 (91.73) | 266 | 224 (84.21) | 266 | 238 (89.47) |
| Moderate Rain | 87 | 76 (87.36) | 87 | 73 (83.91) | 87 | 67 (77.01) |
| Extreme Rain | 03 | 02 (66.67) | 03 | 02 (66.67) | 03 | 03 (100) |
| Rainfall Event/Class | Number of Days Forecasted Ahead | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| Actual Count | Accurately Forecasted Count | Actual Count | Accurately Forecasted Count | Actual Count | Accurately Forecasted Count | |
| Extreme Rain | 4 | 3 (75.00) | 4 | 4 (100) | 4 | 3 (75.00) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saubhagya, S.; Tilakaratne, C.; Lakraj, P.; Mammadov, M. Granger Causality-Based Forecasting Model for Rainfall at Ratnapura Area, Sri Lanka: A Deep Learning Approach. Forecasting 2024, 6, 1124-1151. https://doi.org/10.3390/forecast6040056
Saubhagya S, Tilakaratne C, Lakraj P, Mammadov M. Granger Causality-Based Forecasting Model for Rainfall at Ratnapura Area, Sri Lanka: A Deep Learning Approach. Forecasting. 2024; 6(4):1124-1151. https://doi.org/10.3390/forecast6040056
Chicago/Turabian StyleSaubhagya, Shanthi, Chandima Tilakaratne, Pemantha Lakraj, and Musa Mammadov. 2024. "Granger Causality-Based Forecasting Model for Rainfall at Ratnapura Area, Sri Lanka: A Deep Learning Approach" Forecasting 6, no. 4: 1124-1151. https://doi.org/10.3390/forecast6040056
APA StyleSaubhagya, S., Tilakaratne, C., Lakraj, P., & Mammadov, M. (2024). Granger Causality-Based Forecasting Model for Rainfall at Ratnapura Area, Sri Lanka: A Deep Learning Approach. Forecasting, 6(4), 1124-1151. https://doi.org/10.3390/forecast6040056






