Synthetic Demand Flow Generation Using the Proximity Factor
Abstract
1. Introduction
2. Models
2.1. Proximity Factor
2.2. Gravity Model
Single Parameter Gravity Model
2.3. Numerical Example
3. Model Comparison
3.1. Census Block Group Data
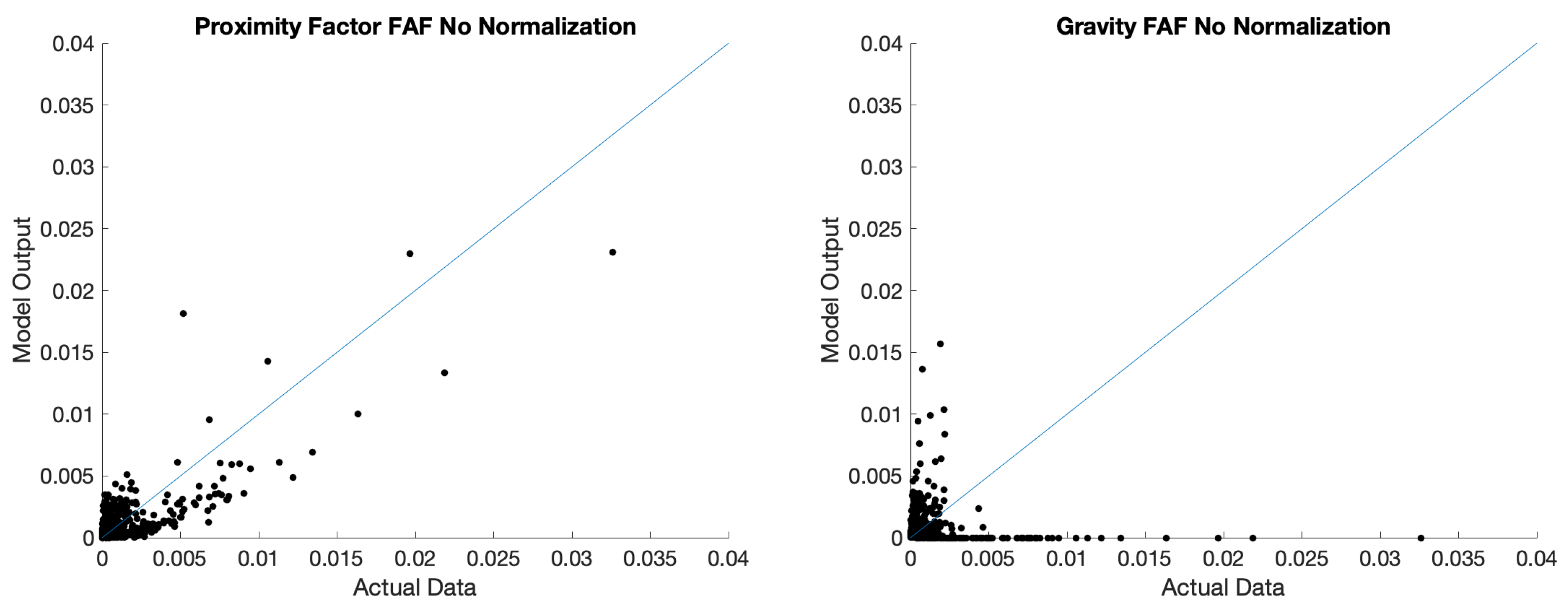
3.2. Logistics Design Application
4. Validation
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
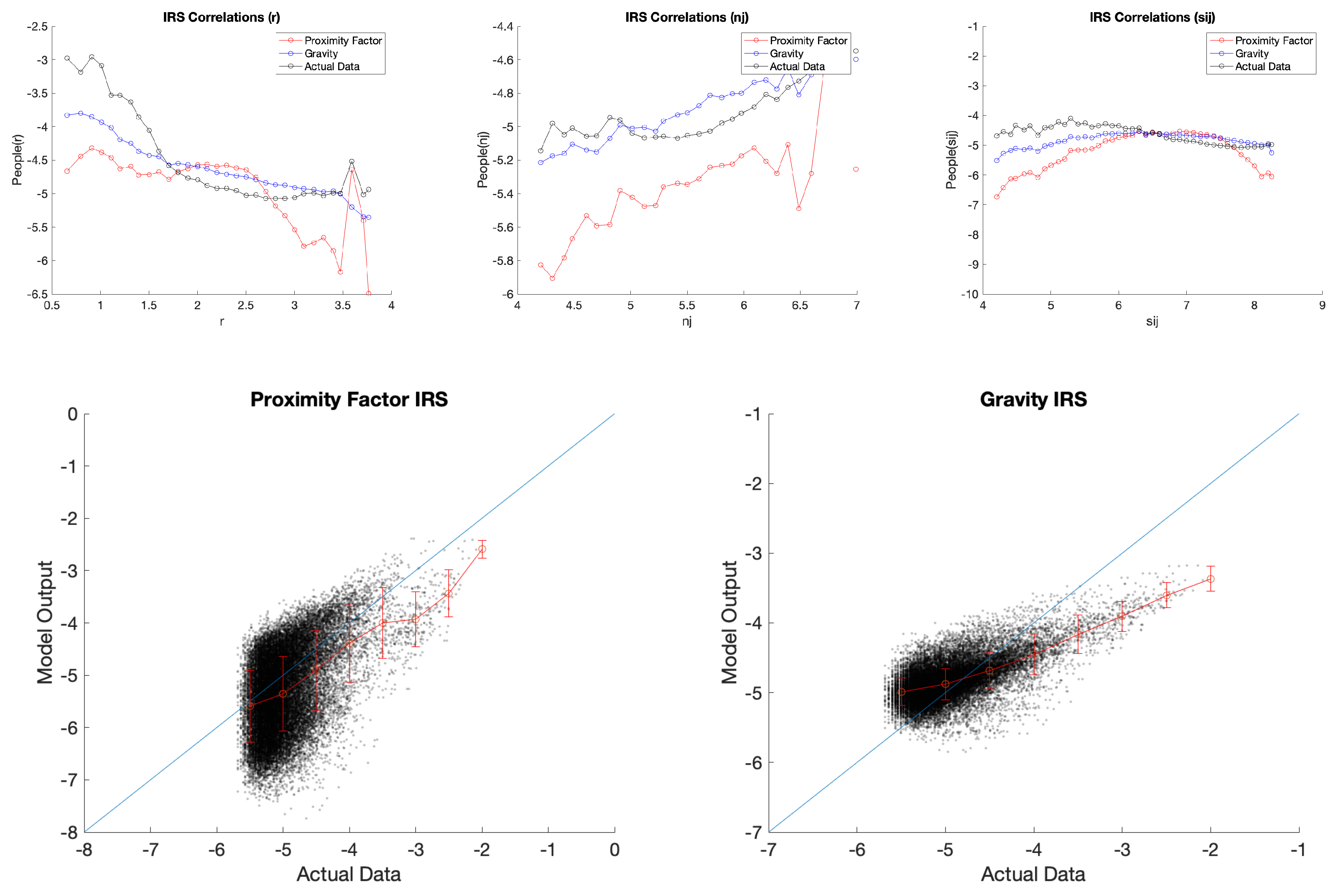
Appendix A.1. Census Data
| Gravity | Proximity Factor | |
|---|---|---|
| Census | 0.0021 | 0.9595 |
| IRS | 0.5550 | 0.1628 |
| Gravity | Proximity Factor | |
|---|---|---|
| Census | 0.2126 | 0.9595 |
| IRS | 0.0936 | 0.1628 |

Appendix A.2. IRS Data
References
- Kay, M.G.; Parlikad, A.N. Material Flow Analysis of Public Logistics Networks. In Progress in Material Handling Research; Meller, R., Ogle, M., Peters, B., Taylor, D., Usher, J., Eds.; The Material Handling Institute: Charlotte, NC, USA, 2002. [Google Scholar]
- Kay, M.G.; Warsing, D.P. Estimating LTL rates using publicly available empirical data. Int. J. Logist. Res. Appl. 2009, 12, 165–193. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Pasin, F.; Solomon, M.M. An Integrated Model for Logistics Network Design. Ann. Oper. Res. 2006, 144, 59–82. [Google Scholar] [CrossRef]
- Melo, M.T.; Nickel, S.; Saldanha-Da-Gama, F. Facility Location and Supply Chain Management—A Review. Eur. J. Oper. Res. 2009, 196, 401–412. [Google Scholar] [CrossRef]
- Guo, W.; Toader, B.; Feier, R.; Mosquera, G.; Ying, F.; Oh, S.W.; Price-Williams, M.; Krupp, A. Global Air Transport Complex Network: Multi-Scale Analysis. SN Appl. Sci. 2019, 1, 1–14. [Google Scholar] [CrossRef]
- Hua, C.; Porell, F. A Critical Review of the Development of the Gravity Model. Int. Reg. Sci. Rev. 1979, 4, 97–126. [Google Scholar] [CrossRef]
- Balcan, D.; Colizza, V.; Gonçalves, B.; Hu, H.; Ramasco, J.J.; Vespignani, A. Multiscale Mobility Networks and the Spatial Spreading of Infectious Diseases. Proc. Natl. Acad. Sci. USA 2009, 106, 21484–21489. [Google Scholar] [CrossRef] [PubMed]
- Kalahasthi, L.; Holguín-Veras, J.; Yushimito, W.F. A Freight Origin-Destination Synthesis Model with Mode Choice. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102595. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Patil, G.R. Integrated Origin–Destination Synthesis Model for Freight with Commodity-Based and Empty Trip Models. Transp. Res. Rec. 2007, 2008, 60–66. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Patil, G.R. A Multicommodity Integrated Freight Origin–Destination Synthesis Model. Netw. Spat. Econ. 2008, 8, 309–326. [Google Scholar] [CrossRef]
- Erlander, S.; Stewart, N.F. The Gravity Model in Transportation Analysis: Theory and Extensions; VSP: Leiden, The Netherlands, 1990. [Google Scholar]
- Zipf, G.K. The P1 P2/D Hypothesis: On the Intercity Movement of Persons. Am. Sociol. Rev. 1946, 11, 677–686. [Google Scholar] [CrossRef]
- Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.J.; Simini, F.; Tomasini, M. Human Mobility: Models and Applications. Phys. Rep. 2018, 734, 1–74. [Google Scholar] [CrossRef]
- Simini, F.; González, M.C.; Maritan, A.; Barabási, A.L. A Universal Model for Mobility and Migration Patterns. Nature 2012, 484, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Masucci, A.P.; Serras, J.; Johansson, A.; Batty, M. Gravity versus Radiation Models: On the Importance of Scale and Heterogeneity in Commuting Flows. Phys. Rev. E 2013, 88, 022812. [Google Scholar] [CrossRef] [PubMed]
- Lenormand, M.; Bassolas, A.; Ramasco, J.J. Systematic Comparison of Trip Distribution Laws and Models. J. Transp. Geogr. 2016, 51, 158–169. [Google Scholar] [CrossRef]
- Jung, W.S.; Wang, F.; Stanley, H.E. Gravity Model in the Korean Highway. EPL Europhys. Lett. 2008, 81, 48005. [Google Scholar] [CrossRef]
- Yang, Y.; Herrera, C.; Eagle, N.; González, M.C. Limits of Predictability in Commuting Flows in the Absence of Data for Calibration. Sci. Rep. 2014, 4, 5662. [Google Scholar] [CrossRef] [PubMed]
- Joines, J.A.; Houck, C.R. On the use of non-stationary penalty functions to solve nonlinear constrained optimization problems with GA’s. In Proceedings of the First IEEE Conference on Evolutionary Computation. IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; pp. 579–584. [Google Scholar]
- De Dios Ortúzar, J.; Willumsen, L.G. Modelling Transport; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mathai, A.M. An Introduction to Geometrical Probability: Distributional Aspects with Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Wilson, R.A. Transportation in America: Statistical Analysis of Transportation in the United States. Historical Compendium 1939–1995; Eno Transportation Foundation: Westport, CT, USA, 2002. [Google Scholar]
- Yalvac, E. Design of a Home Delivery Logistics Network. Ph.D. Dissertation, North Carolina State University, Raleigh, NC, USA, 2023. [Google Scholar]
- Department of Transportation Freight Analysis Framework. Available online: https://faf.ornl.gov/faf5/ (accessed on 18 March 2021).
- Kay, M.G. Matlog: Logistics Engineering Using Matlab. J. Eng. Sci. Des. 2016, 4, 15–20. [Google Scholar]
- Schläpfer, M.; Dong, L.; O’Keeffe, K.; Santi, P.; Szell, M.; Salat, H.; Anklesaria, S.; Vazifeh, M.; Ratti, C.; West, G.B. The Universal Visitation Law of Human Mobility. Nature 2021, 593, 522–527. [Google Scholar] [CrossRef] [PubMed]
- US Census Bureau Commuting Data Statistics. Available online: https://www.census.gov/topics/employment/commuting/data.html (accessed on 31 December 2020).
- Internal Revenue Service SOI Tax Stats—Migration Data. Available online: https://www.irs.gov/statistics/soi-tax-stats-migration-data (accessed on 23 February 2021).
- Bureau of Transportation Monthly Transportation Statistics. Available online: https://data.bts.gov/stories/s/m9eb-yevh (accessed on 30 November 2020).
- Liu, S.; Su, Y. The Impact of the COVID-19 Pandemic on the Demand for Density: Evidence from the US Housing Market. Econ. Lett. 2021, 207, 110010. [Google Scholar] [CrossRef]




| w | ||||||
|---|---|---|---|---|---|---|
| 0.228 | 0.228 | 0.212 | 0.212 | 0.228 | 0.220 | |
| 0.162 | 0.162 | 0.178 | 0.178 | 0.162 | 0.171 | |
| 0.161 | 0.161 | 0.166 | 0.166 | 0.161 | 0.161 | |
| 0.131 | 0.131 | 0.102 | 0.102 | 0.131 | 0.111 | |
| 0.152 | 0.152 | 0.184 | 0.184 | 0.152 | 0.178 | |
| 0.166 | 0.166 | 0.158 | 0.158 | 0.166 | 0.159 | |
| RMSE (in %) | Gainesville, FL | Raleigh, NC | Atlanta, GA | LTL |
|---|---|---|---|---|
| P | ||||
| G | ||||
| – | ||||
| – | ||||
| – | ||||
| – |
| Training Set % | ||
|---|---|---|
| 10 | ||
| 20 | ||
| 30 | ||
| 40 | ||
| 50 | ||
| 60 | ||
| 70 | ||
| 80 | ||
| 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yalvac, E.; Kay, M.G. Synthetic Demand Flow Generation Using the Proximity Factor. Forecasting 2025, 7, 14. https://doi.org/10.3390/forecast7010014
Yalvac E, Kay MG. Synthetic Demand Flow Generation Using the Proximity Factor. Forecasting. 2025; 7(1):14. https://doi.org/10.3390/forecast7010014
Chicago/Turabian StyleYalvac, Ekin, and Michael G. Kay. 2025. "Synthetic Demand Flow Generation Using the Proximity Factor" Forecasting 7, no. 1: 14. https://doi.org/10.3390/forecast7010014
APA StyleYalvac, E., & Kay, M. G. (2025). Synthetic Demand Flow Generation Using the Proximity Factor. Forecasting, 7(1), 14. https://doi.org/10.3390/forecast7010014