White Noise and Its Misapplications: Impacts on Time Series Model Adequacy and Forecasting

Abstract

This paper contributes significantly to time series analysis by discussing the empirical properties of white noise and their implications for model selection. This paper illustrates the ways in which the standard assumptions about white noise typically fail in practice, with a special emphasis on striking differences in sample ACF and PACF. Such findings prove particularly important when assessing model adequacy and discerning between residuals of different models, especially ARMA processes. This study addresses issues involving testing procedures, for instance, the Ljung–Box test, to select the correct time series model determined in the review. With the improvement in understanding the features of white noise, this work enhances the accuracy of modeling diagnostics toward real forecasting practice, which gives it applied value in time series analysis and signal processing.

1. Introduction

The white noise process is a fundamental concept in time series analysis and signal processing, representing a sequence of random variables that are uncorrelated, each having a constant mean and variance [1,2,3,4,5,6,7,8,9,10]. However, despite its importance, the white noise process has often been misapplied in various practical applications and modeling [11,12,13,14,15].

In theory, white noise is an idealized concept where each data point is assumed to be completely independent of the others, with no correlation between observations. It is typically modeled as a Gaussian process, implying a normal distribution with a constant mean and variance [16,17,18]. However, real-world noises are rarely entirely white because most real processes have some forms of correlation or dependency between different times [19,20,21]. Real-world noise may also not behave according to Gaussian assumptions; it can have some skewness or kurtosis [22,23]. Modeling challenges arise when correctly identifying white noise from other types of noise or signal components, as the misidentification of white noise may lead to incorrect model assumptions [24,25]. For example, in ARIMA models, residuals are expected to be white noise, and if they are not, then it indicates that the model is not adequately capturing the underlying process [26,27]. Also, white noise assumes constant variance over time, while for many time series data, heteroscedasticity is observed, thus invalidating the white noise assumption.

Furthermore, real-world data quite often exhibit some form of autocorrelation. Additionally, in information theory and signal processing, it is also difficult to separate a weak signal from white noise, especially when the signal-to-noise ratio is small [28,29,30]. This must be done by designing a filter that can remove white noise without distorting the underlying signal, and especially when the characteristics of the noise are not well known.

Practical implications further relate to the measurement errors that may be obtained in real-world data acquisition, not being those of white noise properties and, hence, adding more complexity to the analysis [31,32,33]. Mathematically, if a time series $Z_t$ representing a stochastic process is proven to be white noise, it means that the future expected values of $Z_t$ (and underlying stochastic process) cannot be forecasted based on past observation of $Z_t$. This absence of temporal correlation indicates that the series has no discernible structure for forecasting purposes. In Gaussian white noise, the behavior of $Z_t$ (and the behavior of its underlying stochastic phenomenon) is entirely random and unpredictable, with each observation being independently drawn from a normal distribution with a constant mean and variance.

The significance of this property of white noise extends beyond merely identifying unpredictable stochastic phenomena. It serves as the foundational principle for using white noise in time series modeling and forecasting, as it represents the benchmark for randomness against which the presence of structure or patterns in data can be evaluated. If a model is able to separate the given time series $\left\{X_t\right\}$ into white noise $\left\{Z_t\right\}$, then it means it can model the predictable part of the $X_t$’s stochastic behavior and separate the complete stochastic part. In this case, the model proposed would be considered an adequate model for modeling and forecasting $\left\{X_t\right\}$. However, if the proposed model reduces the time series $\left\{X_t\right\}$ to a non-white noise time series, it would be considered inadequate since it has not captured all the predictable components of $X_t$’s behavior (i.e., some information from the past values is not adequately extracted to forecast the future values). In this scenario, white noise is a criterion to evaluate the performance of the time series model.

Although white noise serves as a fundamental building block in time series analysis, its actual detection can be challenging, as distinguishing true randomness from subtle patterns or dependencies often requires rigorous statistical testing and careful interpretation of the data. To determine whether a zero-mean, constant variance stationary time series $\left\{Z_t\right\}$ is white noise, or qualifies as white noise, the following tests can be conducted:

$$\begin{array}{c}\hfill H_0:{\rho }_Z\left(h\right)=0,\left|h\right|\ge 1,\end{array}$$

(1)

where ${\rho }_Z\left(h\right)$ denotes the $Z_t$ autocorrelation functions (ACFs) of order h. Most tests proposed for the hypothesis above are those that are based on the asymptotic distribution of the test statistic [17,19,26]. As is evident from several studies, their application in practice may be problematic and lead to incorrect conclusions (see, for instance, [1,2,3]). The aforementioned tests are based on the fundamental theoretical property of white noise processes, where the autocorrelation functions are expected to become asymptotically independent as the sample size increases. For a true white noise process, the ACFs should converge towards a normal distribution with a mean of zero and variance $\frac{1}{n}$, where n represents the sample size. This asymptotic behavior serves as the foundation for statistical tests such as the Ljung–Box test, which evaluates whether the observed ACFs deviate significantly from the theoretical expectation of zero correlation [25]. If the ACFs remain statistically insignificant across multiple lags, the series can be classified as white noise, indicating no underlying structure or serial dependence.

Nevertheless, Hassani’s $-\frac{1}{2}$ theorem indicates that whatever time series is considered, including white noise, the total sum of the sample ACF is always equal to $-\frac{1}{2}$ [24]. Several works emphasize the practical relevance of Hassani’s $-\frac{1}{2}$ theorem in the analysis and modeling of time series [34,35,36,37]. It has important implications in time series modeling [38,39,40] (see also recent work on the relevance of sample ACF and application of Hassani’s theorem [41,42,43,44,45]). In this paper, we delve deeper into the implications of Hassani’s −1/2 theorem in time series analysis, focusing specifically on its effects when applied to a white noise process.

Section 2 provides a detailed theoretical background, wherein we delve into the fundamental principles of white noise and its associated fundamental properties, such as the autocorrelation and partial autocorrelation functions. In Section 3 of the paper, we provide an in-depth simulation study that gives an empirical view on white noise behavior, with particular attention paid to some deviations observed in practice. In Section 3 we also assess to what extent these empirical features influence time series model selection for ARMA modeling, with special reference to the use of diagnostic tests through an analysis for the applicability of the Ljung–Box test. Finally, Section 4 presents our conclusions about the findings of these studies and their general implications for time series analysis before giving an outlook on practical applications and avenues for further research.

2. Theoretical Background

2.1. Definitions

For a stationary process $\left\{X_t\right\}$ of size n, we often define the following key quantities:

2.1.1. Mean

$$\mu =\mathbb{E}\left[X_t\right]$$

Since the process is stationary, the mean is constant over time.

2.1.2. Autocovariance Function

$$\gamma \left(h\right)=\mathbb{E}\left[(X_t-\mu )(X_{t+h}-\mu )\right]$$

where h is the lag. The autocovariance depends only on the lag h and not on the time index t due to stationarity.

2.1.3. Autocorrelation Function (ACF)

$$\rho \left(h\right)={\displaystyle \frac{\gamma \left(h\right)}{\gamma \left(0\right)}}$$

where $\gamma \left(0\right)$ is the variance of the process. The ACF measures the linear correlation between observations separated by lag h.

2.1.4. Sample Mean

$$\widehat{\mu }={\displaystyle \frac{1}{n}}\sum _{t=1}^n{X}_t$$

2.1.5. Sample Autocovariance

$$\widehat{\gamma }\left(h\right)={\displaystyle \frac{1}{n}}\sum _{t=1}^{n-h}(X_t-\widehat{\mu })(X_{t+h}-\widehat{\mu })$$

2.1.6. Sample Autocorrelation

$$\widehat{\rho }\left(h\right)={\displaystyle \frac{\widehat{\gamma }\left(h\right)}{\widehat{\gamma }\left(0\right)}}$$

2.1.7. Spectral Density Function

The spectral density function describes the frequency content of the time series:

$$f\left(\omega \right)={\displaystyle \frac{1}{2\pi }}\sum _{h=-\infty }^{\infty }\gamma \left(h\right)e^{-i\omega h}$$

2.2. Bartlett’s Formula

Assume n observations $X_1,\dots ,X_n$ come from a stationary time series with IID innovations $Z_t$, and n is large enough. Let

$${\widehat{\rho }}_n={(\widehat{\rho }\left(1\right),\dots ,\widehat{\rho }\left(n\right))}^{\prime }$$

and

$${\rho }_n={(\rho \left(1\right),\dots ,\rho \left(n\right))}^{\prime }$$

(here, $\rho \left(i\right)={\rho }_X\left(i\right)$). Then, ${\widehat{\rho }}_n$ is distributed approximately $N(\rho ,n^{-1}W)$, where W is a covariance matrix with elements

$$w_{ij}=\sum _{k=1}^{\infty }(\rho (k+i)+\rho (k-i)-2\rho \left(i\right)\rho \left(k\right))(\rho (k+j)+\rho (k-j)-2\rho \left(j\right)\rho \left(k\right)).$$

2.3. Variance of $\rho \left(h\right)$ and MA(q) Model Identification

• (a) IID Noise: If the process consists of independent and identically distributed (iid) noise such that $\rho \left(k\right)=0$ for all h:

  $$w_{ij}=0\mathrm{for}\mathrm{all}i\ne j,$$

  then the variance of the sample autocorrelation function (ACF) simplifies to

  $$\mathrm{Var}\left(\widehat{\rho }\left(h\right)\right)\approx {\displaystyle \frac{1}{n}}{w}_{hh}={\displaystyle \frac{1}{n}}h\ne 0$$
• (b) Moving Average Process MA(q): Consider the MA(q) process defined by

  $$X_t=Z_t+{\theta }_1{Z}_{t-1}+\dots +{\theta }_q{Z}_{t-q},Z_t\sim \mathrm{IID}(0,{\sigma }_Z^2).$$
  For this process, the autocorrelation coefficients vanish beyond lag q:

  $$\rho (q+j)=0,j=1,2,\dots$$
  Consequently, the variance of the sample ACF for $h>q$ is given by

  $$\mathrm{Var}\left(\widehat{\rho }\left(h\right)\right)\approx {\displaystyle \frac{1}{n}}{w}_{hh}={\displaystyle \frac{1}{n}}\left(1+2\sum _{k=1}^q{\rho }^2\left(k\right)\right).$$
• (c) Asymptotic Distribution: Asymptotically, the distribution of $\widehat{\rho }\left(h\right)$ is approximately normal, with the mean $\rho \left(h\right)$ and variance as derived above. For reliable estimation, Box and Jenkins recommend

  $$n\ge 50,k\le {\displaystyle \frac{n}{4}}.$$
• Examination of the Sample ACF for Model Identification:

  –

  (i) If $|\widehat{\rho }\left(h\right)|<1.96n^{-1/2}$ for all $h\ge 1$, the process can be modeled as MA(0) (a white noise sequence).

  –

  (ii) If $|\widehat{\rho }\left(1\right)|>1.96n^{-1/2}$, compare subsequent values of $\widehat{\rho }\left(h\right)$ with the critical value:

  $$1.96n^{-1/2}{(1+2\rho {\left(1\right)}^2)}^{1/2}.$$

  However, since $\rho {\left(1\right)}^2$ is unknown, two alternatives arise:

  • Replace $\rho \left(1\right)$ with its estimate $\widehat{\rho }\left(1\right)$, and check if

    $$|\widehat{\rho }\left(h\right)|<1.96n^{-1/2}{(1+2\widehat{\rho }{\left(1\right)}^2)}^{1/2},h\ge 2.$$
    If true, assume an MA(1) model.
  • Alternatively, for large n, approximate the term

    $${\displaystyle \frac{2\widehat{\rho }{\left(1\right)}^2}{n}}\approx 0.$$
    Check if

    $$|\widehat{\rho }\left(h\right)|<1.96n^{-1/2},h\ge 2.$$
    If true, assume an MA(1) model.

  –

  (iii) More generally, if $|\widehat{\rho }\left(h_0\right)|>1.96n^{-1/2}$ and $|\widehat{\rho }\left(h\right)|<1.96n^{-1/2}$ for all $h\ge h_0$, then assume an MA(q) model with $q=h_0$.

  –

  Since positive terms $2{\sum }_{i=1}^q{\rho }^2\left(i\right)$ are discarded in the variance calculation, if $\widehat{\rho }\left(h\right)$ is approximately $1.96n^{-1/2}$, it should be considered within the confidence interval.

2.4. Reevaluating White Noise Theoretical Assumptions

In time series analysis and forecasting, the theoretical foundation for modeling often relies on the assumption that white noise possesses no correlation among its observations. This assumption is critical as it forms the basis for the derivation of variance expressions and confidence intervals for sample autocorrelation functions (ACF).

The variance of the sample ACF, as outlined in the theoretical framework above, depends directly on the ACF itself and its summation, particularly through second-order moments. However, the application of Hassani’s $-1/2$ theorem reveals a fundamental contradiction: the sum of the ACF for any stationary process is always $-1/2$ [1,3]. This fixed sum suggests that complete independence among observations in white noise cannot be achieved in practice, raising questions about the theoretical validity of assuming uncorrelated noise when the sum of ACF is constrained.

Moreover, the summation of the squared ACF terms, which directly influences the variance expression, is also under question. The bounded nature of this summation, as implied by Hassani’s theorem, challenges the theoretical assumptions of unbounded variance growth for confidence interval derivations [8]. Consequently, the accuracy of commonly used confidence intervals for the sample ACF becomes questionable.

These theoretical inconsistencies extend beyond the ACF itself to the broader implications for model validation and selection. Specifically, standard tests and models such as ARIMA, which depend on the behavior of the sample ACF for parameter estimation and model selection, may be theoretically flawed under the constraints introduced by Hassani’s theorem.

In the next section, we present a detailed simulation study to further explore these theoretical challenges. We demonstrate that empirical results can deviate significantly from the theoretical predictions, highlighting scenarios where the theoretical variance expressions and confidence intervals break down in practice. These findings emphasize the need for caution when applying traditional modeling techniques based on the theoretical assumptions of stationary processes and uncorrelated white noise.

3. Validating Theory in Practice: A Critical Examination

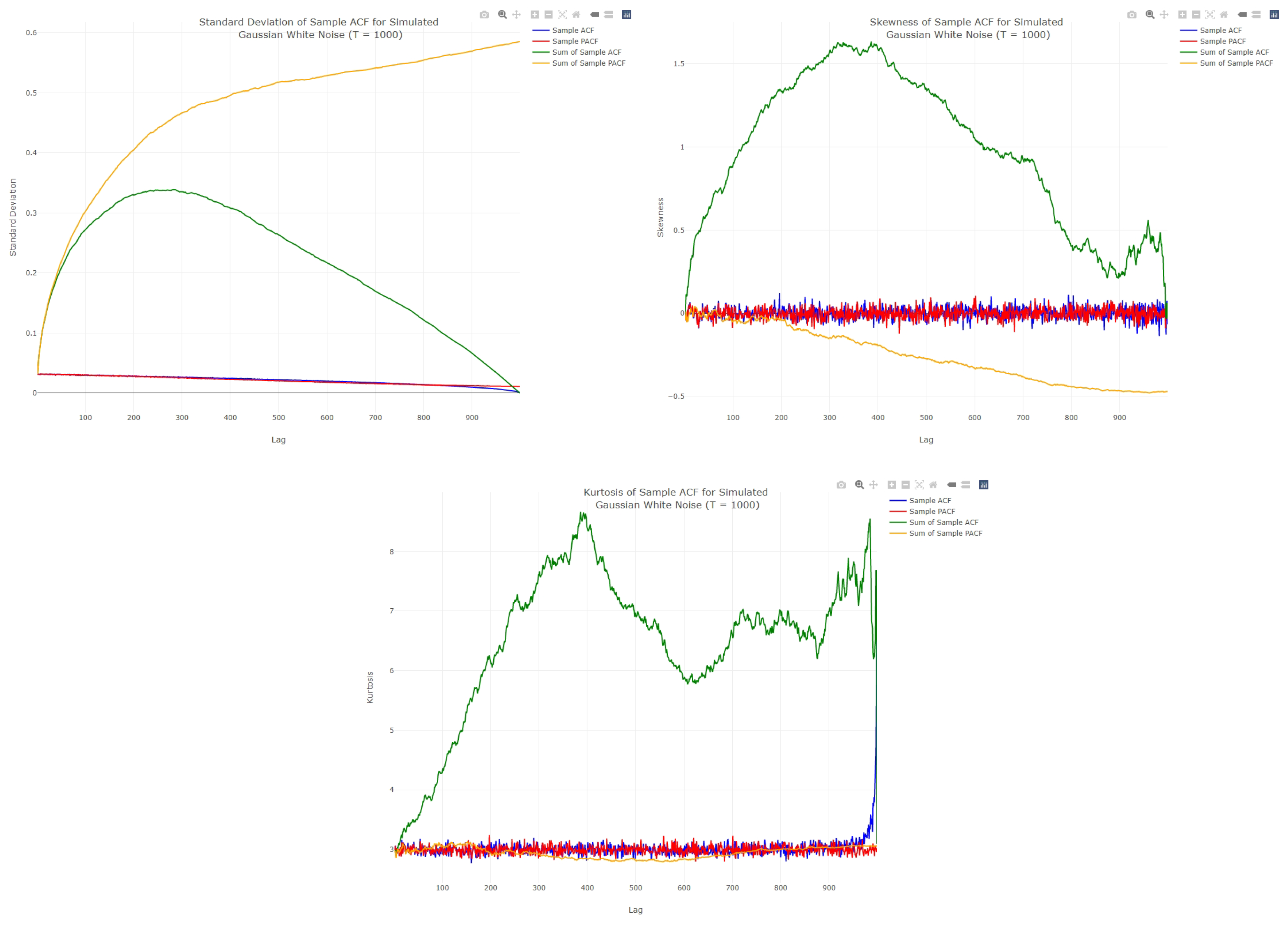
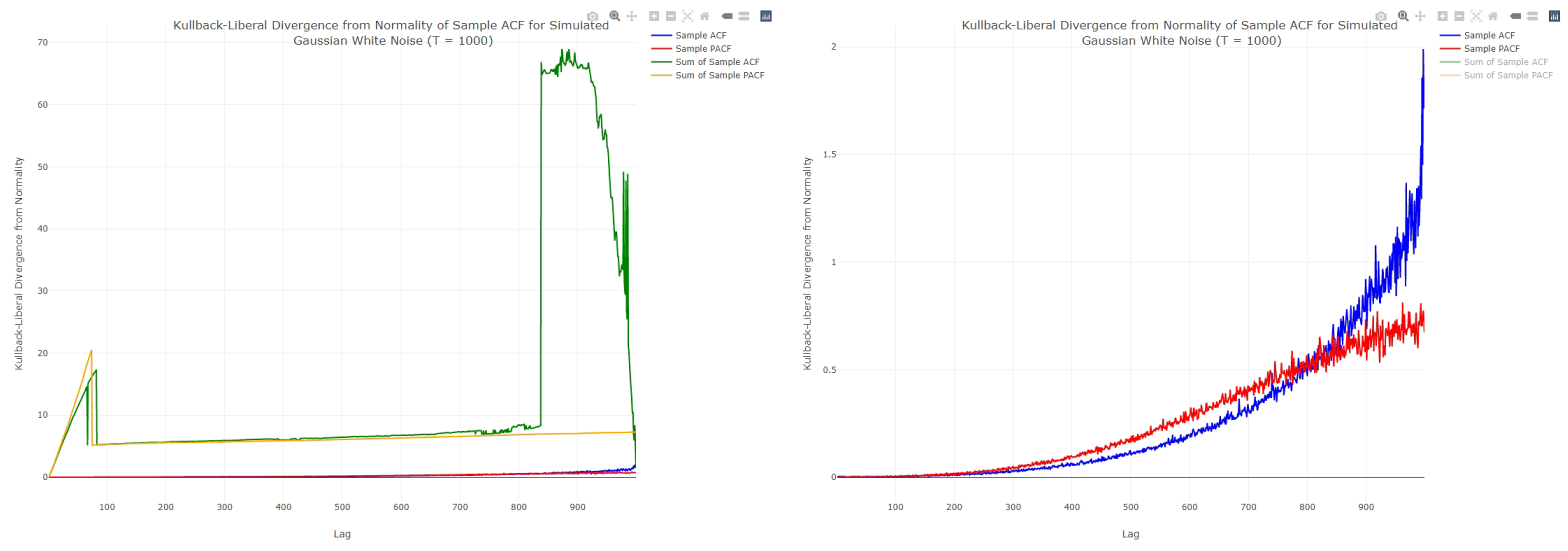
3.1. White Noise Empirical Characteristics

A comprehensive simulation study is conducted to evaluate and compare the behavior of white noise characteristics observed in practice with the theoretical properties described in the previous section. For this purpose, a total of 5000 sample paths, each consisting of 1000 observations, are generated from a Gaussian white noise process. This process is defined to have a mean of zero and a variance of one, ensuring it adheres to the standard properties of white noise.

To analyze the generated white noise, the sample autocorrelation function (ACF) and partial autocorrelation function (PACF) are computed for each of the 5000 sample paths. Additionally, the statistical summaries of these measures are obtained to assess their distribution and variability. Specifically, the focus is on the means, medians, and 95% confidence intervals of the sample ACF and PACF, which are calculated based on the 2.5th and 97.5th percentiles of the observed values.

The results of this analysis are presented in Figure 1. The figure provides a detailed visualization of the mean and median sample ACF and PACF across different lag values, along with the corresponding 95% confidence intervals. Furthermore, the cumulative sums of these functions up to various lags are also illustrated, offering additional insights into how the cumulative behavior evolves as the lag increases. This comprehensive representation highlights the consistency of the simulated results with theoretical expectations, providing a robust validation of the white noise properties under consideration.

As it is evident form the top panels in Figure 1, the variation in sample ACF and sample PACF of the simulated white noise decreases as the lag increases. Furthermore, the mean and median of the sample ACF and sample PACF oscillate near zero, with values slightly smaller than zero.

The bottom panels of Figure 1 illustrate that the cumulative sums of the sample ACF and sample PACF up to a certain lag (${\sum }_{h\le H}\widehat{\rho }\left(h\right)$ and ${\sum }_{h\le H}{\widehat{\varphi }}_{hh}$, for $H=1,\dots ,T-1$) exhibit a decreasing trend. As the number of lags included in the summation increases, the mean and median of the cumulative sum of the sample ACF converge to $-\frac{1}{2}$, consistent with Hassani’s $-\frac{1}{2}$ theorem, while the variation diminishes toward zero after an initial increase.

On the other hand, while the cumulative sum of the sample PACF also shows a decreasing trend, its variation increases as the number of lags in the summation grows, and the summation does not converge to a specific value. Additionally, both the cumulative sums of the sample ACF and sample PACF exhibit slight skewness in their distributions, as indicated by the difference between their mean and median values.

The skewness in the cumulative sum of the sample ACF becomes noticeable at intermediate lags, exhibiting positive skewness, as the mean exceeds the median. Conversely, the skewness in the cumulative sum of the sample PACF appears at later lags and shows negative skewness, with the median positioned above the mean. These patterns are more pronounced in the statistics derived from the sample ACF and PACF of simulated Gaussian white noise. Figure 2 presents the standard deviation, skewness, kurtosis, and Kullback–Leibler divergence from the theoretical asymptotic normal distribution for the sample ACF, sample PACF, and their cumulative sums.

As shown in the top-left panel of Figure 2, the standard deviations of the sample ACF and sample PACF decrease as the lag increases. The standard deviation of the cumulative sum of the sample ACF initially increases with lag up to a certain point before declining, whereas the standard deviation of the cumulative sum of the sample PACF increases monotonically in a nonlinear pattern. The top-right panel of Figure 2 reveals that the cumulative sums of the sample ACF and sample PACF exhibit skewness, with the sum of the sample ACF skewed to the right and the sum of the sample PACF skewed to the left. Meanwhile, the skewness of the sample ACF and sample PACF themselves remains close to zero but gradually shifts negatively as the number of lags increases.

The bottom panel of Figure 2 also shows that the kurtosis of the sample ACF, the sample PACF, and the cumulative sum of the sample PACF remains around 3, which corresponds to the kurtosis of the normal distribution, except for the later lags, where the kurtosis of the sample ACF increases due to its summation as a constant value. The kurtosis of the cumulative sum of the sample ACF, however, is noticeably larger than 3. The skewness deviating from zero (as seen in the top-right panel of Figure 2) and the kurtosis deviating from 3 (as shown in the bottom panel of Figure 2) suggest that the distributions of the sample ACF, sample PACF, and their cumulative sums may deviate from the theoretical asymptotic normal distribution. To assess how closely the distributions of the sample ACF, sample PACF, and their cumulative sums align with the theoretical asymptotic normal distribution, the Kullback–Leibler divergence is computed. The divergence measures the difference between the empirical distributions of the sample ACF, sample PACF, and their cumulative sums (estimated using a kernel density approach) and their theoretical asymptotic distributions, based on the following formulation:

$$\begin{array}{c}\hfill D_{KL}={\displaystyle \frac{1}{2}}\left(\sum _{i=1}^{N}p\left(x_i\right)log{\displaystyle \frac{p\left(x_i\right)}{q\left(x_i\right)}}+\sum _{i=1}^{N}q\left(x_i\right)log{\displaystyle \frac{q\left(x_i\right)}{p\left(x_i\right)}}\right),\end{array}$$

where $p(.)$ is the estimated density based on simulated data, $q(.)$ is the theoretical asymptotic normal density and N is the number of simulated sample paths. The Kullback–Leibler divergence, $D_{KL}$, is calculated for each lag of the sample ACF, sample PACF, cumulative sum of the sample ACF, and cumulative sum of the sample PACF. The resulting values are presented in Figure 3.

As shown in the left panel of Figure 3, the divergence between the density of the cumulative sums of the sample ACF and PACF from their theoretical asymptotic normal distributions increases rapidly, even at small lags. In contrast, the distributions of the sample ACF and sample PACF deviate from the asymptotic normal distribution at higher lags, as illustrated in the right panel of Figure 3.

It is important to recall, as previously shown in Figure 2, that the variance of the cumulative sum of the sample ACF is not monotonic, while the variance of the cumulative sum of the sample PACF follows a nonlinear monotonic pattern. If the sample ACFs at different lags were independent and shared the same variance, the variance of their summation would be expected to follow a linear monotonic pattern as the number of lags increases. The same principle applies to the sample PACF and its summation. To investigate the independence of the sample ACFs and PACFs across different lags, Spearman’s correlation is calculated and statistically tested. Since, in practice, only the first few lags of the sample ACF and sample PACF are commonly utilized, the results are presented for the first 25 lags.

Figure 4 presents the Spearman correlation between the first 25 lags of the sample ACF (left) and the first 25 lags of the sample PACF (right) in the top panels, with diagonal values removed as they are always equal to 1. The correlations fluctuate between approximately −0.04 and 0.04. The bottom panels highlight in bold the correlations that are statistically significant at the 0.05 significance level.

It is not surprising to observe statistically significant correlations among the sample ACFs, even for white noise, despite the theoretical expectation of zero correlation. According to Hassani’s $-\frac{1}{2}$ theorem, the cumulative sum of the sample ACF always converges to $-\frac{1}{2}$, regardless of the type or length of the series. This applies to white noise as well, implying that there must be some degree of correlation among the sample ACF values for a white noise series. Therefore, the theoretical assumption of zero correlation between sample ACF values does not hold perfectly in practice.

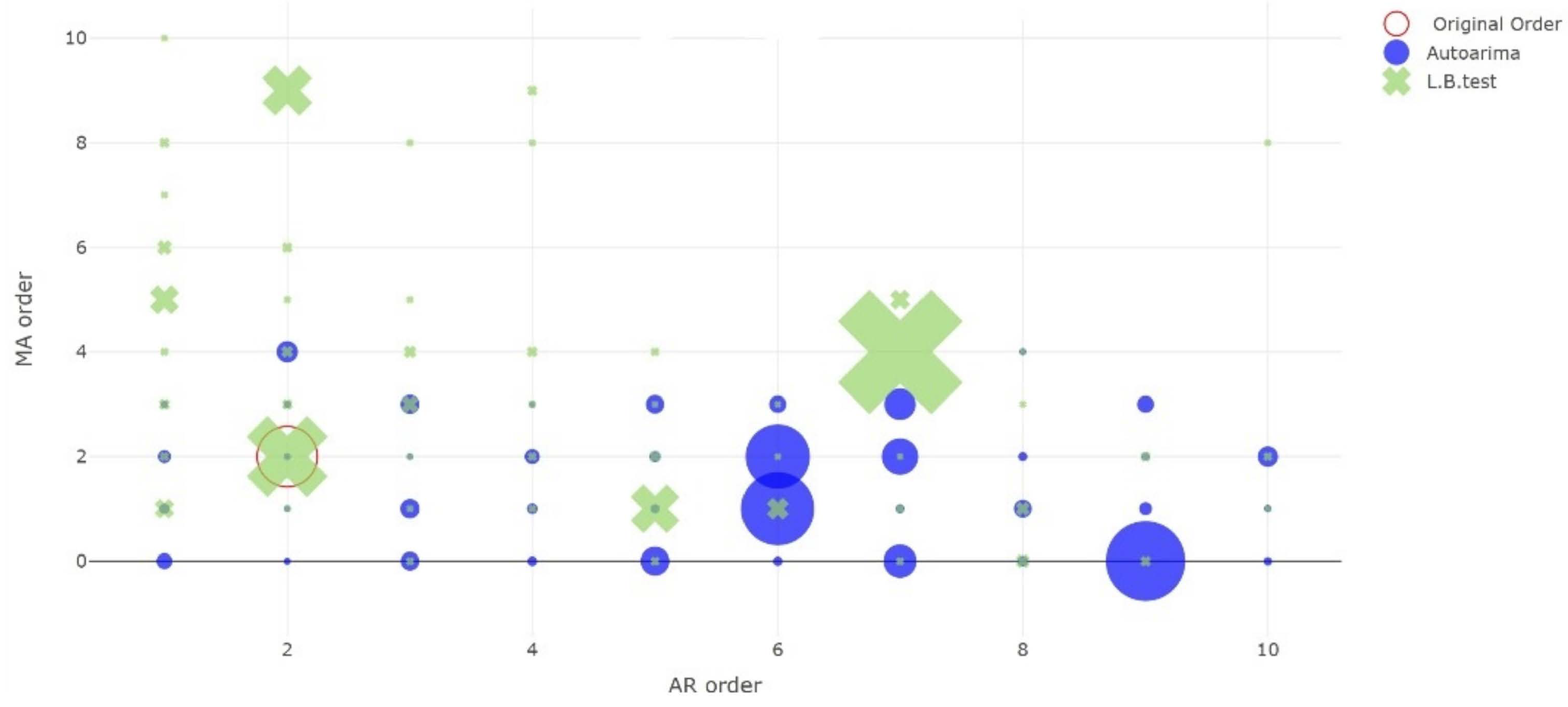
3.2. Impact of White Noise Empirical Characteristics on Models Selection

It should be noted that a fundamental principle in time series analysis and model building is that the extracted residuals should exhibit white noise behavior. In other words, time series models are typically constructed as a combination of a signal component and a white noise component. Based on this foundation, a key criterion for selecting a suitable model is that the extracted residuals should conform to the characteristics of white noise. Consequently, a variety of statistical tests have been developed to assess whether residuals meet this criterion, many of which rely on the sample ACF and PACF.

The gap between the practical characteristics of the sample ACF and PACF raises the question of whether it is possible to distinguish between residuals from different fitted models. For example, it questions whether, when the order of an ARMA model is not correctly identified, the residuals of the fitted model would exhibit a different autocorrelation structure compared to the original white noise (referring to the white noise in the true model from which the data were generated). More importantly, it also raises the question of whether models with incorrect orders result in lower forecasting accuracy.

To investigate the distinction between the residuals of fitted models and the original white noise, a simulation study is conducted. In this study, 5000 sample paths are generated by following ARMA(2,2) model:

$$\begin{array}{c}\hfill X_t=0.1X_{t-1}+0.89X_{t-2}+0.1Z_{t-2}-0.85Z_{t-1}+Z_t,Z_t\stackrel{iid}{\sim }N(0,1).\end{array}$$

The order of the model is selected based on two different methods. In the first method, the model is chosen based on the minimum Bayesian Information Criterion (BIC) using the auto.arima R-function from the package forecast [27,46]. In the second method, the selected model is the smallest model (with the lowest combined AR+MA order) for which the null hypothesis of the Ljung–Box test is not rejected at the 0.05 significance level. The rationale behind this second approach is that, according to theoretical assumptions, if the order of the fitted model is smaller than that of the true model, the residuals will retain some dependency. Therefore, the smallest model yielding uncorrelated residuals would likely be close to the true model.

Figure 5 presents the selected orders from 5000 simulated sample paths. As shown, the orders selected based on both methods exhibit substantial variation. The correct model order (AR = 2, MA = 2) is more frequently identified in models selected using the Ljung–Box test compared to those chosen based on the minimum BIC. Among the models selected by minimum BIC, the null hypothesis of the Ljung–Box test (at five lags) is rejected in 61.68% of the cases, and the correct order ARMA(2,2) is identified in only 26.68% of cases. For models selected using the Ljung–Box test, the null hypothesis is accepted in all cases (as per the selection criterion), with 51.4% of the models correctly identifying the ARMA(2,2) structure. This indicates that even models with incorrect AR and MA orders can still pass the Ljung–Box test for uncorrelated residuals. In line with these observations, Hassani’s $-\frac{1}{2}$ theorem is employed to further explore the limitations and power of the Ljung–Box test in detecting the correct order in ARMA models (for more information, see [3,8]).

Since it has been shown that some models selected based on the minimum BIC produce correlated residuals (i.e., residuals that are not white noise), a further question arises: do such models also exhibit lower forecasting accuracy?

Hassani and Silva’s Kolmogorov–Smirnov Predictive Accuracy (KSPA) test [1] is also employed to compare the residuals of the fitted model with the original white noise to test the following hypothesis.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{H}_0:F_{Original}\left(e^2\right)=F_{Fitted}\left(e^2\right)\hfill \\ H_1:F_{Original}\left(e^2\right)>F_{Fitted}\left(e^2\right)\hfill \end{array}\right.,\end{array}$$

where $F_{Original}\left(e^2\right)$ is the distribution function of the original squared white noise, and $F_{Fitted}\left(e^2\right)$ is the distribution function of squared residuals from the fitted model. Rejection of $H_0$ implies that the original model has better accuracy than the fitted model [1]. The P-values for the above KSPA test are presented in Figure 6.

As can be seen in Figure 6, the minimum BIC method provides fitted models that do not all have the same accuracy as the original model.

Figure 7 shows the out-of-sample forecasting performance, where 20% of the data are used for out-of-sample forecasting and 80% are used for training the model. As can be seen in Figure 7, the minimum BIC method provides fitted models that do not all have the same out-of-sample squared error as the original model. Figure 6 and Figure 7 both confirm that deviations from the original model negatively impact modeling and forecasting performance. It is evident that any departure from the theoretical assumptions affects the model-building process and, consequently, the forecasting accuracy.

The findings of this study highlight critical practical implications for practitioners in finance and economics, particularly in the selection and validation of time series models. In these fields, accurate model specification is paramount, as forecasting errors can have significant financial and policy implications. The results demonstrate that model selection criteria, such as the Bayesian Information Criterion (BIC) and the Ljung–Box test, can yield differing outcomes in identifying the true underlying model order. Notably, while the Ljung–Box test more frequently identifies the correct model, it also allows for models with incorrect orders to pass as valid, raising questions about the robustness of residual diagnostics in practical applications. This insight underscores the importance of supplementing traditional selection methods with additional tests, such as the KSPA test, to ensure residuals closely resemble the original white noise properties.

For financial and economic practitioners, this research emphasizes the potential risks of over-reliance on minimum BIC for model selection, as it may lead to residuals that exhibit autocorrelation and, consequently, reduce forecasting accuracy. Conversely, the Ljung–Box test, while more robust in identifying uncorrelated residuals, does not guarantee perfect model specification. Importantly, these findings suggest that even models with incorrect AR and MA orders can produce forecasting accuracy comparable to the true model. This has significant implications for real-world applications, where perfect model specification may be unattainable. Practitioners are encouraged to prioritize models that achieve uncorrelated residuals over strict adherence to theoretical model order, as such models often perform comparably in terms of forecasting accuracy. These results advocate for a balanced approach, integrating theoretical insights with practical diagnostics, to enhance the reliability of time series modeling in finance and economics.

4. Conclusions

This study provides a comprehensive analysis of white noise properties and their implications for time series modeling and signal processing. Through extensive simulation studies, we have demonstrated that the empirical characteristics of white noise, particularly in terms of sample ACF and PACF, can differ significantly from theoretical assumptions. These deviations impact model selection and diagnostic processes, as evidenced by the varied accuracy of models chosen using minimum BIC and the Ljung–Box test. Our findings underscore the importance of carefully assessing residuals and model diagnostics to ensure that fitted models adequately capture underlying processes. Moreover, this study highlights the limitations of relying solely on theoretical assumptions and emphasizes the need for practical validation in real-world applications. This work contributes valuable insights for researchers and practitioners, improving the robustness of time series analysis and enhancing the reliability of forecasting models in various fields.