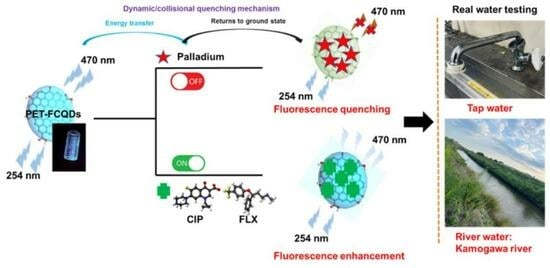
Green One-Step Synthesis and Characterization of Fluorescent Carbon Quantum Dots from PET Waste as a Dual-Mode Sensing Probe for Pd(II), Ciprofloxacin, and Fluoxetine via Fluorescence Quenching and Enhancement Mechanisms
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals and Preparation of Fluorescent Carbon Quantum Dots
2.2. Analytical Techniques
2.3. Thermal Stability Modeling
2.4. Quantum Chemical Analysis-Density Functional Theory
2.5. Fluorescence Sensing of Pd2+, FLX, and CIP
2.5.1. Linearity and Detection Limits
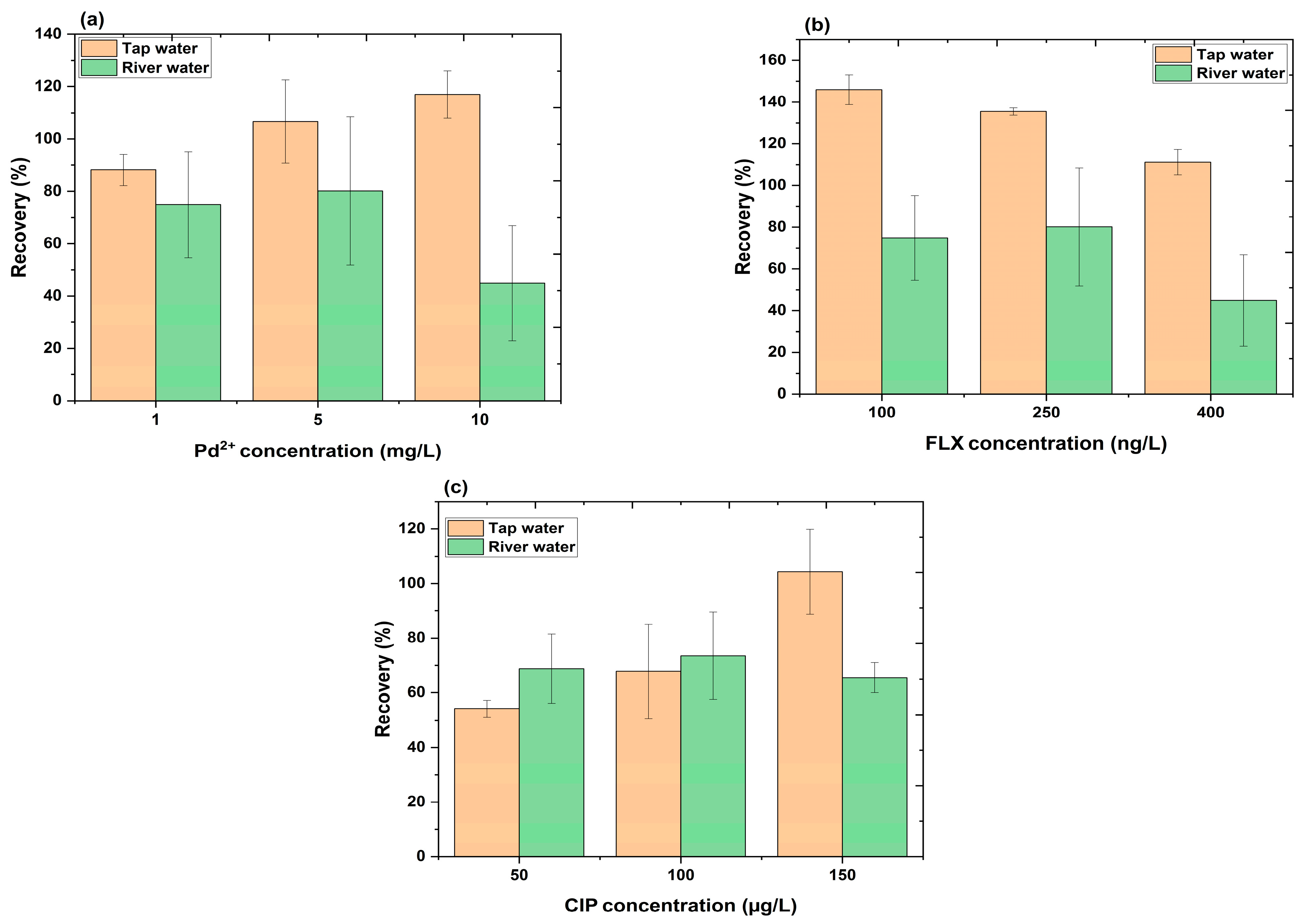
2.5.2. Analysis of Pd2+, FLX, and CIP in Real Water Samples
2.6. Statistical Analysis
3. Results and Discussion
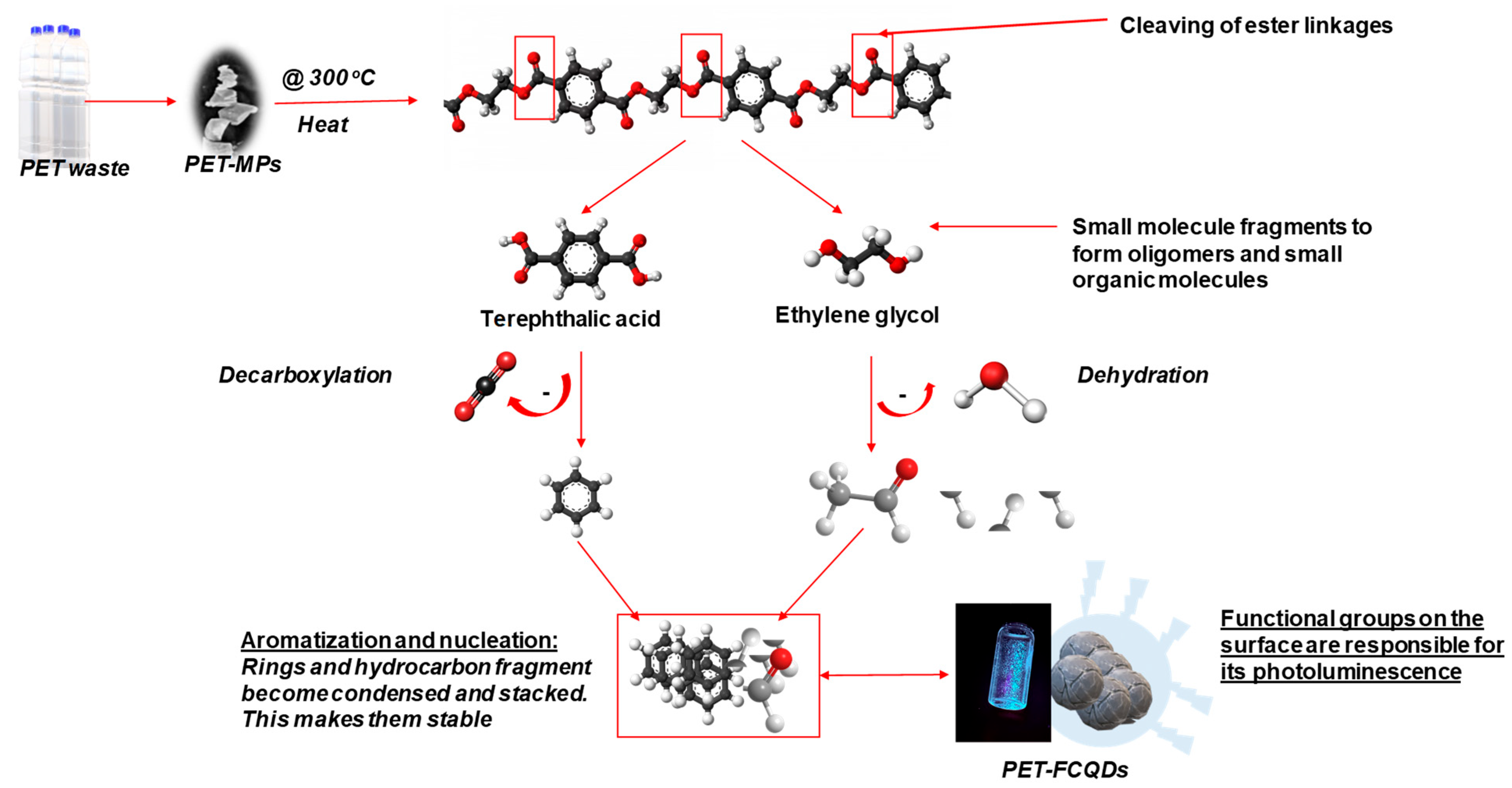
3.1. Quantum Yield of PET-FCQDs
3.2. Characterization of PET-FCQDs
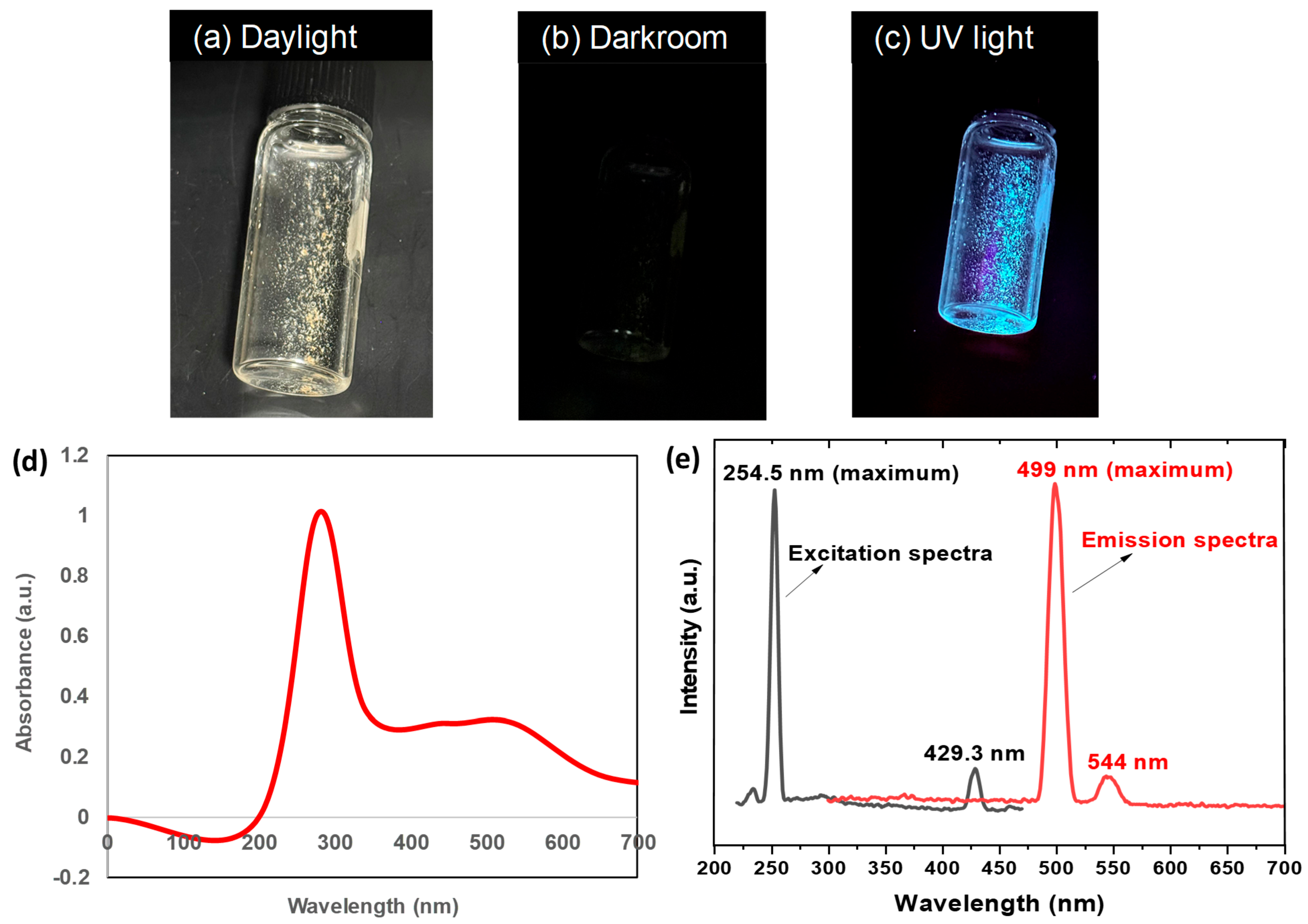
3.2.1. Optical and Fluorescence Analysis
3.2.2. Particle Size Analysis
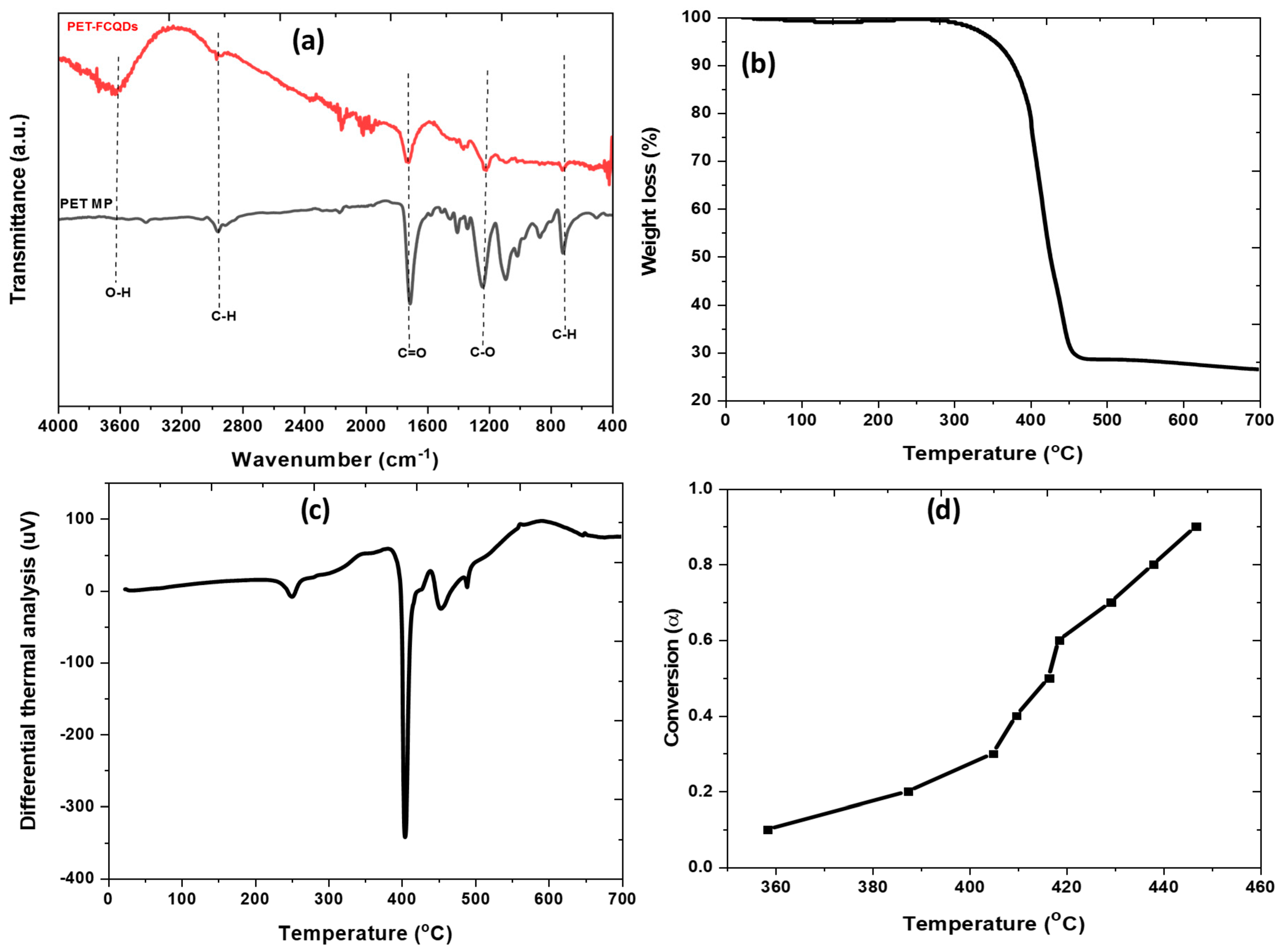
3.2.3. Surface Functional Group Analysis
3.2.4. TGA, DTA, and Conversion Factors
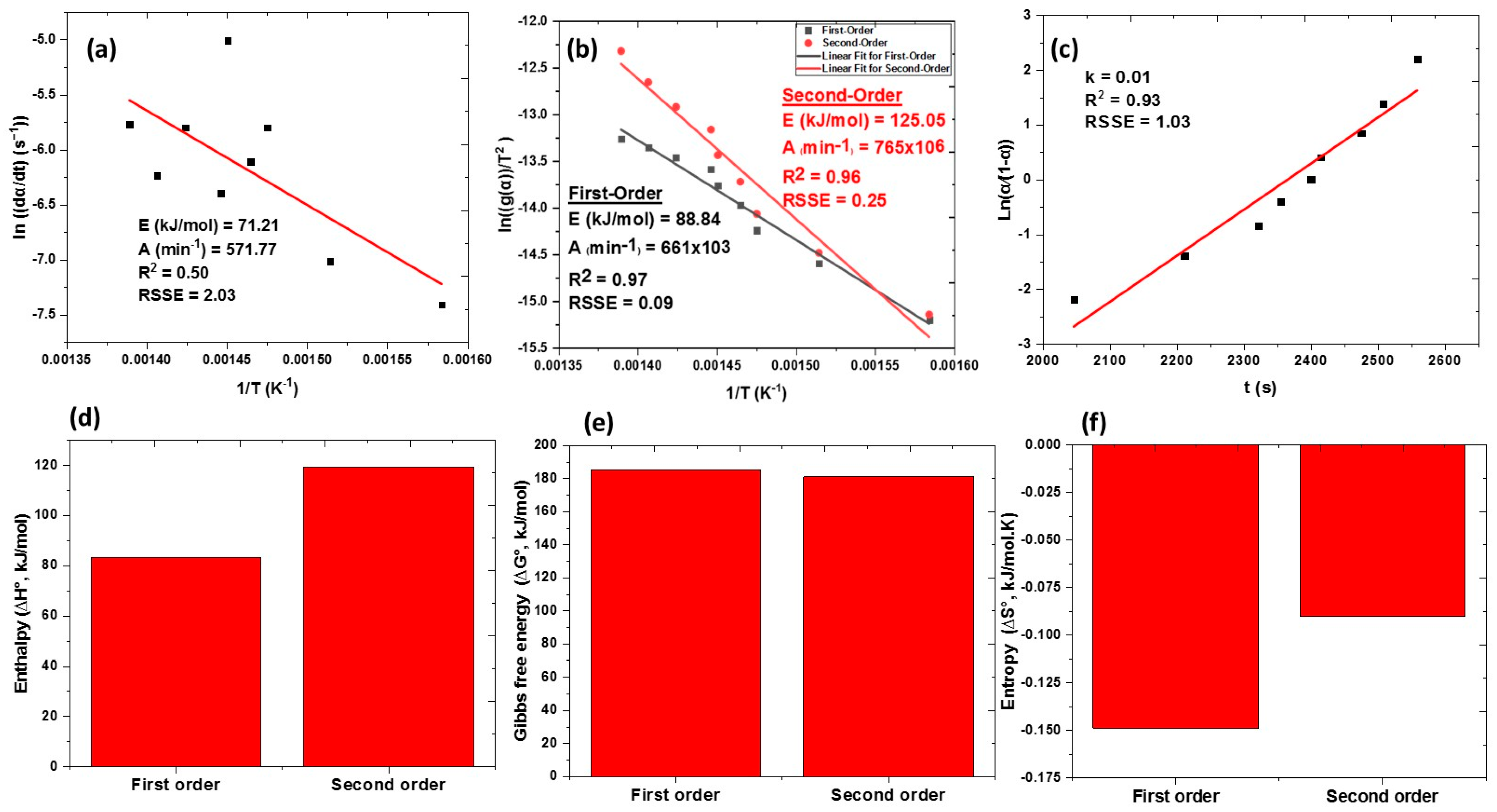
3.3. Kinetic and Thermodynamic Stability Modeling of PET-FCQDs
3.3.1. Kinetic Theory of Breakdown Reaction
3.3.2. Thermodynamic Theory of Breakdown Reaction
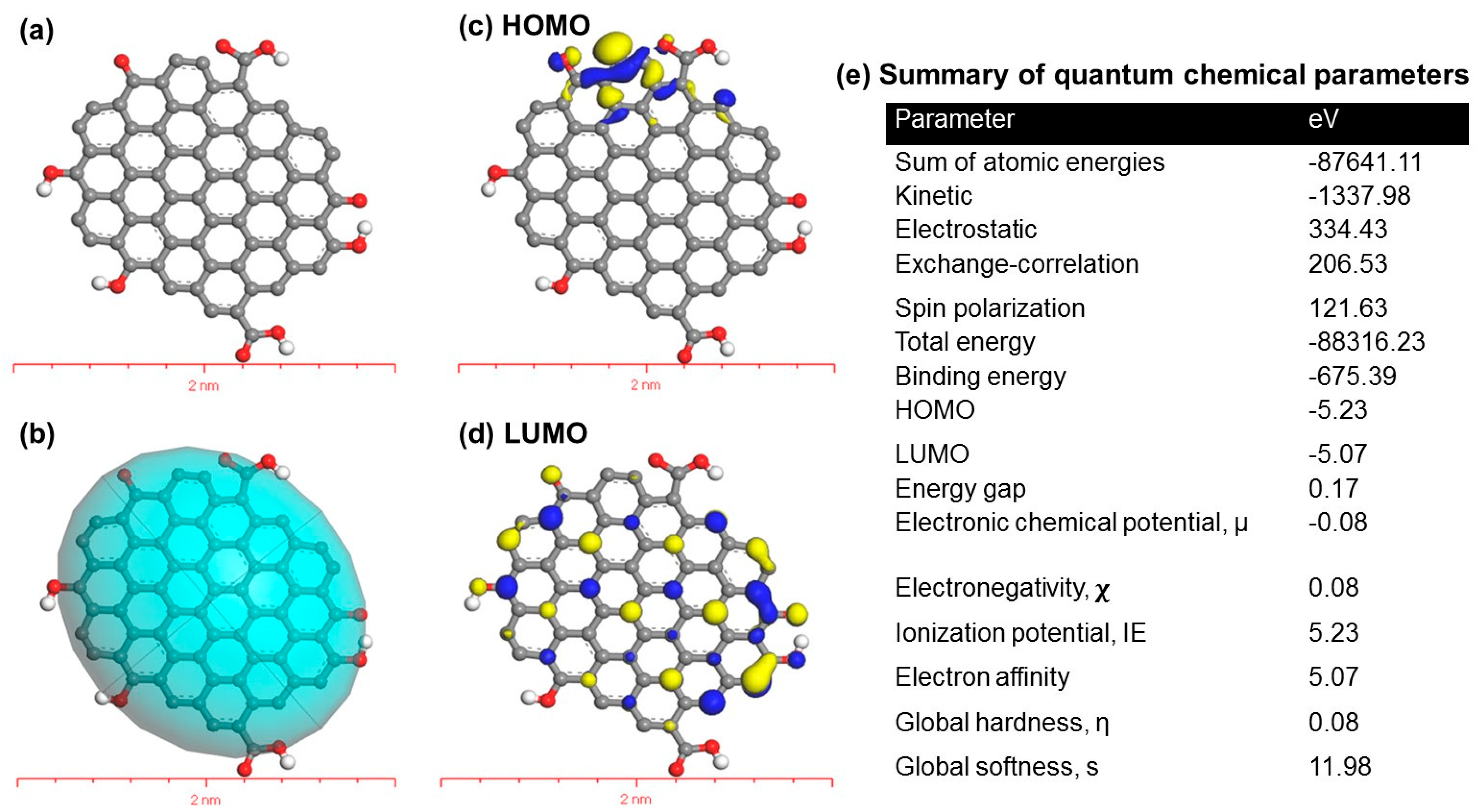
3.4. Quantum Chemical Properties of PET-FCQDs
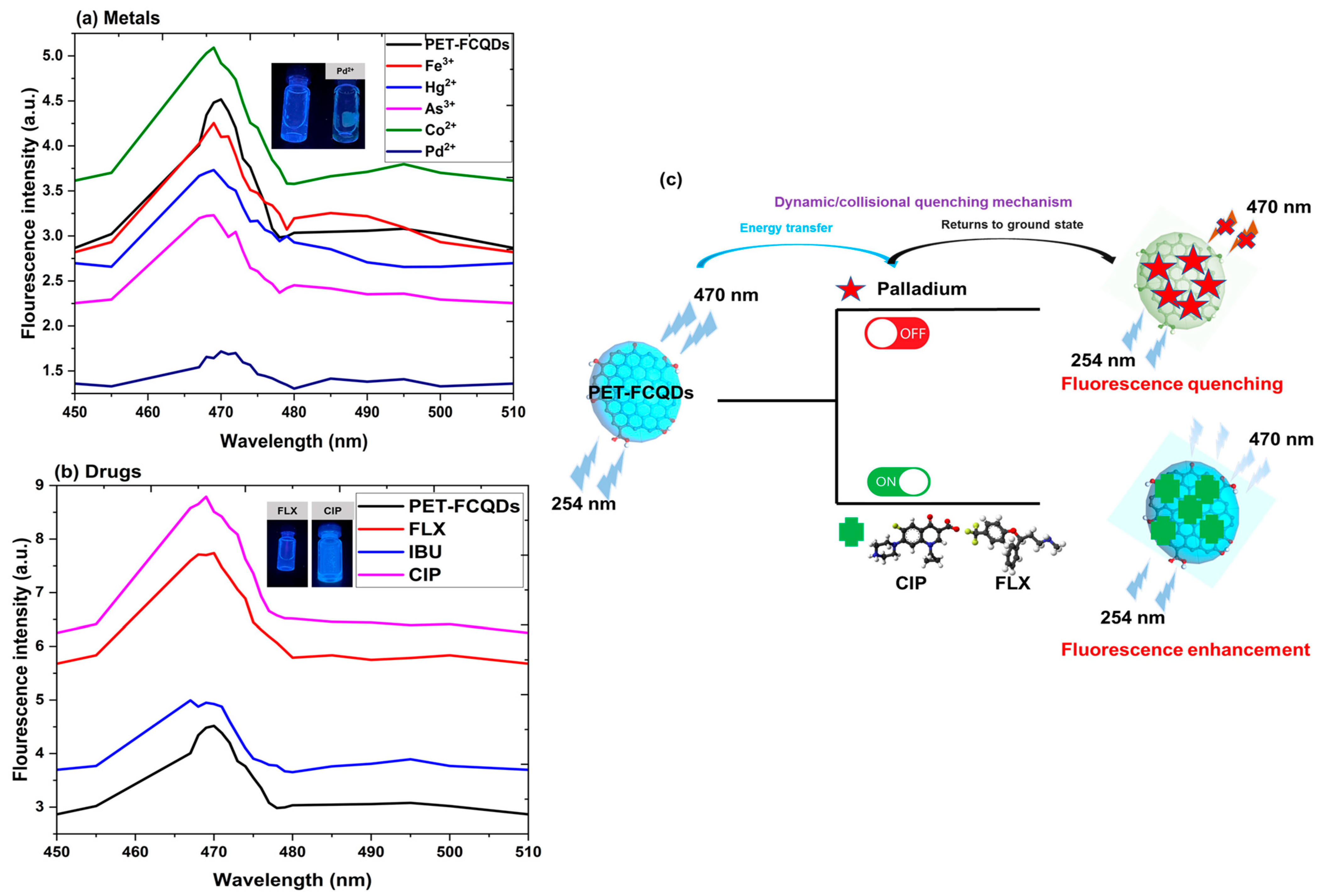
3.5. Fluorescence Assays of Pd2+, CIP, and FLX
Quenching Mechanism, Linearity, and Detection Limits
- Quenching mechanism
- Linearity

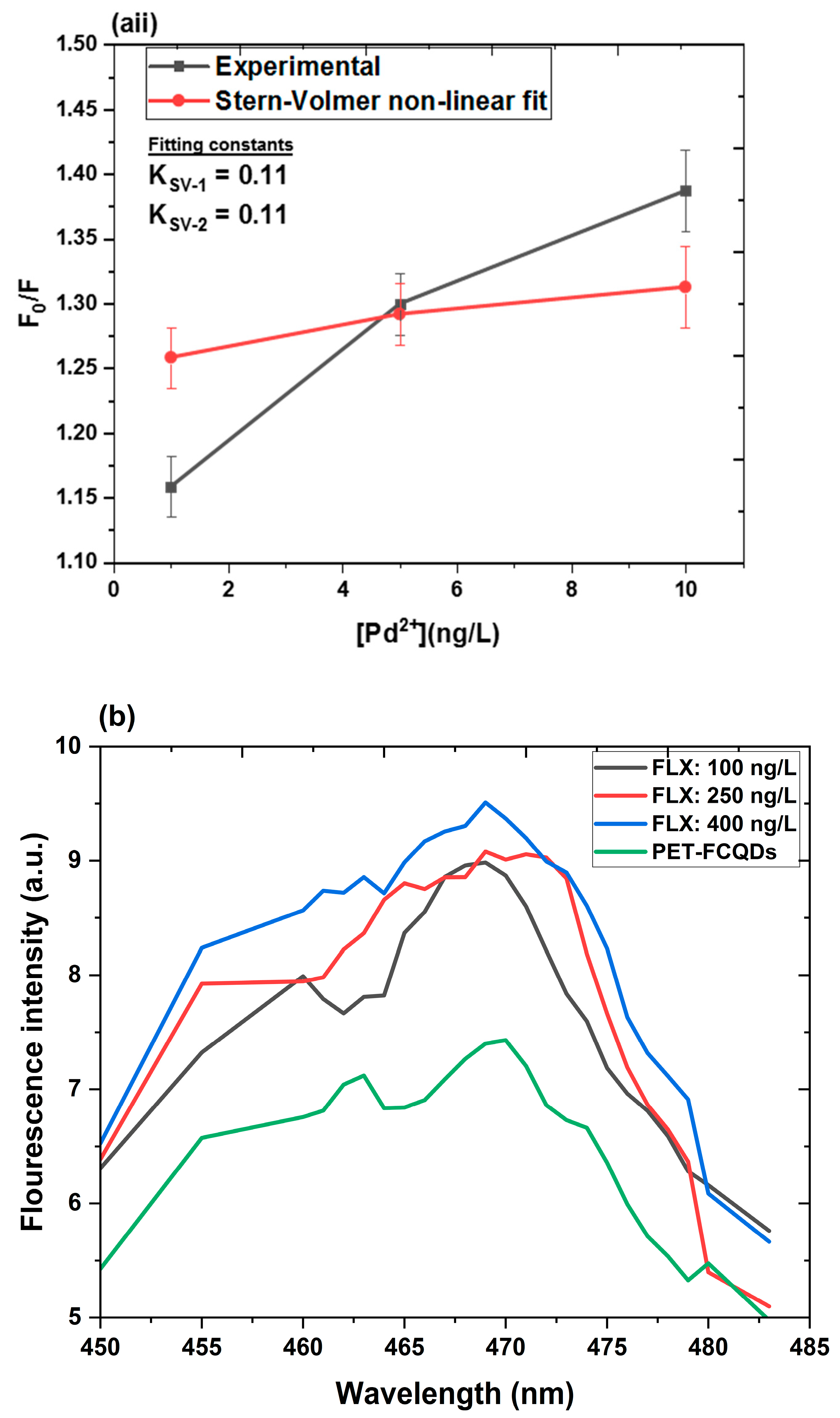

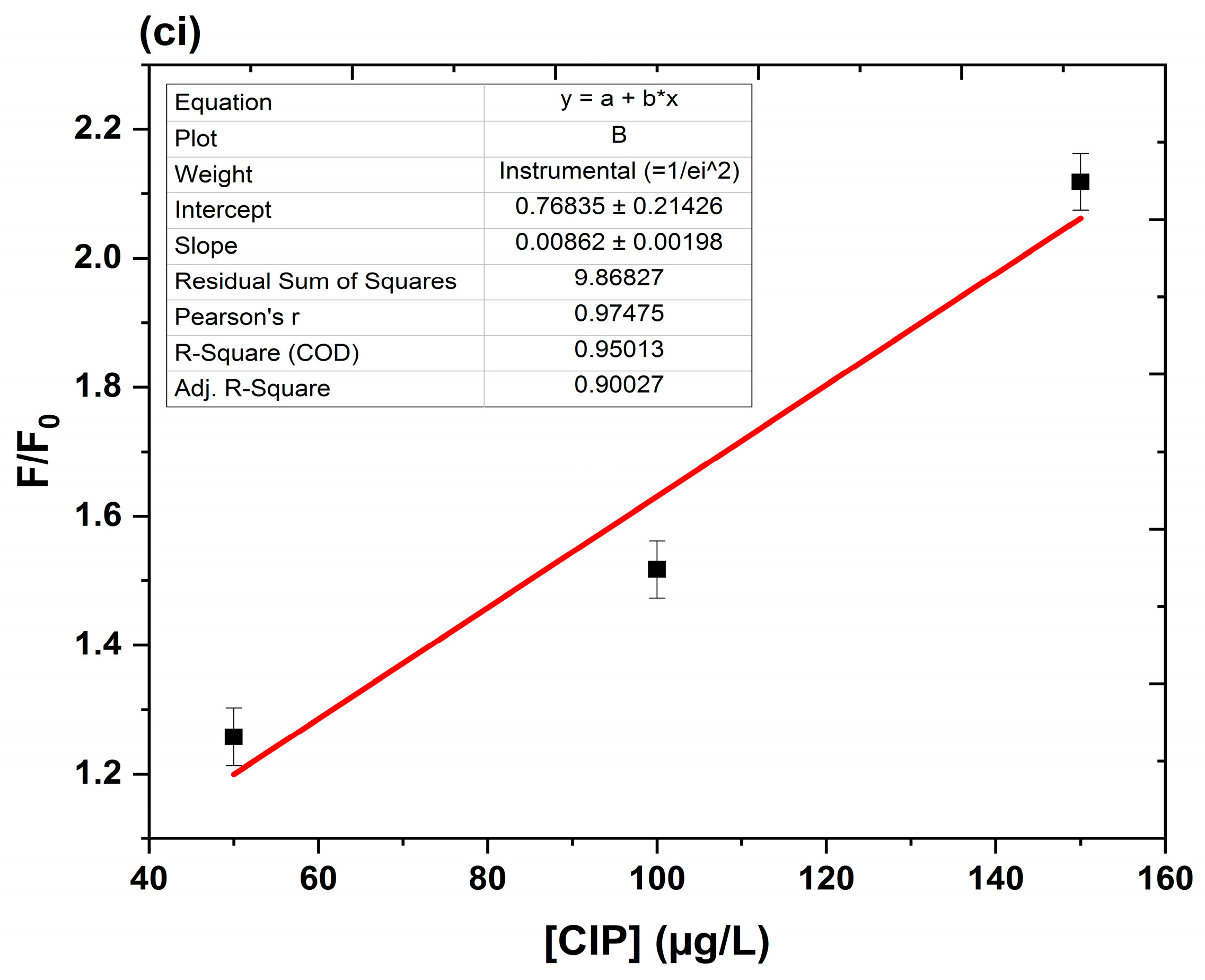
- Limits of detection (LOD) and quantification (LOQ)
3.6. Analytical Sensing Performance of PET-FCQDs in Real Water Samples
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chowdhury, T.; Wang, Q.; Enyoh, C.E. Degradation of Polyethylene Terephthalate Microplastics by Mineral Acids: Experimental, Molecular Modelling and Optimization Studies. J. Polym. Environ. 2022, 30, 5211–5227. [Google Scholar] [CrossRef]
- Hallaji, Z.; Bagheri, Z.; Ranjbar, B. The role of fluorescent carbon dots in the fate of plastic waste. J. Environ. Chem. Eng. 2023, 11, 110322. [Google Scholar] [CrossRef]
- Verla, A.W.; Enyoh, C.E.; Verla, E.N.; Nwarnorh, K.O. Microplastic–toxic chemical interaction: A review study on quantified levels, mechanism and implication. SN Appl. Sci. 2019, 1, 1400. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Ovuoraye, P.E.; Rabin, M.H.; Qingyue, W.; Tahir, M.A. Thermal degradation evaluation of polyethylene terephthalate microplastics: Insights from kinetics and machine learning algorithms using non-isoconversional TGA data. J. Environ. Chem. Eng. 2024, 12, 111909. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, Y.; Waterhouse, G.I.; Shi, R.; Wu, L.-Z.; Zhang, T. Photothermal recycling of waste polyolefin plastics into liquid fuels with high selectivity under solvent-free conditions. Nat. Commun. 2023, 14, 4242. [Google Scholar]
- Al-Tayeb, M.M.; Zeyad, A.M.; Dawoud, O.; Tayeh, B. Experimental and numerical investigations of the influence of partial replacement of coarse aggregates by plastic waste on the impact load. Int. J. Sustain. Eng. 2021, 14, 735–742. [Google Scholar] [CrossRef]
- Lamba, P.; Kaur, D.P.; Raj, S.; Sorout, J. Recycling/reusing plastic waste as construction material for sustainable development: A review. Environ. Sci. Pollut. Res. 2022, 29, 86156–86179. [Google Scholar]
- Feng, Z.; Adolfsson, K.H.; Xu, Y.; Fang, H.; Hakkarainen, M.; Wu, M. Carbon dot/polymer nanocomposites: From green synthesis to energy, environmental and biomedical applications. Sustain. Mater. Technol. 2021, 29, e00304. [Google Scholar] [CrossRef]
- Yaqoob, L.; Noor, T.; Iqbal, N. Conversion of plastic waste to carbon-based compounds and application in energy storage devices. ACS Omega 2022, 7, 13403–13435. [Google Scholar]
- Yuan, X.; Cho, M.K.; Lee, J.G.; Choi, S.W.; Lee, K.B. Upcycling of waste polyethylene terephthalate plastic bottles into porous carbon for CF4 adsorption. Environ. Pollut. 2020, 265 Pt A, 114868. [Google Scholar] [CrossRef]
- Damayanti; Wu, H.S. Strategic possibility routes of recycled PET. Polymers 2021, 13, 1475. [Google Scholar] [CrossRef] [PubMed]
- Bian, X.; Xia, G.; Xin, J.H.; Jiang, S.; Ma, K. Applications of waste polyethylene terephthalate (PET) based nanostructured materials: A review. Chemosphere 2023, 350, 141076. [Google Scholar] [PubMed]
- Aji, M.P.; Rahmawati, I.; Priyanto, A.; Marwoto, P. Novel one-step synthesis of solid-state carbonized polymer dots by heating at around melting point of polyethylene terephthalate (PET) bottle plastic waste. Environ. Nanotechnol. Monit. Manag. 2023, 20, 100892. [Google Scholar] [CrossRef]
- Zhou, X.; Deng, J.; Li, Z.; Cheng, Y.; Zhou, J.; Jiang, M.; Dong, W. One-Pot Synthesis of Multicolor Carbon Dots from PET Plastic Waste for White Light-Emitting Diodes. ACS Sustain. Chem. Eng. 2024, 12, 16592–16602. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Wang, Q. Box–Behnken design and machine learning optimization of PET fluorescent carbon quantum dots for removing fluoxetine and ciprofloxacin with molecular dynamics and docking studies as potential antidepressant and antibiotic. Sep. Purif. Technol. 2025, 362, 131975. [Google Scholar] [CrossRef]
- Soni, V.; Duc Anh, D.; Komal, P.; Rohit, K.; Pardeep, S.; Vinod Kumar, P.; Rangabhashiyam, S.; Archana, S.; Vishal, C.; Sourbh, T.; et al. Upcycling of polyethylene terephthalate (PET) plastic wastes into carbon-based nanomaterials: Current status and future perspectives. Eur. Polym. J. 2024, 215, 113249. [Google Scholar] [CrossRef]
- Umemura, T.; Sato, K.; Kusaka, Y.; Satoh, H. Chapter 26—Palladium Handbook on the Toxicology of Metals, 5th ed.; Volume II: Specific Metals; Academic Press: Cambridge, MA, USA, 2022; pp. 649–662. [Google Scholar] [CrossRef]
- Hosseini, M.J.; Jafarian, I.; Farahani, S.; Khodadadi, R.; Tagavi, S.H.; Naserzadeh, P.; Mohammadi-Bardbori, A.; Arghavanifard, N. New mechanistic approach of inorganic palladium toxicity: Impairment in mitochondrial electron transfer. Metallomics 2016, 8, 252–259. [Google Scholar]
- Laimou-Geraniou, M.; Heath, D.; Heath, E. Analytical methods for the determination of antidepressants, antipsychotics, benzodiazepines and their metabolites through wastewater-based epidemiology. Trends Environ. Anal. Chem. 2023, 37, e00192. [Google Scholar]
- Enyoh, C.E.; Wang, Q. Adsorption and toxicity characteristics of ciprofloxacin on differently prepared polyethylene terephthalate microplastics from both experimental and theoretical perspectives. J. Water Process Eng. 2023, 53, 103909. [Google Scholar] [CrossRef]
- Fergusson, K.N.; Tanner, J.L.; Brand, J.A.; Hannington, S.L.; Pettersen, A.K.; Sundin, J.; Saaristo, M.; Bertram, M.G.; Martin, J.M.; Wong, B.B.M. Effects of long-term fluoxetine exposure on morphology, but not behaviour or metabolic rate, in male guppies (Poecilia reticulata). Aquat. Toxicol. 2024, 276, 107082. [Google Scholar] [CrossRef]
- Fursdon, J.B.; Martin, J.M.; Bertram, M.G.; Lehtonen, T.K.; Wong, B.B.M. The pharmaceutical pollutant fluoxetine alters reproductive behaviour in a fish independent of predation risk. Sci. Total Environ. 2019, 650 Pt 1, 642–652. [Google Scholar] [CrossRef] [PubMed]
- Tymoshuk, O.S.; Fedyshyn, O.S.; Oleksiv, L.V.; Rydchuk, P.V.; Matiychuk, V.S. Spectrophotometric Determination of Palladium(II) Ions Using a New Reagent: 4-(N’-(4-Imino-2-oxo-thiazolidine-5-ylidene)-hydrazino)-benzoic Acid (p-ITYBA). J. Chem. 2020, 2020, 8141853. [Google Scholar] [CrossRef]
- Chowdhury, T.; Wang, Q. Study on Thermal Degradation Processes of Polyethylene Terephthalate Microplastics Using the Kinetics and Artificial Neural Networks Models. Processes 2023, 11, 496. [Google Scholar] [CrossRef]
- Coats, A.W.; Redfern, J.P. Kinetic Parameters from Thermogravimetric Data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Snee, P.T. DFT Calculations of InP Quantum Dots: Model Chemistries, Surface Passivation, and Open-Shell Singlet Ground States. J. Phys. Chem. C 2021, 125, 11765–11772. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Toochukwu, M.; Wang, Q.; Islam, M.R. In Silico Screening of Active Compounds in Garri for the Inhibition of Key Enzymes Linked to Diabetes Mellitus. ACS Food Sci. Technol. 2022, 2, 1597–1611. [Google Scholar] [CrossRef]
- Parr, R.G.; Pearson, R.G. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Pearson, R.G. Absolute Electronegativity and Hardness: Application to Inorganic Chemistry. Inorg. Chem. 1988, 27, 734–740. [Google Scholar] [CrossRef]
- Wang, B.; Lu, S. The light of carbon dots: From mechanism to applications. Matter 2022, 5, 110–149. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, A. Carbon quantum dots: Synthesis, properties and applications. J. Mater. Chem. C 2014, 2, 6921–6939. [Google Scholar] [CrossRef]
- Brouwer, A. Standards for photoluminescence quantum yield measurements in solution (IUPAC Technical Report). Pure Appl. Chem. 2011, 83, 2213–2228. [Google Scholar] [CrossRef]
- Chan, K.; Zinchenko, A. Aminolysis-assisted hydrothermal conversion of waste PET plastic to N-doped carbon dots with markedly enhanced fluorescence. J. Environ. Chem. Eng. 2022, 10, 107749. [Google Scholar] [CrossRef]
- Cruz, M.I.S.D.; Thongsai, N.; de Luna, M.D.G. Preparation of highly photoluminescent carbon dots from polyurethane: Optimization using response surface methodology and selective detection of silver (I) ion. Colloids Surf. A Physicochem. Eng. Asp. 2019, 568, 184–194. [Google Scholar]
- Wu, Y.; Wang, R.; Xie, W.; Ma, G.; Zhang, A.; Liu, B.; Huang, H.; Gao, L.; Qu, M.; Wei, Y.; et al. Solvent-thermal preparation of sulfur and nitrogen-doped carbon dots with PET waste as precursor and application in light-blocking film. J. Nanoparticle Res. 2023, 25, 18. [Google Scholar]
- Chaudhary, S.; Kumari, M.; Chauhan, P.; Ram Chaudhary, G. Upcycling of plastic waste into fluorescent carbon dots: An environmentally viable transformation to biocompatible C-dots with potential prospective in analytical applications. Waste Manag. 2020, 120, 675–686. [Google Scholar] [CrossRef]
- Egorova, M.N.; Tomskaya, A.E.; Kapitonov, A.N.; Smagulova, S.A.; Alekseev, A.A. Investigation of luminescence quantum yields of carbon dots synthesized from ethylene glycol, citric acid and berries. J. Phys. Conf. Ser. 2018, 1124, 081002. [Google Scholar] [CrossRef]
- Karami, M.H.; Abdouss, M.; Rahdar, A.; Pandey, S. Graphene quantum dots: Background, synthesis methods, and applications as nanocarrier in drug delivery and cancer treatment: An updated review. Inorg. Chem. Commun. 2024, 161, 112032. [Google Scholar] [CrossRef]
- Aji, M.P.; Wati, A.L.; Priyanto, A.; Karunawan, J.; Nuryadin, B.W.; Wibowo, E.; Marwoto, P.; Sulhadi. Polymer carbon dots from plastics waste upcycling. Environ. Nanotechnol. Monit. Manag. 2018, 9, 136–140. [Google Scholar] [CrossRef]
- Jayaweera, S.; Yin, K.; Hu, X.; Ng, W.J. Fluorescent N/Al Co-Doped Carbon Dots from Cellulose Biomass for Sensitive Detection of Manganese (VII). J. Fluoresc. 2019, 29, 1291–1300. [Google Scholar] [CrossRef]
- Lu, S.; Sui, L.; Liu, J.; Zhu, S.; Chen, A.; Jin, M.; Yang, B. Near-infrared photoluminescent polymer carbon nanodots with two-Photon fluorescence. Adv. Mater. 2017, 29, 1604436. [Google Scholar]
- Deka, M.J.; Chowdhury, D. Chiral carbon dots and their effect on the optical properties of photosensitizers. RSC Adv. 2017, 7, 53057–53063. [Google Scholar]
- László, K.; Bóta, A.; Dékány, I. Effect of heat treatment on synthetic carbon precursors. Carbon 2003, 41, 1205–1214. [Google Scholar] [CrossRef]
- Kaur, P.; Verma, G. Converting fruit waste into carbon dots for bioimaging applications. Mater. Today Sustain. 2022, 18, 100137. [Google Scholar] [CrossRef]
- Sherka, G.T.; Berry, H.D. Insight into impact of size and shape on optoelectronic properties of InX (X = As, Sb, and P) semiconductor nanoparticles: A theoretical study. Front. Phys. 2024, 12, 1447997. [Google Scholar] [CrossRef]
- Pereira, A.P.; da Silva, M.H.P.; Júnior, É.P.L.; Paula, A.D.S.; Tommasini, F.J. Processing and Characterization of PET Composites Reinforced With Geopolymer Concrete Waste. Mater. Res. 2017, 20, 411–420. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Wang, Q. Combined experimental and molecular dynamics removal processes of contaminant phenol from simulated wastewater by polyethylene terephthalate microplastics. Environ. Technol. 2022, 45, 1183–1202. [Google Scholar] [CrossRef]
- Tao, S.; Song, Y.; Zhu, S.; Shao, J.; Yang, B. A new type of polymer carbon dots with high quantum yield: From synthesis to investigation on fluorescence mechanism. J. Polym. 2017, 116, 472–478. [Google Scholar]
- Gao, Z.; Wang, L.; Su, R.; Huang, R.; Qi, W.; He, Z. A carbon dot-based “off-on” fluorescent probe for highly selective and sensitive detection of phytic acid. Biosens. Bioelectron. 2015, 70, 232–238. [Google Scholar] [CrossRef]
- Sun, H.; Wu, L.; Gao, N.; Ren, J.; Qu, X. Improvement of photoluminescence of graphene quantum dots with a biocompatible photochemical reduction pathway and its bioimaging application. ACS Appl. Mater. Interfaces 2013, 5, 1174–1179. [Google Scholar]
- Mmelesi, O.K.; Mguni, L.L.; Li, F.-t.; Nkosi, B.; Liu, X. Recent development in fluorescent carbon quantum dots-based photocatalysts for water and energy applications. Mater. Sci. Semicond. Process. 2024, 181, 108661. [Google Scholar] [CrossRef]
- Das, S.; Mondal, S.; Ghosh, D. Carbon quantum dots in bioimaging and biomedicines. Front. Bioeng. Biotechnol. 2024, 11, 1333752. [Google Scholar] [CrossRef]
- Uchimiya, M.; Ohno, T.; He, Z. Pyrolysis temperature-dependent release of dissolved organic carbon from plant, manure, and biorefinery wastes. J. Anal. Appl. Pyrolysis 2013, 104, 84–94. [Google Scholar] [CrossRef]
- Fedunik-Hofman, L.; Bayon, A.; Donne, S.W. Kinetics of Solid-Gas Reactions and Their Application to Carbonate Looping Systems. Energies 2019, 12, 2981. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Maduka, T.O.; Suzuki, M.; Lu, S.; Wang, Q. Thermoanalytical and Kinetic Studies for the Thermal Stability of Emerging Pharmaceutical Pollutants Under Different Heating Rates. J. Xenobiotics 2024, 14, 1784–1806. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.E. The Prout-Tompkins rate equation in solid-state kinetics. Thermochim. Acta 1997, 300, 93–106. [Google Scholar] [CrossRef]
- Muraleedharan, K.; Kannan, M.P.; Gangadevi, T. Effects of dopants on the isothermal decomposition kinetics of potassium metaperiodate. J. Serb. Chem. Soc. 2011, 76, 1129–1138. [Google Scholar] [CrossRef]
- Mishra, R.K.; Sahoo, A.; Mohanty, K. Pyrolysis kinetics and synergistic effect in co-pyrolysis of Samanea saman seeds and polyethylene terephthalate using thermogravimetric analyser. Bioresour. Technol. 2019, 289, 121608. [Google Scholar] [CrossRef]
- Das, P.; Tiwari, P. Thermal degradation kinetics of plastics and model selection. Thermochim. Acta 2017, 654, 191–202. [Google Scholar] [CrossRef]
- Chatzieleftheriou, S.; Adendorff, M.R.; Lagaros, N.D. Generalized Potential Energy Finite Elements for Modeling Molecular Nanostructures. J. Chem. Inf. Model. 2016, 56, 1963–1978. [Google Scholar] [CrossRef]
- Benjamin, I.; Ekpong, B.O.; Abdullah, H.Y.; Agwamba, E.C.; Anyambula, I.A.; Adeyinka Adedapo, S.; Louis, H. Surface modification of transition metals (TM: Mn, Fe, Co) decorated Pt-doped carbon quantum dots (Pt@CQDs) nanostructure as nonenzymatic sensors for nitrotyrosine (a biomarker for Alzheimer): Perspective from density functional theory. Mater. Sci. Semicond. Process. 2024, 174, 108245. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Duru, C.E.; Prosper, E.; Wang, Q. Evaluation of Nanoplastics Toxicity to the Human Placenta in Systems. J. Hazard. Mater. 2023, 446, 130600. [Google Scholar] [CrossRef] [PubMed]
- Muhida, R.; Rahman, M.M.; Chowdhury, M.S.H.; Setiyanto, H.; Zainuddin, H.; Azmi, B.Z.; Kasai, H. Density Functional Study of Spin Polarization on a Carbon Material with a Hexagonal Structure Induced by Iron Atoms. J. Comput. Theor. Nanosci. 2014, 11, 58–61. [Google Scholar] [CrossRef]
- Enyoh, C.E.; Wang, Q.; Senlin, L. Optimizing the Efficient Removal of Ciprofloxacin from Aqueous Solutions by Polyethylene Terephthalate Microplastics using Multivariate Statistical Approach. Chem. Eng. Sci. 2023, 278, 118917. [Google Scholar] [CrossRef]
- Wei, K.; Liao, F.; Huang, H.; Shao, M.; Lin, H.; Liu, Y.; Kang, Z. Simple Semiempirical Method for the Location Determination of HOMO and LUMO of Carbon Dots. J. Phys. Chem. C 2021, 125, 7451–7457. [Google Scholar] [CrossRef]
- Vercelli, B. The Role of Carbon Quantum Dots in Organic Photovoltaics: A Short Overview. Coatings 2021, 11, 232. [Google Scholar] [CrossRef]
- Adkins, E.M.; Miller, J.H. Extinction measurements for optical band gap determination of soot in a series of nitrogen-diluted ethylene/air non-premixed flames. Phys. Chem. Chem. Phys. 2015, 17, 2686–2695. [Google Scholar] [CrossRef]
- Silva, T.A.; Stefano, J.S.; Janegitz, B.C. Sensing Materials: Nanomaterials. Encycl. Sens. Biosens. 2023, 2, 212–230. [Google Scholar] [CrossRef]
- Spanedda, N.; McLaughlin, P.F.; Beyer, J.J.; Chakraborty, A. Investigation of Ionization Potential in Quantum Dots Using the Stratified Stochastic Enumeration of Molecular Orbitals Method. J. Chem. Theory Comput. 2022, 18, 5920–5935. [Google Scholar] [CrossRef]
- Xu, D.; Li, M.; Xu, H.; Yu, J.; Wang, Y.; Zhang, P. N,S-doped carbon quantum dots as a fluorescent probe for palladium(II) ions via Förster resonance energy transfer. Results Chem. 2021, 3, 100179. [Google Scholar] [CrossRef]
- Zhang, D.-H.; Yang, L.; Li, N.; Su, K.; Li, L.; Li, C.-Y. Detection of ciprofloxacin and pH by carbon dots and rapid, visual sensing analysis. Food Chem. 2024, 459, 140313. [Google Scholar] [CrossRef]
- Joshi, D.J.; Jha, S.; Malek, N.I.; Park, T.J.; Kailasa, S.K. Facile synthesis of Eu3+-doped niobium carbide MXene quantum dots for parallel detection of hypoxanthine and fluoxetine via fluorescence quenching and enhancement mechanisms. Microchim. Acta 2024, 191, 621. [Google Scholar] [CrossRef]
- Hua, J.; Jiao, Y.; Wang, M.; Yang, Y. Determination of norfloxacin or ciprofloxacin by carbon dots fluorescence enhancement using magnetic nanoparticles as adsorbent. Microchim. Acta 2018, 185, 137. [Google Scholar] [CrossRef] [PubMed]
- Tanwar, A.S.; Parui, R.; Garai, R.; Chanu, M.A.; Iyer, P.K. Dual “Static and Dynamic” Fluorescence Quenching Mechanisms Based Detection of TNT via a Cationic Conjugated Polymer. ACS Meas. Sci. Au 2021, 2, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Gehlen, M.H. The Centenary of the Stern-Volmer Equation of Fluorescence Quenching: From the single line plot to the SV quenching map. J. Photochem. Photobiol. C Photochem. Rev. 2019, 42, 100338. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, Y.D.; Zhi, S.M.; Yang, X.Y.; Yao, C. Green synthesized fluorescent carbon dots from momordica charantia for selective and sensitive detectionof Pd2+ and Fe3+. ChemistrySelect 2021, 6, 123–130. [Google Scholar] [CrossRef]
- Laghari, S.; Khuhawar, M.Y. Colorimetric detection of fluoxetine using citrate-capped silver nanoparticles. SN Appl. Sci. 2020, 2, 581. [Google Scholar] [CrossRef]
- Liu, B.; Huang, Y.; Shen, Q.; Zhu, X.; Hao, Y.; Qu, P.; Xu, M. Turn-on fluorescence detection of ciprofloxacin in tablets based on lanthanide coordination polymer nanoparticles. RSC Adv. 2016, 6, 100743–100747. [Google Scholar] [CrossRef]
- Kawde, A.N.; Aziz, M.A.; Odewunmi, N.; Hassan, N.; AlSharaa, A. Electroanalytical Determination of Antibacterial Ciprofloxacin in Pure Form and in Drug Formulations. Arab. J. Sci. Eng. 2014, 39, 131–138. [Google Scholar] [CrossRef]
- Muhammad, M.; Behisht, A.; Faiz, A.; Izaz, A.; Hafeez, U. Mn-dopped ZnS quantum dots as sensitive sensor for determination of ciprofloxacin in pharmaceutical and biological samples. J. Chil. Chem. Soc. 2021, 66, 5130–5135. [Google Scholar] [CrossRef]
- Awual, M.R.; Hasan, M.M.; Znad, H. Organic–inorganic based nano-conjugate adsorbent for selective palladium(II) detection, separation and recovery. Chem. Eng. J. 2015, 259, 611–619. [Google Scholar] [CrossRef]
- Pawar, S.; Kaja, S.; Nag, A. Red-emitting carbon dots as a dual sensor for In3+ and Pd2+ in water. ACS Omega 2020, 5, 8362–8372. [Google Scholar]


| Probe | Method | Linear Range | LOD | Reference |
|---|---|---|---|---|
| Pd2+ | ||||
| Nano-conjugate adsorbent | Colorimetric | 2.10–72.10 mg/L | 0.14 mg/L | [82] |
| nitrogen-doped red-emitting carbon dots (NRCDs) | Fluorescence | 0–3.51 mg/L | 6.4 × 10−3 mg/L | [83] |
| Blue-emissive CQDs | Fluorescence | 0–34.5 mg/L | 37 × 10−3 mg/L | [77] |
| Green-light-emitting nitrogen-sulfur-doped carbon quantum dots (N,S-GCDs) | Fluorescence | 0–0.15 mg/L | 12.7 × 10−3 mg/L | [70] |
| PET-FCQDs | Fluorescence | 1–10 mg/L | 1.26 mg/L | Present study |
| FLX | ||||
| citrate-capped silver nanoparticles (CIT-AgNPs) | Colorimetry | 6.47–32.3 µM | 0.582 µM (180 × 103 ng/L) | [78] |
| Eu3+-doped niobium carbide MXene quantum dots (Eu3+-Nb2C MQDs) | Fluorescence | 125–100 × 103 ng/L | 4.64 ng/L | [72] |
| PET-FCQDs | Fluorescence | 100–400 ng/L | 134 ng/L | Present study |
| CIP | ||||
| Lanthanide coordination polymer nanoparticle (LCPNP) | Fluorescence | 1.0 and 40 μM | 780 nM (258.453 µg/L) | [79] |
| Mn-doped ZnS quantum dots | Fluorescence | 500–1000 µg/L | 150 µg/L | [81] |
| MPA-CdS quantum dots | Fluorescence | 130–15,000 µg/L | 4 µg/L | [80] |
| PET-FCQDs | Fluorescence | 50–150 µg/L | 3.3 µg/L | Present study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enyoh, C.E.; Wang, Q.; Wang, W.; Suzuki, M.; Masuda, G.; Nakajima, D.; Lu, S. Green One-Step Synthesis and Characterization of Fluorescent Carbon Quantum Dots from PET Waste as a Dual-Mode Sensing Probe for Pd(II), Ciprofloxacin, and Fluoxetine via Fluorescence Quenching and Enhancement Mechanisms. Surfaces 2025, 8, 24. https://doi.org/10.3390/surfaces8020024
Enyoh CE, Wang Q, Wang W, Suzuki M, Masuda G, Nakajima D, Lu S. Green One-Step Synthesis and Characterization of Fluorescent Carbon Quantum Dots from PET Waste as a Dual-Mode Sensing Probe for Pd(II), Ciprofloxacin, and Fluoxetine via Fluorescence Quenching and Enhancement Mechanisms. Surfaces. 2025; 8(2):24. https://doi.org/10.3390/surfaces8020024
Chicago/Turabian StyleEnyoh, Christian Ebere, Qingyue Wang, Weiqian Wang, Miho Suzuki, Go Masuda, Daisuke Nakajima, and Senlin Lu. 2025. "Green One-Step Synthesis and Characterization of Fluorescent Carbon Quantum Dots from PET Waste as a Dual-Mode Sensing Probe for Pd(II), Ciprofloxacin, and Fluoxetine via Fluorescence Quenching and Enhancement Mechanisms" Surfaces 8, no. 2: 24. https://doi.org/10.3390/surfaces8020024
APA StyleEnyoh, C. E., Wang, Q., Wang, W., Suzuki, M., Masuda, G., Nakajima, D., & Lu, S. (2025). Green One-Step Synthesis and Characterization of Fluorescent Carbon Quantum Dots from PET Waste as a Dual-Mode Sensing Probe for Pd(II), Ciprofloxacin, and Fluoxetine via Fluorescence Quenching and Enhancement Mechanisms. Surfaces, 8(2), 24. https://doi.org/10.3390/surfaces8020024