An Improved Rate-Transient Analysis Model of Multi-Fractured Horizontal Wells with Non-Uniform Hydraulic Fracture Properties
Abstract
:1. Introduction
2. RTA Model
2.1. Physical Model
- (1)
- An MFHW is located at a circular-bounded formation with constant thickness (h), porosity (ϕ), total compressibility (Ct), and initial reservoir pressure ().
- (2)
- The horizontal well, with the length of L, is non-uniformly intercepted by multiple fractures. The formation is fully penetrated by hydraulic fractures with half-length (xf), height (hf) and width (wf).
- (3)
- The formation is considered to be anisotropic and homogeneous. kh and kv represent for the permeability in horizontal and vertical direction respectively.
- (4)
- The formation is saturated with single-phase fluid, and total rates (q) are from fractures in the tight reservoir.
- (5)
- The effects of capillary pressure and gravity can be ignored.
2.2. Mathematical Model
2.3. Solution Approach
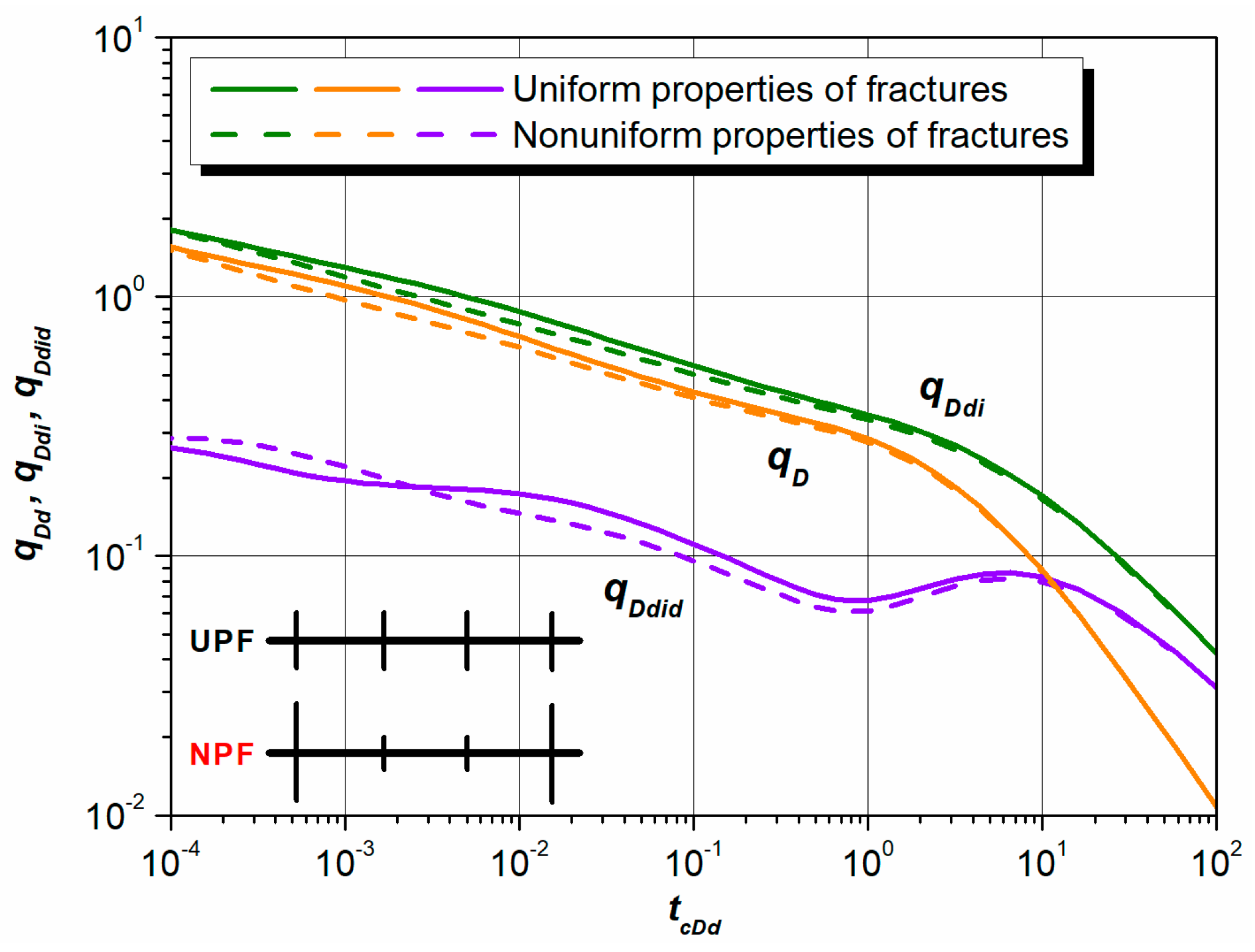
3. Combined Type Curve
4. Sensitivity Analysis
4.1. Fracture Half-Length
4.2. Production of Hydraulic Fractures
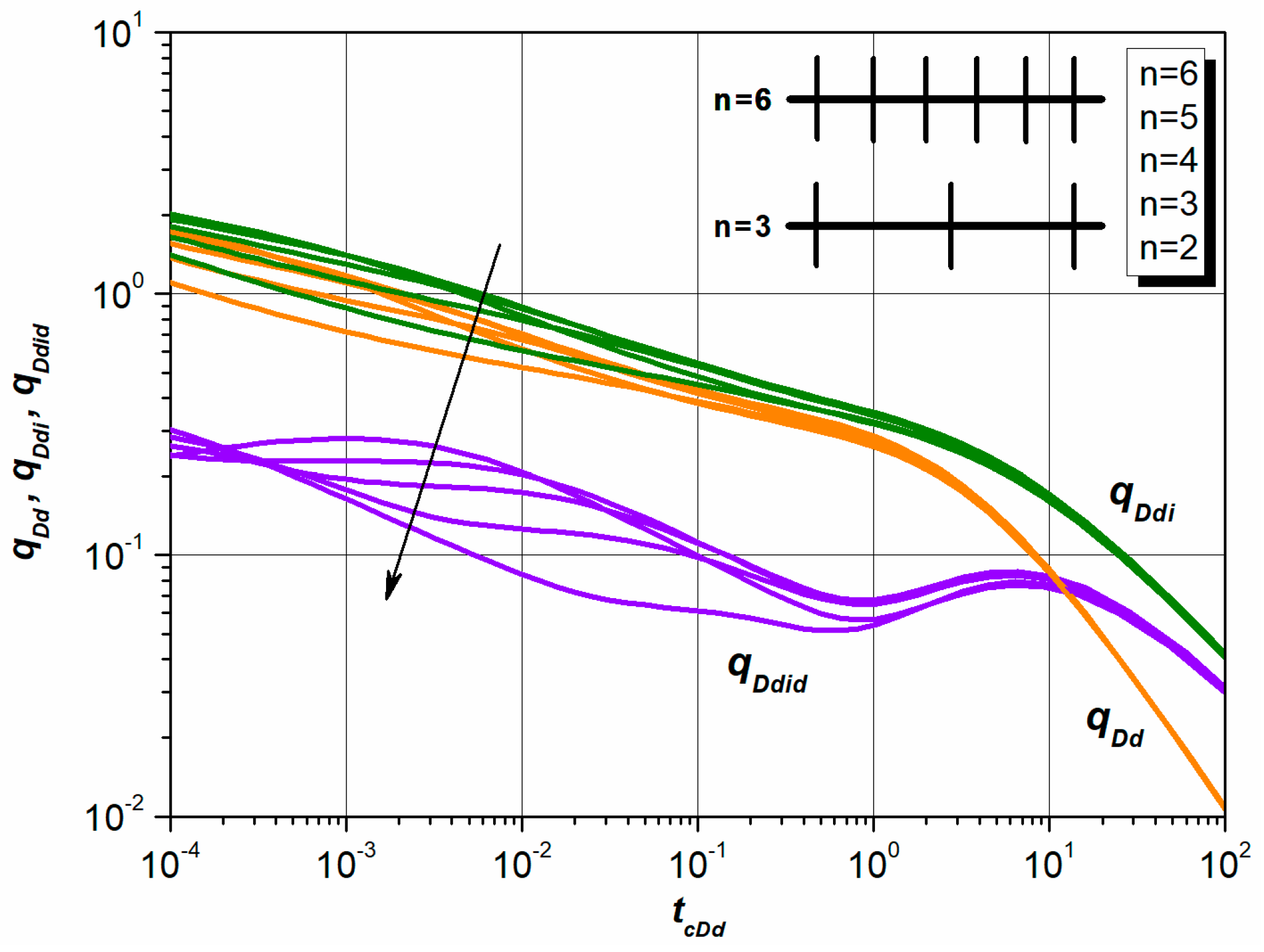
4.3. Number of Hydraulic Fractures
4.4. Fracture Conductivity
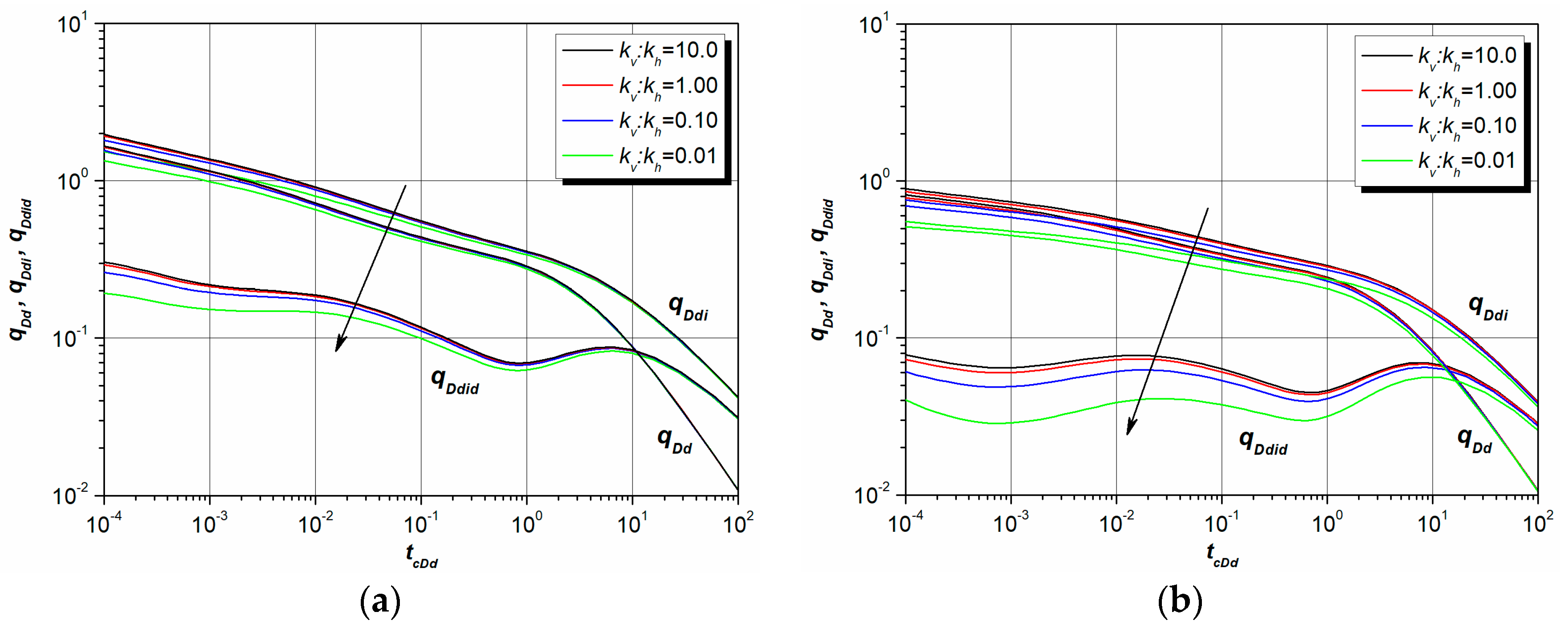
4.5. Ratio of Vertical Permeability to Horizontal Permeability
5. Conclusions
- (1)
- The production distribution along horizontal wellbore is non-uniform, and the properties of different fractures are also unequal, which should be taken into account in the RTA model and later interpretation.
- (2)
- Although the effects of unequal half-length of fractures on type curves are not obvious, the use of the use of dimensionless production integral derivative curve magnifies the differences so that we can identify the production distribution.
- (3)
- Obvious differences can be observed among the type curves of UPF and NPF. Total length of fractures affects the rate decline behaviors more obviously than unequal half-length of fractures with same total length of fractures.
- (4)
- Since the reference point locates at the heel of horizontal wellbore, symmetric distribution of production (i.e., qfD = 0.10:0.10:0.40:0.40; qfD = 0.40:0.40:0.10:0.10) generates different results so that this model can be used to distinguish the symmetric cases.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| B | formation volume factor of fluid, cm3/cm3 |
| C | wellbore-storage coefficient, atm−1 |
| CD | dimensionless wellbore-storage coefficient |
| CfDi | dimensionless fracture conductivity of the ith fracture |
| Ct | total compressibility, atm−1 |
| h | formation thickness, cm |
| hf | height of hydraulic fractures, cm |
| h* | formation thickness considering permeability anisotropy, cm |
| kf | permeability of the ith fracture, D |
| kh | horizontal permeability, D |
| kv | vertical permeability, D |
| L | length of horizontal well, cm |
| LD | dimensionless length of horizontal well |
| n | number of horizontal sections, dimensionless |
| P | pressure, atm |
| PCD | dimensionless pressure drop with wellbore-storage effect |
| PD | dimensionless pressure drop |
| Pf | pressure at fracture tips, atm |
| Pi | initial reservoir pressure, atm |
| Prf | pressure at the boundary of radial-flow region, atm |
| PS | dimensionless pressure drop caused by skin effect |
| PSD | dimensionless total pressure drop with considering skin effect |
| q | total production rate, m3/s |
| qDd | normalized dimensionless decline production |
| qDdi | normalized dimensionless decline production integral |
| qDdid | normalized dimensionless decline production integral derivative |
| rw | wellbore radius, cm |
| rwD | dimensionless wellbore radius |
| S | skin factor |
| t | time, s |
| tD | dimensionless time |
| tDd | dimensionless decline time |
| tcDd | dimensionless material balance time |
| u | Laplace transform variable |
| x, y, z | Cartesian coordinates |
| xf | half-length of hydraulic fractures, cm |
| xfi | half-length of the ith fracture, cm |
| xfDi | half-length of the ith fracture, cm |
| xD, yD, zD | dimensionless Cartesian coordinate |
| wfi | width of the ith fracture, cm |
| ϕ | porosity, fraction |
| ηh | diffusivity in horizontal direction, cm2/s |
| ηv | diffusivity in vertical direction, cm2/s |
| µ | fluid viscosity, cP |
| β | anisotropy coefficient |
| τ | time variable |
| ΔP | pressure drop, atm |
| ΔPTlf | pressure drop resulted by linear flow, atm |
| ΔPrf | pressure drop caused by radial flow, atm |
| ΔPs | pressure drop with considering the skin-factor effect, atm |
| ΔPTf | total pressure drops in a hydraulic fracture, atm |
| dimensionless pressure in Laplace space with considering wellbore-storage | |
| dimensionless pressure in Laplace space without considering wellbore-storage | |
| pressure solution of an MFHW in circular-bounded formation | |
| pressure in which the formation is infinite in horizontal direction and impermeable in vertical direction | |
| pressure response caused by the circular-bounded formation | |
| dimensionless rate in Laplace space |
Appendix A
Appendix A.1. Pressure Drop Caused by Linear Flow with Non-Uniform-Rate-Density
Appendix A.2. Pressure Drop Caused by Radial Flow
Appendix B
References
- Clarkson, C.R. Production Data Analysis of Unconventional Gas Wells: Review of Theory and Best Practices. Int. J. Coal Geol. 2013, 109, 101–146. [Google Scholar] [CrossRef]
- Uzun, I.; Kurtoglu, B.; Kazemi, H. Multiphase Rate-Transient Analysis in Unconventional Reservoirs: Theory and Application. SPE Reserv. Eval. Eng. 2016, 19, 553–566. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.; Zhang, R.; Rui, Z. Review of Multi-Scale and Multi-Physical Simulation Technologies for Shale and Tight Gas Reservoir. J. Nat. Gas Sci. Eng. 2017, 37, 560–578. [Google Scholar] [CrossRef]
- Cui, G.; Ren, S.; Rui, Z.; Ezekiel, J.; Zhang, L.; Wang, H. The influence of complicated fluid-rock interactions on the geothermal exploitation in the CO2 plume geothermal system. Appl. Energy 2018. [Google Scholar] [CrossRef]
- Clarkson, C.R. Production Data Analysis of Unconventional Gas Wells: Workflow. Int. J. Coal Geol. 2013, 109, 147–157. [Google Scholar] [CrossRef]
- Rui, Z.; Han, G.; Zhang, H.; Wang, S.; Pu, H.; Ling, K. A new model to evaluate two leak points in a gas pipeline. J. Nat. Gas Sci. Eng. 2017, 46, 491–497. [Google Scholar] [CrossRef]
- Chai, Z.; Yan, B.; Killough, J.E.; Wang, Y. Dynamic Embedded Discrete Fracture Multi-Continuum Model for the Simulation of Fractured Shale Reservoirs. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 14–16 November 2016; International Petroleum Technology Conference: Richardson, TX, USA, 2016. [Google Scholar]
- Sun, J.; Gamboa, E.; Schechter, D.; Rui, Z. An Integrated Workflow for Characterization and Simulation of Complex Fracture Networks Utilizing Microseismic and Horizontal Core Data. J. Nat. Gas Sci. Eng. 2016, 34, 1347–1360. [Google Scholar] [CrossRef]
- Sun, Z.; Espinoza, D.N.; Balhoff, M.T. Discrete Element Modeling of Indentation Tests to Investigate Mechanisms of CO2-Related Chemomechanical Rock Alteration. J. Geophys. Res. Solid Earth. 2016, 121, 7867–7881. [Google Scholar] [CrossRef]
- Rui, Z.; Wang, X.; Zhang, Z.; Lu, J.; Chen, G.; Zhou, X.; Patil, S. A realistic and integrated model for evaluating oil sands development with steam assisted gravity drainage technology in Canada. Appl. Energy 2018, 213, 76–91. [Google Scholar] [CrossRef]
- Tang, H.; Killough, J.E.; Heidari, Z. A New Technique To Characterize Fracture Density by Use of Neutron Porosity Logs Enhanced by Electrically Transported Contrast Agents. SPE J. 2016, 22, 1034–1045. [Google Scholar] [CrossRef]
- He, Y.; Cheng, S.; Qin, J.; Chen, J.; Wang, Y.; Feng, N.; Yu, H. Successful Application of Well Testing and Electrical Resistance Tomography to Determine Production Contribution of Individual Fracture and Water-Breakthrough Locations of Multifractured Horizontal Well in Changqing Oil Field, China. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; Society of Petroleum Engineers: Richardson, TX, USA, 2017. SPE-187285-MS. [Google Scholar] [CrossRef]
- Qin, J.; Liu, Y.; Feng, Y.; Ding, Y.; Liu, L.; He, Y. New Well Pattern Optimization Methodology in Mature Low-Permeability Anisotropic Reservoirs. J. Geophys. Eng. 2018, 15, 93–105. [Google Scholar] [CrossRef]
- He, Y.; Cheng, S.; Li, L.; Mu, G.; Zhang, T.; Xu, H.; Qin, J.; Yu, H. Waterflood Direction and Front Characterization with Four-Step Work Flow: A Case Study in Changqing Oil Field, China. SPE Reserv. Eval. Eng. 2017, 20, 708–725. [Google Scholar] [CrossRef]
- Rui, Z.; Li, C.; Peng, F.; Ling, K.; Chen, G.; Zhou, X. Chang, H. Development of Industry Performance Metrics For Offshore Oil and Gas Project. J. Nat. Gas Sci. Eng. 2017, 39, 44–53. [Google Scholar] [CrossRef]
- Jing, J.; Sun, J.; Tan, J. Investigation on Flow Patterns and Pressure Drops of Highly Viscous Crude Oil–Water Flows in a Horizontal Pipe. Exp. Therm. Fluid Sci. 2016, 72, 88–96. [Google Scholar] [CrossRef]
- He, Y.; Cheng, S.; Li, L.; Mu, G.; Zhang, T.; Xu, H.; Qin, J.; Yu, H. Waterflood Direction and Front Characterization with Multiple Methods: A Case Study in Changqing Oilfield, China. In Proceedings of the SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 24–26 November 2015; Society of Petroleum Engineers: Richardson, TX, USA, 2015. SPE-178053-MS. [Google Scholar] [CrossRef]
- Ren, W.; Li, G.; Tian, S.; Sheng, M.; Geng, L. Adsorption and Surface Diffusion of Supercritical Methane in Shale. Ind. Eng. Chem. Res. 2017, 56, 3446–3455. [Google Scholar] [CrossRef]
- Rui, Z.; Peng, F.; Ling, K.; Chang, H.; Chen, G.; Zhou, X. Investigation Into The Performance of Oil and Gas Projects. J. Pet. Sci. Eng. 2017, 38, 12–20. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, C.; Rui, Z.; Yu, Y.; Chen, Z. Fractured horizontal well productivity prediction in tight oil reservoirs. J. Pet. Sci. Eng. 2017, 151, 159–168. [Google Scholar] [CrossRef]
- Rui, Z.; Lu, J.; Zhang, Z.; Guo, R.; Ling, K.; Zhang, R.; Patil, S. A Quantitative Oil and Gas Reservoir Evaluation System for Development. J. Nat. Gas Sci. Eng. 2017, 42, 31–39. [Google Scholar] [CrossRef]
- Sarisittitham, S.; Jamiolahmady, M. Decline Curve Analysis for Tight Gas and Gas Condensate Reservoirs. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 10–12 December 2014; International Petroleum Technology Conference: Richardson, TX, USA, 2014. IPTC-18188-MS. [Google Scholar]
- Zuo, L.; Yu, W.; Wu, K. A fractional decline curve analysis model for shale gas reservoirs. Int. J. Coal Geol. 2016, 163, 140–148. [Google Scholar] [CrossRef]
- He, Y.; Cheng, S.; Qin, J.; Wang, Y.; Feng, N.; Hu, L.; Huang, Y.; Fang, R.; Yu, H. A semianalytical approach to estimate the locations of malfunctioning horizontal wellbore through bottom-hole pressure and its application in Hudson oilfield. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Manama, Kingdom of Bahrain, 6–9 March 2017; Society of Petroleum Engineers: Richardson, TX, USA, 2017. SPE-183796-MS. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, S.; Feng, N.; He, Y.; Yu, H. The Physical Process and Pressure-Transient Analysis Considering Fractures Excessive Extension in Water Injection Wells. J. Pet. Sci. Eng. 2017, 151, 439–454. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Hou, X.; Xu, W. Rate Decline Analysis of Vertically Fractured Wells in Shale Gas Reservoirs. Energies 2017, 10, 1602. [Google Scholar] [CrossRef]
- Wang, M.; Fan, Z.; Xing, G.; Zhao, W.; Song, H.; Su, P. Rate Decline Analysis for Modeling Volume Fractured Well Production in Naturally Fractured Reservoirs. Energies 2018, 11, 43. [Google Scholar] [CrossRef]
- Arps, J.J. Analysis of Decline Curves. Pet. Trans. 1945, 160, 228–247. [Google Scholar] [CrossRef]
- Fetkovich, M.J. Decline Curve Analysis Using Type Curves. J. Pet. Technol. 1980, 32, 1065–1077. [Google Scholar] [CrossRef]
- Fetkovich, M.J.; Vienot, M.E.; Bradley, M.D.; Kiesow, U.G. Decline Curve Analysis Using Type Curves: Case Histories. SPE Form. Eval. 1987, 2, 637–656. [Google Scholar] [CrossRef]
- Chen, H.; Teufel, L.W. A New Rate-Time Type Curve for Analysis of Tight-Gas Linear and Radial Flows. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000; Society of Petroleum Engineers: Richardson, TX, USA, 2000. SPE 63094-MS. [Google Scholar]
- Blasingame, T.A.; McCray, T.L.; Lee, W.J. Decline curve analysis for variable pressure drop/variable flowrate systems. In Proceedings of the SPE Gas Technology Symposium, Houston, TX, USA, 22–24 January 1991; Society of Petroleum Engineers: Richardson, TX, USA, 1991. SPE-21513-MS. [Google Scholar]
- Agarwal, R.G.; Gardner, D.C.; Kleinsteiber, S.W.; Fussell, D.D. Analyzing Well Production Data Using Combined-Type-Curve and Decline-Curve Analysis Concepts. SPE Reserv. Eval. Eng. 1999, 2, 478–486. [Google Scholar] [CrossRef]
- Wattenbarger, R.A.; El-Banbi, A.H.; Villegas, M.E.; Maggard, J.B. Production Analysis of Linear Flow into Fractured Tight Gas Wells. In Proceedings of the SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 5–8 April 1998; Society of Petroleum Engineers: Richardson, TX, USA, 1998. SPE-39931-MS. [Google Scholar]
- Pratikno, H.; Rushing, J.A.; Blasingame, T.A. Decline curve analysis using type curves-fractured wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; Society of Petroleum Engineers: Richardson, TX, USA, 2003. SPE-84287-MS. [Google Scholar]
- Badazhkov, D.; Dmitry, O.; Kovalenko, A. Analysis of Production Data with Elliptical Flow Regime in Tight Gas Reservoirs. In Proceedings of the SPE Russian Oil and Gas Technical Conference and Exhibition, Moscow, Russia, 28–30 October 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. SPE-117023-MS. [Google Scholar]
- Kupchenko, C.L.; Gault, B.W.; Mattar, L. Tight Gas Production Performance Using Decline Curves. In Proceedings of the CIPC/SPE Gas Technology Symposium 2008 Joint Conference, Calgary, AB, Canada, 16–19 June 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. SPE-114991-MS. [Google Scholar]
- Ilk, D.; Rushing, J.A.; Perego, A.D.; Blasingame, T.A. Exponential vs. hyperbolic decline in tight gas sands: Understanding the origin and implications for reserve estimates using Arps’ decline curves. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. SPE-116731-MS. [Google Scholar]
- Clarkson, C.R.; Beierle, J.J. Integration of microseismic and other post-fracture surveillance with production analysis: A tight gas study. J. Nat. Gas Sci. Eng. 2011, 3, 382–401. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Pedersen, P.K. Tight oil production analysis: Adaptation of existing rate-transient analysis techniques. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010; Society of Petroleum Engineers: Richardson, TX, USA, 2010. SPE-137352-MS. [Google Scholar]
- Bello, R.O.; Wattenbarger, R.A. Rate transient analysis in naturally fractured shale gas reservoirs. In Proceedings of the CIPC/SPE Gas Technology Symposium 2008 Joint Conference, Calgary, AB, Canada, 16–19 June 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2010. SPE-114591-MS. [Google Scholar]
- Mattar, L. Production analysis and forecasting of shale gas reservoirs: Case history-based approach. In Proceedings of the SPE Shale Gas Production Conference, Fort Worth, TX, USA, 16–18 November 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. SPE-119897-MS. [Google Scholar]
- Valko, P.P.; Lee, W.J. A better way to forecast production from unconventional gas wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010; Society of Petroleum Engineers: Richardson, TX, USA, 2010. SPE-134231-MS. [Google Scholar]
- Duong, A.N. Rate-decline analysis for fracture-dominated shale reservoirs. SPE Reserv. Eval. Eng. 2011, 14, 377–387. [Google Scholar] [CrossRef]
- Nobakht, M.; Clarkson, C.R.; Kaviani, D. New and improved methods for performing rate-transient analysis of shale gas reservoirs. SPE Reserv. Eval. Eng. 2014, 15, 335–350. [Google Scholar] [CrossRef]
- Belyadi, H.; Yuyi, S.; Junca-Laplace, J.-P. Production analysis using rate transient analysis. In Proceedings of the SPE Eastern Regional Meeting, Morgantown, WV, USA, 13–15 October 2015; Society of Petroleum Engineers: Richardson, TX, USA, 2015. SPE-177293-MS. [Google Scholar]
- Kuchuk, F.; Morton, K.; Biryukov, D. Rate-transient analysis for multistage fractured horizontal wells in conventional and un-conventional homogeneous and naturally fractured reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, Dubai, UAE, 26–28 September 2016; Society of Petroleum Engineers: Richardson, TX, USA, 2016. SPE-181488-MS. [Google Scholar]
- Al-Shamma, B.; Nicole, H.; Nurafza, P.R. Evaluation of Multi-Fractured Horizontal Well Performance: Babbage Field Case Study. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014; Society of Petroleum Engineers: Richardson, TX, USA, 2014. SPE-168623-MS. [Google Scholar]
- He, Y.; Cheng, S.; Li, S.; Huang, Y.; Qin, J.; Hu, L.; Yu, H. A semianalytical methodology to diagnose the locations of underperforming hydraulic fractures through pressure-transient analysis in tight gas reservoir. SPE J. 2017, 22, 924–939. [Google Scholar] [CrossRef]
- Qin, J.; Cheng, S.; He, Y.; Luo, L.; Wang, Y.; Fang, N.; Zhang, T.; Qin, G.; Yu, H. Estimation of non-uniform production rate distribution of multi-fractured horizontal well through pressure transient analysis: Model and case study. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; Society of Petroleum Engineers: Richardson, TX, USA, 2017. SPE-187412-MS. [Google Scholar] [CrossRef]
- He, Y.; Cheng, S.; Hu, L.; Fang, R.; Li, S.; Wang, Y.; Huang, Y.; Yu, H. A pressure transient analysis model of multi-fractured horizontal well in consideration of unequal production of each fracture. J. China Univ. Pet. (Ed. Nat. Sci.) 2017, 41, 116–123. [Google Scholar] [CrossRef]
- Qin, J.; Cheng, S.; He, Y.; Li, D.; Zhang, J.; Feng, D.; Yu, H. Rate Decline Analysis for Horizontal Wells with Multiple Sections. Geofluids 2018, in press. [Google Scholar]
- Van Everdingen, A.F.; Hurst, W. The Application of the Laplace Transformation to Flow Problems in Reservoirs. J. Pet. Technol. 1949, 1, 305–324. [Google Scholar] [CrossRef]
- Stehfest, H. Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 624. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J. The use of source and Green’s Functions in solving unsteady-flow problems in reservoirs. SPE J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Van Everdingen, A.F. The Skin Effect and Its Influence on the Productive Capacity of a Well. J. Pet. Technol. 1953, 5, 171–176. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Thickness of formation (h) | 20.0 × 102 cm |
| Permeability in the horizontal direction (kh) | 1.0 × 10−3 D |
| Permeability in the horizontal direction (kv) | 0.1 × 10−3 D |
| Length of horizontal wellbore (L) | 1200 × 102 cm |
| Radius of horizontal wellbore (rw) | 0.1 × 102 cm |
| Dimensionless wellbore-storage coefficient (CD) | 2 × 10−5 |
| Skin factor (S) | 1.0 |
| Parameters | Value | |
|---|---|---|
| Case1 (UPF) | Case 2 (NPF) | |
| Number of fractures (n) | 4 | |
| Dimensionless fracture half-length (xfD) | 0.05:0.05:0.05:0.05 | 0.09:0.01:0.01:0.09 |
| Dimensionless production of fractures (qfD) | 0.25:0.25:0.25:0.25 | 0.48:0.02:0.02:0.48 |
| Dimensionless fracture conductivity (CfD) | 0.50:0.50:0.50:0.50 | 0.90:0.10:0.10:0.90 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Cheng, S.; Rui, Z.; Qin, J.; Fu, L.; Shi, J.; Wang, Y.; Li, D.; Patil, S.; Yu, H.; et al. An Improved Rate-Transient Analysis Model of Multi-Fractured Horizontal Wells with Non-Uniform Hydraulic Fracture Properties. Energies 2018, 11, 393. https://doi.org/10.3390/en11020393
He Y, Cheng S, Rui Z, Qin J, Fu L, Shi J, Wang Y, Li D, Patil S, Yu H, et al. An Improved Rate-Transient Analysis Model of Multi-Fractured Horizontal Wells with Non-Uniform Hydraulic Fracture Properties. Energies. 2018; 11(2):393. https://doi.org/10.3390/en11020393
Chicago/Turabian StyleHe, Youwei, Shiqing Cheng, Zhenhua Rui, Jiazheng Qin, Liang Fu, Jianguo Shi, Yang Wang, Dingyi Li, Shirish Patil, Haiyang Yu, and et al. 2018. "An Improved Rate-Transient Analysis Model of Multi-Fractured Horizontal Wells with Non-Uniform Hydraulic Fracture Properties" Energies 11, no. 2: 393. https://doi.org/10.3390/en11020393
APA StyleHe, Y., Cheng, S., Rui, Z., Qin, J., Fu, L., Shi, J., Wang, Y., Li, D., Patil, S., Yu, H., & Lu, J. (2018). An Improved Rate-Transient Analysis Model of Multi-Fractured Horizontal Wells with Non-Uniform Hydraulic Fracture Properties. Energies, 11(2), 393. https://doi.org/10.3390/en11020393









