Differentiation of SCC Susceptibility with EIS of Alloy 182 in High Temperature Water
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Environment
2.3. Electrode Set-Up
2.4. EIS Measurements
3. Results
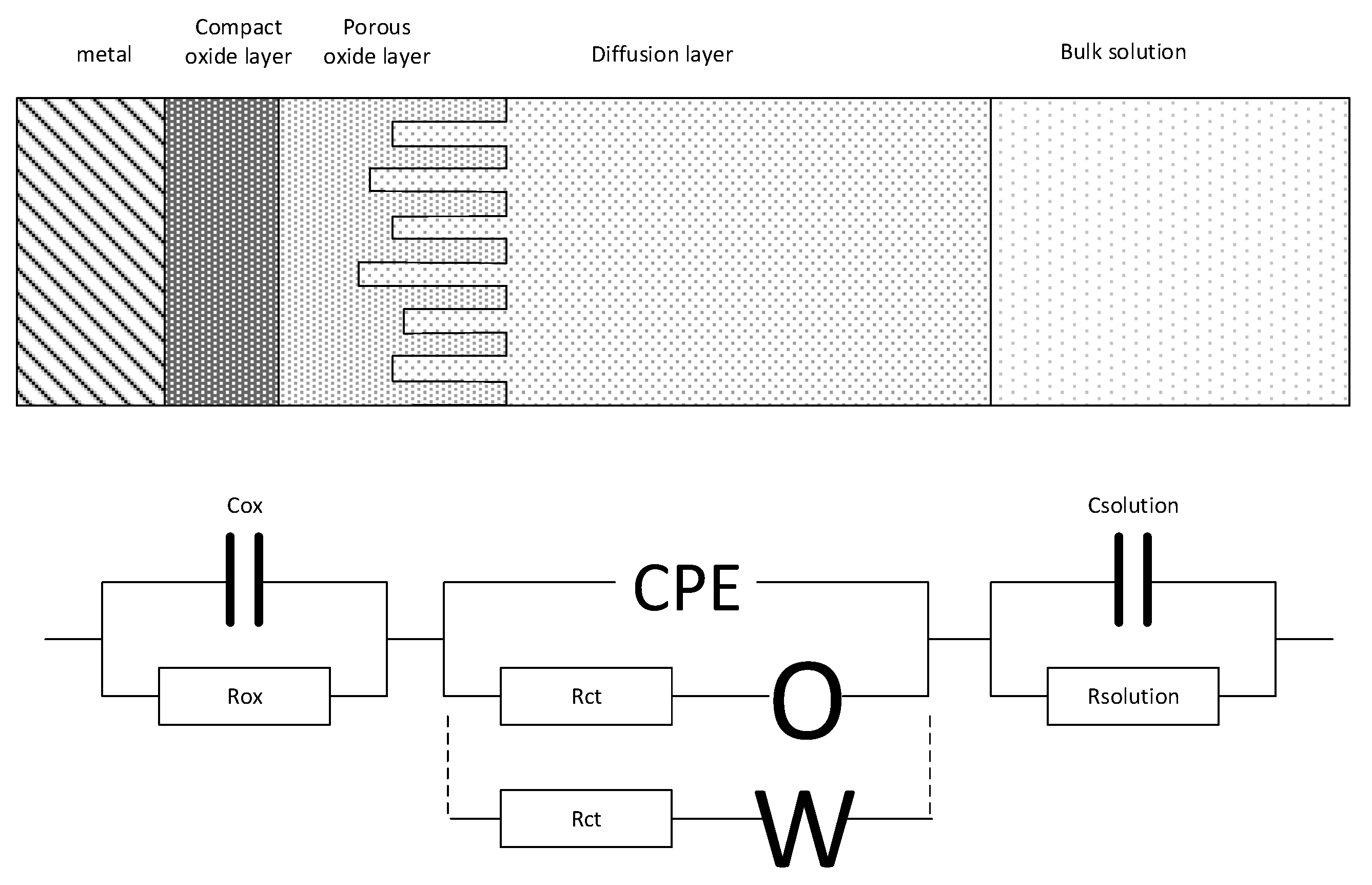
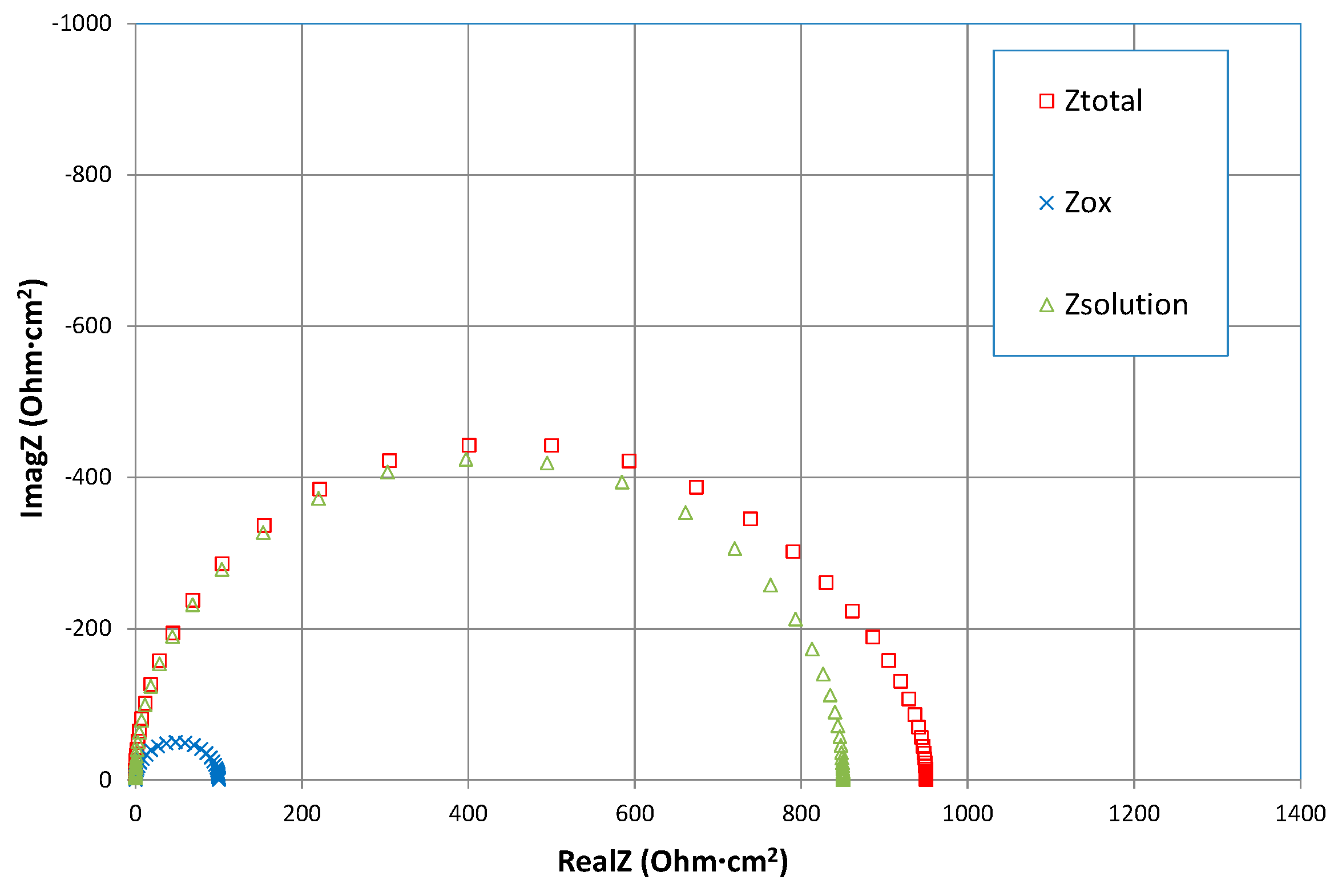
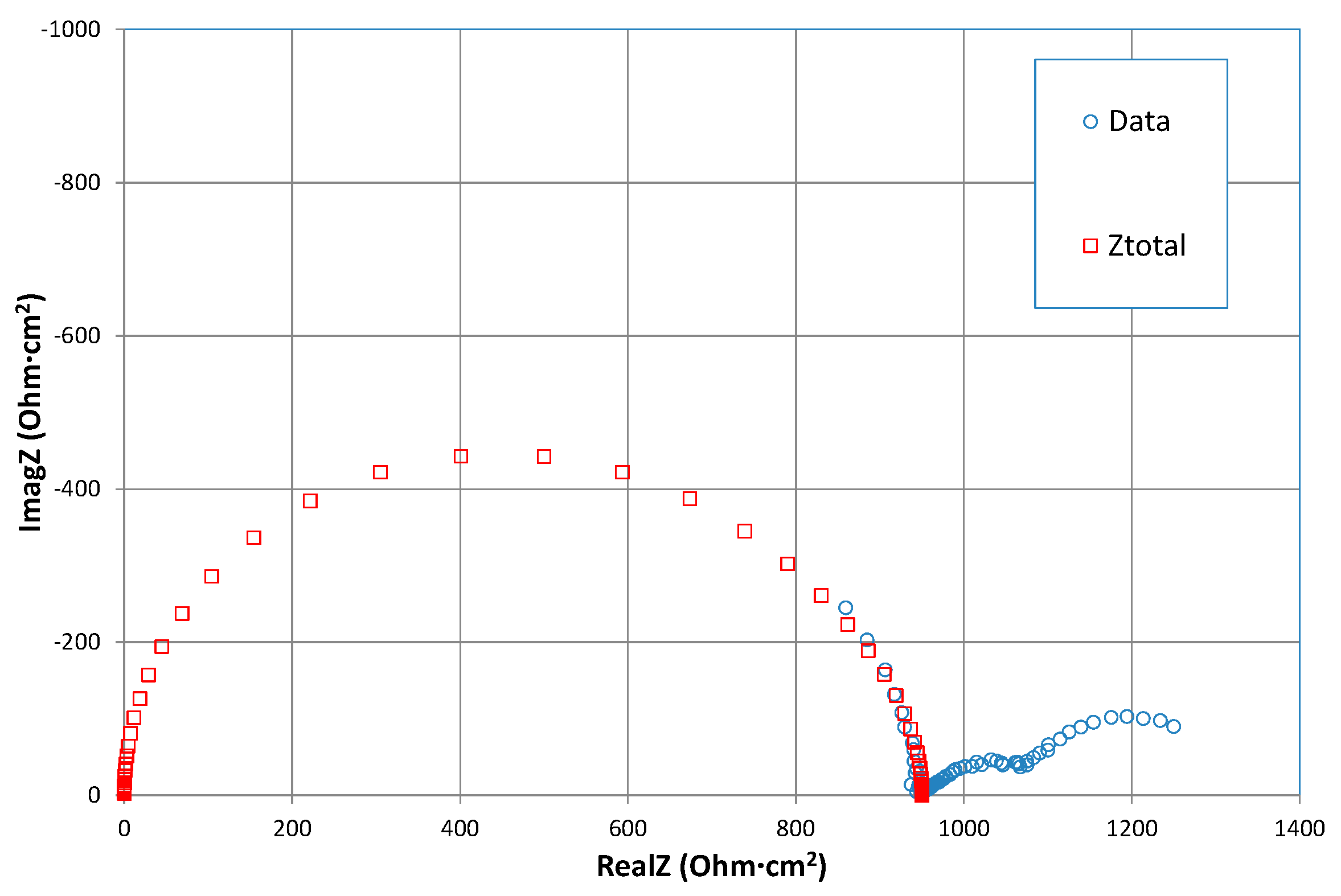
3.1. Equivalent Circuit Modelling
- Cox: the capacity of the oxide layer, that is present on the metal surface
- Rox: the (ohmic) resistance of the oxide layer
- Rct: charge transfer resistance of the electrochemical reactions that take place at the oxide layer water interface
- O: diffusion resistance related to the electrochemical active species moving from and to the oxide layer water interface, assuming a finite length of the diffusion layer (first alternative). The impedance (ZO) is given by:where σ is the Warburg coefficient and B a Warburg fit parameter represented by B = δ/√D. Here δ is the diffusion layer thickness and D is some average value of the diffusion coefficients of the diffusion species.
- W: diffusion resistance related to electrochemical active species moving from and to the oxide layer water interface, assuming an infinite length of the diffusion layer (second alternative). The impedance (ZW) is given by:where σ is the Warburg coefficient.
- CPE: Constant Phase Element representing the electrochemical double layer capacity on a heterogeneous/dispersed substrate. The impedance is given by:where Yo is the CPE constant or pseudo capacitance and n the CPE exponent.
- Csolution: diffuse double layer capacity
- Rsolution: solution resistance of the test water
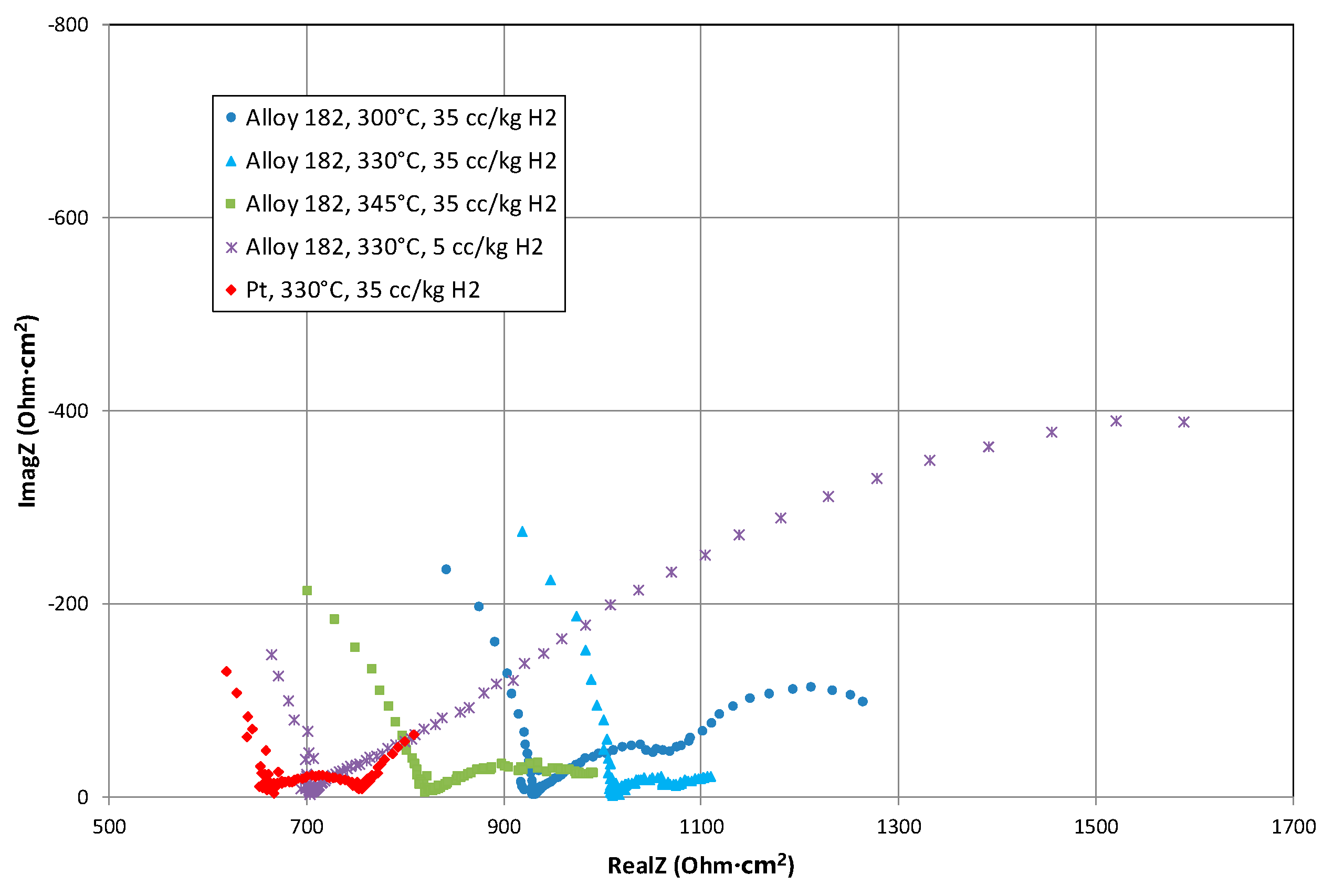
3.2. Interpretation of the High Frequency Arc
3.3. Interpretation of the Warburg Coefficient
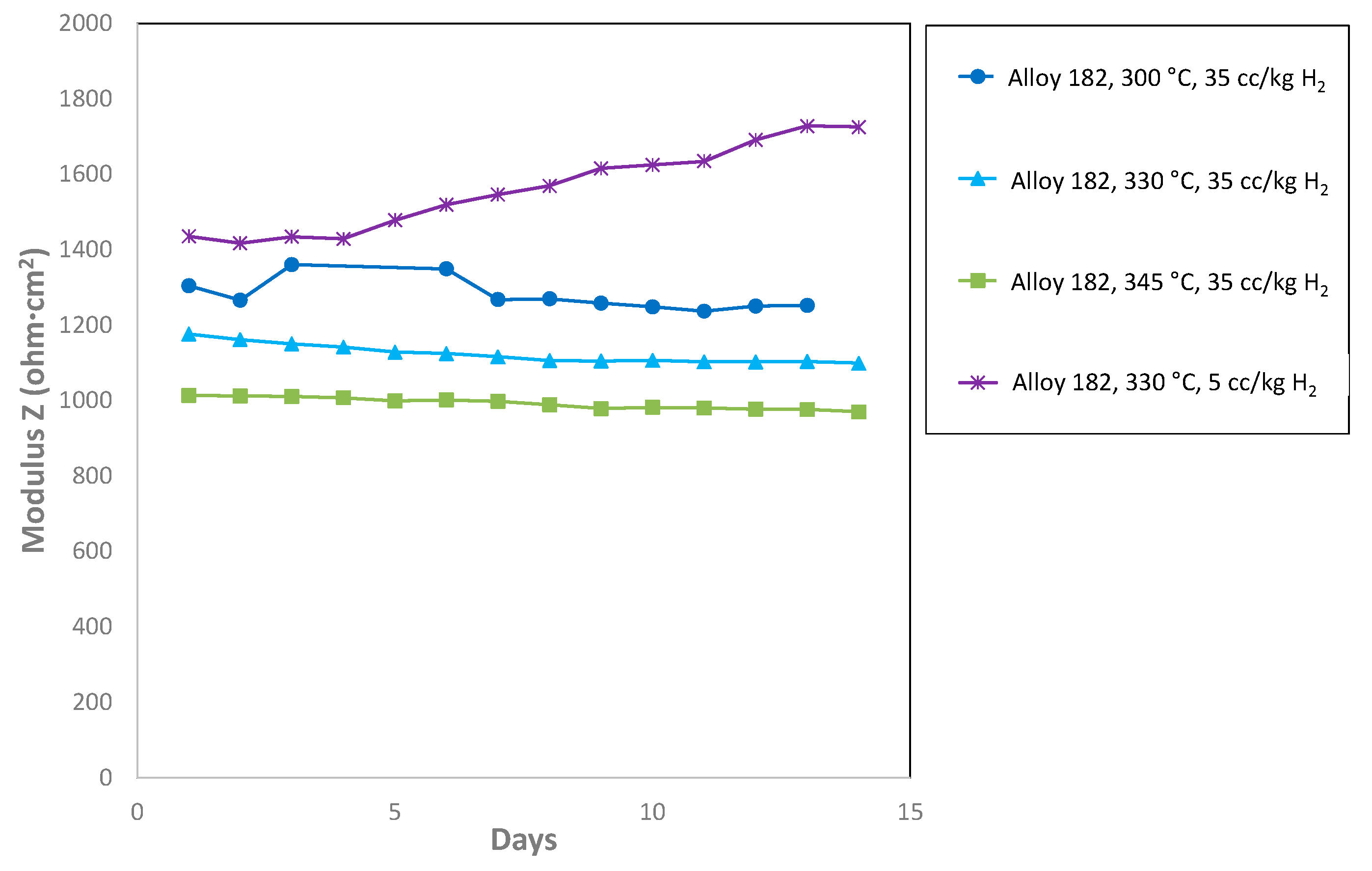
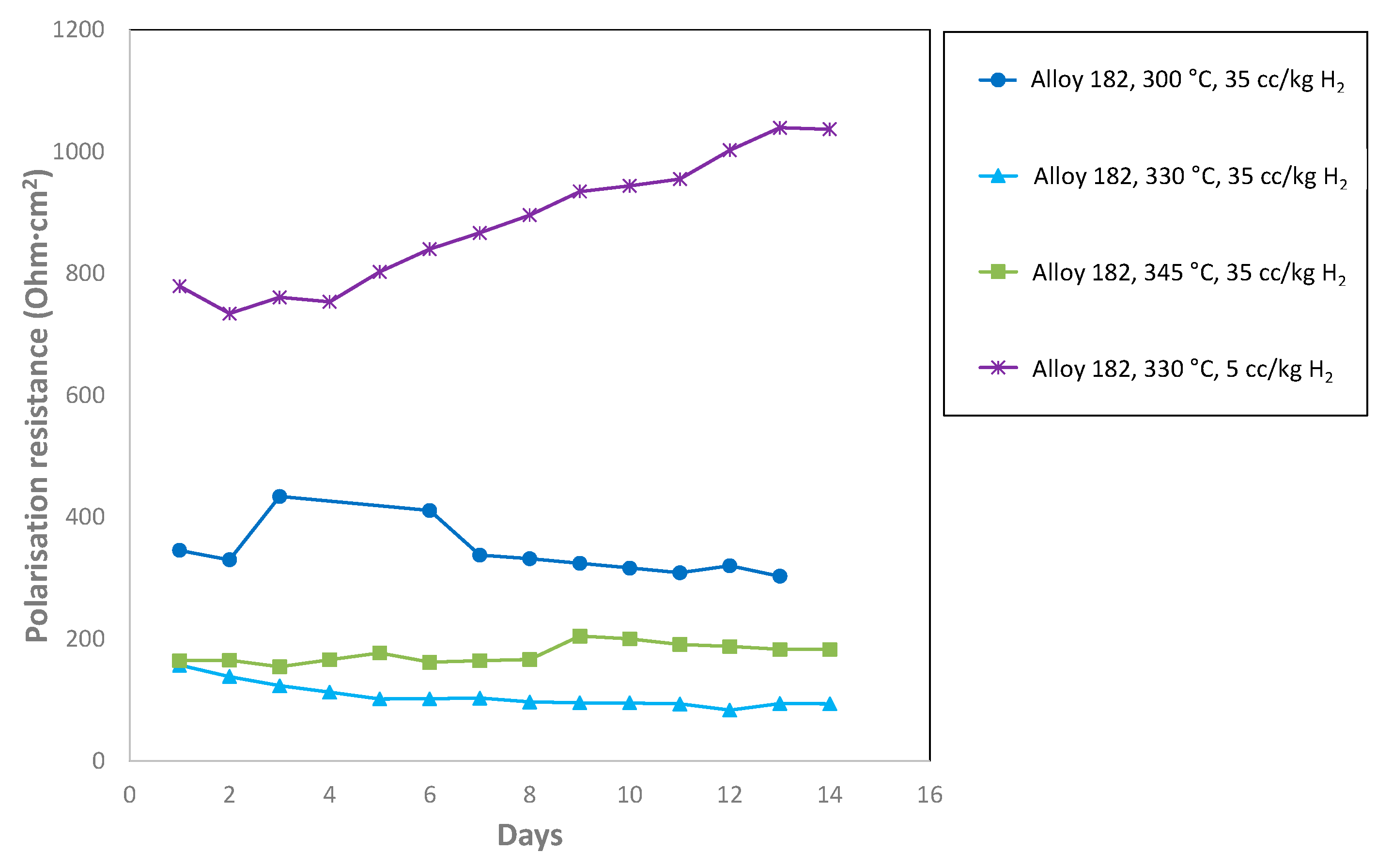
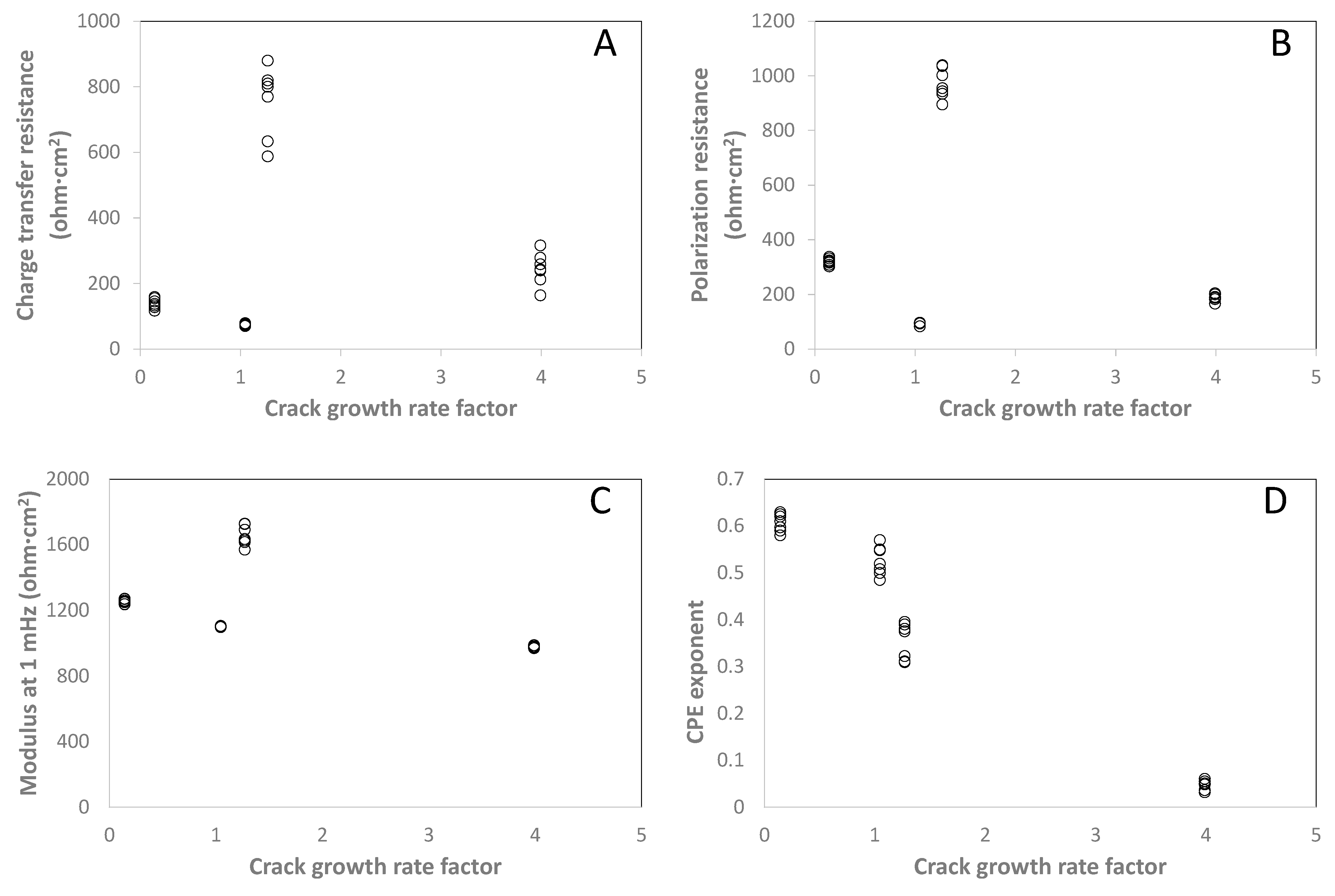
3.4. Trend Analysis of the Equivalent Circuit Fit Parameters
3.5. Low Frequency Impedance Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scott, P.M.; Combrade, P. Corrosion in Pressurized Water Reactors. In ASM Handbook, Volume 13C Corrosion: Environments and Industries; ASM International: Materials Park, OH, USA, 2006; ISBN 13: 978-0-87170-709-3. [Google Scholar]
- Vaillant, F.; Boursier, J.-M.; Amzallag, C.; Bibollet, C.; Pons, S. Environmental Behaviour and weldability of Ni-base weld in PWRs. Rev. Générale Nucléaire 2007, 6, 62–71. [Google Scholar] [CrossRef]
- Andresen, P.L.; Hickling, J.; Ahluwalia, A.; Wilson, J. Effects of Hydrogen on SCC Growth Rate of nickel Alloys in high temperature water. Corrosion 2008, 64, 707–720. [Google Scholar] [CrossRef]
- Attanasio, S.A.; Morton, D.S. Measurement of the Nickel Oxide Transition in Ni-Cr-Fe Alloys and Updated Data and Correlations to Quantify the Effect of Aqueous Hydrogen on Primary Water SCC. In Proceedings of the 11th International Conference Environmental Degradation of Materials in Nuclear Power Systems, Stevenson, WA, USA, 10–14 August 2003. [Google Scholar]
- Liu, J.-H.; Mendonça, R.; Bosch, R.-W.; Konstantinović, M.J. Characterization of oxide films formed on alloy 182 in simulated PWR primary water. J. Nucl. Mater. 2009, 393, 242–248. [Google Scholar] [CrossRef]
- Terachi, T.; Totsuka, N.; Yamada, T.; Nakagawa, T.; Deguchi, H.; Masaki, H.; Oshitani, M. Influence of dissolved hydrogen on structure of oxide film on alloy 600 formed in primary water of pressurized water reactors. J. Nucl. Sci. Technol. 2003, 40, 509–516. [Google Scholar] [CrossRef]
- Kuang, W.; Wu, X.; Han, E.-H. Influence of dissolved oxygen concentration on the oxide film formed on Alloy 690 in high temperature water. Corros. Sci. 2013, 69, 197–204. [Google Scholar] [CrossRef]
- Dozaki, K.; Akutagawa, D.; Nagata, N.; Takiguchi, H.; Norring, K. Effects of dissolved hydrogen content in PWR primary water on PWSCC initiation property. E-J. Adv. Maint. Jpn. Soc. Maintenology 2010, 2, 65–76. [Google Scholar]
- Mendonça, R.; Bosch, R.W.; van Renterghem, W.; Vankeerberghen, M.; Figueiredo, C.d. Effect of temperature and dissolved hydrogen on oxide films formed on Ni and Alloy 182 in simulated PWR water. J. Nucl. Mater. 2016, 477, 280–291. [Google Scholar] [CrossRef]
- Figueiredo, C.; Bosch, R.-W.; Vankeerberghen, M. Electrochemical investigation of oxide films formed on nickel alloys 182, 600 and 52 in high temperature water. Electrochim. Acta 2011, 56, 7871–7879. [Google Scholar] [CrossRef]
- Bosch, R.W.; Vankeerberghen, M. In-pile electrochemical tests of stainless steel under PWR conditions: Interpretation of electrochemical impedance spectroscopy data. Electrochim. Acta 2007, 52, 7538. [Google Scholar] [CrossRef]
- Xu, J.; Shoji, T. The corrosion behavior of Alloy 182 in a cyclic hydrogenated and oxygenated water chemistry in high temperature aqueous environment. Corros. Sci. 2016, 104, 248. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Ming, H.; Zhang, Z.; Han, E.H. Effect of temperature on corrosion behavior of alloy 690 in high temperature hydrogenated water. J. Mater. Sci. Technol. 2018, 34, 1419. [Google Scholar] [CrossRef]
- Yang, J.; Li, Y.; Xu, A.; Fekete, B.; Macdonald, D.D. The electrochemical properties of alloy 690 in simulated pressurized water reactor primary water: Effect of temperature. J. Nucl. Mater. 2019, 518, 305. [Google Scholar] [CrossRef]
- Yang, J.; Li, Y.; Macdonald, D.D. Effects of temperature and pH on the electrochemical behaviour of alloy 600 in simulated pressurized water reactor primary water. J. Nucl. Mater. 2020, 528, 151850. [Google Scholar] [CrossRef]
- Xu, J.; Shoji, T.; Jang, C. The effects of dissolved hydrogen on the corrosion behavior of Alloy 182 in simulated primary water. Corros. Sci. 2015, 97, 115. [Google Scholar] [CrossRef]
- Bai, J.; Bosch, R.W.; Ritter, S.; Schneider, C.; Seifert, H.P.; Virtanen, S. Electrochemical and spectroscopic characterization of oxide films formed on Alloy 182 in simulated boiling water reactor environments: Effects of dissolved hydrogen. Corros. Sci. 2018, 133, 204. [Google Scholar] [CrossRef]
- Macak, J.; Sajdl, P.; Kucera, P.; Novotny, R.; Vosta, J. In situ electrochemical impedance and noise measurements of corroding stainless steel in high temperature water. Electrochim. Acta 2006, 51, 3566. [Google Scholar] [CrossRef]
- Macak, J.; Novotny, R.; Sajdl, P.; Bystriansky, V.; Tuma, L.; Novak, M. In-situ electrochemical impedance measurements of corrosing stainless steel in high subcritical water. Corros. Sci. 2019, 150, 9. [Google Scholar] [CrossRef]
- Morton, D.S.; Attanasio, S.A.; Richey, E.; Young, G.A. In search of the true temperature and stress intensity factor dependencies for PWSCC. In Proceedings of the 12th International Conference Environmental Degradation of Materials in Nuclear Power Systems, TMS (The Minerals, Metals & Materials Society), Salt Lake, UT, USA, 14–18 August 2005. [Google Scholar]
- PWR Primary Water Chemistry Guidelines: Volume 1, Revision 4; EPRI: Palo Alto, CA, USA, 1999.
- Wood, C.J. 5.02 Water Chemistry control in LWRs. Compr. Nucl. Mater. 2012, 5, 17. [Google Scholar]
- Basics of Electrochemical Impedance Spectroscopy. In Application Note Gamry Instruments; Gamry Instruments: Warminster, PA, USA, 2006.
- Cottis, R.A.; Turgoose, S.; Neuman, R. Electrochemical Impedance and Noise. In Corrosion Testing Made Easy; NACE International: Houston, TX, USA, 1999. [Google Scholar]
- Stewart, K.C.; Kolman, D.G.; Taylor, S.R. The effect of parasitic conduction pathways on EIS measurements in low conductivity media. In Electrochemical Impedance: Analysis and Interpretation; Scully, J., Silverman, D., Kendig, M., Eds.; ASTM STP1188: West Conshohocken, PA, USA, 1993. [Google Scholar]
- Quick check of EIS System Performance. In Appliction Note Gamry Instruments; Gamry Instruments: Warminster, PA, USA, 2013.
- Bockris, J.O.M.; Reddy, A.K.N. Modern Electrochemistry; Plenum Press: New York, NY, USA, 1970. [Google Scholar]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods; Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Bojinov, M.; Kinnunen, P.; Sundholm, G. Electrochemical behavior of Nickel-Chromium Alloys in a high-temperature aqueous electrolyte. Corrosion 2003, 59, 91. [Google Scholar] [CrossRef]
- Kalligras, D.T.; Plugatry, A.Y.; Svishchev, I.M. High temperature diffusion coefficients for O2, H2 and OH in water, and for pure water. J. Chem. Eng. Data 2014, 59, 1964. [Google Scholar] [CrossRef]
- Materials Reliability Program: Mitigation of PWSCC in Nickel-Base Alloys by Optimizing Hydrogen in the Primary Water (MRP-213); EPRI: Palo Alto, CA, USA, 2007; p. 1015288.
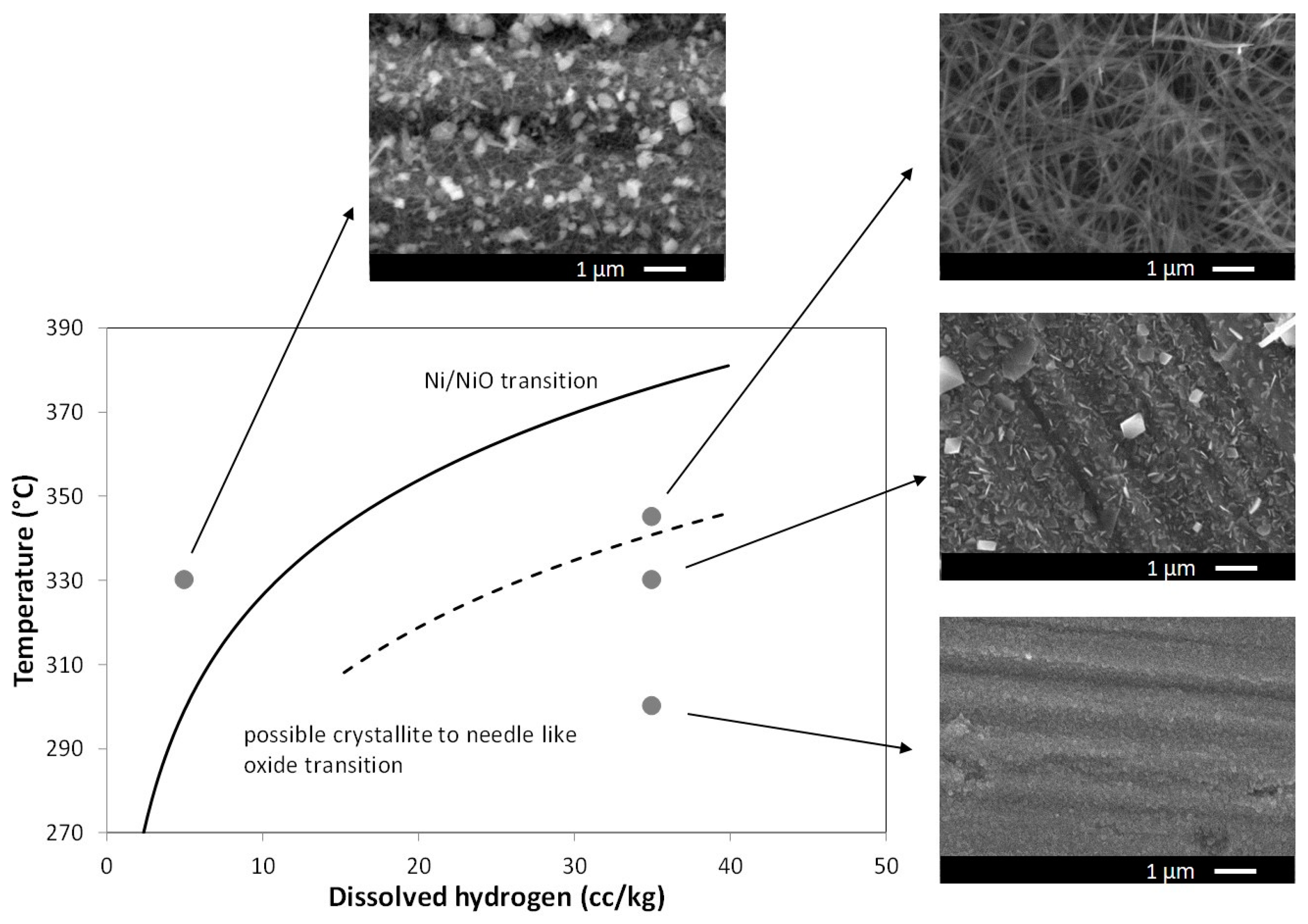

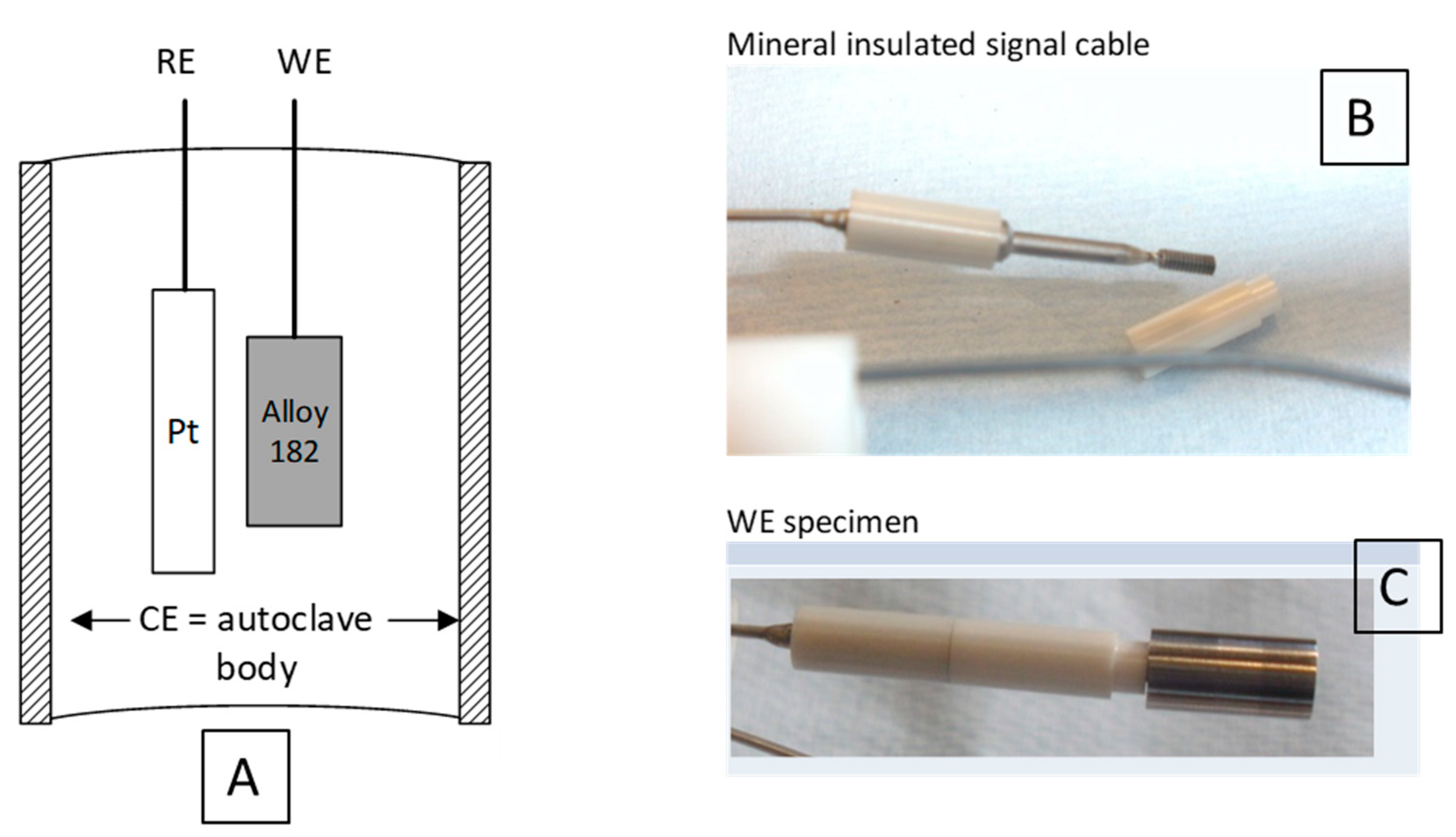




| Alloy | C | Cr | Fe | Ni | Mn | Si | P | S | Nb | Ti | Cu | Mo |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 182 | 0.047 | 14.9 | Bal. | 71.8 | 5.81 | 0.015 | 0.015 | 0.006 | 1.89 | 0.183 | 0.019 | 0.24 |
| Test nr | Working Electrode | Temperature | Hydrogen Concentration |
|---|---|---|---|
| 1 | Alloy 182 | 300 °C | 35 cc/kg H2 |
| 2 | Alloy 182 | 330 °C | 35 cc/kg H2 |
| 3 | Alloy 182 | 345 °C | 35 cc/kg H2 |
| 4 | Alloy 182 | 330 °C | 5 cc/kg H2 |
| 5 | Pt | 330 °C | 35 cc/kg H2 |
| Test Condition | Material | Rsolution (Ohm·cm2) | Yo (Ohm−1·sn·cm−2) | n | σ (Ohm·s−½·cm2) | B | Rct (Ohm·cm2) |
|---|---|---|---|---|---|---|---|
| 300 °C, 35 cc/kg H2 | Alloy 182 | 940 | 6.74 × 10−3 | 0.580 | 18.36 | 13.5 | 155 |
| 330 °C, 35 cc/kg H2 | Alloy 182 | 1009 | 7.15 × 10−3 | 0.519 | 2.96 | -- | 74 |
| 345 °C, 35 cc/kg H2 | Alloy 182 | 717 | 4.22 × 10−3 | 0.037 | 719 | 134.0 | 259 |
| 330 °C, 5 cc/kg H2 | Alloy 182 | 694 | 4.65 × 10−3 | 0.376 | 249 | 8.5 | 588 |
| 330 °C, 35 cc/kg H2 | Pt | 652 | 1.48 × 10−3 | 0.459 | 6.88 | 23.8 | 103 |
| Oxide Layer Impedance | |
| Rox | 100 Ohm cm2 |
| Cox | 10.7 nF/cm2 |
| Solution Resistance and Capacitance (“Space Charge” or Diffuse Double Layer) | |
| Rsolution | 850 Ohm cm2 |
| Csolution | 0.1 nF/cm2 |
| Test Condition | Material | Temperature (K) | Hydrogen Concentration (mol/cm3) | Hydrogen Diffusion Coefficient (cm2/s) | σ Calculated (Ohm·s−½·cm2) | σ Measured (Ohm·s−½·cm2) |
|---|---|---|---|---|---|---|
| 300 °C, 35 cc/kg H2 | Alloy 182 | 573 | 1.56 × 10−6 | 4.81 × 10−4 | 3.71 | 18.36 |
| 330 °C, 35 cc/kg H2 | Alloy 182 | 603 | 1.56 × 10−6 | 5.64 × 10−4 | 4.02 | 2.96 |
| 345 °C, 35 cc/kg H2 | Alloy 182 | 618 | 1.56 × 10−6 | 6.12 × 10−4 | 4.22 | 719 |
| 330 °C, 5 cc/kg H2 | Alloy 182 | 603 | 2.23 × 10−7 | 5.64 × 10−4 | 28.12 | 249 |
| 330 °C, 35 cc/kg H2 | Pt | 603 | 1.56 × 10−6 | 5.64 × 10−4 | 4.02 | 6.88 |
| Description | Value |
|---|---|
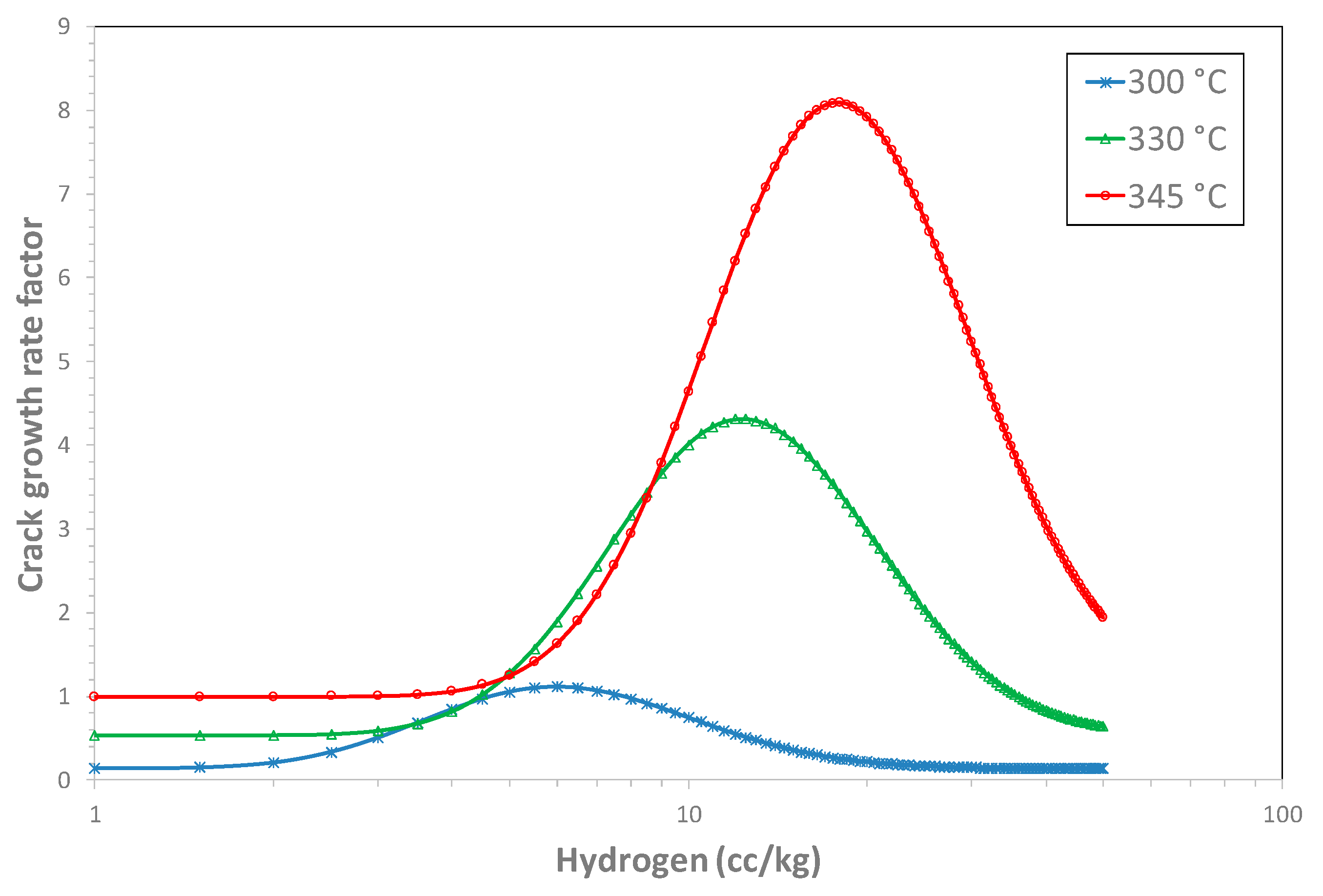
| H2(peak) at 300 °C | 5.50 cc/kg |
| H2(peak) at 330 °C | 11.83 cc/kg |
| H2(peak) at 345 °C | 17.34 cc/kg |
| P | 8.09 |
| ECPos | 0 |
| λ | 20.2 mV |
| Q | 130 kJ/mol |
| R | 8.314 J/mol-K |
| 300 °C, 35 cc/kg H2 | 330 °C, 35 cc/kg H2 | 345 °C, 35 cc/kg H2 | 330 °C, 5 cc/kg H2 | |
|---|---|---|---|---|
| CGR factor | 0.142 | 1.045 | 3.99 | 1.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bosch, R.-W.; Vankeerberghen, M. Differentiation of SCC Susceptibility with EIS of Alloy 182 in High Temperature Water. Corros. Mater. Degrad. 2021, 2, 341-359. https://doi.org/10.3390/cmd2030018
Bosch R-W, Vankeerberghen M. Differentiation of SCC Susceptibility with EIS of Alloy 182 in High Temperature Water. Corrosion and Materials Degradation. 2021; 2(3):341-359. https://doi.org/10.3390/cmd2030018
Chicago/Turabian StyleBosch, Rik-Wouter, and Marc Vankeerberghen. 2021. "Differentiation of SCC Susceptibility with EIS of Alloy 182 in High Temperature Water" Corrosion and Materials Degradation 2, no. 3: 341-359. https://doi.org/10.3390/cmd2030018
APA StyleBosch, R.-W., & Vankeerberghen, M. (2021). Differentiation of SCC Susceptibility with EIS of Alloy 182 in High Temperature Water. Corrosion and Materials Degradation, 2(3), 341-359. https://doi.org/10.3390/cmd2030018





