Acoustic Black Holes in Structural Design for Vibration and Noise Control
Abstract
:1. Introduction
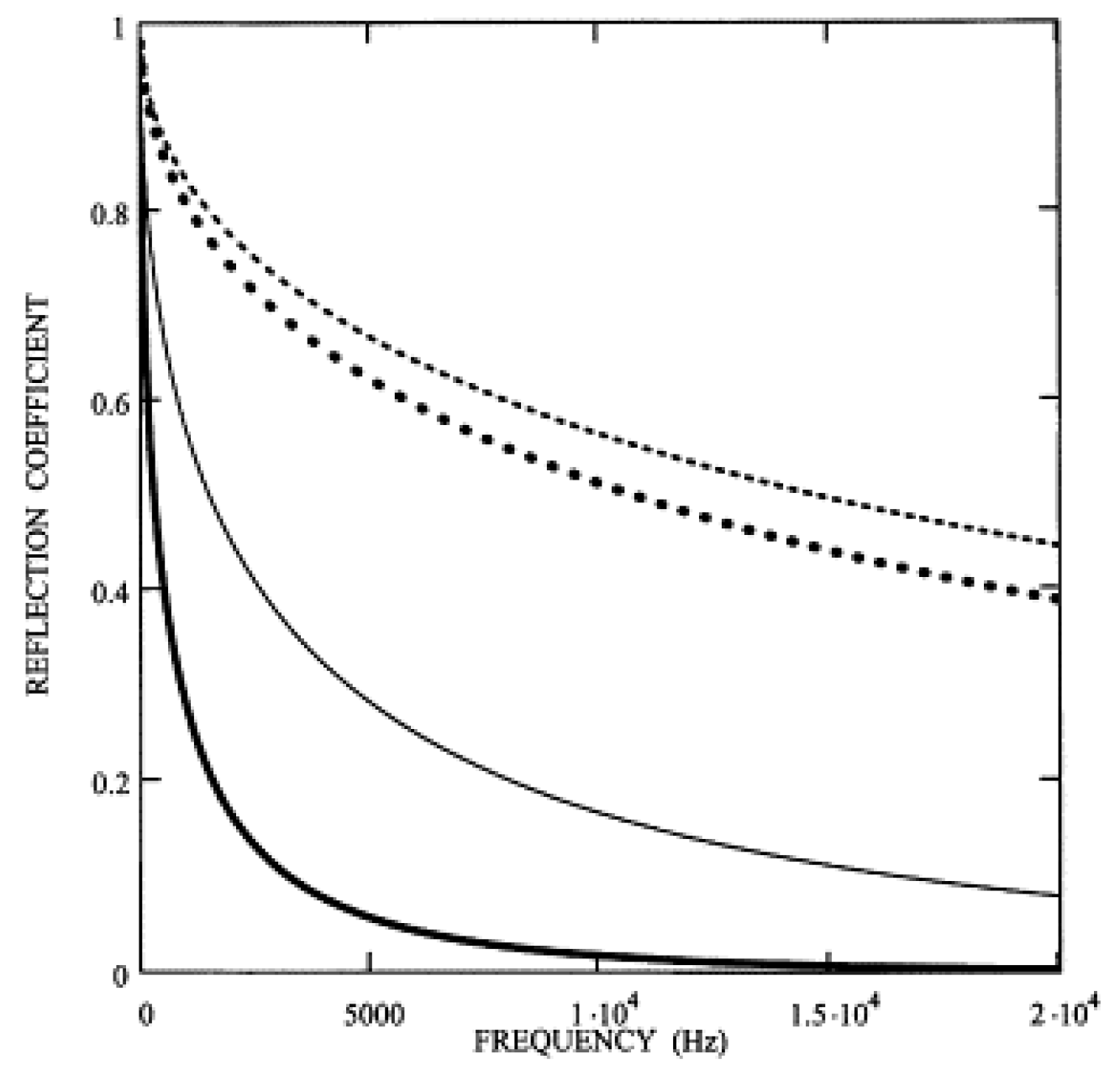
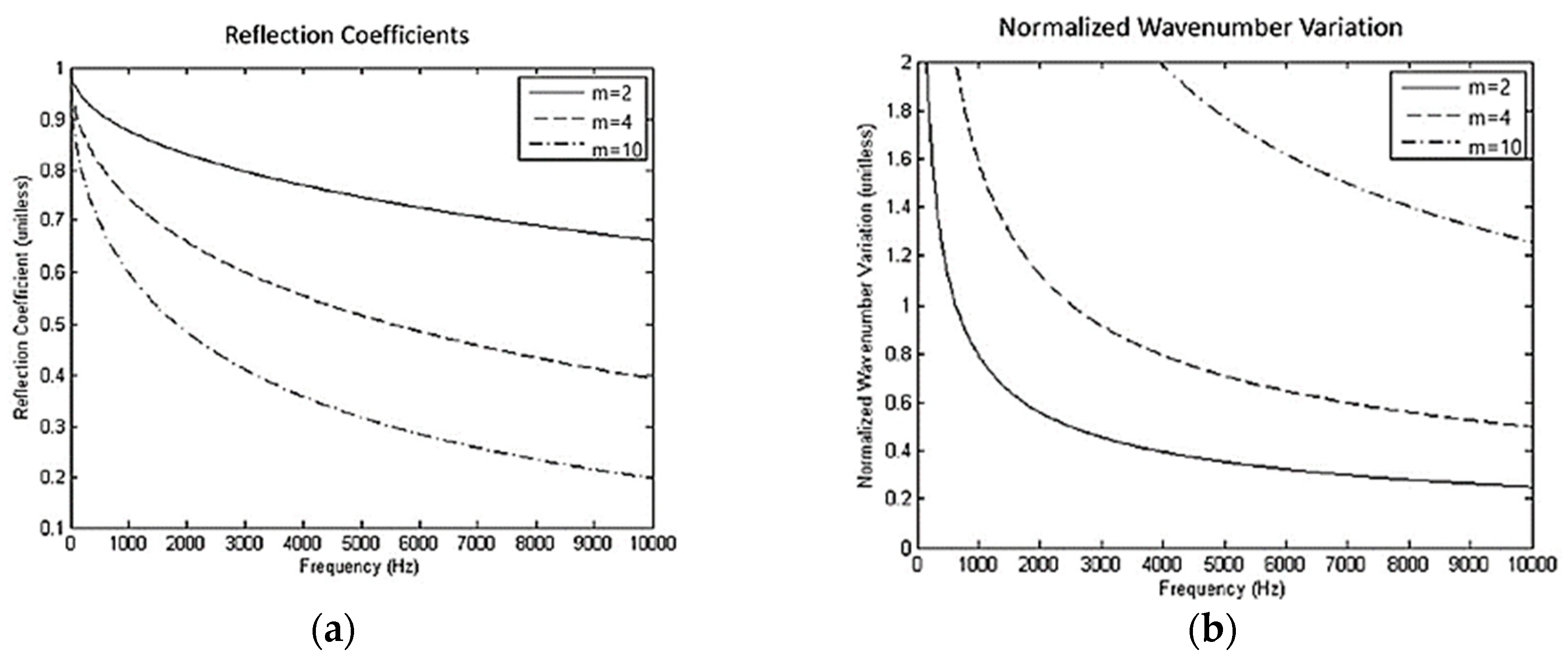
2. Theoretical Analysis
3. Applications to Structural Design with Acoustic Black Holes
3.1. Application of ABHs to Vibration Control
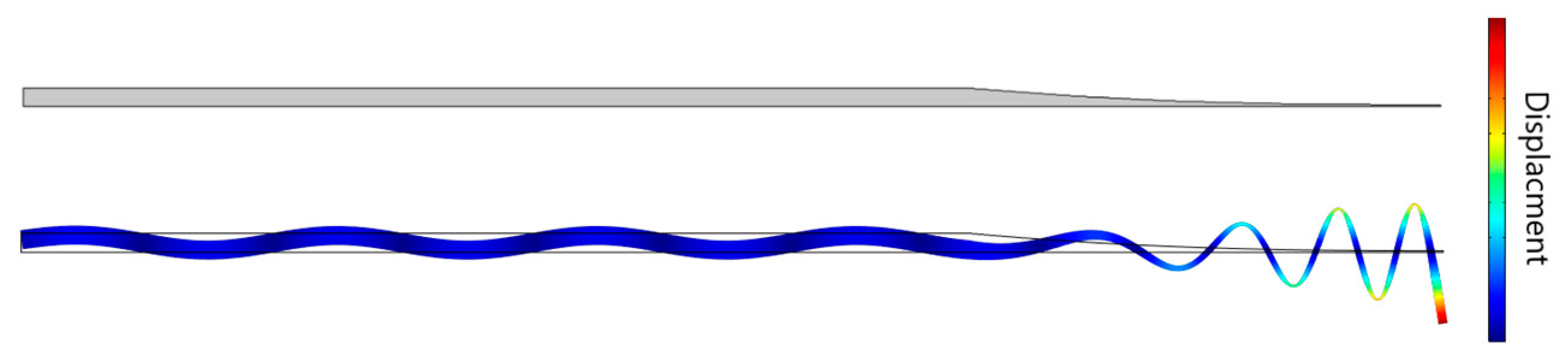
3.1.1. Vibration Control of Beams with ABHs
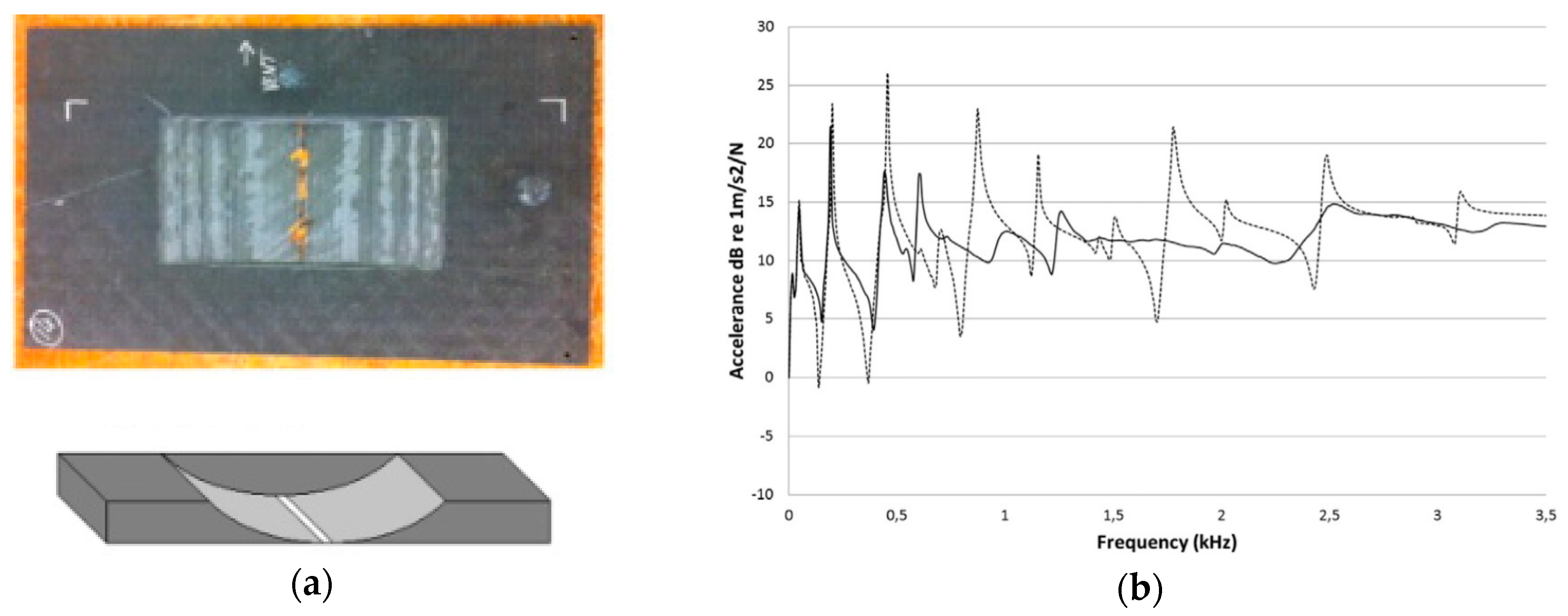
3.1.2. Vibration Damping of Plates with ABH
3.1.3. Vibration Damping of Turbofan Blades with ABH
3.2. Application of ABH to Sound Reduction
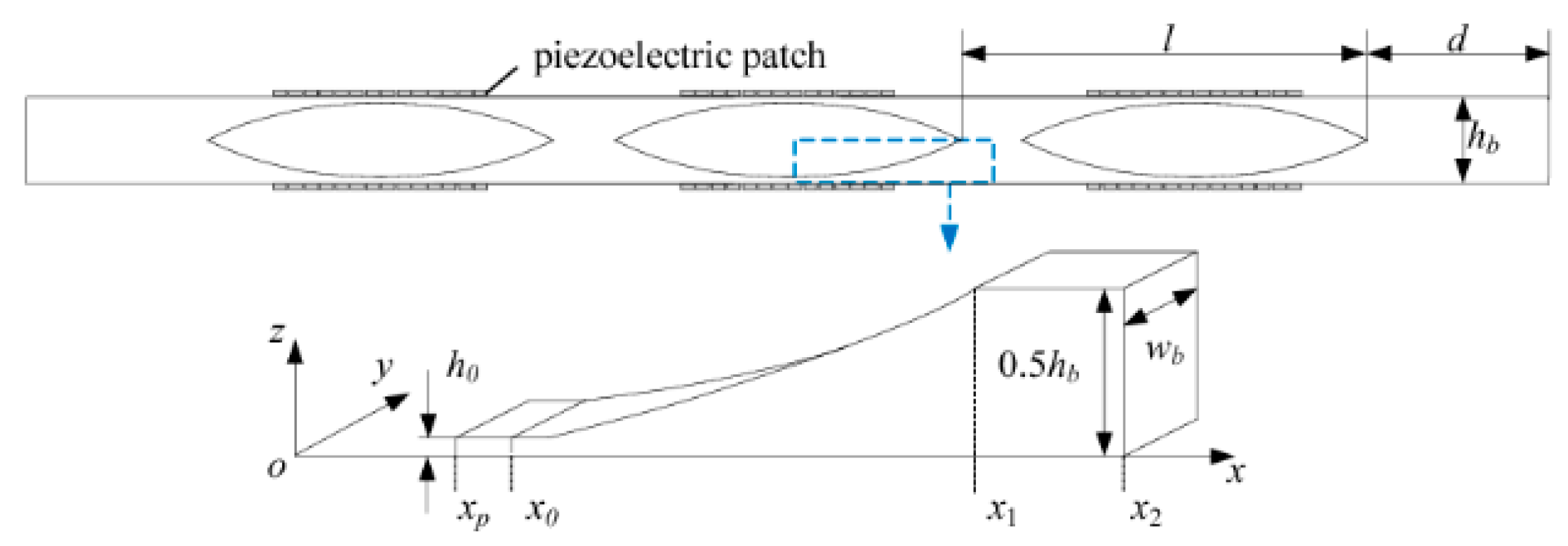
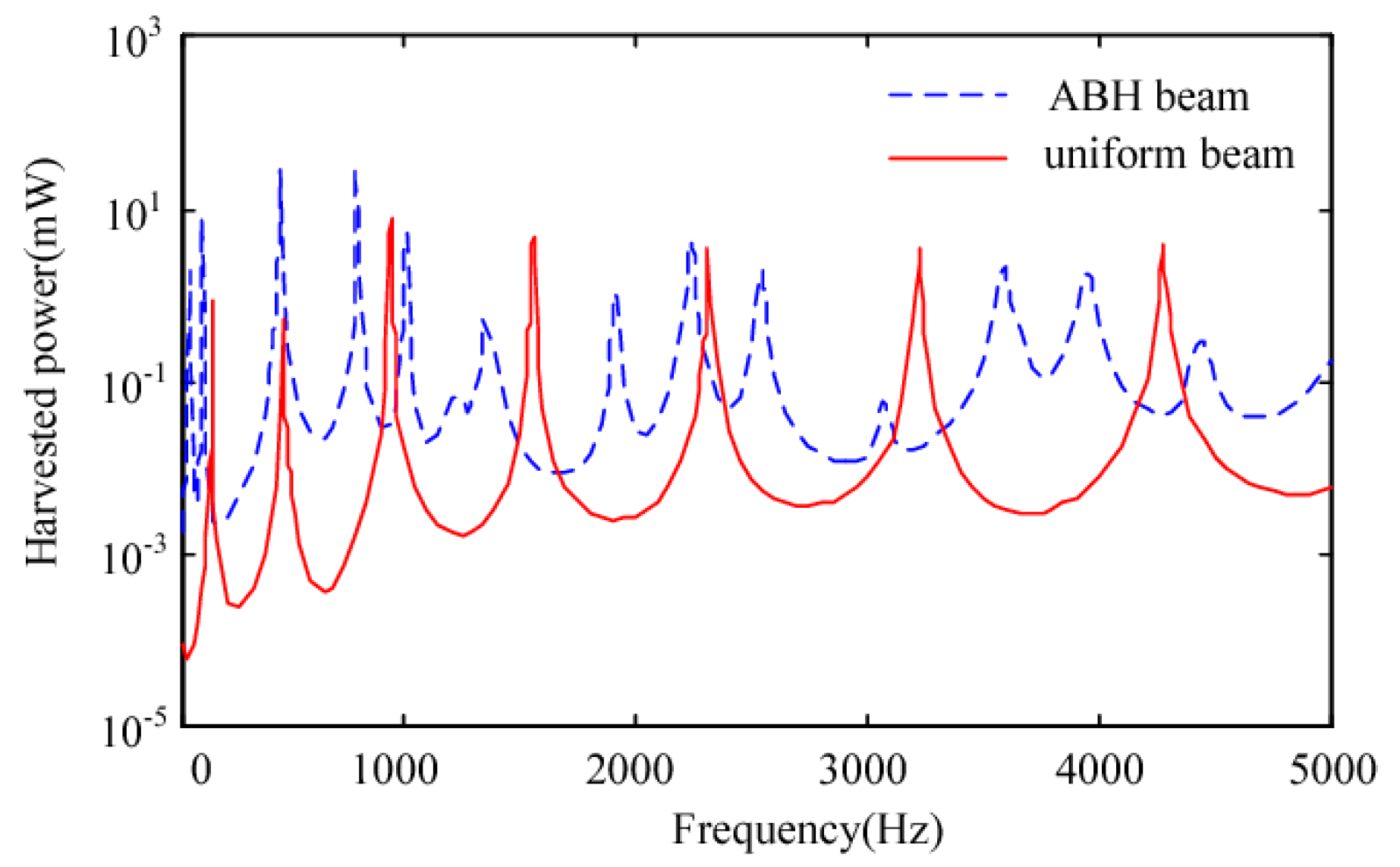
3.3. Application of ABH to Vibration Energy Harvesting
3.4. Discussion
4. Design of Structures Using Acoustic Black Holes
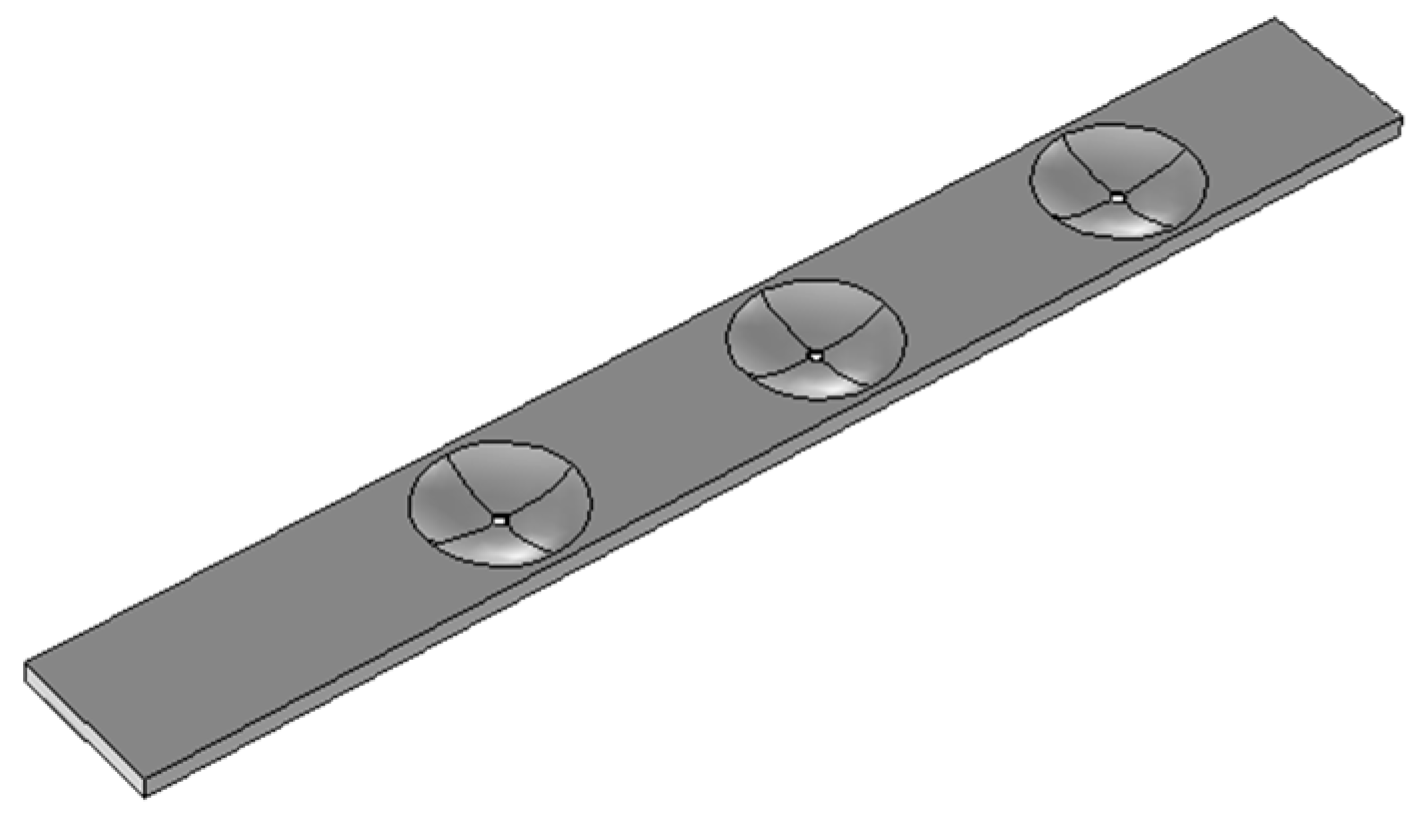
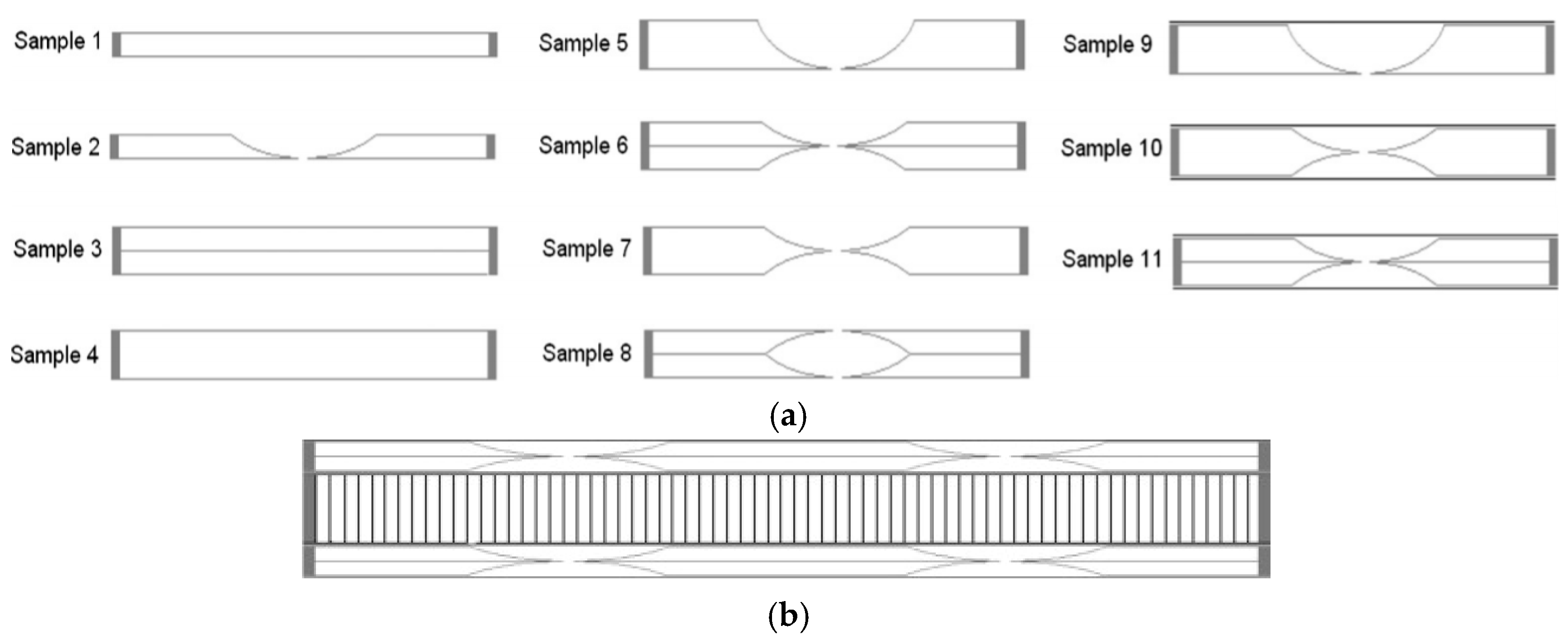
4.1. Design of 1D ABH
4.2. Design of a 2D ABH
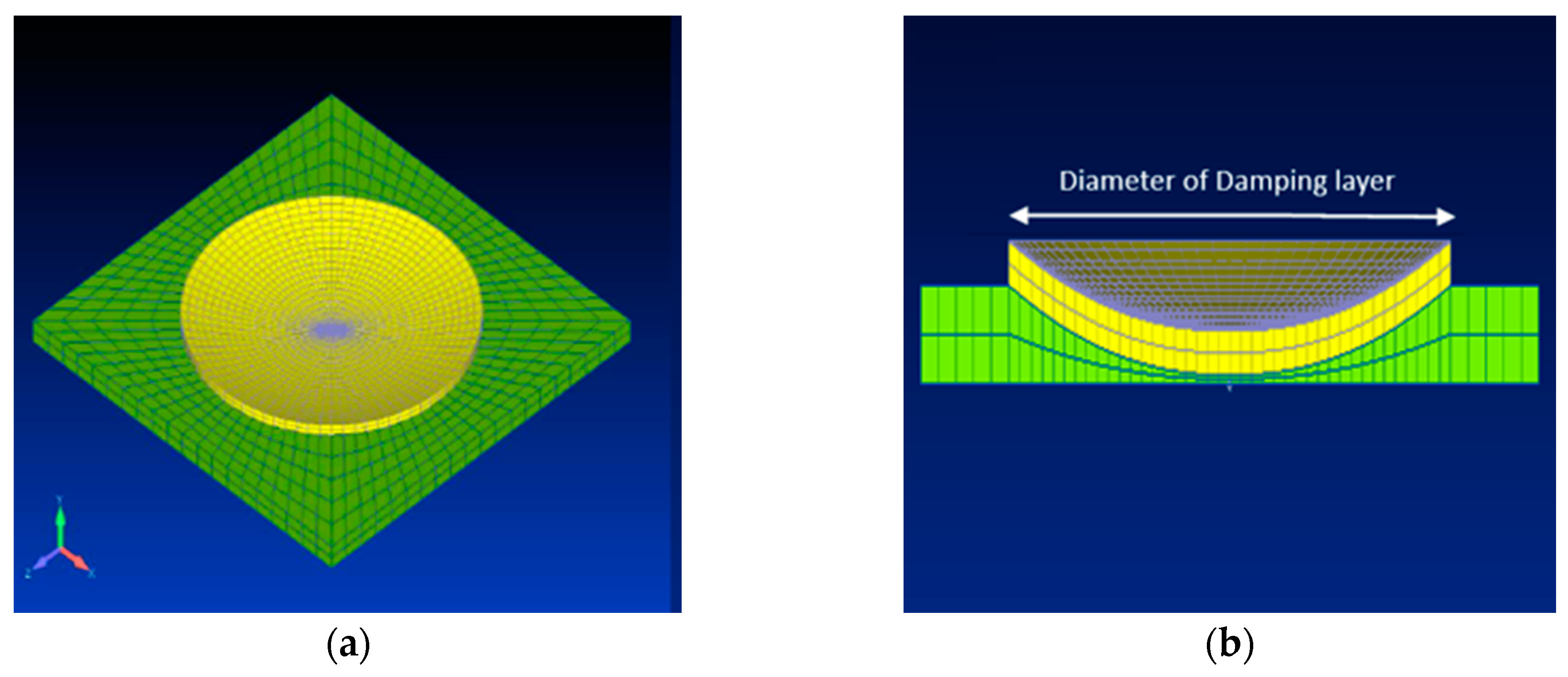
4.3. Design of Damping Layer
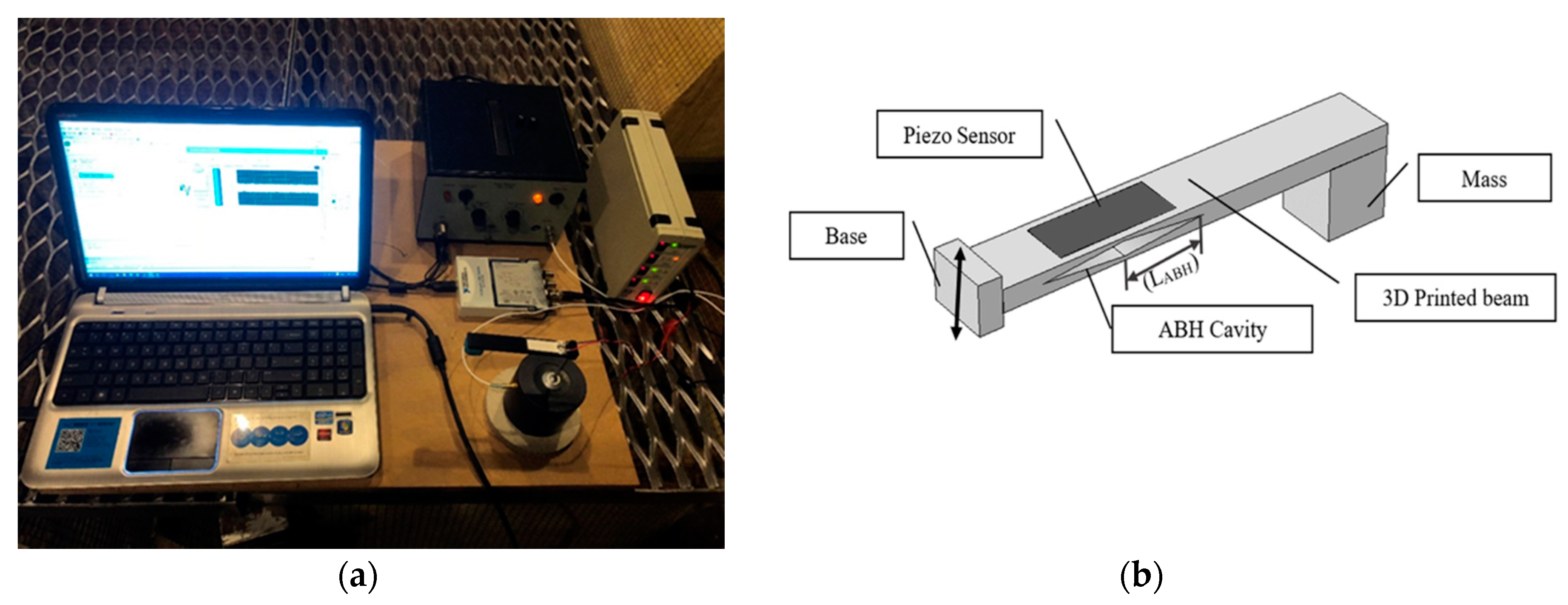
4.4. Studies on 3D-Printed Structures with ABH
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Rao, M.D. Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. J. Sound Vib. 2003, 262, 457–474. [Google Scholar] [CrossRef]
- Denis, V. Vibration Damping in Beams Using the Acoustic Black Hole Effect. Ph.D. Thesis, Universit´e du Maine, Le Mans, France, 2014. [Google Scholar]
- Bowyer, E.P.; O’Boy, D.J.; Krylov, V.V.; Gautier, F. Experimental investigation of damping flexural vibrations using two-dimensional Acoustic ‘Black Holes’. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA 2010), Leuven, Belgium, 20–22 September 2010. [Google Scholar]
- Nishimura, I.; Kobori, T.; Sakamoto, M.; Koshika, N.; Sasaki, K.; Ohrui, S. Active tuned mass damper. Smart Mater. Struct. 1992, 1, 306. [Google Scholar] [CrossRef]
- Mead, D.J. Passive Vibration Control; Wiley: Chichester, UK, 1999. [Google Scholar]
- Li, H.; Tian, C.; Deng, Z. Energy harvesting from low frequency applications using piezoelectric materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]
- Sojan, S.; Kulkarni, R. A Comprehensive Review of energy harvesting techniques and its potential applications. Int. J. Comput. Appl. 2016, 139, 14–19. [Google Scholar] [CrossRef]
- Zhao, C.; Prasad, M.G. Studies on vibration energy harvesting using a cantilever beam with a modified Acoustic Black Hole cavity. In Proceedings of the Inter-Noise 2018, Chicago, IL, USA, 26–29 August 2018. [Google Scholar]
- Feurtado, P.A.; Conlon, S.C.; Semperlotti, F.A. Normalized wave number variation parameter for Acoustic Black Hole design. J. Acoust. Soc. Am. 2014, 136, 148–152. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Conlon, S.C.; Semperlotti, F. Broadband energy harvesting using Acoustic Black Hole structural tailoring. Smart Mater. Struct. 2014, 23, 065021. [Google Scholar] [CrossRef]
- Pekeris, C.L. Theory of propagation of sound in a half-space of variable sound velocity under conditions of formation of a shadow zone. J. Acoust. Soc. Am. 1946, 18, 295–315. [Google Scholar] [CrossRef]
- Mironov, M.A. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval. Sov. Phys. Acoust. 1988, 34, 318–319. [Google Scholar]
- Krylov, V.V.; Bowyer, E.P. Acoustic Black Holes: A new approach to vibration damping in light-weight structures. Proc. Inst. Acoust. 2003, 35, 184–191. [Google Scholar]
- Krylov, V.V.; Shuvalov, A.L. Propagation of localised flexural vibrations along plate edges described by a power law. Proc. Inst. Acoust. 2000, 22, 263–270. [Google Scholar]
- Krylov, V.V. Acoustic Black Holes and their applications for vibration damping and sound absorption. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA 2012), Leuven, Belgium, 17–19 September 2012; pp. 933–944. [Google Scholar]
- Bowyer, E.P.; Krylov, V.V. Experimental investigation of damping flexural vibrations in glass fiber composite plates containing one- and two-dimensional Acoustic Black Holes. Compos. Struct. 2014, 107, 406–415. [Google Scholar] [CrossRef]
- Krylov, V.V. Acoustic Black Holes: Recent developments in the theory and applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1296–1306. [Google Scholar] [CrossRef] [PubMed]
- Conlon, S.C.; Fahnline, J.; Semperlotti, F. Numerical analysis of the vibroacoustic properties of plates with embedded grids of Acoustic Black Holes. J. Acoust. Soc. Am. 2015, 137, 447. [Google Scholar] [CrossRef] [PubMed]
- Conlon, S.C.; Semperlotti, F. Passive control of vibration and sound transmission for vehicle structures via embedded Acoustic Black Holes. In Proceedings of the Noise-Con 2013, Denver, CO, USA, 26–28 August 2013. [Google Scholar]
- Conlon, S.C.; Feurtado, P.A. Progressive phase trends in plates with embedded Acoustic Black Holes. J. Acoust. Soc. Am. 2018, 143, 921. [Google Scholar] [CrossRef] [PubMed]
- Ji, H.; Huang, W.; Qiu, J.; Cheng, L. Mechanics problems in application of Acoustic Black Hole structures. Adv. Mech. 2017, 47, 201710. [Google Scholar]
- Chong, B.M.P.; Tan, L.B.; Lim, K.M.; Lee, H.P. A review on Acoustic Black-Holes (ABH) and the experimental and numerical study of ABH-featured 3D printed beams. Int. J. Appl. Mech. 2017, 9, 1750078. [Google Scholar] [CrossRef]
- Bowyer, E.P.; Krylov, V.V. Acoustic Black Hole manufacturing for practical applications and the effect of geomatical and material imperfections. In Proceedings of the Inter-Noise 2016, Hamburg, Germany, 21–24 August 2016. [Google Scholar]
- Zhou, T.; Tang, L.; Ji, H.; Qiu, J.; Cheng, L. Dynamic and static properties of double-layered compound Acoustic Black Hole structures. Int. J. Appl. Mech. 2017, 9, 1750074. [Google Scholar] [CrossRef]
- Rothe, S.; Blech, C.; Watschke, H.; Vietor, T.; Langer, S.C. Numerical modelling of additively manufactured Acoustic Black Holes. In Proceedings of the Inter-Noise 2018, Chicago, IL, USA, 26–29 August 2018. [Google Scholar]
- Liang, Y.; Ji, H.; Qiu, J.; Cheng, L.; Wu, Y.; Zhang, C. Enhancement of piezoelectric energy harvesting using ABH structural tailoring. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018. [Google Scholar]
- Zhao, C.; Prasad, M.G. Studies on influence of geometrical parameters of an Acoustic Black Hole. In Proceedings of the Noise-Con 2017, Grand Rapids, MI, USA, 12–14 June 2017. [Google Scholar]
- O’Boy, D.J.; Krylov, V.V.; Kralovic, V. Damping of flexural vibrations in rectangular plates using the Acoustic Black Hole effect. J. Sound Vib. 2010, 329, 4672–4688. [Google Scholar] [CrossRef]
- Krylov, V.V.; Tilman, F.J.B.S. Acoustic ‘Black Holes’ for flexural waves as effective vibration dampers. J. Sound Vib. 2004, 274, 605–619. [Google Scholar] [CrossRef]
- Zhao, L. Passive vibration control based on embedded Acoustic Black Holes. J. Vib. Acoust. 2016, 138, 041002. [Google Scholar] [CrossRef]
- Ji, H.; Luo, J.; Qiu, J.; Cheng, L. Investigations on flexural wave propagation and attenuation in a modified one-dimensional Acoustic Black Hole using a laser excitation technique. Mech. Syst. Signal Process. 2018, 104, 19–35. [Google Scholar] [CrossRef]
- Huang, W.; Ji, H.; Qiu, J.; Cheng, L. Analysis of ray trajectories of flexural waves propagation over generalized Acoustic Black Hole indentations. J. Sound Vib. 2018, 417, 216–226. [Google Scholar] [CrossRef]
- O’Boy, D.J.; Bowyer, E.P.; Krylov, V.V. Damping of flexural vibrations in thin plates using one and two dimensional Acoustic Black Hole Effect. In Proceedings of the 10th International Conference on Recent Advances in Structural Dynamics (RASD 2010), Southampton, UK, 12–14 July 2010. [Google Scholar]
- Tang, L.; Cheng, L.; Ji, H.; Qiu, J. Characterization of Acoustic Black Hole effect using a one-dimensional fully-coupled and wavelet-decomposed semi-analytical model. J. Sound Vib. 2016, 374, 172–184. [Google Scholar] [CrossRef]
- Jeon, W. Vibration damping using a spiral Acoustic Black Hole. In Proceedings of the Inter-Noise 2016, Hamburg, Germany, 21–24 August 2016. [Google Scholar]
- Lee, J.Y.; Jeon, W. Vibration damping using a spiral Acoustic Black Hole. J. Acoust. Soc. Am. 2017, 141, 1437. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Cheng, L. A resonant beam damper tailored with Acoustic Black Hole features for broadband vibration reduction. J. Sound Vib. 2018, 430, 174–184. [Google Scholar] [CrossRef]
- Bowyer, E.P.; Krylov, V.V. Slots of power-law profile as Acoustic Black Holes for flexural waves in metallic and composite plates. Structures 2016, 6, 48–58. [Google Scholar] [CrossRef]
- Bowyer, E.P.; O’Boy, D.J.; Krylov, V.V.; Gautier, F. Experimental investigation of damping flexural vibrations in plates containing tapered indentations of power-law profile. Appli. Acoust. 2013, 74, 553–560. [Google Scholar] [CrossRef]
- O’Boy, D.J.; Krylov, V.V. Damping of flexural vibrations in circular plates with tapered central holes. J. Sound Vib. 2011, 330, 2220–2236. [Google Scholar] [CrossRef]
- Georgiev, V.B.; Cuenca, J.; Gautier, F.; Simon, L.; Krylov, V.V. Damping of structural vibrations in beams and elliptical plates using the Acoustic Black Hole effect. J. Sound Vib. 2011, 330, 2497–2508. [Google Scholar] [CrossRef]
- Jia, X.; Du, Y.; Zhao, K. Vibration Control of variable thickness plates with embedded Acoustic Black Holes and dynamic vibration absorbers. In Proceedings of the ASME 2015 Noise Control and Acoustics Division Conference, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- Krylov, V.V. Acoustic black holes as elements of metamaterials. In Proceedings of the IOP Physical Acoustics Group Tutorial Day, Loughborough, UK, 17 September 2015. [Google Scholar]
- Semperlotti, F.; Zhu, H. Acoustic meta-structures based on periodic Acoustic Black Holes. J. Acoust. Soc. Am. 2015, 137, 2265. [Google Scholar] [CrossRef]
- Foucaud, S.; Michon, G.; Gourinat, Y.; Pelat, A.; Gautier, F. Artificial Cochlea and Acoustic Black Hole travelling waves observation: Model and experimental results. J. Sound Vib. 2014, 333, 3428–3439. [Google Scholar] [CrossRef]
- Bowyer, E.P.; Krylov, V.V. Damping of flexural vibrations in turbofan blades using the Acoustic Black Hole effect. Appl. Acoust. 2014, 76, 359–365. [Google Scholar] [CrossRef]
- Bowyer, E.P.; Krylov, V.V. Sound Radiation of rectangular plates containing tapered indentations of power-law profile. In Proceedings of the 164th Meeting of the Acoustical Society of America, Kansas City, MO, USA, 22–26 October 2012. [Google Scholar]
- Feurtado, P.A.; Conlon, S.C. Experimental analysis of vibration and radiated sound power reduction using an array of Acoustic Black Holes. In Proceedings of the Inter-Noise 2015, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- Bowyer, E.P.; Krylov, V.V. A review of experimental investigations into the Acoustic Black Hole effect and its applications for reduction of flexural vibrations and structure-borne sound. In Proceedings of the Inter-Noise 2015, The 44th International Congress and Exposition on Noise Control Engineering, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- Mironov, M.A.; Pislyakov, V.V. One-dimensional acoustic waves in retarding structures with propagation velocity tending to zero. Acoust. Phys. 2002, 48, 347–352. [Google Scholar] [CrossRef]
- Azbaid, E.; Krylov, V.V.; O’Boy, D.J. Experimental investigation of the Acoustic Black Hole for sound absorption in air. In Proceedings of the 22nd International Congress on Sound and Vibration, Florence, Italy, 12–16 July 2015. [Google Scholar]
- Azbaid, E.; Krylov, V.; O’Boy, D.J. Investigation of the Acoustic Black Hole termination for sound waves propagating in cylindrical waveguides. In Proceedings of the Inter-Noise 2015, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- Zhou, X.; Semperlotti, F. The energy absorption properties of Helmholtz resonators enhanced by Acoustic Black Holes. In Proceedings of the Inter-Noise 2016, Hamburg, Germany, 21–24 August 2016. [Google Scholar]
- Zhao, L.; Conlon, S.C.; Semperlotti, F. An experimental study of vibration based energy harvesting in dynamically tailored structures with embedded Acoustic Black Holes. Smart Mater. Struct. 2015, 24, 065039. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q. Sound radiation of a beam with a wedge-shaped edge embedding Acoustic Black Hole feature. J. Sound Vib. 2019, 439, 287–299. [Google Scholar] [CrossRef]
- Tang, L.; Cheng, L. Broadband locally resonant band gaps in periodic beam structures with embedded Acoustic Black Holes. J. Appl. Phys. 2017, 121, 194901. [Google Scholar] [CrossRef]
- Zhao, C.; Prasad, M.G. Studies on sound radiation from beam with Acoustic Black Hole. In Proceedings of the Noise-Con 2016, Providence, RI, USA, 13–15 June 2016. [Google Scholar]
- Mustakerov, I.; Borissova, D. Multi-criteria model for optimal number and placement of sensors for structural health monitoring: lexicographic method implementation. Adv. Model. Optim. 2014, 16, 103–112. [Google Scholar]
- Li, X.; Ding, Q. Analysis on vibration energy concentration of the one-dimensional wedges-shaped Acoustic Black Hole structure. J. Intell. Mater. Syst. Struct. 2018, 29, 2137–2148. [Google Scholar] [CrossRef]
- Feurtado, P.A.; Conlon, S.C. Investigation of boundary-taper reflection for Acoustic Black Hole design. Noise Control Eng. J. 2015, 63, 460–466. [Google Scholar] [CrossRef]
- Denis, V.; Pelat, A.; Touzé, C.; Gautier, F. Improvement of the Acoustic Black Hole effect by using energy transfer due to geometric nonlinearity. Int. J. Non-Linear Mech. 2017, 94, 134–145. [Google Scholar] [CrossRef]
- McCormick, C.A.; Shepherd, M.R. Optimal design and position of an embedded one-dimensional Acoustic Black Hole. In Proceedings of the Inter-Noise 2018, Chicago, IL, USA, 26–29 August 2018. [Google Scholar]
- Tang, L.; Cheng, L. Loss of Acoustic Black Hole effect in a structure of finite size. Appl. Phys. Lett. 2016, 109, 014102. [Google Scholar] [CrossRef]
- Huang, W.; Ji, H.; Qiu, J.; Cheng, L. Wave energy focalization in a plate with imperfect two-dimensional Acoustic Black Hole indentation. J. Vib. Acoust. 2016, 138, 061004. [Google Scholar] [CrossRef]
- Denis, V.; Pelat, A.; Gautier, F. Scattering effects induced by imperfections on an Acoustic Black Hole placed at a structural waveguide termination. J. Sound Vib. 2016, 362, 56–71. [Google Scholar] [CrossRef]
- Conlon, S.C.; Fahnline, J.B.; Shepherd, M.R.; Feurtado, P.A. Vibration control using grids of Acoustic Black Holes: How many is enough? In Proceedings of the Inter-Noise 2015, San Francisco, CA, USA, 9–12 August 2015. [Google Scholar]
- Conlon, S.C.; Fahnline, J.B.; Semperlotti, F.; Feurtado, P.A. Enhancing the low frequency vibration reduction performance of plates with embedded Acoustic Black Holes. In Proceedings of the Inter-Noise 2014, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Zhu, H.; Semperlotti, F. Phononic thin plates with embedded Acoustic Black Holes. Phys. Rev. B 2015, 91, 104304. [Google Scholar] [CrossRef]
- Lee, J.; Jeon, W. An optimal design of 1D Acoustic Black Hole with damping layer for plate geometry. In Proceedings of the 23rd International Congress of Sound and Vibration, Athens, Greece, 10–14 July 2016; pp. 99–104. [Google Scholar]
- Kamran, M.; Saxena, A.A. Comprehensive study on 3D printing technology. MIT Int. J. Mech. Eng. 2016, 6, 63–69. [Google Scholar]









































© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Prasad, M.G. Acoustic Black Holes in Structural Design for Vibration and Noise Control. Acoustics 2019, 1, 220-251. https://doi.org/10.3390/acoustics1010014
Zhao C, Prasad MG. Acoustic Black Holes in Structural Design for Vibration and Noise Control. Acoustics. 2019; 1(1):220-251. https://doi.org/10.3390/acoustics1010014
Chicago/Turabian StyleZhao, Chenhui, and Marehalli G. Prasad. 2019. "Acoustic Black Holes in Structural Design for Vibration and Noise Control" Acoustics 1, no. 1: 220-251. https://doi.org/10.3390/acoustics1010014
APA StyleZhao, C., & Prasad, M. G. (2019). Acoustic Black Holes in Structural Design for Vibration and Noise Control. Acoustics, 1(1), 220-251. https://doi.org/10.3390/acoustics1010014





