Aerodynamic and Aeroacoustic Analysis of a Harmonically Morphing Airfoil Using Dynamic Meshing
Abstract
:1. Introduction
2. Computational Methodology
2.1. Governing Equations
2.1.1. Fluid Dynamics
2.1.2. Turbulence Modelling
2.1.3. Ffowcs-Williams and Hawkings Model
- ui = fluid velocity component in the xi direction
- un = fluid velocity component normal to the surface f = 0
- vi = surface velocity components in the xi direction
- vn = surface velocity component normal to the surface
- δ(f) = Dirac delta function
- H(f) = Heaviside function
- p′ = the sound pressure at the far field
- Tij = the Lighthill’s stress tensor
- a0 = far-field sound speed
- (f = 0) = corresponds to the source (emission) surface
- Pij is the compressive stress tensor
- nj is the unit normal vector pointing toward the exterior region
2D vs. 3D Analysis
Source Correlation Length and Acoustic Corrections
- = Span length simulated
- = Span length targeted (i.e., experimental setup)
- = Microphone distance in the simulation
- = Microphone targeted
2.2. Mathematical Model of the Trailing-Edge Flap Motion
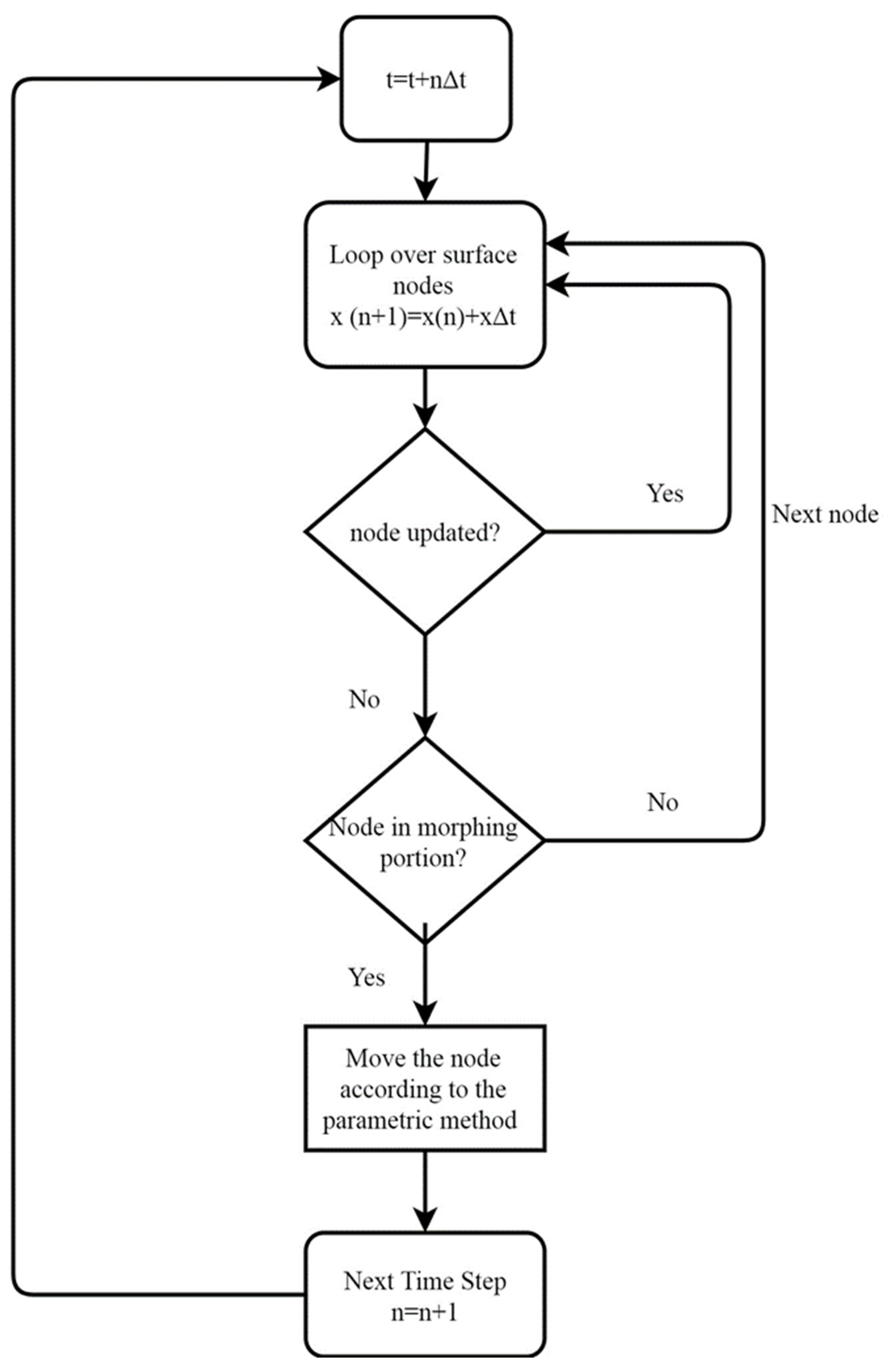
2.3. Dynamic Mesh Update Method
3. Numerical Procedure
4. Results and Discussion
4.1. Verification and Validation
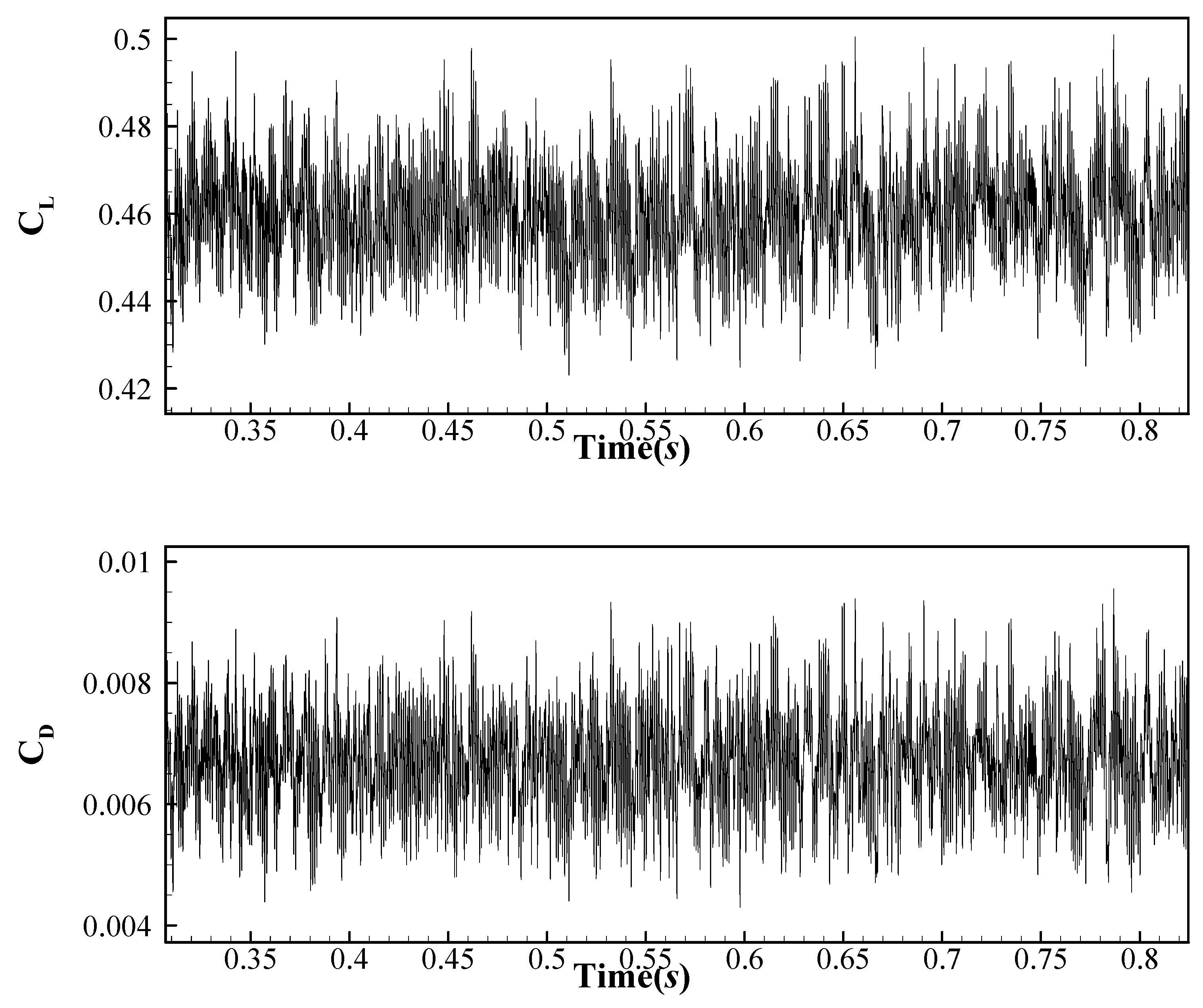
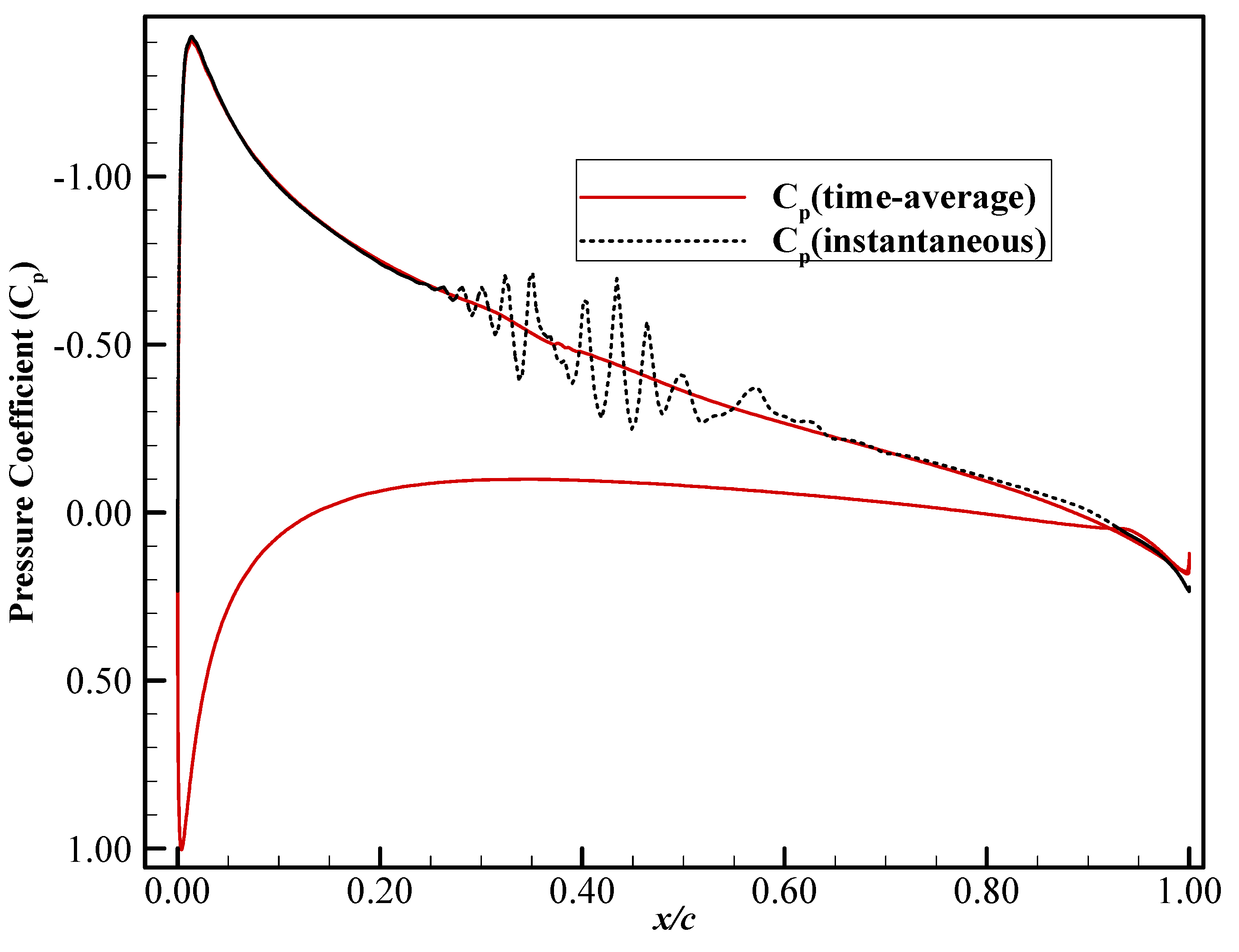
4.1.1. Unmorphed Case: M = 0.115, AoA = 4°, Re = 0.62 × 106
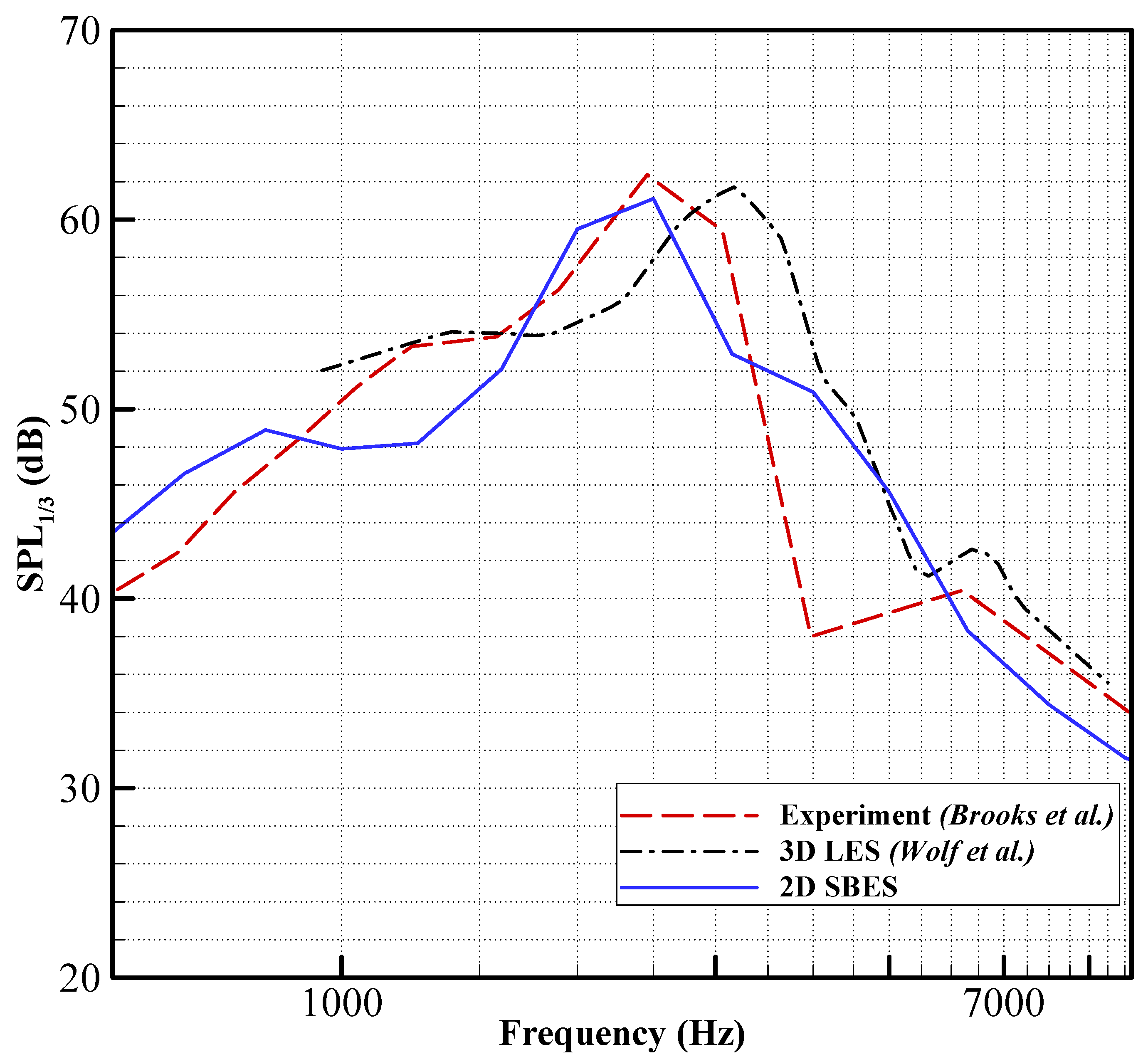
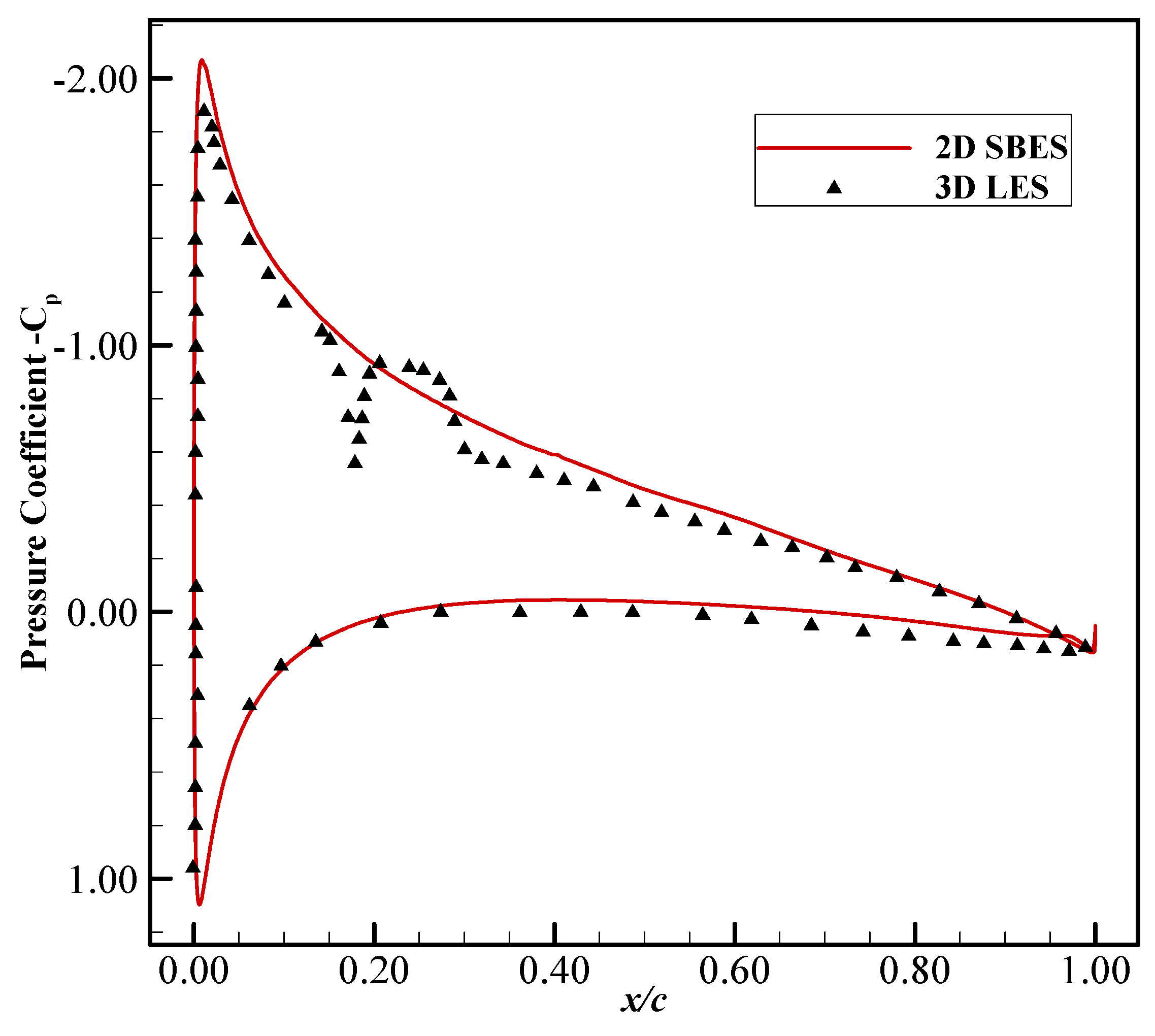
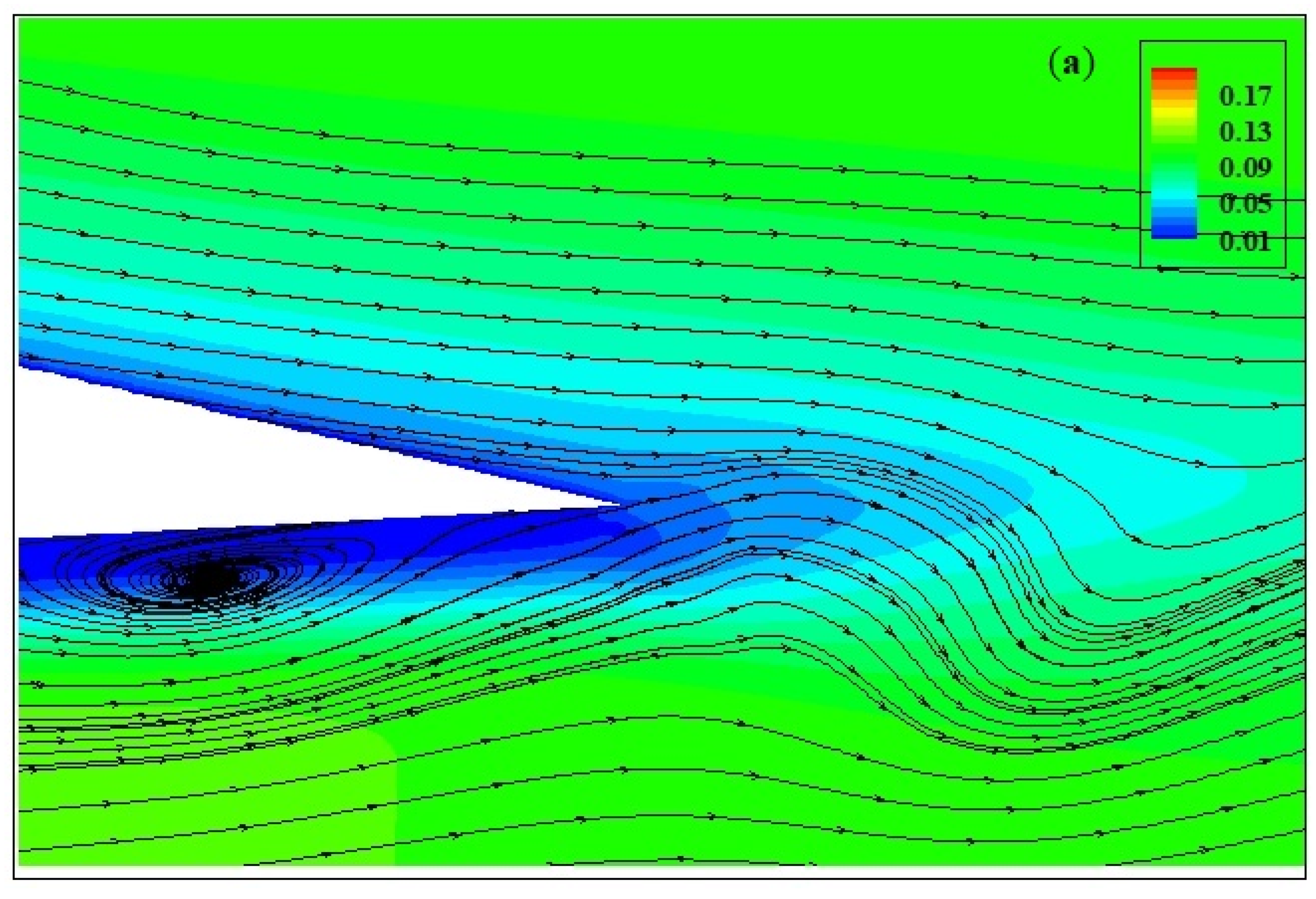
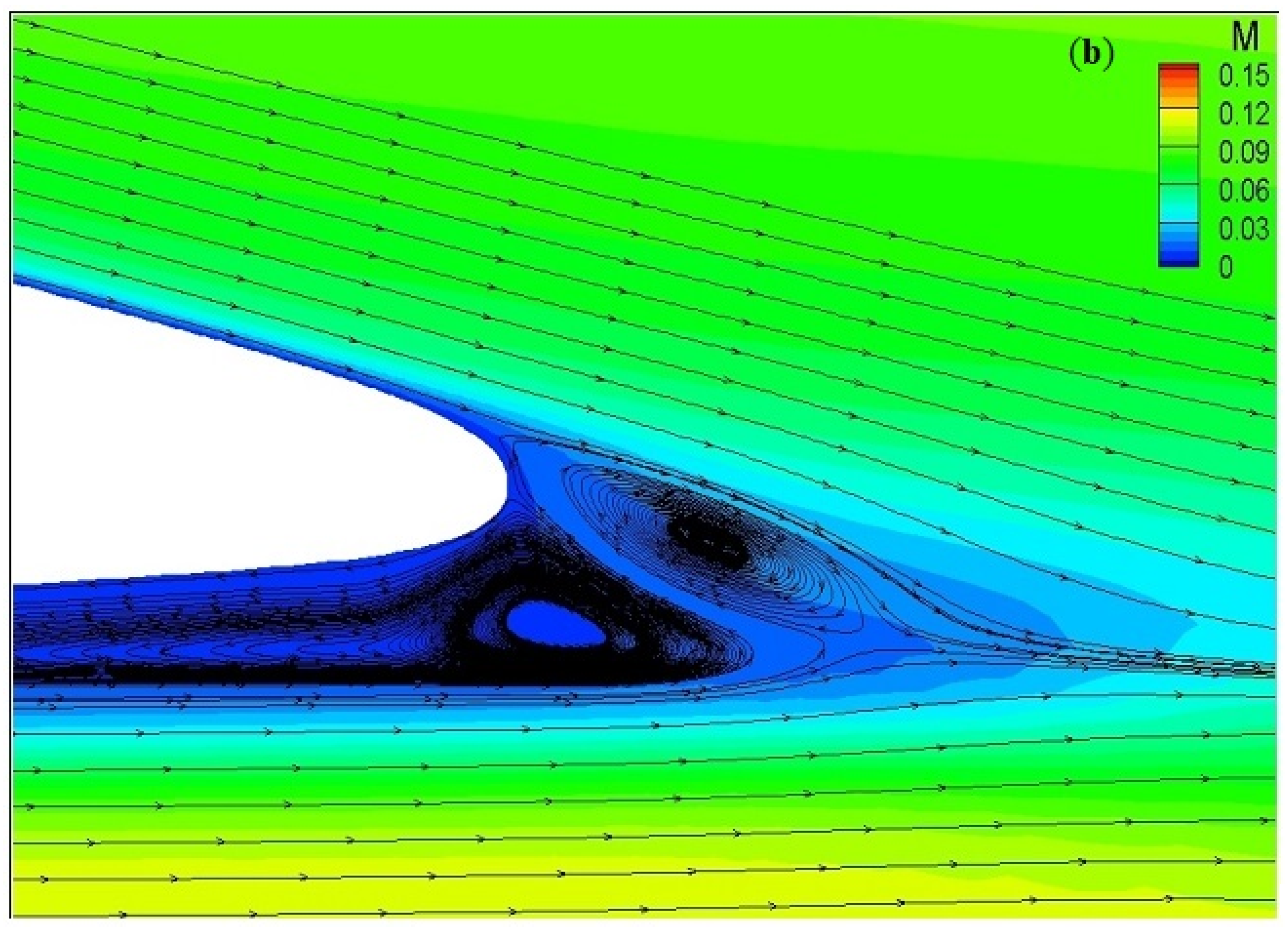
4.1.2. Unmorphed 2D vs. 3D case: M = 0.115, AoA = 5°, Re = 0.408 × 106
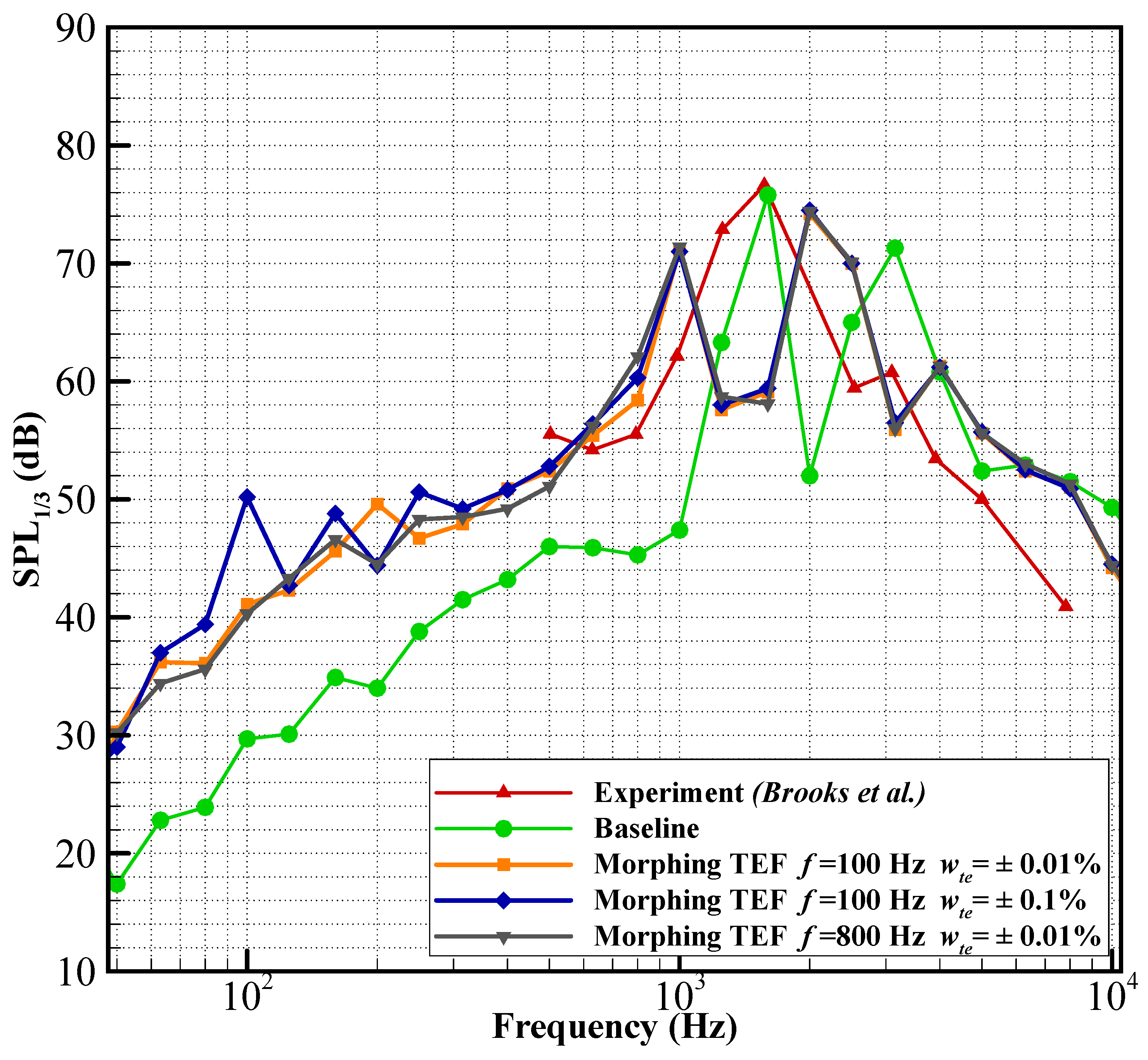
4.2. Harmonically Morphing Trailing Edge Flap
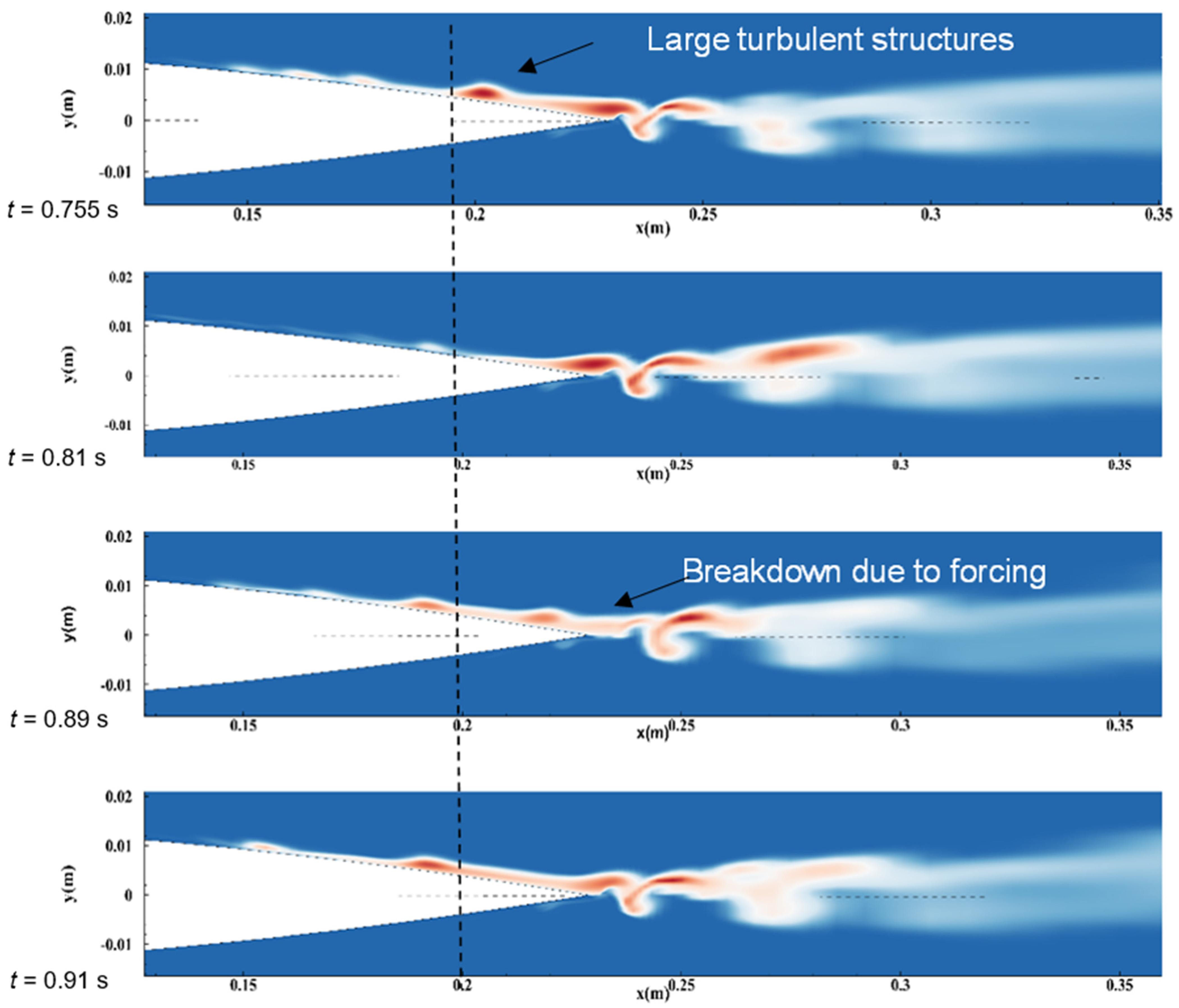
Effect of Harmonic Morphing
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Commission; Dareki, M.; Edelstenne, C.; Enders, T.; Fernandez, E.; Hartman, P.; Herteman, J.-P.; Kerkloh, M.; King, I.; Ky, P.; et al. Flightpath 2050: Europe’s Vision for Aviation. European Commission: Brussels, Belgium, 2011; 24p, ISBN 978-92-79-19724-6. [Google Scholar] [CrossRef]
- Nguyen, N. Project Elastically Shaped Future Air Vehicle Concept; NASA Innovation Fund Award: Washington, DC, USA, 2010.
- Macaraeg, M. Fundamental investigations of airframe noise. In Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998; American Institute of Aeronautics and Astronautics: Toulouse, France, 1998; pp. 123–132. [Google Scholar] [CrossRef] [Green Version]
- Abdessemed, C.; Yao, Y.; Bouferrouk, A.; Narayan, P. Analysis of a 3D Unsteady Morphing Wing with Seamless Side-edge Transition. In Proceedings of the 36th AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; AIAA: Atlanta, GA, USA, 2018; p. 2897416. [Google Scholar] [CrossRef] [Green Version]
- Kota, S.; Flick, P.; Collier, F.S. Flight Testing of FlexFloilTM Adaptive Compliant Trailing Edge. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; pp. 1–13. [Google Scholar] [CrossRef]
- NASA Hear This: 30 Percent Less Noise. Available online: https://www.nasa.gov/centers/armstrong/feature/ACTE_30_percent_less_noise.html (accessed on 8 October 2018).
- Fincham, J.H.S.; Friswell, M.I. Aerodynamic optimisation of a camber morphing aerofoil. Aerosp. Sci. Technol. 2015, 43, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Afonso, F.; Vale, J.; Lau, F.; Suleman, A. Performance based multidisciplinary design optimization of morphing aircraft. Aerosp. Sci. Technol. 2017, 67, 1–12. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, I.J. Control of flow separation by periodic excitation. Prog. Aerosp. Sci. 2000, 36, 487–545. [Google Scholar] [CrossRef]
- Winant, C.D.; Browand, F.K. Vortex pairing: The mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 1974, 63, 237. [Google Scholar] [CrossRef]
- Cattafesta, L.N.; Sheplak, M. Actuators for Active Flow Control. Annu. Rev. Fluid Mech. 2011, 43, 247–272. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Huang, P.G.; LeBeau, R.P.; Hauser, T. Numerical Study of Blowing and Suction Control Mechanism on NACA0012 Airfoil. J. Aircr. 2004, 41, 1005–1013. [Google Scholar] [CrossRef]
- Hue, D.; François, C.; Dandois, J.; Gebhardt, A. Simulations of an aircraft with constant and pulsed blowing flow control at the engine/wing junction. Aerosp. Sci. Technol. 2017, 69, 659–673. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Liou, M. Flow simulation and drag decomposition study of N3-X hybrid wing-body configuration. Aerosp. Sci. Technol. 2019, 85, 24–39. [Google Scholar] [CrossRef]
- Jukes, T.N.; Choi, K.-S. Flow control around a circular cylinder using pulsed dielectric barrier discharge surface plasma. Phys. Fluids 2009, 21, 084103. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Hajipour, M. Flow separation control over an airfoil using dual excitation of DBD plasma actuators. Aerosp. Sci. Technol. 2018, 79, 658–668. [Google Scholar] [CrossRef]
- Krzysiak, A.; Narkiewicz, J. Aerodynamic Loads on Airfoil with Trailing-Edge Flap Pitching with Different Frequencies. J. Aircr. 2006, 43, 407–418. [Google Scholar] [CrossRef]
- Jones, G.; Santer, M.; Debiasi, M.; Papadakis, G. Control of flow separation around an airfoil at low Reynolds numbers using periodic surface morphing. J. Fluids Struct. 2018, 76, 536–557. [Google Scholar] [CrossRef] [Green Version]
- Abdessemed, C.; Yao, Y.; Bouferrouk, A.; Narayan, P. Aerodynamic Analysis of a harmonically Morphing Flap Using a Hybrid Turbulence Model and Dynamic Meshing. In Proceedings of the 36th AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018; pp. 1–15. [Google Scholar] [CrossRef]
- Seifert, A.; Eliahu, S.; Greenblatt, D.; Wygnanski, I. Use of Piezoelectric Actuators for Airfoil Separation Control. AIAA J. 1998, 36, 1535–1537. [Google Scholar] [CrossRef]
- Kegerise, M.A.; Cabell, R.H.; Cattafesta, L.N. Real-time feedback control of flow-induced cavity tones-Part 1: Fixed-gain control. J. Sound Vib. 2007, 307, 906–923. [Google Scholar] [CrossRef]
- Liggett, N.; Smith, M.J. The physics of modeling unsteady flaps with gaps. J. Fluids Struct. 2013, 38, 255–272. [Google Scholar] [CrossRef]
- Scheller, J.; Chinaud, M.; Rouchon, J.F.; Duhayon, E.; Cazin, S.; Marchal, M.; Braza, M. Trailing-edge dynamics of a morphing NACA0012 aileron at high Reynolds number by high-speed PIV. J. Fluids Struct. 2015, 55, 42–51. [Google Scholar] [CrossRef] [Green Version]
- Jodin, G.; Motta, V.; Scheller, J.; Duhayon, E.; Döll, C.; Rouchon, J.F.; Braza, M. Dynamics of a hybrid morphing wing with active open loop vibrating trailing edge by time-resolved PIV and force measures. J. Fluids Struct. 2017, 74, 263–290. [Google Scholar] [CrossRef] [Green Version]
- Abdessemed, C.; Yao, Y.; Bouferrouk, A.; Narayan, P. Morphing airfoils unsteady flow analysis using dynamic meshing. Int. J. Numer. Methods Heat Fluid Flow 2017, 23. [Google Scholar] [CrossRef] [Green Version]
- Abdessemed, C.; Yao, Y.; Narayan, P.; Bouferrouk, A. Unsteady parametrization of a morphing wing design for improved aerodynamic performance. In Proceedings of the 52rd 3AF International Conference on Applied Aerodynamics, Lyon, France, 27–29 March 2017; pp. 1–10. [Google Scholar]
- Alqash, S.; Dhote, S.; Behdinan, K. Predicting far-field noise generated by a landing gear using multiple two-dimensional simulations. Appl. Sci. 2019, 9, 4485. [Google Scholar] [CrossRef] [Green Version]
- Doolan, C.J. Computational bluff body aerodynamic noise prediction using a statistical approach. Appl. Acoust. 2010, 71, 1194–1203. [Google Scholar] [CrossRef]
- Brentner, K.S.; Rumsey, C.L.; Cox, J.S.; Younis, B.A. Computation of Sound Generated By Flow Over A Circular Cylinder: An Acoustic Analogy Approach. In Proceedings of the NASA Conference Publication; NASA: Washington, DC, USA, 1996; pp. 1–7. [Google Scholar]
- Arunajatesan, S.; Sinha, N. Hybrid RANS-LES Modeling for Cavity Aeroacoutics Predictions. Int. J. Aeroacoust. 2003, 2, 65–93. [Google Scholar] [CrossRef]
- Housman, J.A.; Stich, G.D.; Kiris, C.C. Predictions of slat noise from the 30P30N at high angles of attack using zonal hybrid rans-les. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019; p. 2438. [Google Scholar] [CrossRef] [Green Version]
- Mahak, M.; Naqavi, I.Z.; Tucker, P.G. Cost-effective hybrid RANS-LES type method for jet turbulence and noise prediction. Int. J. Aeroacoust. 2017, 16, 97–111. [Google Scholar] [CrossRef]
- Syawitri, T.P.; Yao, Y.; Yao, J.; Chandra, B. Assessment of stress-blended eddy simulation model for accurate performance prediction of vertical axis wind turbine. Int. J. Numer. Methods Heat Fluid Flow 2020. [Google Scholar] [CrossRef]
- Pratomo, H.P.S.; Suprianto, F.D.; Sutrisno, T. Hybrid turbulence models: Recent progresses and further researches. In Proceedings of the 1st International Conference on Automotive, Manufacturing, and Mechanical Engineering, Bali, Indonesia, 26−28 September 2018; EDP Sciences: Les Ulis, France, 2019; Volume 130, p. 1013. [Google Scholar] [CrossRef]
- Wolf, W.R.; Lele, S.K. Trailing-Edge Noise Predictions Using Compressible Large-Eddy Simulation and Acoustic Analogy. AIAA J. 2012, 50, 2423–2434. [Google Scholar] [CrossRef]
- Brooks, T.F.; Pope, D.S.; Marcolini, M. Airfoil Self-Noise and Prediction; NASA Technical Report; 1989.
- ANSYS Release 18.2, Help System; ANSYS Inc.: Canonsburg, PA, USA, 2018.
- Menter, F. Stress-blended eddy simulation (SBES)—A new paradigm in hybrid RANS-LES modeling. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Cham, Switzerland, 2016; Volume 137, pp. 27–37. ISBN 978-3-319-70031-1. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Weihing, P.; Letzgus, J.; Lutz, T.; Krämer, E. Development of alternative shielding functions for detached-eddy simulations. In Progress in Hybrid RANS-LES Modelling; Springer: Cham, Switzerland, 2020; pp. 109–118. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Williams, J.E.F.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. A R. Soc. 1952, 211, 564–587. [Google Scholar]
- Garipova, L.I.; Batrakov, A.S.; Kusyumov, A.N.; Mikhaylov, S.A.; Barakos, G. Aerodynamic and acoustic analysis of helicopter main rotor blade tips in hover. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2101–2118. [Google Scholar] [CrossRef]
- Lockard, D.P. Efficient, two-dimensional implementation of the Ffowcs Williams and Hawkings equation. J. Sound Vib. 2000, 229, 897–911. [Google Scholar] [CrossRef]
- De Gennaro, M.; Kühnelt, H.; Zanon, A. Numerical Prediction of the Tonal Airborne Noise for a NACA 0012 Aerofoil at Moderate Reynolds Number Using a Transitional URANS Approach. Arch. Acoust. 2017, 42, 653–675. [Google Scholar] [CrossRef] [Green Version]
- Golubev, V.V.; Nguyen, L.; Mankbadi, R.R.; Roger, M.; Visbal, M.R. On Flow-Acoustic Resonant Interactions in Transitional Airfoils. Int. J. Aeroacoust. 2014, 13, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Singer, B.A.; Lockard, D.P.; Brentner, K.S. Computational Aeroacoustic Analysis of Slat Trailing-Edge Flow. AIAA J. 2000, 38, 1558–1564. [Google Scholar] [CrossRef]
- Golubev, V.; Nguyen, L.; Roger, M.; Visbal, M. On Interaction of Airfoil Leading and Trailing Edge Noise Sources in Turbulent Flow. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5–8 June 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011; p. 2859. [Google Scholar] [CrossRef]
- Golubev, V.; Nguyen, L.; Roger, M.; Visbal, M. High-Accuracy Simulations of Flow-Acoustic Resonant Interactions in Airfoil Transitional Boundary Layers. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; pp. 4–6. [Google Scholar] [CrossRef]
- Golubev, V.V.; Nguyen, L.; Mankbadi, R.R.; Dudley, J.G.; Visbal, M.R. On Self-Sustained Flow-Acoustic Resonant Interactions in Airfoil Transitional Boundary Layers. In Proceedings of the 43rd Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013; pp. 1–16. [Google Scholar] [CrossRef]
- Kato, C.; Iida, A.; Takano, Y.; Fujita, H.; Ikegawa, M. Numerical prediction of aerodynamic noise radiated from low Mach number turbulent wake. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1993. [Google Scholar] [CrossRef]
- Orselli, R.; Meneghini, J.; Saltara, F. Two and Three-Dimensional Simulation of Sound Generated by Flow Around a Circular Cylinder. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009; American Institute of Aeronautics and Astronautics: Miami, FL, USA, 2009; p. 3270. [Google Scholar] [CrossRef] [Green Version]
- Seo, J.H.; Moon, Y.J. Aerodynamic noise prediction for long-span bodies. J. Sound Vib. 2007, 306, 564–579. [Google Scholar] [CrossRef]
- Bies, D.; Hansen, C. Engineering Noise Control: Theory and Practice; Taylor and Francis: New York, NY, USA, 2009; Volume 3, ISBN 9780203872406. [Google Scholar]
- Jacobs, E.; Ward, K.; Pinkerton, R. The characteristics of 78 related airfoil sections from tests in the variable-density wind tunnel. Natl. Advis. Comm. Aeronaut. 1933, 299–354. [Google Scholar] [CrossRef]
- Abdessemed, C. Dynamic Mesh Framework for Morphing Wings CFD. Ph.D. Thesis, University of the West of England, Bristol, UK, 2019. [Google Scholar]
- Abdessemed, C. Dynamic Mesh Framework for Morphing Wings CFD—User Defined Function; Zenodo: Genève, Switzerland, 2020. [Google Scholar] [CrossRef]
- Menter, F.R. Best Practice: Scale-Resolving Simulations in ANSYS CFD; ANSYS Inc.: Canonsburg, PA, USA, 2012; pp. 1–70. [Google Scholar] [CrossRef]
- Abdessemed, C.; Yao, Y.; Bouferrouk, A.; Narayan, P. Influence of non-iterative time-advancement schemes on the aerodynamic prediction of pitching airfoils using dynamic mesh. In Proceedings of the 8th International Symposium on Physics of Fluids (ISPF8), Xi’an, China, 10–13 June 2019. [Google Scholar]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; SAND-80-2114; Sandia National Laboratories: Albuquerque, NM, USA, 1981.
- Nash, E.C.; Lowson, M.V.; Mcalpine, A. Boundary-layer instability noise on aerofoils. J. Fluid Mech. 1999, 382. [Google Scholar] [CrossRef]
- Arbey, H.; Bataille, J. Noise generated by airfoil profiles placed in a uniform laminar flow. J. Fluid Mech. 1983, 134, 33–47. [Google Scholar] [CrossRef] [Green Version]
- Paterson, R.W.; Vogt, P.G.; Fink, M.R.; Munch, C.L. Vortex noise of isolated airfoils. J. Aircr. 1973, 10, 296–302. [Google Scholar] [CrossRef]
- Trümner, J.; Mundt, C. Comparison of Two Different CAA Methods for the Prediction of Far-Field Noise from Heated and Unheated Jets. In Proceedings of the 7th European Conference for Aeronautics and Aerospace Sciences, Milan, Italy, 3–6 July 2017; Volume 37, pp. 1–14. [Google Scholar]
- Munday, P.M.; Taira, K. On the lock-on of vortex shedding to oscillatory actuation around a circular cylinder. Phys. Fluids 2013, 25. [Google Scholar] [CrossRef]





| Configuration | Reynolds Number | Angle of Attack (°) | Mach Number |
|---|---|---|---|
| Unmorphed case | 0.62 × 106 | 4 | 0.115 |
| Unmorphed case: 2D SBES vs. 3D LES | 0.408 × 106 | 5 | 0.115 |
| Harmonically Morphing TEF | 0.62 × 106 | 4 | 0.115 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdessemed, C.; Bouferrouk, A.; Yao, Y. Aerodynamic and Aeroacoustic Analysis of a Harmonically Morphing Airfoil Using Dynamic Meshing. Acoustics 2021, 3, 177-199. https://doi.org/10.3390/acoustics3010013
Abdessemed C, Bouferrouk A, Yao Y. Aerodynamic and Aeroacoustic Analysis of a Harmonically Morphing Airfoil Using Dynamic Meshing. Acoustics. 2021; 3(1):177-199. https://doi.org/10.3390/acoustics3010013
Chicago/Turabian StyleAbdessemed, Chawki, Abdessalem Bouferrouk, and Yufeng Yao. 2021. "Aerodynamic and Aeroacoustic Analysis of a Harmonically Morphing Airfoil Using Dynamic Meshing" Acoustics 3, no. 1: 177-199. https://doi.org/10.3390/acoustics3010013
APA StyleAbdessemed, C., Bouferrouk, A., & Yao, Y. (2021). Aerodynamic and Aeroacoustic Analysis of a Harmonically Morphing Airfoil Using Dynamic Meshing. Acoustics, 3(1), 177-199. https://doi.org/10.3390/acoustics3010013








