A Hybrid Multistep Procedure for the Vibroacoustic Simulation of Noise Emission from Wind Turbines
Abstract
:1. Introduction
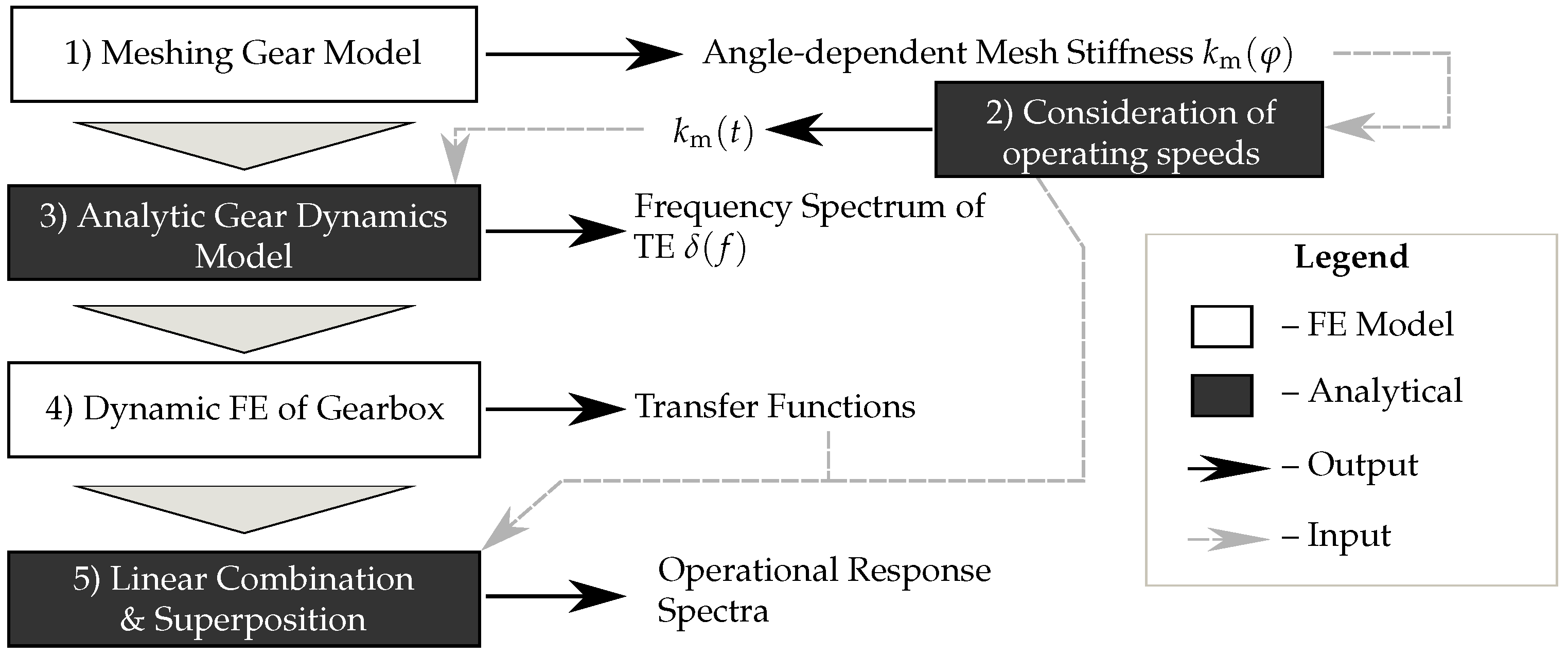
2. Hybrid Analytical-Computational Procedure
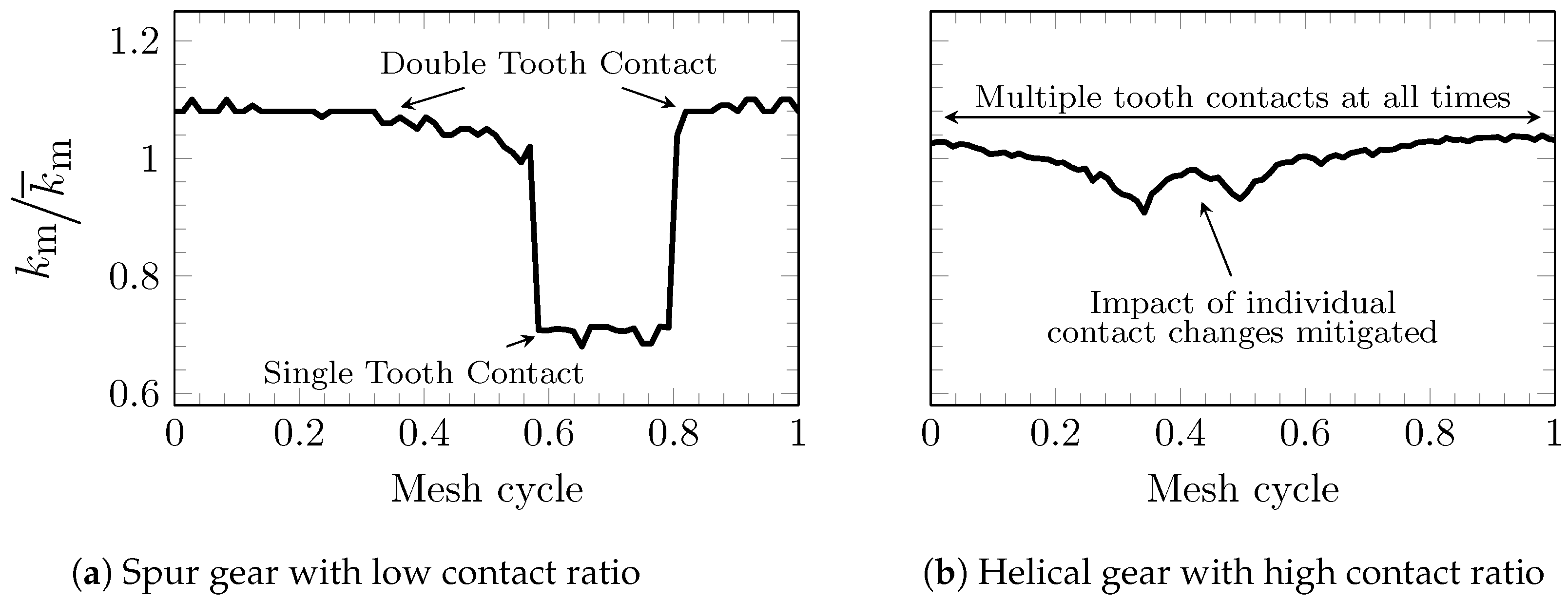
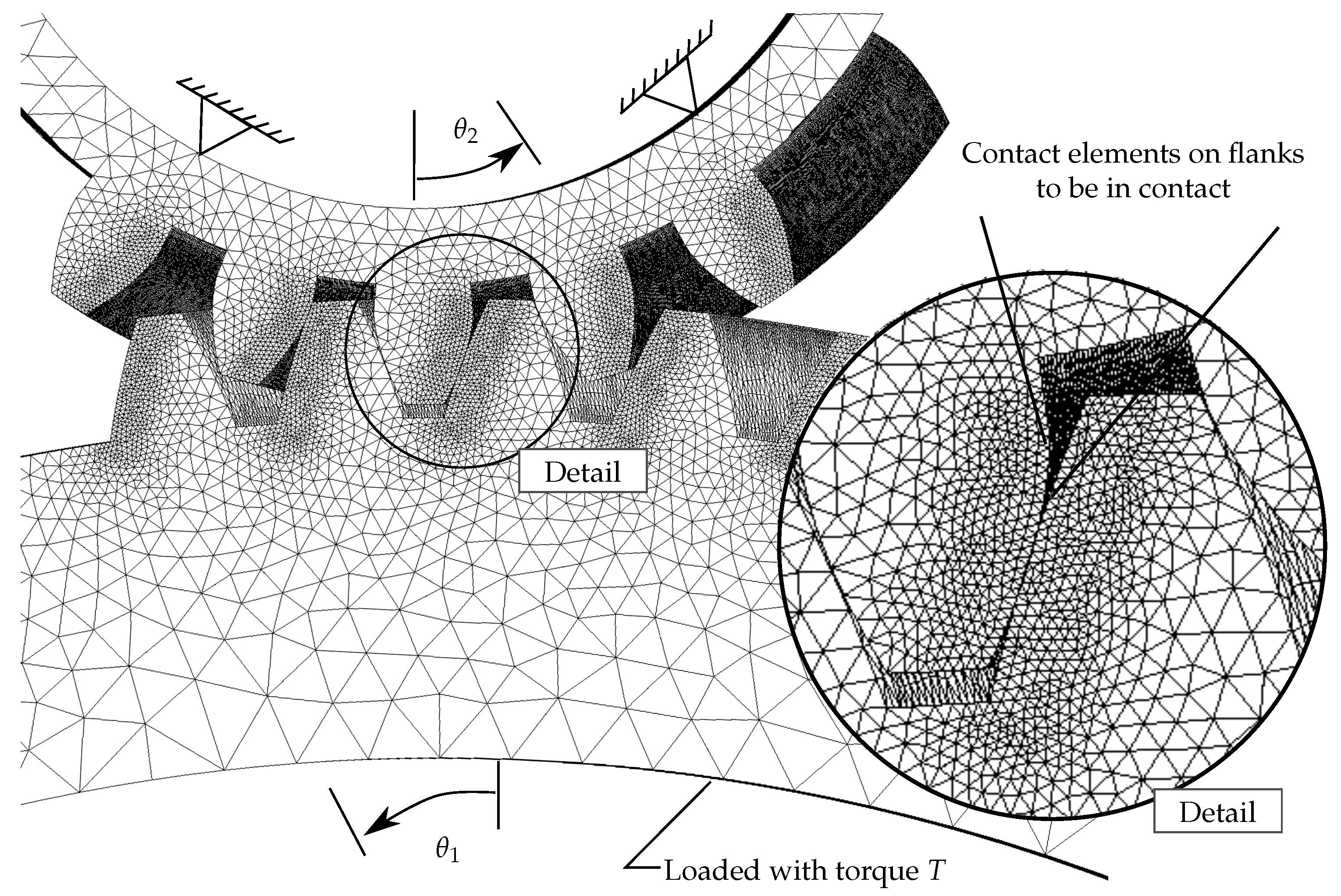
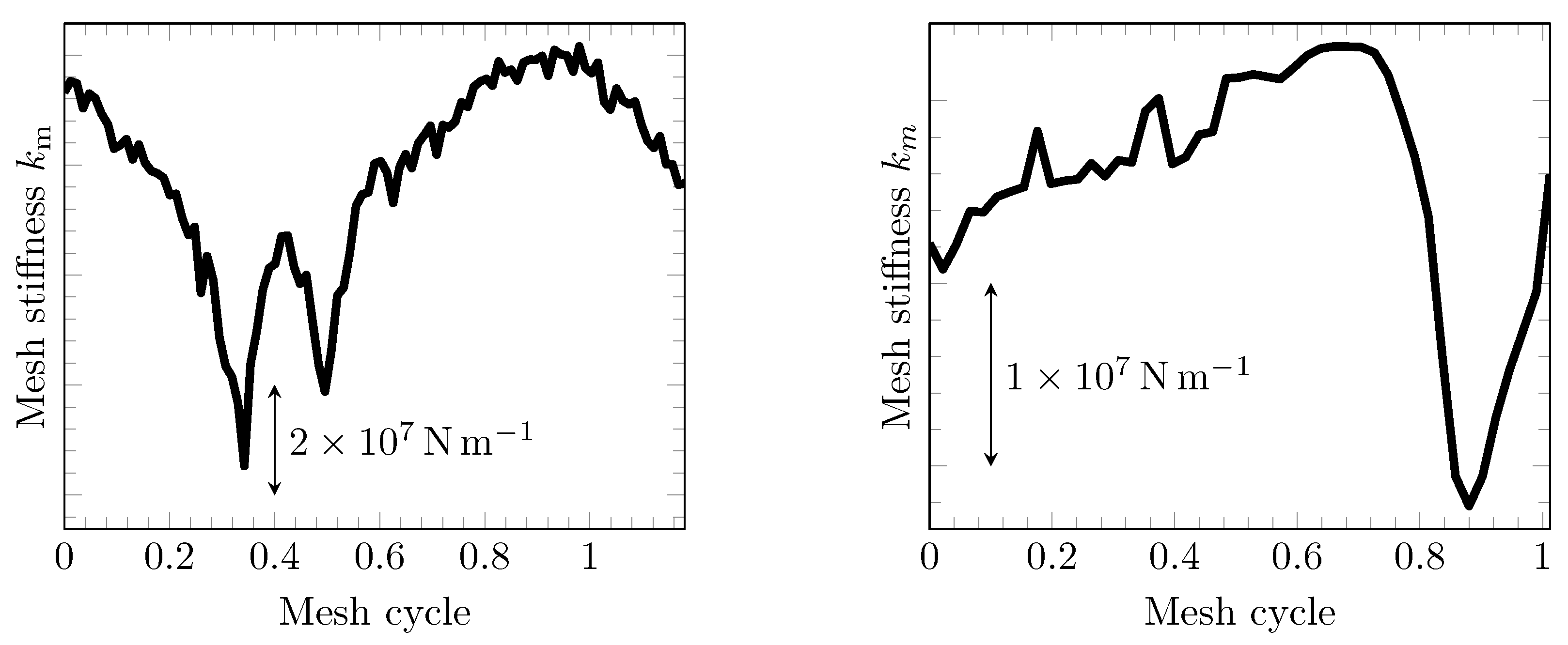
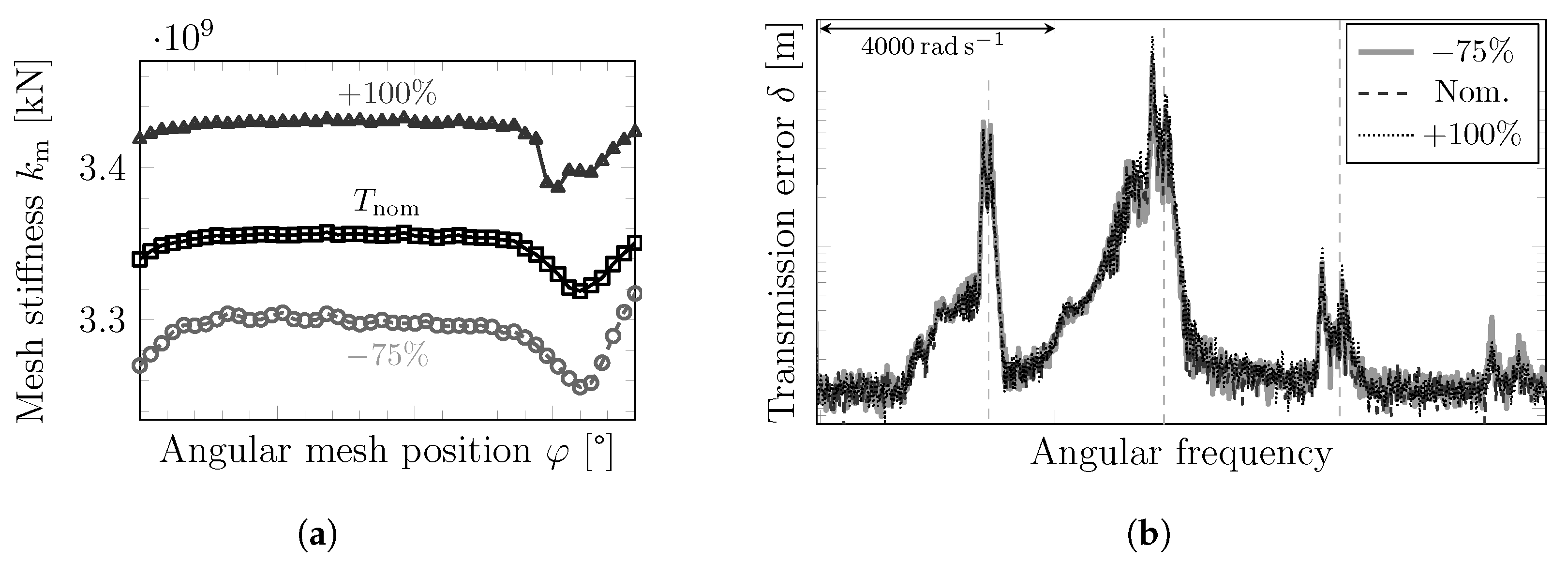
2.1. Angle-Dependent Mesh Stiffness (Step 1)
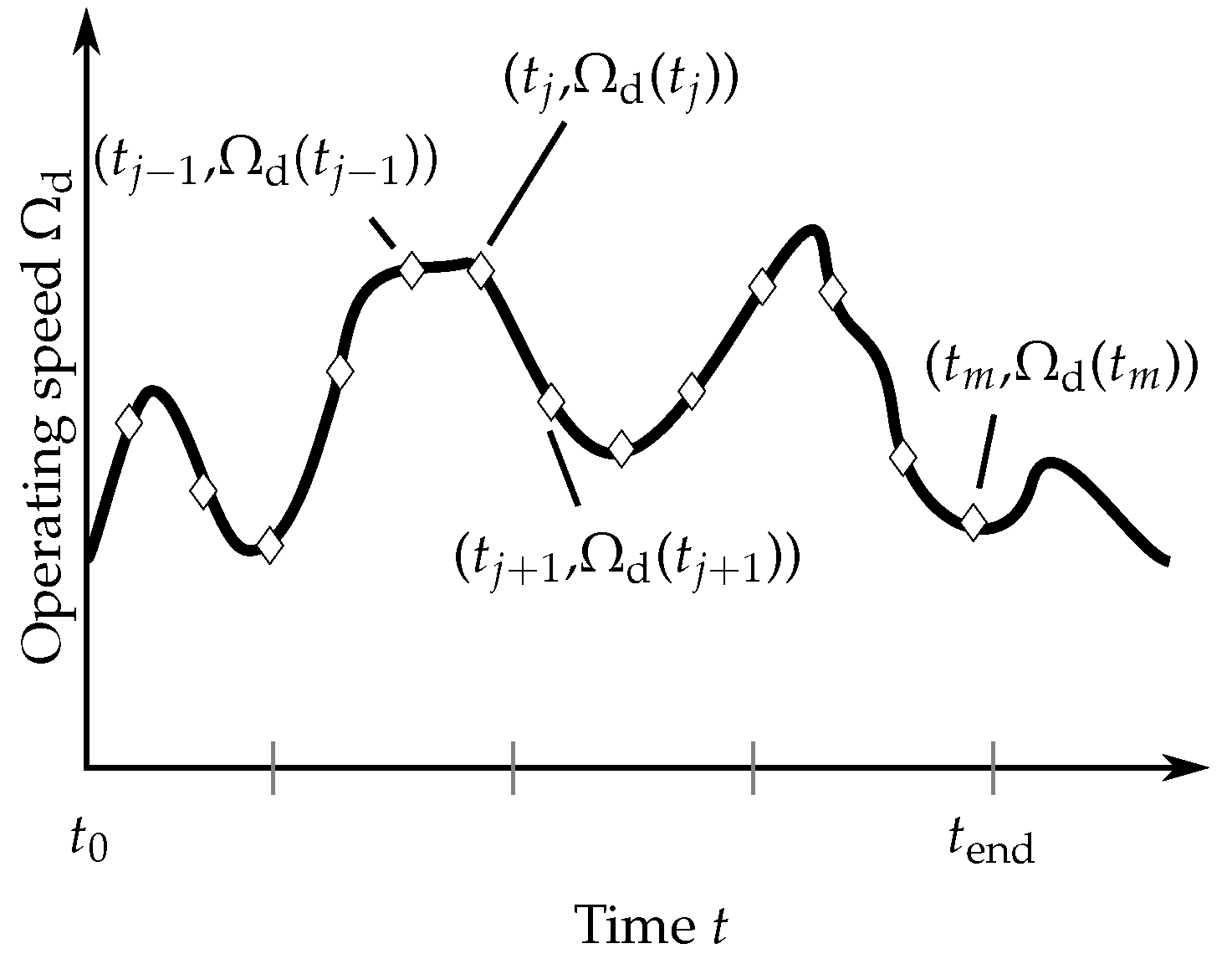
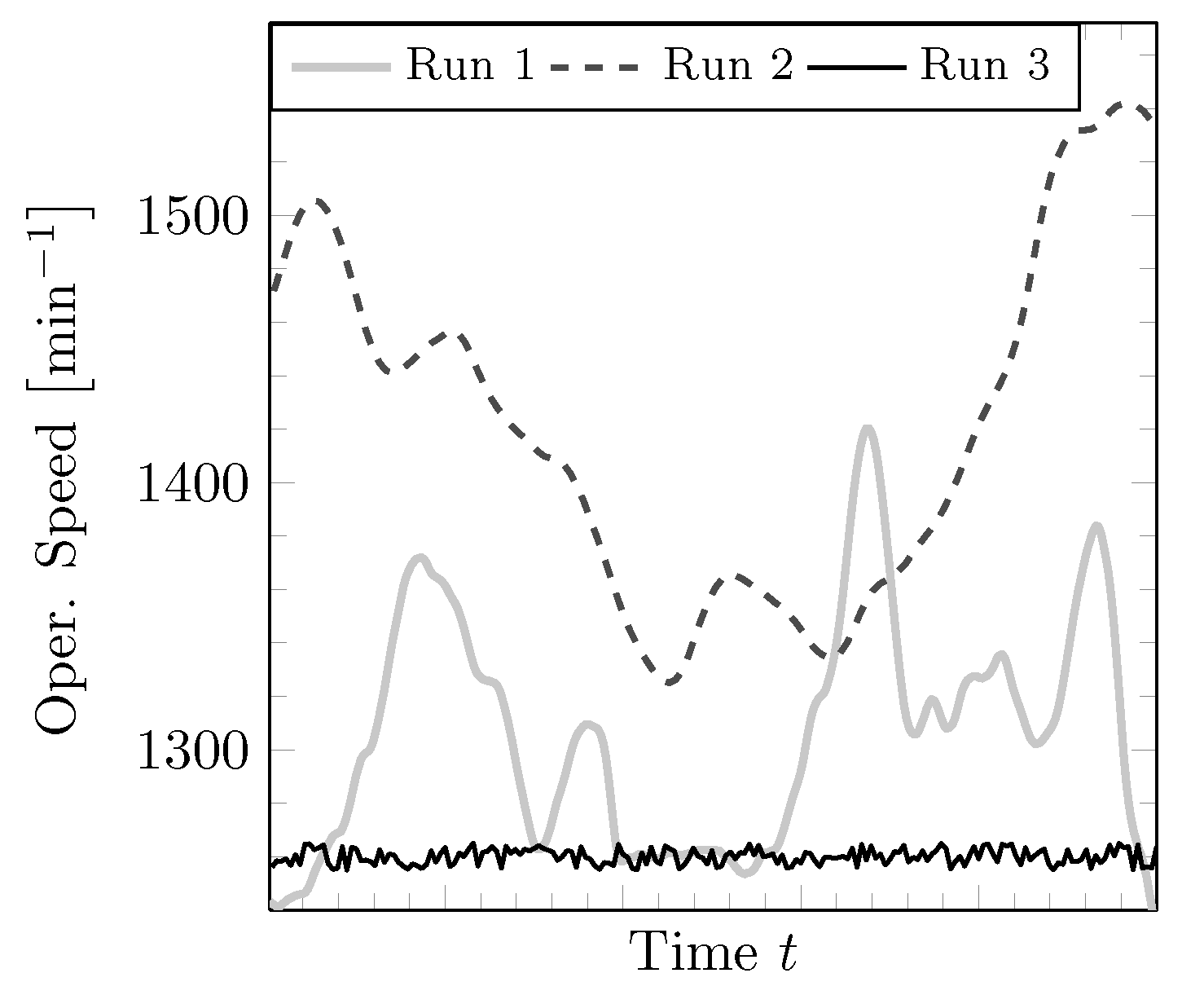
2.2. Consideration of Time-Varying Operating Conditions (Step 2)
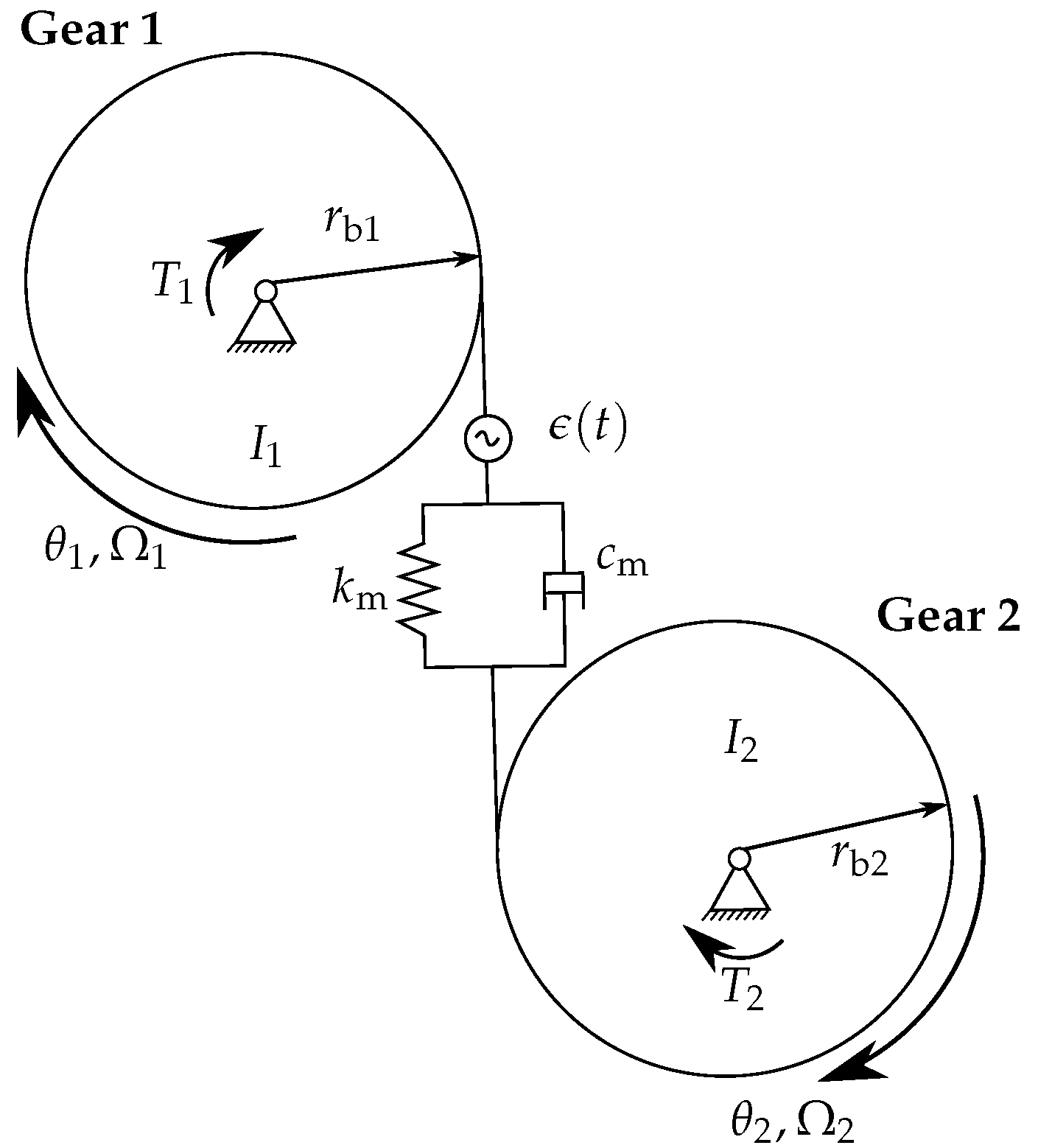
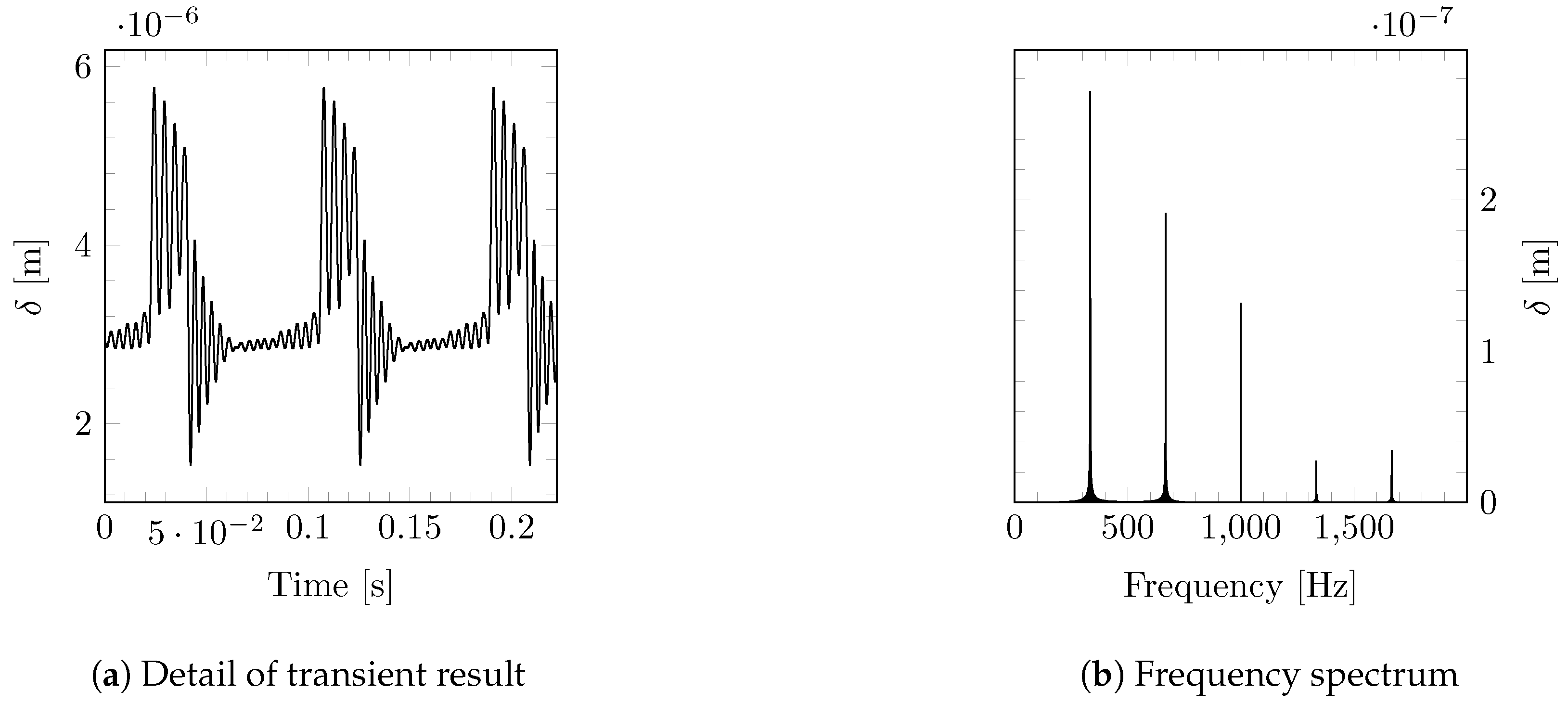
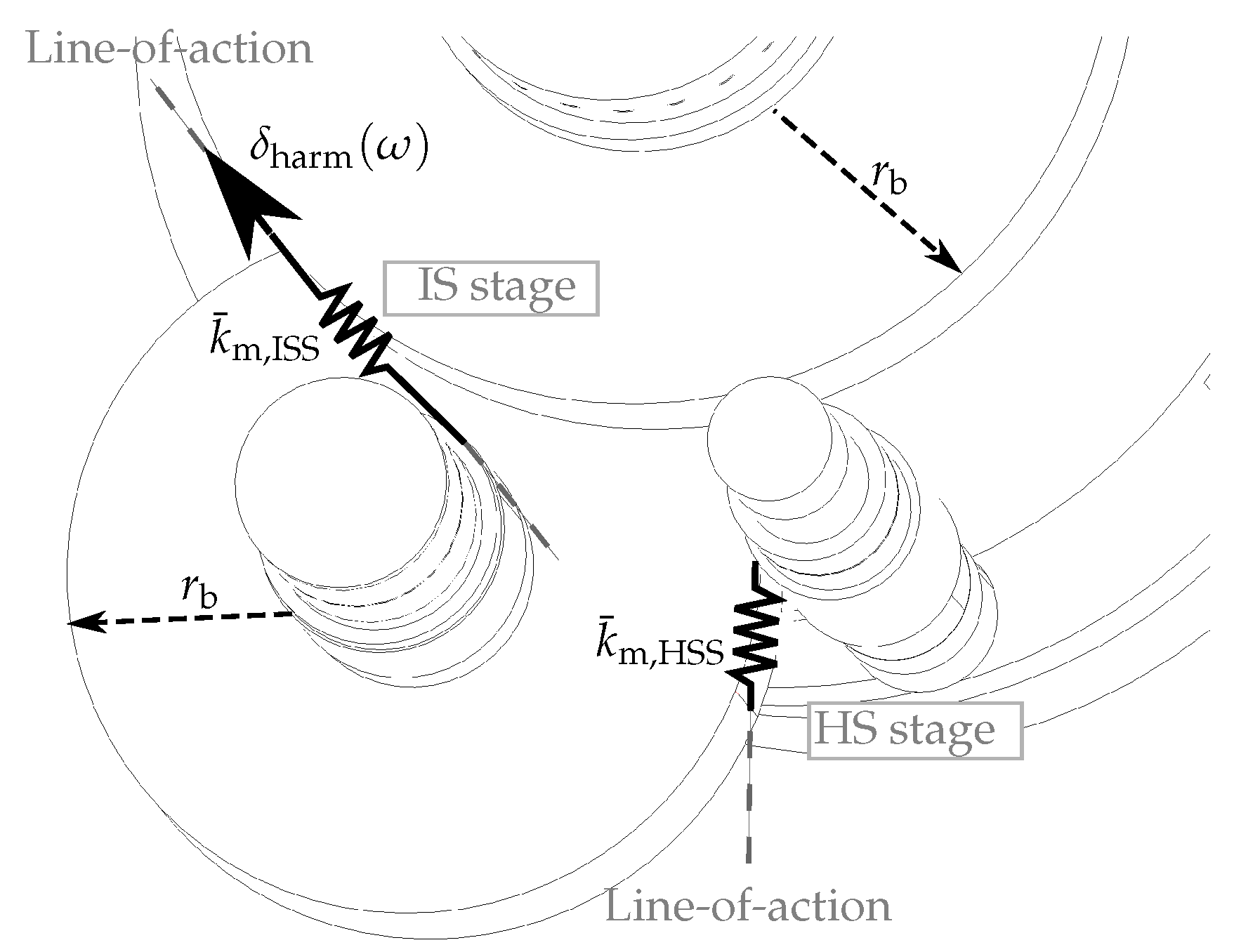
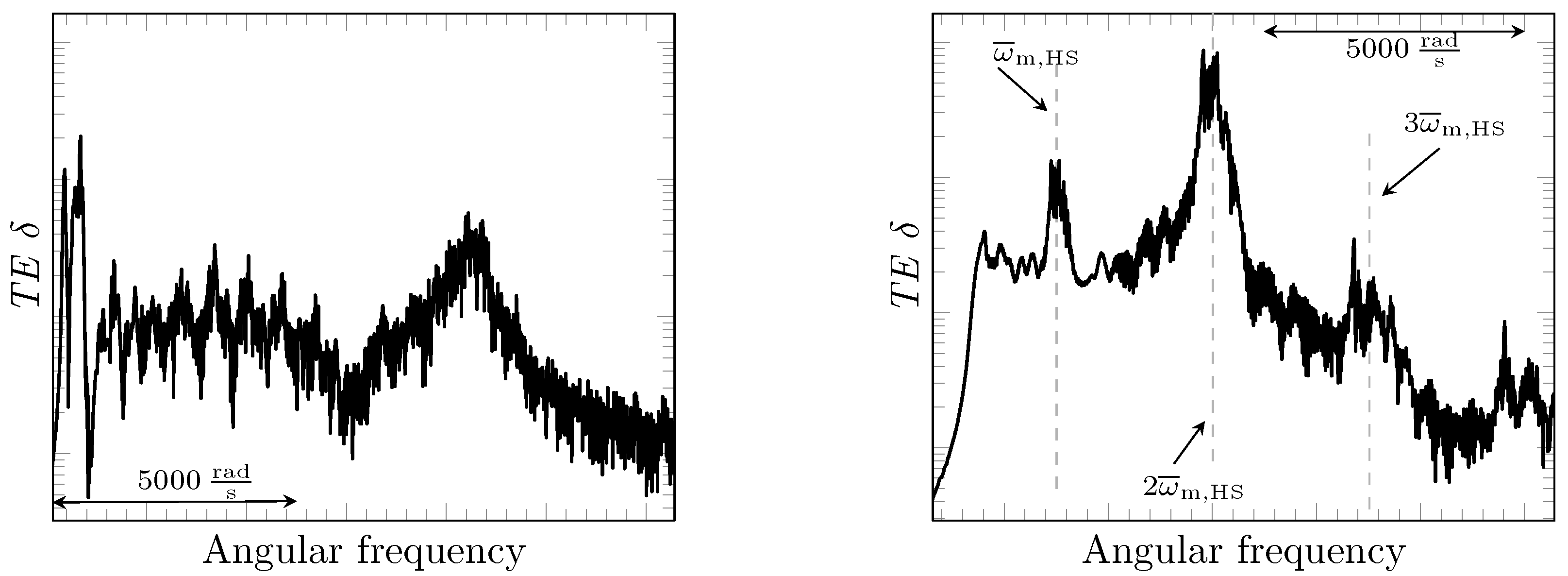
2.3. Transient Gear Dynamics (Step 3)
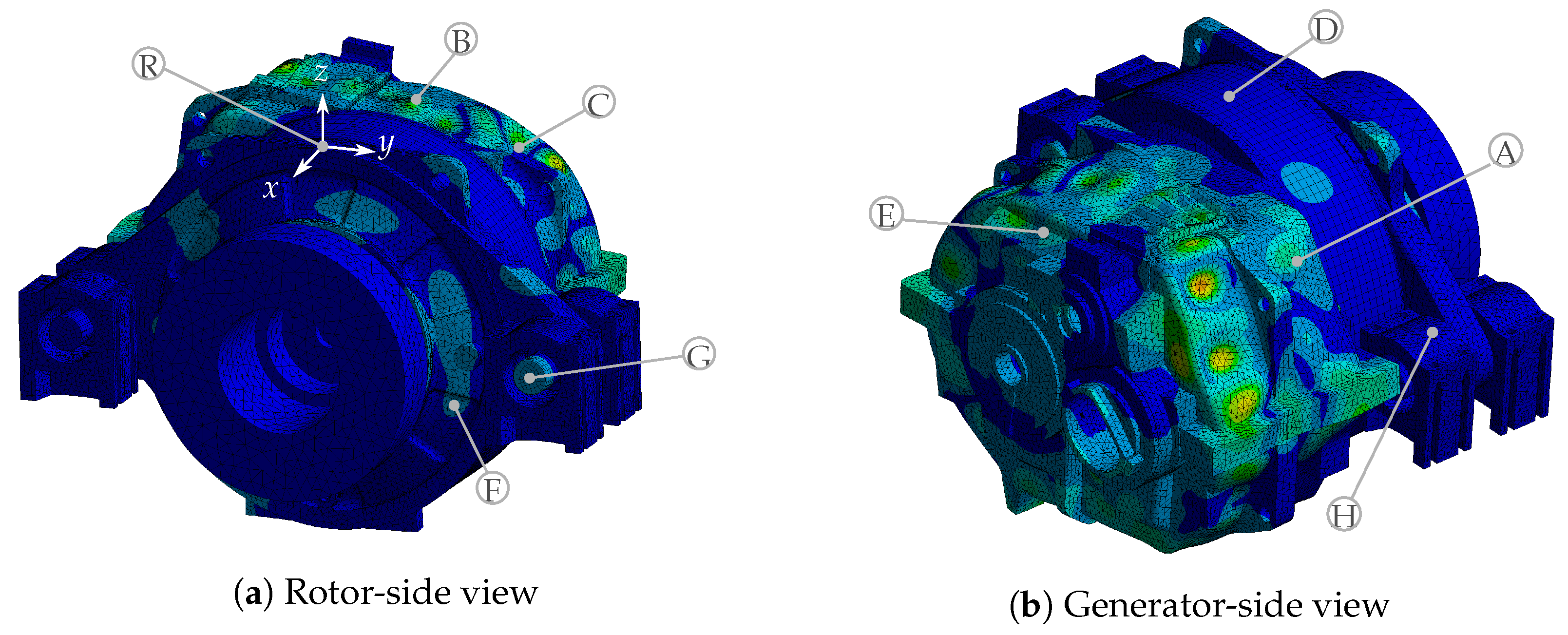
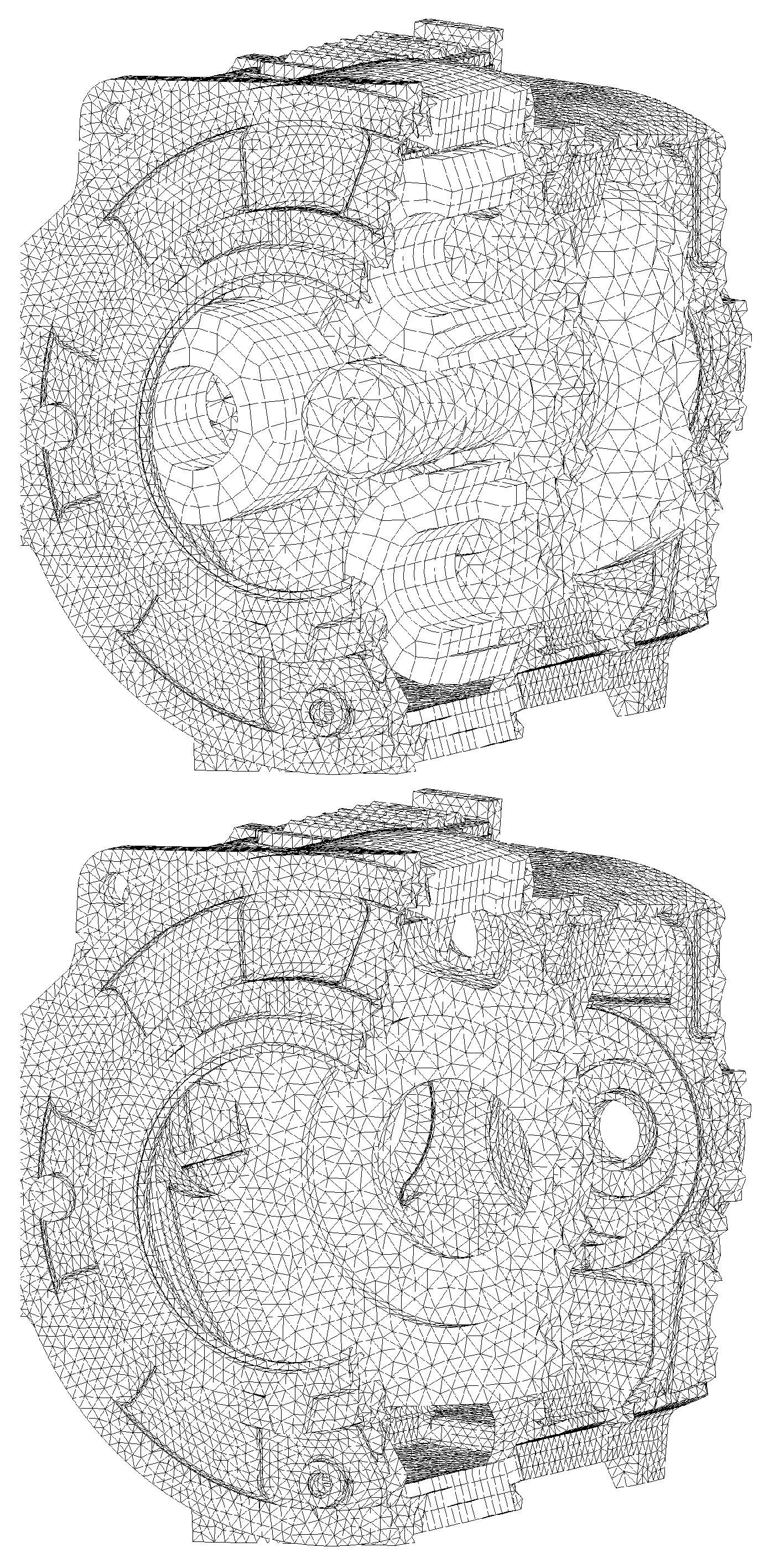
2.4. Structural Response and Transfer Behavior Using Dynamic Finite Element Analysis (Step 4)
2.5. Response at Operating Conditions (Step 5)
3. Numerical Results and Experimental Validation
3.1. Application of the Integrated Computational Procedure
3.2. Computational Costs
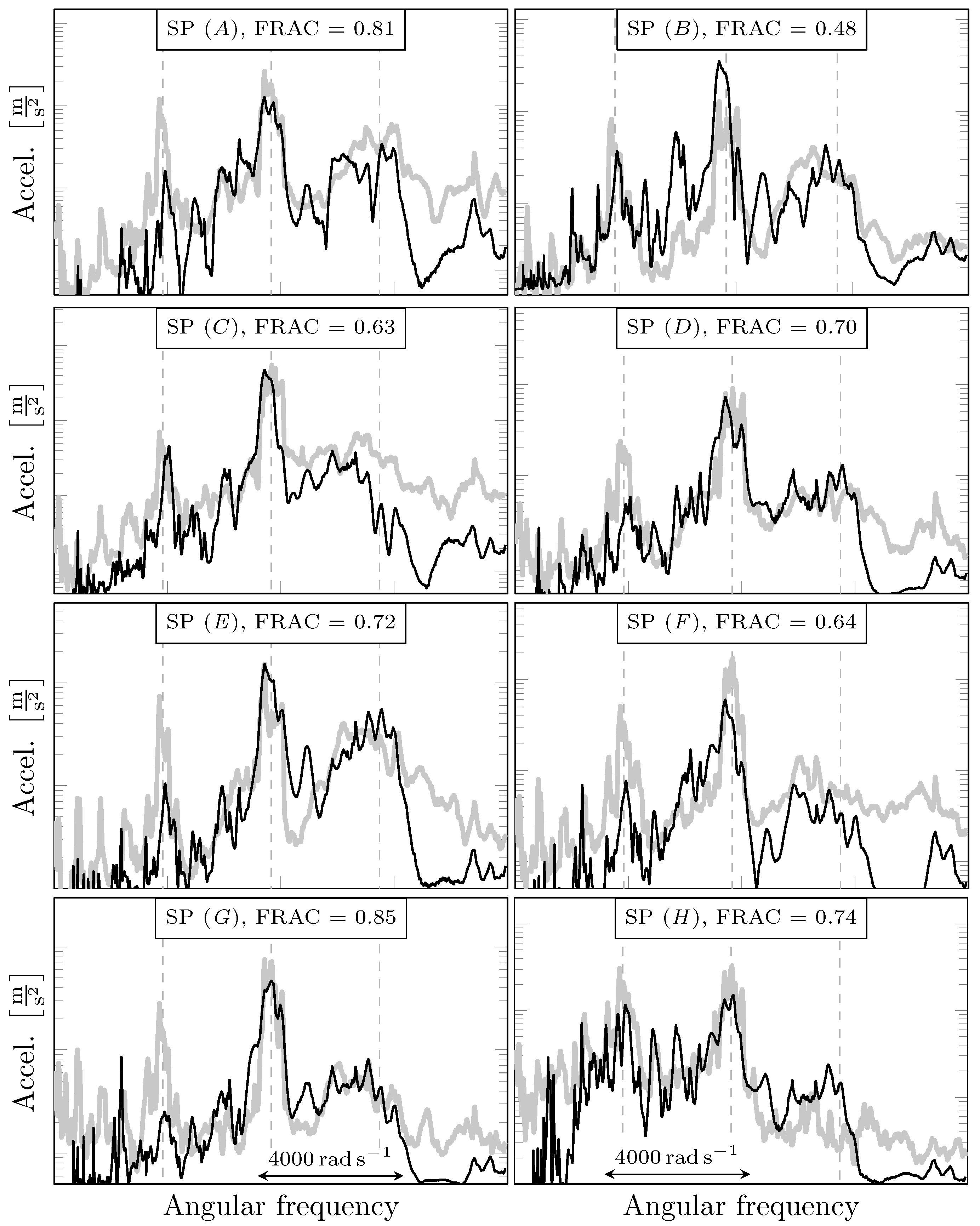
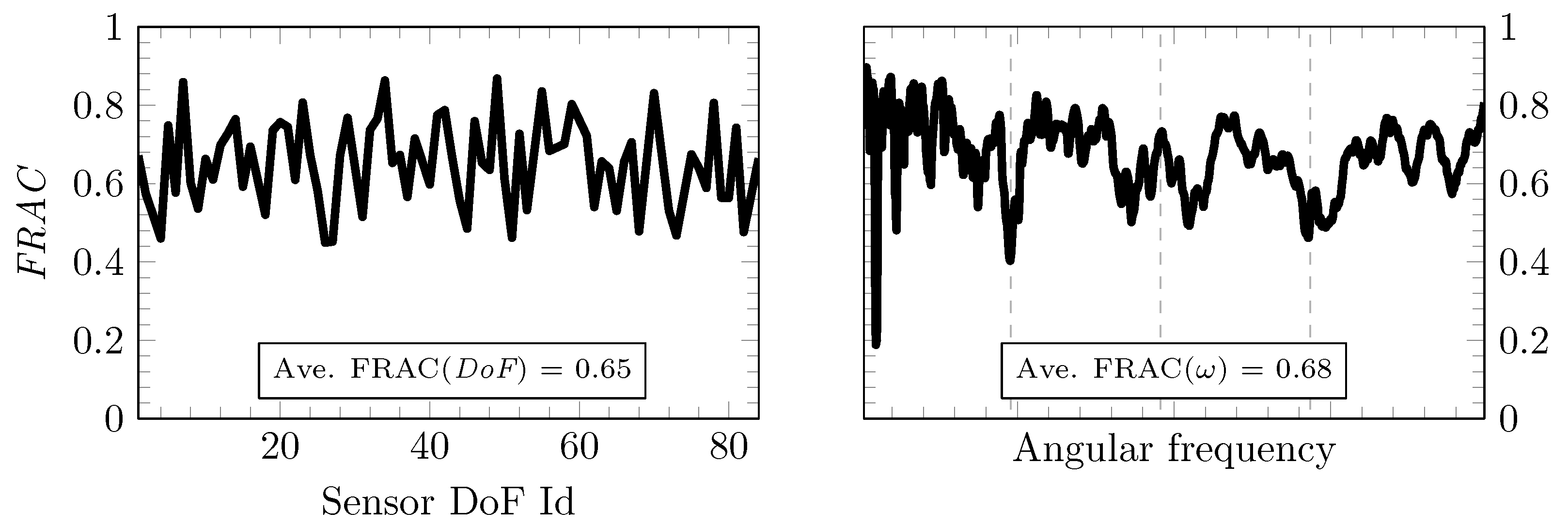
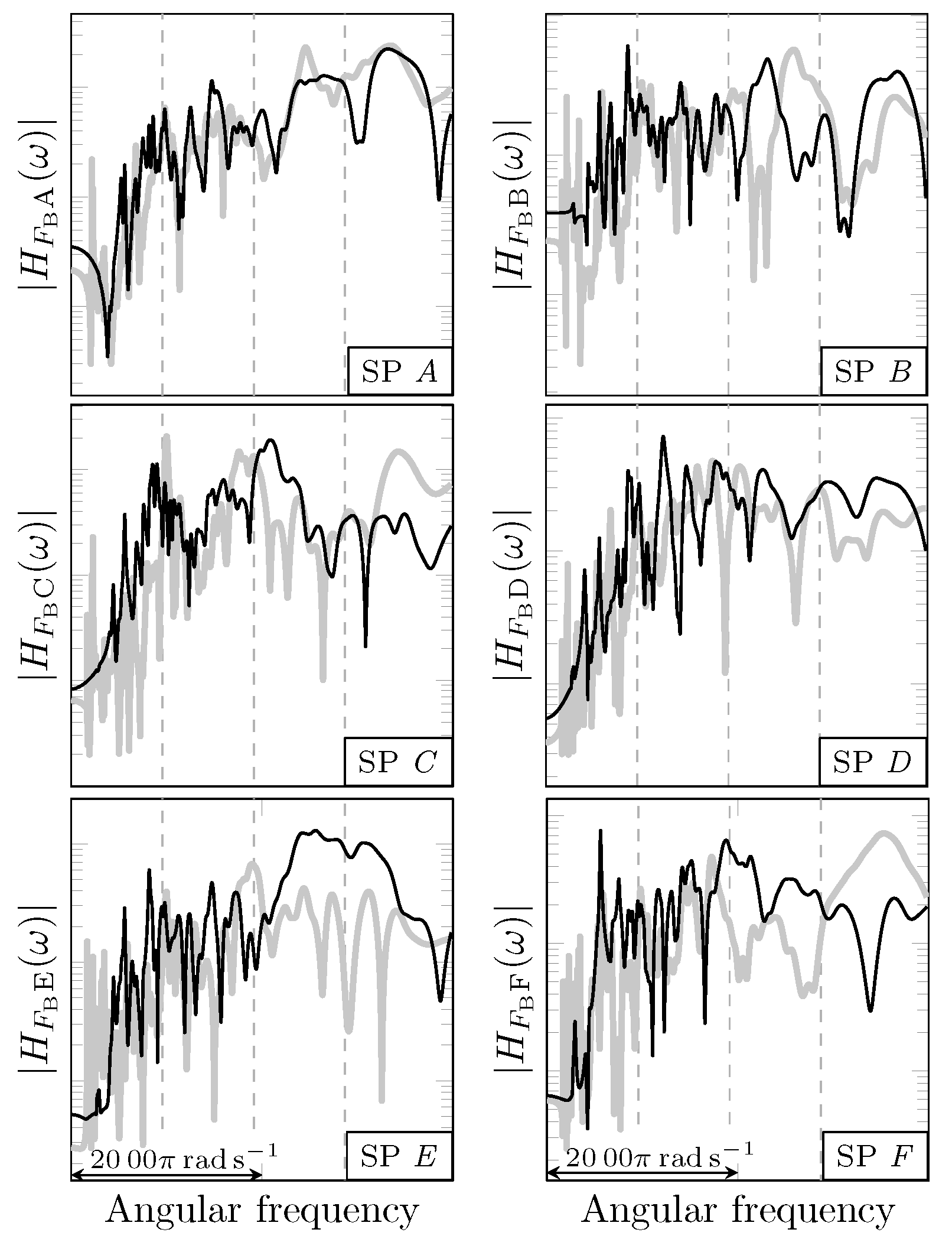
3.3. Comparison with Measurements
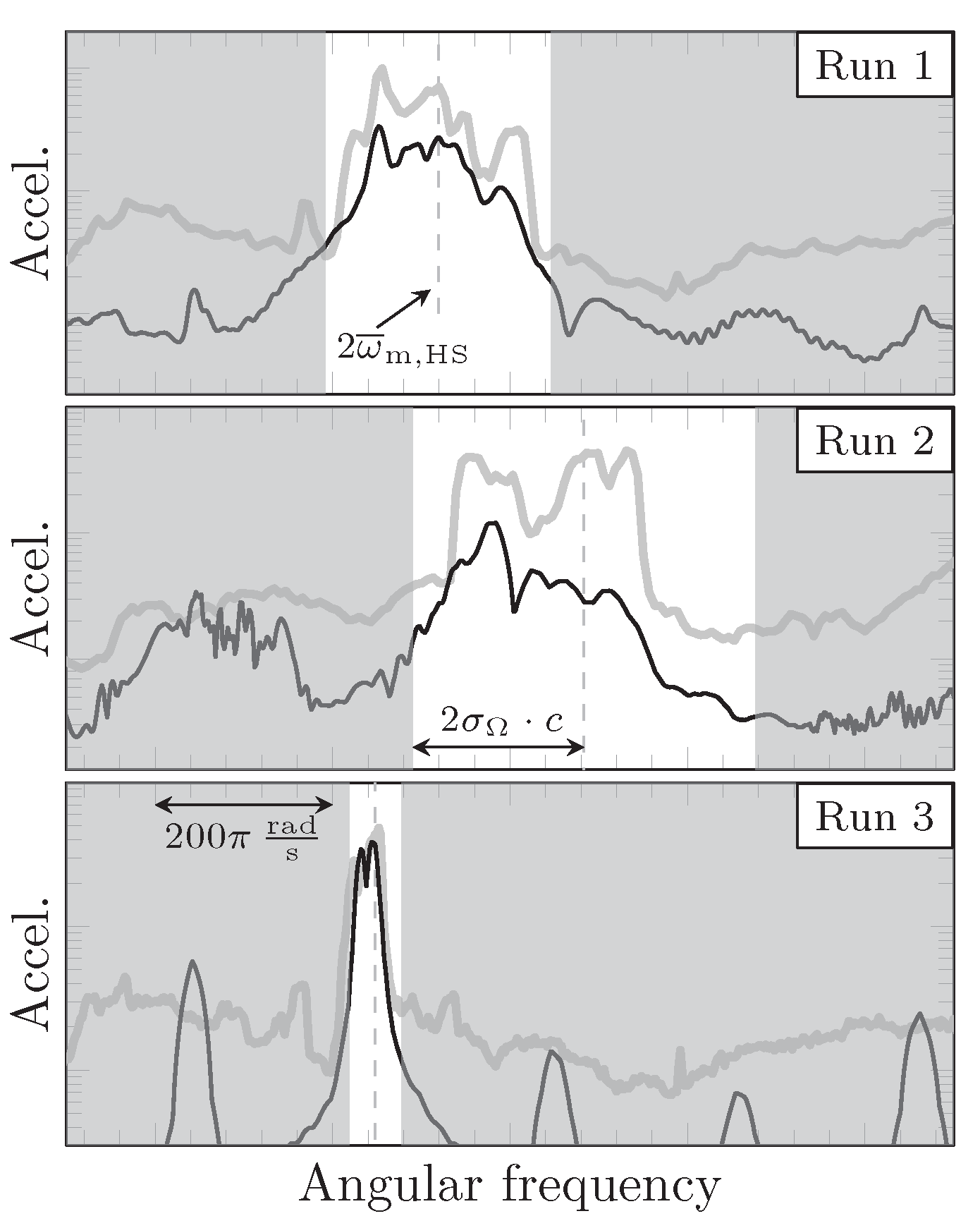
3.4. Influence of Varying Operating Conditions
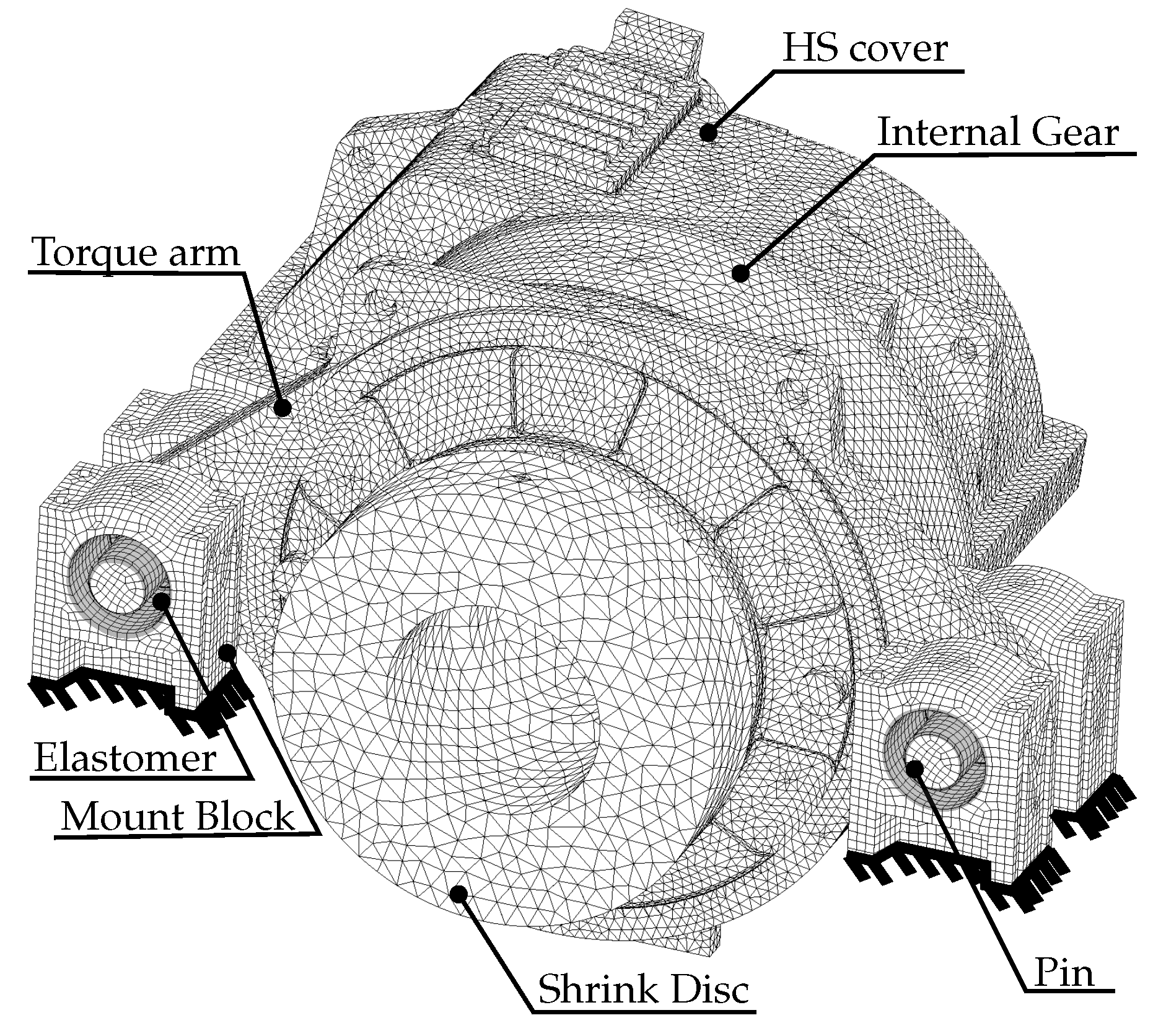
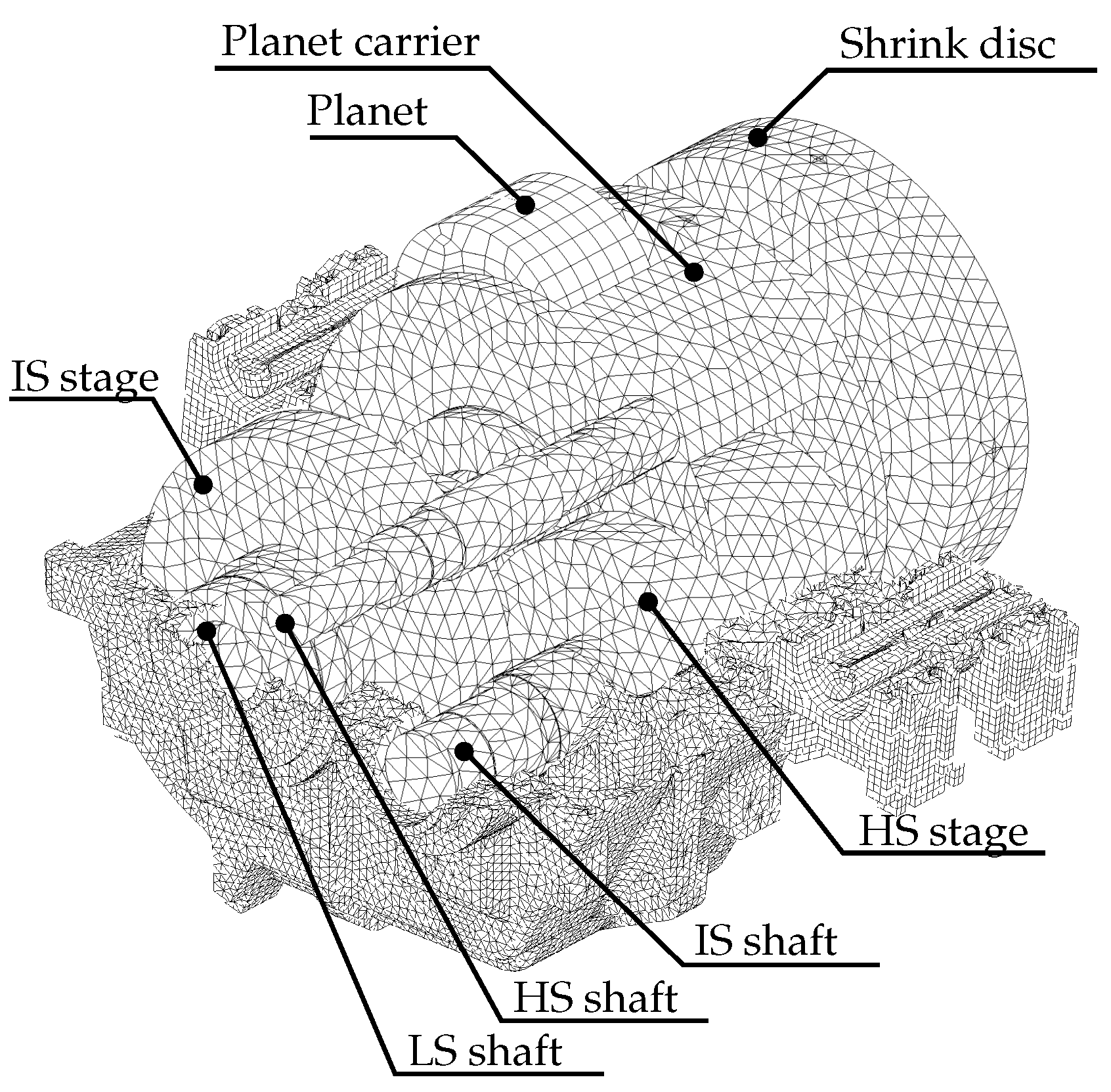
3.5. Influence of the Internal Components
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pinder, J.N. Mechanical Noise from Wind Turbines. Wind. Eng. 1992, 16, 158–168. [Google Scholar]
- Wagner, S.; Bareiß, R.; Guidati, G. Wind Turbine Noise; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Pedersen, E.; Persson Waye, K. Perception and annoyance due to wind turbine noise—A dose–response relationship. J. Acoust. Soc. Am. 2004, 116, 3460–3470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pedersen, E.; Waye, K.P. Wind turbine noise, annoyance and self-reported health and well-being in different living environments. Occup. Environ. Med. 2007, 64, 480–486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pedersen, E.; van den Berg, F.; Bakker, R.; Bouma, J. Response to noise from modern wind farms in The Netherlands. J. Acoust. Soc. Am. 2009, 126, 634–643. [Google Scholar] [CrossRef] [Green Version]
- Warren, C.R.; McFadyen, M. Does community ownership affect public attitudes to wind energy? A case study from south-west Scotland. Land Use Policy 2010, 27, 204–213. [Google Scholar] [CrossRef]
- Janssen, S.A.; Vos, H.; Eisses, A.R.; Pedersen, E. A comparison between exposure-response relationships for wind turbine annoyance and annoyance due to other noise sources. J. Acoust. Soc. Am. 2011, 130, 3746–3753. [Google Scholar] [CrossRef] [Green Version]
- McCunney, R.J.; Mundt, K.A.; Colby, W.D.; Dobie, R.; Kaliski, K.; Blais, M. Wind Turbines and Health: A Critical Review of the Scientific Literature. J. Occup. Environ. Med. 2014, 56, 108–130. [Google Scholar] [CrossRef]
- Klæboe, R.; Sundfør, H.B. Windmill Noise Annoyance, Visual Aesthetics, and Attitudes towards Renewable Energy Sources. Int. J. Environ. Res. Public Health 2016, 13, 746. [Google Scholar] [CrossRef]
- Vanhollebeke, F. Dynamic analysis of wind turbine gearbox components. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2015. [Google Scholar]
- Ozguven, H.; Houser, D. Dynamic analysis of high speed gears by using loaded static transmission error. J. Sound Vib. 1988, 125, 71–83. [Google Scholar] [CrossRef]
- Zhao, M.; Ji, J. Nonlinear torsional vibrations of a wind turbine gearbox. Appl. Math. Model. 2015, 39, 4928–4950. [Google Scholar] [CrossRef]
- Magnus, K.; Popp, K.S.W. Schwingungen, 11th ed.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Cao, H.; He, D.; Xi, S.; Chen, X. Vibration signal correction of unbalanced rotor due to angular speed fluctuation. Mech. Syst. Signal Process. 2018, 107, 202–220. [Google Scholar] [CrossRef]
- Hong, L.; Yongzhi, Q.; Jaspreet, S.; Sheng, S.; Tan, Y.; Zhou, Z. A novel vibration-based fault diagnostic algorithm for gearboxes under speed fluctuations without rotational speed measurement. Mech. Syst. Signal Process. 2017, 94, 14–32. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, R.; Peng, X. Survey of nonlinear vibration of gear transmission systems. Appl. Mech. Rev. 2003, 56, 309–328. [Google Scholar] [CrossRef]
- Liu, G.; Hong, J.; Parker, R.G. Influence of simultaneous time-varying bearing and tooth mesh stiffness fluctuations on spur gear pair vibration. Nonlinear Dyn. 2019, 97, 1403–1424. [Google Scholar] [CrossRef]
- Henriksson, M. On noise generation and dynamic transmission error of gears. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2009. [Google Scholar]
- Radzevich, S. Dudley’s Handbook of Practical Gear Design and Manufacture, 2nd ed.; Taylor & Francis: Abingdon, UK, 2012. [Google Scholar]
- Mao, K. An approach for powertrain gear transmission error prediction using the non-linear finite element method. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2006, 220, 1455–1463. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Chen, K.; Ma, H.; Che, L.; Li, Z.; Wen, B. Comparison of meshing characteristics of helical gears with spalling fault using analytical and finite-element methods. Mech. Syst. Signal Process. 2019, 121, 279–298. [Google Scholar] [CrossRef]
- Gu, X.; Velex, P.; Sainsot, P.; Bruyère, J. Analytical investigations on the mesh stiffness function of solid spur and helical gears. J. Mech. Des. Trans. ASME 2015, 137, 063301. [Google Scholar] [CrossRef]
- Cooley, C.G.; Liu, C.; Dai, X.; Parker, R.G. Gear tooth mesh stiffness: A comparison of calculation approaches. Mech. Mach. Theory 2016, 105, 540–553. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Cao, H.; He, W.; Chen, Y. Mesh stiffness calculation using an accumulated integral potential energy method and dynamic analysis of helical gears. Mech. Mach. Theory 2015, 92, 447–463. [Google Scholar] [CrossRef]
- Meagher, J.; Wu, X.; Kong, D.; Lee, C.H. A Comparison of Gear Mesh Stiffness Modeling Strategies. In Structural Dynamics, Proceedings of the 28th IMAC, A Conference on Structural Dynamics, 2010; Springer: New York, NY, USA, 2011; Volume 3, pp. 255–263. [Google Scholar] [CrossRef]
- Dai, X.; Cooley, C.G.; Parker, R.G. An Efficient Hybrid Analytical-Computational Method for Nonlinear Vibration of Spur Gear Pairs. J. Vib. Acoust. Trans. ASME 2019, 141, 011006. [Google Scholar] [CrossRef]
- Zhou, J.; Wenlei, S. Vibration and Noise Radiation Characteristics of Gear Transmission System. J. Low Freq. Noise Vib. Act. Control 2014, 30, 485–502. [Google Scholar] [CrossRef]
- Blankenship, G.W.; Singh, R. A new gear mesh interfache Dynamic Model to predict multi-dimensional Force Coupling and Excitation. Mech. Mach. Theory 1995, 30, 43–57. [Google Scholar] [CrossRef]
- Blankenship, G.W.; Singh, R. Dynamic force transmissibility in helical gear pairs. Mech. Mach. Theory 1995, 30, 323–339. [Google Scholar] [CrossRef]
- Velex, P.; Matar, M. A mathematical model for analyzing the influence of shape deviations and mounting errors on gear dynamics. J. Sound Vib. 1996, 191, 629–660. [Google Scholar] [CrossRef]
- Eritenel, T.; Parker, R.G. Three-dimensional nonlinear vibration of gear pairs. J. Sound Vib. 2012, 331, 3628–3648. [Google Scholar] [CrossRef]
- Eritenel, T.; Parker, R.G. An investigation of tooth mesh nonlinearity and partial contact loss in gear pairs using a lumped-parameter model. Mech. Mach. Theory 2012, 56, 28–51. [Google Scholar] [CrossRef]
- Velex, P.; Ajmi, M. On the modelling of excitations in geared systems by transmission errors. J. Sound Vib. 2006, 290, 882–909. [Google Scholar] [CrossRef]
- Ozguven, H.; Houser, D.R. Mathematical models used in gear dynamics—A review. J. Sound Vib. 1988, 121, 383–411. [Google Scholar] [CrossRef]
- Parey, A.; Tandon, N. Spur Gear Dynamic Models Including Defects: A Review. Shock Vib. Dig. 2003, 35, 465–478. [Google Scholar] [CrossRef]
- Li, F.; Qin, Y.; Ge, L.; Pang, Z.; Liu, S.; Lin, D. Influences of planetary gear parameters on the dynamic characteristics—A review. J. Vibroengineering 2015, 17, 574–586. [Google Scholar]
- Cooley, C.G.; Parker, R.G. A review of planetary and epicyclic gear dynamics and vibrations research. Appl. Mech. Rev. 2014, 66, 040804. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Huo, Z. Analysis of dynamic behavior of multiple-stage planetary gear train used in wind driven generator. Sci. World J. 2014, 2014, 627045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, J.; Zhang, A.; Qin, D.; Lim, T.C.; Shu, R.; Lin, X.; Meng, F. A coupling dynamics analysis method for a multistage planetary gear system. Mech. Mach. Theory 2017, 110, 27–49. [Google Scholar] [CrossRef]
- Jia, S.; Howard, I. Comparison of localised spalling and crack damage from dynamic modelling of spur gear vibrations. Mech. Syst. Signal Process. 2006, 20, 332–349. [Google Scholar] [CrossRef]
- Sun, W.; Ding, X.; Wei, J.; Zhang, A. A method for analyzing sensitivity of multi-stage planetary gear coupled modes to modal parameters. J. Vibroeng. 2015, 17, 3133–3146. [Google Scholar]
- Wang, J.; Yang, S.; Liu, Y.; Mo, R. Analysis of load-sharing behavior of the multistage planetary gear train used in wind generators: Effects of random wind load. Appl. Sci. 2019, 9, 5501. [Google Scholar] [CrossRef] [Green Version]
- Grajaa, O.; Zghala, B.; Dziedziech, K.; Chaaria, F.; Jablonski, A.; Barszcz, T.; Haddara, M. Simulating the dynamic behavior of planetary gearbox based on improved Hanning function. C. R. Mec. 2019, 347, 49–61. [Google Scholar] [CrossRef]
- Zghal, B.; Graja, O.; Dziedziech, K.; Chaari, F.; Jablonski, A.; Barszcz, T.; M, H. A new modeling of planetary gear set to predict modulation phenomenon. Mech. Syst. Signal Process. 2019, 127, 234–261. [Google Scholar] [CrossRef]
- Luo, Y.; Baddour, N.; Liang, M. Dynamical modeling of gear transmission considering gearbox casing. In Proceedings of the ASME Design Engineering Technical Conference, Quebec City, QC, Canada, 26–29 August 2018; Volume 8, pp. 1–7. [Google Scholar] [CrossRef]
- Xu, H.; Qin, D.; Liu, C.; Yi, Y.; Jia, H. Dynamic modeling of multistage gearbox and analysis method of resonance danger path. IEEE Access 2019, 7, 154796–154807. [Google Scholar] [CrossRef]
- Abousleiman, V.; Velex, P. A hybrid 3D finite element/lumped parameter model for quasi-static and dynamic analyses of planetary/epicyclic gear sets. Mech. Mach. Theory 2006, 41, 725–748. [Google Scholar] [CrossRef]
- Abousleiman, V.; Velex, P.; Becquerelle, S. Modeling of spur and helical gear planetary drives with flexible ring gears and planet carriers. J. Mech. Des. Trans. ASME 2007, 129, 95–106. [Google Scholar] [CrossRef]
- Bettaïeb, M.N.; Velex, P.; Ajmi, M. A static and dynamic model of geared transmissions by combining substructures and elastic foundations - Applications to thin-rimmed gears. J. Mech. Des. Trans. ASME 2007, 129, 184–194. [Google Scholar] [CrossRef]
- Guilbert, B.; Velex, P.; Dureisseix, D.; Cutuli, P. A Mortar-Based Mesh Interface for Hybrid Finite-Element/Lumped-Parameter Gear Dynamic Models - Applications to Thin-Rimmed Geared Systems. J. Mech. Des. Trans. ASME 2016, 138, 123301. [Google Scholar] [CrossRef]
- Vijayakar, S.M.; Busby, H.R.; Houser, D.R. Linearization of multibody frictional contact problems. Comput. Struct. 1988, 29, 569–576. [Google Scholar] [CrossRef]
- Vijayakar, S.; Busby, H.; Wilcox, L. Finite element analysis of three-dimensional conformal contact with friction. Comput. Struct. 1989, 33, 49–61. [Google Scholar] [CrossRef]
- Vijayakar, S. A combined surface integral and finite element solution for a three-dimensional contact problem. Int. J. Numer. Methods Eng. 1991, 31, 525–545. [Google Scholar] [CrossRef]
- Parker, R.G.; Agashe, V.; Vijayakar, S.M. Dynamic response of a planetary gear system using a finite element/contact mechanics model. J. Mech. Des. Trans. ASME 2000, 122, 304–310. [Google Scholar] [CrossRef]
- Parker, R.; Vijayakar, S.; Imajo, T. Non-linear dynamic response of a spur gear Pair: Modelling and experimental comparison. J. Sound Vib. 2000, 237, 435–455. [Google Scholar] [CrossRef] [Green Version]
- Eritenel, T.; Parker, R.G. Nonlinear Vibration of Gears With Tooth Surface Modifications. J. Vib. Acoust. 2013, 135. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Eritenel, T.; Ericson, T.M.; Parker, R.G. Vibro-acoustic propagation of gear dynamics in a gear-bearing-housing system. J. Sound Vib. 2014, 333, 5762–5785. [Google Scholar] [CrossRef]
- Helsen, J. The Dynamics of High Power Density Gear Units with Focus on the Wind Turbine Application. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2012. [Google Scholar]
- Helsen, J.; Marrant, B.; Vanhollebeke, F.; Coninck, F.D.; Berckmans, D.; Vandepitte, D.; Desmet, W. Assessment of excitation mechanisms and structural flexibility influence in excitation propagation in multi-megawatt wind turbine gearboxes: Experiments and flexible multibody model optimization. Mech. Syst. Signal Process. 2013, 40, 114–135. [Google Scholar] [CrossRef]
- Helsen, J.; Peeters, P.; Vanslambrouck, K.; Vanhollebeke, F.; Desmet, W. The dynamic behavior induced by different wind turbine gearbox suspension methods assessed by means of the flexible multibody technique. Renew. Energy 2014, 69, 336–346. [Google Scholar] [CrossRef]
- Vanhollebeke, F.; Helsen, J.; Peeters, J.; Vandepitte, D.; Desmet, W. Combining multibody and acoustic simulation models for wind turbine gearbox NVH optimisation. In Proceedings of the International Conference on Noise and Vibration Engineering ISMA 2012, Leuven, Belgium, 17–19 September 2012; pp. 4463–4477. [Google Scholar]
- Vanhollebeke, F.; Peeters, J.; Vandepitte, D.; Desmet, W. Using transfer path analysis to assess the influence of bearings on structural vibrations of a wind turbine gearbox. Wind Energy 2015, 18, 797–810. [Google Scholar] [CrossRef]
- Vanhollebeke, F.; Peeters, P.; Helsen, J.; Di Lorenzo, E.; Manzato, S.; Peeters, J.; Vandepitte, D.; Desmet, W. Large Scale Validation of a Flexible Multibody Wind Turbine Gearbox Model. J. Comput. Nonlinear Dyn. 2015, 10, 041006. [Google Scholar] [CrossRef]
- Sika, G.; Velex, P. Analytical and numerical dynamic analysis of gears in the presence of engine acyclism. J. Mech. Des. Trans. ASME 2008, 130, 1245021–1245026. [Google Scholar] [CrossRef]
- Sika, G.; Velex, P. Instability analysis in oscillators with velocity-modulated time-varying stiffness-Applications to gears submitted to engine speed fluctuations. J. Sound Vib. 2008, 318, 166–175. [Google Scholar] [CrossRef]
- Zarnekow, M.; Ihlenburg, F.; Grätsch, T. An Efficient Approach to the Simulation of Acoustic Radiation from Large Structures with FEM. J. Theor. Comput. Acoust. 2020, 28, 1950019. [Google Scholar] [CrossRef]
- Umezawa, K.; Sato, T.; Ishikawa, J. Simulation on rotational vibration of spur gears. Bull. Jpn. Soc. Mech. Eng. 1984, 27, 102–109. [Google Scholar] [CrossRef] [Green Version]
- Umezawa, K.; Sato, T. Influence of gear error on rotational vibration of power transmission spur gears. Bull. Jpn. Soc. Mech. Eng. 1985, 28, 2143–2148. [Google Scholar] [CrossRef]
- Kubo, A. Stress Condition, Vibrational Exciting Force, and Contact Pattern of Helical Gears with Manufacturing and Alignment Error. J. Mech. Des. 1978, 100, 77–84. [Google Scholar] [CrossRef]
- Chang, L.; Liu, G.; Wu, L. A robust model for determining the mesh stiffness of cylindrical gears. Mech. Mach. Theory 2015, 87, 93–114. [Google Scholar] [CrossRef]
- Palermo, A.; Mundo, D.; Hadjit, R.; Desmet, W. Multibody element for spur and helical gear meshing based on detailed three-dimensional contact calculations. Mech. Mach. Theory 2013, 62, 13–30. [Google Scholar] [CrossRef]
- Vaishya, M.; Singh, R. Analysis of periodically varying gear mesh systems with Coulomb friction using Floquet theory. J. Sound Vib. 2001, 243, 525–545. [Google Scholar] [CrossRef] [Green Version]
- Amabili, M.; Rivola, A. Dynamic Analysis of Gear Pairs: Steady-State Response and Stability of SDoF Model with time-Varying Mesh Damping. Mech. Syst. Signal Process. 1997, 11, 375–390. [Google Scholar] [CrossRef]
- Amabili, M.; Fregolent, A. A method to identify modal parameters and gear errors by vibrations of a spur gear pair. J. Sound Vib. 1998, 214, 339–357. [Google Scholar] [CrossRef]
- Oliveri, L.; Rosso, C.; Zucca, S. Influence of Actual Static Transmission Error and Contact Ratio on Gear Engagement Dynamics. In Nonlinear Dynamics, Proceedings of the 35th IMAC, A Conference and Exposition on Structural Dynamics; Kerschen, G., Ed.; Springer: Garden Grove, CA, USA, 2017; pp. 143–154. [Google Scholar] [CrossRef]
- Umezawa, K.; Ajima, T.; Houjoh, H. Vibration of three axis gear system. Bull. JSME 1986, 29, 950–957. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Hayashi, T. The Linear Approximated Equation of Vibration of a Pair of Spur Gears (Theory and Experiment). J. Mech. Des. 1994, 116, 558. [Google Scholar] [CrossRef]
- Kasuba, R.; Evans, J.W. An extended model for determining dynamic loads in spur gearing. J. Mech. Des. 1981, 103, 398. [Google Scholar] [CrossRef]
- Cattani, C.; Grebenikov, E.A.; Prokopenya, A.N. On stability of the Hill equation with damping. Nonlinear Oscil. 2004, 7, 168–178. [Google Scholar] [CrossRef]
- Ishida, K.; Matsuda, T.; Kukui, M. Effect of gearbox on noise reduction of geared devices. In Proceedings of the International Symposium on Gearing and Power Transmissions, Tokyo, Japan, 30 August–3 September 1981; pp. 13–18. [Google Scholar]
- Mitchell, A.; Oswald, F.B.; Coe, H. Testing of uh-60a Helicopter Transmission in NASA Lewis 2240kw (3000-hp) Facility; Technical Paper 2538; NASA: Washington, DC, USA, 1986.
- Guo, Y.; Parker, R.G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model. Mech. Mach. Theory 2012, 51, 32–45. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice Hall, Pearson Education Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Zienkiewicz, O.; Taylor, R.; Zhu, J. Chapter 15—Errors, Recovery Processes, and Error Estimates. In The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2013; pp. 493–543. [Google Scholar] [CrossRef]
- Cooley, C.G.; Parker, R.G.; Vijayakar, S.M. A frequency domain finite element approach for three-dimensional gear dynamics. J. Vib. Acoust. Trans. ASME 2011, 133, 041004. [Google Scholar] [CrossRef]
- Grätsch, T.; Zarnekow, M.; Ihlenburg, F. Simulation of sound radiation of wind turbines using large scale finite element models. In Proceedings of the 8th International Conference on Wind Turbine Noise, Lisbon, Portugal, 12–14 June 2019. [Google Scholar]
- Nefske, D.J.; Sung, S.H. Correlation of a coarse-mesh finite element model using structural system identification and a frequency response criterion. In Proceedings-SPIE the International Society for Optical Engineering; SPIE: Bellingham, WA, USA, 1996; Volume 1, pp. 597–602. [Google Scholar]
- Zang, C.; Grafe, H.; Imregun, M. Frequency-domain criteria for correlating and updating dynamic finite element models. Mech. Syst. Signal Process. 2001, 15, 139–155. [Google Scholar] [CrossRef]
- Zarnekow, M.; Grätsch, T.; Ihlenburg, F. A multi-level approach for the numerical simulation of mechanical noise in wind turbines. In Proceedings of the 14th World Congress in Computational Mechanics and ECCOMAS Congress, Virtual, 11–15 January 2020. [Google Scholar]
- Ihlenburg, F.; Zarnekow, M.; Grätsch, T. Simulation of vibrational sources and vibroacoustic transfer in wind turbine drivetrains. PAMM 2019, 19, e201900101. [Google Scholar] [CrossRef]






| Step | Analysis Task | Method | Time |
|---|---|---|---|
| 1 | Angle-varying mesh stiffness | Static FEM | 10 |
| 2 | Time-varying mesh stiffness | Analytical | |
| 3 | Transmission Error (TE) | Runge-Kutta scheme | 10 |
| 4 | Frequency Response | Time-harmonic FEM | |
| 5 | Linear Combination and Superposition | Analytical |
| Run | |||
|---|---|---|---|
| [] | [] | [] | |
| 1 | 290.1 | 9.6 | 42.3 |
| 2 | 315.7 | 14.6 | 48.2 |
| 3 | 280 | 0.6 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarnekow, M.; Grätsch, T.; Ihlenburg, F. A Hybrid Multistep Procedure for the Vibroacoustic Simulation of Noise Emission from Wind Turbines. Acoustics 2023, 5, 1-27. https://doi.org/10.3390/acoustics5010001
Zarnekow M, Grätsch T, Ihlenburg F. A Hybrid Multistep Procedure for the Vibroacoustic Simulation of Noise Emission from Wind Turbines. Acoustics. 2023; 5(1):1-27. https://doi.org/10.3390/acoustics5010001
Chicago/Turabian StyleZarnekow, Marc, Thomas Grätsch, and Frank Ihlenburg. 2023. "A Hybrid Multistep Procedure for the Vibroacoustic Simulation of Noise Emission from Wind Turbines" Acoustics 5, no. 1: 1-27. https://doi.org/10.3390/acoustics5010001
APA StyleZarnekow, M., Grätsch, T., & Ihlenburg, F. (2023). A Hybrid Multistep Procedure for the Vibroacoustic Simulation of Noise Emission from Wind Turbines. Acoustics, 5(1), 1-27. https://doi.org/10.3390/acoustics5010001





