Comparison of Semi-Empirical Impedance Models for Locally-Reacting Acoustic Liners in a Wide Range of Sound Pressure Levels
Abstract
:1. Introduction
- To derive the impedance formula, it is necessary to use simplified mathematical formulations that do not completely consider some complex physical effects that are important for an accurate description of impedance under certain conditions (for example, the process of vortex formation ignored in perforation at a high SPL; it is assumed that the velocity in the perforation is transformed only into the acoustic mode); and
- Obtaining experimental data that allow us to compare the impedance of both a single resonator and the entire sample from an acoustic liner;
- Comparison of the impedance calculated by known, well-developed, semi-empirical models with experimental results;
- Interpretation of the reasons for the possible discrepancies between the calculated and experimental values of the impedance; and
- Identification of more accurate semi-empirical models with semi-empirical dependencies and constants known from the literature for different SPL ranges.
2. Considered Semi-Empirical Impedance Models
2.1. Goodrich Model
2.2. Sobolev Model
2.3. Eversman Model
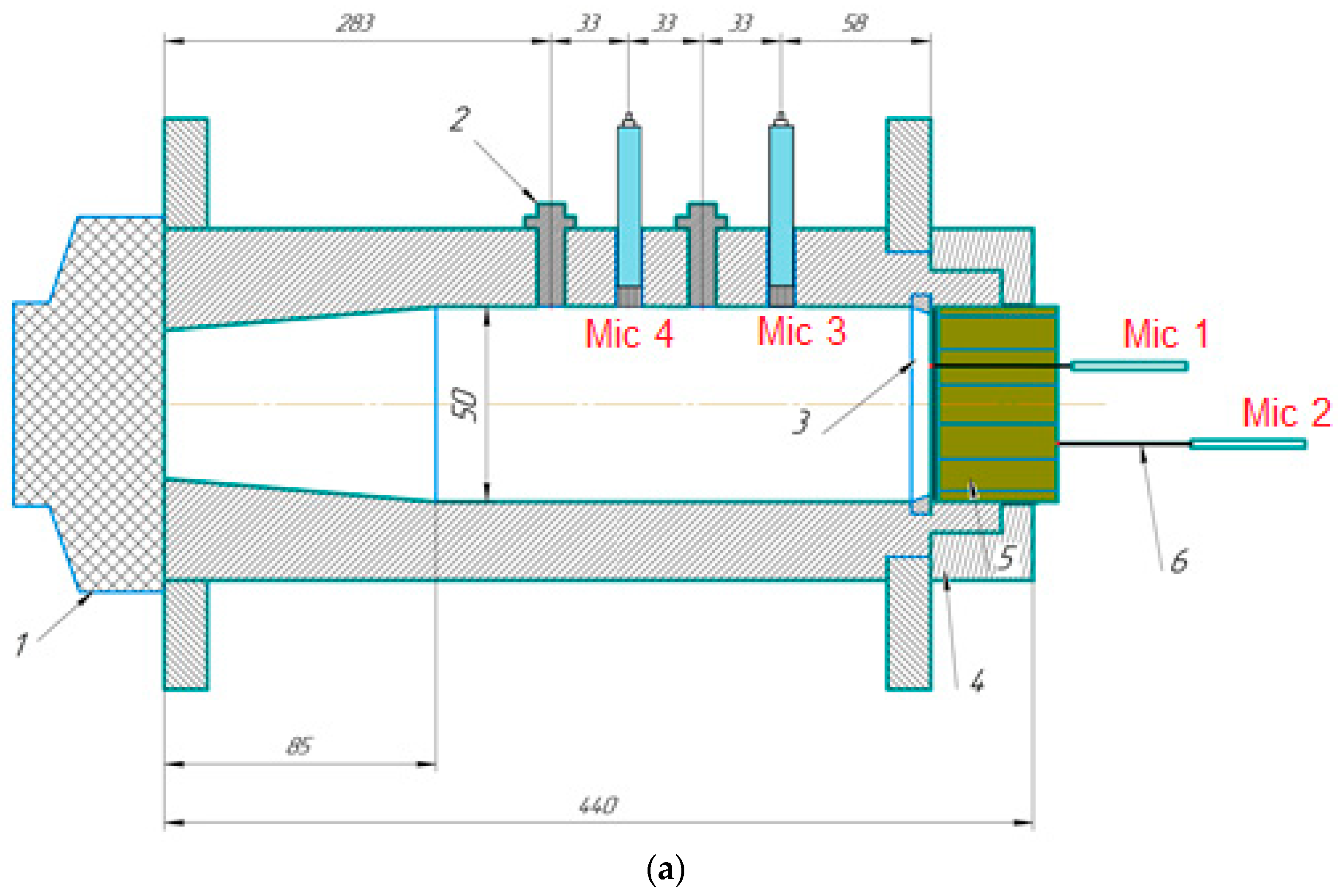
3. Details of the Experiment
- The wavelength changes as the frequency changes, so SPL changes along an impedance tube and consequently on the face of a sample;
- The absorption of sound energy changes with frequency (especially in a region of resonance frequencies); therefore, the SPL on the face of a sample changes too; and
- The characteristics of the acoustic driver change in frequency (for example, to maintain a required SPL at low frequencies of sound generation, less voltage should be applied to the acoustic driver than at high frequencies).
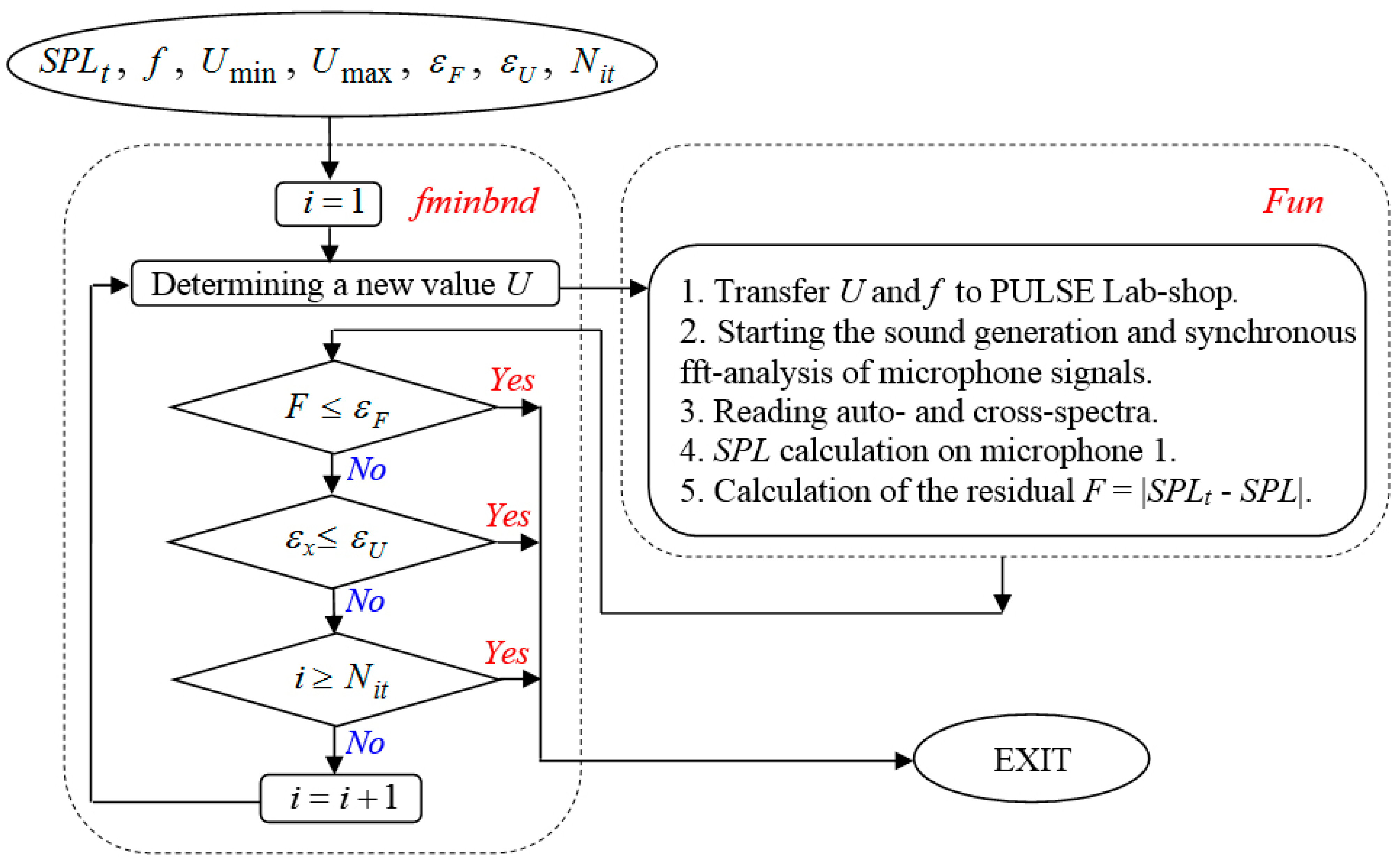
- Transfers the required voltage value and the sound generation frequency to PULSE Labshop;
- Starts the generation of the sound signal and synchronous fft-analysis of the signals registered on the microphones; and
- Reads from the PULSE Labshop the auto- and cross-spectra obtained in the fft-analysis.
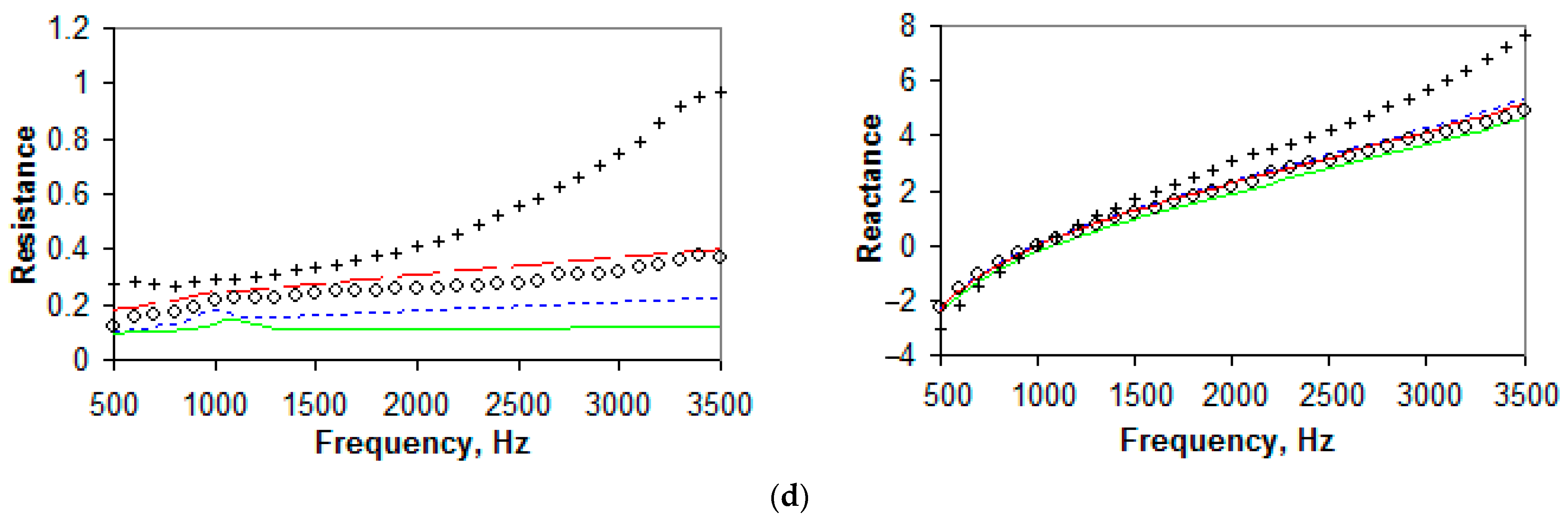
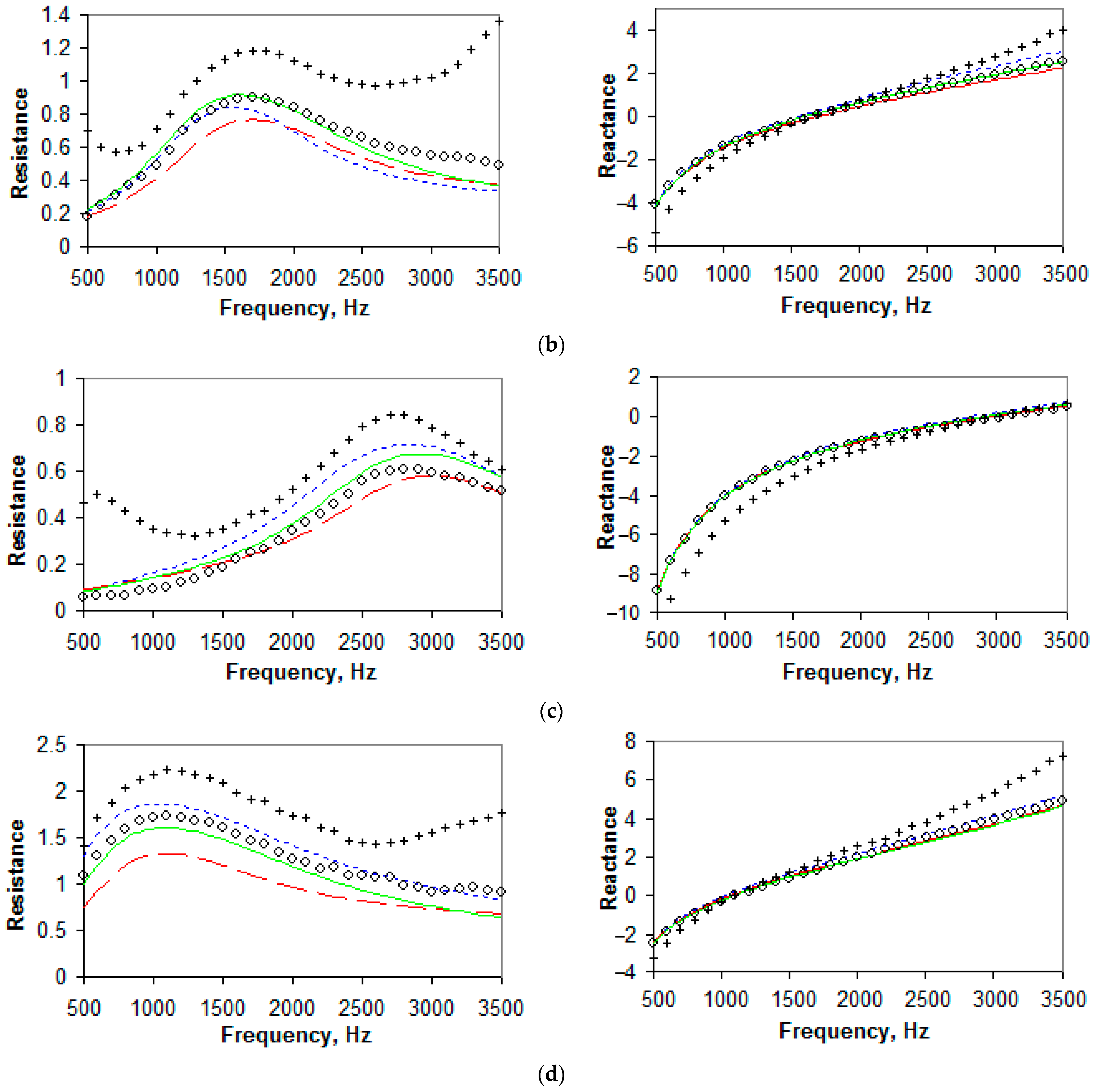
4. Results of the Study
5. Discussion
6. Conclusions
- If the validation of a semi-empirical impedance model of locally reacting liner is carried out by measurements on a normal incidence impedance tube, then it is better to use “sine” excitation and Dean’s method because they better correspond to the conditions used when deriving an impedance model;
- At a low SPL on the face of a liner sample, the impedance is better described by the Sobolev model;
- At a high SPL on the face of a liner sample, the impedance is well described by the Goodrich or Eversman model (depending on the geometry of a sample); and
- In the presence of a variable SPL on the face of a liner sample (e.g., grazing incidence), it is obviously necessary to use several different impedance models, each in certain sections of the liner, ensuring a smooth change in the impedance when transferring from one model to another.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ISO 10534-1; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes. Part 1: Method Using Standing Wave Ratio. ISO: Geneva, Switzerland, 1996.
- ISO 10534-2; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedances Tubes. Part 2: Transfer-Function Method. ISO: Geneva, Switzerland, 1996.
- Dean, P.D. An in-situ method of wall acoustic impedance measurement in flow duct. J. Sound Vib. 1974, 34, 97–130. [Google Scholar] [CrossRef]
- Watson, W.R.; Jones, M.G. A comparative study of four impedance eduction methodologies using several test liners. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013. [Google Scholar]
- Ostrikov, N.N.; Yakovets, M.A.; Ipatov, M.S. Confirmation of an analytical model of the sound propagation in a rectangular duct in the presence of impedance transitions and development of an impedance eduction method based on it. Acoust. Phys. 2020, 66, 105–122. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Kurbatskii, K.A. A numerical and experimental investigation of the dissipation mechanisms of resonant acoustic liners. J. Sound Vib. 2001, 245, 545–557. [Google Scholar] [CrossRef]
- Roche, J.M.; Leylekian, L.; Delattre, G.; Vuillot, F. Aircraft fan noise absorption: DNS of the acoustic dissipation of resonant liners. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009. [Google Scholar]
- Zhang, Q.; Bodony, D.J. Impedance predictions of 3D honeycomb liner with circular apertures by DNS. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5–8 June 2009. [Google Scholar]
- Palchikovskiy, V.; Khramtsov, I.; Kustov, O. On the influence of certain geometric characteristics of the resonator on the impedance determined by the Dean’s method. Acoustics 2022, 4, 382–393. [Google Scholar] [CrossRef]
- Ou, Y.; Zhao, Y. Prediction of the absorption characteristics of non-uniform acoustic absorbers with grazing flow. Appl. Sci. 2023, 13, 2256. [Google Scholar] [CrossRef]
- Melling, T.H. The acoustic impendance of perforates at medium and high sound pressure levels. J. Sound Vib. 1973, 21, 1–65. [Google Scholar] [CrossRef]
- Guess, A.W. Calculation of perforated plate liner parameters from specified acoustic resistance and reactance. J. Sound Vib. 1975, 40, 119–137. [Google Scholar] [CrossRef]
- Kooi, J.W.; Sarin, S.L. An experimental study of the acoustic impedance of Helmholtz resonator arrays under a turbulent boundary layer. In Proceedings of the 7th Aeroacoustics Conference, Palo Alto, CA, USA, 5–7 October 1981. [Google Scholar]
- Motsinger, R.E.; Kraft, R.E. Design and performance of duct acoustic treatment. In Aeroacoustics of Flight Vehicles. Theory and Practice. Volume 2: Noise Control; Hubbard, H.H., Ed.; NASA Langley Research Center: Hampton, VA, USA, 1991; pp. 165–206. [Google Scholar]
- Hersh, A.S.; Walker, B.E.; Celano, J.W. Helmholtz resonator impedance model, Part 1: Nonlinear behavior. AIAA J. 2003, 41, 795–808. [Google Scholar] [CrossRef]
- Yu, J.; Ruiz, M.; Kwan, H.W. Validation of Goodrich perforate liner impedance model using NASA Langley test data. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference), Vancouver, BC, Canada, 5–7 May 2008. [Google Scholar]
- Sobolev, A.F. A semiempirical theory of a one-layer cellular sound-absorbing lining with a perforated face panel. Acoust. Phys. 2007, 53, 762–771. [Google Scholar] [CrossRef]
- Murray, P.B.; Astley, R.J. Development of a single degree of freedom perforate impedance model under grazing flow and high SPL. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 May 2012. [Google Scholar]
- Murray, P.B.; Donnan, C.; Richter, C.; Astley, J. Development of a single degree of freedom microperforate impedance model under grazing flow and high SPL. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar]
- Rienstra, S.W.; Singh, D.K. Nonlinear asymptotic impedance model for a Helmholtz resonator of finite depth. AIAA J. 2018, 56, 1792–1802. [Google Scholar] [CrossRef] [Green Version]
- Eversman, W.; Drouin, M.; Locke, J.; McCartney, J. Impedance models for single and two degree of freedom linings and correlation with grazing flow duct testing. Int. J. Aeroacoustics 2021, 20, 497–529. [Google Scholar] [CrossRef]
- Stinson, M.R.; Shaw, E.A. Acoustic impedance of small, circular orifices in thin plates. J. Acoust. Soc. Am. 1985, 77, 2039–2042. [Google Scholar] [CrossRef]
- Elnady, T.; Boden, H. On semi-empirical liner impedance modeling with grazing flow. In Proceedings of the 9th AIAA/CEAS Aeroacoustics Conference and Exhibit, Hilton Head, SC, USA, 12–14 May 2003. [Google Scholar]
- Komkin, A.; Bykov, A.; Saulkina, O. Evaluation of the oscillation velocity in the neck of the Helmholtz resonator in nonlinear regimes. Acoustics 2022, 4, 564–573. [Google Scholar] [CrossRef]
- Kraft, R.E.; Yu, J.; Kwan, H.W. Acoustic treatment impedance models for high frequencies. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 12–14 May 1997. [Google Scholar]
- Yu, J.; Kwan, H.W.; Chiou, S. Microperforate plate acoustic property evaluation. In Proceedings of the 5th AIAA/CEAS Aeroacoustics Conference and Exhibit, Bellevue, WA, USA, 10–12 May 1999. [Google Scholar]
- Fok, V.A. Theoretical study of the conductance of a circular hole in a partition across a tube. Proc. USSR Acad. Sci. 1941, 31, 875–882. [Google Scholar]
- Parrott, T.L.; Jones, M.G. Chapter 6—Uncertainty in acoustic liner impedance measurement and prediction. In Assessment of NASA’s Aircraft Noise Prediction Capability; Dahl, M.H., Ed.; NASA Glenn Research Center: Cleveland, Ohio, USA, 2012; pp. 157–204. [Google Scholar]
- Schultz, T.; Liu, F.; Cattafesta, L.; Sheplak, M.; Jones, M. A comparison study of normal-incidence acoustic impedance measurementsof a perforate liner. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009. [Google Scholar]
- Spillere, A.M.; Braga, D.S.; Seki, L.A.; Bonomo, L.A.; Cordioli, J.A.; Rocamora, B.M., Jr.; Greco, P.C., Jr.; dos Reis, D.C.; Coelho, E.L. Design of a single degree of freedom acoustic liner for a fan noise test rig. Int. J. Aeroacoustics 2021, 20, 708–736. [Google Scholar] [CrossRef]
- Palchikovskiy, V.V.; Kustov, O.Y.; Korin, I.A.; Cherepanov, I.E.; Khramtsov, I.V. Investigation of acoustic characteristics of liner samples in interferometers with different duct diameter. PNRPU Aerosp. Eng. Bull. 2017, 51, 62–73. [Google Scholar] [CrossRef]
- Khramtsov, I.; Kustov, O.; Palchikovskiy, V.; Ershov, V. Investigation of the reason for the difference in the acoustic liner impedance determined by the transfer function method and Dean’s method. Akustika 2021, 39, 224–229. [Google Scholar] [CrossRef]

 “white noise” excitation;
“white noise” excitation;  “sine” excitation.
“sine” excitation.
 “white noise” excitation;
“white noise” excitation;  “sine” excitation.
“sine” excitation.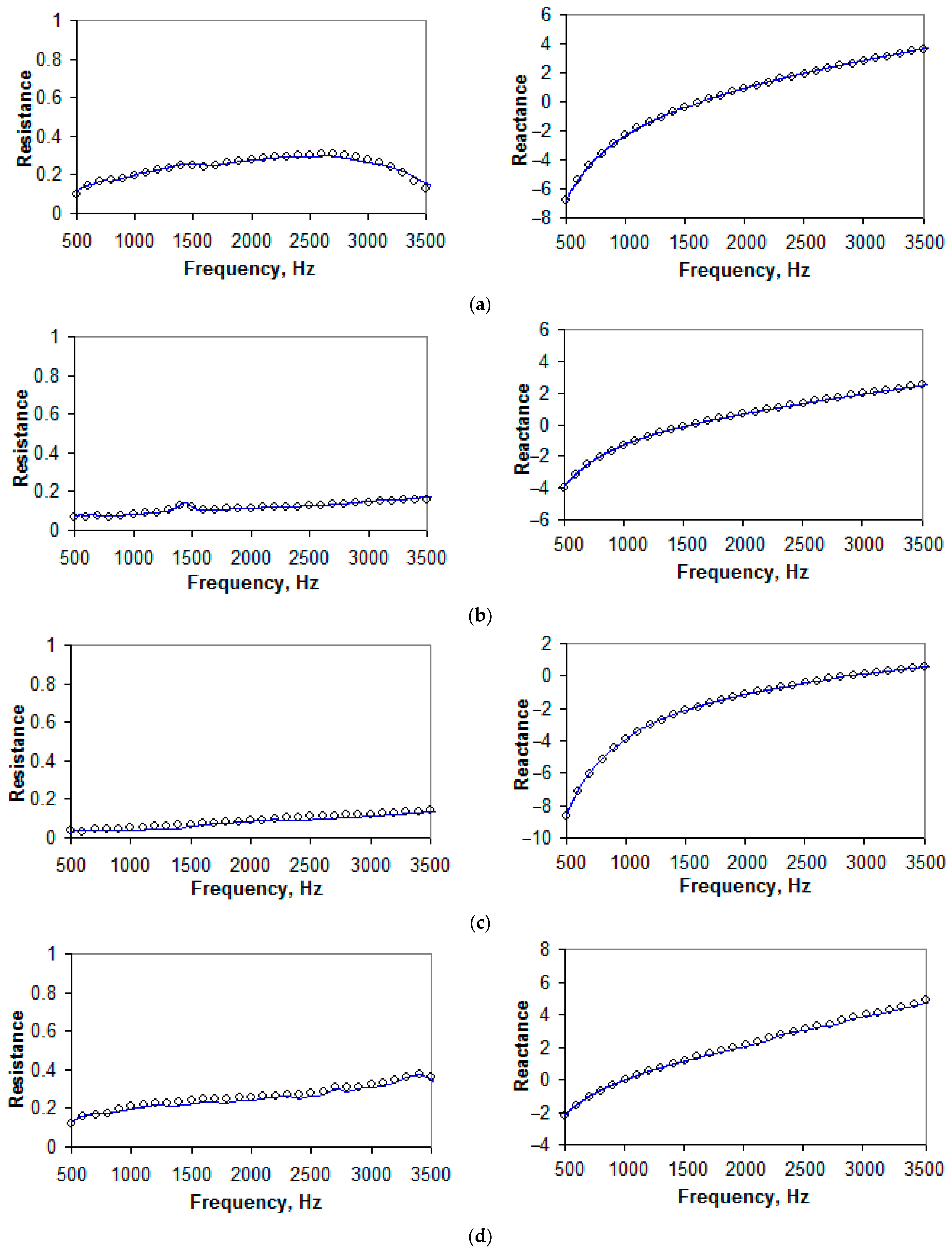
 “white noise” excitation;
“white noise” excitation;  “sine” excitation.
“sine” excitation.
 “white noise” excitation;
“white noise” excitation;  “sine” excitation.
“sine” excitation.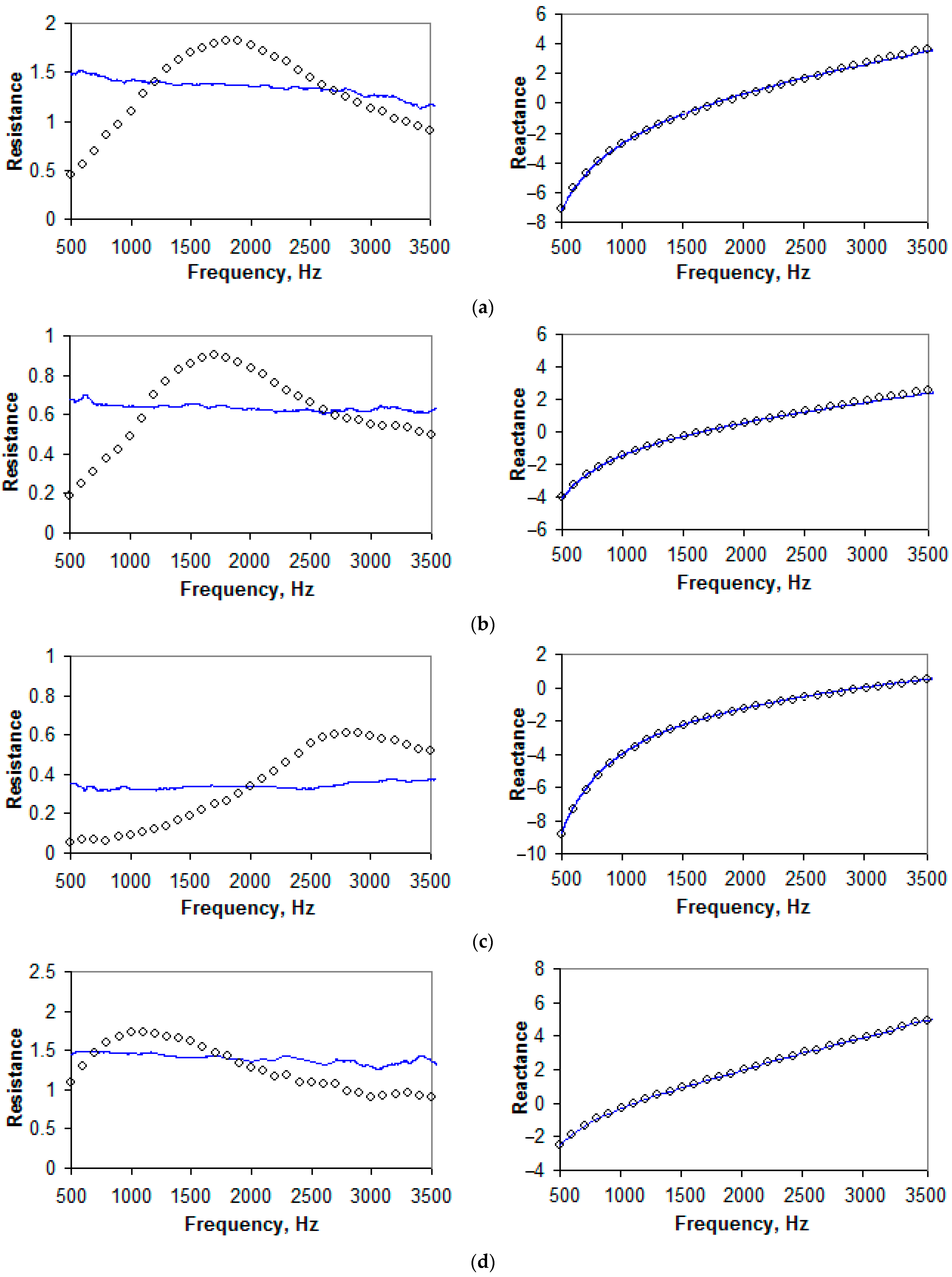
 transfer function method;
transfer function method;  Dean’s method;
Dean’s method;  Goodrich’s model;
Goodrich’s model;  Sobolev’s model;
Sobolev’s model;  Eversman’s model.
Eversman’s model.
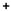 transfer function method;
transfer function method;  Dean’s method;
Dean’s method;  Goodrich’s model;
Goodrich’s model;  Sobolev’s model;
Sobolev’s model;  Eversman’s model.
Eversman’s model.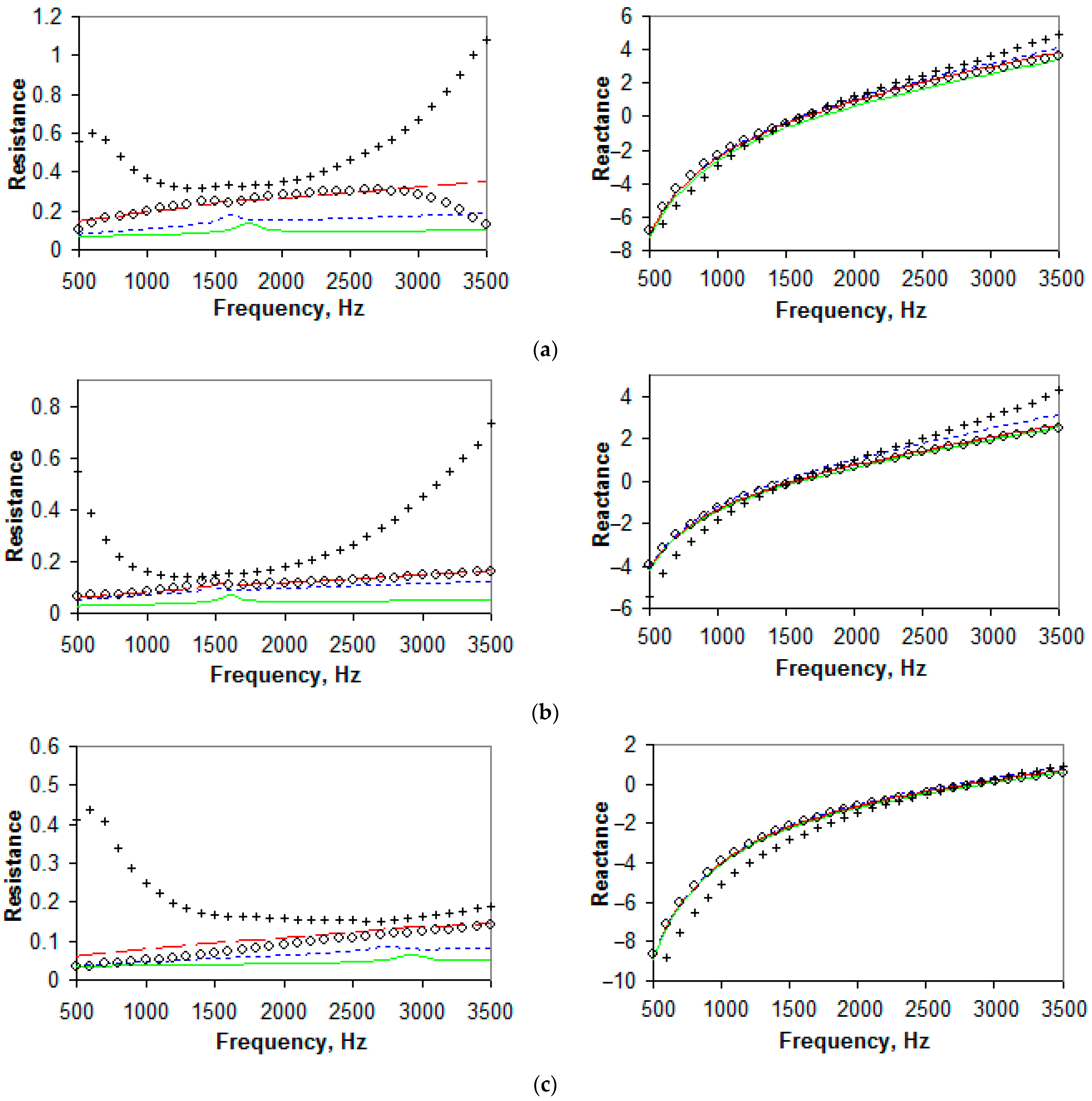
 transfer function method;
transfer function method;  Dean’s method;
Dean’s method;  Goodrich’s model;
Goodrich’s model;  Sobolev’s model;
Sobolev’s model;  Eversman’s model.
Eversman’s model.
 transfer function method;
transfer function method;  Dean’s method;
Dean’s method;  Goodrich’s model;
Goodrich’s model;  Sobolev’s model;
Sobolev’s model;  Eversman’s model.
Eversman’s model.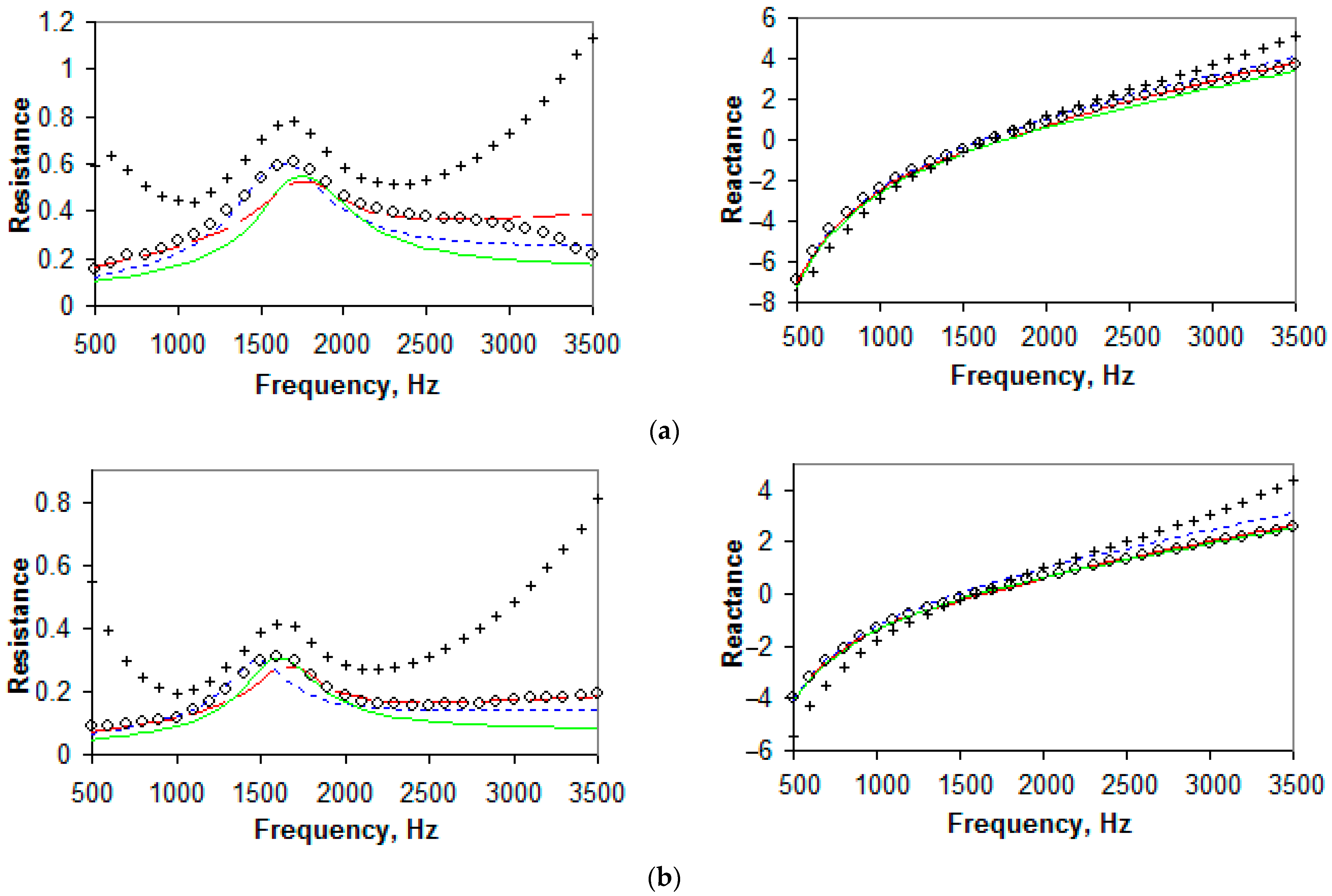
 transfer function method;
transfer function method;  Dean’s method;
Dean’s method;  Goodrich’s model;
Goodrich’s model;  Sobolev’s model;
Sobolev’s model;  Eversman’s model.
Eversman’s model.
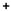 transfer function method;
transfer function method;  Dean’s method;
Dean’s method;  Goodrich’s model;
Goodrich’s model;  Sobolev’s model;
Sobolev’s model;  Eversman’s model.
Eversman’s model.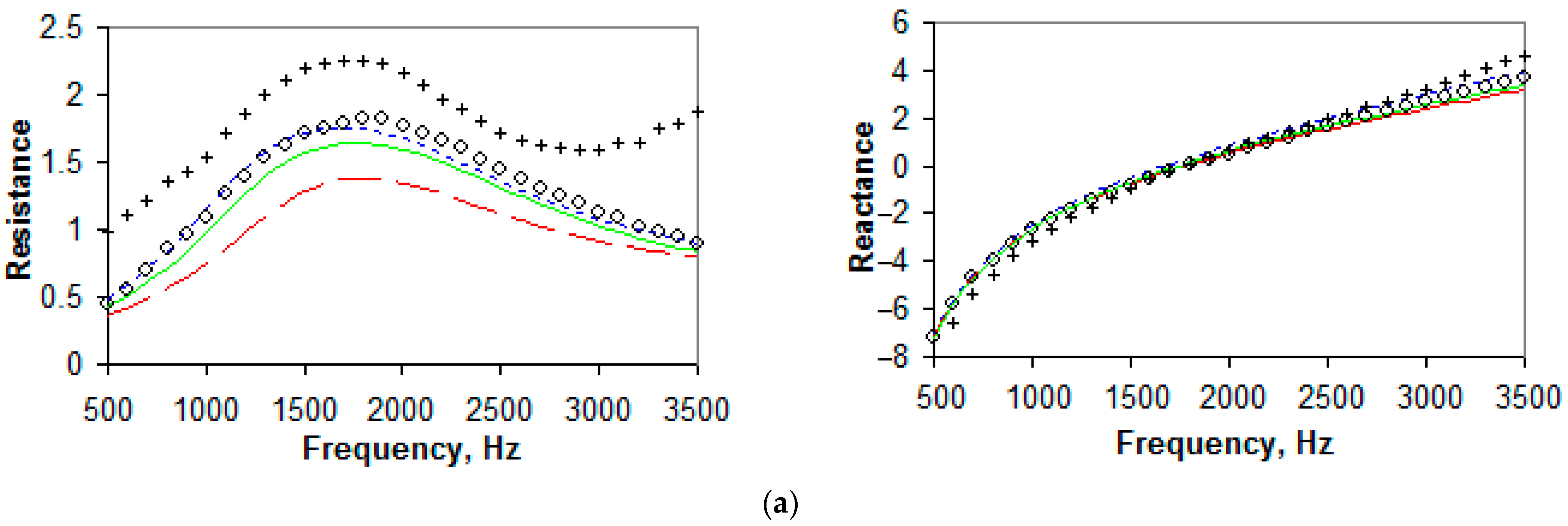
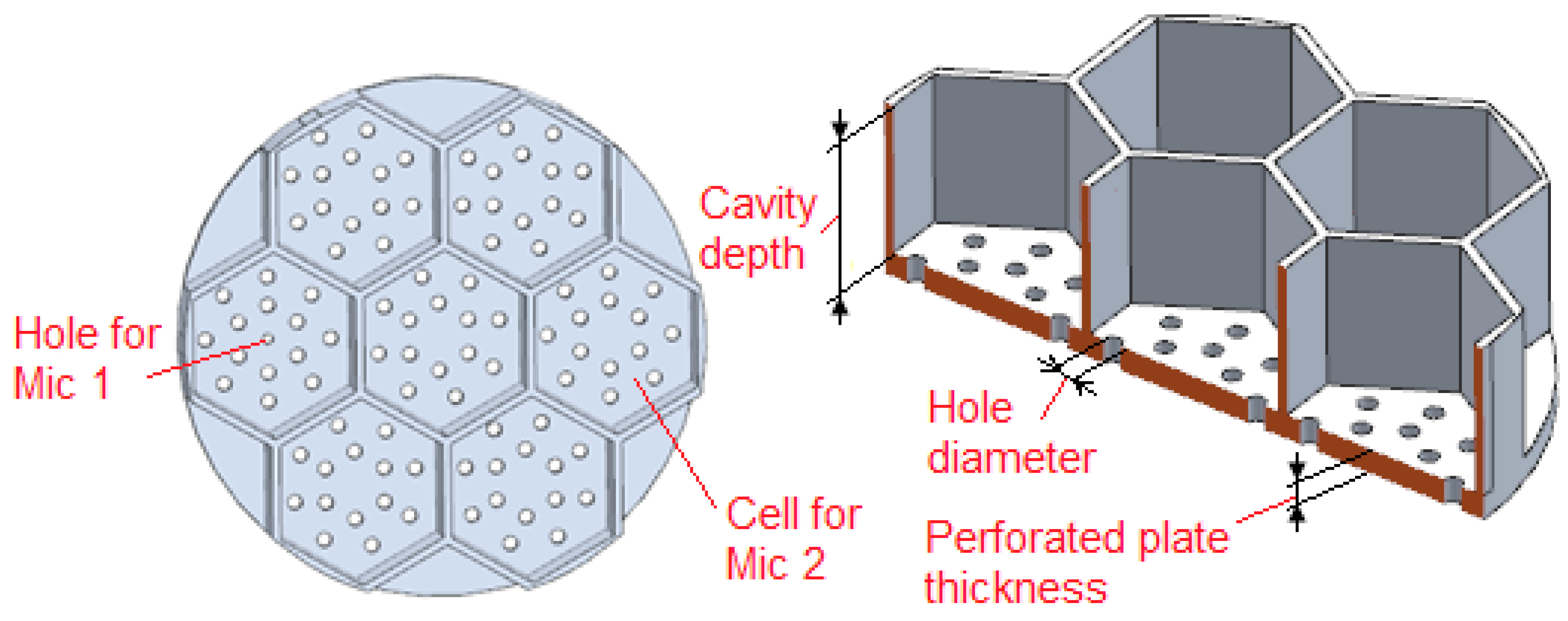
| Characteristic | Sample 1 | Sample 2 | Sample 3 | Sample 4 |
|---|---|---|---|---|
| Cavity depth, mm | 14 | 24 | 12 | 35 |
| Perforated plate thickness, mm | 2 | 2 | 2 | 2 |
| Hole diameter, mm | 1.5 | 2 | 1.4 | 1.2 |
| Number of holes in a resonator | 5 | 5 | 14 | 8 |
| Resonator open area ratio | 0.420 | 0.746 | 0.102 | 0.430 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palchikovskiy, V.; Kuznetsov, A.; Khramtsov, I.; Kustov, O. Comparison of Semi-Empirical Impedance Models for Locally-Reacting Acoustic Liners in a Wide Range of Sound Pressure Levels. Acoustics 2023, 5, 676-692. https://doi.org/10.3390/acoustics5030041
Palchikovskiy V, Kuznetsov A, Khramtsov I, Kustov O. Comparison of Semi-Empirical Impedance Models for Locally-Reacting Acoustic Liners in a Wide Range of Sound Pressure Levels. Acoustics. 2023; 5(3):676-692. https://doi.org/10.3390/acoustics5030041
Chicago/Turabian StylePalchikovskiy, Vadim, Aleksandr Kuznetsov, Igor Khramtsov, and Oleg Kustov. 2023. "Comparison of Semi-Empirical Impedance Models for Locally-Reacting Acoustic Liners in a Wide Range of Sound Pressure Levels" Acoustics 5, no. 3: 676-692. https://doi.org/10.3390/acoustics5030041
APA StylePalchikovskiy, V., Kuznetsov, A., Khramtsov, I., & Kustov, O. (2023). Comparison of Semi-Empirical Impedance Models for Locally-Reacting Acoustic Liners in a Wide Range of Sound Pressure Levels. Acoustics, 5(3), 676-692. https://doi.org/10.3390/acoustics5030041






