1. Introduction
Sound radiation simulations from vibrating surfaces can be achieved by means of linear structural finite element, boundary element or analytical models [
1,
2,
3,
4,
5,
6,
7,
8], sometimes overly simplified on the real and effective boundary conditions, frictions, mistuning and non-linearities from actual parts and mounting pre-loads, but also without real-life errors. The shape of the error patterns on structural vibrations might be therefore unknown, or disregarded as minor issues as in [
9], but the question of whether these errors might be a concern for vibro-acoustic simulations may arise, independently from the specific algorithm used. In the presentation of the work [
10], it was underlined how the error in the vibration measurement does not affect the simulations of the acoustic field, since the effects on the Rayleigh integral approximation cancel them out as the error should be uniformly distributed. By using the same approximation, this statement asked for an extended check, based instead on real, more accurate, higher spatial resolution and broad frequency band full-field optical measurements, as can be found in the present extended discussion, working on the
receptances obtained in [
11,
12,
13,
14], where, instead, the measurement noises were found with different patterns than the simplistic uniform distributions.
Furthermore, most of the times, the vibro-acoustic investigations may be limited to a single active structural eigenmode at its eigenfrequency, taken alone as a distributed vibrating source in a single tonal or resonance propagation, disregarding the neglected adjacent structural dynamics’ contributions. Spatially detailed operative deflection shapes and
receptances, coming from broad frequency band real testing as in [
14,
15], instead, may be a viable dataset for the best achievable representation in the spatial and frequency domains of the real behaviour of manufactured and mounted components around their working load levels, without any simplifications, usable also with a modally dense and damped structural dynamics and complex patterns in the dynamic signature of the excitations, with broad frequency spectra.
At the core of this paper, therefore, the exploitation of experiment-based optical full-field technologies is proposed for sound radiation numerical simulations. A trace of the author’s background needs to be given to the interested reader, to understand how the experience with full-field techniques has grown before the recent works [
16,
17,
18,
19,
20,
21,
22], which are spin-off activities after the end of the TEFFMA project (
Towards Experimental Full Field Modal Analysis, funded by the European Commission with the Marie Curie FP7-PEOPLE-IEF-2011 PIEF-GA-2011-298543 grant and carried out by the author from 1 February 2013 to 31 July 2015 at the Vienna University of Technology, Austria; note: A. Zanarini was the unique scientific proposer and experienced researcher in the TEFFMA project). The early steps were made in the HPMI-CT-1999-00029
Speckle Interferometry for Industrial Needs Post-doctoral Marie Curie Industry Host Fellowship project held by the author in 2004-2005 at Dantec Ettemeyer GmbH, Germany. Since the early measurements [
23,
24] it became clear how the ESPI approach, a
native full-field optical technology, allows a dense mapping of the structural dynamics for enhanced assessments [
25] and fatigue spectral methods [
26,
27]. The TEFFMA project’s ideas were born in the works of [
25], with the first presentations in [
11,
28], followed by [
12,
29,
30,
31]. In [
13] a gathering of the works of TEFFMA was firstly attempted, whereas [
14] made an extensive description of the whole
receptance testing and [
32] detailed the successful EFFMA and the full-field based model updating attempts. Only in [
33] the full-field techniques were scrutinised to find the potential error distributions on the shapes at each frequency line: this analysis underlined the specific noise patterns in full-field dynamic testing later here used for the results and the discussion. Furthermore, the precise comparison in [
34], about new achievements for
rotational and
strain FRF high resolution experiment-based
maps, put again into evidence the quality of full-field datasets, as the numerical derivatives can easily spread errors across the spatial domain. The interested reader can appreciate in [
13,
29,
34] the effect of the measurement noise on derivative quantities; however, unfortunately due to the complexity of their measurement, the
rotational dofs are usually disregarded, whilst they are relevant for the successful build of a reliable dynamic model for complex structures [
35,
36,
37,
38,
39,
40,
41,
42]. Based on the achievable
strain FRF mapping, in [
17] a risk index was introduced as a metric to distinguish failure-exposed areas in a dynamically loaded component, with a focus also on the evidences from a damaged fibreglass reinforced composite panel [
16,
24]. In [
19] a comparison among risk index maps was made, when the same white noise spectrum was changed in injection locations, whereas in [
20] the variability of risk maps was analysed by the changes in the excitation dynamic signature. In [
21] two excitation signatures and two energy injection locations were combined for risk grading. Therefore, various works have been published recently by the author on the full-field optical measurements and on their perspectives in NVH [
11,
12,
13,
14,
16,
17,
18,
19,
20,
21,
22,
28,
29,
30,
31,
32,
34]. Especially the latest works [
11,
13,
14,
16,
17,
18,
19,
20,
21,
22,
29,
32,
34] from the TEFFMA project highlighted the tangible advances for the consistency and continuity of the data fields, which have become available by the growing full-field techniques, with clear effects in model updating, derivatives’ calculations (
rotational dofs,
strains,
stresses and
risk index maps) and vibro-acoustics. Optical full-field
receptance maps are becoming an increasingly consistent non-contacting experiment-based means in the estimation of high spatial resolution dynamic deflection shapes, and are appreciated especially in the case of lightweight structures or panels. These experiment-based shapes come with low, but not null, noise on the fields, across a broad frequency range, with all the blending, and potential phase delays, of a modally dense dynamics, without the need of any analytical model nor of a truncated modal base identification [
36,
39].
To be recalled is that full-field optical measurements started as a qualitative design aid, thanks to the larger and denser vision offered and the high consistency of the viewed field [
43]; but, as based on the chemical development of film compounds, they were not competitive in terms of time-to-result [
44] with the digital instruments of the time. But they were proficiently used to show the whole response shape of a structure at a particular frequency of interest, as they already offered a highly detailed picture of the spatial domain against the coarse representation obtained by traditional lumped sensors (e.g., accelerometers or strain gauges, at that time, the only quantitative instruments). Indeed full-field optical approaches were among the first techniques that showed the entire field ODSs with rapidly changing patterns during the frequency sweeps. These ODSs appeared for the first time as functions of the complex blending of the structural dynamics in non-conventional patterns, highlighting where the best location for the lumped vibration sensors, used in contemporary structural dynamics’ approaches, could have been.
SLDV [
39] introduced the concept of contactless measurement—adding no mass to the specimen—in time/frequency domains in the 1980s, expanding it to finer grids of scanned locations, thus extending the concept of the velocity sensors to a spatially detailed acquisition. Therefore SLDV is considered
the reference in NVH when spatially detailed FRF measurements are needed: SLDV keeps the same peculiarities of lumped sensor technologies (and of established procedures, born to exploit few dofs only), but adds many dofs in the spatial domain at a reasonable cost, with a trade-off at high frequency in the sensitivity between displacements and accelerations. Due to the
asynchronous scanning process, however, SLDV can not be properly called a
native full-field instrumentation.
Only the optical full-field technologies that acquire the motion-related information from photons
synchronously recorded at every sensible site of an imaging sensor, normally in a much denser grid, can be instead called
native. Earlier, in [
23,
24], the author proved the high quality of the datasets obtainable in the spatial domain from the native full-field measurement techniques, acknowledged in terms of consistency of the motion field among the neighbouring dofs. Since the 2000s, ESPI, among the
native full-field technologies, has given extremely accurate displacement fields up to several kHz of frequency. Due to a lack of complete processing automation, up to now the main drawback of ESPI remains the time-consuming stepped sine excitation/acquisition, in order to have data at all the lines of a broad frequency band in stroboscopic light acquisitions [
25,
45].
High-speed DIC is another
native technology, with its first commercial prototypes starting around 2005. DIC can have good detail in the time-resolved displacement maps, but the processing of the correlated data can be time consuming [
12,
13]. Due to both a sensor/electronics bandwidth trade-off, between resolution and sampling rate, and the difficulty in properly exciting the higher frequency displacement components, DIC is generally more limited for complex structural dynamics in a broad frequency domain, although rapid electronics and processing improvements can be easily foreseen in the near future.
Indeed, nowadays,
scanning and
native full-field optical technologies allow displacement and velocity measurements in a non-contact way with dense spatial mapping, without inertia-related distortions of the dynamics (due to added sensors, fixtures and cabling), and without any structural finite element (FE) or analytical models to be accurately tuned for the lumped sensor data expansion [
42,
46,
47]. As it was previously shown in [
13,
34], ESPI technology actually permits the most precise estimation from non-contacting testing of superficial
receptance FRF maps, which turn out to be optimal also for derived quantities like dense mapping of
rotational dofs and
strains.
The Rayleigh integral formulation (e.g., in [
1,
4,
5,
6,
8,
48,
49,
50,
51]) can be adopted for the numerical approximation of the Helmholtz equation for the sound pressure field induced by a vibrating surface. The Rayleigh approach has undergone a slight re-formulation to take advantage of the spatial oversampling of full-field
receptances [
36,
39], here from a lightweight rectangular plate in a broad frequency band. The re-formulation shows how the most advanced experiment-based knowledge available can augment the fidelity of the acoustic field mapping. The results are well detailed maps of the vibro-acoustic frequency response functions (pressure over force), or of the radiated acoustic pressure, once the structural excitation is defined in its dynamic signature and energy injection location. This underlines the importance of the test-based
complex-valued structural dynamics in reliable sound radiation predictions. The usage of experiment-based optical full-field
receptances for the acoustic field prediction has already been introduced by the author in the works [
18,
22], with interest on the excitation dynamic signature and on the energy injection location. Therefore the accuracy in the maps of experiment-based optical full-field
receptances becomes crucial for assessing error effects, by means of the here-proposed experiment-based approximation of sound radiation from a vibrating plate, thanks to the high quality estimations of the real structural dynamics with accurate spatial description for complex pattern sensing, especially for lightweight structures in broad frequency bands.
A thin and lightweight rectangular plate was the sample used here, whose dynamics was sensed using the SLDV technology, in a broad frequency band, during the fundamental research project TEFFMA. The TEFFMA project made a comparison between the state-of-the-art technologies in image-based (
native, DIC and ESPI) full-field optical measurements and the
scanning SLDV as reference, to understand if these approaches, not completely established, can provide NVH applications with enhanced peculiarities. A dual-shaker-driven broad frequency band excitation was used successfully for a complete EFFMA as in [
32]. The
experiment-based full-field FRF approach in [
14] can bring the complete and real structural dynamics into sound radiation approximations, therefore, as proposed here, assessing the effect of errors, spread on the experiment-based full-field
receptances, onto the vibro-acoustic simulations. From the perspective of using only experiment-based quantities—for the retained dynamics, for the broad frequency spectra of the excitation and for the high resolution mapping achievable—the quality of the raw dataset plays an uttermost relevance in the accurate and reliable acoustic field reconstruction.
The novel strength of this paper deals with the findings of experiment-based specific noise patterns on the
raw receptances of the testing, specifically as a uniformly distributed and amplitude-modulated noise, a measurement-related noise and a filtering-related noise. This approach is different from discussing the methods for the best reconstruction of the acoustic fields, as can be found in [
52]. Here the errors are in the full-field
raw receptances only, while the Rayleigh integral is kept as the unique computational means to see the impact on the vibro-acoustic FRFs. The use of a
complex-valued re-formulation of the Rayleigh integral approximation permits the usage of real measurements without any assumptions, except those concerning the linearity of the system during the
receptances’ estimations [
36,
39,
53]. The assessed noise patterns from real testing, being different from the generally assumed uniform distribution of random noise, have therefore been extensively discussed here, by means of quantitative comparative tools, regarding their potential to create distortions on the simulated vibro-acoustic frequency response function maps, at different distances from the vibrating plate.
This paper is organised as follows. After this introductory
Section 1, the main methodological
Section 2 comprises what is needed to understand and replicate the analyses of this work: the experiment-based FRF modelling is sketched in
Section 2.1; the testing is briefly outlined in
Section 2.2, with attention on the set-up; the Rayleigh integral re-formulation is recalled in
Section 2.3; the tools to quantitatively compare the simulations are gathered in
Section 2.4. The main results’
Section 3 proposes the simulations of the vibro-acoustic frequency response functions and the potential error effects, with detailed figures and comments.
Section 3.1 deals, after notes on the meshing of the acoustic domain, with examples in the space and frequency domains of vibro-acoustic transfer functions, simulated from the
experiment-based full-field receptance maps, with and without noise; furthermore, the comparative tools are applied to these simulations.
Section 3.2 discusses the effects of a uniformly distributed and amplitude-modulated noise.
Section 3.3 discusses the effects of a measurement-related noise.
Section 3.4 discusses the effects of a filtering-related noise. The main discussion is done in
Section 4, which synthesises the comments of the achieved results, before
Section 5 for the final statements. “Abbreviations” finally gathers the nomenclature used in the manuscript without explicit explanation.
4. Discussion
The purpose of this article is to discuss how the noise measured on the structural dynamics can influence the vibro-acoustic FRF simulations. In
Section 3 examples of the whole
acoustic transfer matrix from
Section 2.3 were shown over the entire acoustic mesh at specific frequencies and distances, when shaker 2 was used; in particular, in
Section 3.2,
Section 3.3 and
Section 3.4, three different types of noise patterns were highlighted over the structural
receptances from real testing. The frequencies were selected on the whole broad frequency band, therefore also outside the resonances, as presenting specific behaviours, which may enter into the acoustic responses when the structure is excited with a broad signature. Furthermore, they may leave traces in the modal identification [
13,
32]. These results were precisely discussed by means of the quantitative tools proposed in
Section 2.4. Note again how the vibro-acoustic simulations retained the real-life, unsimplified,
complex-valued relations and phase delays, coming from the underneath
complex-valued receptance matrix in Equation (
1), obtained directly from the experiments of
Section 2.1, but blended in the
complex-valued summation in
of Equation (
14), without any artificial noise model nor regularisation.
Table 17 summarises the ratio between the evaluated vibro-acoustic error against the raw vibro-acoustic transfer function value in acoustic dof 941; each pair of columns (first-second, third-fourth, fifth-sixth) is related to each type of error in the
receptance source as discussed in
Section 3. This ratio goes from a negligible to a strong relevance of noise issues in the vibro-acoustic simulations, showing when the smoothed results can clearly be distorted in comparison with those obtainable from the raw experiments. After the development of such a quantitative comparison of datasets, run at four distances from nearfield to medium distance, it can be easily stated that only a uniformly distributed random noise on experimental structural
raw receptances has a very limited impact on vibro-acoustic FRF simulations, at close distance from the vibrating plate. However, it is sufficient that an ODS modulates—in the spatial domain—the amplitude of the scattered noise, to start noticing some divergence in the results, as commented on
Section 3.2. Once the noise on the experimental structural
raw receptances has specific patterns, such as those related to a specific measurement system, also modulated by the ODS pattern, the assumption of uniform distribution in the noise is lost, and clear effects were commented on
Section 3.3. The stronger distortions—here documented in
Section 3.4—originated from the excessive filtering of experimental datasets, by means of a filter with a lower spatial complexity than that found on the experimental structural
raw receptances and real noise distributions (e.g., the specific measurement-related noise, modulated in amplitude and phase by the
complex-valued ODS). This latter problem suggests the usage in future research of a smoothing filter with adaptive spatial order to the complexity of the specific structural dynamics and real-life noise patterns.
Figure 30.
Examples of
receptance shapes with their experiment-related noise (in (
), Equation (
1)) against the smoothed version (in (
), Equation (
2)) and related error pattern (in (
), Equation (
3)) at the specific frequency of 991 Hz, with excitation from shaker 2.
Figure 30.
Examples of
receptance shapes with their experiment-related noise (in (
), Equation (
1)) against the smoothed version (in (
), Equation (
2)) and related error pattern (in (
), Equation (
3)) at the specific frequency of 991 Hz, with excitation from shaker 2.
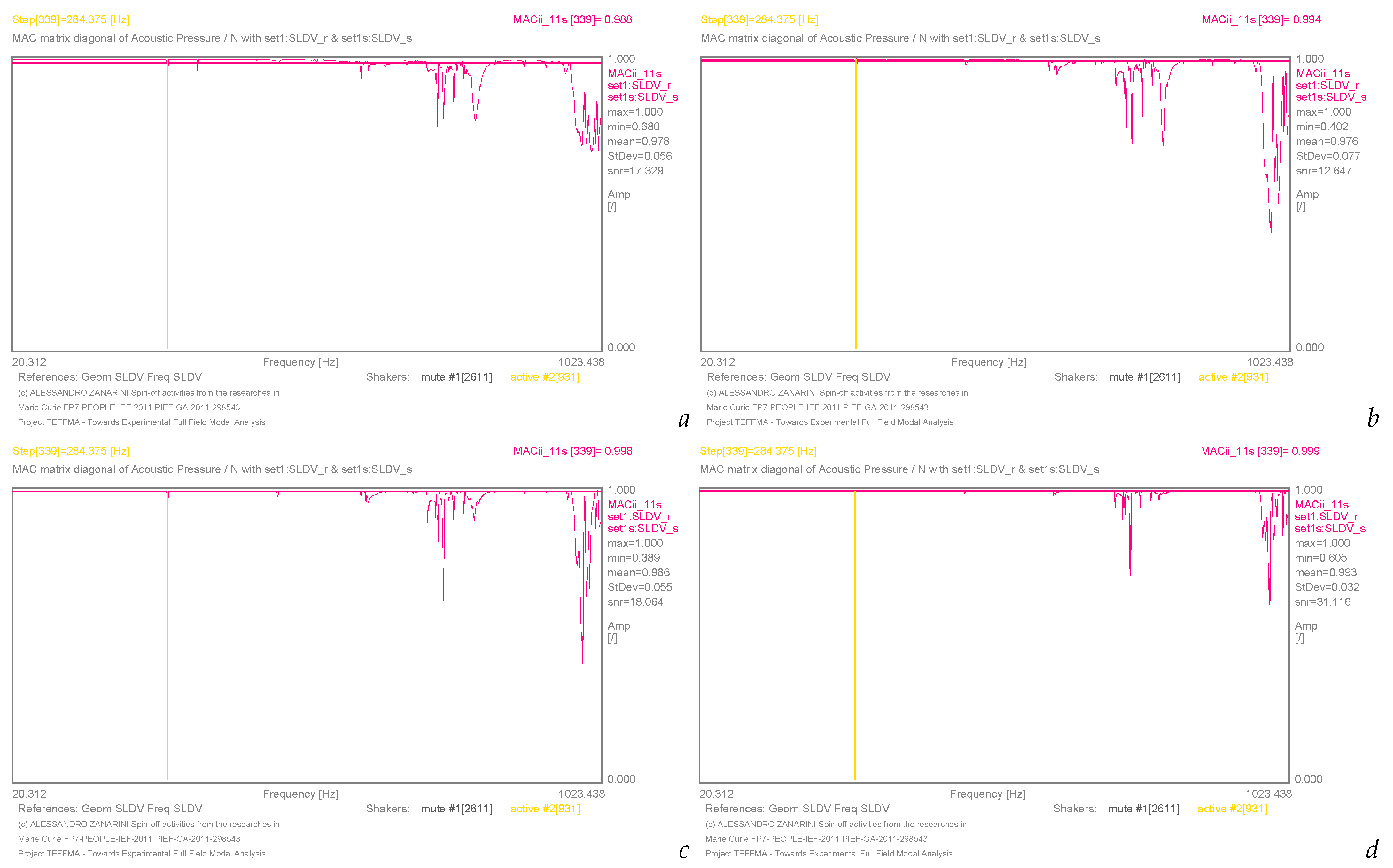
Figure 31.
MACii graphs in the comparison of the
acoustic transfer matrix as in Equations (
14) and (
18), at specific distances of 25 mm in (
), 75 mm in (
), 150 mm in (
), and 300 mm in (
) at the specific frequency of 991 Hz, with excitation from shaker 2.
Figure 31.
MACii graphs in the comparison of the
acoustic transfer matrix as in Equations (
14) and (
18), at specific distances of 25 mm in (
), 75 mm in (
), 150 mm in (
), and 300 mm in (
) at the specific frequency of 991 Hz, with excitation from shaker 2.