Data-Driven Discovery of Anomaly-Sensitive Parameters from Uvula Wake Flows Using Wavelet Analyses and Poincaré Maps

Abstract

This study presents a data-driven approach to identifying anomaly-sensitive parameters through a multiscale, multifaceted analysis of simulated respiratory flows. The anomalies under consideration include a pharyngeal model with three levels of constriction (M1, M2, M3) and a flapping uvula with two types of kinematics (K1, K2). Direct numerical simulations (DNS) were implemented to solve the wake flows induced by a flapping uvula; instantaneous vortex images, as well as pressures and velocities at seven probes, were recorded for twelve cycles. Principal component analysis (PCA), wavelet-based multifractal spectrum and scalogram, and Poincaré mapping were implemented to identify anomaly-sensitive parameters. The PCA results demonstrated a reasonable periodicity of instantaneous vortex images in the leading vector space and revealed distinct patterns between models with varying uvula kinematics (K1, K2). At higher PCA ranks, the periodicity gradually decays, eventually transitioning to a random pattern. The multifractal spectra and scalograms of pressures in the pharynx (P6, P7) show high sensitivity to uvula kinematics, with the pitching mode (K2) having a wider spectrum and a left-skewed peak than the heaving mode (K1). Conversely, the Poincaré maps of velocities and pressures in the pharynx (Vel6, Vel7, P6, P7) exhibit high sensitivity to pharyngeal constriction levels (M1–M3), but not to uvula kinematics. The parameter sensitivity to anomaly also differs with the probe site; thus, synergizing measurements from multiple probes with properly extracted anomaly-sensitive parameters holds the potential to localize the source of snoring and estimate the collapsibility of the pharynx.

1. Introduction

Conventional methods for diagnosing breathing-related disorders often rely on acoustic recordings or EGG signals. An inherent limitation of such methods is the lack of detailed understanding regarding how externally measured signals correlate with underlying airway abnormalities, which themselves need to be diagnosed or clarified. This gap in signal–disease correlation renders most signal-based diagnoses inaccurate and, at best, empirical. It should be noted that not all signals are useful. Acoustic signals are integrative, embedding a myriad of pressure components originating from both disease site and surroundings [1,2,3]. Thus, isolating disease-specific signals from recorded acoustics can be challenging.

Lumped analytical models have been implemented widely to understand and intervene in respiratory dynamics. Various models of respiratory dynamics have been proposed, offering differing levels of detail, complexity, and rigor. Models comprising single or multiple compartments with a network of resistors (R_i) and capacitors (C_i) are well received by clinicians because of their simplicity [4,5]. Most commercial devices for respiration assistance or diagnosis are based on such models. For instance, most mechanical ventilators assess a patient’s lung health by estimating the lung’s resistance R and compliance C [6,7,8]. Electrical analog models do capture major dynamics in a time-/resource-efficient way; however, they also suffer from setbacks of neglecting nonlinearity and lack of details. In this vein, nonlinear corrections, such as a sigmoidal equation, have been introduced to more accurately assess tissue compliance or airway resistance [9,10]. However, flow-induced sounds, or aeroacoustics, are inherently a highly nonlinear process, not only due to the nonlinearity of tissue properties but also to the multiple flow regimes and the dynamic fluid–structure interactions [11,12,13]. As a result, lumped electrical analog models have rarely been used to study acoustics in breathing-related disorders.

Physiology-based modeling and simulations have emerged as a viable alternative to understanding the correlations between internal anomalies and externally measurable signals, such as lung sounds and flow–volume curves [14,15,16]. This approach has become an ideal tool for examining the mechanisms behind snoring and sleep apnea, especially since current diagnostics for snoring are predominantly confined to specialized sleep labs where patients are required to stay overnight [17,18,19,20]. Compared to experimental testing, computational aeroacoustics offers a more detailed temporal and spatial insight into respiratory flows. Past research has significantly enhanced our understanding of this vortex-driven, flow-induced phenomenon, providing clarity on sound production [21,22]. However, contemporary transient numerical simulations can easily generate data in the order of gigabytes and even terabytes. Vortex images, despite their vivid visual representations, are complex to interpret. It is still challenging to use these simulation results for diagnostic or prognostic purposes, e.g., to predict pharynx collapse, identify snoring source, or quantify tissue property variation [20,23,24,25,26,27]. Further analysis of such data promises to reveal new information critical to understanding both respiratory physiology and pathology.

Several studies have analyzed simulation data generated by LES or DNS to search for anomaly-sensitive parameters hidden within the seemingly chaotic flow images/videos to effectively differentiate health from disease [28,29,30,31]. Analytical methods include principal component analysis (PCA) [32], proper orthogonal decomposition (POD) [33], dynamic mode decomposition (DMD) [34], balanced modes [35], global eigenmodes [36], etc. These methods have shed useful light on the underlying dynamics of fluid flows from different perspectives. Analytical approaches of time-series pointwise flow parameters (pressure, velocity, vorticity, etc.) have been employed even more widely to study the system’s temporal and spatial dynamics. These include fast Fourier transform (FFT), continuous wavelet transformation, semblance, autocorrelation, Shannon entropy, multifractal, Lyapunov exponent, and Poincaré maps [37,38,39]. The multifractal spectrum has been demonstrated to be sensitive to anomaly-induced differences in acoustic signals and exhaled aerosol distributions [40,41,42]. Poincaré maps, or recurrent maps, have often been used to study the stability of dynamic systems under periodic forcing [43,44]. Bramburger and Kutz used Poincaré maps to study a multiscale dynamical system close to invariant manifolds, and demonstrated that Poincaré maps could offer forecasting of long-term dynamics [45]. In practice, a Poincaré map can be challenging to implement due to its requirement for a large number of intersection points to reveal the hidden pattern. The advent of high-fidelity physiology-based DNS simulations in recent years provides the needed inputs for data-driven discoveries of reduced-dimensional, anomaly-sensitive features.

In this study, we will simulate the wake flows from a vibrating uvula using direct numerical simulation (DNS), and analyze the wake flows to seek anomaly-sensitive variables or features. Particularly, instantaneous vortex structures of multiple uvula vibration cycles will be analyzed using PCA. Additionally, the time series of pressures and velocities at different probes will be examined using wavelet transform and Poincaré section analysis to identify the appropriate measurement points for predicting pharynx constrictions or uvula vibration modes. The goal is to identify low-dimensional, anomaly-aware parameters from a large dataset of DNS results that are sensitive to either uvula kinematics or pharyngeal constriction levels.

2. Methods

Airway models and uvula motions are described in Section 2.1. Numerical methods using direct numerical simulations (DNS) are explained in Section 2.2. Regarding the DNS-predicted wake flows, the 2D vortex images analyzed using principal component analysis (Section 2.3); while the time-series pressure signals were analyzed using wavelet transform (Section 2.4) and Poincaré section analysis (Section 2.5), respectively.

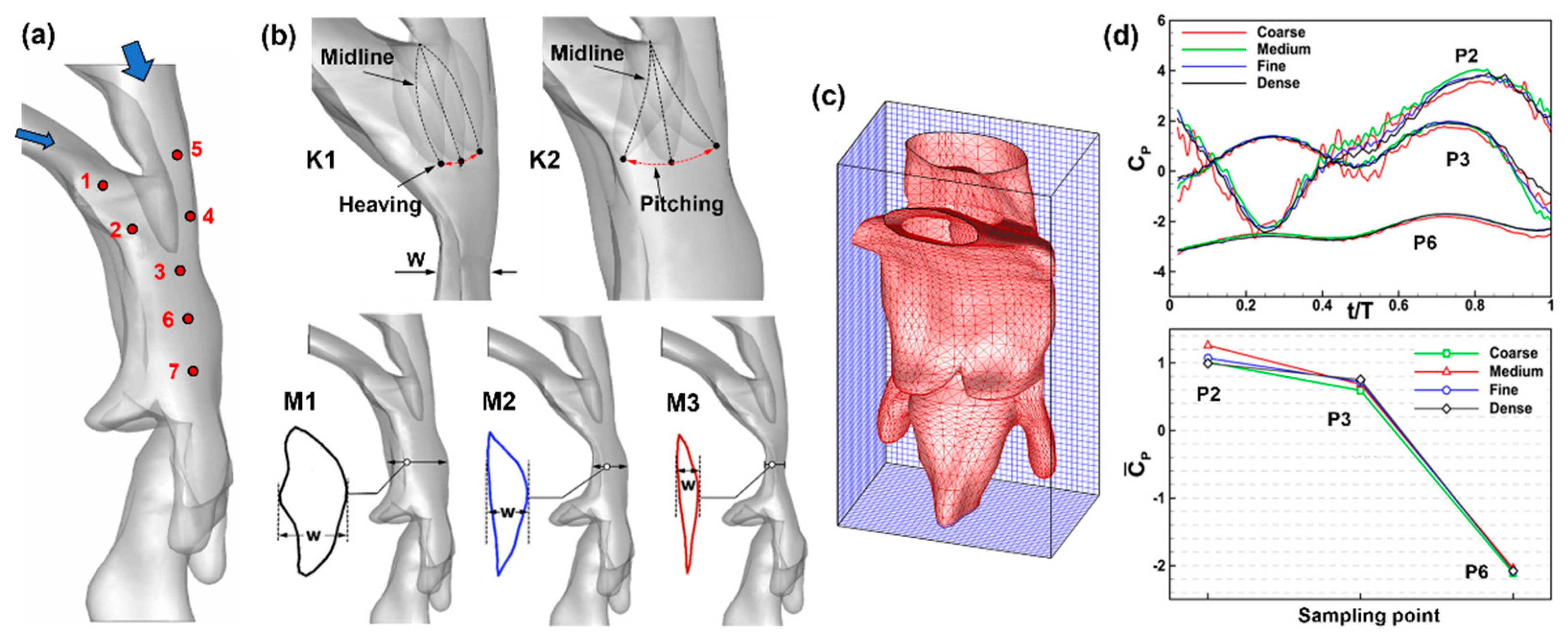
2.1. Airway Model with a Vibrating Uvula and Constricted Pharynx

The mouth-nose-throat airway model (Figure 1a) was adapted from an airway geometry originally reconstructed from MRI scans of an adult male using Mimics (Materialise, Leuven, Belgium) [46]. To simulate pharynx collapses that lead to apnea, three progressive models of pharyngeal constriction were developed, namely, M1, M2, and M3 (Figure 1b). The uvula vibrations were determined from a high-speed recording of uvula motions [28] exhibiting two distinct kinematics. The heaving mode (K1) had the largest flapping amplitude at the middle uvula, while the pitching mode (K2) had the largest amplitude at the uvula tip (Figure 1b). The vibration frequency was 100 Hz, and the inhalation flow rate was set at 20 L/min, following [47,48]. The inhaled air was distributed, with 80% entering the nose and 20% entering the mouth. Ambient conditions were specified at zero pressure (Figure 1a). Seven sampling points or probes were utilized to record instantaneous pressure and velocity, as indicated in Figure 1a. Specifically, probes 1 and 5 were positioned near the base of the uvula, probes 2 and 4 were located close to the middle of the uvula, probe 3 was situated directly beneath the uvula, probe 6 was at the site of pharyngeal constriction, and probe 7 was positioned near the epiglottis.

2.2. Numerical Methods

Direct numerical simulations (DNS) were implemented to resolve the inspiratory flows with high-frequency uvula oscillations. The immersed boundary method (IBM) was used to control the uvula kinematics based on a Cartesian-grid finite-difference approach (Figure 1d) [49], which has undergone extensive testing in simulations of flapping propulsion for insects [50,51], birds [52,53], fish [54,55], and breathing [56]. In summary, the airway surface with tetrahedral meshes was immersed in a structured hexahedral grid (Figure 1c), with the boundary conditions specified on the immersed surfaces via the ghost-cell approach [57]. Constant flows were inhaled into the mouth and nose, and the tracheal outlet had a zero-gradient condition, ensuring vortices could move through freely. Second-order central differencing was used for discretizing the flow variables p and u_i. The time step size was 0.02 ms; a second-order accurate fractional-step method was used for time marching. Each case simulated twelve cycles of uvula vibrations, spanning 0–0.12 s. One-way coupling was assumed, i.e., from dynamic structures to fluid only. Convergence was assumed until the first three energetic modes changed less than 1 × 10⁻⁵ in two successive time steps. The pressure p was normalized as p/(0.5ρU₀²), with U₀ being the inlet velocity into the mouth (U₀ = 0.5 m/s). A grid independence study was conducted on the C_P variation with meshes from 0.8, 2.8, 5.3 to 9.0 million (i.e., from extra-coarse, coarse, fine, to ultrafine), as shown in Figure 1d. Less than 1.5% in C_P was obtained at the sampling point 3 between the fine and ultrafine meshes, and thus the 5.3-million mesh was utilized for all following predictions.

2.3. Principal Component Analysis (PCA) of 2D Time Series Vortex Images

Principal component analysis (PCA) is a linear dimensionality reduction technique that identifies a series of orthogonal spatial features derived from the singular value decomposition (SVD) of a data matrix. PCA was selected to analyze uvula wake flows in this study because of its computational efficiency and its successful usages in previous studies. PCA offers computational simplicity and efficiency, especially when dealing with large datasets, as in this study. PCA has been widely implemented to glean insights from vortex flows, even with its inherent linearity [58,59]. To prepare for PCA, each 2D vortex image was represented with 427 × 960 data points, translating to a vector with 409,920 values that served as a single column in the data matrix. For a category containing 288 images, the matrix X had dimensions of 409,920 × 288. The mathematical representation of the SVD method can be expressed as X = UΣV*, where ‘U’ denotes the matrix of principal components (PCs) or vectors. To project a sample image, x, into a 3D vector space spanned by the PCs (i, j, k), the formula ϕ(i, j, k) = <x, U(i, j, k)> is used, where < > denote a dot product [60]. It should be noted that when performing PCA on the 2D vortex images, each image was treated as a high-dimensional vector. At each pixel location there was one dimension for grey images and three dimensions for color images, while the pixel location (x, y) was preserved in its relative location in the vector column. In this way, the spatial information of a 2D image was preserved even though it was written as a vector for mathematical purposes, i.e., to perform SVD.

2.4. Wavelet Transform Analyses of Time-Series Pressures

To analyze pressure signals from a periodically oscillating uvula, we chose the wavelet transform over standard time-frequency transform for its variable resolution and transient detection. The oscillating uvula could produce pressure signals with both low-frequency components (representing the primary oscillation) and high-frequency components (potentially arising from rapid transient events or perturbations). The wavelet transform’s ability to provide high frequency resolution at low frequencies and high time resolution at high frequencies makes it particularly suitable to capture and analyze both these aspects of the signal. Moreover, the wavelet transform is adept at detecting transient events or anomalies in signals. Considering the uvula wake flows, there could be irregularities or sudden changes in the pressure signal, which wavelets can capture effectively due to their localized nature.

Wavelet transform analyses were performed in MATLAB. We employed the continuous wavelet transform (CWT) to break down the instantaneous pressure coefficients C_P across multiple scales, aiming to uncover correlations less evident in the original C_P profiles. Various wavelets were utilized to adjust and modulate the signal f(t):

$$wt(a,b)=\frac{1}{\sqrt{a}}{\displaystyle {\int }_{-\infty }^{\infty }f(t)\psi }(\frac{t-b}{a})dt\begin{array}{cc},& \end{array}a>0$$

(1)

Here, a is the scaling factor, b is the time lag, and $\psi (t)$ is the Morlet wavelet [61]. The wavelet coefficient wt represents the degree of similarity between the signal and the wavelet at a particular a and b. By adjusting a and b, spatial and temporal anomalies (i.e., abrupt change in patterns) can be isolated [61]. A smaller a denoted a condensed wavelet and higher frequency, highlighting swift and sharp fluctuations. Adjusting the time lag b either forwarded or pushed back the wavelet’s starting point. The scalogram visualized the time-frequency energy distribution and was derived through the CWT.

The discrete wavelet transform was employed to derive the multifractal spectrum of signals, establishing a normalized measure µ_i(q, ε) with a series of scaling exponents q, to investigate various segments of the singularities (i.e., rapid or infinite changes of a specific measure) [62].

$${\mu }_i(q,\epsilon )={\left[P_i(\epsilon )\right]}^q/{\displaystyle \sum {\left[P_i(\epsilon )\right]}^q}$$

(2)

When q < 1, µ_i(q, ε) highlighted the regions with weaker singularities, whereas when q < 1, it emphasized areas with stronger singularities. The multifractal spectrum function f(α), as well as the strength of the singularity α(q), were determined as a function of µ_i(q, ε):

$$\alpha (q)=\underset{\epsilon \to 0}{\lim }\frac{{\displaystyle \sum {\mu }_i(q,\epsilon )\ln P_i(\epsilon )}}{\ln \epsilon };\hspace{1em}\hspace{1em}\begin{array}{cc}& f({\alpha }_q)=\underset{\epsilon \to 0}{\lim }\frac{{\displaystyle \sum {\mu }_i(q,\epsilon )\ln {\mu }_i(q,\epsilon )}}{\ln \epsilon }\end{array}$$

(3)

2.5. Poincaré Section Analysis of Time-Series Pressures/Velocities

The Poincaré section, also known as Poincaré map or first return map, is a technique to study dynamical systems, particularly in analyzing periodic or quasi-periodic system behaviors [63,64]. It is a lower dimensional slice of the phase space, and can be visualized as the intersection points where a trajectory (or flow) cuts through the section. There are different ways to define these slices in the phase space, i.e., mean/plane Poincaré map, maxima/minima maps, and period map. The mean Poincaré section is defined by a specific plane in phase space. Every time a trajectory crosses this plane in a specified direction (for example, from below to above), an intersection point is plotted [65]. Likewise, for a maxima/minima map, the plane is defined by its local maxima/minima, with a point plotted each time the variable reaches the extrema. The period Poincaré section (or period map) is defined by a fixed time interval. A point is plotted at every fixed time period and describes how the system’s state evolves over regular time intervals. Different types of sections can reveal different characteristics or attributes of the system, such as chaotic behaviors, stable orbits, and other invariant measures. In this study, we used a sampling period of 10 ms, based on the observed dominant frequency of vortex flows and to capture sufficient detail without oversampling. MATLAB was used to conduct the Poincaré section analysis of time-series pressure and velocity signals.

3. Results

3.1. DNS-Predicted Inspiratory Vortex Dynamics

Figure 2 showcases the vortex structures across the six models at t/T = ¾, a moment when the uvula tip is at its furthest left position. Vortex shedding, originating from the oscillating uvula, is observed for all models. However, the vortex intensity is notably higher in the two M3 models compared to the M1 and M2 models, especially in the proximity of the uvula and within the pharynx. Considering the uvula kinematic effects (K1 vs. K2), differences in vortex structures are noted on the rear side of the uvula, with K2 models exhibiting weaker vortices near the middle uvula and more left-skewed vortices at the uvula tip than the counterpart K1 models (i.e., Figure 3a vs. Figure 3d at t/T = $\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$. The temporal evolution of the vortex structures is also shown in Figure 2a. The uvula undergoes a vibration cycle, flapping from the middle position (t/T = 0) to the dorsal oropharynx ($\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$), reverting back to the middle ($\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$), then continuing to the ventral oropharynx ($\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$), before returning to its initial middle position. The vortices generated from the uvula demonstrate variations throughout the vibration cycle, imposing a constantly changing influence on the downstream flows.

Figure 3 shows the 2D vorticity images at t/T = ¾, where the red and blue colors denote the positive and negative vorticity, respectively. For each uvula vibration cycle, a series of 48 images were captured for subsequent principal component analysis (PCA). Images were recorded for six cycles, leading to 288 images in total for each model. The lower panels of Figure 3 show the averaged vortex image from the 288 images. The PCA results shown in the next section are based on the difference between each image and the average.

3.2. PCA Analysis

Figure 4 shows the projections of 2D vortex images onto the vector spaces spanned by the principal components (PCs) at different scales. The first panel in Figure 4a represents the temporospatial evolution of 48 images (i.e., one uvula vibration cycle) projected onto the PC1–3-spanned vector space. The projected points approximately form a closed loop/orbit, with blue denoting the starting point and red indicating the end of one cycle. The second panel shows six cycles of the PC1–3 projections, demonstrating good periodicity/repeatability among cycles. Smooth, periodic curves were also observed in the PC3–5 and PC5–7 vector spaces; however, deteriorations in periodicity became perceivable starting from PC7–9 and continued growing to be highly random in PC39–41.

Interestingly, from 48 images of one uvular cycle, the projected curves exhibited one orbit in the vector space spanned by PC1–3, two orbits by PC3–5, and three orbits by PC5–7, which could correlate with the fundamental frequency and the two harmonics. It should be noted that this observation held true for both models presented in Figure 4. The number of orbits became less countable starting from PC7–9, and became entirely unrecognizable in PC39–41. This decaying regularity in PC projections is a good example that respiratory flows are a combination of deterministic chaos and random components, which can be separated according to their scales.

For a given scale, the projected curves differ notably between K1M3 and K2M3 in the PC1–3 and PC3–5 vector spaces (Figure 4a vs. Figure 4b). Thus, the PC-projected curves can be a highly sensitive index, individually or as a combination, to study uvula vibration kinematics. Because the uvular kinematics is dictated by both the external excitation forces and material physical properties, this method holds the potential to estimate tissue properties when excited at known specifications. Conversely, flow controls to augment or attenuate flow-induced sounds or structural motions are possible, for instance, by exerting promoting/stimulating or counteractive/opposing flow/acoustic components (i.e., scale- or frequency-specific) onto the current flow.

From PC5–7, the curves started to converge in appearance between K1M3 and K2M3, with the orbits in both models exhibiting a butterfly shape, indicating a gradual decrease in signature flow feature at higher scales (Figure 4a,b, three lower panels). No distinctive features are noted in PC39–41, where low-energy, high-frequency flow fluctuations dominate, regardless of uvula vibration modes.

Figure 5a,b compare PC projections among six models in the vector space spanned by PC1–3 and PC2–4, with each model comprising 288 vortex images from six consecutive uvular vibration cycles. It should be noted that Figure 5a,b contain both PC2 and PC3. It is evident that PC1 is more dominant and effectively separates the six curves in terms of either the vibration mode (K1 vs. K2, or heaving vs. pitching) or pharyngeal constriction level (M1, M2, M3). Of these two factors, the vibration mode/kinematics appears to have a more pronounced impact than the pharyngeal constriction level, as indicated by the gross cluster of the K1 models to the right vs. the K2 models to the left. By comparison, PC4 contains much lower energy or fewer features, as evident by the mingling of curves among the six models.

3.3. Wavelet Analyses of DNS-Predicted Pressures (P1–7)

In addition to the 2-D vortex images, wavelet analyses of the time series of pressures were undertaken at seven sampling points, as depicted in Figure 6. Figure 6a shows the pressures at sampling point 3 in K1M3 and K2M3 for ten consecutive uvula vibration cycles, while Figure 6b compares the pressures among the three K1 models (i.e., K1M1, K1M2, K1M3, upper panel) and K2 models (lower panel) within one vibration cycle. Overall, the pressures contain complex fluctuations within one cycle, while also exhibiting gross periodicity/repeatability from cycle to cycle (Figure 6a). All pressures have an approximate bimodal profile, presumably resulting from the uvula stopping twice within one cycle. This observation was consistent with the two hiatuses at high frequencies of the scalograms (Figure 6c), regardless of the model.

However, when considering the average pressures, notable differences exist. In K1 models, the pressure peaks are relatively symmetric in both site and magnitude. In contrast, the pressure peaks in the K2 models skew to the right. Moreover, the pressure fluctuating amplitudes in K1 models are smaller than those in K2 models, and increase with the pharyngeal constriction level. These differences also manifest themselves in the scalogram (Figure 6c). At the high frequencies, the scalogram intensity in a K1 model is lower than that in its K2 counterpart. For both categories, the scalogram intensity increases with the level of pharyngeal constriction.

Figure 7 displays the pressures for six models at sampling point 6, where the pharyngeal constriction occurs. As expected, the absolute pressure magnitude increased nonlinearly with increasing pharyngeal constriction level, regardless of the uvula vibration mode (Figure 7a, upper and lower panels). The pressure increased slightly from M1 to M2, but abruptly from M2 to M3 for both vibration modes. This occurred because the flow velocity increased in the constricted pharynx, and the pressure varied with the square of velocity.

Significant differences in multifractal spectra were noted between K1 and K2 models (solid vs. dashed lines, upper row, Figure 7b); in contrast, the differences among the three models with varying pharyngeal constrictions were insignificant. Differences between K1 and K2 models were also predicted in their τ(q)-spectra, which converged for the three K1 models but not for K2 models (zoomed insert, lower row, Figure 7b), lending further support to the fact that multifractals are more sensitive to the dynamic structures than static geometry variations.

Large differences in high-frequency scalograms existed between K1 and K2 models (left vs. right, Figure 7c); this was in contrast to the high similarity in high-frequency scalograms among M1, M2, and M3 for a given vibration mode, despite large variations in the mean pressure among them. It was thus concluded that the vibration mode (K1, K2) mainly influenced the pressure fluctuation amplitudes (vortices and turbulence, Figure 7b,c), while the pharyngeal constriction affected the mean pressure in the pharynx (Figure 7a). Complex scalogram distributions are observed at low frequencies (100–1000 Hz), with no apparent patterns among models.

Figure 8 shows the pressures, multifractals, and scalograms at point 7, which is downstream of the constricted pharynx. As a result, the mean pressure and fluctuation magnitude are considerably affected by the pharyngeal constriction level, both of which increased quickly (Figure 8a). A phase shift occurred between K1 and K2 models, leading to the coincidence of peaks and valleys between these two models. Unlike P6, both the multifractal and scalogram of P7 are sensitive to pharyngeal variations. Conversely, the kinematics-induced differences were much smaller than those at P6. This was evident from the clear separation of multifractal spectra among M1–M3 models, in contrast to the close proximity between any K1–K2 pairs (solid vs. dashed, Figure 8b). The high-frequency scalograms look alike for each of the three pairs (Figure 8c), as opposed to the distinctive patterns between each pair at P6 (Figure 8c vs. Figure 7c). Location-wise, the scalograms varied remarkably from P6 to P7 at both low and high frequencies, reflecting the drastic transition in flow regimes. Moreover, the flow transition was more significant in the constricted pharynx in a nonlinear manner, a hallmark of turbulent flows.

3.4. Poincaré Analyses of DNS-Predicted Pressures and Velocities

3.4.1. P3: Immediately Downstream of the Uvula

Figure 9 shows the Poincaré analyses of the time series DNS-predicted pressures immediately downstream of the uvula (P3). Figure 9a compares the P3 Poincaré maps between the K1 and K2 models (pink vs. green), which exhibit both overlapping and separated regions, indicating the potential of Poincaré maps as discriminatory, yet suboptimal, features.

Figure 9b,c compare the Poincaré maps among M1 (black), M2 (red), and M3 (blue) with K1 (heaving) and K2 (pitching) vibration modes, respectively. For both kinematics, significant overlapping was noted among M1–3 models with negligible separation, suggesting the inability of the Poincaré map to differentiate P3 from different uvula vibration modes and pharyngeal constrictions.

In Figure 9d, the period map shows highly regular points in the range 0–0.025, and becomes more dispersed beyond this range to the right. Thus, the fluctuating components of P3 were mainly the result of the uvula flapping frequency and its harmonics, rather than the flow instabilities and turbulences. Due to their close proximity, the vibrating uvula imparted periodic energy onto the airflow on contact, which further affected the neighboring airflows and pressures. Considering the maxima maps, which exhibited much less dispersion for any model, both overlapping and separation were observed among the M1–M3 models, regardless of the K1 or K2 vibration mode (Figure 9e,f).

3.4.2. P6: Site of Pharyngeal Constriction

The Poincaré analyses of P6 are shown in Figure 10 in terms of the Poincaré map, period map, and maxima map. In comparison to Figure 9, the overlapping increases between the K1 and K2 Poincaré maps at P6 compared to P3. This is reasonable, considering that P6 is situated further downstream from the vibrating uvula than P3. Figure 10b,c consider the sensitivity of the P3 Poincaré map to the level of pharyngeal constrictions (M1, M2, M3) with K1 and K2 uvula kinematics. Only the most constricted M3 model is separatable, while M1 and M2 cannot be differentiated, regardless of the vibration kinematics.

The period map of P6 is more concentrated in the lower end (0–0.02) than that of P3 (Figure 10d vs. Figure 9d); however, the scatters in the higher end are more random than those of P3, indicating the attenuation of direct impact from the flapping uvula and the augmentation of vortices or turbulences. Surprisingly, the maxima maps of P6 signals display highly concentrated patterns, shifting from M1 in the upper right to M2 in the middle to M3 in the lower left (black to red to blue), with non-insignificant overlapping for both kinematics (Figure 10e,f). Notably, the maxima map of K2M3 (Figure 10f) is more widespread than the other five models, likely due to the long excursions of a pitching uvula within a wider airspace where more complex vortices are generated. However, the maxima maps at P6 are not sensitive to the vibration mode (Figure 10e vs. Figure 10f).

3.4.3. P1, P2, and P7: Sampling Points in the Mouth-Throat Tract

The Poincaré and maxima maps of pressure signals at the other three points in the mouth-throat respiratory tract, 1, 2, and 7, are shown in Figure 11, with expected results. At P1, the less random Poincaré map can be attributed to its further upstream location with minimal impacts from downstream disturbances. At P2, the Poincaré map becomes more dispersed than P1. On the other hand, the K1 (heaving vibration mode) Poincaré map, even though not separated from the K2 (pitching vibration mode) Poincaré map, occupies a much smaller region (Figure 11b). At P7, which is located far downstream of the pharynx, indistinguishable Poincaré maps are observed between K1 and K2, testifying to the diminishing impacts from the uvula vibration. All maxima maps of the three points display a diagonal profile with varying levels of scattering, overlapping, and distinguishability (lower panels, Figure 11a–c). One observation worth noting is the relative positions in the maxima map vs. pharyngeal constriction. At P1 and P2 (upstream), the clusters of M1, M2, and M3 are located from the lower left to upper right (Figure 11a,b), while at P7, this order is reversed (Figure 11c). Moreover, the occupied region of P7 is much smaller in M1, and grows progressively with increasing pharyngeal constriction levels, leading to adequate partition of the maxima maps among M1, M2, and M3.

3.4.4. Velocity Magnitude at Sampling Points 3, 6, and 7

In Figure 12a, the Poincaré maps of Vel3 exhibit significant overlapping between K1 (pink) and K2 (green) models with moderate separations, suggesting an acceptable but weak parameter of the Poincaré map to capture the vibration-related differences. The overlapping of the Vel3 Poincaré maps between K1M1, K1M2, and K1M3 is even more widespread, and thus will not be able to differentiate the constriction-related differences in Vel3. By contrast, the Poincaré map sufficiently separates Vel6 signals among K1M1, K1M2, and K1M3, and perfectly separates Vel6 signals among K2M1, K2M2, and K2M3 models (Figure 12b). The closer proximity between M1 and M2 models, compared to the much greater distance between M2 and M3, signifies the nonlinear dynamics in Vel6 in response to pharyngeal constrictions (Figure 12b). Similar observations were made for the downstream Vel 7 (Figure 12c), except for the weak separation between K1M1 and K1M2 models.

It is noted that not all parameters at those selected points correlate well with abnormalities in uvula vibration and/or pharyngeal constriction. For comparison purposes, significantly more overlapping and worse separation were found in the Poincaré maps of U3, U6, and U7 (i.e., the transverse velocity components at sampling points 3, 6, and 7), except M3 at points 6 and 7, as illustrated in Figure 13.

4. Discussion

A data-driven discovery of anomaly-sensitive parameters/features was conducted using multiscale, multifaceted analyses of simulated respiratory flows. Anomalies include a collapsible pharynx with three constriction levels (M1–M3), and an oscillating uvula with two kinematics (K1, K2). The flows were solved using direct numerical simulation (DNS) and the immersed boundary method (IBM). The instantaneous vortex images were analyzed using principal component analysis (PCA), while time-series pressures/velocities were analyzed using wavelet-transform-based multifractals and scalograms, as well as Poincaré maps. Insights from this study concerning the algorithms, anomaly-sensitive features, and their implications are discussed below.

4.1. Evaluation of PC Curves, Multifractal Spectra, and Poincaré Maps

Overall, discriminatory features among different models were analytically extracted from instantaneous vortex images and pointwise pressures/velocities. Different aspects of the same flows were captured, either temporally or spatially, and at varying scales. Principal component analysis (PCA) is a statistical method that reduces data dimensionality while preserving variance. In this study, each 2D image was projected as one point in the vector spaces spanned by principal components (PCs) (Figure 4). In the PC1–3 vector space, 48 images in one uvula cycle formed one closed loop (first panel, Figure 4a), and 288 images from six cycles approximately repeated themselves in six orbits, indicating good periodicity in dominant flow structures (second panel, Figure 4a). This also justified the Poincaré analysis, which is specifically suited for periodic dynamical systems. The PCA also captured a gradual decay in periodicity with increasing scales (2nd–6th panels, Figure 4a), and provided information on energy distributions. In addition, different temporospatial orbits were predicted by PCA between K1M3 and K2M3 (Figure 4a vs. Figure 4b), thereby permitting a comparative analysis and anomaly detection. In our previous studies, PCA features were used to train SVM algorithms, and obtained high classification accuracies.

A multifractal spectrum reveals multiple scaling behaviors of the flow, including its complexity, intermittency, and heterogeneity; a wider spectrum implies a flow having stronger singularities and more localized vortices, and being more heterogeneous. This is consistent with Figure 7, where K2 models (dashed lines) exhibit more complex flows and have wider spectra than K1 models (solid lines). All models contain a single peak in Figure 7 and Figure 8, suggesting the existence of only one dominant flow process, which is associated with the uvular oscillation. No abrupt changes or discontinuity occur in spectra in Figure 7 and Figure 8, consistent with the fully turbulent flow regimes in the pharynx with no flow transitions or bifurcations. In Figure 7b, the K1 spectra are more skewed to the right than the K2 spectra, hinting that a heaving uvula (K1) induces more positive fluctuations in the pharynx than a pitching uvula (K2).

Like PC curves, Poincaré maps provide qualitative information on flows’ stability, periodicity, nonlinearity, state, and chaos/turbulence. There are two clusters in Figure 9c (P3 in K2 models), mirroring the two vortex streets shedding from a pitching uvula. By contrast, the separation of clusters in Figure 9b (P3 in K1 models) is less apparent, which is in line with a shorter tip excursion and closer vortex shedding from a heaving uvula. Likewise, the separation of M3 model (pharynx with severe constriction) from M1 and M2 models in Figure 10b,c mirrors the nonlinear, abrupt changes in flow structures from mild to severe pharyngeal constriction. The increased cluster dispersion from P3 to P6 and P7 signifies the increase in turbulence in the pharynx.

As seen from above, each approach provides unique insights into the nature of the flow. The PC curve extracts the dominant flow with the most energy or variance (i.e., eigenvectors); the multifractal spectrum is fitting for understanding the scale-dependent nature of turbulence or complexity in a signal, while the Poincaré map can identify periodicity, state, chaos, and stability in a system. It is also noted that fast Fourier transform (FFT) of the time-series pressure signals was also performed in our previous study, which exhibited distinct patterns in terms of the wave amplitudes at the fundamental and harmonic frequencies [13]. There are many indices that have been developed and used to assess the complexity of signals, and all of them come with different specificities. Readers interested in embedded dimension, mutual information, and other analytical methods are referred to [66,67,68,69]. Future complementary experiments are also needed to validate the simulations in this study.

4.2. Anomaly-Sensitive Parameters/Features

In Figure 12, we observed a high sensitivity of the Poincaré maps of Vel6 and Vel7 to the level of pharyngeal constrictions. This is consistent with the fact that the velocity magnitude increases in a narrowing pharynx. It should be noted that the multifractals/scalograms of P7 (Figure 8), as well as the maxima maps of P6 and P7 (Figure 10 and Figure 11), are also sensitive to the pharyngeal constriction level; thus, measuring acoustics at these two points is recommended to gauge the constriction levels of the pharynx, thus, to estimate pharynx collapsibility, as explained in Wang et al. [13].

On the other hand, the P3 scalogram (Figure 6), P6 multifractal/scalogram (Figure 7), and P2 Poincaré map (Figure 11) are all sensitive to the uvula vibration kinematics, and thus can be exploited, individually or in combination, to gauge the abnormality in uvula vibration kinematics. The uvula vibration is a passive process dictated by external excitation, uvula morphology, and uvula tissue properties. Knowing the uvula kinematics via measuring acoustics at multiple points (2, 3, and 6 herein) can also facilitate the estimation of the variation in uvula structures and/or tissue properties.

Sensitivity to anomalies also varies with the location of the sampling point. There are seven sampling points in total, with probes 1, 2, 3, 4, and 5 situated around the uvula, and probes 6 and 7 in the downstream pharynx. It is not surprising that the extracted features or parameters close to the anomalies are more intensified, such as probes 2 and 3 for the uvula, and probes 6 and 7 for the collapsible pharynx. The clear separation among Poincaré maps for the velocities at probe 6 (Vel6) might be strongly correlated to the velocity increase in a narrowing channel (Figure 10). However, a similar clear separation for Vel7, which is 2 mm downstream from the pharyngeal constriction site, suggests that the Poincaré maps consider more flow features than merely the velocity magnitude (Figure 11). The observation that the anomaly sensitivity differs among probe sites provides an opportunity to use multiple probes in a synergic way to localize the source or quantify the source severity. A similar concept has also recently been pursued by Khalili et al., who characterized sound signals through stenosis using spectral decomposition, with the aim to localize the stenosis with points of measurement [70].

Regarding the uvula kinematics, it is acknowledged that a wider range of uvula flapping modes may exist in addition to the heaving and pitching modes considered herein, which warrants future studies of their impacts on pressure signals. Also, it is still challenging to mathematically define the sensitivity to anomalies for most features presented in this study, despite their visual distinctions.

4.3. Implications of New Anomaly-Sensitive Features for AI-Based Diagnosis

The reduced-dimensional, etiology-sensitive parameters/features extracted from DNS results can assist the development of AI-based diagnostic tools in two ways, i.e., (1) improving the classifier performance, and (2) improving the interpretability of conifers, especially the AI-extracted features. In the past several years, AI, and deep learning in particular, has quickly gained popularity in anomaly detection [71]. They have demonstrated great usage and effectiveness in learning/extracting distinguishing features and facilitating disease diagnosis (binary classification) or stage gauging (multi-class classification) [72]. Machine learning algorithms, such as SVM and random forest (RF), need hand-crafted features as the training dataset [42,73,74]. Thus, identifying anomaly-sensitive features is of the utmost importance to ensure an accurate classifier; discovering new features, as shown in Figure 4, Figure 7, Figure 8, Figure 11 and Figure 12, has the potential to further improve the classifier’s accuracy. Future studies leveraging flow-derived features and machine learning algorithms such as SVM or RF are needed for respiration anomaly detection.

On the other hand, convolutional neural networks (CNN) train classifiers directly on images, eliminating the need for pre-extracted features [75]. Moreover, CNN models can learn label-related features during training in the form of activation layers and/or heat maps. One drawback of these features is that they become increasingly abstract in deeper layers, as demonstrated in [76]. This trend mirrors the diminishing consistency observed in PC curves as scales rise (Figure 4), and the transition from simplicity to complexity with growing frequencies in scalograms in Figure 6, Figure 7 and Figure 8. A standout feature of this study is that we search for anomaly-sensitive features from DNS predictions with known inputs. This ensures a clear understanding of the underlying reasons for any predicted or extracted features, creating a direct correlation from external symptoms to internal causes. In this sense, the sought features at multiscale, particularly at high scales, are likely to shed light on AI-learned abstract features and thus improve the classifier’s interpretability.

In summary, the utility of the flow-derived, anomaly-sensitive features in AI-based diagnosis can be twofold. First, the quantitative features can be incorporated with machine learning techniques like SVM and random forest to create a classification model. Second, the qualitative features offer insights into the correlation between flow and pathology, potentially elucidating features that convolutional neural networks autonomously extract.

5. Conclusions

In summary, this study analyzed DNS-predicted respiratory flows to search for reduced-dimensional parameters/features that are sensitive to the uvula vibration mode and/or pharyngeal constriction level. The immersed boundary method was used to solve the flow field at 0.02 ms and specify two uvula vibration kinematics. Principal component analysis (PCA) was used to study the flow’s periodicity vs. rank (variance), wavelet-transform-based multifractal spectra (discrete) and scalograms (continuous) were used to study multiscale properties, and Poincaré maps were used to study the state and chaos. Specific findings include the following:

• The vortex images were projected in the PC1–3 vector space as a closed orbit for those from one vibration cycle and six closed orbits from six vibration cycles, suggesting the periodicity and regularity of the dominant flows.
• The regularity in PC projections decays gradually with increasing ranks, and eventually becomes random.
• The PC projections reveal significant differences among models in the leading vector space (PC1–3).
• The multifractal spectra of pressures in the pharynx (P6, P7) show high sensitivity to the uvula vibration modes; the pitching mode (K2) has a wider spectrum, with the peak more skewed to the left than the heaving mode (K1).
• Mean Poincaré maps of velocities in the pharynx (Vel6, Vel7) successfully separate three pharyngeal constriction levels (M1–M3). Maxima Poincaré maps of pressures in the pharynx (P6, P7) also show distinct clusters among M1–M3.
• Sensitivity to anomalies differs among probes and analytical algorithms. Synergizing measurements from multiple probes and their anomaly-sensitive features extracted with proper algorithms can aid source localization and stage gauging.