Low-Frequency-Noise Attenuation through Extended-Neck Double-Degree-of-Freedom Helmholtz Resonators

Abstract

The use of acoustic liners, based on double-degree-of-freedom Helmholtz resonators, for low-frequency-noise attenuation is limited by the volume of individual resonating cavities. This study investigates the effect of the septum neck length on the acoustic performance of double-degree-of-freedom resonators, both experimentally and numerically, for varying cavity volume ratios. The underlying sound attenuation mechanism is studied by analysing the acoustic pressure fields within the resonator cavities. An increase in the septum neck is shown to lower the frequencies affected by the resonator. In addition, it deteriorates and significantly improves the sound attenuation performance at the primary and secondary peak transmission-loss frequencies, respectively.

1. Introduction

Aero-engines have gone through considerable development over the past decades to significantly reduce jet engine noise through the use of high bypass ratios [1]. However, an increase in the bypass ratio of the engines has led to a decrease in the blade passing frequency (BPF) which necessitates the need for aero-engine acoustic liners to attenuate lower frequencies and target the BPF. Low-frequency-sound attenuation remains a challenge for the scientific community due to its inherited physical characteristics, as low-frequency content can travel farther from its source with less attenuation compared to high-frequency content. Helmholtz resonator sound attenuation depends on various geometrical parameters and is governed by Equation (1),

$${\mathit{f}}_{\mathit{o}}=\left(\frac{c}{2\pi }\right)\sqrt{\frac{S_{neck}}{V_{cavity}(l_{neck}+{\delta }_{neck})}},$$

(1)

where the speed of sound in air is given by c, $S_{neck}$ is the neck opening area, $V_{cavity}$ is the volume of the resonating cavity, and $l_{neck}$ is the length of the neck. The end-correction factor ${\delta }_{neck}$ compensates for any discontinuities inside the resonator that result in the formation of higher-order modes [2,3]. Equation (1) suggests an increase in the resonating cavity volume or decrease in the neck-opening area, to target low-frequency sound. However, both these characteristics would be undesirable for an acoustic liner due to size, weight, and manufacturing constraints. The effect of the changing neck geometry and location has been studied extensively in the past [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]; however, the influence of extending the neck into the Helmholtz resonator cavity has not been investigated in detail. Past research has shown neck extensions leading to lower-frequency sound attenuation [19,20,21,22,23], due to the introduction of multiple resonance frequencies, when the neck extensions become significantly large [24,25,26,27]. Following the recent surge in studies such as Simon et al. [28] and Jones et al. [29] investigating the use of extended-neck resonators for low-frequency-sound absorption, this paper presents the underlying mechanism of sound attenuation from double-degree-of-freedom (2-DoF) resonators with varying neck extensions.

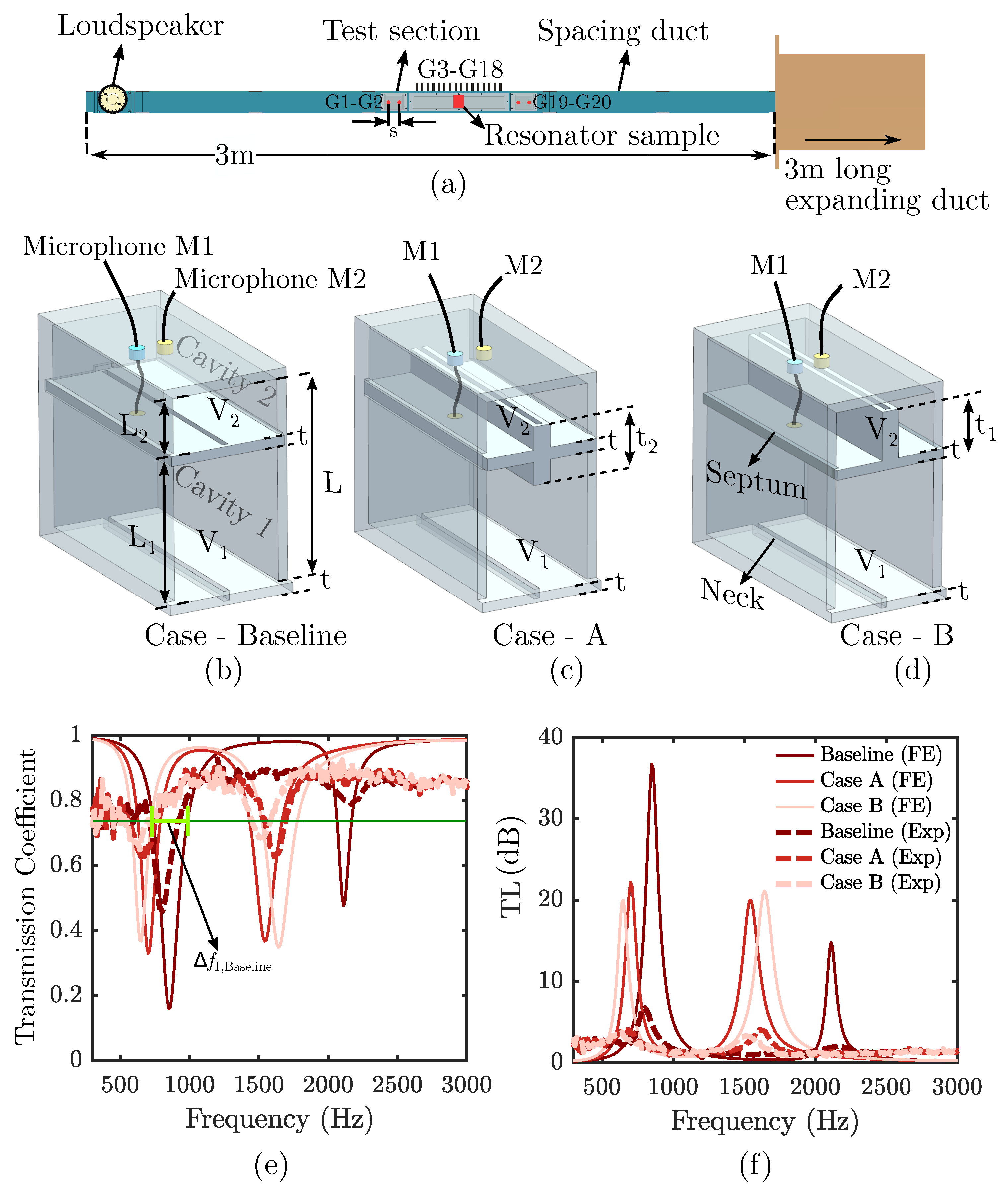
2. Experimental and Numerical Methodology

The experiments were performed at the University of Bristol Grazing Flow Impedance Tube Facility (UoB-GFIT) which is illustrated in Figure 1a. The impedance tube’s internal duct has a square cross-section of 50.4 mm × 50.4 mm and measures 3000 mm in length. The test section, 762 mm in length, is placed at a distance of 23 tube hydraulic diameters from the acoustic source, in order to ensure plane wave propagation. The facility is intended to allow experiments both with and without airflow in the duct. However, experiments in this study have been conducted without airflow. In the presence of airflow, a 3000 mm long diffusing section can be added to the facility to minimize acoustic reflections into the test section by promoting a gradual reduction in air velocity along the length of the section. The impedance tube acoustic source consisted of two BMS 4592ND compression drivers, capable of generating sound pressure levels of up to 130 dB in the test section. A Tektronix AFG3011C arbitrary waveform generator (Beaverton, OR, USA) was utilised to produce a white-noise excitation with an amplitude of 10 V_pp. G.R.A.S. 40PL free-field array microphones were used to obtain the noise data in the tube. A National Instruments PXIe-1082 data acquisition system (Austin, TX, USA) with a PXIe-4499 sound and vibration module was used to acquire data. The data acquisition code enabled the utilisation of Matlab R2016a to interface between the data acquisition device and the signal generator.

The experiments were performed at a sampling rate of 2¹⁵ Hz for 16 s in order to satisfy the Nyquist criterion. The two upstream (G1–G2) and downstream microphones (G19–G20) (see Figure 1a) were used to collect data for transmission loss and transmission coefficient eduction following the ASTM E2611-19 standard [30]. The spacing between the microphones was determined by the frequency range of interest. The distance between the upstream microphones (G1 and G2) and downstream microphones (G19 and G20) was selected following the ASTM E2611-19 standard [30] as,

$$\frac{0.01c}{f_{lower}}<s<\frac{0.4c}{f_{upper}},$$

(2)

where s is the spacing, $f_{upper}$ and $f_{lower}$ are the upper and lower frequency limits, respectively. The distance between the upstream microphones (G1 and G2) and downstream reference microphones (G19 and G20) was set at 40 mm, which ensured sound waves were captured accurately between 85 Hz to 3400 Hz. The effect of test samples on the acoustic field propagation in the tube was captured using an array of 16 G.R.A.S. microphones, G3 to G18. The spacing between these microphones was set at 25 mm, which enabled capturing frequencies between 137.5 Hz and 5488 Hz.

The Helmholtz resonator test samples used in this study, shown in Figure 1, were manufactured using stereolithography (SLA), in an Elegoo Mars 2 Pro Mono LCD Resin 3D printer. The 3D-printed samples were flush-mounted to one of the side walls of the impedance tube, with Cavity 1’s neck receiving the incoming acoustic field. The resonator was manufactured as a single chamber with a rectangular cross-section of 22 mm × 40 mm and a depth of 46.8 mm. In addition, the sidewalls of the resonators consisted of indents to enable the insertion of a septum. Moreover, a key–lock relation was designed into the resonator covers to ensure sealing.

Three different types of resonator septum configurations were tested in this study, namely, a baseline two-degree-of-freedom configuration (2-DoF) shown in Figure 1b, a septum neck extension towards both Cavity 1 and Cavity 2 (Case A), shown in Figure 1c, and a septum neck extension towards Cavity 2 only (Case B), shown in Figure 1d. The 2-DoF resonators consisted of two cavities with volumes $V_1$ and $V_2$. The volumes could be adjusted by changing the location of the septum. The ratio between $V_1$ and the entire chamber volume ($V_1$ + $V_2$) is defined by the parameter “m” and is called the volume ratio. For example, a volume ratio of $m=0.3$ suggests that the volume $V_1$ for Cavity 1 is 30 percent of the entire chamber volume. The experiments in this study were conducted for a range of volume ratios $0.3<m<0.7$. In addition, two different septum neck extension configurations for both one-sided and double-sided extensions were studied in detail. The extension of the septum neck $t_1$ or $t_2$ was represented as a ratio with the total chamber length (L). Therefore, a septum neck extension of $t_1=0.1$ would mean that the one-sided neck extension towards Cavity 2 was 10 percent of the total chamber length (L).

The acoustic signals for Cavity 1 and Cavity 2 were obtained using a pair of Knowles (Santa Clara, CA, USA) Omni-Directional (FG) 2.56 DIA electret condenser microphones (FG-23329-P07) flush-mounted to the internal walls of both cavities for all resonator volume ratio and neck extension configurations. Microphones M1 and M2, as shown in Figure 1, were utilised to capture Cavity 1 and Cavity 2 signals, respectively. Prior to the experiments, the microphones were magnitude- and phase-calibrated using a GRAS 40PL free-field microphone as the reference pressure transducer, with a known sensitivity value. The calibration procedure followed that outlined by Ali [31]. For a frequency range of 100 Hz to 3000 Hz, the calibration results indicated a phase shift of less than 7${}^{\circ }$, with a fairly consistent amplitude sensitivity, which is not shown here for brevity.

The finite element analysis conducted in this study employed COMSOL Multiphysics 5.5${}^{TM}$ [32], a widely used commercial software package. The primary focus of these simulations was to gather data within the acoustic domain and calculate transmission coefficients and losses for different test sample configurations. The overarching goal was to closely emulate the outcomes of experimental tests, thereby ensuring the dependability of the simulation results for a subsequent acoustic field analysis of both the impedance tube and resonators. In order to enhance the precision of representing the physical phenomena, the acoustic domain was partitioned into two discrete regions. The region encompassing the resonator setups was modelled using a thermoviscous physics approach, while the sections before and after the resonators were described using a simplified pressure acoustics model. These two regions were linked through a multiphysics interface. It is important to note that the presence of boundary layers, especially in confined areas such as the resonator necks, can lead to substantial thermal and viscous losses. Therefore, to address these effects, the simulation incorporated the thermoviscous interface, utilizing COMSOL’s thermoviscous acoustic module to solve linearized Navier–Stokes equations and comprehensively address continuity, momentum, and energy equations.

The computational domain of the impedance tube was discretized through the utilization of a freely structured triangular mesh. For regions employing the thermoviscous acoustics model, a boundary layer mesh configuration was employed. To facilitate the analysis, an acoustic source was introduced at one end of the impedance tube domain, employing a port boundary condition to establish an incident wave at the upstream boundary. Conversely, another port boundary condition was employed at the opposite end of the impedance tube domain, serving as an acoustic termination to enforce a nonreflecting condition for the waveguide. The mesh resolution was determined by setting a maximum element size equal to one-sixth of the wavelength corresponding to the highest frequency of interest (3000 Hz). Additionally, a minimum element size was established at one-tenth of the wavelength associated with this highest frequency. The mesh refinement strategy incorporated a maximum element growth rate of 1.2, with a curvature factor of 0.3. Furthermore, precise resolution was achieved in the narrow regions of interest by adjusting the number of layers to a value of 3. The computational analysis involved the determination of the acoustic transmission loss within the simulation domain, computed as follows,

$$\mathit{TL}=10lo{g}_{10}\left(\frac{W_{in}}{W_{out}}\right),$$

(3)

where

$$\begin{array}{c}\hfill {\mathit{W}}_{\mathit{in}}={\int }_{S_{in}}\frac{p_{o,s}^2}{\rho c_0}ds,\\ \hfill {\mathit{W}}_{\mathit{out}}={\int }_{S_{out}}\frac{\mid p^2\mid }{\rho c_0}ds.\end{array}$$

(4)

In the above equations, $c_0$ denotes the speed of sound (343 m/s), $\rho$ signifies the air density (1.173 kg/m³), p represents the estimated pressure parameter, $p_{o,s}$ corresponds to the inlet pressure set at 1 pascal, and $W_{in}$ and $W_{out}$ denote the computed total acoustic power values at the inlet and outlet regions, respectively, calculated over the respective port areas $S_{in}$ and $S_{out}$.

In the context of transient simulations, a model for transient pressure acoustics was employed for the impedance tube model, with the exception of the region containing the Helmholtz resonator, where a transient thermoviscous model was utilized. The Transient Pressure Acoustics Model node incorporates equations tailored for the simulation of predominantly time-dependent (transient) acoustics. It deals with the scalar wave equation,

$$\frac{1}{\rho c^2}\frac{{\partial }^2{p}_t}{\partial t^2}+\nabla ·\left(-\frac{1}{\rho }\nabla (p_t-q_d)\right)=Q_m,$$

(5)

where $p_t$ represents the complete acoustic pressure, $\rho$ corresponds to the fluid density, c denotes the speed of sound, $q_d$ is attributed to the dipole domain source, and $Q_m$ signifies the monopole domain source. This formulation of the wave equation allows for the possibility that the speed of sound and density can be spatially dependent. However, it was assumed that these properties changed relatively slowly over time, particularly when compared to the variations in the acoustic signal.

The mesh parameters, including element order, size, and type remained consistent with those employed in steady-state simulations. To simulate an incident pressure plane wave, a background pressure field node with an initial pressure amplitude of 1 pascal, denoted as $p_{in}$, was introduced. To prevent acoustic reflections and ensure anechoic termination at both ends of the impedance tube, perfectly matched layers (PMLs) were applied. Two distinct time scales were utilized in the transient simulations: one corresponding to the frequency of the incoming pressure wave and another governing the time step used by the numerical solver. Time integration was achieved by employing the generalised alpha method [33], with a time step size set to $T/60$, where T represented the time period of the acoustic wave. The simulations were conducted at resonant frequencies tailored to various resonator configurations, each running for a duration of $30T$ to achieve convergence. In order to obtain pressure data within the resonator cavities, 50 domain probe points were placed strategically along the resonator’s length. These probe points were evenly spaced at 1 mm intervals, with the initial point situated 10 mm below the resonator’s opening. The schematics for both the steady and transient simulation are shown in Figure 2a with a detailed view of the mesh in the narrow regions, i.e., the neck of the resonator sample shown in Figure 2b. The transient simulations were utilised to extract the time sensitivity of the acoustic pressure and velocity within the impedance tube duct and the resonator test samples. The extracted information could be presented in the form of contour pressure and velocity maps which aid in better visualising the change in acoustic field within the whole system.

3. Results and Discussion

A comparison of the transmission coefficient and transmission loss induced by the 2-DoF and 2-DoF extended-neck configurations is presented in Figure 1e and Figure 1f, respectively, for a fixed volume ratio $m=0.5$. The results illustrate the primary ($f_1$) and secondary ($f_2$) peak transmission-loss frequencies for the 2-DoF resonator configurations, which are consistent with findings by Xu et al. [34]. In addition, it can be seen that for a fixed volume ratio (m), the peak transmission-loss frequencies of a Helmholtz resonator could be altered significantly by extending the septum neck length, resulting in the resonator targeting lower frequencies. The direction of the septum neck extension, i.e., towards Cavity 2 ($t_1$) or both cavities ($t_2$), also reduced the peak transmission-loss frequencies; however, this effect was not significant.

The effect of neck extensions on both peak transmission-loss frequencies is better visualised in Figure 3a,b, which presents the two frequencies for an extended-neck resonator configuration normalised with the peak transmission-loss frequencies of the baseline 2-DoF configuration ($f/f_{2\text{-}DoF}$). The results clearly indicate a substantial decrease in $f_1$ as the neck extension is increased from $t_1,t_2=0.1$ to $t_1,t_2=0.3$, for both Case A and Case B. However, as the volume ratio increases, the peak transmission-loss frequency approaches that of a baseline 2-DoF resonator, a trend consistent with the findings of Gautam et al. [35] for a standard 2-DoF resonator. The opposite can be seen for $f_2$, in Figure 3b, where the peak transmission-loss frequency decreases further with an increasing volume ratio and increasing neck extension. It can also be seen that the direction of the neck extension does not have a considerable effect on the peak transmission loss frequencies. The observations are similar for Cases A and B. In order to assess the effect of neck extensions on the range of frequencies affected, a nondimensional bandwidth coefficient was defined as follows,

$$\mathit{Bandwidth}\mathit{Coefficient}=\frac{\Delta f_{n,Case}}{\Delta f_{n,Baseline}},$$

(6)

where $\Delta f_{n,Case}$ is the bandwidth of frequencies obtained at a transmission coefficient of 0.75, n is the order of the peak transmission-loss frequencies and “Case” refers to Case A or Case B. The same value for the baseline 2-DoF resonator is given by $\Delta f_{n,Baseline}$, as shown in Figure 1e. The bandwidth coefficient for the different resonator configurations, at $f_1$ and $f_2$, is presented in Figure 3c and Figure 3d, respectively. Similarly, the magnitude of sound attenuated by different configurations is presented by defining another nondimensional parameter, the normalised transmission loss (TL), which is defined as,

$$\mathit{Normalised}\mathit{TL}=\frac{T{L}_{n,Case}}{T{L}_{n,Baseline}}.$$

(7)

The normalised TL for the different resonator configurations, at $f_1$ and $f_2$, is presented in Figure 3e and Figure 3f, respectively. The bandwidth coefficient and normalised TL results at $f_1$ and $f_2$ illustrate a similar behaviour for all resonator configurations. There is a significant reduction in both the magnitude of sound attenuated and frequency bandwidth affected, at $f_1$, as the neck extension is increased. However, as the volume ratio is increased, both parameters approach that of a baseline 2-DoF resonator. The opposite is evident at $f_2$, where both parameters significantly increase with the increasing neck extension and volume ratio. This shows the significant effect of changing the septum neck length on improving the resonators’ sound absorption capacity at $f_2$. The finite element results matched the experimental findings, but small differences could be due to difficulties in accurately replicating the experimental boundary conditions. The resonators were assumed to have a hard wall in the finite element analysis simulations, which may not be the case for the test samples, which were 3D-printed. In addition, it was also evident that the direction of the septum neck extension had no significant effect on the performance of the resonator. Therefore, all further analysis is focused on the “Case A” neck extension direction configuration.

The trends in Figure 3 and the inverse relation of the peak transmission-loss frequencies with the volume and neck length (Equation (1)) illustrate that variations in the volume ratio and the length of the septum neck have an influence on the acoustic environment within the resonator cavities, which leads to the different noise attenuation characteristics. In order to characterize this influence on the acoustic pressure field inside these cavities, transient finite element simulations were conducted using commercially available software COMSOL Multiphysics 5.5${}^{TM}$. These simulations were performed at both frequencies $f_1$ and $f_2$. Figure 4 presents the internal cavity acoustic pressure field, at $f_1$, for the $t_2=0.3$ configuration, in comparison with a standard 2-DoF resonator, at different volume ratios. Figure 5 presents similar results but at $f_2$. The acoustic field data were obtained via domain probe points placed along the centreline of the resonator, shown by the dotted red lines in Figure 4 and Figure 5. The pressure field results at $f_1$ illustrate both cavities being excited in phase, with Cavity 2 being the dominant cavity (higher pressure magnitude), regardless of the volume ratio and neck extension. In addition, an increase in the volume ratio shifts the trend towards an equalised pressure magnitude between the two cavities. Moreover, increasing the septum neck length increases the pressure magnitude within Cavity 2 and reduces the magnitude in Cavity 1. The pressure field results at $f_2$, shown in Figure 5, illustrate an interesting behaviour, with both cavities being excited out of phase and the pressure magnitude being concentrated in Cavity 1 at lower volume ratios, shifting to Cavity 2 at higher volume ratios. In addition, the septum neck extension leads to an increase in pressure magnitude in Cavity 1, regardless of the volume ratio. Recall that an opposite behaviour was observed at $f_1$ where Cavity 1’s pressure decreased with the increasing septum neck extension. The incoming sound field reaching a resonator neck is efficiently scattered and absorbed at the resonance frequency of the Helmholtz resonator. This is enabled by a very low impedance around the resonator neck at its resonance frequency, which makes the neck act as a pressure release surface [36]. Since Cavity 1 directly interacts with the incoming acoustic field, it acts as the pressure release surface, and a reduction in acoustic pressure within Cavity 1 would lead to a loss in the acoustic performance of the resonator at $f_1$, with increasing neck extension. Conversely, an increase in Cavity 1’s pressure at $f_2$ would improve the resonator performance, which is evident in Figure 3.

The finite element analysis results for the acoustic pressure field within the resonator cavity illustrated interesting underlying mechanisms which may be related to the sound attenuation behaviours observed; however, these needed to be validated with experimental results. Recall that every resonator configuration was instrumented with two microphones to measure the acoustic pressure field in both Cavity 1 (microphone M1) and Cavity 2 (microphone M2), as shown in Figure 1. Figure 6 presents the sound pressure level (SPL) inside each cavity, at $f_1$ and $f_2$, for volume ratios of $m=0.3,0.5,0.7$ plotted against the septum neck extension ($t_2$). The experimental results are consistent with the findings of the finite element transient simulations. The SPL within Cavity 1, at the primary peak transmission-loss frequency $f_1$, can be seen to decrease with an increasing septum neck extension as well as an increasing volume ratio. The opposite is true for the SPL observed within Cavity 2, which increases with the increasing volume ratio and neck extension length. The results for the secondary peak transmission-loss frequency $f_2$ are also consistent with the transient simulations, with Cavity 1 having a concentration of acoustic pressure at lower volume ratios and Cavity 2 having a higher concentration at larger volume ratios. In addition, SPL within Cavity 1 increases significantly with an increase in septum neck extension, whereas the opposite is true for SPL within Cavity 2 until $m=0.5$. At $m=0.7$ and $t_2=0.3$, both Cavity 1 and Cavity 2 can be seen to have a significantly higher concentration of acoustic pressure compared to all other volume ratio and neck extension cases.

The relationship in phase difference ($\phi$) between the two cavities within the 2-DoF resonator setups can also offer valuable insights into how an extended septum neck and changes in volume ratio might impact the resonator’s ability to attenuate sound. Cross-spectral calculations between the data acquired from microphones M1 and M2 were used to obtain the relative phase between the two cavities. The relative phase data for the three resonator septum neck extension configurations at volume ratios of $m=0.3,0.5,$ and $0.7$ are presented in Figure 6. The first ($f_1$) and second ($f_2$) peak transmission-loss frequencies for each septum neck extension configuration are marked by a coloured triangle and a coloured circle, respectively. The results indicate that increasing the septum neck extension reduces the bandwidth of frequencies within which the two cavities are in phase. At $m=0.3$, shown in Figure 6g, the standard 2-DoF resonator cavities are in phase up to around 1000 Hz, whereas for the $t_2=0.3$ configuration, the two cavities are in phase up to 500 Hz. As the volume ratio increases, this bandwidth becomes even larger. At $m=0.7$ (Figure 6i), the standard 2-DoF resonator cavities are in phase up to around 1600 Hz compared to the $t_2=0.3$ configuration, where the cavities are in phase up to 900 Hz. The loss in resonator performance at $f_1$ and the improvement at $f_2$, seen in Figure 3, may be attributed to this relative phase behaviour. Recall that at $f_1$, both cavities resonate in phase whereas at $f_2$ they resonate out of phase. Therefore, an increase in the septum neck extension promoting an out-of-phase behaviour may be the reason for the improved resonator performance at $f_2$.

The relative phase of microphones M1 and M2 and the microphone directly opposite to the resonator neck opening (G8), flush-mounted to the side wall of the test section, may also shed some light on the effect of the different resonator configurations on the sound field in the test section. The relative phase of microphones M1 and G8, for volume ratios $m=0.3,0.5$, and $0.7$, is presented in Figure 7a, Figure 7b, and Figure 7c, respectively. The same data but for the relative phase between microphones M2 and G8 are presented in Figure 7d–f. In addition, the areas of interest around the peak transmission-loss frequencies are presented within shaded regions in the figure. The results for the relative phase between Cavity 1 (microphone M1) and the impedance tube duct (microphone G8) show the cavity’s acoustic field and impedance tube’s acoustic field being out of phase near the peak transmission-loss frequencies. This would lead to destructive interference and attenuate the sound field. The bandwidth of the out-of-phase frequencies, around $f_2$, increases as the septum neck is increased, which may lead to the improvement in the resonator performance at $f_2$, as seen in Figure 3d,f. The opposite is observed for the relative phase between Cavity 2 (microphone M2) and the impedance tube (microphone G8). An increase in the septum neck extension leads to a reduction in the bandwidth of frequencies at which the cavity and the duct acoustic field are out of phase. This reduction in the frequency bandwidth may aid in the improvement in the resonator performance at $f_2$, leading to a destructive interference between Cavity 1 and Cavity 2.

4. Conclusions

The effect of the septum neck length on the sound attenuation performance of a 2-DoF Helmholtz resonator with different internal volume ratios was studied experimentally and numerically. Experiments were performed in a grazing flow impedance tube with 3D-printed test samples. The results showed that increasing the septum neck length of a 2-DoF resonator significantly affected both the primary ($f_1$) and secondary ($f_2$) peak transmission-loss frequencies. Both $f_1$ and $f_2$ were reduced significantly with the increasing septum neck length at lower volume ratios. However, an increase in the volume ratio of the resonator increased $f_1$ but decreased $f_2$ even further. The induced transmission loss and the targeted bandwidth of frequencies at $f_1$ reduced with the increasing septum neck length but increased with the increasing volume ratio, albeit remaining below the baseline 2-DoF resonator values. However, at $f_2$, both the induced transmission loss and the targeted range of frequencies significantly increased with increasing neck length. In addition, the induced transmission loss and the targeted range of frequencies increased further at higher volume ratios. Finite element analysis results were utilised to assist the understanding of the underlying sound attenuation mechanism by investigating the acoustic field inside the resonator cavities. The acoustic pressure results for $f_1$ showed that Cavity 2 acted as the dominant resonant cavity, and the acoustic pressure magnitude increased as the septum neck extension length increased. This led to a decrease in Cavity 1’s acoustic pressure, which subsequently resulted in a deteriorated sound attenuation performance at $f_1$. The results at $f_2$ showed that Cavity 1 acted as the dominant cavity at lower volume ratios, and as the volume ratio increased, Cavity 2 became dominant with an increased pressure magnitude. Moreover, the Cavity 1 acoustic pressure magnitude increased with the increasing septum neck extension, which may have led to the improved resonator performance observed at $f_2$. The SPL data collected from experiments using flush-mounted microphones placed inside the resonators matched the findings from the finite element analysis. This alignment reinforced the observed acoustic characteristics within the resonator cavities. Furthermore, the relative phase measurements between the resonator cavities and the impedance tube duct demonstrated a more pronounced out-of-phase behaviour as the septum neck extension increased. This outcome further confirmed the observed trend in sound performance. The results of this study suggest that 2-DoF resonators can be adapted to achieve a specific low-frequency-noise attenuation behaviour, by altering septum neck length, for application in modern high-bypass-ratio engines without altering the dimensions of the engine nacelle. Moreover, observations from this study can be used to design acoustic liners with improve low-frequency-noise attenuation characteristics.