Identification of the Aeroacoustic Emission Source Regions Within a Ceiling Swirl Diffuser
Abstract
1. Introduction
2. Methods
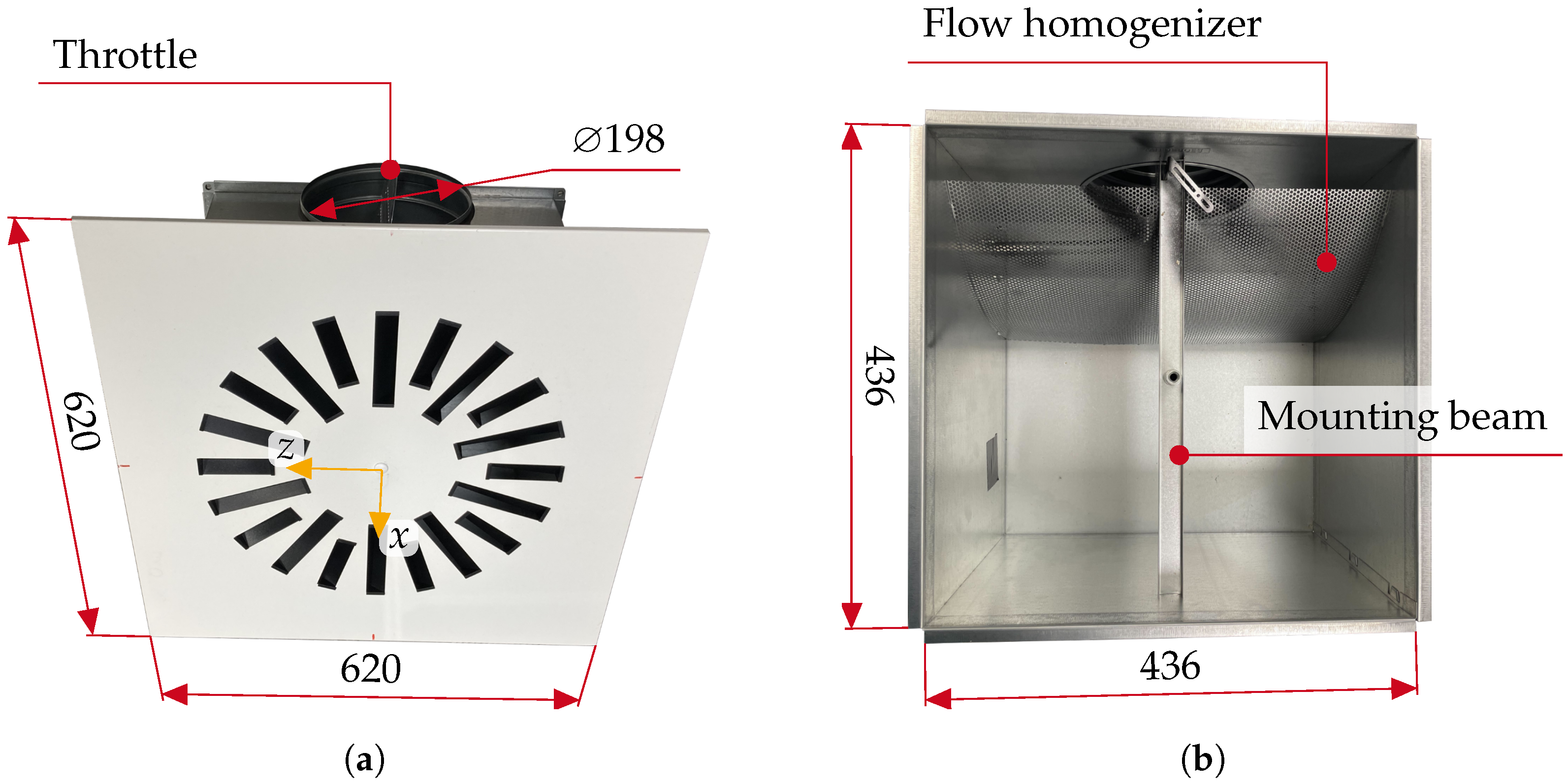
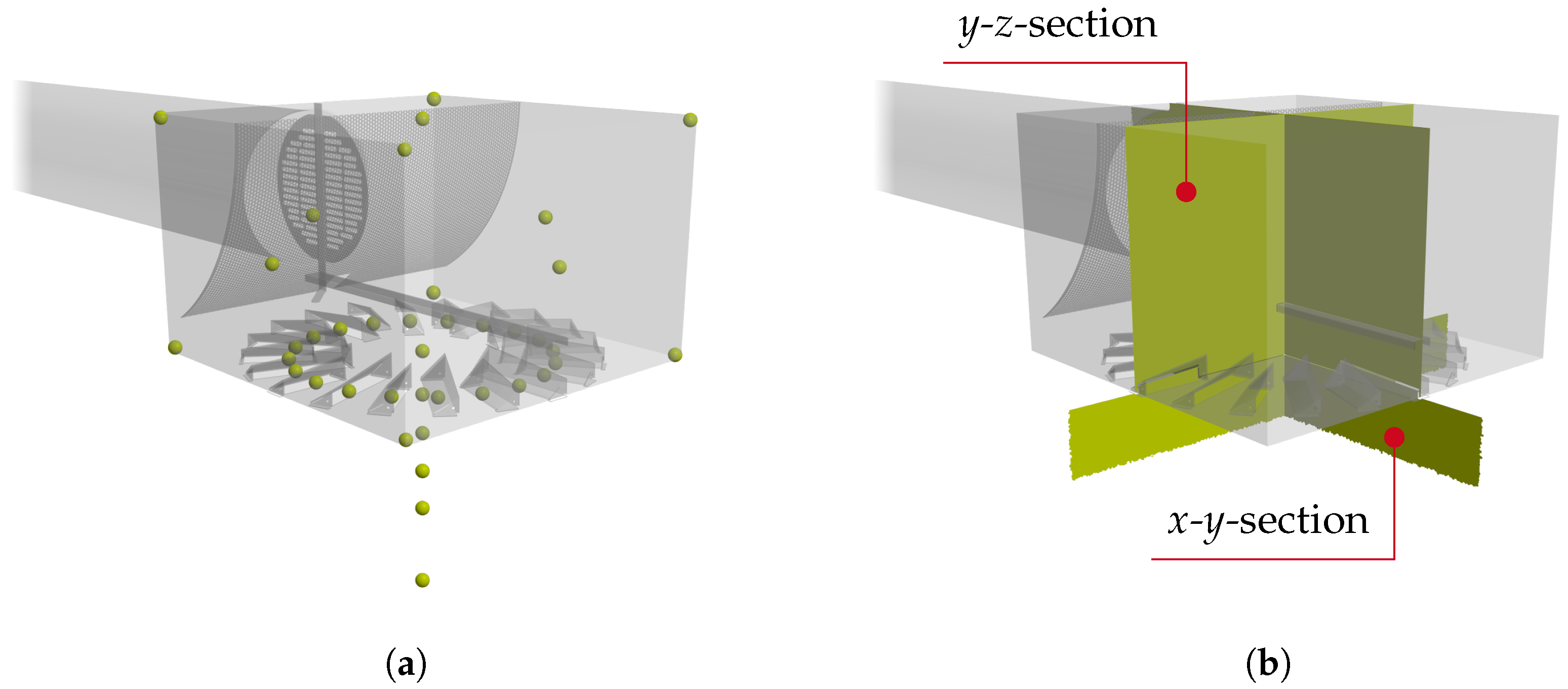
2.1. Investigated Swirl Diffuser
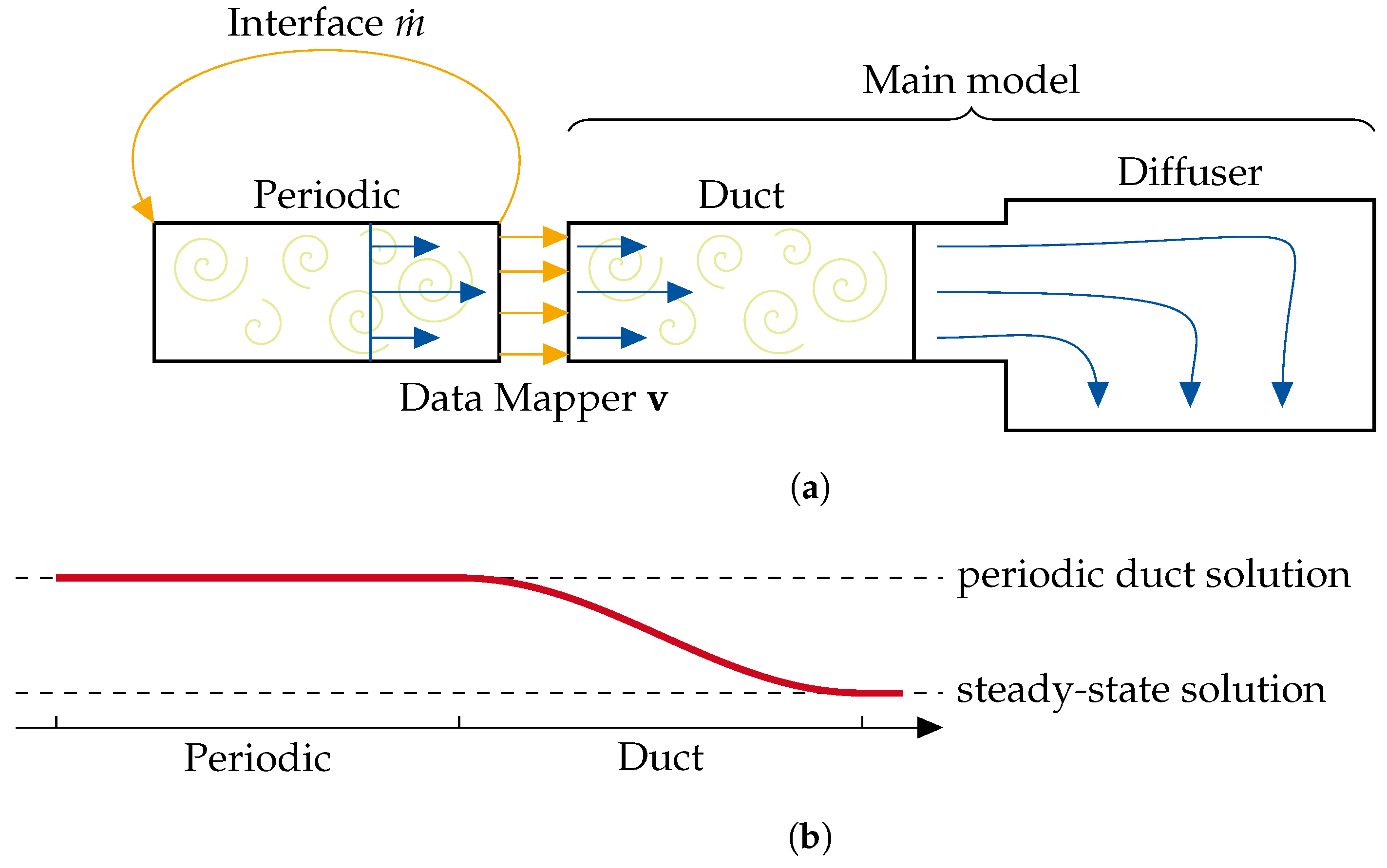
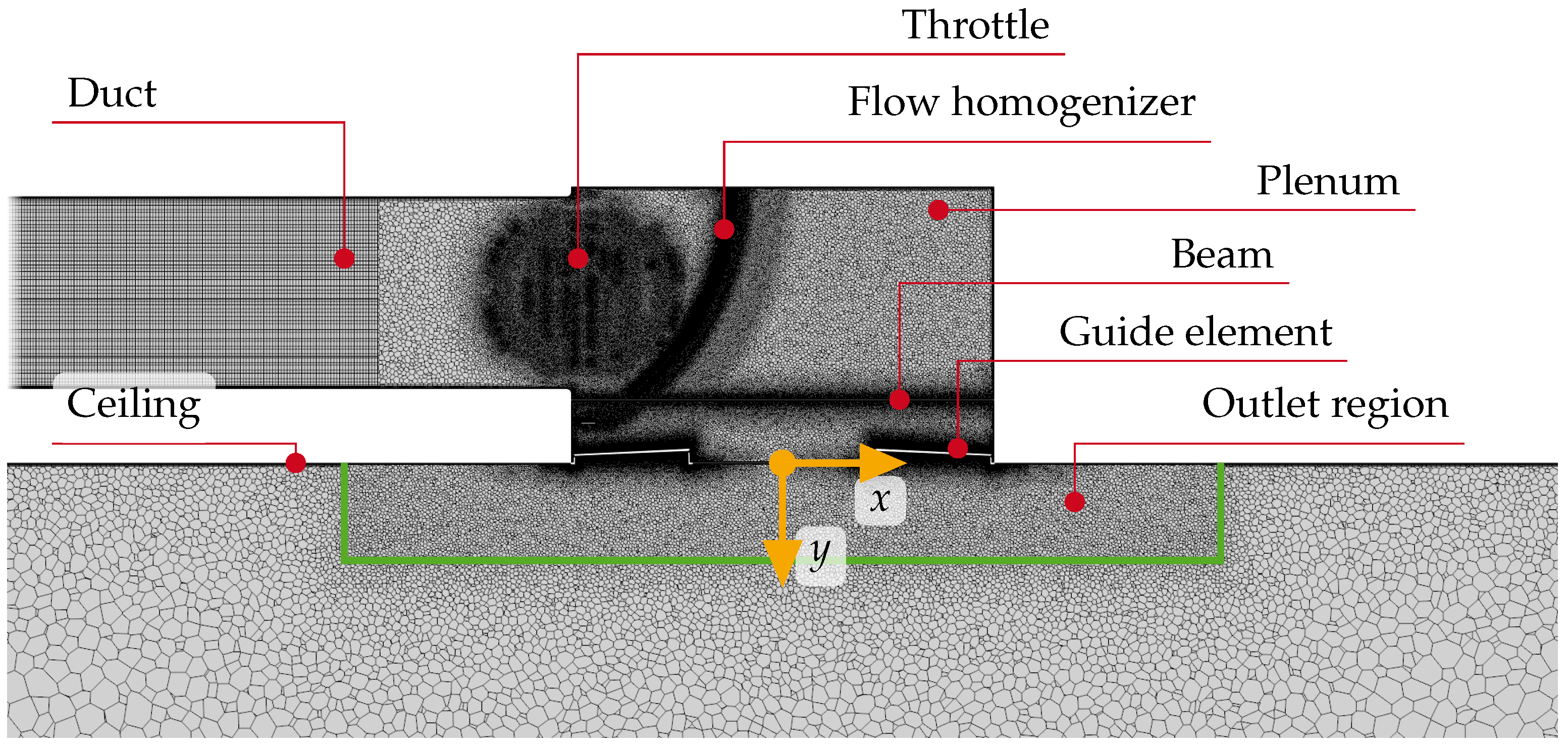
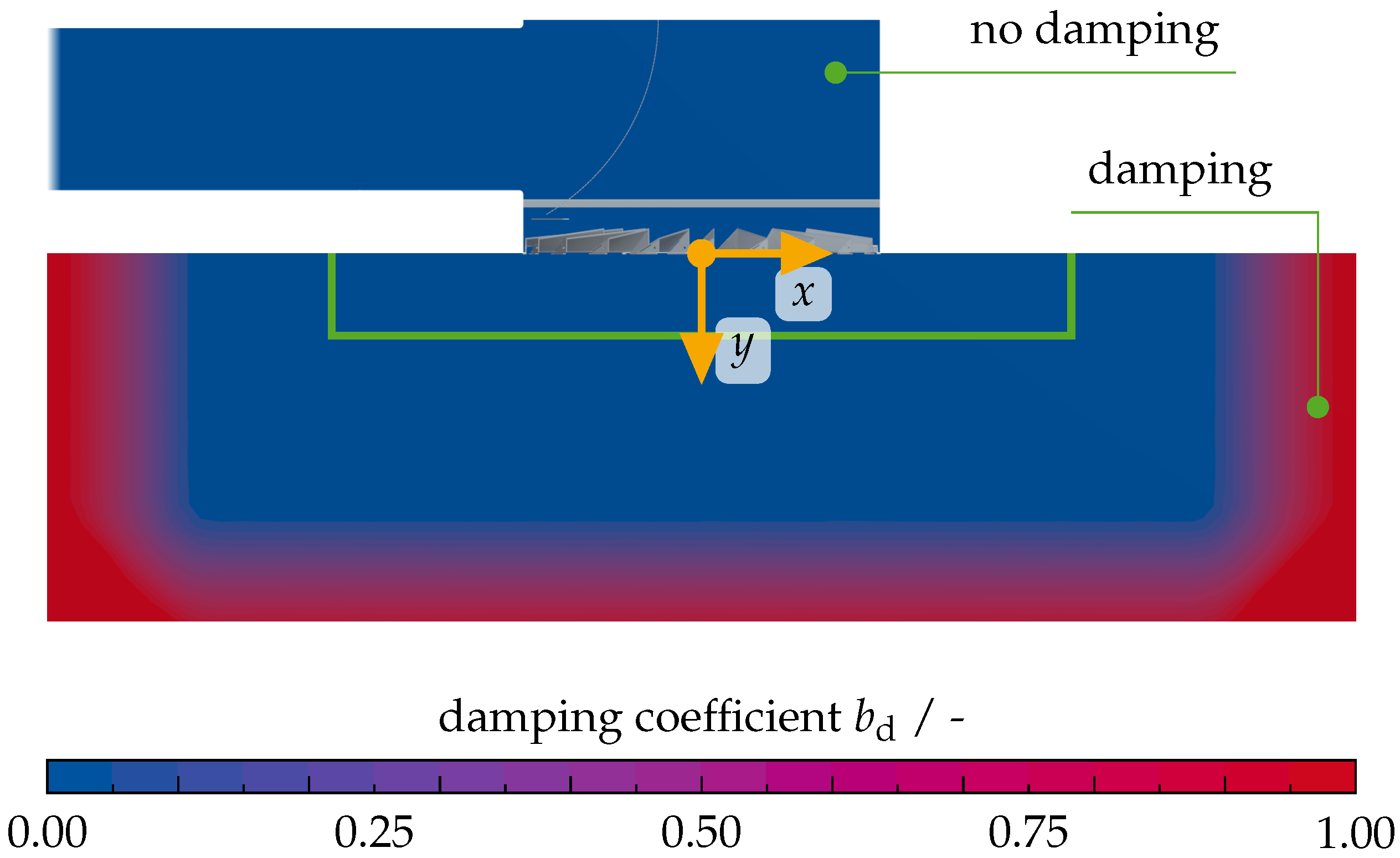
2.2. Numerical Model
2.3. Evaluation of the Flow Model
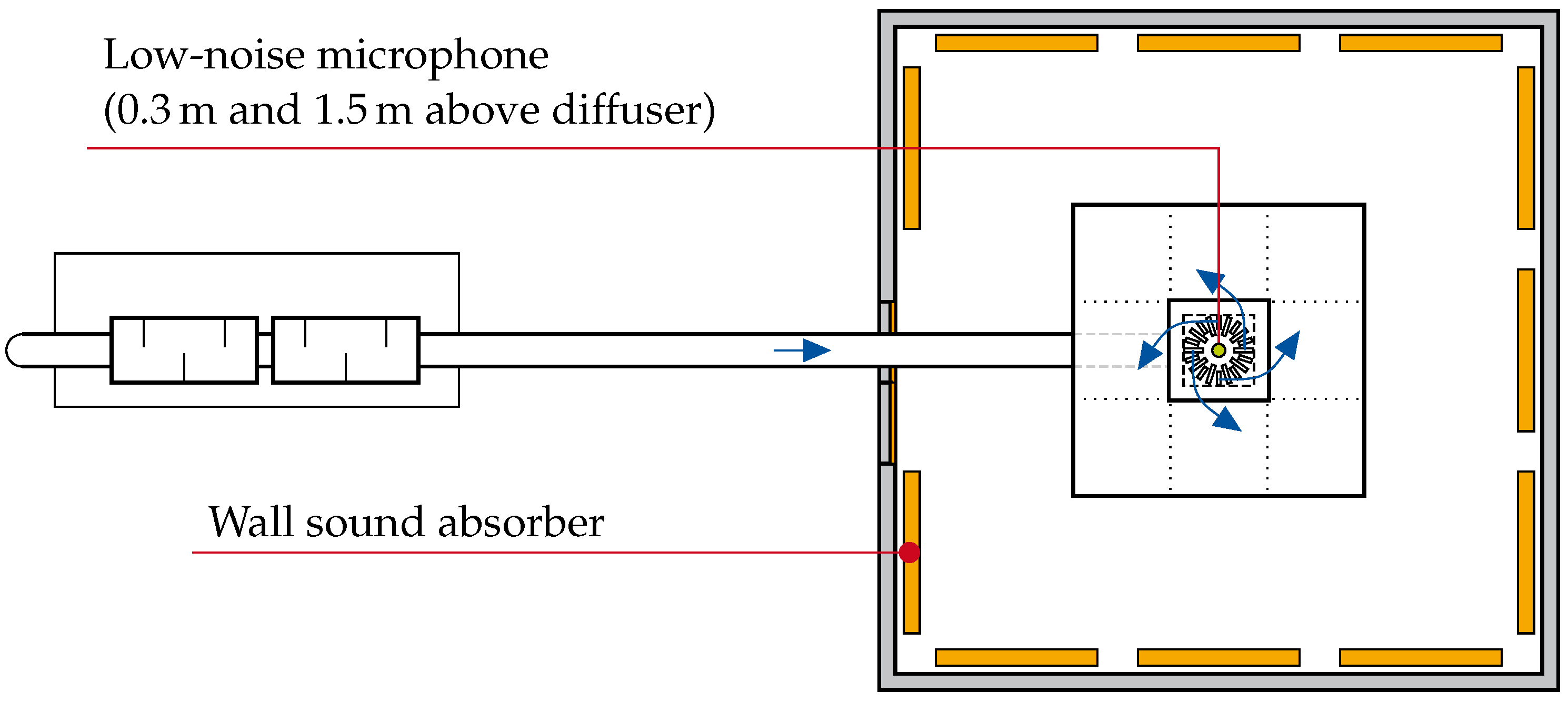
2.4. Experimental Setup
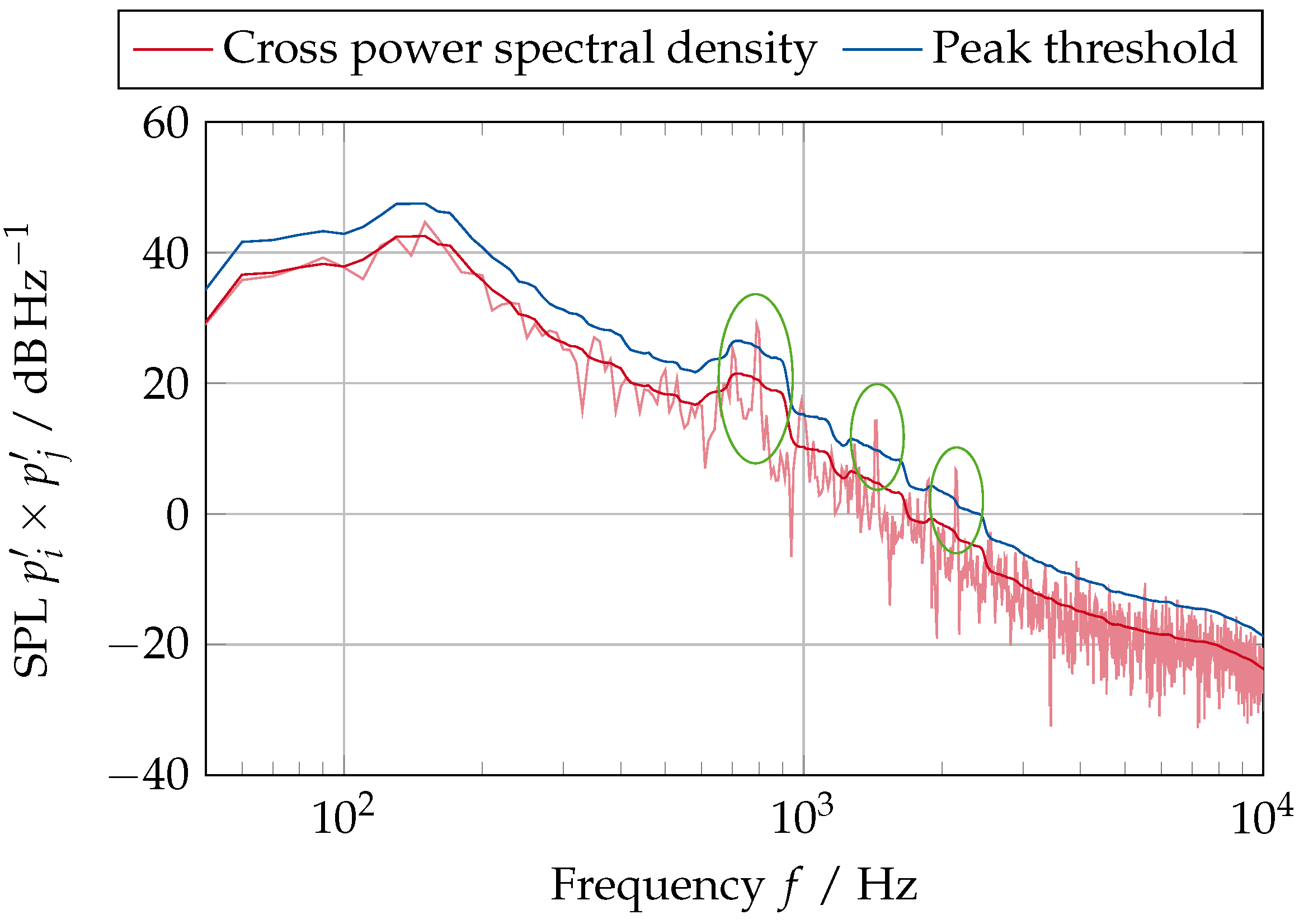
2.5. Evaluation of Acoustic Signals
3. Results
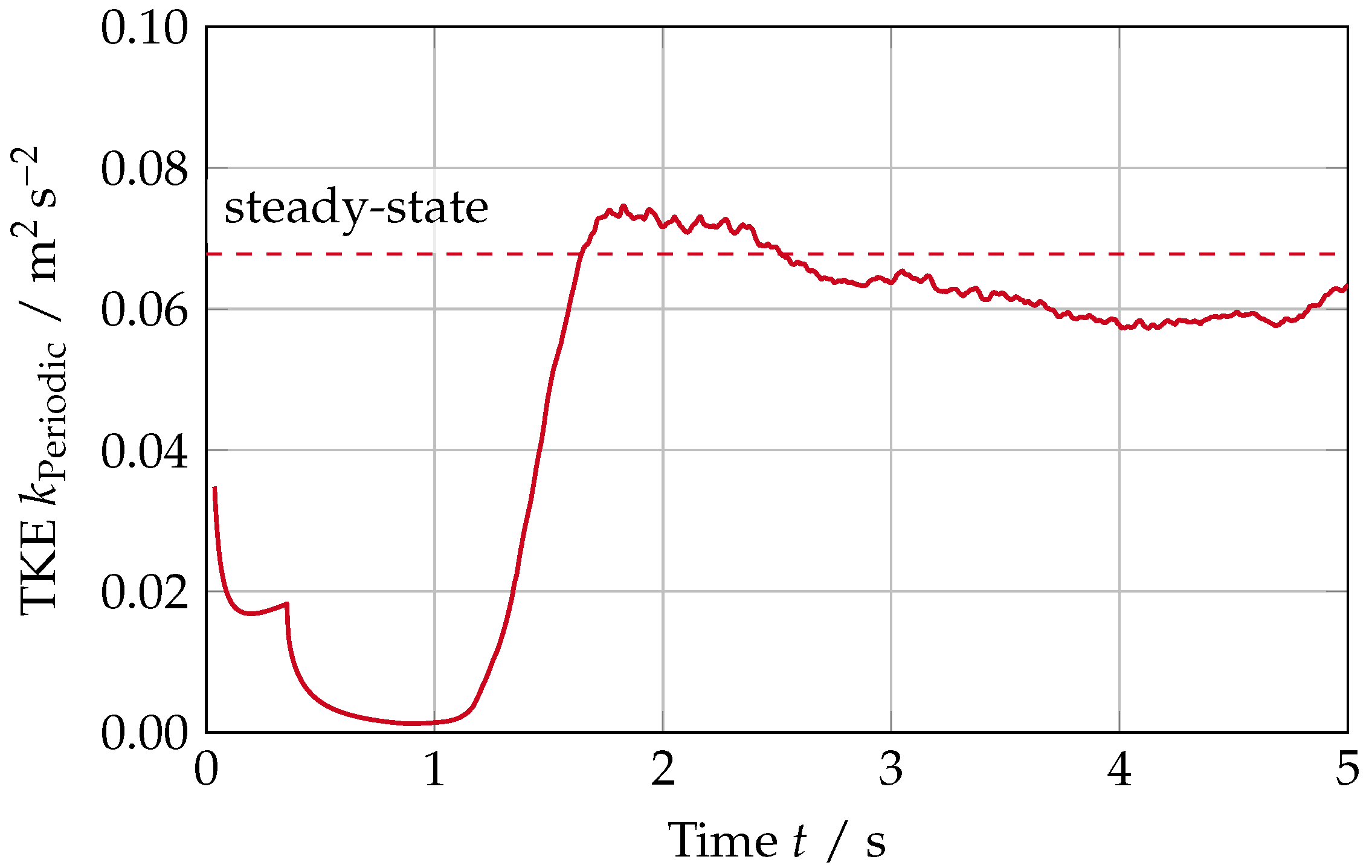
3.1. Computed Initial Solution for the Transient Calculation
3.2. Validation of the Computed Flow Model Results
3.2.1. Aerodynamic Pressure Losses
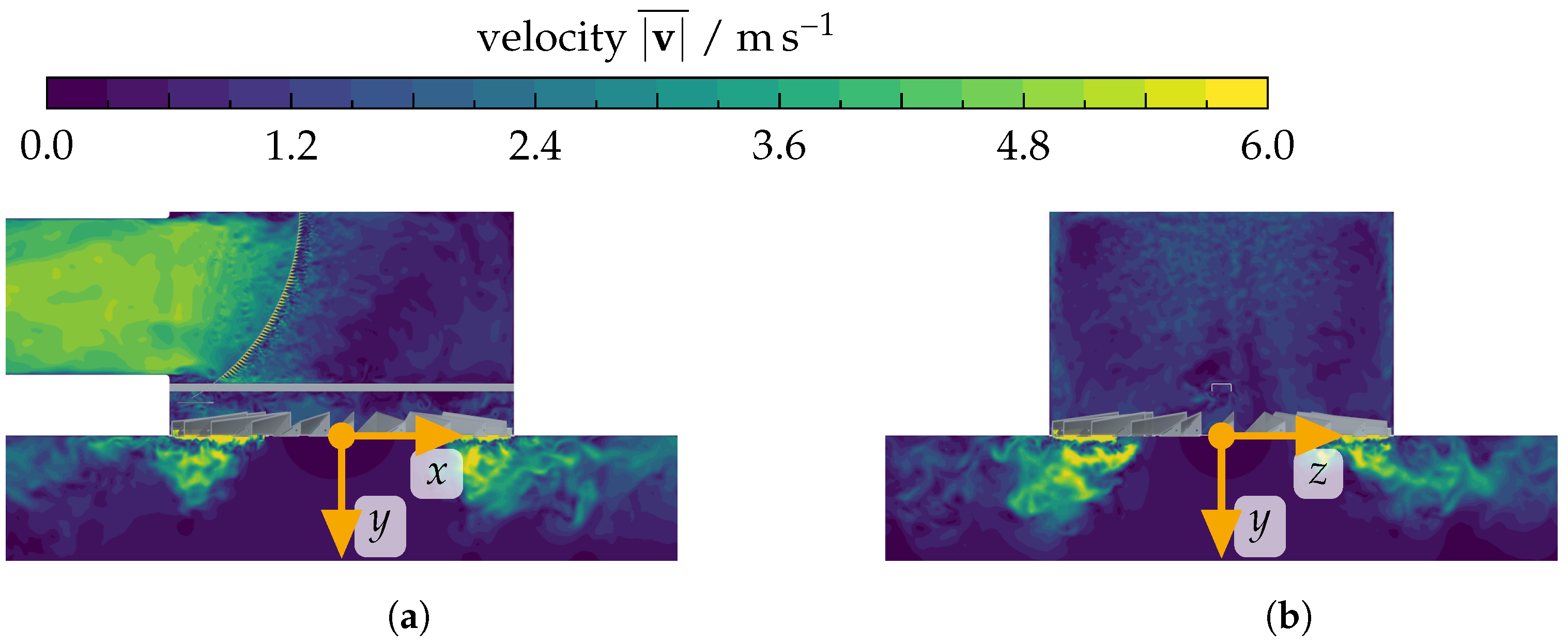
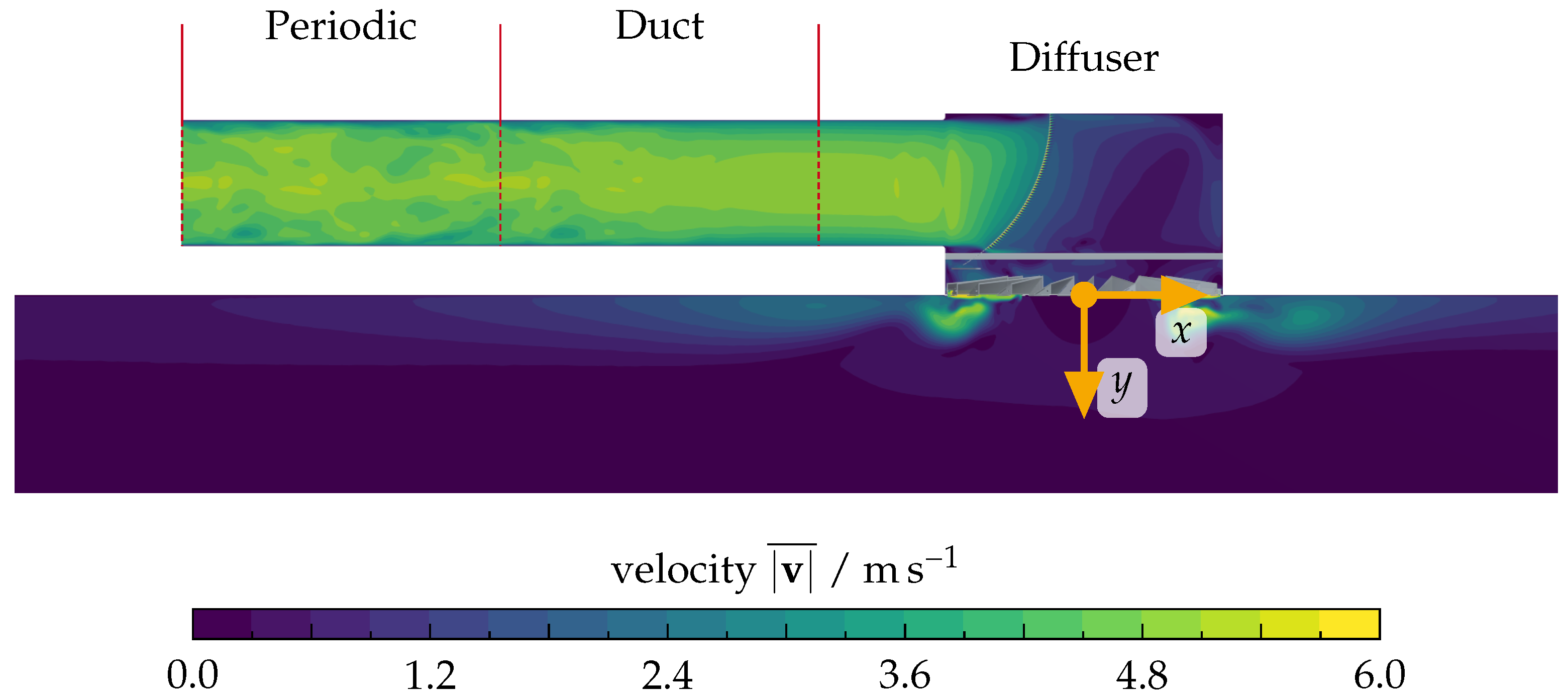
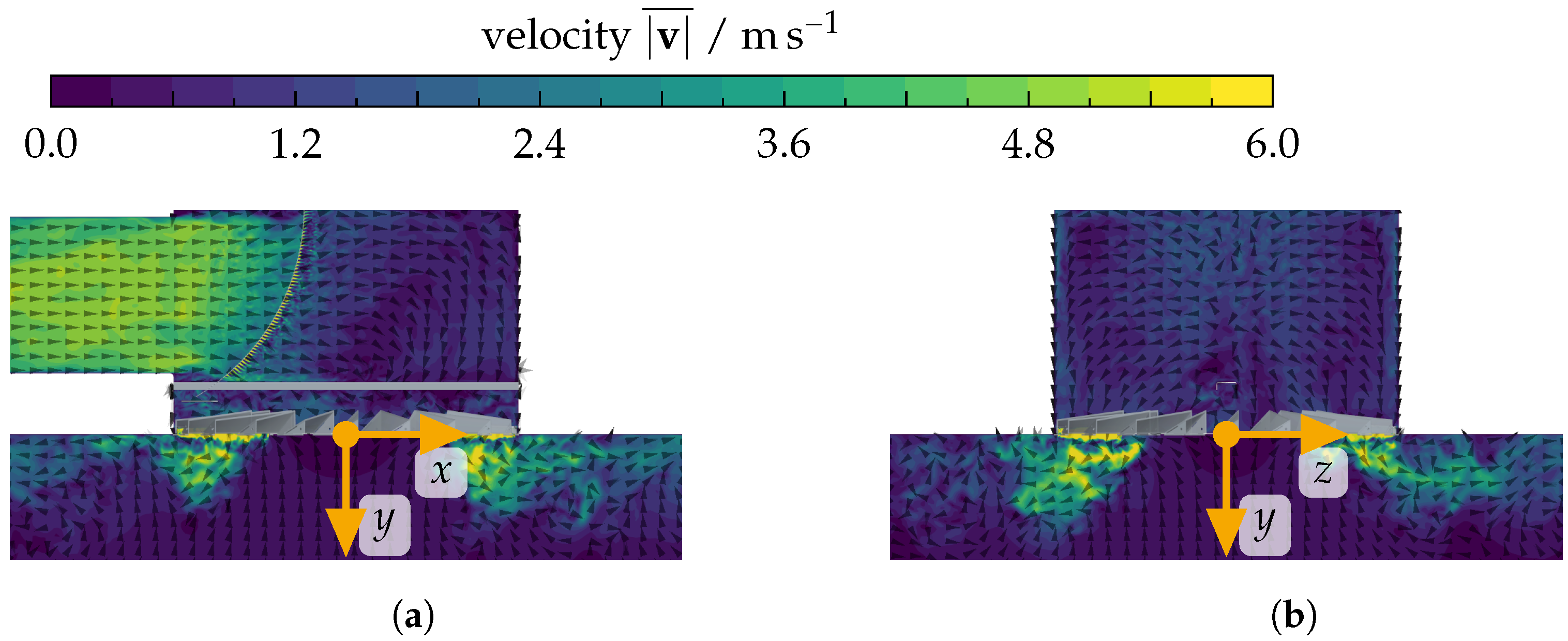
3.2.2. Flow-Field Evaluation
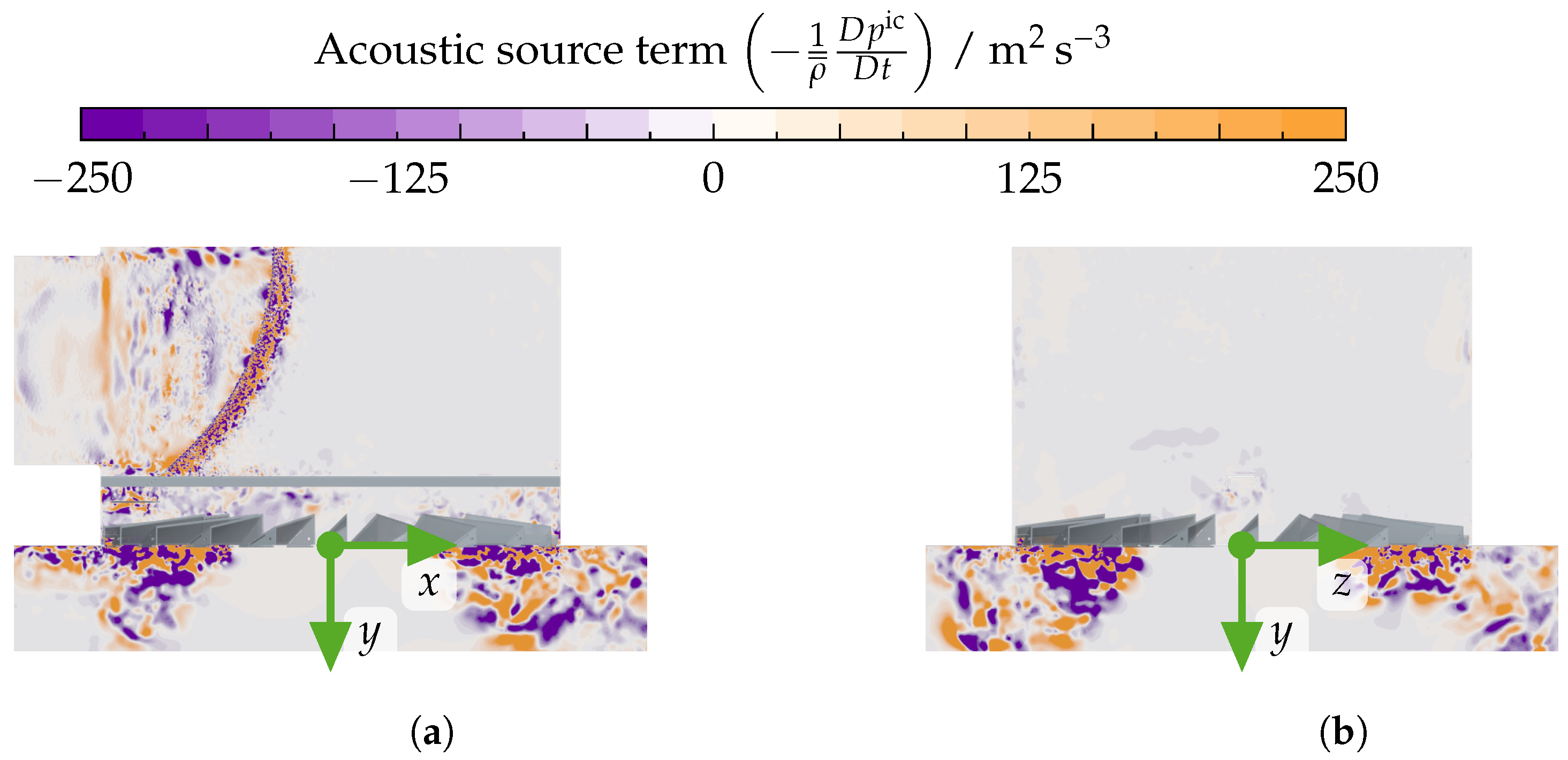
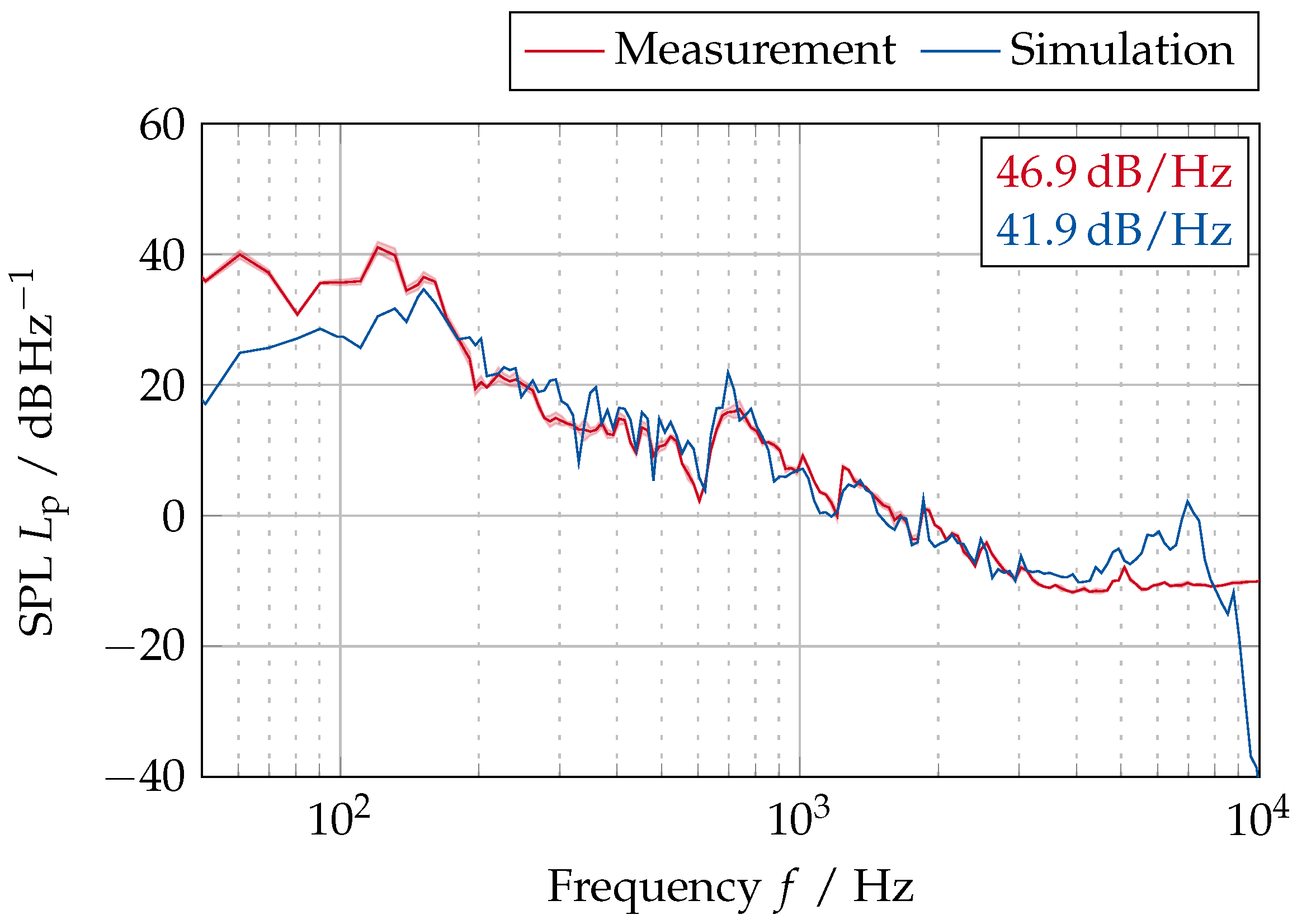
3.2.3. Acoustic Emissions
3.3. Simulation Results of the “Base” Model
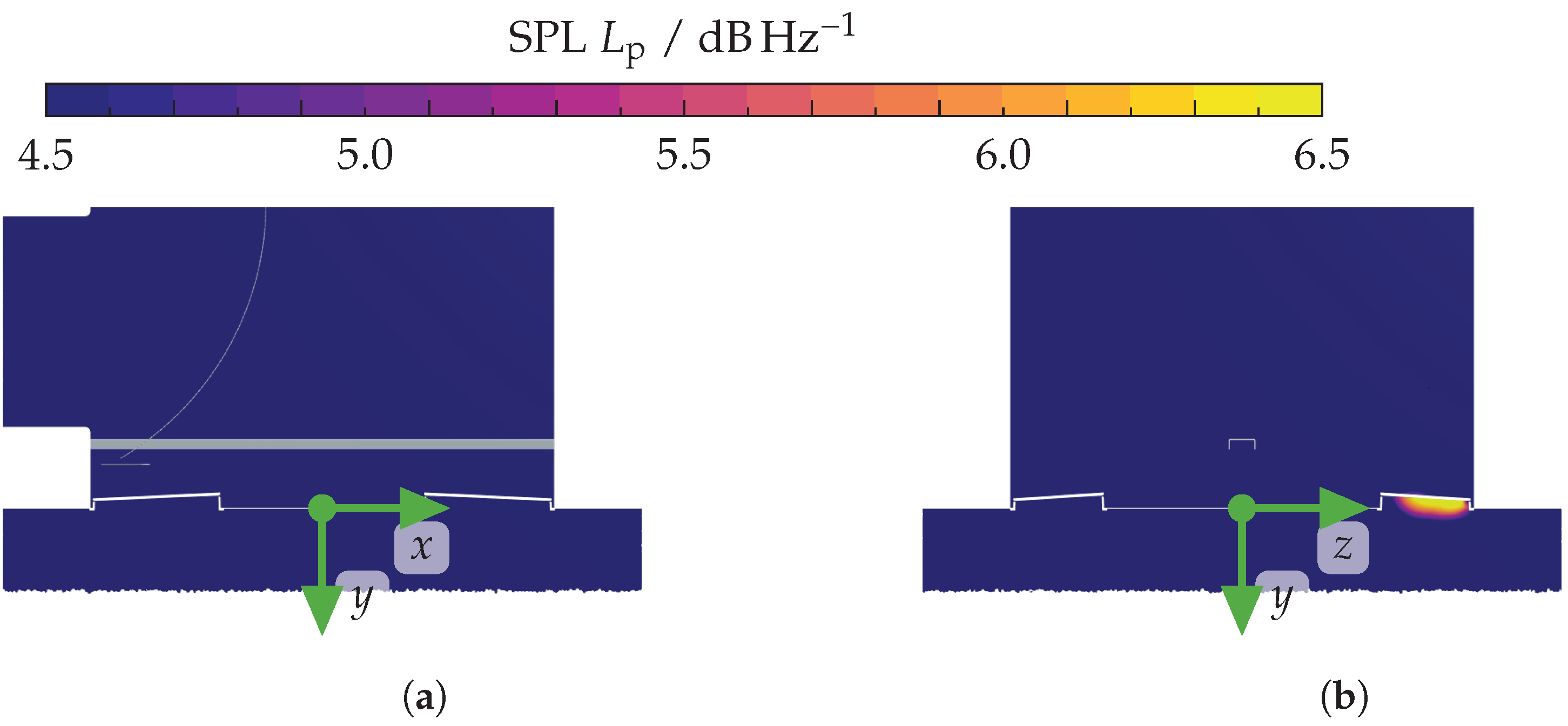
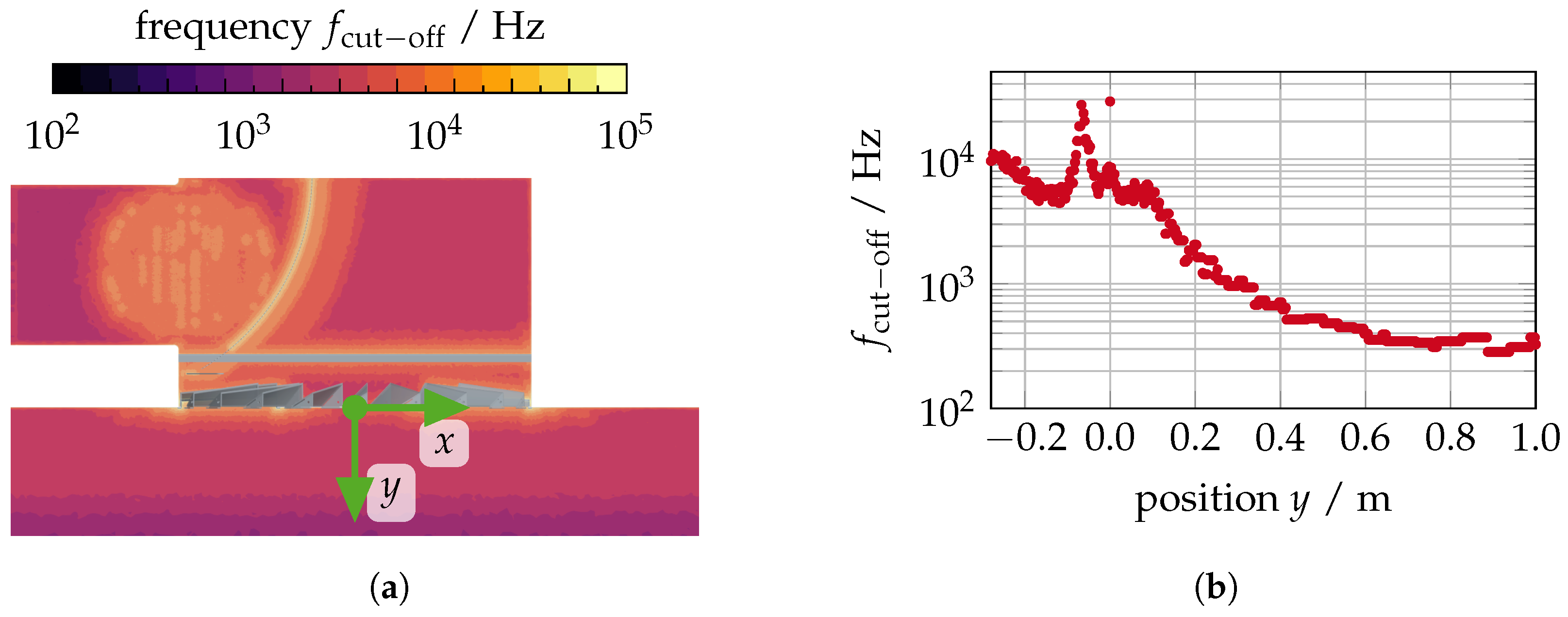
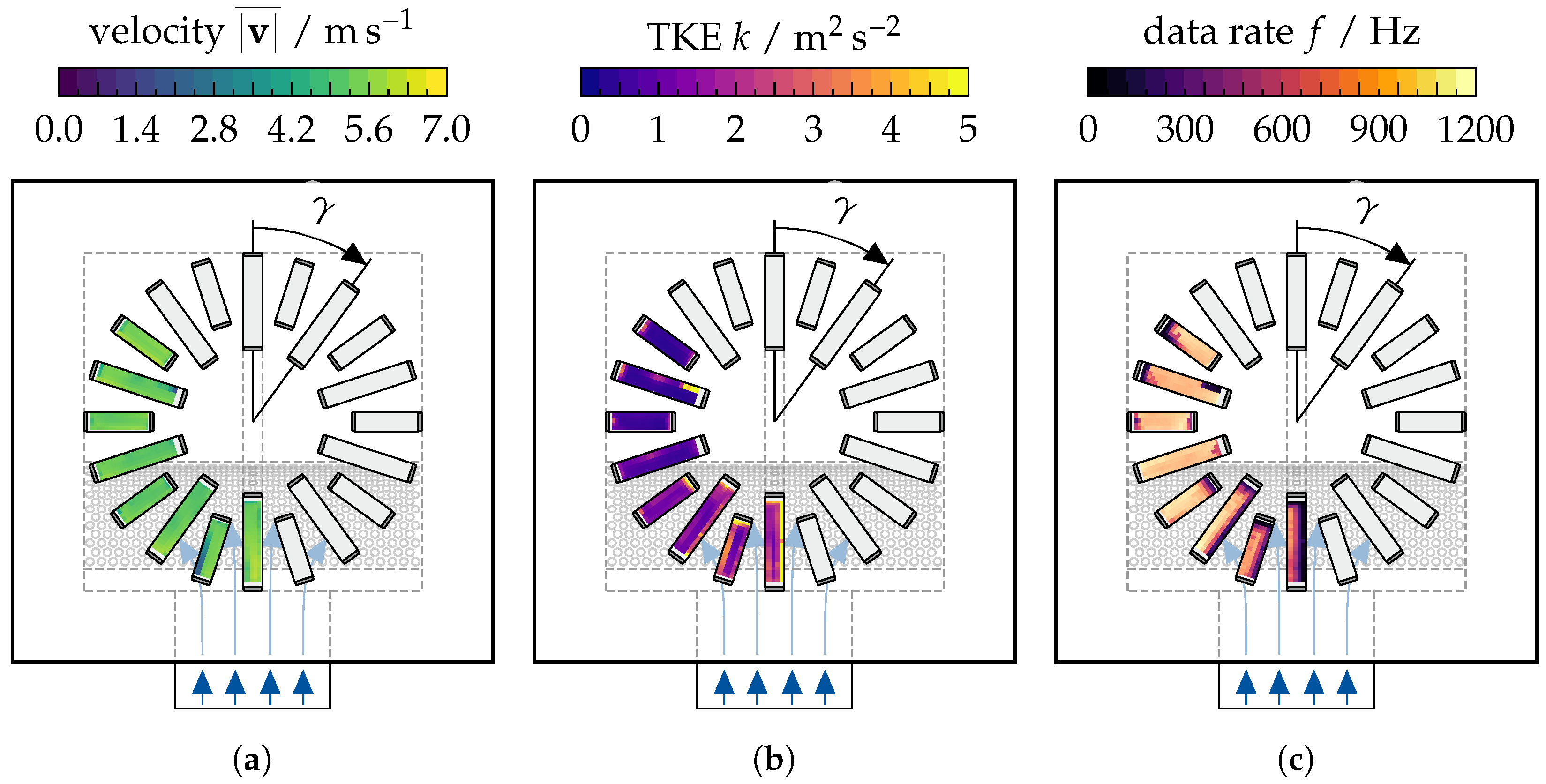
3.4. Identification of Emission Sources
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHU | Air handling unit |
| APE | Acoustic Perturbed Equation |
| BPF | Blade passing frequency |
| CAA | Computational Aeroacoustics |
| CFD | Computational Fluid Dynamics |
| CPSD | Cross-Power spectral density |
| FW-H | Ffowcs–Williams Hawkings |
| GUM | Guide to the expression of uncertainty in measurement |
| LDA | Laser-Doppler-Anemometry |
| LES | Large-Eddy Simulation |
| OASPL | Overall sound-pressure level |
| PPW | points per wavelength |
| PSD | Power spectral density |
| RANS | Reynolds-Averaged Navier–Stokes |
| SPL | Sound-pressure level |
| TKE | Turbulent Kinetic Energy |
| WALE | Wall-Adapting Local-Eddy Viscosity |
| wLPCE | wave Linearized Perturbed Compressible Equation |
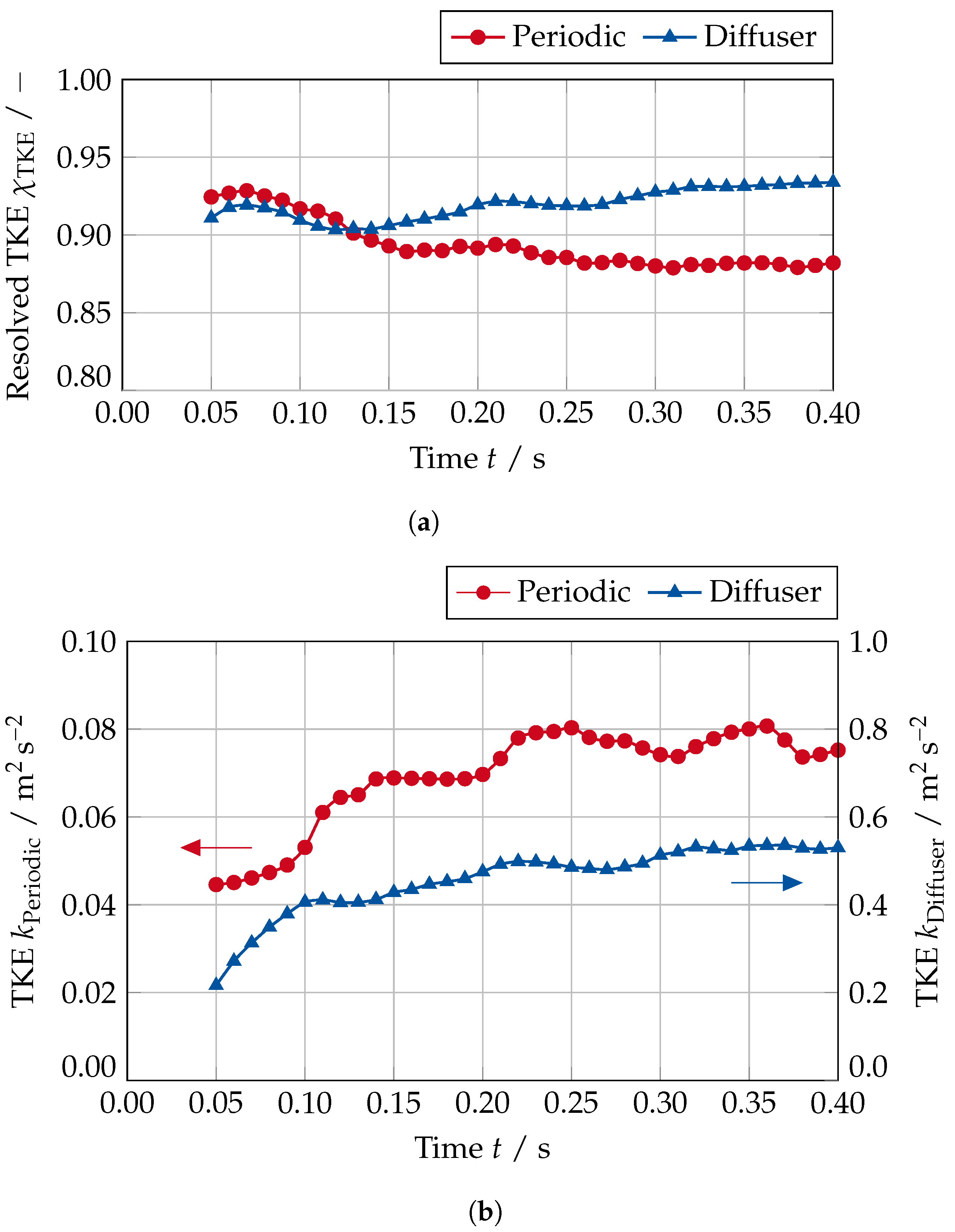
Appendix A. Evaluation of the Turbulent Kinetic Energy
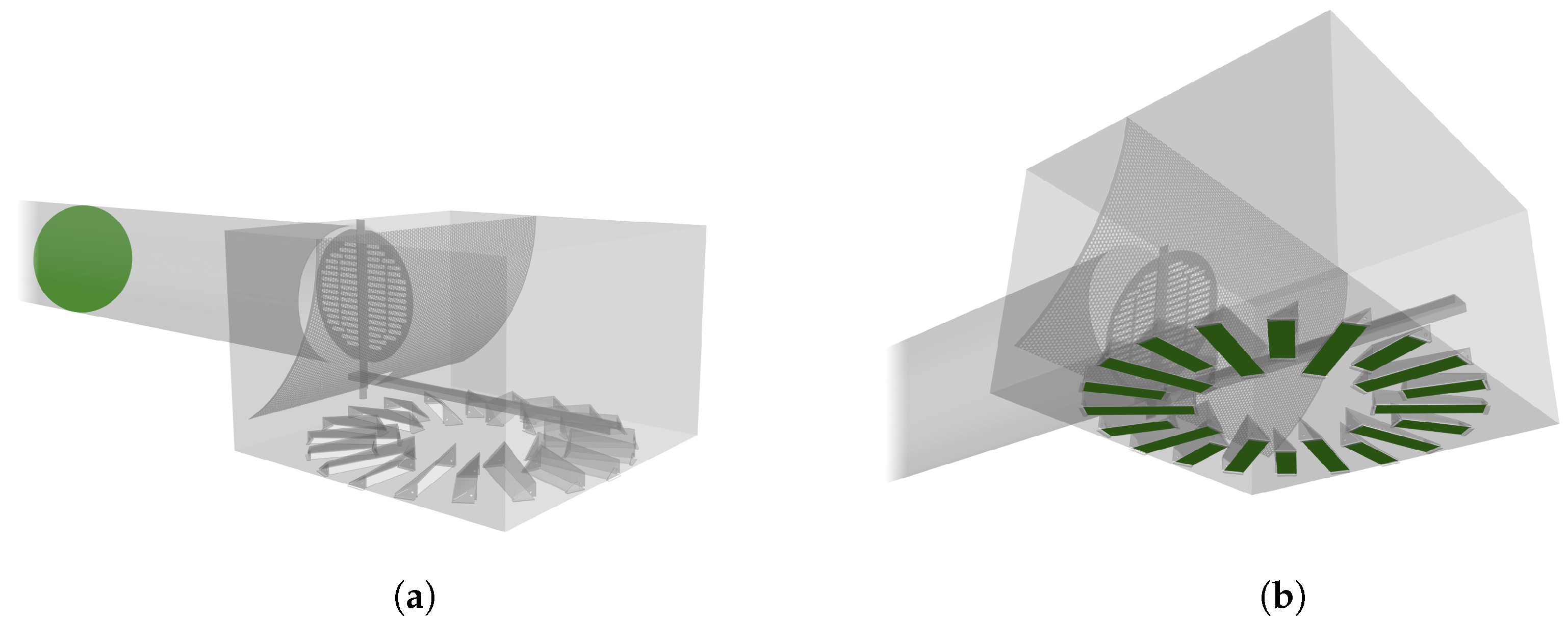
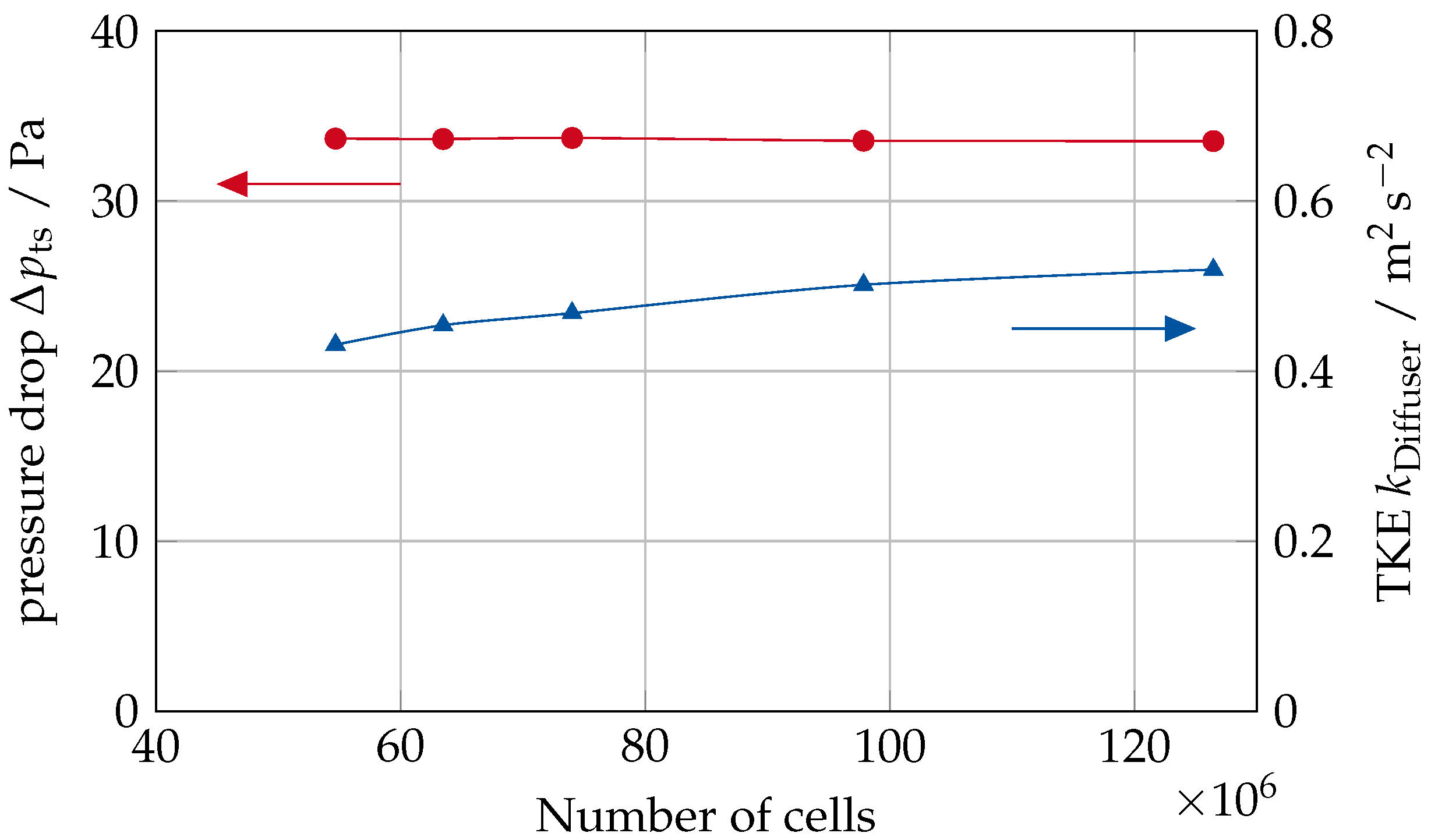
Appendix B. Results of the Mesh Independence Study
Appendix C. Additional Evaluation of the “Base” Model
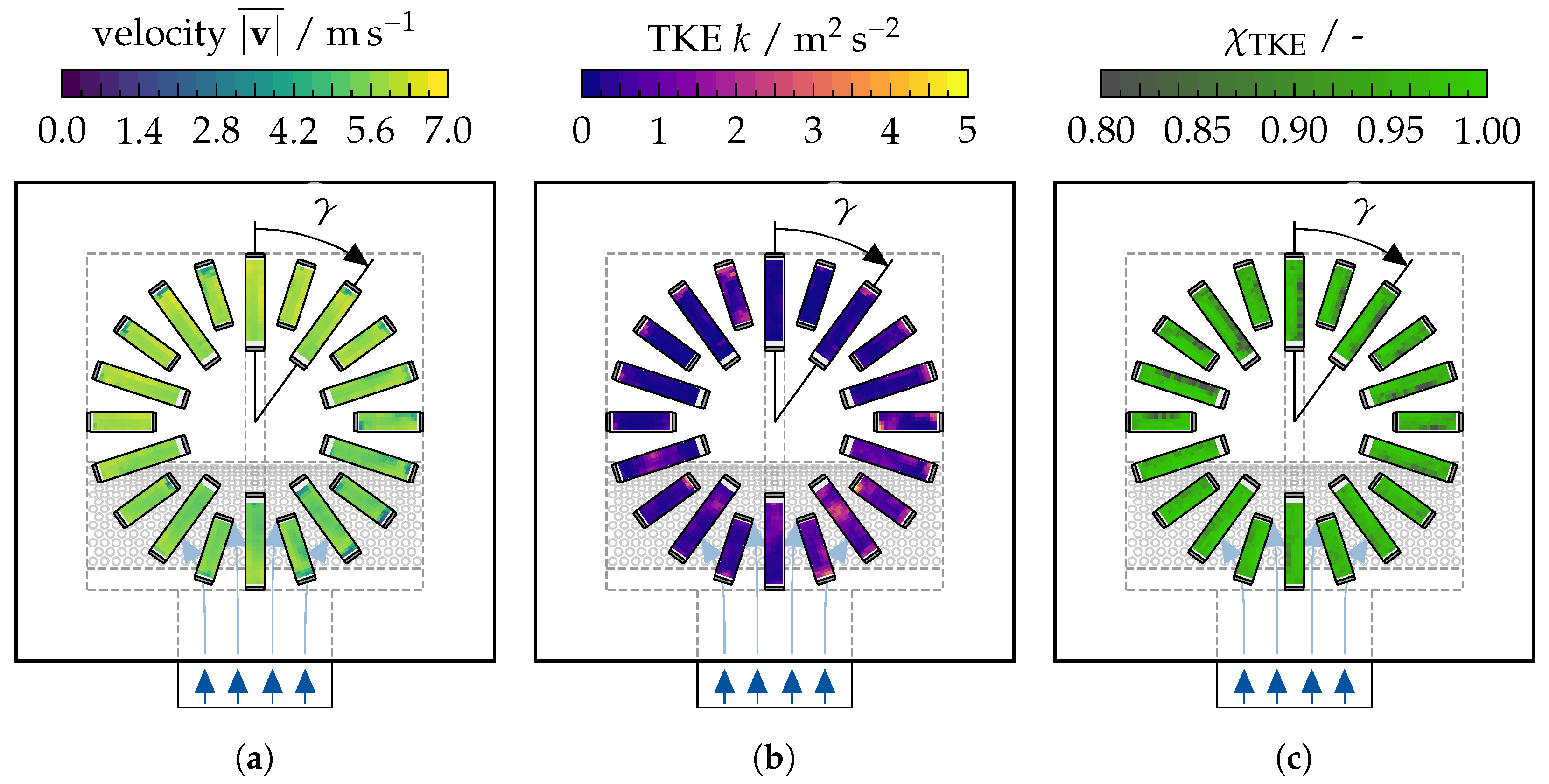

Appendix C.1. Measurement Results
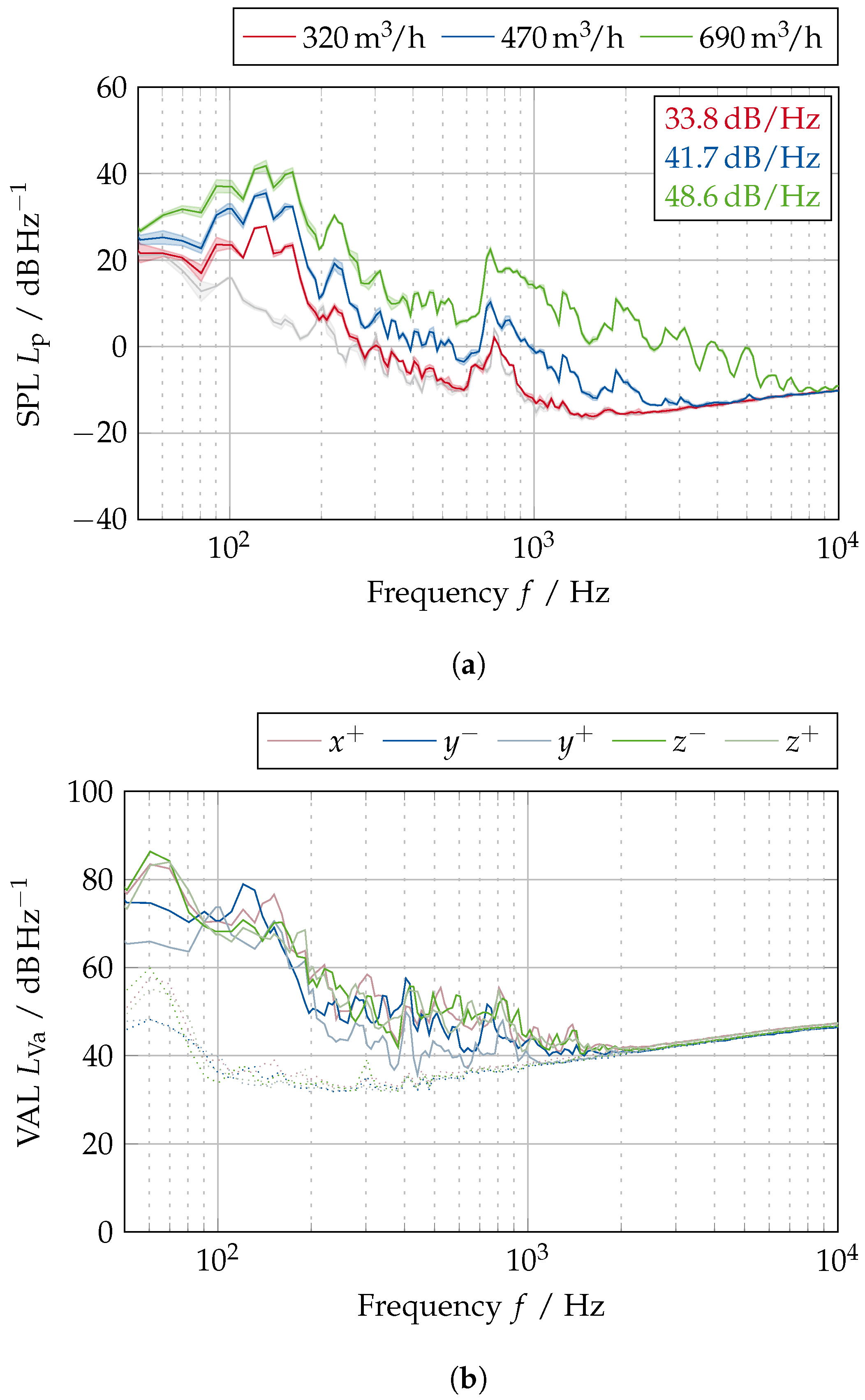
Appendix C.2. Sound-Pressure Level at Additional Receiver Locations for the “Base” Model

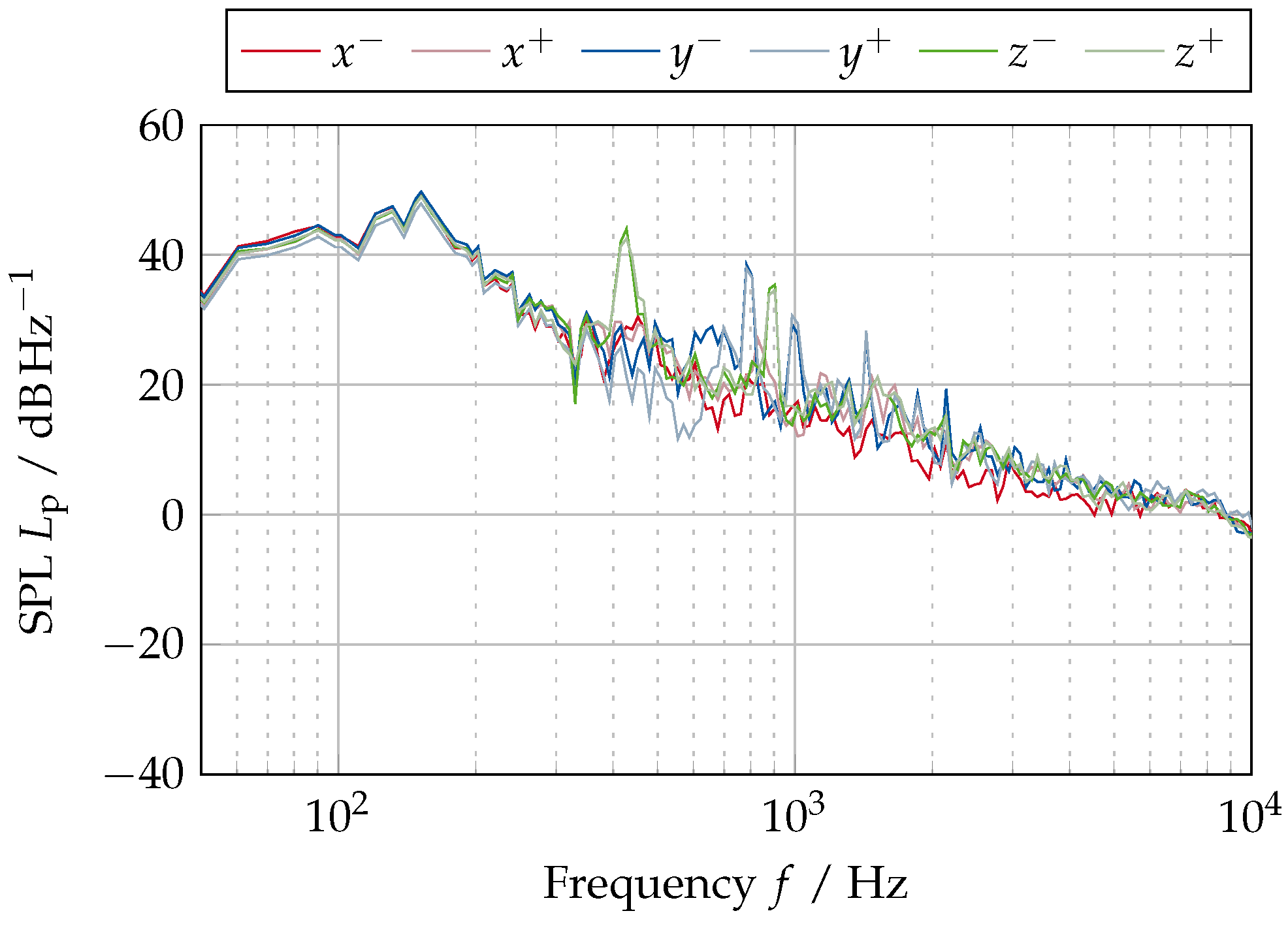
Appendix C.3. Evaluation of the Surface Sound-Pressure Level at Additional Frequency Bands for the “Base” Model

Appendix D. Additional Evaluation of the “Absorbing” Model
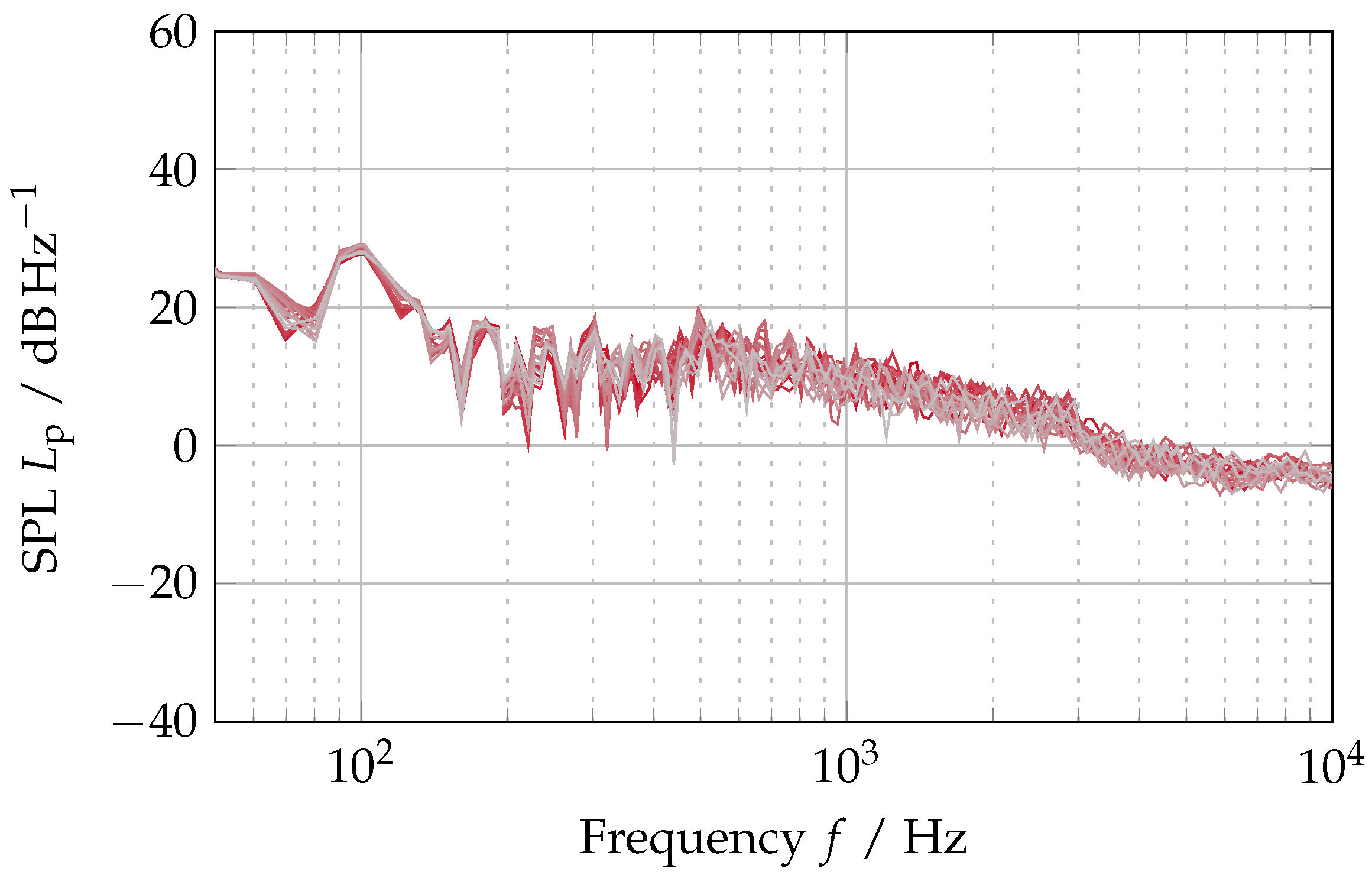
Appendix D.1. Sound-Pressure Level at Additional Receiver Locations for the “Absorbing” Model
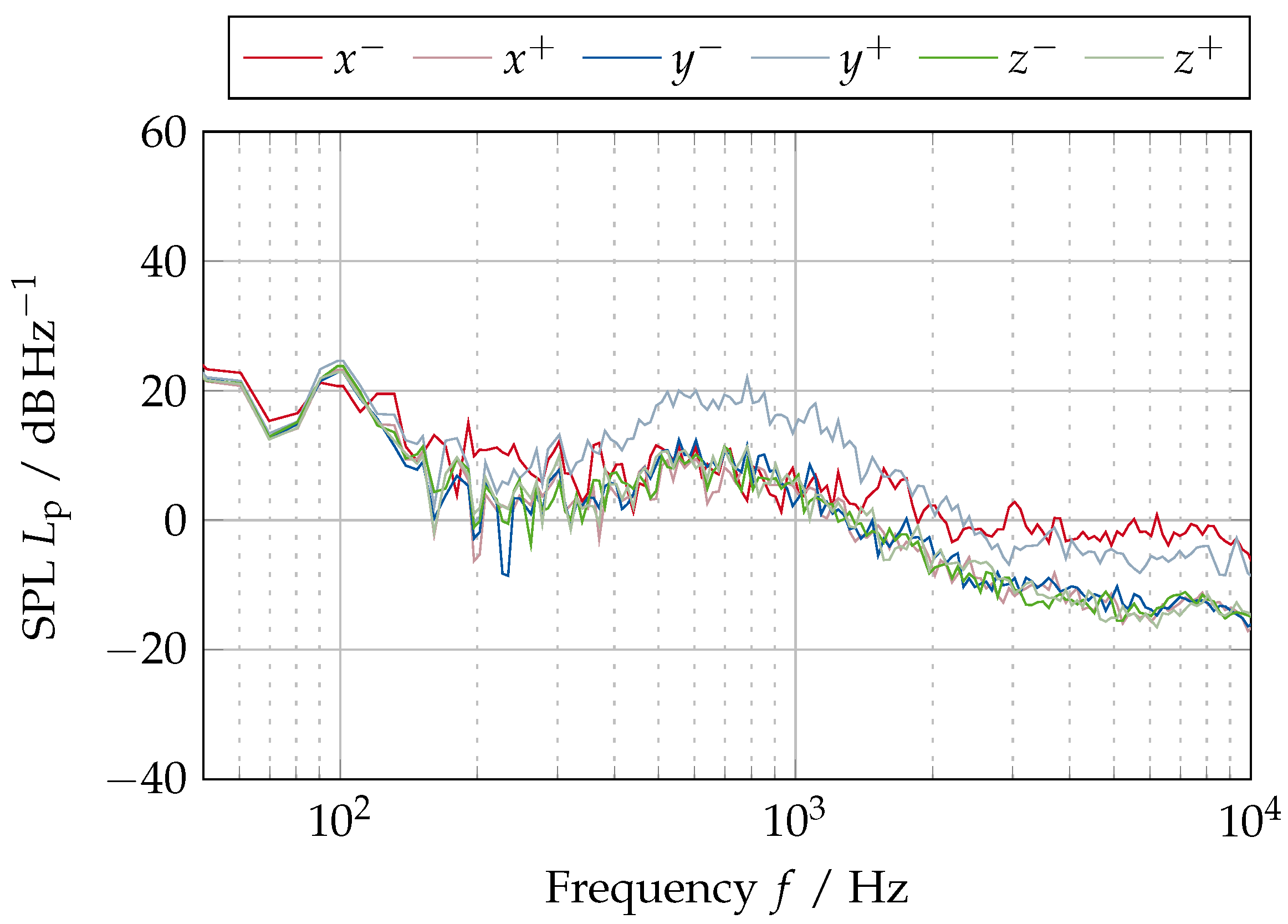
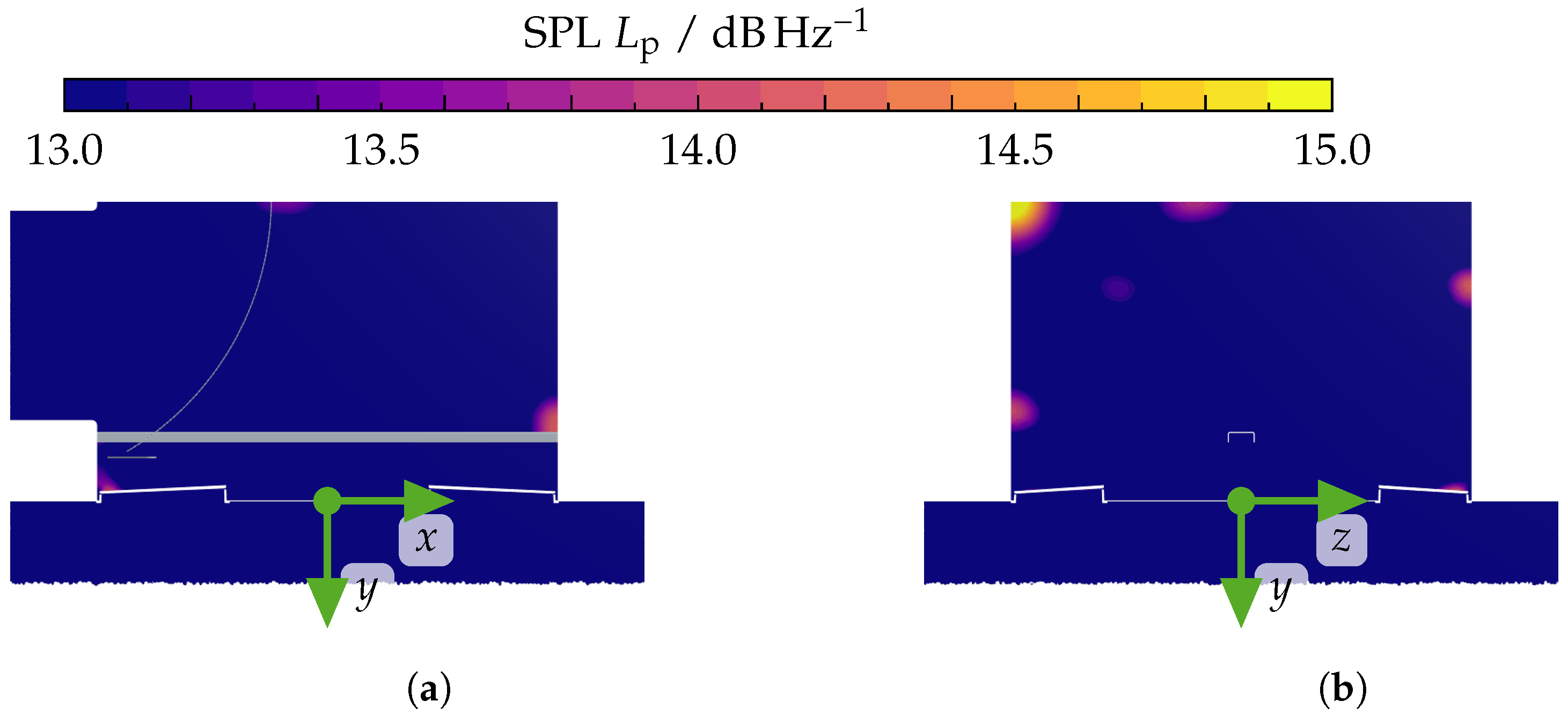
Appendix D.2. Evaluation of the Surface Power Spectral Density at Additional Frequency Bands for the “Absorbing” Model
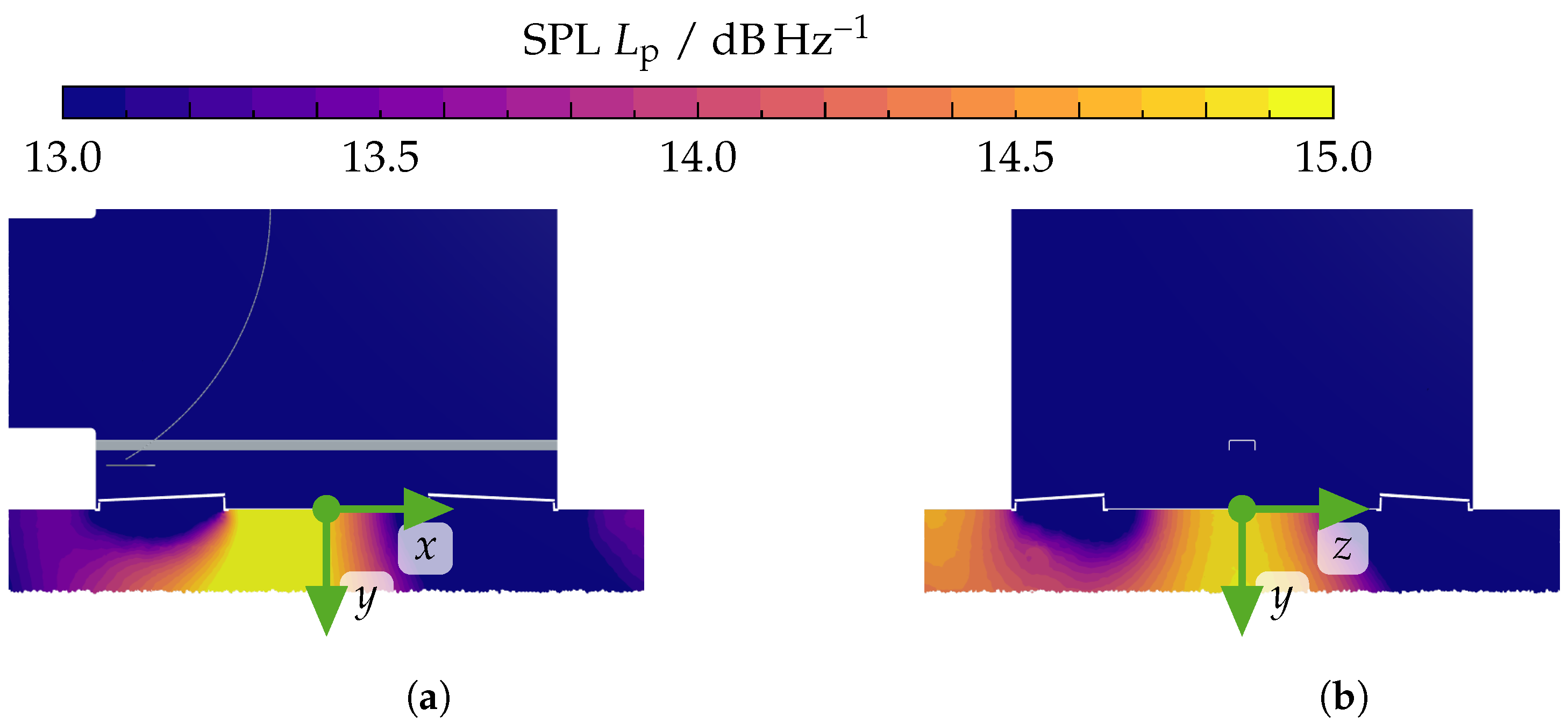
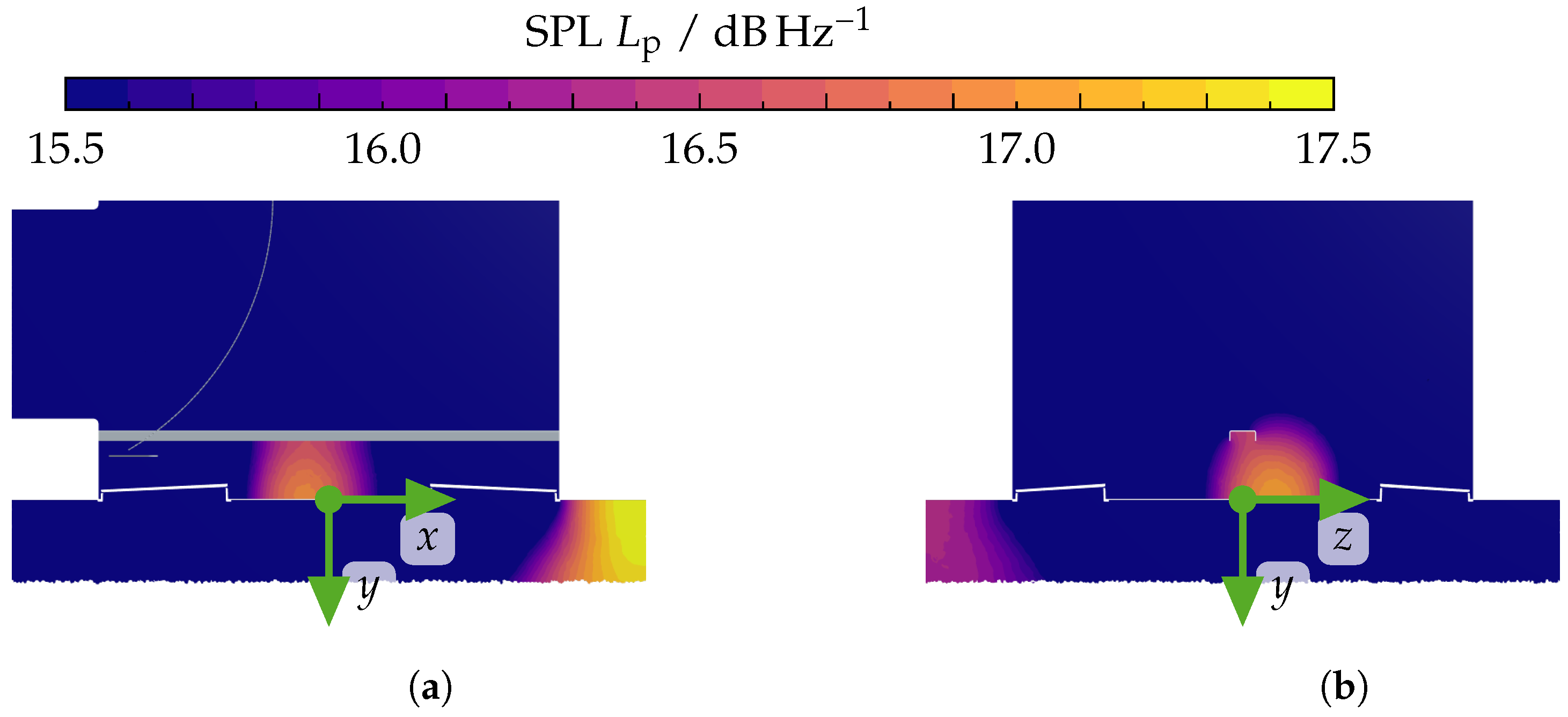
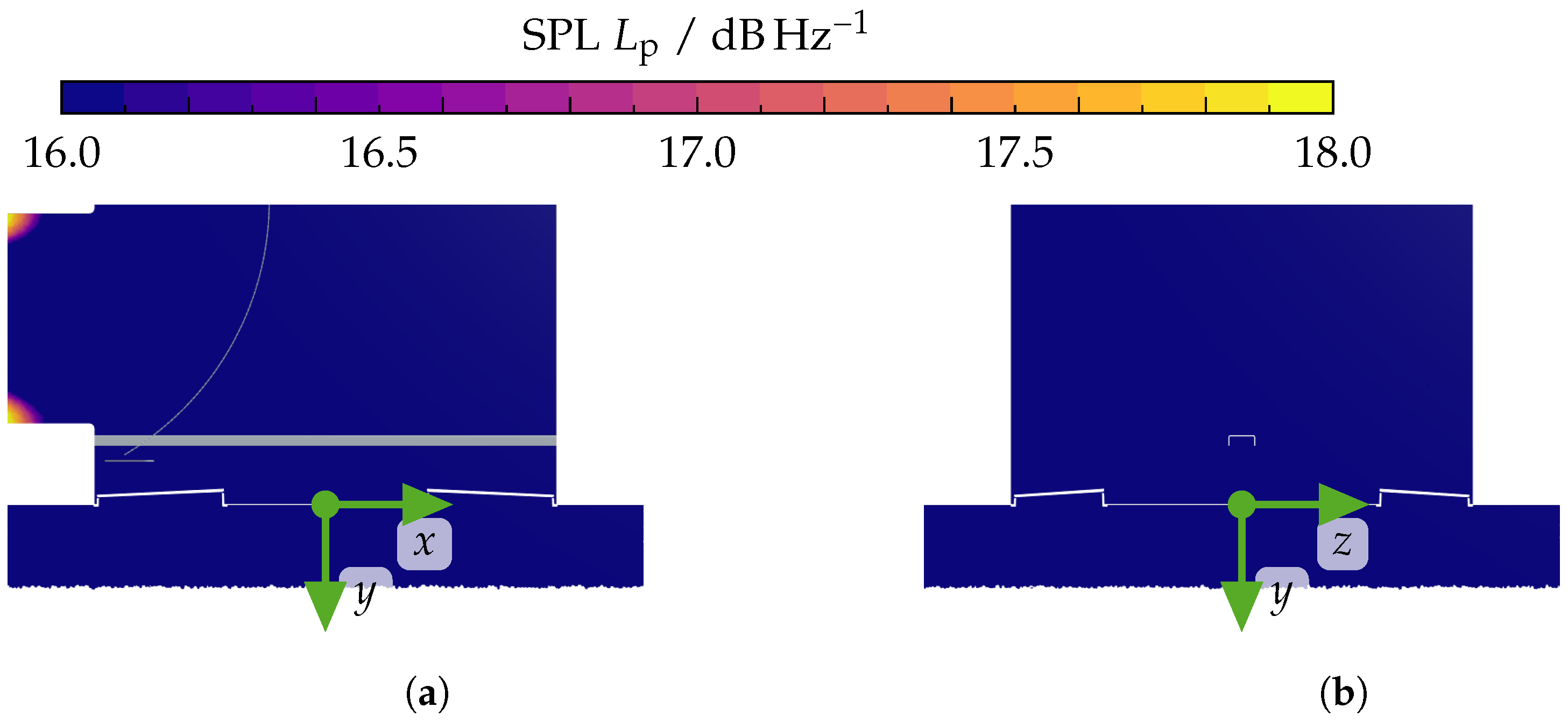
References
- Bundesanstalt für Arbeitsschutz und Arbeitsmedizin. Technische Regeln Für Arbeitsstätten. Lärm. 2021.
- Winkelmann, S.; Stürenburg, L.; Schiller, I.; Fels, J.; Schlittmeier, S. Subjektiver Akustischer Komfort von Luftdurchlässen Für Gebäudebelüftungen. In Proceedings of the Fortschritte Der Akustik—DAGA 2023, Hamburg, Germany, 6–9 May 2023. [Google Scholar]
- Stürenburg, L.; Ostmann, P.; Aspöck, L.; Fels, J.; Müller, D. Acoustic measurements and psychoacoustic analyses of ventilation diffusers. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Glasgow, UK, 21–24 August 2022. [Google Scholar] [CrossRef]
- Stürenburg, L.; Ostmann, P.; Aspock, L.; Müller, D.; Fels, J. Herausforderungen bei Messungen von Lüftungsgeräuschen in einem reflexionsfreien Halbraum. In Proceedings of the Fortschritte der Akustik—DAGA 2024, Hannover, Germany, 18–21 May 2024. [Google Scholar]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Ewert, R.; Schröder, W. Acoustic Perturbation Equations Based on Flow Decomposition via Source Filtering. J. Comput. Phys. 2003, 188, 365–398. [Google Scholar] [CrossRef]
- Seo, J.H.; Moon, Y.J. Perturbed Compressible Equations for Aeroacoustic Noise Prediction at Low Mach Numbers. AIAA J. 2005, 43, 1716–1724. [Google Scholar] [CrossRef]
- Seo, J.H.; Moon, Y.J. Linearized Perturbed Compressible Equations for Low Mach Number Aeroacoustics. J. Comput. Phys. 2006, 218, 702–719. [Google Scholar] [CrossRef]
- Hüppe, A. Spectral Finite Elements for Acoustic Field Computation; Measurement-, Actuator-, and Simulation-Technology, Shaker: Aachen, Germany, 2013. [Google Scholar] [CrossRef]
- Piepiorka, J.; von Estorff, O. Numerical Investigation of Hydrodynamic/Acoustic Splitting Methods in Finite Volumes Including Rotating Domains. In Proceedings of the 23rd International Congress on Acoustics, Aachen, Germany, 9–13 September 2019; pp. 1827–1834. [Google Scholar]
- Ocker, C.; Geyer, T.F.; Czwielong, F.; Krömer, F.; Becker, S.; Merkel, M.; Pannert, W. Experimental Investigation of the Impact of 3D-Metal-Printed Perforated Leading Edges on Airfoil and Axial Fan Noise. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020. [Google Scholar] [CrossRef]
- Ocker, C.; Czwielong, F.; Chaitanya, P.; Pannert, W.; Becker, S. Aerodynamic and Aeroacoustic Properties of Axial Fan Blades with Slitted Leading Edges. Acta Acust. 2022, 6, 48. [Google Scholar] [CrossRef]
- Czwielong, F.; Berchtenbreiter, B.; Ocker, C.; Geyer, T.; Stockmeier, G.; Merkel, M.; Becker, S. On the Application and Limitations of Sound-Absorbing Materials for Axial Fan Blades. In Proceedings of the Fan 2022–International Conference on Fan Noise, Aerodynamics, Applications and Systems, Senlis, France, 27–29 June 2022. [Google Scholar] [CrossRef]
- Clark, I.A.; Alexander, W.N.; Devenport, W.; Glegg, S.; Jaworski, J.W.; Daly, C.; Peake, N. Bioinspired Trailing-Edge Noise Control. AIAA J. 2017, 55, 740–754. [Google Scholar] [CrossRef]
- Lendvai, B.; Benedek, T. Experimental and Numerical Investigation of the Blade Tip-Related Aeroacoustic Sound Source Mechanisms of a Ducted Low-Speed Axial Flow Fan. Appl. Acoust. 2024, 215, 109705. [Google Scholar] [CrossRef]
- Sun, Z.; Tian, J.; Zheng, Y.; Zhu, X.; Du, Z.; Ouyang, H. Design of Sinusoidal-Shaped Inlet Duct for Acoustic Mode Modulation Noise Reduction of Cooling Fan. Appl. Acoust. 2024, 216, 109741. [Google Scholar] [CrossRef]
- Lörcher, F.; Hub, S. Effizientes Und Schallarmes Axialventilatorsystem Mit Neuartigem Zonal Optimiertem Nachleitrad. In Proceedings of the Fortschritte Der Akustik—DAGA 2023, Hamburg, Germany, 6–9 May 2023; pp. 1564–1567. [Google Scholar]
- Schäfer, R.; Böhle, M. Validation of the Lattice Boltzmann Method for Simulation of Aerodynamics and Aeroacoustics in a Centrifugal Fan. Acoustics 2020, 2, 735–752. [Google Scholar] [CrossRef]
- Tautz, M. Aeroacoustic Noise Prediction of Automotive HVAC Systems. Ph.D. Thesis, FAU University Press, Erlangen, Germany, 2019. [Google Scholar] [CrossRef]
- Yadegari, M.; Ommi, F.; Karimian Aliabadi, S.; Saboohi, Z. Reducing the Aerodynamic Noise of the Axial Flow Fan with Perforated Surface. Appl. Acoust. 2024, 215, 109720. [Google Scholar] [CrossRef]
- Zurbano-Fernández, I.; Guedel, A.; Robitu, M.; Roger, M. Noise Reduction of a Centrifugal Plenum Fan with Leading Edge or Trailing Edge Serrations. In Proceedings of the Fan 2022—International Conference on Fan Noise, Aerodynamics, Applications and Systems, Senlis, France, 27–29 June 2022. [Google Scholar] [CrossRef]
- Perot, F.; Kim, M.S.; Freed, D.; Lee, D.; Ih, K.D.; Ih, K.D.; Kim, M.S. Direct Aeroacoustics Prediction of Ducts and Vents Noise. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Reston, Virigina, Stockholm, Sweden, 7–9 June 2010. [Google Scholar] [CrossRef]
- Curle, N. The Influence of Solid Boundaries upon Aerodynamic Sound. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1955, 231, 505–514. [Google Scholar] [CrossRef]
- Proudman, I. The Generation of Noise by Isotropic Turbulence. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1952, 214, 119–132. [Google Scholar] [CrossRef]
- Khondge, A.D.; Sovani, S.D.; Kim, S.E.; Guzy, S.C.; Farag, A.A. On Predicting Aeroacoustic Performance of Ducts with Broadband Noise Source Models. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2005. [Google Scholar] [CrossRef]
- Mohamud, O.M.; Johnson, P. Broadband Noise Source Models as Aeroacoustic Tools in Designing Low NVH HVAC Ducts. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef]
- Ravichandran, A.; Logdesser, A.; Peller, N.; Manhart, M. Experimentelle Und Numerische Untersuchung Des Effekts Der Zuströmbedingungen Auf Die Schallabstrahlung Eines Generischen Ausströmers. In Proceedings of the Fortschritte Der Akustik—DAGA 2022, Stuttgart und Online, 21–24 May 2022; pp. 1250–1253. [Google Scholar]
- Ravichandran, A.; Manhart, M.; Schwertfirm, F.; Peller, N. Wake Flow-Acoustic Resonance in a Generic Air Outlet. In Proceedings of the TSFP12, Osaka, Japan, 19–22 July 2022. [Google Scholar]
- Ewert, R.; Kreuzinger, J. Hydrodynamic/Acoustic Splitting Approach with Flow-Acoustic Feedback for Universal Subsonic Noise Computation. J. Comput. Phys. 2021, 444, 110548. [Google Scholar] [CrossRef]
- Fenini, L. Numerical Modelling Of Flow-Induced Noise Emitted by Control Devices. Ph.D. Thesis, Politecnico Di Milano, Mailand, Italy, 2019. [Google Scholar]
- Bechara, W.; Bailly, C.; Lafon, P.; Candel, S.M. Stochastic Approach to Noise Modeling for Free Turbulent Flows. AIAA J. 1994, 32, 455–463. [Google Scholar] [CrossRef]
- Saarinen, P.; Koskela, H. Flow Noise from an Exhaust Valve - Prediction by Simulations as Compared with Measurements. In Proceedings of the 12th International Conference on Air Distribution in Rooms, Austin, TX, USA, 5–10 June 2011. [Google Scholar]
- Saarinen, P.; Mustakallio, P. Simulation of Flow Noise Generation in a Circular Ceiling Diffuser: A Comparison Between a Silent and a Noisy Design by Using CFD and Lighthill’s Acoustic Analogy. In Proceedings of the ISHVAC 2011, Shanghai, China, 6–9 November 2011. [Google Scholar]
- Ostmann, P.; Krüger, L.; Kremer, M.; Müller, D. Contribution of Geometric Features on the Aeroacoustic Behaviour of a Slot Diffuser. In Proceedings of the 36th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2023), Las Palmas De Gran Canaria, Spain, 25–30 June 2023; pp. 500–511. [Google Scholar] [CrossRef]
- Krüger, L.; Ostmann, P.; Kremer, M.; Müller, D. Numerical Investigation of the Aeroacoustic Properties of a Slot Diffuser. In Proceedings of the RoomVent Conference, Stockholm, Sweden, 22–25 April 2024. [Google Scholar]
- Ostmann, P.; Kremer, M.; Müller, D. Evaluation of the Aeroacoustic Sources of a Swirl Diffusor. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Shiba, Japan, 20–23 August 2023; pp. 127–138. [Google Scholar] [CrossRef]
- Siemens. STAR-CCM+ UserGuide v.18.04.008; Siemens: München, Germany, 2023. [Google Scholar]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A Synthetic-Eddy-Method for Generating Inflow Conditions for Large-Eddy Simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef]
- de Laage Meux, B.; Audebert, B.; Manceau, R.; Perrin, R. Anisotropic Linear Forcing for Synthetic Turbulence Generation in Large Eddy Simulation and Hybrid RANS/LES Modeling. Phys. Fluids 2015, 27. [Google Scholar] [CrossRef]
- Skillen, A.; Revell, A.; Craft, T. Accuracy and Efficiency Improvements in Synthetic Eddy Methods. Int. J. Heat Fluid Flow 2016, 62, 386–394. [Google Scholar] [CrossRef]
- Xie, Z.T.; Castro, I.P. Efficient Generation of Inflow Conditions for Large Eddy Simulation of Street-Scale Flows. Flow Turbul. Combust. 2008, 81, 449–470. [Google Scholar] [CrossRef]
- DIN EN 61672-1; Elektroakustik-Schallpegelmesser-Teil 1: Anforderungen. Deutsches Institut für Normung: Berlin, Germany, 2014.
- Nyquist, H. Certain Topics in Telegraph Transmission Theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Whittaker, J.M. The “Fourier” Theory of the Cardinal Function. Proc. Edinb. Math. Soc. 1928, 1, 169–176. [Google Scholar] [CrossRef]
- Kotelnikov, V.A. On the Transmission Capacity of the “Ether” and Wire in Electrocommunications. In Proceedings of the Material for the First All-Union Conference on Questions of Communication, 1933.
- Stotz, D. Computergestützte Audio- Und Videotechnik: Multimediatechnik in Der Anwendung, 3rd ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Zingg, D.W.; Lomax, H.; Jurgens, H. High-Accuracy Finite-Difference Schemes for Linear Wave Propagation. SIAM J. Sci. Comput. 1996, 17, 328–346. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.W.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. Über Die Partiellen Differenzengleichungen Der Mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Jongen, T. Simulation and Modeling of Turbulent Incompressible Fluid Flows. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 1998. [Google Scholar] [CrossRef]
- Wolfshtein, M. The Velocity and Temperature Distribution in One-Dimensional Flow with Turbulence Augmentation and Pressure Gradient. Int. J. Heat Mass Transf. 1969, 12, 301–318. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Welch, P. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Magnus, G. Versuche Über Die Spannkräfte Des Wasserdampfs. Ann. Phys. 1844, 137, 225–247. [Google Scholar] [CrossRef]
- JCGM. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; BIPM: Sèvres, France, 2008. [Google Scholar]
- Hall, B.D.; Borbely, J.S. MSLNZ/GTC: V1.4.0; Zenodo: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]
- Buchhave, P.; George, W.K.; Lumley, J.L. The Measurement of Turbulence with the Laser-Doppler Anemometer. Annu. Rev. Fluid Mech. 1979, 11, 443–503. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Pope, S.B. Ten Questions Concerning the Large-Eddy Simulation of Turbulent Flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]



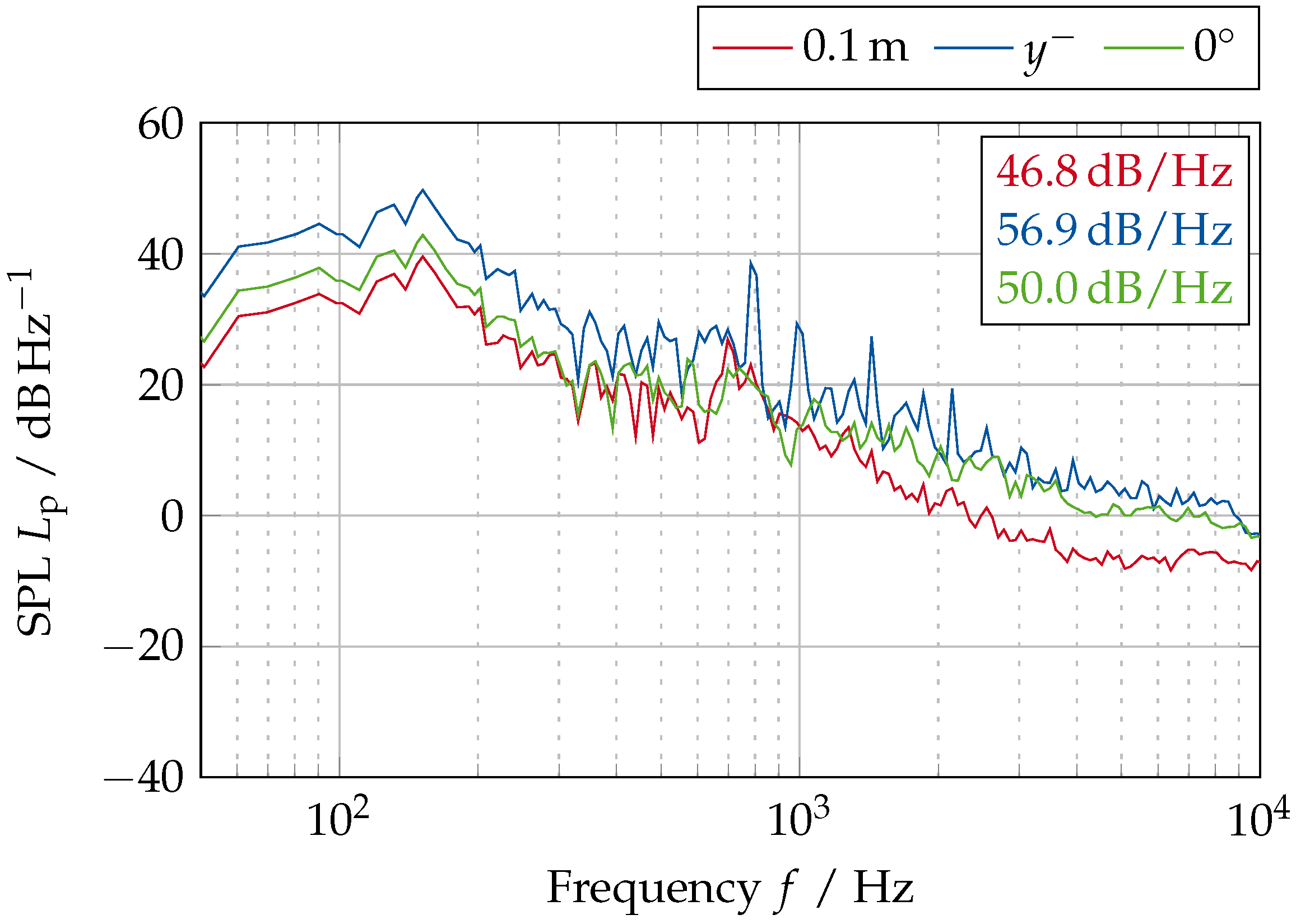
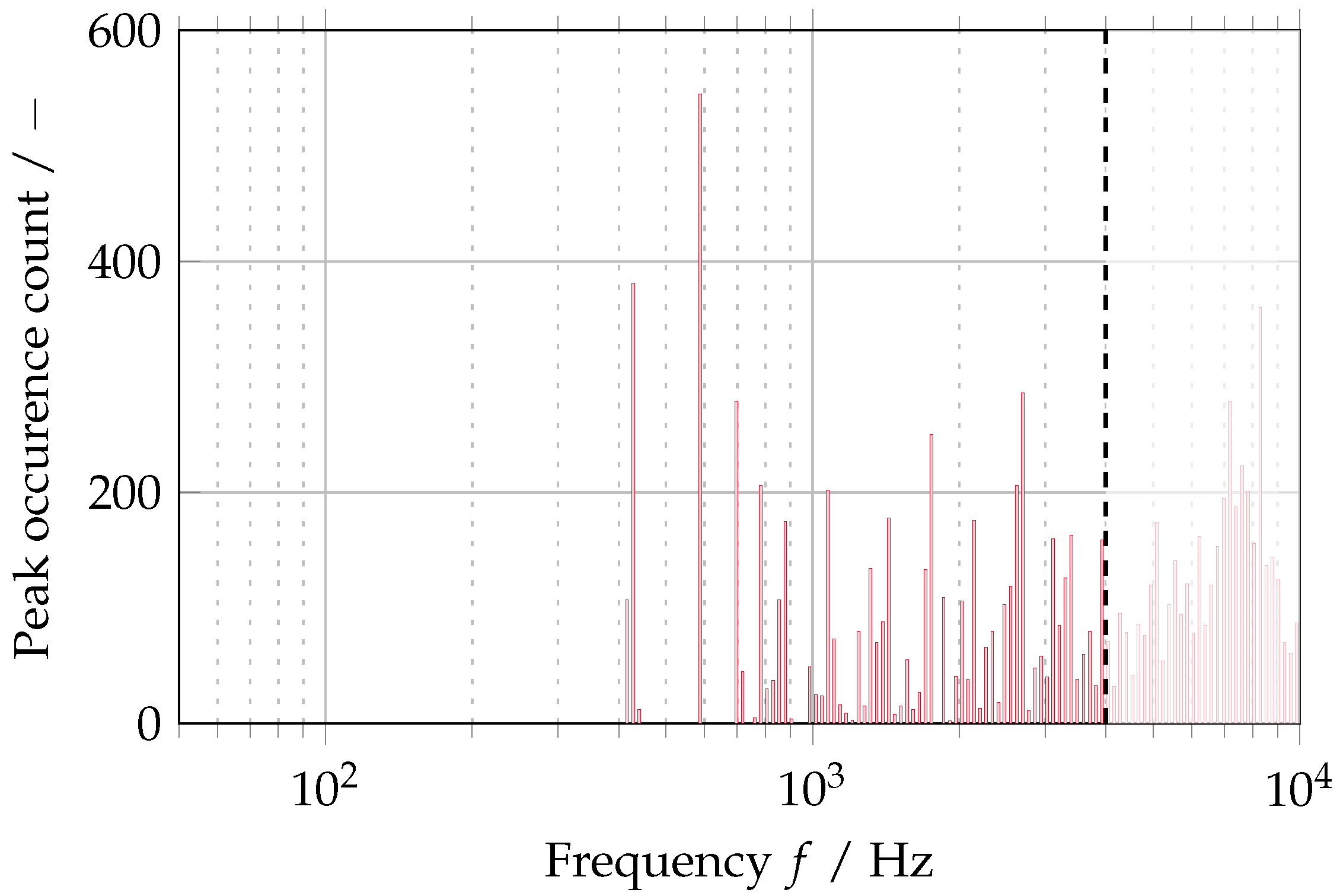

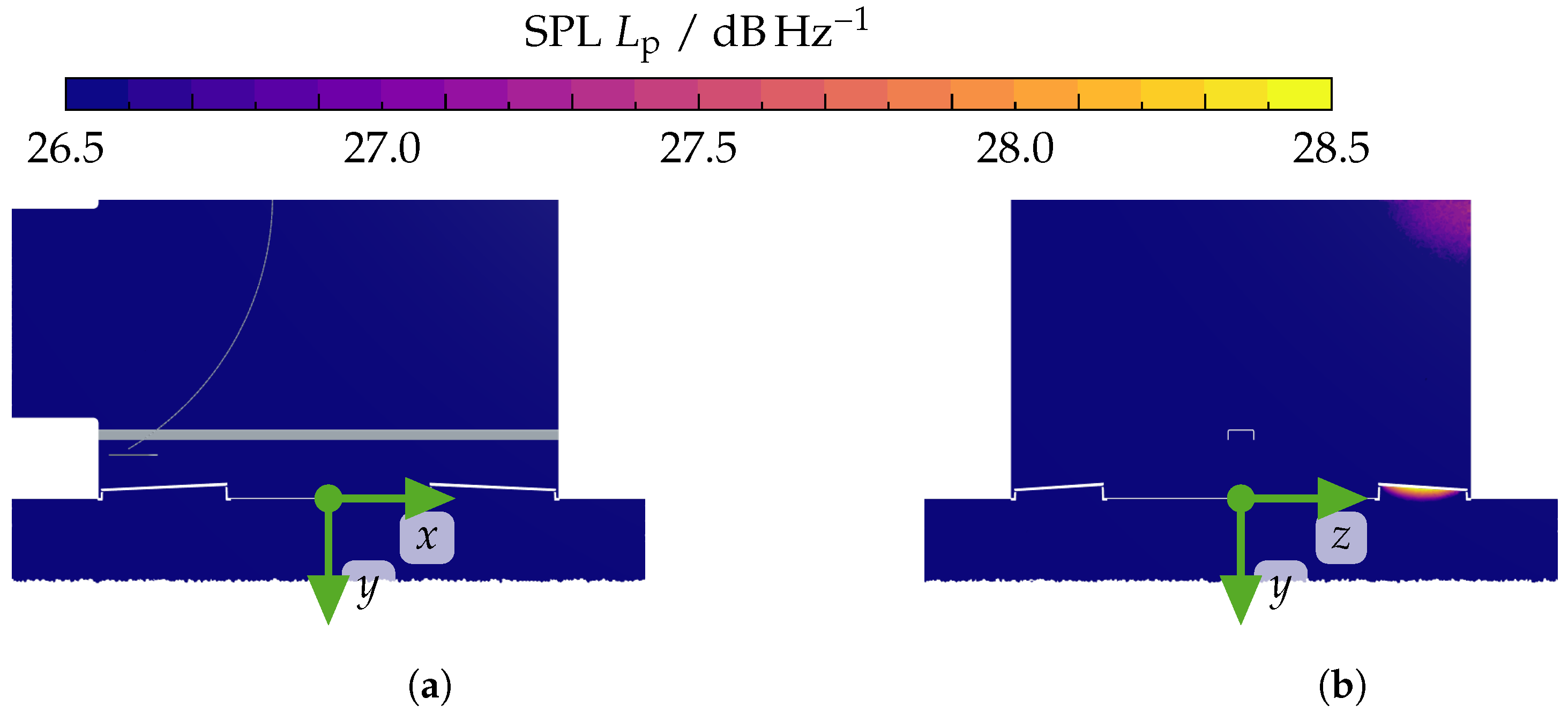
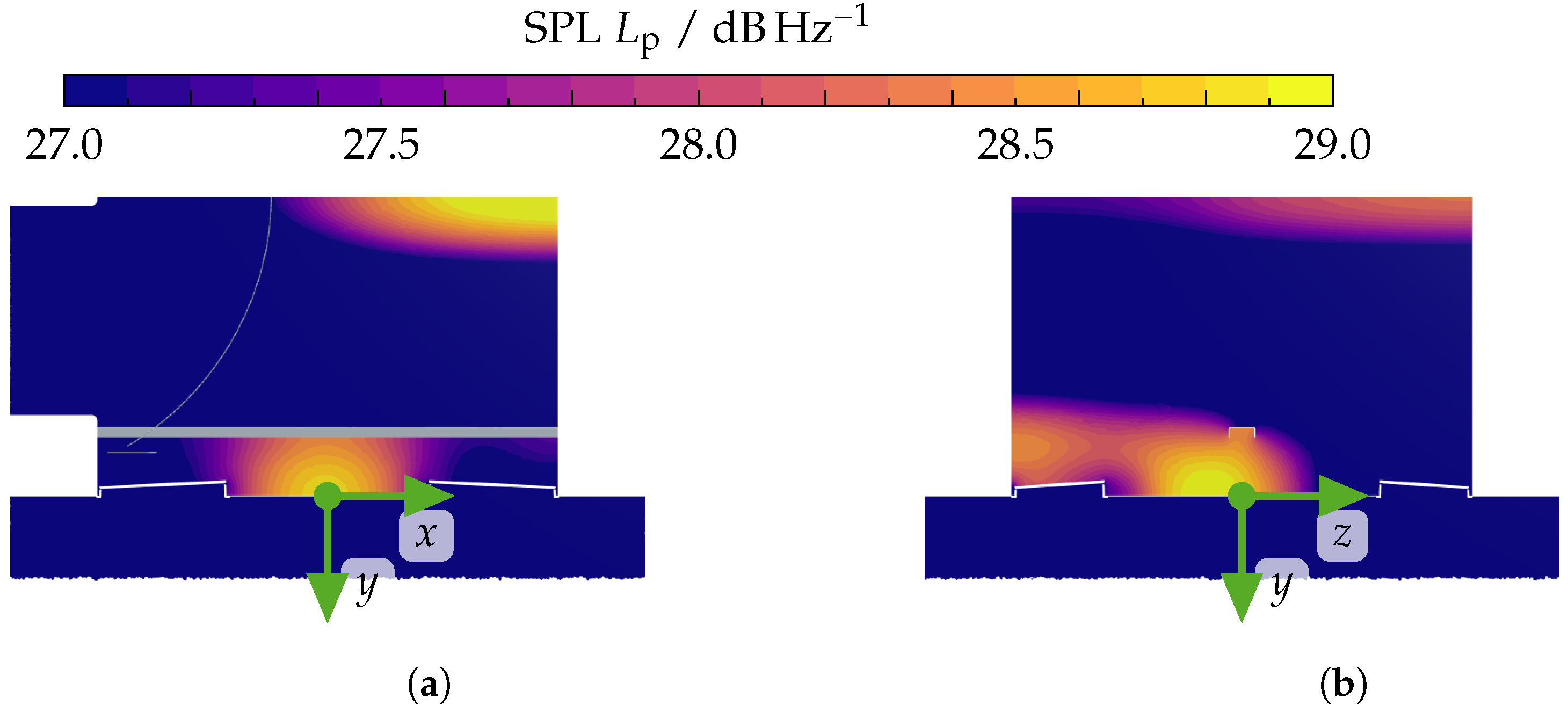
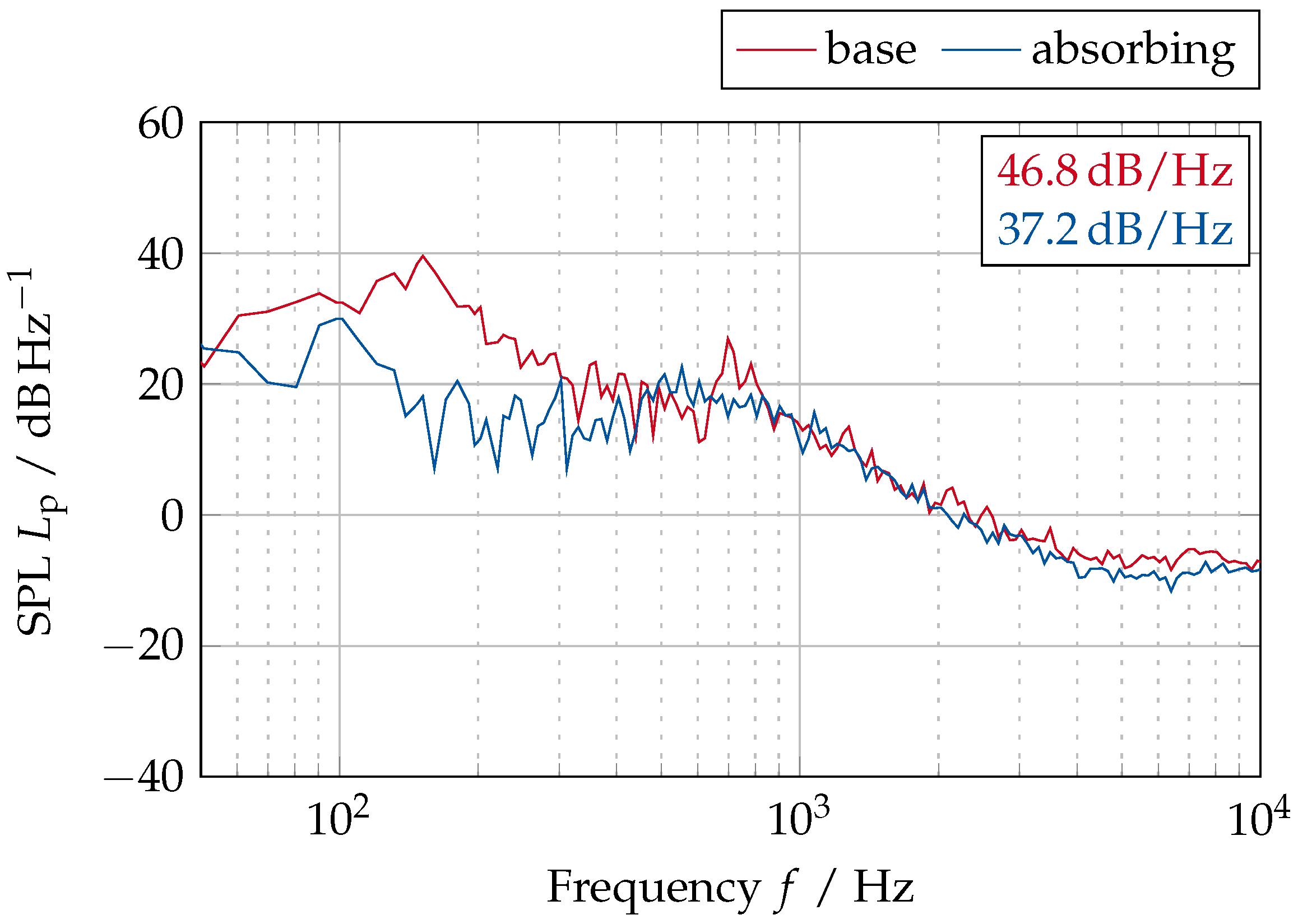

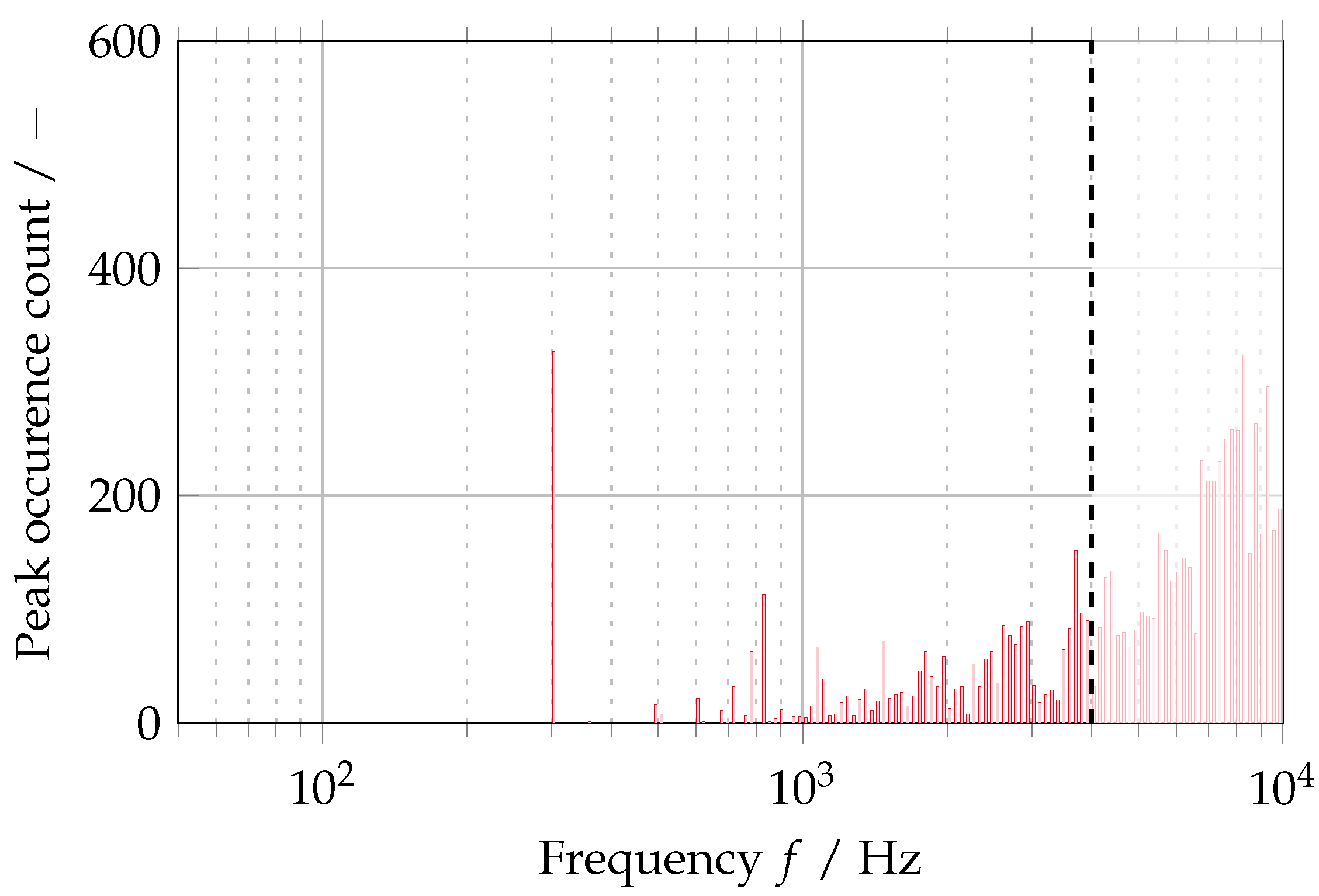
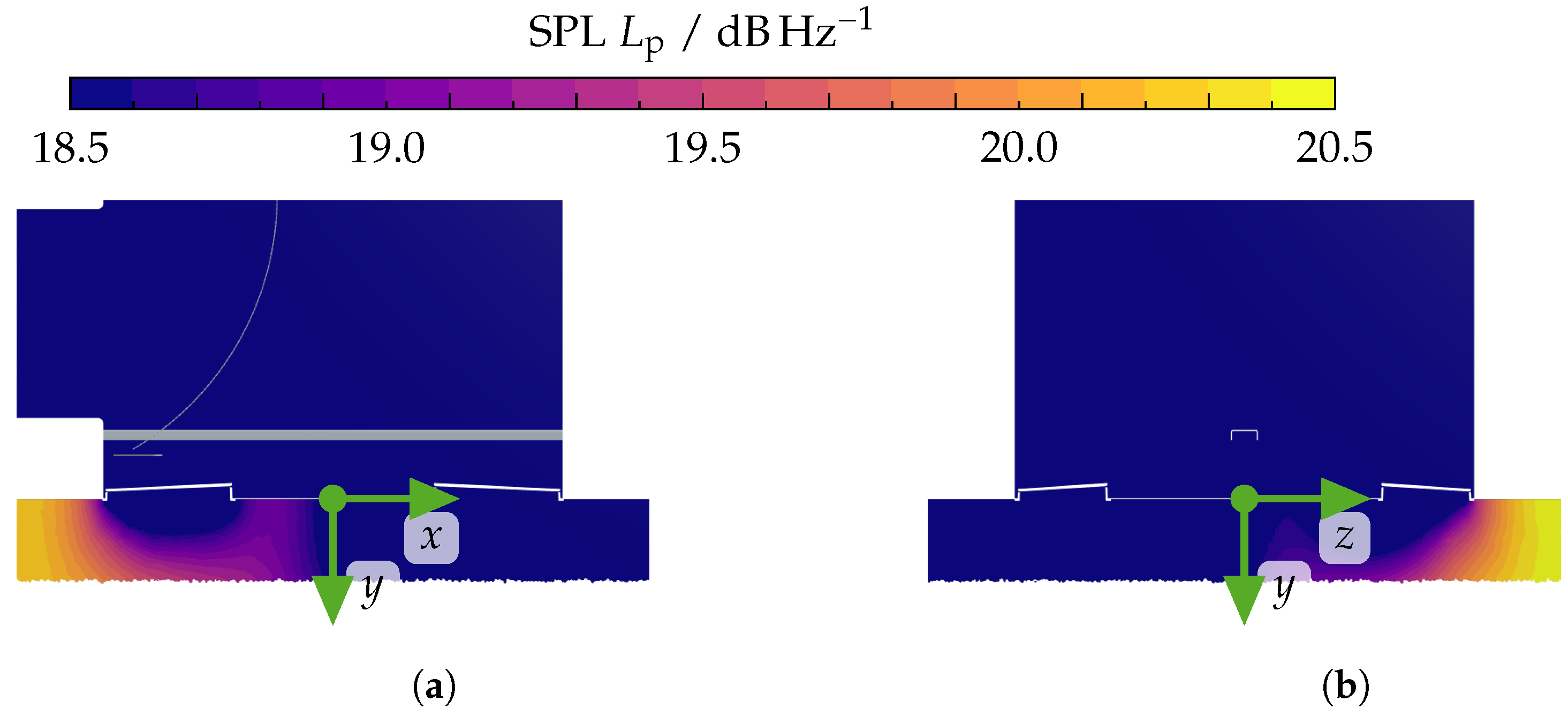


| Property | Value | |
|---|---|---|
| Temperature | Θ | 293.15 K |
| absolute Pressure | 101.325 Pa | |
| Heat Capacity Ratio | 1.402 | |
| Density | 1.204 kg/m3 | |
| Speed of Sound | c | 343.48 m/s |
| Variable | Range | Type | Manufacturer |
|---|---|---|---|
| 0.7–1.2 bar | AMS 4710-1200-B | AMSYS | |
| −40–80°C | DKRF400 | Driesen & Kern | |
| 0–100% | |||
| 0–3500 Pa | SDP2000-L | Sensirion | |
| 0–3500 Pa | SDP2000-L | Sensirion | |
| 0–500 Pa | SDP1000-L | Sensirion |
| Volumeflow | Total-Static Pressure Drop Δpts/Pa | |||
|---|---|---|---|---|
| /m3/h−1 | Data Sheet | Measurement | RANS | LES |
| 320.00 | 15 | 15.1 ± 1.2 | 15.7 | - |
| 470.00 | 32 | 33.2 ± 1.2 | 33.5 | 33.5 ± 0.3 |
| 690.00 | 70 | 73 ± 12 | 71.9 | - |
| Velocity | TKE | Volumeflow | |||||||
|---|---|---|---|---|---|---|---|---|---|
| /−1 | k/−2 | /−1 | |||||||
| Position γ | LDA | LES | Δ | LDA | LES | Δ | LDA | LES | Δ |
| 234° | 5.22 | 5.59 | −6.7% | 1.257 | 0.548 | +129.5% | 14.7 | 15.9 | −7.3% |
| 252° | 5.24 | 5.79 | −9.5% | 0.788 | 0.602 | +31.0% | 21.4 | 23.5 | −8.6% |
| 270° | 5.43 | 6.06 | −10.4% | 0.552 | 0.268 | +106.1% | 16.4 | 17.5 | −6.3% |
| 288° | 5.32 | 6.02 | −11.6% | 0.539 | 0.199 | +170.8% | 22.7 | 24.4 | −7.0% |
| Total | 5.30 | 5.87 | −9.7% | 0.764 | 0.404 | +89.2% | 75.3 | 81.3 | −7.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostmann, P.; Kremer, M.; Müller, D. Identification of the Aeroacoustic Emission Source Regions Within a Ceiling Swirl Diffuser. Acoustics 2025, 7, 9. https://doi.org/10.3390/acoustics7010009
Ostmann P, Kremer M, Müller D. Identification of the Aeroacoustic Emission Source Regions Within a Ceiling Swirl Diffuser. Acoustics. 2025; 7(1):9. https://doi.org/10.3390/acoustics7010009
Chicago/Turabian StyleOstmann, Philipp, Martin Kremer, and Dirk Müller. 2025. "Identification of the Aeroacoustic Emission Source Regions Within a Ceiling Swirl Diffuser" Acoustics 7, no. 1: 9. https://doi.org/10.3390/acoustics7010009
APA StyleOstmann, P., Kremer, M., & Müller, D. (2025). Identification of the Aeroacoustic Emission Source Regions Within a Ceiling Swirl Diffuser. Acoustics, 7(1), 9. https://doi.org/10.3390/acoustics7010009








