A Z-Test-Based Evaluation of a Least Mean Square Filter for Noise Reduction
Abstract
:1. Introduction
2. Method
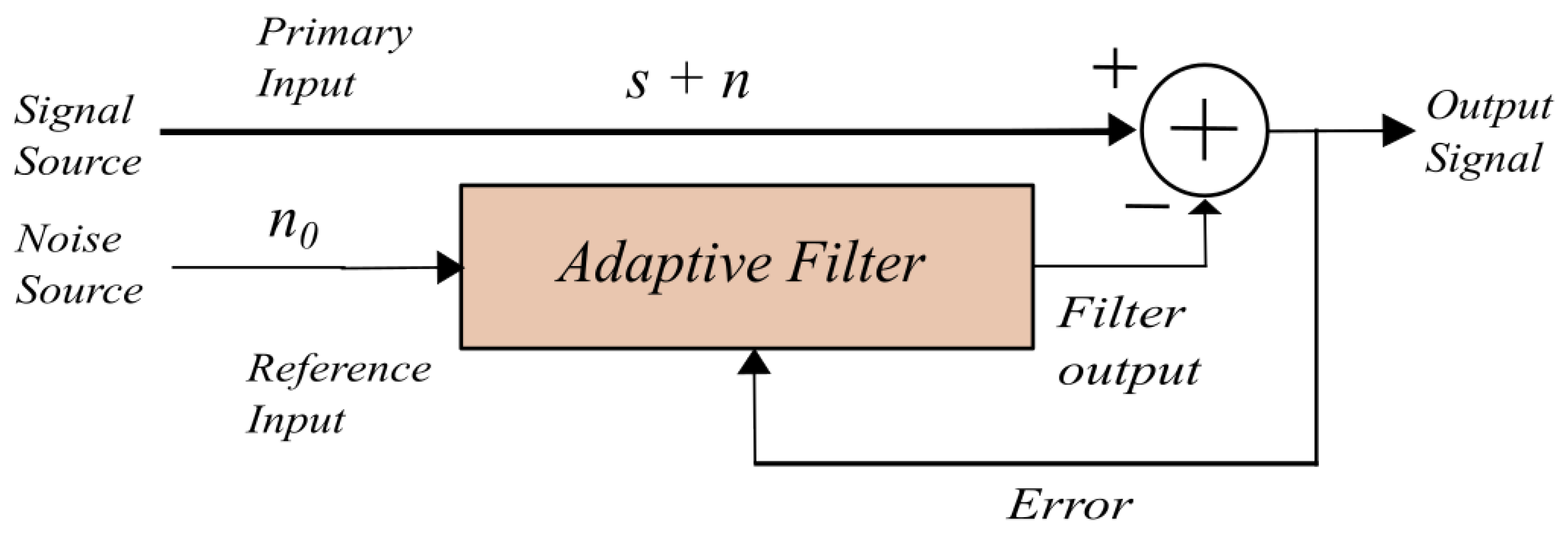
2.1. Least Mean Squares (LMS) Algorithm
- The filter output is calculated as: ;
- Calculate the error signal: ;
- Update filter coefficients and repeat procedure: .
2.2. Signal Processing
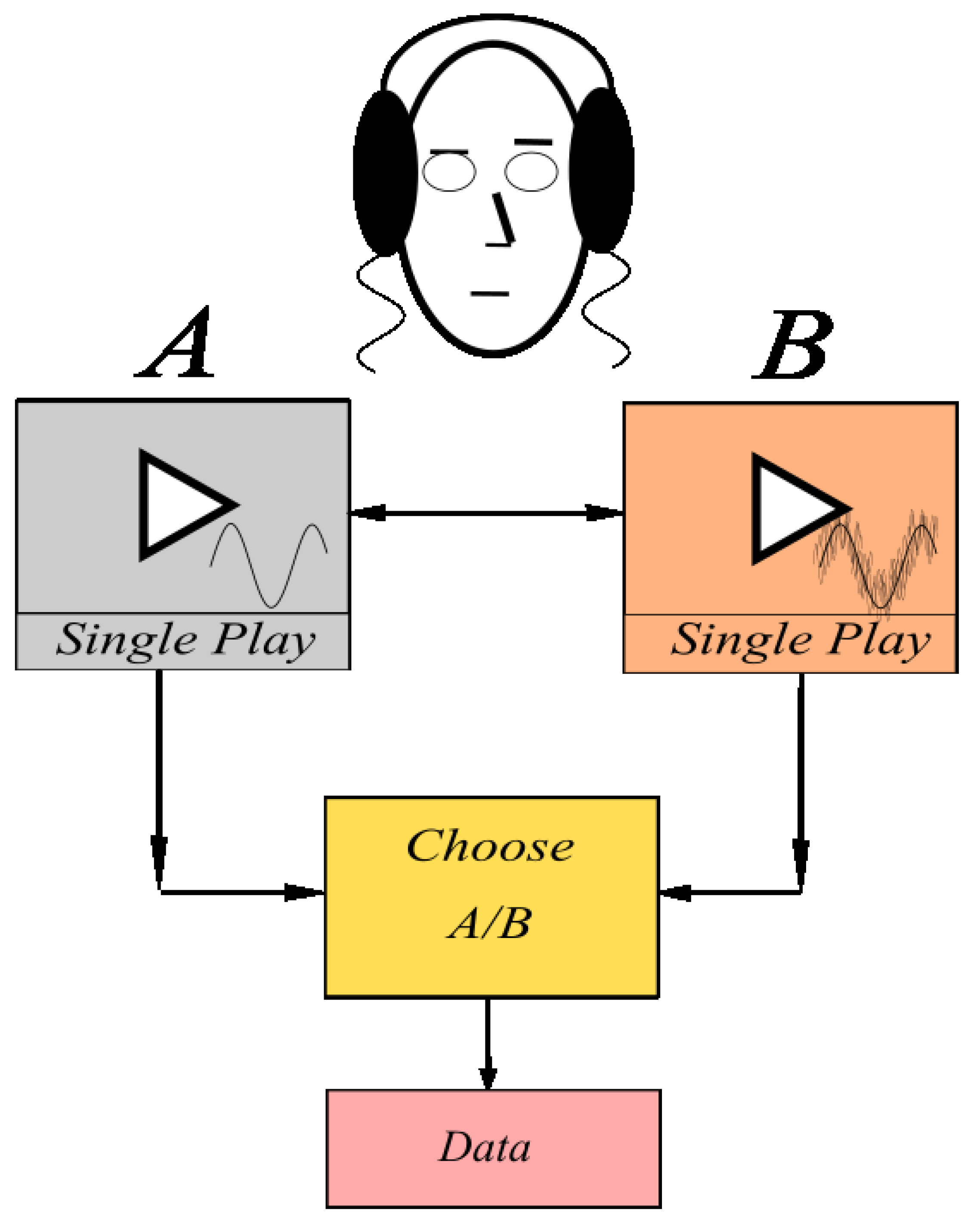
2.3. Blind Test Design
2.4. Data Collection
2.5. Statistical Analysis
- Hypotheses:
2.6. Confidence Interval
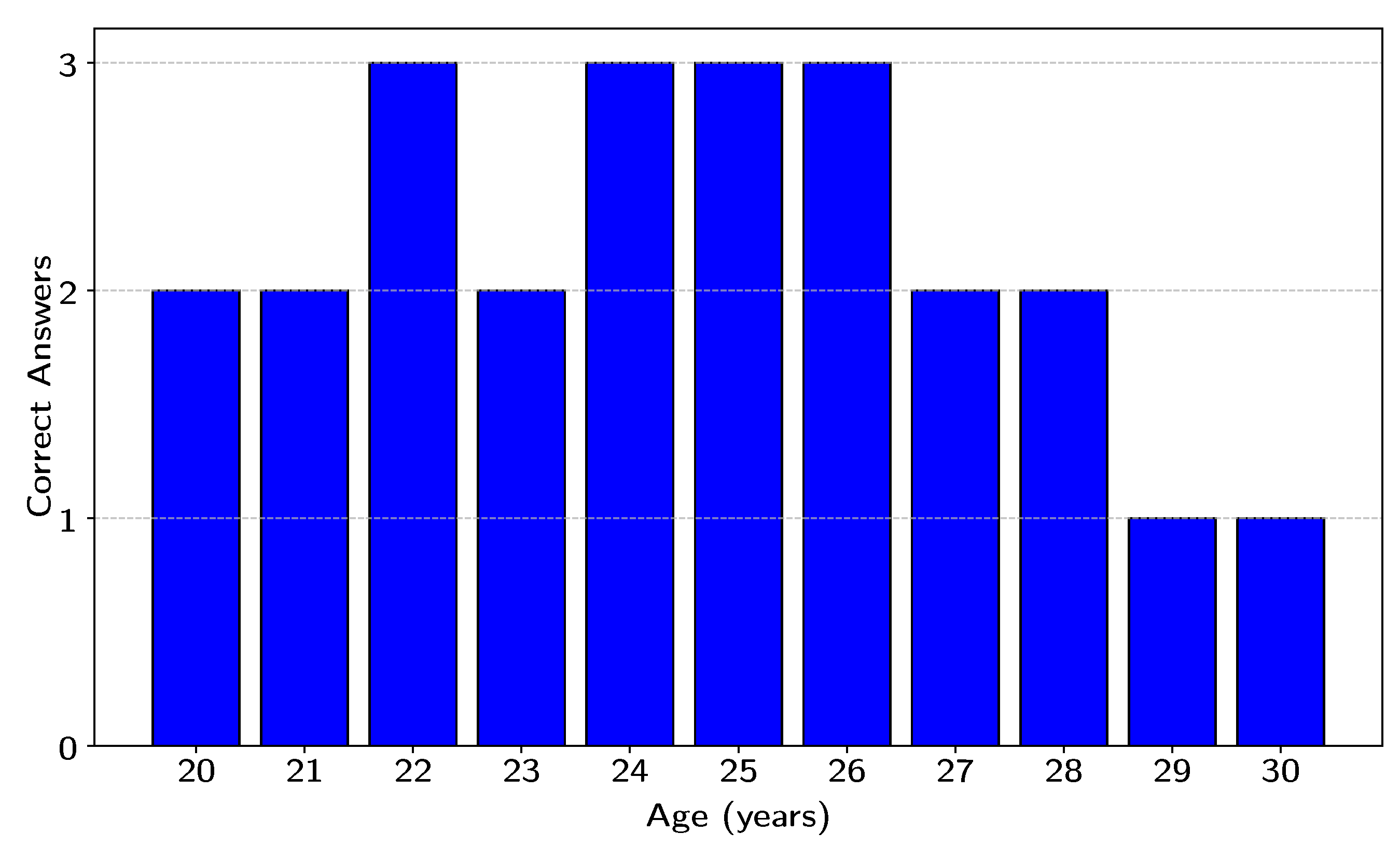
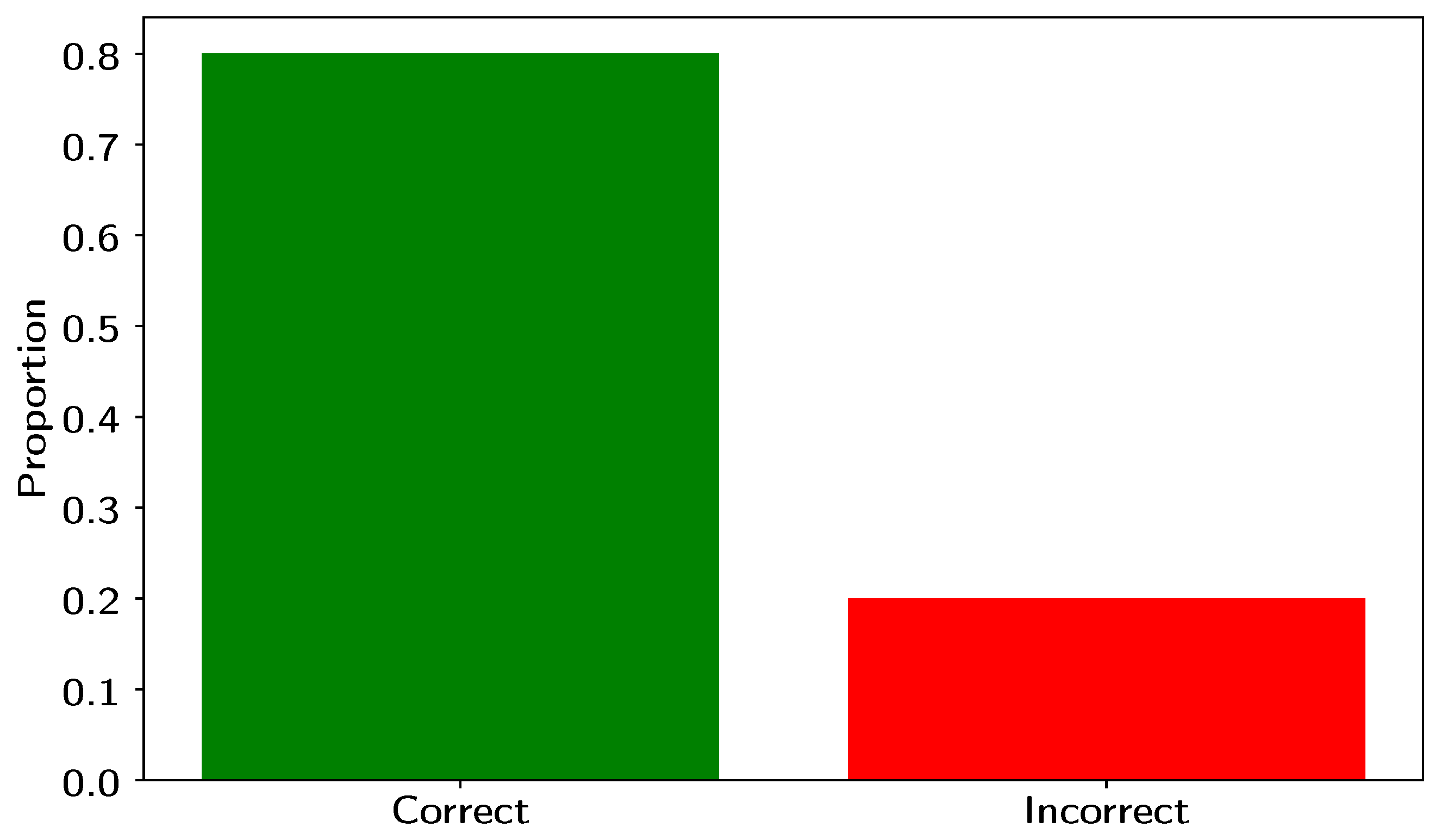
3. Results
3.1. Statistical Analysis and Interpretation
3.2. Test Results
3.3. Statistical Significance
3.4. Confidence Interval
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
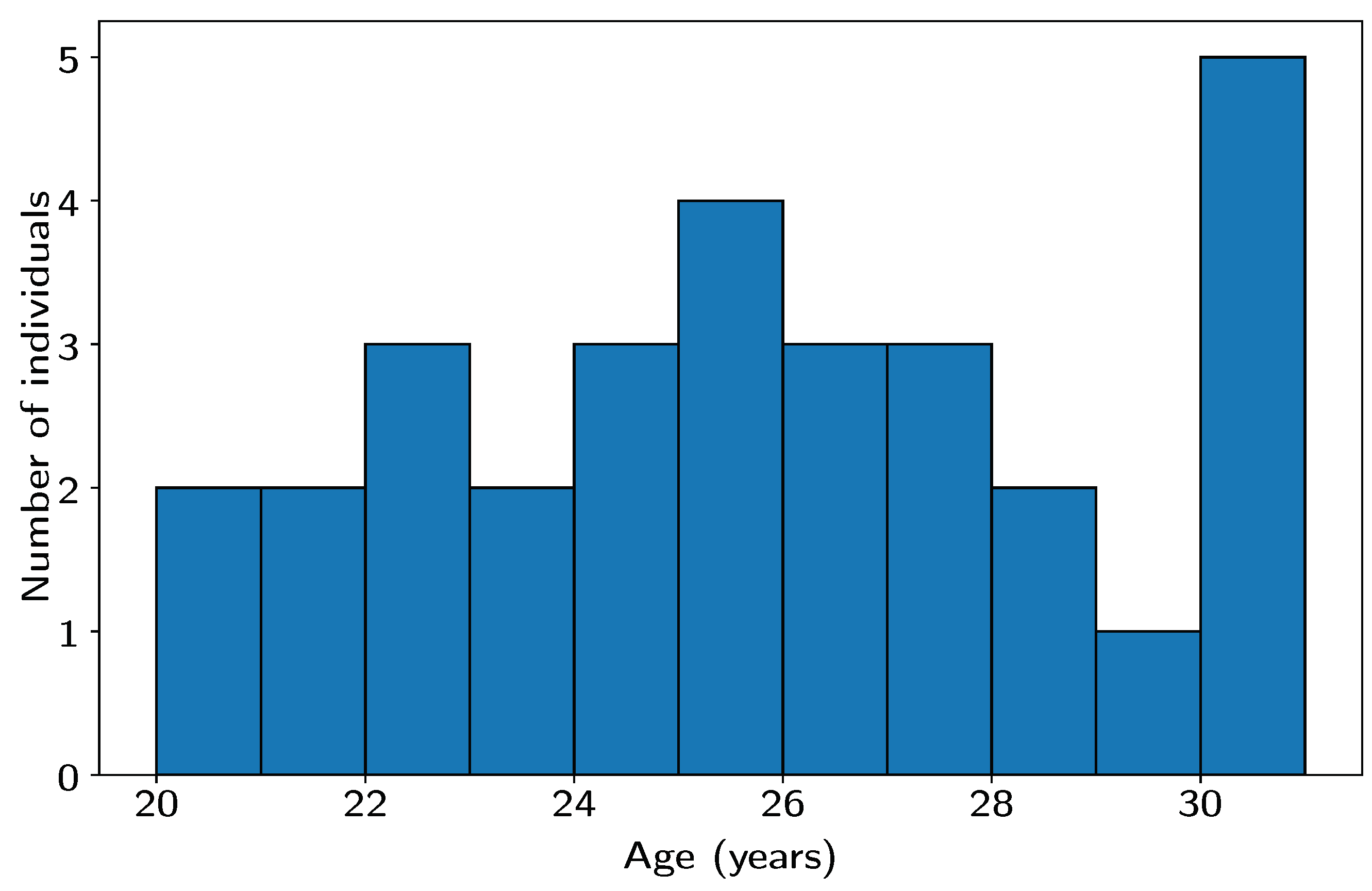
| Subject | Age | A Signal | B Signal | Signal Selected |
|---|---|---|---|---|
| P1 | 20 | Filtered | Corrupted | A |
| P2 | 20 | Filtered | Corrupted | A |
| P3 | 20 | Filtered | Corrupted | A |
| P4 | 21 | Corrupted | Filtered | B |
| P5 | 21 | Filtered | Corrupted | A |
| P6 | 22 | Corrupted | Filtered | B |
| P7 | 22 | Filtered | Corrupted | A |
| P8 | 22 | Corrupted | Filtered | B |
| P9 | 22 | Corrupted | Filtered | B |
| P10 | 24 | Corrupted | Filtered | B |
| P11 | 24 | Filtered | Corrupted | A |
| P12 | 24 | Filtered | Corrupted | A |
| P13 | 25 | Filtered | Corrupted | A |
| P14 | 25 | Filtered | Corrupted | B |
| P15 | 25 | Corrupted | Filtered | B |
| P16 | 25 | Corrupted | Filtered | B |
| P17 | 26 | Corrupted | Filtered | B |
| P18 | 26 | Filtered | Corrupted | A |
| P19 | 26 | Corrupted | Filtered | B |
| P20 | 27 | Filtered | Corrupted | A |
| P21 | 27 | Corrupted | Filtered | A |
| P22 | 28 | Corrupted | Filtered | B |
| P23 | 28 | Filtered | Corrupted | A |
| P24 | 28 | Corrupted | Filtered | B |
| P25 | 29 | Filtered | Corrupted | B |
| P26 | 30 | Corrupted | Filtered | A |
| P27 | 30 | Corrupted | Filtered | A |
| P28 | 30 | Corrupted | Filtered | A |
| P29 | 30 | Filtered | Corrupted | B |
| P30 | 30 | Filtered | Corrupted | B |
Appendix B
Appendix B.1. Mathematical Derivation of the Steepest Descent Method
Appendix B.2. Objective Function to Minimize
Appendix B.3. Gradient of the Function
Appendix B.4. Update Rule
- is the vector of parameters at iteration k;
- is the step size (learning rate), which determines how much the parameters should change at each iteration;
- is the gradient of the function at iteration k.
Appendix B.5. In the Context of the LMS Filter
- is the desired signal at time k;
- is the vector of filter coefficients;
- is the input vector (features or signals) at time k.
Appendix B.6. Summary of the Mathematical Development
- Objective Function: The error function is defined, which we aim to minimize.
- Gradient of the Function: The gradient of the error function is computed, indicating the direction of steepest increase.
- Update Rule: The filter coefficients are updated in the opposite direction of the gradient, applying a step size to control the speed of convergence.
Appendix C
MATLAB Version: 9.13.0 (R2022b), Natick, Massachusetts: The MathWorks Inc.; 2022. Script for LMS and SDM Implmentation
- % Load the audio files[signal1, fs] = audioread(’Corrupted_signal.wav’);[signal2, fs] = audioread(’Filtered_signal.wav’);[signal3, fs] = audioread(’PRUEBA_LMS_L.wav’);% Define the sample interval (for example, from sample 1000 to 2000)start_sample = 132300;end_sample = 308700;
- % Extract the section of the signal that we are interested insignal1_interval = signal1(start_sample:end_sample);signal2_interval = signal2(start_sample:end_sample);signal3_interval = signal3(start_sample:end_sample);% Number of samples in the intervalN1 = length(signal1_interval);N2 = length(signal2_interval);% Perform the FFT of the signal in the intervalY1 = fft(signal1_interval);Y2 = fft(signal2_interval);
- % Calculate the frequency vectorf1 = (0:N1-1)∗(fs/N1); % Frequency in Hzf2 = (0:N2-1)∗(fs/N2);% Get the magnitude of the FFT (only the positive half of the spectrum)magnitude1 = abs(Y1(1:N1/2+1));magnitude2 = abs(Y2(1:N2/2+1));f1 = f1(1:N1/2+1);f2 = f2(1:N1/2+1);
- % Calculate the signal and noise powersignal_power_before = rms(signal3_interval)^2;noise_power_before = rms(signal1_interval − signal3_interval)^2;
- signal_power_after = rms(signal2_interval)^2;noise_power_after = rms(signal2_interval − signal3_interval)^2;
- % Calculate the SNR before and after filtering (in dB)SNR_before = 10 ∗ log10(signal_power_before/noise_power_before);SNR_after = 10 ∗ log10(signal_power_after/noise_power_after);
- % Display the resultsfprintf(’SNR before processing: %.2f dB\n’, SNR_before);fprintf(’SNR after processing: %.2f dB\n’, SNR_after);fprintf(’The SNR improvement is: %.2f dB\n’, SNR_after - SNR_before);
- % Load the audio signal% Make sure to have the audio file[signal, Fs] = audioread(’PRUEBA_LMS_L.wav’);signal = signal(:,1); % If it is stereo, select one of the~channels
- % Generate white noiseSNR_dB = 40; % Signal-to-noise ratio in decibelsnoise = randn(length(signal), 1); % White noisesignal_power = var(signal); % Power of the original signalnoise_power = var(noise); % Power of the~noise
- % Calculate the necessary noise for the signal-to-noise ratio (SNR)adjusted_noise_power = signal_power/(10^(SNR_dB/10));noise = noise ∗ sqrt(adjusted_noise_power/noise_power);
- % Signal with noise (add the original signal and the noise)signal_with_noise = signal + noise;
- % LMS filter parametersN = 30; % Number of filter coefficientsmu = 0.01; % Adaptation rate (LMS algorithm step)M = length(signal_with_noise); % Length of the signal with noisex = zeros(N, 1); % Initialize the filter coefficientsy = zeros(M, 1); % Filtered signale = zeros(M, 1); % Error
- % LMS adaptive filterfor n = N:M% Filter input: vector of the last N samples of the signal with noisex_vec = signal_with_noise(n:-1:n-N+1);
- % Filter output (prediction)y(n) = x’ ∗ x_vec;
- % Error (desired signal − filtered output)e(n) = signal(n) − y(n);
- % Update the LMS filter coefficientsx = x + mu ∗ e(n) ∗ x_vec;end
- % Convert the signals
- audiowrite(’Corrupted_signal.wav’, signal_with_noise, Fs);% Filtered signalaudiowrite(’Filtered_signal.wav’, y, Fs);
References
- Agnew, J. Audible circuit noise in hearing aid amplifiers. J. Acoust. Soc. Am. 1997, 102, 2793–2799. [Google Scholar] [CrossRef] [PubMed]
- Keizer, G. The Unwanted Sound of Everything We Want: A book About Noise; PublicAffairs: New York, NY, USA, 2010. [Google Scholar]
- Kim, S.; Arzac, S.; Dokic, N.; Donnelly, J.; Genser, N.; Nortwich, K.; Rooney, A. Cortical and Subjective Measures of Individual Noise Tolerance Predict Hearing Outcomes with Varying Noise Reduction Strength. Appl. Sci. 2024, 14, 6892. [Google Scholar] [CrossRef]
- Ding, T.; Yan, A.; Liu, K. What is noise-induced hearing loss? Br. J. Hosp. Med. 2019, 80, 525–529. [Google Scholar] [CrossRef]
- Mueller, B.J.; Liebl, A.; Herget, N.; Kohler, D.; Leistner, P. Using active noise-cancelling headphones in open-plan offices: No influence on cognitive performance but improvement of perceived privacy and acoustic environment. Front. Built Environ. 2022, 8, 962462. [Google Scholar] [CrossRef]
- Alvarsson, J.J.; Wiens, S.; Nilsson, M.E. Stress recovery during exposure to nature sound and environmental noise. Int. J. Environ. Res. Public Health 2010, 7, 1036–1046. [Google Scholar] [CrossRef]
- Münzel, T.; Sørensen, M.; Schmidt, F.; Schmidt, E.; Steven, S.; Kröller-Schön, S.; Daiber, A. The adverse effects of environmental noise exposure on oxidative stress and cardiovascular risk. Antioxid. Redox Signal. 2018, 28, 873–908. [Google Scholar] [CrossRef] [PubMed]
- Frühholz, S.; Belin, P. The Science of Voice Perception; Oxford University Press: Oxford, UK, 2018; Volume 1. [Google Scholar]
- Wang, X.; Xu, L. Speech perception in noise: Masking and unmasking. J. Otol. 2021, 16, 109–119. [Google Scholar] [CrossRef] [PubMed]
- Masullo, M.; Yamauchi, K.; Dan, M.; Cioffi, F.; Maffei, L. Influence of Infotainment-System Audio Cues on the Sound Quality Perception Onboard Electric Vehicles in the Presence of Air-Conditioning Noise. Acoustics 2024, 7, 1. [Google Scholar] [CrossRef]
- Ballou, G. Handbook for Sound Engineers; Taylor & Francis: Abingdon, UK, 2013. [Google Scholar]
- Cheng, H.L.; Han, J.Y.; Chu, Y.C.; Cheng, Y.F.; Lin, C.M.; Chiang, M.C.; Wu, S.L.; Lai, Y.H.; Liao, W.H. Evaluating the hearing screening effectiveness of active noise cancellation technology among young adults: A pilot study. J. Chin. Med Assoc. 2023, 86, 105–112. [Google Scholar] [CrossRef]
- Zacharov, N.; Ramsgaard, J.; Le Ray, G.; Jørgensen, C.V. The multidimensional characterization of active noise cancelation headphone perception. In Proceedings of the 2010 Second International Workshop on Quality of Multimedia Experience (QoMEX), Trondheim, Norway, 21–23 June 2010; pp. 130–135. [Google Scholar]
- Jurado, C.; Gallegos, P.; Gordillo, D.; Moore, B.C. The detailed shapes of equal-loudness-level contours at low frequencies. J. Acoust. Soc. Am. 2017, 142, 3821–3832. [Google Scholar] [CrossRef]
- Rasetshwane, D.M.; Trevino, A.C.; Gombert, J.N.; Liebig-Trehearn, L.; Kopun, J.G.; Jesteadt, W.; Neely, S.T.; Gorga, M.P. Categorical loudness scaling and equal-loudness contours in listeners with normal hearing and hearing loss. J. Acoust. Soc. Am. 2015, 137, 1899–1913. [Google Scholar] [CrossRef] [PubMed]
- Glasberg, B.R.; Moore, B.C. Prediction of absolute thresholds and equal-loudness contours using a modified loudness model. J. Acoust. Soc. Am. 2006, 120, 585–588. [Google Scholar] [CrossRef]
- Motlagh Zadeh, L.; Silbert, N.H.; Sternasty, K.; Swanepoel, D.W.; Hunter, L.L.; Moore, D.R. Extended high-frequency hearing enhances speech perception in noise. Proc. Natl. Acad. Sci. USA 2019, 116, 23753–23759. [Google Scholar] [CrossRef]
- Kreiman, J.; Gerratt, B.R. Perceptual interaction of the harmonic source and noise in voice. J. Acoust. Soc. Am. 2012, 131, 492–500. [Google Scholar] [CrossRef]
- Titze, I.R.; Palaparthi, A. Vocal loudness variation with spectral slope. J. Speech, Lang. Hear. Res. 2020, 63, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Tait, B.L. Applied Fletcher-Munson curve algorithm for improved voice recognition. Int. J. Electron. Secur. Digit. Forensics 7 2012, 4, 178–186. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Y.; Hero, A.O. Regularized least-mean-square algorithms. arXiv 2010, arXiv:1012.5066. [Google Scholar]
- McKenzie, T.; Armstrong, C.; Ward, L.; Murphy, D.T.; Kearney, G. Predicting the colouration between binaural signals. Appl. Sci. 2022, 12, 2441. [Google Scholar] [CrossRef]
- Ang, L.Y.L.; Koh, Y.K.; Lee, H.P. The performance of active noise-canceling headphones in different noise environments. Appl. Acoust. 2017, 122, 16–22. [Google Scholar] [CrossRef]
- Hayes, M.H. Statistical Digital Signal Processing and Modeling; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Lee, J.H.; Ooi, L.E.; Ko, Y.H.; Teoh, C.Y. Simulation for noise cancellation using LMS adaptive filter. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Busan, Republic of Korea, 25–27 August 2017; IOP Publishing: Bristol, UK, 2017; Volume 211, p. 012003. [Google Scholar]
- Ferdouse, L.; Akhter, N.; Nipa, T.H.; Jaigirdar, F.T. Simulation and performance analysis of adaptive filtering algorithms in noise cancellation. arXiv 2011, arXiv:1104.1962. [Google Scholar]
- He, Y.; He, H.; Li, L.; Wu, Y.; Pan, H. The applications and simulation of adaptive filter in noise canceling. In Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Wuhan, China, 12–14 December 2008; Volume 4, pp. 1–4. [Google Scholar]
- Foley, J.; Boland, F. Comparison between steepest descent and LMS algorithms in adaptive filters. In IEE Proceedings F (Communications, Radar and Signal Processing); IET: London, UK, 1987; Volume 134, pp. 283–289. [Google Scholar]
- Martag, V.L. ; Rosa, A C. Bioestadística; Editorial El Manual Moderno: Mexico City, Mexico, 2014. [Google Scholar]
- Yoshizawa, T.; Hirobayashi, S.; Misawa, T. Noise reduction for periodic signals using high-resolution frequency analysis. EURASIP J. Audio Speech Music Process. 2011, 2011, 5. [Google Scholar] [CrossRef]
- Suzuki, Y.; Takeshima, H.; Kurakata, K. Revision of ISO 226 “Normal Equal-Loudness-Level Contours” from 2003 to 2023 edition: The background and results. Acoust. Sci. Technol. 2024, 45, 1–8. [Google Scholar] [CrossRef]
- Stevens, S. Calculation of the loudness of complex noise. J. Acoust. Soc. Am. 1956, 28, 807–832. [Google Scholar] [CrossRef]
- Narayan, S.S.; Peterson, A. Frequency domain least-mean-square algorithm. Proc. IEEE 1981, 69, 124–126. [Google Scholar] [CrossRef]
- Rao, H.I.; Farhang-Boroujeny, B. Fast LMS/Newton algorithms for stereophonic acoustic echo cancelation. IEEE Trans. Signal Process. 2009, 57, 2919–2930. [Google Scholar] [CrossRef]
- Carlile, S.; Hyams, S.; Delaney, S. Systematic distortions of auditory space perception following prolonged exposure to broadband noise. J. Acoust. Soc. Am. 2001, 110, 416–424. [Google Scholar] [CrossRef]
- Srivastava, D.; Narayanan, V.; Singh, B.; Verma, A. A Novel Steepest Descent Least Mean Square Control for Smooth Mode Transfer of a Single-Stage SPVA-BES Hybrid Microgrid. IEEE Trans. Ind. Appl. 2024, 60, 7250–7263. [Google Scholar] [CrossRef]
- Schäffer, B.; Pieren, R.; Schlittmeier, S.J.; Brink, M. Effects of different spectral shapes and amplitude modulation of broadband noise on annoyance reactions in a controlled listening experiment. Int. J. Environ. Res. Public Health 2018, 15, 1029. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bojorjes, A.R.; Garcia-Barrientos, A.; Cárdenas-Juárez, M.; Pineda-Rico, U.; Arce, A.; Velasquez, S.M.; Cortés, O.P. A Z-Test-Based Evaluation of a Least Mean Square Filter for Noise Reduction. Acoustics 2025, 7, 20. https://doi.org/10.3390/acoustics7020020
Bojorjes AR, Garcia-Barrientos A, Cárdenas-Juárez M, Pineda-Rico U, Arce A, Velasquez SM, Cortés OP. A Z-Test-Based Evaluation of a Least Mean Square Filter for Noise Reduction. Acoustics. 2025; 7(2):20. https://doi.org/10.3390/acoustics7020020
Chicago/Turabian StyleBojorjes, Alan Rodríguez, Abel Garcia-Barrientos, Marco Cárdenas-Juárez, Ulises Pineda-Rico, Armando Arce, Sharon Macias Velasquez, and Obed Pérez Cortés. 2025. "A Z-Test-Based Evaluation of a Least Mean Square Filter for Noise Reduction" Acoustics 7, no. 2: 20. https://doi.org/10.3390/acoustics7020020
APA StyleBojorjes, A. R., Garcia-Barrientos, A., Cárdenas-Juárez, M., Pineda-Rico, U., Arce, A., Velasquez, S. M., & Cortés, O. P. (2025). A Z-Test-Based Evaluation of a Least Mean Square Filter for Noise Reduction. Acoustics, 7(2), 20. https://doi.org/10.3390/acoustics7020020







