Next Article in Journal
Internet of Spacecraft for Multi-Planetary Defense and Prosperity
Next Article in Special Issue
Saliency-Guided Local Full-Reference Image Quality Assessment
Previous Article in Journal
Manual 3D Control of an Assistive Robotic Manipulator Using Alpha Rhythms and an Auditory Menu: A Proof-of-Concept
Previous Article in Special Issue
A Survey on MIMO-OFDM Systems: Review of Recent Trends
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Signals
Volume 3
Issue 2
10.3390/signals3020025
signals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Perspective on Information Optimality in a Neural Circuit and Other Biological Systems

by
Robert Friedman
†
Department of Biological Sciences, University of South Carolina, Columbia, SC 29208, USA
†
Retired.
Signals 2022, 3(2), 410-427; https://doi.org/10.3390/signals3020025
Submission received: 24 April 2022 / Revised: 12 May 2022 / Accepted: 13 June 2022 / Published: 20 June 2022
(This article belongs to the Special Issue The 2022 7th International Conference on Intelligent Information Processing)
Browse Figures
Versions Notes

Abstract

:
The nematode worm Caenorhabditis elegans has a relatively simple neural system for analysis of information transmission from sensory organ to muscle fiber. Consequently, this study includes an example of a neural circuit from the nematode worm, and a procedure is shown for measuring its information optimality by use of a logic gate model. This approach is useful where the assumptions are applicable for a neural circuit, and also for choosing between competing mathematical hypotheses that explain the function of a neural circuit. In this latter case, the logic gate model can estimate computational complexity and distinguish which of the mathematical models require fewer computations. In addition, the concept of information optimality is generalized to other biological systems, along with an extended discussion of its role in genetic-based pathways of organisms.

1. Introduction

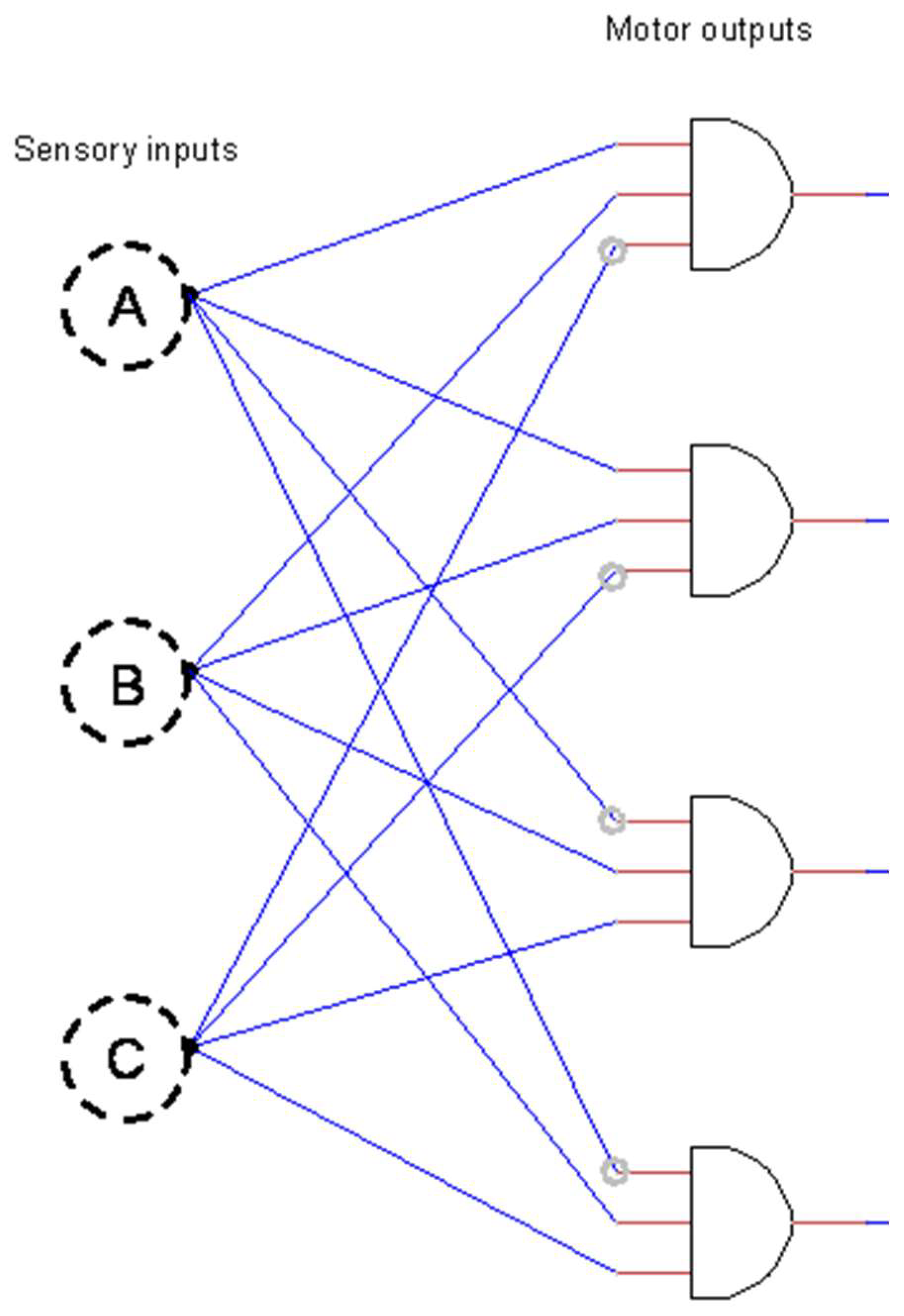
1.1. The Logic Gate Model

McCulloch and Pitts introduced the concept of a logic gate model for explaining the processing of information in an animal neuronal system, based on the concept that a neuron is in a resting or active state, and the synaptic connections exhibit specific non-dynamic behaviors [1]. The logic gate design is an efficient model of Boolean algebraic operations, including the basic operators AND, OR, and NOT (Figure 1) [2,3,4,5,6]. However, others consider the biological design of a neuronal network inconsistent with the assumptions of this model [7,8,9,10,11,12,13,14,15,16,17]. Even though the logic gate model is not expected to predict the behavior of a neuron at the cellular level, it does offer a measurement of expected computational efficiency for a neural network. Given knowledge of a neural system and its layer of nodes of inputs, its layer of nodes of outputs, and an assumption that a neuron is at a resting or active state, it is possible to estimate the optimal number of logic gates to model information optimality, and potentially the behavior of the system. This metric of optimality is also applicable for making comparisons between neural circuits, and potentially as a source of intuition on network structure and function. The assumption where a neuron as active or at rest can be represented by the binary values one and zero.
One problem with modeling neuronal communication is the availability of reliable data on the activity of a neural system. This activity is dependent on external effects, such as the environment, the interactions between the organism and the environment, and its nonlinear dynamics at the spatial and temporal scales. The complexity of the system is expected to grow exponentially with variation in the environmental conditions, and likewise with organism complexity, such as in the physiological states. This phenomenon is observed in the sociality of ants [18].
Evolution can lead to adaptation for efficient communication in a neural system. One kind of adaptation is modularity, which can enhance the efficiency of information processing, such as that observed in the social behavior of honeybees [19]. Another strategy is where multiple functions are handled by neurons in neural circuits, otherwise separate neural circuits would be required for changes in the surrounding environment. This is a confounding factor for disentangling the workings of a neural circuit. However, in the case of a simple example, along with a controlled environment, then it should be possible to gain insight on information processing by mapping a neural circuit to a simple model [20], and therefore avoid the effects of the increasingly complex dynamics that often occur in Nature.

1.2. Efficiency of Mathematical Operations

It is also possible to consider the efficiency of multiplication and division operations in the context of Boolean algebra and logic gates. Hypotheses and models of fly motion detection involve the use of these operations.
Borst and Helmstaedter [21] had reviewed prior work on visual motion detection in the fly. In their review of potential models of motion detection, they discussed a model’s dependence on sampling the luminance values at two or more points across a visual space. One mathematical model includes a calculation of velocity, along with a division operation. Another model relies on a computation with a correlation between two spatially separated luminance values. They further discuss that the correlation-based model is the preferred one because it fits better with current knowledge about the information processing in the fly visual system.
Theory and empirical studies led to a later study, and in support of the latter model, otherwise referred to as a “delay-and-compare model” of fly motion detection, where Groschner and others [22] showed evidence of a “multiplication-like nonlinearity” in a single neuron of this system, a prediction expected by prior theory on information flow [22,23]. This process was also shown to be dependent on a biological mechanism involving “pairs of shunting inhibitory and excitatory synapses” [22,23]. This merging of theory with biological evidence has the potential for producing biologically realistic models of neural circuits, with an expectation of applicability to animals in general, given an evolutionary convergence at the level of the neural circuit, and similarity in the molecular mechanisms of neuronal communication [21,22].
Even though biologically realistic models are preferred in neurobiology, it is still possible to idealize information flow in making predictions on optimality in a neural system, as pursued in this study. If theory predicts a high complexity in the computation of information, regardless of the type of system, then physical limitations will constrain the rate of computation. Therefore, this study includes simple examples using Boolean models for modeling information optimality, including in the case of multiplication and division, operations not native to Boolean algebra.

1.3. Optimality of a Neuronal System

This question of optimality in a neural system has been examined at the level of structure and function in a neural network [13,24,25,26,27,28]. In the case of the nematode worm Caenorhabditis elegans, one type of optimization is observed in the neuronal wiring length and minimization of the overall path length for efficient information communication [25].
Furthermore, it is expected that the neural system is optimized for its roles across the development of an animal. In support of this hypothesis is that evolutionary adaptation typically leads to a reasonably optimal design in the case of anatomical and physiological features. A similar argument is from the role of natural selection that tends to disfavor individuals with inefficient use of energy, such as in evolving a large brain size, along with its higher energy requirements, in the case where it offers no benefit over a smaller ancestral form. This example shows costly energy use and would result in individuals weakening their chances of survival during the “struggle for existence” against conspecifics.
Other structural properties of the C. elegans neural network have been described, such as an observation of a small-world architecture [10,29,30], sparsity of neuronal connectiveness [16], and commonly observed motifs [8,31]. The neural network may also be described at the informational level.
A simpler neural system, or neural circuit, is more tractable for measuring information flow efficiency. Past studies have observed the coding of animal behavior in these neural circuits of the nervous system [9,12,14,25,32,33,34,35]. It is also of interest to relate these systems with the informational processes [10,36]. The concept of information flow, efficiency, and the presence of neural circuits suggest an applicability of information flow theory, and use of a logic gate model for estimating the rate of information flow in a system [8,37]. Other applications of models for explaining neural system function include studies by Yan and others [27], Karbowski [16], and Lysiak and Paszkiel [38]. In particular, Yan and others [27] proposed a model based on control theory to explain and predict the structure of a neural circuit involved in C. elegans locomotion. Their predictions were further verified by empirical work. The prospect of building models at the small and large scales of life is also present in the study of ecological systems, another area involving nonlinear dynamical processes, where the efficiency and flow of energy and matter are measured without parameterizing the properties of the living organisms themselves [39].

1.4. Biological Model of a Neuron

The perspective of a neural system as an informational network requires a simplification of the complexity inherent in neuronal communication [40,41]. For specific measurements of the computational complexity in a neural network, it is assumed that the network has the same limitations as other communication networks, that information moves by a physical process, and this information travels in the network at a cost of time and energy. In this study, computational complexity and information flow are approached by estimating the ideal number of computational units for operations in a neural network. An alternative approach is to employ theory on information processing, which includes metrics of entropy, and methods to study the neural code and the transmission of information [20].
Another influential factor in the above approach is the coding of information in the network. The biological model of the neuron shows that information is transmitted from neuron to neuron by a diverse set of coding schemes, including a simple method of communication that is based on an on/off electrically based signal [41].
Instead, the neuronal system model may specify a complex signal for communication across the neural network, such as a spike train. The spike train has spatial and temporal dynamics, since it occurs as a series of signals over a span of time. The dynamics include how time varies between signals and the number of signals in a series [41]. Furthermore, these dynamics, the mechanisms of the neural code, and hypotheses for explaining these phenomena have been reviewed [42] and studied in practice [43,44]. In the particular case of taste in a mammal, one study showed evidence that the dynamics of a spike train code for the many dimensions in taste perception [45]. In addition, information encoding includes not only spike-train dynamics, but also the role of populations of neurons in encoding information [46,47]. However, the approach of this study is to employ the simpler model of neuronal communication, since it requires fewer assumptions and parameters, and therefore minimizes the many sources of error [20].

1.5. Approaches of This Study

A neural circuit in C. elegans is modeled as a minimal set of logic gates, which is equivalent to fitting Boolean algebraic expressions to the known sets of input and output values of a neural circuit. This example is a demonstration of the approach, and to offer a null hypothesis on the activity of neurons and their connections. There is a second demonstration, similar in its information-based perspective, where mathematical hypotheses on a neural circuit are ranked by their optimality according to competing truth tables of binary values.
In this article, a neural circuit is considered a portion of a neural system, or a neural network, that has a distinct role in information processing. It is implied that the neural circuit is local in scale, although it is possible that a circuit spans across a larger portion of a neural network. In contrast, a neural system refers to a large clustering of neurons and synapses in an animal, while a neural network refers to the more abstract organization of nodes and their connections. A neural system is a type of neural network, as is a deep-learning architecture of computer science.
The above approaches for problem solving in neural systems are complemented by a broad perspective on information in biological processes, including from genetics and immunology. The aim is to consider these biological examples as algorithms, both for insights into these processes in general, and to associate them with methods in information processing.

2. Methods

2.1. Data Retrieval

The web-based interface at WormAtlas.Org documents the sensory and motor neurons in the adult hermaphroditic form of C. elegans [48,49,50,51,52,53]. This species has two distinct nervous systems: a somatic system of 282 neurons [48] and a pharyngeal system of 20 neurons [49]. Several of these neurons are not fully characterized, and others do not have distinctive membership to either the pharyngeal or somatic system, so it is possible to make assignments based on the curated databases at WormAtlas.Org.
The neural circuit for gentle touch in C. elegans locomotion is described by Yan and others [27] and Driscoll and Kaplan [32]. This study assumes that any neural circuit operates by a forward feedback loop, a biologically plausible assertion [31]. In particular, Yan and others [27] examined the sensory neurons involved in gentle touch, the interneurons for control, and the motor neurons that synapse with muscle by neuromuscular junctions [32]. They isolated the essential members of the circuit, as predicted by control theory in engineering. The inputs include three sensory neurons, while the outputs correspond to four motor neurons that synapse on locomotory muscles involved in forward and backward motion, and interneurons that may act as intermediaries of information flow between sensory and motor neurons.

2.2. Data Processing and Visualization

Minitab statistical software [54], version 14, provided for data organization and processing. The diagram of the digital circuit was drawn in TinyCAD [55]. It includes the software libraries 74TTL and gen_Logic, which include graphical symbols for the commonly used logic gates.

2.3. Logic Gate Analysis

The Espresso software computes solutions for the minimal number of logic gates, given a number of inputs and outputs in a circuit [56]. Below is an example of the input data with 3 inputs and 4 outputs, corresponding to the AND/NOT case (Table 1):
.i 3
.o 4
.ilb A B C
.ob E F G H
000 0000
100 0000
010 0000
001 0000
110 1100
101 0000
011 0011
111 0000
.e
The above list is a computer-readable list of truth-table values where each of the lines of input (A, B, C) and output (E, F, G, H) are separated by a space character. The header information includes the count of columns of input and output values, along with a human-readable variable name for each of the columns of number values. The software resolves the truth table into a set of logic gates, as represented in Boolean algebraic form:
E = (A & B & !C)
F = (A & B & !C)
G = (!A & B & C)
H = (!A & B & C)
The software performs the calculation and solution by this command line:
espresso.exe -oeqntott -Dso -S1 -t input_datafile
As the columns of input values increase, the time complexity increases exponentially.
For an example of enumerating the input state values for a truth table, a line of bash shell code is shown below:
for i in $(seq 0 4095); do echo "obase=2;$i" | bc | tr -d ’\r’ | xargs printf "%012d\n"; done

3. Results

3.1. Optimality of an Idealized Neural Circuit

In this study, the logic gate model was designed for the above number of sensory inputs and motor outputs. Table 1 shows the data as represented by a truth table and suggests two logic gate models that are abstract representatives of the gentle touch circuit in C. elegans [27]. Each zero or one in the truth table corresponds to an OFF or ON state in the neural circuit. The OR/NOT logic gate model allows for multiple neurons to independently code for forward or backward locomotion, while the AND/NOT model requires a neuron to depend on another neuron for any activation of animal locomotion. The method is also dependent on the assumption of unidirectional information flow from sensory input to motor output.
Figure 2 shows a logic gate diagram that corresponds to the solution for the AND/NOT case (Table 1). The diagram is an abstraction of the flow of information from sensory input to motor output. The priors for the model are listed in Section 2.1 and Section 2.3, and these are the number of sensory inputs, a value of three, and the number of motor outputs, which is four. This procedure may be applied to other kinds of neural circuits, given a sufficient knowledge of the circuit’s inputs and outputs.

3.2. Efficiency of Mathematical Operations in a Neural Circuit

The information-based cost of the operations of multiplication and division provide insight on the information processing in an idealized neural circuit. Table 2 shows a case where a 2-bit value is multiplied by another 2-bit value. This is repeated for the case of division to provide a contrast in the cost of these binary operations.
The truth table for binary multiplication and division (Table 2) was formatted as an input file for use in the Espresso software [56]. The multiplication operation results in a cost of eight Boolean operations, while division has a cost of 12. This result is dependent on the precision in the remainder value, so increasing this value leads to a higher number of operations. This procedure may be used to compare prior mathematical hypotheses that reflect the kinds of computations that are expected to occur in a neural circuit. It also offers a procedure for estimating the complexity of information processing in a circuit. In reference to computational complexity, the above result supports that multiplication is favored over division in an optimally designed system, at least in a computational sense.

4. Discussion

4.1. The Utility of a Logic Gate Model

Figure 2 shows a logic gate model of an idealized neural circuit. This assumes a level of abstraction of the individual parts of the system, and a static snapshot of neuronal dynamics. In a larger network, such as in advanced information processing, it is expected that the use of nonlinear dynamics will better capture the deeper complexity of the system, such as that used in comparisons of an animal’s neural network to an artificial neural network [57,58]. However, at these scales, there is typically a limitation in the explainability of a model, particularly at the neuronal level. Instead, use of a logic gate model may provide better explainability and offer intuition on the routing and efficiency of information flow in a neural network.
The logic gate model is also more applicable for a neural circuit in an unchanging environment. For a dynamic environment, it becomes difficult to disentangle the inner workings of a neural circuit, since it is expected that some of its many functions remain unknown. This is a reminder that past studies have identified roles of neurons in a controlled setting; however, these roles are often specific to a single environment, or a few environments, and are not tested across all potential environments (Figure 3). This problem is compounded by the complexity inherent in the dynamics of an animal’s physiology and its interactions. This complexity may also be described as a system of high dimensionality, so that the number of parameters is large and difficult to estimate in practice.
The use of the logic-gate model depends on information flowing from sensory input to output, such as in the case of a sensory neuron to a motor neuron [59]. The organization of a neural network and its circuits is expected to depend on the values at the input and output layers, especially during the relatively rapid modifications in an animal’s early development. These systems are essentially programmable network systems of neurons and synaptic connections. The connections, at least as idealized features, are dynamic with respect to gain, loss, and in the strength of connection. The connectivity and the network structure show evidence of optimality in structure, as described in the Introduction, and so it is reasonable to consider optimality in the information flow across a neural system, too. Theory provides an important guide, while the above method offers an alternative method where theory is not applicable, or interpretable.

4.2. Information Processing as an Algorithm in Biological Systems

4.2.1. Overview of Information-Based Systems

The logic gate model applies to the information processing of logical operations. While it is based on a binary number system, it provides general insight into information flow and routing. The reason is that information-based systems in Nature, particularly the evolved systems of biological organisms, are typically an optimal solution within the constraints of their biological design. Further, the processing of information in these systems is, in essence, an algorithm and a model. This description of information processing is also mirrored in the process of genetic inheritance, neural systems in biology, and detection of intracellular pathogens in the jawed vertebrates.
An animal neural system processes information, and the information processing operates like an algorithm. The algorithm is encoded in the neural network, so it is expected to be represented by a very complex data structure, and is contained in a higher dimensional space than that expected from the more common use of the term algorithm. We describe this system, and other examples in Nature, in the following sections.

4.2.2. Genetic Inheritance

It is possible to frame the inheritance of genetic material through an information-based perspective (Figure 4). The genetic material is a sequence of elements, where each element is a nucleic acid molecule, and is inherited by an individual and serves as the informational code to form the new organism. These processes are usually presented with terminology and pathways that originate in the chaotic path of scientific discovery, and a pre-Linnaean approach to ontology of natural systems, but these informational processes are generalizable and categorical in nature. In the case of generating proteins, the above genetic sequence is the informational template that is processed for creating multiple copies, and then processed further to convert the copies to molecular sequences of amino acids—the protein sequence. These proteins then fold to form complex shapes in three-dimensional space. This higher dimensional form leads to complex dynamics, such as in its interactions with other molecules, its potential to increase the rate of biochemical reactions, and transformation of stored energy in molecular bonds to motion at the molecular level.
The presumption is that the processing of a linear sequence of genetic information to a protein shape is optimally designed, such as in the genetic code for protein translation, although an idealized optimality is constrained by biological processes. The linear sequence is one-dimensional, a compression of the three-dimensional shape of the protein, along with its corresponding spatiotemporal dynamics in a cellular environment. Biological molecules are the operators to convert the information along the steps of this pathways, like an algorithm.

4.2.3. Cellular Immunity in Jawed Vertebrates

The immune system of jawed vertebrates includes a similar strategy. In this case, the genetic information of interest is not from the process of inheritance, but instead originates from a foreign source, such as a virus or bacterium, which may infect and lead to changes in the host organism. To deter these foreign invaders, a jawed vertebrate has cellular processes that search for intracellular and extracellular proteins, whether the source is foreign, or from itself, for detection and identification of proteins that are specific to a pathogen, and to potentially activate a pathway to eliminate the infected host cells.
A virus is defined as a pathogen that is dependent on a host cell for genetic replication, and to generate proteins (Figure 5). After intracellular infection, the viral proteins are produced in the cells of the host, so these proteins and their sequences are available for host detection. This involves a pathway which has similarities to the information processing in the genetic inheritance of cellular organisms. The protein information, a sequence of amino acids, is processed by the host to a set of subsequences. These subsequences are small in size as compared to the original sequence, and they are further combined with a type of specialized cell-surface receptor [60,61]. This combination of biological molecules leads to a cellular presentation of its corresponding three-dimensional shape, so the one-dimensional protein subsequence has been converted to a three-dimensional arrangement, and this latter arrangement, in combination with the receptor, is used in detection by specific immune cells that are surveilling the surface of host cells [62].
This mechanism of cellular surveillance, by these “specific immune cells”, involves another cell-surface protein receptor (Figure 5D). This receptor is also formed by an informational process with similarities to the mechanisms of genetic inheritance. It is formed by different combinations of proteins that have undergone genetic-level processes that include mutation and recombination, thereby modifying the protein sequences, and changing the resultant receptor shape, which leads to a very large diversity of receptor types as compared to the genetic instructions that code for the initial receptor [63]. This increased diversity of host receptor types has a greater potential for detecting many types of pathogens, including those that are novel to the host. This pathway is a probabilistic solution to the evolution of a pathogen that can escape host detection [64].
There is an additional layer of complexity that occurs in this process, where many different cellular receptors are mutually acting in detection of an intracellular pathogen. This overall process may be considered optimal in the efficient use of genetic information that is derived from the pathogen, along with high precision in detection of proteins that are pathogen specific [64], while avoiding reactions to host-specific proteins, because otherwise host cells without infection would be eliminated by host immunity [65].
The contest between survival of the host and that of the intracellular pathogen is dependent on the generation of these pathogen-specific protein subsequences by the host. The length of the relevant portion of these subsequences is typically short. For the intracellular case, they are often about nine amino acids in sequence [63]. This short length is expected for efficiency in the host detection of a pathogen. For example, if the pathogen is rapidly evolving, such as by the mechanisms of mutation and recombination, then its genetic sequence is expected to become unrecognizable to the host immune system. However, the evolutionary process is not likely to act on every portion of the genetic sequence of the virus, so subsequences are expected to remain unmodified over time, and likewise, a shorter-length subsequence is more likely to remain unmodified than one of longer length.
Furthermore, a pathogen population is constrained in its evolvability, since genetic change may lead to loss of biological function, such as in the change of a protein sequence, which may lead to changes in essential regions of its three-dimensional shape. This is a further constraint on the evolution of a pathogen for escaping host immune detection.
In addition, the typical protein subsequence length is sufficiently long for high precision in detection by the host; otherwise, a very short subsequence would likely originate from another source, including from the host itself. This process is further regulated by its dependence on sampling a variety of pathogenic protein subsequences in order to evoke a strong immune response. Lastly, a pathogen population must replicate and spread to multiple hosts in a host population, otherwise the pathogen will cease to replicate and exist. So, the virus must encounter many host immune systems, along with the corresponding potential of the host population to generate a larger number of immune-cell receptor types than any single individual by itself. Therefore, the host population employs a strategy of pathogen detection at multiple levels, each one additive or multiplicative in its generation of molecular diversity toward the process of pathogen detection.
From the perspective of the pathogen population, its genetic changes, including recombination within and between populations, may lead to evasion of host immunity, such as in the above example. The pathogen can avoid detection along the steps of the pathway of intracellular host immunity (Figure 5). One method is by interruption of the path as shown in Figure 5B, so that a previously spliced protein subsequence is no longer spliced by the host. Another method is by interruption of the path in Figure 5C, so that a spliced protein subsequence is no longer adequately combined with the host-cell receptor [66]. A third method is by the path in Figure 5D, so that the specific immune cell and its receptor no longer has recognition of the combinational pattern on a host cell, where the combinational pattern is defined as the protein subsequence bound with a cellular receptor [67].
In essence, for this pathway, the host is detecting the pathogen by sampling protein subsequences, while the evolution of the pathogen would tend to favor genetic change to evade host immunity. These favorable genetic changes in the pathogen are likely to lead to changes in its proteins, and therefore increasing its chance of evasion of host immunity; but these particular genetic changes, which lead to modified protein shapes, and possibly loss of biological function, are not favored in the pathogen population.
The above process is considered optimal, since the host is sampling information of sufficiently high complexity in identification of a pathogen, while avoiding detection of itself. Furthermore, the host–pathogen interactions are a dynamical process, and these population dynamics may persist over a long time-period, since each of the two populations has the potential to adapt to the other’s strategy, in which the host population is learning the genetic sequence of the pathogen and the pathogen is evolving for evasion of the outcome of this learning process by the host. The persistence of the system depends on many factors, including population sizes, rates of molecular evolution, and number of populations involved, so it can be considered a complex and high-dimensional phenomenon.

4.2.4. Neural Systems in Animals

Lastly, the neural network of animals can be considered as yet another example of an information-based system. It represents an algorithm that processes information as input and for output. For example, visual input is received across a two-dimensional surface, but visual perception is in three dimensions. Therefore, the neural network is processing the information for generating a perception in multiple dimensions [68]. For example, a visual scene may be initially processed as segments for subsequent detection of objects and boundaries in the scene [69].
Visual processing typically occurs at the millisecond time-scale [70], so there is a requirement of a process for constructing a visual scene from prior perception [71], otherwise the perception is a past scene. These processes are dependent on visual input, and in the case of humans, the optic nerve transmits around 108 bits of information per second [72]. This value is comparable to the maximum capacity of a computer network. This rate of information flow leads to a visual perception, and this information is conserved in a neural system, like that of energy in a closed system [73], so the downstream processes are creating visual representations that do not exceed the information content that originates from the visual input (Figure 6). The assumption of this statement is that the system is closed to other sources of information.
In cognition, information processing is not caused by a biological enzyme, or by the strength of a protein interaction, but the electrochemical-based communication of the neural network. To robustly recognize visual objects [74], this analog of an algorithmic system is expected to use the informational processes of combination and recombination, along with other mechanisms, to generate large diversity of informational patterns and to match an observation to objects stored in the memory (Figure 7). The process of matching, and therefore knowledge, is also dependent on the labeling of objects, and building on that knowledge by relating them to other objects. It may be represented as a graph of nodes and connections. Where the neural network is very large, then it is possible to model a large number of objects and their associations [75].
As in the previous examples, the neural system is formed by an evolutionary process that favors a form of information optimality [76,77]. In addition, the neural system may be considered as an analog, particularly at the level of information flow, of the deep-learning system, as developed by computer scientists [78,79,80]. They both may be described as neural networks which mediate the flow of information.

5. Conclusions

5.1. Information-Based Perspective of Biological Processes

The earlier approach to analysis of a neural circuit is derived from an information-based perspective, and for gaining insight into the workings of a neural system. This perspective seems applicable for examining neural systems at a small scale, while a larger scale is better suited for another approach, such as at the level of communication across a neural network. The communication of information is expected to show behavior, as expected in other physical processes, including the law of conservation, and so it is useful to construct models and make predictions in neural systems that are based on informational approaches and theory. The neural system is also expected to reflect the evolutionary history of an animal, and the tendency for solutions that favor optimality, at least within the constraints of biology.
Across the natural systems, processes sometimes have the potential to construct a near-infinite number of combinations from an initial set of elements. This can also be viewed as an informational process. An example is in the genetic inheritance of information from parent to offspring. In this case, the genes undergo mutation and recombination. Recombination allows for an exchange of genetic material among individuals, whether through a mating process or, in the case of a virus population, through a genetic mechanism during co-infection of a host cell by a variety of individuals of the population. The process of genetic recombination is expected to lead to an increase in new variants in a population. Another example is in jawed vertebrates and their adaptive immune system. They have a variety of genes that code for a cell-surface receptor with a role in detection of pathogenic proteins. These receptors undergo somatic, not genetic, processes of mutation and recombination for generating a very large diversity of receptor types.

5.2. Future Directions of Study

To facilitate comparative work across studies in neuroscience, it is ideal to collect, annotate, and curate as much data as possible. Likewise, experimental work in identifying neural circuits should record the surrounding environmental conditions, and the physiological states of an organism. At a broader scale, at the informational level, then it is of interest to compare the neural systems with the deep learning systems of computer science. It is expected that the different kinds of neural networks and their computational problems will converge on similar or analogous solutions, given the universality of informational processes.
In the case of vertebrate immunity, it is of continued interest to study the mechanisms for detection of pathogenic proteins, not as a deterministic process, but one that is probabilistic in forming an immune response. So, the pathogenic proteins and immune-cell receptors may be considered as populations of molecules instead of as ideal types, and that these populations are diverse and dynamic in their distributions. These molecular-level dynamics are expected to lead to a diversity of interactions between the pathogen and the host that altogether cause a robust host response. The methods to study this area, especially in molecular dynamics, are dependent on an information-based perspective, and often a dependency on very large datasets, particularly in the case of employing deep-learning methods [81,82,83,84,85].
For the case of a virus population, genetic recombination may occur between a common form and one that is rarely observed, such as where the rare type originates in a reservoir host population. This process is better described in an ecological context, where the virus is described as a population that inhabits patches with resources that facilitate replication. This is a reminder that a virus population can acquire genetic material from both the host of interest and other host species. Given these dynamics across populations, it is necessary to robustly sample genetic types so that the data are not biased and missing the rare variants. Modeling these complex dynamics is also suitable for deep-learning approaches, including that the data have a genetic and ecological context.
In addition, the dynamics of host immunity and the genetics of populations can be approached by computational modeling. Consequently, it is possible to extend an empirical dataset with data from theoretical methods. For example, the types of genetic changes can be assigned probabilities by frequency of expected occurrence, including the types and rates of mutation and substitution, and the recombinational events. This prior knowledge, where it exists, may be incorporated into a deep-learning-based methodology. The deep learning methods have also been successful in robust prediction of three-dimensional protein structure, and these and future models may be applied for predictions about the interacting molecules between a host and pathogen.
Lastly, some of the cognitive processes in animals are possibly based on combinational mechanisms in the neural system. For an animal that relies on advanced visual navigation, the visual scene is segmented into sections and the visual objects are classified. It is possible, or even probable, that classification involves comparisons to internal representations of objects, and also recombinations of these objects. These combinational mechanisms would also apply to natural language, so the words and phonemes are undergoing similar processes of mutation, combination, and recombination for creating a set of internal representational patterns that may be matched to those received by the sensory systems. Without a kind of combinational process in forming new internal representations, it is difficult to imagine how it is possible to classify specific objects that have not yet been experienced.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

An anonymous reviewer kindly suggested references in a section on neuronal biology and communication.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
  2. Boole, G. The Mathematical Analysis of Logic, Being an Essay towards a Calculus of Deductive Reasoning; Macmillan, Barclay, & Macmillan: London, UK, 1847. [Google Scholar]
  3. Leibniz, G.W.; Gerhardt, C.I. Die Philosophischen Schriften VII; Weidmannsche Buchhandlung: Berlin, Germany, 1890; pp. 236–247. [Google Scholar]
  4. Malink, M. The logic of Leibniz’s Generales Inquisitiones de Analysi Notionum et Veritatum. Rev. Symb. Log. 2016, 9, 686–751. [Google Scholar] [CrossRef] [Green Version]
  5. Schmidhuber, J. 1931: Kurt Godel, Founder of THEORETICAL computer Science, Shows Limits of Math, Logic, Computing, and Artificial Intelligence. Available online: people.idsia.ch/~juergen/goedel-1931-founder-theoretical-computer-science-AI.html (accessed on 4 April 2022).
  6. Leibniz, G.W. De Progressione Dyadica Pars I. 1679; Herrn von Leibniz’ Rechnung mit Null und Einz; Hochstetter, E., Greve, H.-J., Eds.; Siemens Aktiengesellschaft: Berlin, Germany, 1966. [Google Scholar]
  7. Smith, M.; Pereda, A.E. Chemical synaptic activity modulates nearby electrical synapses. Proc. Natl. Acad. Sci. USA 2003, 100, 4849–4854. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Reigl, M.; Alon, U.; Chklovskii, D.B. Search for computational modules in the C. elegans brain. BMC Biol. 2004, 2, 25. [Google Scholar] [CrossRef] [Green Version]
  9. Gray, J.M.; Hill, J.J.; Bargmann, C.I. A circuit for navigation in Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA 2005, 102, 3184–3191. [Google Scholar] [CrossRef] [Green Version]
  10. Varshney, L.R.; Chen, B.L.; Paniagua, E.; Hall, D.H.; Chklovskii, D.B. Structural properties of the C. elegans neuronal network. PLoS Comput. Biol. 2011, 7, e1001066. [Google Scholar] [CrossRef] [Green Version]
  11. Bargmann, C.I. Beyond the connectome: How neuromodulators shape neural circuits. Bioessays 2012, 34, 458–465. [Google Scholar] [CrossRef]
  12. Zhen, M.; Samuel, A.D. C. elegans locomotion: Small circuits, complex functions. Curr. Opin. Neurobiol. 2015, 33, 117–126. [Google Scholar] [CrossRef]
  13. Niven, J.E.; Chittka, L. Evolving understanding of nervous system evolution. Curr. Biol. 2016, 26, R937–R941. [Google Scholar] [CrossRef] [Green Version]
  14. Rakowski, F.; Karbowski, J. Optimal synaptic signaling connectome for locomotory behavior in Caenorhabditis elegans: Design minimizing energy cost. PLoS Comput. Biol. 2017, 13, e1005834. [Google Scholar] [CrossRef] [Green Version]
  15. Jabeen, S.; Thirumalai, V. The interplay between electrical and chemical synaptogenesis. J. Neurophysiol. 2018, 120, 1914–1922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Karbowski, J. Deciphering neural circuits for Caenorhabditis elegans behavior by computations and perturbations to genome and connectome. Curr. Opin. Syst. Biol. 2019, 13, 44–51. [Google Scholar] [CrossRef]
  17. Niebur, E.; Erdos, P. Theory of the locomotion of nematodes: Control of the somatic motor neurons by interneurons. Math. Biosci. 1993, 118, 51–82. [Google Scholar] [CrossRef]
  18. Kamhi, J.F.; Gronenberg, W.; Robson, S.K.; Traniello, J.F. Social complexity influences brain investment and neural operation costs in ants. Proc. R. Soc. B Biol. Sci. 2016, 283, 20161949. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  19. Traniello, I.M.; Chen, Z.; Bagchi, V.A.; Robinson, G.E. Valence of social information is encoded in different subpopulations of mushroom body Kenyon cells in the honeybee brain. Proc. R. Soc. B 2019, 286, 20190901. [Google Scholar] [CrossRef] [Green Version]
  20. Cover, T.M.; Thomas, J.A. Information Theory and Statistics. In Elements of Information Theory, 1st ed.; John Wiley & Sons: New York, NY, USA, 1991; pp. 279–335. [Google Scholar]
  21. Borst, A.; Helmstaedter, M. Common circuit design in fly and mammalian motion vision. Nat. Neurosci. 2015, 18, 1067–1076. [Google Scholar] [CrossRef]
  22. Groschner, L.N.; Malis, J.G.; Zuidinga, B.; Borst, A. A biophysical account of multiplication by a single neuron. Nature 2022, 603, 119–123. [Google Scholar] [CrossRef]
  23. Schnupp, J.W.; King, A.J. Neural processing: The logic of multiplication in single neurons. Curr. Biol. 2001, 11, R640–R642. [Google Scholar] [CrossRef] [Green Version]
  24. Laughlin, S.B.; Sejnowski, T.J. Communication in neuronal networks. Science 2003, 301, 1870–1874. [Google Scholar] [CrossRef] [Green Version]
  25. Chen, B.L.; Hall, D.H.; Chklovskii, D.B. Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. USA 2006, 103, 4723–4728. [Google Scholar] [CrossRef] [Green Version]
  26. Bullmore, E.; Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 2012, 13, 336–349. [Google Scholar] [CrossRef] [PubMed]
  27. Yan, G.; Vertes, P.E.; Towlson, E.K.; Chew, Y.L.; Walker, D.S.; Schafer, W.R.; Barabasi, A.L. Network control principles predict neuron function in the Caenorhabditis elegans connectome. Nature 2017, 550, 519–523. [Google Scholar] [CrossRef] [PubMed]
  28. Poznanski, R.R. Dendritic integration in a recurrent network. J. Integr. Neurosci. 2002, 1, 69–99. [Google Scholar] [CrossRef]
  29. Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
  30. Towlson, E.K.; Vertes, P.E.; Ahnert, S.E.; Schafer, W.R.; Bullmore, E.T. The rich club of the C. elegans neuronal connectome. J. Neurosci. 2013, 33, 6380–6387. [Google Scholar] [CrossRef] [Green Version]
  31. Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network motifs: Simple building blocks of complex networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Driscoll, M.; Kaplan, J. Mechanotransduction. In The Nematode C. elegans, II; Cold Spring Harbor Press, Cold Spring Harbor: New York, NY, USA, 1997; pp. 645–677. [Google Scholar]
  33. Wakabayashi, T.; Kitagawa, I.; Shingai, R. Neurons regulating the duration of forward locomotion in Caenorhabditis elegans. Neurosci. Res. 2004, 50, 103–111. [Google Scholar] [CrossRef]
  34. Chatterjee, N.; Sinha, S. Understanding the mind of a worm: Hierarchical network structure underlying nervous system function in C. elegans. Prog. Brain Res. 2008, 168, 145–153. [Google Scholar]
  35. Campbell, J.C.; Chin-Sang, I.D.; Bendena, W.G. Mechanosensation circuitry in Caenorhabditis elegans: A focus on gentle touch. Peptides 2015, 68, 164–174. [Google Scholar] [CrossRef]
  36. Poznanski, R.R. Biophysical Neural Networks: Foundations of Integrative Neuroscience; Mary Ann Liebert: New York, NY, USA, 2001; pp. 177–214. [Google Scholar]
  37. Goldental, A.; Guberman, S.; Vardi, R.; Kanter, I. A computational paradigm for dynamic logic-gates in neuronal activity. Front. Comput. Neurosci. 2014, 8, 52. [Google Scholar] [CrossRef] [Green Version]
  38. Lysiak, A.; Paszkiel, S. A Method to Obtain Parameters of One-Column Jansen–Rit Model Using Genetic Algorithm and Spectral Characteristics. Appl. Sci. 2021, 11, 677. [Google Scholar] [CrossRef]
  39. Odum, E.P. Energy flow in ecosystems—A historical review. Am. Zool. 1968, 8, 11–18. [Google Scholar] [CrossRef]
  40. Van Hemmen, J.L.; Sejnowski, T.J. (Eds.) 23 Problems in Systems Neuroscience; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
  41. Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
  42. Brette, R. Philosophy of the Spike: Rate-Based vs. Spike-Based Theories of the Brain. Front. Syst. Neurosci. 2015, 9, 151. [Google Scholar] [CrossRef] [PubMed]
  43. Pregowska, A.; Szczepanski, J.; Wajnryb, E. Temporal code versus rate code for binary Information Sources. Neurocomputing 2016, 216, 756–762. [Google Scholar] [CrossRef] [Green Version]
  44. Pregowska, A.; Kaplan, E.; Szczepanski, J. How Far can Neural Correlations Reduce Uncertainty? Comparison of Information Transmission Rates for Markov and Bernoulli Processes. Int. J. Neural Syst. 2019, 29, 1950003. [Google Scholar] [CrossRef] [Green Version]
  45. Di Lorenzo, P.M.; Chen, J.Y.; Victor, J.D. Quality Time: Representation of a Multidimensional Sensory Domain through Temporal Coding. J. Neurosci. 2009, 29, 9227–9238. [Google Scholar] [CrossRef]
  46. Crumiller, M.; Knight, B.; Kaplan, E. The Measurement of Information Transmitted by a Neural Population: Promises and Challenges. Entropy 2013, 15, 3507–3527. [Google Scholar] [CrossRef] [Green Version]
  47. Saxena, S.; Cunningham, J.P. Towards the neural population doctrine. Curr. Opin. Neurobiol. 2019, 55, 103–111. [Google Scholar] [CrossRef]
  48. White, J.G.; Southgate, E.; Thomson, J.N.; Brenner, S. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. B Biol. Sci. 1986, 314, 1–340. [Google Scholar]
  49. Albertson, D.G.; Thomson, J.N. The pharynx of Caenorhabditis elegans. Philos. Trans. R. Soc. B Biol. Sci. 1976, 275, 299–325. [Google Scholar]
  50. Durbin, R.M. Studies on the Development and Organisation of the Nervous System of Caenorhabditis elegans. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1987. [Google Scholar]
  51. Achacoso, T.B.; Yamamoto, W.S. AY’s Neuroanatomy of C. elegans for Computation; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
  52. Hall, D.H.; Russell, R.L. The posterior nervous system of the nematode Caenorhabditis elegans: Serial reconstruction of identified neurons and complete pattern of synaptic interactions. J. Neurosci. 1991, 11, 1–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Hobert, O.; Hall, D.H. Neuroanatomy: A second look with GFP reporters and some comments. Worm Breeder’s Gazette 1999, 16, 24. [Google Scholar]
  54. Wild, D.J. MINITAB Release 14. J. Chem. Inf. Modeling 2005, 45, 212. [Google Scholar] [CrossRef]
  55. Pyne, M. TinyCAD Source Code (version 2.90.00). Available online: Sourceforge.net/projects/tinycad (accessed on 4 April 2022).
  56. Brayton, R.K.; Hachtel, G.D.; McMullen, C.T.; Sangiovanni-Vincentelli, A.L. Logic Minimization Algorithms for VLSI Synthesis; Kluwer Academic: Berlin, Germany, 1985. [Google Scholar]
  57. Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef] [Green Version]
  58. Bengio, Y.; Lecun, Y.; Hinton, G. Deep learning for AI. Commun. ACM 2021, 64, 58–65. [Google Scholar] [CrossRef]
  59. Friedman, R. Test of robustness of pharyngeal neural networks in Caenorhabditis elegans. NeuroReport 2021, 32, 169–176. [Google Scholar] [CrossRef] [PubMed]
  60. Klein, J.; Figueroa, F. Evolution of the major histocompatibility complex. Crit. Rev. Immunol. 1986, 6, 295–386. [Google Scholar]
  61. Germain, R.N. MHC-dependent antigen processing and peptide presentation: Providing ligands for T lymphocyte activation. Cell 1994, 76, 287–299. [Google Scholar] [CrossRef]
  62. Davis, M.M.; Bjorkman, P.J. T-cell antigen receptor genes and T-cell recognition. Nature 1988, 334, 395–402. [Google Scholar] [CrossRef]
  63. Nikolich-Zugich, J.; Slifka, M.K.; Messaoudi, I. The many important facets of T-cell repertoire diversity. Nat. Rev. Immunol. 2004, 4, 123–132. [Google Scholar] [CrossRef]
  64. Wucherpfennig, K.W. The structural interactions between T cell receptors and MHC-peptide complexes place physical limits on self-nonself discrimination. Curr. Top. Microbiol. Immunol. 2005, 296, 19–37. [Google Scholar] [PubMed]
  65. Starr, T.K.; Jameson, S.C.; Hogquist, K.A. Positive and negative selection of T cells. Annu. Rev. Immunol. 2003, 21, 139–176. [Google Scholar] [CrossRef] [PubMed]
  66. O’Donnell, T.J.; Rubinsteyn, A.; Laserson, U. MHCflurry 2.0: Improved Pan-Allele Prediction of MHC Class I-Presented Peptides by Incorporating Antigen Processing. Cell Syst. 2020, 11, 42–48. [Google Scholar] [CrossRef] [PubMed]
  67. Montemurro, A.; Schuster, V.; Povlsen, H.R.; Bentzen, A.K.; Jurtz, V.; Chronister, W.D.; Crinklaw, A.; Hadrup, S.R.; Winther, O.; Peters, B.; et al. NetTCR-2.0 enables accurate prediction of TCR-peptide binding by using paired TCRα and β sequence data. Commun. Biol. 2021, 4, 1–13. [Google Scholar] [CrossRef] [PubMed]
  68. Clarke, A.; Tyler, L.K. Understanding what we see: How we derive meaning from vision. Trends Cogn. Sci. 2015, 19, 677–687. [Google Scholar] [CrossRef] [Green Version]
  69. Engel, A.K.; Konig, P.; Singer, W. Direct physiological evidence for scene segmentation by temporal coding. Proc. Natl. Acad. Sci. USA 1991, 88, 9136–9140. [Google Scholar] [CrossRef] [Green Version]
  70. Lamme, V.A. Why visual attention and awareness are different. Trends Cogn. Sci. 2003, 7, 12–18. [Google Scholar] [CrossRef]
  71. Spratling, M.W. A review of predictive coding algorithms. Brain Cogn. 2017, 112, 92–97. [Google Scholar] [CrossRef] [Green Version]
  72. Itti, L.; Koch, C. Computational modelling of visual attention. Nat. Rev. Neurosci. 2001, 2, 194–203. [Google Scholar] [CrossRef] [Green Version]
  73. Barrett, T.W. Conservation of information. Acta Acust. United Acust. 1972, 27, 44–47. [Google Scholar]
  74. Chang, L.; Tsao, D.Y. The code for facial identity in the primate brain. Cell 2017, 169, 1013–1028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  75. Leibniz, G. Dissertatio de Arte Combinatoria, 1666; Akademie Verlag: Berlin, Germany, 1923; Manuscript later published in Smtliche Schriften und Briefe. [Google Scholar]
  76. Stringer, C.; Pachitariu, M.; Steinmetz, N.; Carandini, M.; Harris, K.D. High-dimensional geometry of population responses in visual cortex. Nature 2019, 571, 361–365. [Google Scholar] [CrossRef] [PubMed]
  77. Goni, J.; Avena-Koenigsberger, A.; de Mendizabal, N.V.; van den Heuvel, M.P.; Betzel, R.F.; Sporns, O. Exploring the Morphospace of Communication Efficiency in Complex Networks. PLoS ONE 2013, 8, e58070. [Google Scholar] [CrossRef] [PubMed]
  78. Hinton, G.E. Connectionist learning procedures. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef] [Green Version]
  79. Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
  80. Silver, D.; Singh, S.; Precup, D.; Sutton, R.S. Reward is enough. Artif. Intell. 2021, 299, 103535. [Google Scholar] [CrossRef]
  81. Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
  82. Hekkelman, M.L.; de Vries, I.; Joosten, R.P.; Perrakis, A. AlphaFill: Enriching the AlphaFold models with ligands and co-factors. bioRxiv 2021. bioRxiv: 2021.11.26.470110. [Google Scholar]
  83. Gao, M.; Nakajima An, D.; Parks, J.M.; Skolnick, J. Predicting direct physical interactions in multimeric proteins with deep learning. Nat. Commun. 2022, 13, 1744. [Google Scholar] [CrossRef]
  84. Akdel, M.; Pires, D.E.; Pardo, E.P.; Janes, J.; Zalevsky, A.O.; Mészáros, B.; Bryant, P.; Good, L.L.; Laskowski, R.A.; Pozzati, G.; et al. A structural biology community assessment of AlphaFold 2 applications. bioRxiv 2021. bioRxiv: 2021.09.26.461876. [Google Scholar]
  85. Mirdita, M.; Schutze, K.; Moriwaki, Y.; Heo, L.; Ovchinnikov, S.; Steinegger, M. ColabFold-Making protein folding accessible to all. bioRxiv 2021. bioRxiv: 2021.08.15.456425. [Google Scholar] [CrossRef] [PubMed]
Signals 03 00025 g001 550
Figure 1. (A). Truth table for the basic Boolean operations AND, OR, and NOT. (B). The logic gate symbols represent the operations in (A).
Figure 1. (A). Truth table for the basic Boolean operations AND, OR, and NOT. (B). The logic gate symbols represent the operations in (A).
Signals 03 00025 g001
Signals 03 00025 g002 550
Figure 2. Diagram of a neural circuit with three sensory inputs and four logic gates that correspond to the four motor outputs and shows a solution for the AND/NOT case (Table 1). The small gray circles between red and blue lines represent a potential inversion of the input signal, a NOT operation. The sensory inputs are labeled A to C.
Figure 2. Diagram of a neural circuit with three sensory inputs and four logic gates that correspond to the four motor outputs and shows a solution for the AND/NOT case (Table 1). The small gray circles between red and blue lines represent a potential inversion of the input signal, a NOT operation. The sensory inputs are labeled A to C.
Signals 03 00025 g002
Signals 03 00025 g003 550
Figure 3. Abstract diagram of neurons and their connections. Two neural circuits are represented, one with connections shown by black lines, and the other by green lines. The information flow in this neural system is from input neuron to output neuron. Only a single neural circuit is activated at a time, and its activation is dependent on specific environmental conditions. Therefore, the neurons may be recorded as having different roles if there is not an experimental control on the environmental conditions.
Figure 3. Abstract diagram of neurons and their connections. Two neural circuits are represented, one with connections shown by black lines, and the other by green lines. The information flow in this neural system is from input neuron to output neuron. Only a single neural circuit is activated at a time, and its activation is dependent on specific environmental conditions. Therefore, the neurons may be recorded as having different roles if there is not an experimental control on the environmental conditions.
Signals 03 00025 g003
Signals 03 00025 g004 550
Figure 4. Simplification of the pathway for conversion of a one-dimensional genetic sequence to a three-dimensional protein shape. (A). Genetic sequence where each word is 2 bits in width. This sequence is representative of the proximate code of a protein molecule; (B) multiple copies of the genetic sequence are created from (A); (C) protein sequence is formed from (B), encoded by each word of the genetic sequence of a width of 6 bits, although the bit size is compressible in the corresponding protein code; (D) protein shape in three dimensions, where the shape is formed by the dynamics of physical interactions within the protein and between other molecules.
Figure 4. Simplification of the pathway for conversion of a one-dimensional genetic sequence to a three-dimensional protein shape. (A). Genetic sequence where each word is 2 bits in width. This sequence is representative of the proximate code of a protein molecule; (B) multiple copies of the genetic sequence are created from (A); (C) protein sequence is formed from (B), encoded by each word of the genetic sequence of a width of 6 bits, although the bit size is compressible in the corresponding protein code; (D) protein shape in three dimensions, where the shape is formed by the dynamics of physical interactions within the protein and between other molecules.
Signals 03 00025 g004
Signals 03 00025 g005 550
Figure 5. One simplified pathway of jawed vertebrate immunity—from intracellular pathogenic protein to its detection by a host cell. (A) Shape of viral protein in three dimensions; (B) protein is spliced into protein subsequences; (C) subsequence of viral protein is combined with a host cell receptor; (D) the protein subsequence and receptor from (C) are bound to the surface of a host cell (on the left). A specific immune cell (on the right) with a cell-surface receptor scans the host cell for evidence of pathogenic protein subsequences. Positive detection of a pathogenic protein may contribute to an immune response, so that host cells infected with a pathogen are eliminated by the immune system.
Figure 5. One simplified pathway of jawed vertebrate immunity—from intracellular pathogenic protein to its detection by a host cell. (A) Shape of viral protein in three dimensions; (B) protein is spliced into protein subsequences; (C) subsequence of viral protein is combined with a host cell receptor; (D) the protein subsequence and receptor from (C) are bound to the surface of a host cell (on the left). A specific immune cell (on the right) with a cell-surface receptor scans the host cell for evidence of pathogenic protein subsequences. Positive detection of a pathogenic protein may contribute to an immune response, so that host cells infected with a pathogen are eliminated by the immune system.
Signals 03 00025 g005
Signals 03 00025 g006 550
Figure 6. Abstract diagram of layers of a neural network that contain information. It is a closed system and the information flows from input to output. The information content from one layer to the next can stay the same or decrease, but not increase, because information moves by a physical process, and therefore is constrained by the Laws of Thermodynamics.
Figure 6. Abstract diagram of layers of a neural network that contain information. It is a closed system and the information flows from input to output. The information content from one layer to the next can stay the same or decrease, but not increase, because information moves by a physical process, and therefore is constrained by the Laws of Thermodynamics.
Signals 03 00025 g006
Signals 03 00025 g007 550
Figure 7. Plot of combinatorial explosion, the growth in number of possible combinations with respect to number of elements. For comparison, a plot of exponential growth is shown.
Figure 7. Plot of combinatorial explosion, the growth in number of possible combinations with respect to number of elements. For comparison, a plot of exponential growth is shown.
Signals 03 00025 g007
Table
Table 1. Truth table for a digital circuit with 3 input and 4 output operations. Each row corresponds to 1 of the 8 possible input and resulting output states. The binary digit 1 is an ON state and 0 is an OFF state. An OR operation resolves to an ON state if either of two specific inputs are ON, while an AND operation resolves to an ON state where two specific inputs are ON. NOT modifies the state from ON to OFF or OFF to ON.
Table 1. Truth table for a digital circuit with 3 input and 4 output operations. Each row corresponds to 1 of the 8 possible input and resulting output states. The binary digit 1 is an ON state and 0 is an OFF state. An OR operation resolves to an ON state if either of two specific inputs are ON, while an AND operation resolves to an ON state where two specific inputs are ON. NOT modifies the state from ON to OFF or OFF to ON.
OR/NOTAND/NOT
InputsOutputsInputsOutputs
0 0 00 0 0 00 0 00 0 0 0
1 0 01 1 0 01 0 00 0 0 0
0 1 00 0 0 00 1 00 0 0 0
0 0 10 0 1 10 0 10 0 0 0
1 1 01 1 0 01 1 01 1 0 0
1 0 10 0 0 01 0 10 0 0 0
0 1 10 0 1 10 1 10 0 1 1
1 1 10 0 0 01 1 10 0 0 0
Table
Table 2. Truth table for binary multiplication and division in the case of two 2-bit input values. Input 1 is a 2-bit value labeled AA; Input 2 is a 2-bit value labeled BB. The output value for multiplication is the product of AA multiplied by BB. The output value for division is AA divided by BB; the quotient value QQ is stored in the 2 most significant bits, and the divide-by-zero error bit is the next adjacent bit, while the 3 least significant bits store the unrounded remainder value (RRR). Specific to this case of lower precision, the remainder value is stored in a 3-bit value since the highest possible remainder value is not greater than 7 (base 10 number system).
Table 2. Truth table for binary multiplication and division in the case of two 2-bit input values. Input 1 is a 2-bit value labeled AA; Input 2 is a 2-bit value labeled BB. The output value for multiplication is the product of AA multiplied by BB. The output value for division is AA divided by BB; the quotient value QQ is stored in the 2 most significant bits, and the divide-by-zero error bit is the next adjacent bit, while the 3 least significant bits store the unrounded remainder value (RRR). Specific to this case of lower precision, the remainder value is stored in a 3-bit value since the highest possible remainder value is not greater than 7 (base 10 number system).
Mathematical Operations
Input 1Input 2Output (Multiplication)Output (Division)
A AB BAA × BB =AA/BB = QQ (ERRR)
0 00 00 0 0 00 0 1 0 0 0
0 00 10 0 0 00 0 0 0 0 0
0 01 00 0 0 00 0 0 0 0 0
0 01 10 0 0 00 0 0 0 0 0
0 10 00 0 0 00 0 1 0 0 0
0 10 10 0 0 10 1 0 0 0 0
0 11 00 0 1 00 0 0 1 0 1
0 11 10 0 1 10 0 0 0 1 1
1 00 00 0 0 00 0 1 0 0 0
1 00 10 0 1 01 0 0 0 0 0
1 01 00 1 0 00 1 0 0 0 0
1 01 10 1 1 00 0 0 1 1 0
1 10 00 0 0 00 0 1 0 0 0
1 10 10 0 1 11 1 0 0 0 0
1 11 00 1 1 00 1 0 1 0 1
1 11 11 0 0 10 1 0 0 0 0
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Friedman, R. A Perspective on Information Optimality in a Neural Circuit and Other Biological Systems. Signals 2022, 3, 410-427. https://doi.org/10.3390/signals3020025

AMA Style

Friedman R. A Perspective on Information Optimality in a Neural Circuit and Other Biological Systems. Signals. 2022; 3(2):410-427. https://doi.org/10.3390/signals3020025

Chicago/Turabian Style

Friedman, Robert. 2022. "A Perspective on Information Optimality in a Neural Circuit and Other Biological Systems" Signals 3, no. 2: 410-427. https://doi.org/10.3390/signals3020025

APA Style

Friedman, R. (2022). A Perspective on Information Optimality in a Neural Circuit and Other Biological Systems. Signals, 3(2), 410-427. https://doi.org/10.3390/signals3020025

Article Metrics

Back to TopTop