A Survey of Adaptive Multi-Agent Networks and Their Applications in Smart Cities
Abstract
:1. Introduction
2. Definition Frameworks
2.1. Entities
2.2. Actions
2.3. Environment
2.4. Information Flow
3. Monitoring Paradigms
3.1. Dimension Reduction and Filtering
3.2. Anomaly Detection
3.3. Predictive Models
3.4. Clustering
3.5. Pattern Recognition
4. Development Approaches
4.1. Main Platform
4.2. Learning Mechanism
4.3. Control Solutions
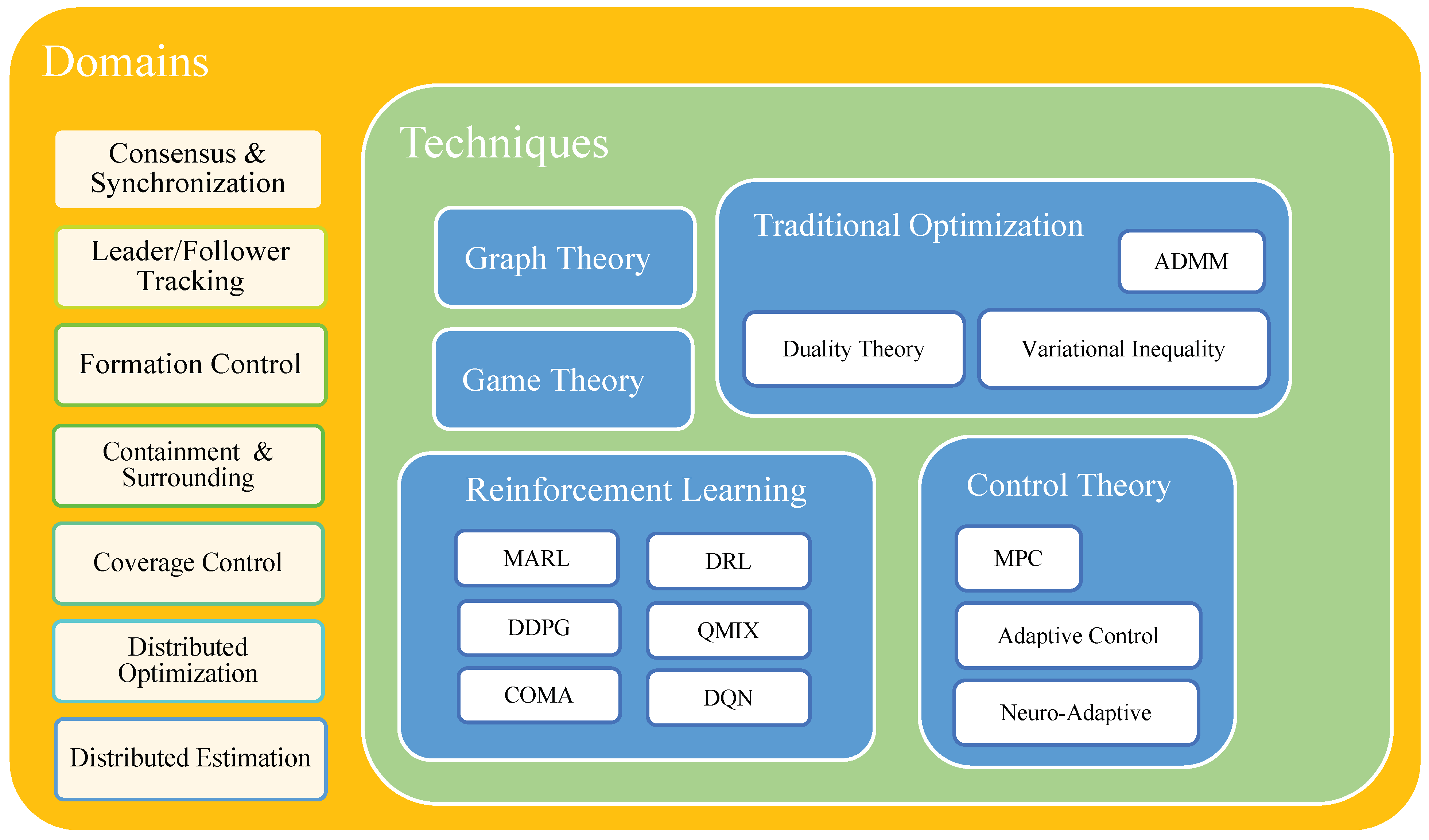
4.3.1. MASs Applications
4.3.2. Control Techniques
5. Evaluation Metrics
5.1. Performance Indicators
5.2. Test Datasets and Platforms
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cocchia, A. Smart and digital city: A systematic literature review. In Smart City; Springer: Cham, Switzerland, 2014; pp. 13–43. [Google Scholar]
- Kim, T.; Ramos, C.; Mohammed, S. Smart city and IoT. Future Gener. Comput. Syst. 2017, 76, 159–162. [Google Scholar] [CrossRef]
- Khan, J.Y.; Yuce, M.R. Internet of Things (IoT): Systems and Applications; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Park, E.; Del Pobil, A.P.; Kwon, S.J. The role of Internet of Things (IoT) in smart cities: Technology roadmap-oriented approaches. Sustainability 2018, 10, 1388. [Google Scholar] [CrossRef] [Green Version]
- Mukhopadhyay, S.C.; Suryadevara, N.K. Internet of things: Challenges and opportunities. In Internet of Things; Springer: Berlin/Heidelberg, Germany, 2014; Volume 9, pp. 1–17. [Google Scholar]
- Iqbal, A.; Suryani, M.A.; Saleem, R.; Suryani, M.A. Internet of things (IoT): On-going security challenges and risks. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 671. [Google Scholar]
- Roscia, M.; Longo, M.; Lazaroiu, G.C. Smart City by multi-agent systems. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013; pp. 371–376. [Google Scholar]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-agent systems: A survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- do Nascimento, N.M.; de Lucena, C.J.P. FIoT: An agent-based framework for self-adaptive and self-organizing applications based on the Internet of Things. Inf. Sci. 2017, 378, 161–176. [Google Scholar] [CrossRef]
- Forestiero, A. Multi-agent recommendation system in Internet of Things. In Proceedings of the 2017 17th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGRID), Madrid, Spain, 14–17 May 2017; pp. 772–775. [Google Scholar]
- Aseere, A.M. Multiagent Systems Applied to Smart City. J. Eng. Appl. Sci. 2020, 7, 29–36. [Google Scholar]
- Longo, M.; Roscia, M.; Lazaroiu, C. Innovating multi-agent systems applied to smart city. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 4296–4302. [Google Scholar] [CrossRef]
- Krupitzer, C.; Roth, F.M.; VanSyckel, S.; Schiele, G.; Becker, C. A survey on engineering approaches for self-adaptive systems. Pervasive Mob. Comput. 2015, 17, 184–206. [Google Scholar] [CrossRef]
- Boes, J.; Migeon, F. Self-organizing multi-agent systems for the control of complex systems. J. Syst. Softw. 2017, 134, 12–28. [Google Scholar] [CrossRef] [Green Version]
- Kantamneni, A.; Brown, L.E.; Parker, G.; Weaver, W.W. Survey of multi-agent systems for microgrid control. Eng. Appl. Artif. Intell. 2015, 45, 192–203. [Google Scholar] [CrossRef]
- Kaviani, S. Multi-Agent Clinical Decision Support Systems: A Survey. In Proceedings of the 1st Korea Artificial Intelligence Conference, Jeju Island, Korea, 23–25 April 2020. [Google Scholar]
- Dominguez, R.; Cannella, S. Insights on multi-agent systems applications for supply chain management. Sustainability 2020, 12, 1935. [Google Scholar] [CrossRef] [Green Version]
- Gjikopulli, A.A.; Banerjee, A. A survey on Multi-Agent Systems (MAS). Netw. Archit. Serv. 2020, 55–59. [Google Scholar]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Z.; Han, Q.L.; Liu, Y. Consensus control of stochastic multi-agent systems: A survey. Sci. China Inf. Sci. 2017, 60, 120201. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Tan, C. A survey of the consensus for multi-agent systems. Syst. Sci. Control Eng. 2019, 7, 468–482. [Google Scholar] [CrossRef] [Green Version]
- Rahmani, A.; Ji, M.; Mesbahi, M.; Egerstedt, M. Controllability of multi-agent systems from a graph-theoretic perspective. SIAM J. Control Optim. 2009, 48, 162–186. [Google Scholar] [CrossRef]
- Diaconescu, I.M.; Wagner, G. Modeling and simulation of web-of-things systems as multi-agent systems. In German Conference on Multiagent System Technologies; Springer: Cham, Switzerland, 2015; pp. 137–153. [Google Scholar]
- Liang, H.; Liu, G.; Zhang, H.; Huang, T. Neural-Network-Based Event-Triggered Adaptive Control of Nonaffine Nonlinear Multiagent Systems With Dynamic Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2239–2250. [Google Scholar] [CrossRef]
- Lowe, R.; Gupta, A.; Foerster, J.; Kiela, D.; Pineau, J. On the interaction between supervision and self-play in emergent communication. arXiv 2020, arXiv:2002.01093. [Google Scholar]
- Fouad, H.; Moskowitz, I.S. Meta-Agents: Using Multi-Agent Networks to Manage Dynamic Changes in the Internet of Things. In Artificial Intelligence for the Internet of Everything; Elsevier: Cambridge, MA, USA, 2019; pp. 271–281. [Google Scholar]
- Xu, X.; Chen, S.; Huang, W.; Gao, L. Leader-following consensus of discrete-time multi-agent systems with observer-based protocols. Neurocomputing 2013, 118, 334–341. [Google Scholar] [CrossRef]
- D’Angelo, M.; Gerasimou, S.; Ghahremani, S.; Grohmann, J.; Nunes, I.; Pournaras, E.; Tomforde, S. On learning in collective self-adaptive systems: State of practice and a 3d framework. In Proceedings of the 2019 IEEE/ACM 14th International Symposium on Software Engineering for Adaptive and Self-Managing Systems (SEAMS), Montreal, QC, Canada, 25 May 2019; pp. 13–24. [Google Scholar]
- Zheng, Y.; Wang, L. Consensus of heterogeneous multi-agent systems without velocity measurements. Int. J. Control 2012, 85, 906–914. [Google Scholar] [CrossRef]
- Gottifredi, S.; Tamargo, L.H.; García, A.J.; Simari, G.R. Arguing about informant credibility in open multi-agent systems. Artif. Intell. 2018, 259, 91–109. [Google Scholar] [CrossRef] [Green Version]
- Kendrick, P.; Hussain, A.; Criado, N.; Randles, M. Multi-agent systems for scalable internet of things security. In Proceedings of the Second International Conference on Internet of things, Data and Cloud Computing, Cambridge, UK, 22–23 March 2017; pp. 1–6. [Google Scholar]
- Chen, F.; Ren, W. On the control of multi-agent systems: A survey. Found. Trends® Syst. Control 2019, 6, 339–499. [Google Scholar] [CrossRef]
- Zuo, Z.; Zhang, J.; Wang, Y. Adaptive fault-tolerant tracking control for linear and Lipschitz nonlinear multi-agent systems. IEEE Trans. Ind. Electron. 2014, 62, 3923–3931. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2021, 2021, 1–39. [Google Scholar] [CrossRef]
- Jiang, C.; Du, H.; Zhu, W.; Yin, L.; Jin, X.; Wen, G. Synchronization of nonlinear networked agents under event-triggered control. Inf. Sci. 2018, 459, 317–326. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, B.; Lin, C.; Shang, Y. Fuzzy adaptive finite-time consensus tracking control for nonlinear multi-agent systems. Int. J. Syst. Sci. 2021, 52, 1346–1358. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, H.; Pan, Y.; Liang, H. Adaptive neural networks event-triggered fault-tolerant consensus control for a class of nonlinear multi-agent systems. AIMS Math. 2020, 5, 2780–2800. [Google Scholar] [CrossRef]
- Guan, Y.; Ji, Z.; Zhang, L.; Wang, L. Controllability of heterogeneous multi-agent systems under directed and weighted topology. Int. J. Control 2016, 89, 1009–1024. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Desaraju, V.R.; How, J.P. Decentralized path planning for multi-agent teams with complex constraints. Auton. Robot. 2012, 32, 385–403. [Google Scholar] [CrossRef]
- Movric, K.H.; Lewis, F.L. Cooperative optimal control for multi-agent systems on directed graph topologies. IEEE Trans. Autom. Control 2013, 59, 769–774. [Google Scholar] [CrossRef]
- De Nijs, F. Resource-Constrained Multi-Agent Markov Decision Processes. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Radulescu, R.; Mannion, P.; Roijers, D.M.; Nowé, A. Recent Advances in Multi-Objective Multi-Agent Decision Making; Benelux Association for Artificial Intelligence: Leiden, The Netherlands, 2020; pp. 392–394. [Google Scholar]
- Lee, D.; Hu, J. Primal-dual distributed temporal difference learning. arXiv 2018, arXiv:1805.07918. [Google Scholar]
- Rizk, Y.; Awad, M.; Tunstel, E.W. Decision making in multiagent systems: A survey. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 514–529. [Google Scholar] [CrossRef]
- Rossi, F.; Bandyopadhyay, S.; Wolf, M.; Pavone, M. Review of multi-agent algorithms for collective behavior: A structural taxonomy. IFAC-PapersOnLine 2018, 51, 112–117. [Google Scholar] [CrossRef]
- Aydin, M.E. Coordinating metaheuristic agents with swarm intelligence. J. Intell. Manuf. 2012, 23, 991–999. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Xiang, Z. Aggregation analysis for competitive multiagent systems with saddle points via switching strategies. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 2931–2943. [Google Scholar] [CrossRef]
- Yang, T.; Yi, X.; Wu, J.; Yuan, Y.; Wu, D.; Meng, Z.; Hong, Y.; Wang, H.; Lin, Z.; Johansson, K.H. A survey of distributed optimization. Annu. Rev. Control 2019, 47, 278–305. [Google Scholar] [CrossRef]
- Xiao, W.; Cao, L.; Li, H.; Lu, R. Observer-based adaptive consensus control for nonlinear multi-agent systems with time-delay. Sci. China Inf. Sci. 2020, 63, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Brown, R.; Rossi, F.; Solovey, K.; Tsao, M.; Wolf, M.T.; Pavone, M. On Local Computation for Network-Structured Convex Optimization in Multi-Agent Systems. IEEE Trans. Control Netw. Syst. 2021, 8, 542–554. [Google Scholar] [CrossRef]
- Shen, Q.; Shi, P.; Zhu, J.; Wang, S.; Shi, Y. Neural Networks-Based Distributed Adaptive Control of Nonlinear Multiagent Systems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1010–1021. [Google Scholar] [CrossRef]
- Calvaresi, D.; Cid, Y.D.; Marinoni, M.; Dragoni, A.F.; Najjar, A.; Schumacher, M. Real-time multi-agent systems: Rationality, formal model, and empirical results. Auton. Agents Multi-Agent Syst. 2021, 35, 12. [Google Scholar] [CrossRef]
- Eriksson, A.; Hansson, J. Distributed Optimisation in Multi-Agent Systems Through Deep Reinforcement Learning; TRITA-EECS-EX: Stockholm, Sweden, 2019. [Google Scholar]
- Yu, H.; Shen, Z.; Leung, C.; Miao, C.; Lesser, V.R. A survey of multi-agent trust management systems. IEEE Access 2013, 1, 35–50. [Google Scholar]
- Tariverdi, A.; Talebi, H.A.; Shafiee, M. Fault-tolerant consensus of nonlinear multi-agent systems with directed link failures, communication noise and actuator faults. Int. J. Control 2021, 94, 60–74. [Google Scholar] [CrossRef]
- Calvaresi, D.; Marinoni, M.; Sturm, A.; Schumacher, M.; Buttazzo, G. The challenge of real-time multi-agent systems for enabling IoT and CPS. In Proceedings of the International Conference on Web Intelligence, Leipzig, Germany, 23–26 August 2017; pp. 356–364. [Google Scholar]
- Cheng, L.; Hou, Z.G.; Tan, M.; Lin, Y.; Zhang, W. Neural-network-based adaptive leader-following control for multiagent systems with uncertainties. IEEE Trans. Neural Netw. 2010, 21, 1351–1358. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Han, Q.L.; Ge, X.; Zhang, X.M. An overview of recent advances in event-triggered consensus of multiagent systems. IEEE Trans. Cybern. 2017, 48, 1110–1123. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Wang, Z.; Liu, X. A Stochastic Sampled-Data Approach to Distributed H∞ Filtering in Sensor Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 2237–2246. [Google Scholar] [CrossRef]
- Heemels, W.H.; Donkers, M.; Teel, A.R. Periodic event-triggered control for linear systems. IEEE Trans. Autom. Control 2012, 58, 847–861. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L.; Ding, L.; Wang, Y.L.; Zhang, X.M. Dynamic event-triggered distributed coordination control and its applications: A survey of trends and techniques. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3112–3125. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Zhang, B.L. An overview and deep investigation on sampled-data-based event-triggered control and filtering for networked systems. IEEE Trans. Ind. Inform. 2016, 13, 4–16. [Google Scholar] [CrossRef]
- Negenborn, R.; Maestre, J. Distributed Model Predictive Control: An overview of features and research opportunities. In Proceedings of the 11th IEEE International Conference on Networking, Sensing and Control, Miami, FL, USA, 7–9 April 2014. [Google Scholar]
- Liu, P.; Xiao, F.; Wei, B.; Wang, A. Distributed constrained optimization problem of heterogeneous linear multi-agent systems with communication delays. Syst. Control Lett. 2021, 155, 105002. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Chen, C.P. Adaptive neural control of uncertain MIMO nonlinear systems with state and input constraints. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1318–1330. [Google Scholar] [CrossRef] [PubMed]
- Wen, G.; Duan, Z.; Yu, W.; Chen, G. Consensus in multi-agent systems with communication constraints. Int. J. Robust Nonlinear Control 2012, 22, 170–182. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, H.; Ma, H.; Zhou, Q.; Yu, Z. Distributed adaptive consensus tracking control for nonlinear multi-agent systems with state constraints. Appl. Math. Comput. 2018, 326, 16–32. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, Z.; Srinivasan, D.; Yu, L. Leader-follower consensus of multiagent systems with energy constraints: A Markovian system approach. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1727–1736. [Google Scholar] [CrossRef]
- Marcotte, R.J.; Wang, X.; Mehta, D.; Olson, E. Optimizing multi-robot communication under bandwidth constraints. Auton. Robot. 2020, 44, 43–55. [Google Scholar] [CrossRef]
- Ricci, A.; Piunti, M.; Viroli, M. Environment programming in multi-agent systems: An artifact-based perspective. Auton. Agents Multi-Agent Syst. 2011, 23, 158–192. [Google Scholar] [CrossRef]
- Weyns, D.; Omicini, A.; Odell, J. Environment as a first class abstraction in multiagent systems. Auton. Agents Multi-Agent Syst. 2007, 14, 5–30. [Google Scholar] [CrossRef] [Green Version]
- Platon, E.; Mamei, M.; Sabouret, N.; Honiden, S.; Parunak, H.V.D. Mechanisms for environments in multi-agent systems: Survey and opportunities. Auton. Agents Multi-Agent Syst. 2007, 14, 31–47. [Google Scholar] [CrossRef]
- Johansson, K.; Rosolia, U.; Ubellacker, W.; Singletary, A.; Ames, A.D. Mixed Observable RRT: Multi-Agent Mission-Planning in Partially Observable Environments. arXiv 2021, arXiv:2110.01002. [Google Scholar]
- Bourne, R.A.; Excelente-Toledo, C.B.; Jennings, N.R. Run-time selection of coordination mechanisms in multi-agent systems. In 14th European Conference on Artificial Intelligence (ECAI-2000); IOS Press: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Chen, S.; Wang, M.; Li, Q. Second-order consensus of hybrid multi-agent systems with unknown disturbances via sliding mode control. IEEE Access 2020, 8, 34973–34980. [Google Scholar] [CrossRef]
- Hernandez-Leal, P.; Kartal, B.; Taylor, M.E. A survey and critique of multiagent deep reinforcement learning. Auton. Agents Multi-Agent Syst. 2019, 33, 750–797. [Google Scholar] [CrossRef] [Green Version]
- Wagner, G.; Choset, H. Path planning for multiple agents under uncertainty. In Proceedings of the Twenty-Seventh International Conference on Automated Planning and Scheduling, Pittsburgh, PA, USA, 18–23 June 2017. [Google Scholar]
- Li, Z.; Duan, Z.; Xie, L.; Liu, X. Distributed robust control of linear multi-agent systems with parameter uncertainties. Int. J. Control 2012, 85, 1039–1050. [Google Scholar] [CrossRef] [Green Version]
- Amato, C. Decision-Making Under Uncertainty in Multi-Agent and Multi-Robot Systems: Planning and Learning. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018; pp. 5662–5666. [Google Scholar]
- Peng, Z.; Zhang, J.; Hu, J.; Huang, R.; Ghosh, B.K. Optimal containment control of continuous-time multi-agent systems with unknown disturbances using data-driven approach. Sci. China Inf. Sci. 2020, 63, 209205. [Google Scholar] [CrossRef]
- Hu, G. Robust consensus tracking for an integrator-type multi-agent system with disturbances and unmodelled dynamics. Int. J. Control 2011, 84, 1–8. [Google Scholar] [CrossRef]
- Khazaeni, Y.; Cassandras, C.G. Event-driven cooperative receding horizon control for multi-agent systems in uncertain environments. IEEE Trans. Control Netw. Syst. 2016, 5, 409–422. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, C.; Ding, Z. Robust consensus control of uncertain multi-agent systems with input delay: A model reduction method. Int. J. Robust Nonlinear Control 2017, 27, 1874–1894. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Xu, H. Mean field game and decentralized intelligent adaptive pursuit evasion strategy for massive multi-agent system under uncertain environment. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 5382–5387. [Google Scholar]
- Busoniu, L.; Babuska, R.; De Schutter, B. A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 156–172. [Google Scholar] [CrossRef] [Green Version]
- Khan, N. Learning to Cooperate Using Deep Reinforcement Learning in a Multi-Agent System. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2020. [Google Scholar]
- Omidshafiei, S.; Pazis, J.; Amato, C.; How, J.P.; Vian, J. Deep decentralized multi-task multi-agent reinforcement learning under partial observability. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 2681–2690. [Google Scholar]
- Shang, W.; Li, Q.; Qin, Z.; Yu, Y.; Meng, Y.; Ye, J. Partially observable environment estimation with uplift inference for reinforcement learning based recommendation. Mach. Learn. 2021, 110, 2603–2640. [Google Scholar] [CrossRef]
- Wang, R.E.; Everett, M.; How, J.P. R-MADDPG for partially observable environments and limited communication. arXiv 2020, arXiv:2002.06684. [Google Scholar]
- Li, W.; Xie, L.; Zhang, J.F. Containment control of leader-following multi-agent systems with Markovian switching network topologies and measurement noises. Automatica 2015, 51, 263–267. [Google Scholar] [CrossRef]
- Perez, J.; Silander, T. Non-markovian control with gated end-to-end memory policy networks. arXiv 2017, arXiv:1705.10993. [Google Scholar]
- Mansour, A.M. Cooperative Multi-Agent Vehicle-to-Vehicle Wireless Network in a Noisy Environment. Int. J. Circuits, Syst. Signal Process. 2021, 15, 135–148. [Google Scholar] [CrossRef]
- Búrdalo, L.; Terrasa, A.; Julián, V.; García-Fornes, A. The information flow problem in multi-agent systems. Eng. Appl. Artif. Intell. 2018, 70, 130–141. [Google Scholar] [CrossRef]
- Baki, B.; Bouzid, M.; Ligęza, A.; Mouaddib, A.I. A centralized planning technique with temporal constraints and uncertainty for multi-agent systems. J. Exp. Theor. Artif. Intell. 2006, 18, 331–364. [Google Scholar] [CrossRef]
- Ge, M.; Bangui, H.; Buhnova, B. Big data for internet of things: A survey. Future Gener. Comput. Syst. 2018, 87, 601–614. [Google Scholar] [CrossRef]
- Khan, A.; Zhang, C.; Lee, D.D.; Kumar, V.; Ribeiro, A. Scalable centralized deep multi-agent reinforcement learning via policy gradients. arXiv 2018, arXiv:1805.08776. [Google Scholar]
- Huang, D.; Jiang, H.; Yu, Z.; Hu, C.; Fan, X. Cluster-delay consensus in MASs with layered intermittent communication: A multi-tracking approach. Nonlinear Dyn. 2019, 95, 1713–1730. [Google Scholar] [CrossRef]
- Ge, X.; Yang, F.; Han, Q.L. Distributed networked control systems: A brief overview. Inf. Sci. 2017, 380, 117–131. [Google Scholar] [CrossRef]
- Sayed, A.H. Adaptive networks. Proc. IEEE 2014, 102, 460–497. [Google Scholar] [CrossRef]
- Zhuge, H. Knowledge flow network planning and simulation. Decis. Support Syst. 2006, 42, 571–592. [Google Scholar] [CrossRef]
- Zhang, C.; Lesser, V.R.; Abdallah, S. Self-organization for coordinating decentralized reinforcement learning. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems: IFAAMAS, Richland, SC, USA, 9–13 May 2010; Volume 1, pp. 739–746. [Google Scholar]
- Althnian, A.; Agah, A. Evolutionary learning of goal-oriented communication strategies in multi-agent systems. J. Autom. Mob. Robot. Intell. Syst. 2015, 9, 52–64. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Q. Informational design of dynamic multi-agent system. arXiv 2021, arXiv:2105.03052. [Google Scholar]
- Das, A.; Gervet, T.; Romoff, J.; Batra, D.; Parikh, D.; Rabbat, M.; Pineau, J. Tarmac: Targeted multi-agent communication. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 1538–1546. [Google Scholar]
- Wang, D.; Wang, Z.; Chen, M.; Wang, W. Distributed optimization for multi-agent systems with constraints set and communication time-delay over a directed graph. Inf. Sci. 2018, 438, 1–14. [Google Scholar] [CrossRef]
- Jiang, X.; Xia, G.; Feng, Z. Output consensus of high-order linear multi-agent systems with time-varying delays. IET Control Theory Appl. 2019, 13, 1084–1094. [Google Scholar] [CrossRef]
- Tan, X.; Cao, J.; Li, X.; Alsaedi, A. Leader-following mean square consensus of stochastic multi-agent systems with input delay via event-triggered control. IET Control Theory Appl. 2017, 12, 299–309. [Google Scholar] [CrossRef]
- Han, F.; Wei, G.; Ding, D.; Song, Y. Local condition based consensus filtering with stochastic nonlinearities and multiple missing measurements. IEEE Trans. Autom. Control 2017, 62, 4784–4790. [Google Scholar] [CrossRef]
- Cholvy, L.; da Costa Pereira, C. Usefulness of information for goal achievement. In International Conference on Principles and Practice of Multi-Agent Systems; Springer: Cham, Switzerland, 2019; pp. 123–137. [Google Scholar]
- Djaidja, S.; Wu, Q.H.; Fang, H. Leader-following consensus of double-integrator multi-agent systems with noisy measurements. Int. J. Control Autom. Syst. 2015, 13, 17–24. [Google Scholar] [CrossRef]
- Bacciu, D.; Micheli, A.; Podda, M. Edge-based sequential graph generation with recurrent neural networks. Neurocomputing 2020, 416, 177–189. [Google Scholar] [CrossRef] [Green Version]
- Atluri, G.; Karpatne, A.; Kumar, V. Spatio-temporal data mining: A survey of problems and methods. ACM Comput. Surv. (CSUR) 2018, 51, 1–41. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [Green Version]
- Laurence, E.; Doyon, N.; Dubé, L.J.; Desrosiers, P. Spectral dimension reduction of complex dynamical networks. Phys. Rev. X 2019, 9, 011042. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Cui, P.; Zhu, W. Structural deep network embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1225–1234. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Mahdavi, S.; Khoshraftar, S.; An, A. Dynamic joint variational graph autoencoders. arXiv 2019, arXiv:1910.01963. [Google Scholar]
- Barros, C.D.; Mendonça, M.R.; Vieira, A.B.; Ziviani, A. A Survey on Embedding Dynamic Graphs. arXiv 2021, arXiv:2101.01229. [Google Scholar] [CrossRef]
- Sayama, H.; Laramee, C. Generative network automata: A generalized framework for modeling adaptive network dynamics using graph rewritings. In Adaptive Networks; Springer: Heidelberg, Germany, 2009; pp. 311–332. [Google Scholar]
- Taheri, A.; Gimpel, K.; Berger-Wolf, T. Learning Graph Representations with Recurrent Neural Network Autoencoders; KDD Deep Learning Day: London, UK, 2018. [Google Scholar]
- Papoudakis, G.; Albrecht, S.V. Variational autoencoders for opponent modeling in multi-agent systems. arXiv 2020, arXiv:2001.10829. [Google Scholar]
- Zhang, K.; Ying, H.; Dai, H.N.; Li, L.; Peng, Y.; Guo, K.; Yu, H. Compacting Deep Neural Networks for Internet of Things: Methods and Applications. IEEE Internet Things J. 2021, 8, 11935–11959. [Google Scholar] [CrossRef]
- Lomuscio, A.; Qu, H.; Russo, F. Automatic data-abstraction in model checking multi-agent systems. In International Workshop on Model Checking and Artificial Intelligence; Springer: Heidelberg, Germany, 2010; pp. 52–68. [Google Scholar]
- Rassam, M.A.; Zainal, A.; Maarof, M.A. An adaptive and efficient dimension reduction model for multivariate wireless sensor networks applications. Appl. Soft Comput. 2013, 13, 1978–1996. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Lin, T.; Huh, J.; Stauffer, C.; Lim, S.N.; Isola, P. Learning to Ground Multi-Agent Communication with Autoencoders. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–14 December 2021; Volume 34. [Google Scholar]
- García, N.M. Multi-agent system for anomaly detection in Industry 4.0 using Machine Learning techniques. ADCAIJ Adv. Distrib. Comput. Artif. Intell. J. 2019, 8, 33–40. [Google Scholar]
- Tahsien, S.M. A Neural Network Guided Genetic Algorithm for Flexible Flow Shop Scheduling Problem with Sequence Dependent Setup Time. Ph.D. Thesis, The University of Guelph, Guelph, ON, Canada, 2020. [Google Scholar]
- Ma, X.; Wu, J.; Xue, S.; Yang, J.; Sheng, Q.Z.; Xiong, H. A Comprehensive Survey on Graph Anomaly Detection with Deep Learning. arXiv 2021, arXiv:2106.07178. [Google Scholar] [CrossRef]
- Ding, K.; Li, J.; Liu, H. Interactive anomaly detection on attributed networks. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, VIC, Australia, 11–15 February 2019; pp. 357–365. [Google Scholar]
- Duan, D.; Tong, L.; Li, Y.; Lu, J.; Shi, L.; Zhang, C. AANE: Anomaly Aware Network Embedding For Anomalous Link Detection. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 1002–1007. [Google Scholar]
- Zheng, M.; Zhou, C.; Wu, J.; Pan, S.; Shi, J.; Guo, L. Fraudne: A joint embedding approach for fraud detection. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Ruff, L.; Vandermeulen, R.; Goernitz, N.; Deecke, L.; Siddiqui, S.A.; Binder, A.; Müller, E.; Kloft, M. Deep one-class classification. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4393–4402. [Google Scholar]
- Louati, F.; Ktata, F.B. A deep learning-based multi-agent system for intrusion detection. SN Appl. Sci. 2020, 2, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Zhao, L. A systematic survey on deep generative models for graph generation. arXiv 2020, arXiv:2007.06686. [Google Scholar]
- You, J.; Ying, R.; Ren, X.; Hamilton, W.; Leskovec, J. Graphrnn: Generating realistic graphs with deep auto-regressive models. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5708–5717. [Google Scholar]
- Zhou, D.; Zheng, L.; Han, J.; He, J. A data-driven graph generative model for temporal interaction networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 23–27 August 2020; pp. 401–411. [Google Scholar]
- Peng, H.; Wang, H.; Du, B.; Bhuiyan, M.Z.A.; Ma, H.; Liu, J.; Wang, L.; Yang, Z.; Du, L.; Wang, S.; et al. Spatial temporal incidence dynamic graph neural networks for traffic flow forecasting. Inf. Sci. 2020, 521, 277–290. [Google Scholar] [CrossRef]
- Li, L.; Yao, J.; Wenliang, L.; He, T.; Xiao, T.; Yan, J.; Wipf, D.; Zhang, Z. GRIN: Generative Relation and Intention Network for Multi-agent Trajectory Prediction. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–14 December 2021; Volume 34. [Google Scholar]
- Guastella, D.; Camps, V.; Gleizes, M.P. Multi-agent Systems for Estimating Missing Information in Smart Cities. In 11th International Conference on Agents and Artificial Intelligence-ICAART 2019; SCITEPRESS-Science and Technology Springer: Prague, Czech Republic, 2019; pp. 214–223. [Google Scholar]
- Feng, W.; Zhang, C.; Zhang, W.; Han, J.; Wang, J.; Aggarwal, C.; Huang, J. STREAMCUBE: Hierarchical spatio-temporal hashtag clustering for event exploration over the Twitter stream. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Korea, 13–17 April 2015; pp. 1561–1572. [Google Scholar]
- Zhao, L.; Akoglu, L. On using classification datasets to evaluate graph outlier detection: Peculiar observations and new insights. Big Data 2021, 2021, 69. [Google Scholar] [CrossRef] [PubMed]
- Teng, X.; Yan, M.; Ertugrul, A.M.; Lin, Y.R. Deep into hypersphere: Robust and unsupervised anomaly discovery in dynamic networks. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018. [Google Scholar]
- Ierardi, C.; Orihuela, L.; Jurado, I. Distributed estimation techniques for cyber-physical systems: A systematic review. Sensors 2019, 19, 4720. [Google Scholar] [CrossRef] [Green Version]
- Jing, G.; Zheng, Y.; Wang, L. Flocking of multi-agent systems with multiple groups. Int. J. Control 2014, 87, 2573–2582. [Google Scholar] [CrossRef]
- Chen, K.; Wang, J.; Zhang, Y.; Lewis, F.L. Cluster consensus of heterogeneous linear multi-agent systems. IET Control Theory Appl. 2018, 12, 1533–1542. [Google Scholar] [CrossRef]
- Belghache, E.; Georgé, J.P.; Gleizes, M.P. DREAM: Dynamic data relation extraction using adaptive multi-agent systems. In Proceedings of the 2017 Twelfth International Conference on Digital Information Management (ICDIM), Fukuoka, Japan, 12–14 September 2017; pp. 292–297. [Google Scholar]
- Li, W.; Yang, J.Y. Comparing networks from a data analysis perspective. In International Conference on Complex Sciences; Springer: Heidelberg, Germany, 2009; pp. 1907–1916. [Google Scholar]
- Kim, J.; Lee, J.G. Community detection in multi-layer graphs: A survey. ACM SIGMOD Rec. 2015, 44, 37–48. [Google Scholar] [CrossRef]
- Banka, A.A.; Naaz, R. Large Scale Graph Analytics for Communities Using Graph Neural Networks. In International Conference on Computational Data and Social Networks; Springer: Cham, Switzerland, 2020; pp. 39–47. [Google Scholar]
- Liu, F.; Xue, S.; Wu, J.; Zhou, C.; Hu, W.; Paris, C.; Nepal, S.; Yang, J.; Yu, P.S. Deep learning for community detection: Progress, challenges and opportunities. arXiv 2020, arXiv:2005.08225. [Google Scholar]
- Cazabet, R.; Rossetti, G.; Amblard, F. Dynamic Community Detection; Springer: New York, NY, USA, 2017. [Google Scholar]
- Rossetti, G.; Cazabet, R. Community discovery in dynamic networks: A survey. ACM Comput. Surv. (CSUR) 2018, 51, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Liao, H.; Chu, T. Aggregation and splitting in self-driven swarms. Phys. A Stat. Mech. Appl. 2012, 391, 3988–3994. [Google Scholar] [CrossRef]
- Ogston, E.; Overeinder, B.; Van Steen, M.; Brazier, F. A method for decentralized clustering in large multi-agent systems. In Proceedings of the Second International Joint Conference on Autonomous Agents and Multiagent Systems, Melbourne, VIC, Australia, 14–18 July 2003; pp. 789–796. [Google Scholar]
- Cai, N.; Diao, C.; Khan, M.J. A novel clustering method based on quasi-consensus motions of dynamical multiagent systems. Complexity 2017, 2017, 4978613. [Google Scholar] [CrossRef] [Green Version]
- Kadar, M.; Muntean, M.V.; Csabai, T. A Multi-agent System with Self-optimization for Automated Clustering (MASAC). In Agents and Multi-Agent Systems: Technologies and Applications 2019; Springer: Singapore, 2019; pp. 117–128. [Google Scholar]
- Sequeira, P.; Antunes, C. Real-time sensory pattern mining for autonomous agents. In International Workshop on Agents and Data Mining Interaction; Springer: Heidelberg, Germany, 2010; pp. 71–83. [Google Scholar]
- Fournier-Viger, P.; He, G.; Cheng, C.; Li, J.; Zhou, M.; Lin, J.C.W.; Yun, U. A survey of pattern mining in dynamic graphs. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2020, 10, e1372. [Google Scholar] [CrossRef]
- Halder, S.; Samiullah, M.; Lee, Y.K. Supergraph based periodic pattern mining in dynamic social networks. Expert Syst. Appl. 2017, 72, 430–442. [Google Scholar] [CrossRef]
- Jin, R.; McCallen, S.; Almaas, E. Trend motif: A graph mining approach for analysis of dynamic complex networks. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; pp. 541–546. [Google Scholar]
- Cheng, Z.; Flouvat, F.; Selmaoui-Folcher, N. Mining recurrent patterns in a dynamic attributed graph. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Cham, Switzerland, 2017; pp. 631–643. [Google Scholar]
- Kaytoue, M.; Pitarch, Y.; Plantevit, M.; Robardet, C. Triggering patterns of topology changes in dynamic graphs. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China, 17–20 August 2014; pp. 158–165. [Google Scholar]
- Fournier-Viger, P.; Cheng, C.; Cheng, Z.; Lin, J.C.W.; Selmaoui-Folcher, N. Mining significant trend sequences in dynamic attributed graphs. Knowl.-Based Syst. 2019, 182, 104797. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; Ahmad, M.S.; Mostafa, S.A. Norm-based behavior regulating technique for multi-agent in complex adaptive systems. IEEE Access 2019, 7, 126662–126678. [Google Scholar] [CrossRef]
- Venkatesan, D. A Novel Agent-Based Enterprise Level System Development Technology. Ph.D. Thesis, Anna University, Tamil Nadu, India, 2018. [Google Scholar]
- Bellifemine, F.; Bergenti, F.; Caire, G.; Poggi, A. JADE—A java agent development framework. In Multi-Agent Programming; Springer: Boston, MA, USA, 2005; pp. 125–147. [Google Scholar]
- DeLoach, S.A.; Garcia-Ojeda, J.C. O-MaSE: A customisable approach to designing and building complex, adaptive multi-agent systems. Int. J. Agent-Oriented Softw. Eng. 2010, 4, 244–280. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, R.C.; Ferrando, A. A Review of Agent-Based Programming for Multi-Agent Systems. Computers 2021, 10, 16. [Google Scholar] [CrossRef]
- Kravari, K.; Bassiliades, N. A survey of agent platforms. J. Artif. Soc. Soc. Simul. 2015, 18, 11. [Google Scholar] [CrossRef]
- Bordini, R.H.; El Fallah Seghrouchni, A.; Hindriks, K.; Logan, B.; Ricci, A. Agent programming in the cognitive era. Auton. Agents Multi-Agent Syst. 2020, 34, 37. [Google Scholar] [CrossRef]
- Costantini, S. ACE: A flexible environment for complex event processing in logical agents. In International Workshop on Engineering Multi-Agent Systems; Springer: Cham, Switzerland, 2015; pp. 70–91. [Google Scholar]
- Araujo, P.; Rodríguez, S.; Hilaire, V. A metamodeling approach for the identification of organizational smells in multi-agent systems: Application to ASPECS. Artif. Intell. Rev. 2018, 49, 183–210. [Google Scholar] [CrossRef]
- Boissier, O.; Bordini, R.H.; Hübner, J.F.; Ricci, A. Dimensions in programming multi-agent systems. Knowl. Eng. Rev. 2019, 34, e2. [Google Scholar] [CrossRef]
- Rahimi, H.; Trentin, I.F.; Ramparany, F.; Boissier, O. SMASH: A Semantic-enabled Multi-agent Approach for Self-adaptation of Human-centered IoT. arXiv 2021, arXiv:2105.14915. [Google Scholar]
- Baek, Y.M.; Song, J.; Shin, Y.J.; Park, S.; Bae, D.H. A meta-model for representing system-of-systems ontologies. In Proceedings of the 2018 IEEE/ACM 6th International Workshop on Software Engineering for Systems-of-Systems (SESoS), Gothenburg, Sweden, 29 May 2018; pp. 1–7. [Google Scholar]
- Pigazzini, I.; Briola, D.; Fontana, F.A. Architectural Technical Debt of Multiagent Systems Development Platforms. In Proceedings of the WOA 2021: Workshop “From Objects to Agents”, Bologna, Italy, 1–3 September 2021. [Google Scholar]
- Jazayeri, A.; Bass, E.J. Agent-Oriented Methodologies Evaluation Frameworks: A Review. Int. J. Softw. Eng. Knowl. Eng. 2020, 30, 1337–1370. [Google Scholar] [CrossRef]
- Logan, B. An agent programming manifesto. Int. J. Agent-Oriented Softw. Eng. 2018, 6, 187–210. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, F.L.; Costa, A.H.R. A survey on transfer learning for multiagent reinforcement learning systems. J. Artif. Intell. Res. 2019, 64, 645–703. [Google Scholar] [CrossRef] [Green Version]
- Dusparic, I.; Cahill, V. Autonomic multi-policy optimization in pervasive systems: Overview and evaluation. ACM Trans. Auton. Adapt. Syst. (TAAS) 2012, 7, 1–25. [Google Scholar] [CrossRef]
- Sharma, P.K.; Fernandez, R.; Zaroukian, E.; Dorothy, M.; Basak, A.; Asher, D.E. Survey of recent multi-agent reinforcement learning algorithms utilizing centralized training. In Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications III; International Society for Optics and Photonics: Orlando, FL, USA, 2021; Volume 11746, p. 117462K. [Google Scholar]
- Foerster, J.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual multi-agent policy gradients. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- De Lemos, R.; Giese, H.; Müller, H.A.; Shaw, M.; Andersson, J.; Litoiu, M.; Schmerl, B.; Tamura, G.; Villegas, N.M.; Vogel, T.; et al. Software engineering for self-adaptive systems: A second research roadmap. In Software Engineering for Self-Adaptive Systems II; Springer: Heidelberg, Germany, 2013; pp. 1–32. [Google Scholar]
- Panait, L.; Luke, S. Cooperative multi-agent learning: The state of the art. Auton. Agents Multi-Agent Syst. 2005, 11, 387–434. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. Qmix: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4295–4304. [Google Scholar]
- Chen, G. A New Framework for Multi-Agent Reinforcement Learning–Centralized Training and Exploration with Decentralized Execution via Policy Distillation. arXiv 2019, arXiv:1910.09152. [Google Scholar]
- Pesce, E.; Montana, G. Improving coordination in small-scale multi-agent deep reinforcement learning through memory-driven communication. Mach. Learn. 2020, 109, 1727–1747. [Google Scholar] [CrossRef] [Green Version]
- Czarnowski, I.; Jędrzejowicz, P. An agent-based framework for distributed learning. Eng. Appl. Artif. Intell. 2011, 24, 93–102. [Google Scholar] [CrossRef]
- D’Angelo, M. Engineering Decentralized Learning in Self-Adaptive Systems. Ph.D. Thesis, Linnaeus University Press, Vaxjo, Sweden, 2021. [Google Scholar]
- Shi, P.; Yan, B. A survey on intelligent control for multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 161–175. [Google Scholar] [CrossRef]
- Poveda, J.I.; Benosman, M.; Teel, A.R. Hybrid online learning control in networked multiagent systems: A survey. Int. J. Adapt. Control Signal Process. 2019, 33, 228–261. [Google Scholar] [CrossRef]
- Tahbaz-Salehi, A.; Jadbabaie, A. A necessary and sufficient condition for consensus over random networks. IEEE Trans. Autom. Control 2008, 53, 791–795. [Google Scholar] [CrossRef] [Green Version]
- Svítek, M.; Skobelev, P.; Kozhevnikov, S. Smart City 5.0 as an urban ecosystem of Smart services. In International Workshop on Service Orientation in Holonic and Multi-Agent Manufacturing; Springer: Cham, Switzerland, 2019; pp. 426–438. [Google Scholar]
- Alves, B.R.; Alves, G.V.; Borges, A.P.; Leitão, P. Experimentation of negotiation protocols for consensus problems in smart parking systems. In International Conference on Industrial Applications of Holonic and Multi-Agent Systems; Springer: Cham, Switzerland, 2019; pp. 189–202. [Google Scholar]
- Yu, H.; Yang, Z.; Sinnott, R.O. Decentralized big data auditing for smart city environments leveraging blockchain technology. IEEE Access 2018, 7, 6288–6296. [Google Scholar] [CrossRef]
- Yang, S.; Tan, S.; Xu, J.X. Consensus based approach for economic dispatch problem in a smart grid. IEEE Trans. Power Syst. 2013, 28, 4416–4426. [Google Scholar] [CrossRef]
- De Sousa, A.L.; De Oliveira, A.S. Distributed MAS with Leaderless Consensus to Job-Shop Scheduler in a Virtual Smart Factory with Modular Conveyors. In Proceedings of the 2020 Latin American Robotics Symposium (LARS), 2020 Brazilian Symposium on Robotics (SBR) and 2020 Workshop on Robotics in Education (WRE), Natal, Brazil, 9–13 November 2020; pp. 1–6. [Google Scholar]
- Cardona, G.A.; Calderon, J.M. Robot swarm navigation and victim detection using rendezvous consensus in search and rescue operations. Appl. Sci. 2019, 9, 1702. [Google Scholar] [CrossRef] [Green Version]
- Saad, A.; Faddel, S.; Youssef, T.; Mohammed, O.A. On the implementation of IoT-based digital twin for networked microgrids resiliency against cyber attacks. IEEE Trans. Smart Grid 2020, 11, 5138–5150. [Google Scholar] [CrossRef]
- Lee, S.; Yang, Y.; Nayel, M.; Zhai, Y. Leader-follower irrigation system management with Shapley value. In International Workshop on Automation, Control, and Communication Engineering (IWACCE 2021); SPIE: Beijing, China, 2021; Volume 11929, pp. 8–14. [Google Scholar]
- Song, Z.; Liu, Y.; Tan, M. Robust pinning synchronization of complex cyberphysical networks under mixed attack strategies. Int. J. Robust Nonlinear Control 2019, 29, 1265–1278. [Google Scholar] [CrossRef]
- Miao, G.; Ma, Q. Group consensus of the first-order multi-agent systems with nonlinear input constraints. Neurocomputing 2015, 161, 113–119. [Google Scholar] [CrossRef]
- Yamakami, T. A dimensional framework to evaluate coverage of IoT services in city platform as a service. In Proceedings of the 2017 International Conference on Service Systems and Service Management, Dalian, China, 16–18 June 2017; pp. 1–5. [Google Scholar]
- Etemadyrad, N.; Li, Q.; Zhao, L. Deep Graph Spectral Evolution Networks for Graph Topological Evolution. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 7358–7366. [Google Scholar]
- Ren, W.; Beard, R.W. Formation feedback control for multiple spacecraft via virtual structures. IEE Proc. Control Theory Appl. 2004, 151, 357–368. [Google Scholar] [CrossRef] [Green Version]
- Cortés, J. Global and robust formation-shape stabilization of relative sensing networks. Automatica 2009, 45, 2754–2762. [Google Scholar] [CrossRef]
- Krick, L.; Broucke, M.E.; Francis, B.A. Stabilisation of infinitesimally rigid formations of multi-robot networks. Int. J. Control 2009, 82, 423–439. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Jalalkamali, P. Collaborative target tracking using distributed Kalman filtering on mobile sensor networks. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 1100–1105. [Google Scholar]
- Wang, H.; Shi, D.; Song, B. A dynamic role assignment formation control algorithm based on hungarian method. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018; pp. 687–696. [Google Scholar]
- Barve, A.; Nene, M.J. Survey of Flocking Algorithms in multi-agent Systems. Int. J. Comput. Sci. Issues (IJCSI) 2013, 10, 110–117. [Google Scholar]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef] [Green Version]
- Abdelwahab, S.; Hamdaoui, B. Flocking virtual machines in quest for responsive iot cloud services. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Haghshenas, H.; Badamchizadeh, M.A.; Baradarannia, M. Containment control of heterogeneous linear multi-agent systems. Automatica 2015, 54, 210–216. [Google Scholar] [CrossRef]
- Ji, M.; Ferrari-Trecate, G.; Egerstedt, M.; Buffa, A. Containment control in mobile networks. IEEE Trans. Autom. Control 2008, 53, 1972–1975. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, H.T.; Meng, H.; Hu, B.; Chen, D.; Chen, G. Moving target surrounding control of linear multiagent systems with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 1705–1715. [Google Scholar] [CrossRef]
- Hu, B.B.; Zhang, H.T.; Liu, B.; Meng, H.; Chen, G. Distributed Surrounding Control of Multiple Unmanned Surface Vessels With Varying Interconnection Topologies. IEEE Trans. Control Syst. Technol. 2021, 30, 400–407. [Google Scholar] [CrossRef]
- Li, M.; Wang, Z.; Li, K.; Liao, X.; Hone, K.; Liu, X. Task Allocation on Layered Multiagent Systems: When Evolutionary Many-Objective Optimization Meets Deep Q-Learning. IEEE Trans. Evol. Comput. 2021, 25, 842–855. [Google Scholar] [CrossRef]
- Amini, M.H.; Mohammadi, J.; Kar, S. Promises of fully distributed optimization for iot-based smart city infrastructures. In Optimization, Learning, and Control for Interdependent Complex Networks; Springer: Cham, Switzerland, 2020; pp. 15–35. [Google Scholar]
- Raju, L.; Sankar, S.; Milton, R. Distributed optimization of solar micro-grid using multi agent reinforcement learning. Procedia Comput. Sci. 2015, 46, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, M.A.; Jin, T.; Su, W. Multi-agent energy management of smart islands using primal-dual method of multipliers. Energy 2020, 208, 118306. [Google Scholar] [CrossRef]
- Olszewski, R.; Pałka, P.; Turek, A. Solving “Smart City” Transport Problems by Designing Carpooling Gamification Schemes with Multi-Agent Systems: The Case of the So-Called “Mordor of Warsaw”. Sensors 2018, 18, 141. [Google Scholar] [CrossRef] [Green Version]
- Euchi, J.; Zidi, S.; Laouamer, L. A new distributed optimization approach for home healthcare routing and scheduling problem. Decis. Sci. Lett. 2021, 10, 217–230. [Google Scholar] [CrossRef]
- Lin, F.r.; Kuo, H.c.; Lin, S.m. The enhancement of solving the distributed constraint satisfaction problem for cooperative supply chains using multi-agent systems. Decis. Support Syst. 2008, 45, 795–810. [Google Scholar] [CrossRef]
- Hsieh, F.S. Dynamic configuration and collaborative scheduling in supply chains based on scalable multi-agent architecture. J. Ind. Eng. Int. 2019, 15, 249–269. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Yang, S.; Wang, J. A collective neurodynamic approach to distributed constrained optimization. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1747–1758. [Google Scholar] [CrossRef]
- Necoara, I.; Nedelcu, V.; Dumitrache, I. Parallel and distributed optimization methods for estimation and control in networks. J. Process Control 2011, 21, 756–766. [Google Scholar] [CrossRef] [Green Version]
- Rana, M.M.; Abdelhadi, A.; Shireen, W. Monitoring Operating Conditions of Wireless Power Transfer Systems Using Distributed Estimation Process. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–4. [Google Scholar]
- Guastella, D.A.; Campss, V.; Gleizes, M.P. A Cooperative Multi-Agent System for Crowd Sensing Based Estimation in Smart Cities. IEEE Access 2020, 8, 183051–183070. [Google Scholar] [CrossRef]
- Tan, R.K.; Bora, Ş. Exploiting of Adaptive Multi Agent System Theory in Modeling and Simulation: A Survey. J. Appl. Math. Comput. (JAMC) 2018, 1, 21–26. [Google Scholar] [CrossRef]
- Rossi, F.; Bandyopadhyay, S.; Wolf, M.T.; Pavone, M. Multi-Agent Algorithms for Collective Behavior: A structural and application-focused atlas. arXiv 2021, arXiv:2103.11067. [Google Scholar]
- Chen, F.; Ren, W. Multi-Agent Control: A Graph-Theoretic Perspective. J. Syst. Sci. Complex. 2021, 34, 1973–2002. [Google Scholar] [CrossRef]
- Zelazo, D.; Rahmani, A.; Mesbahi, M. Agreement via the edge laplacian. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 2309–2314. [Google Scholar]
- You, K.; Xie, L. Network topology and communication data rate for consensusability of discrete-time multi-agent systems. IEEE Trans. Autom. Control 2011, 56, 2262–2275. [Google Scholar] [CrossRef]
- Shi, C.X.; Yang, G.H. Robust consensus control for a class of multi-agent systems via distributed PID algorithm and weighted edge dynamics. Appl. Math. Comput. 2018, 316, 73–88. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y. Cluster synchronization of a class of multi-agent systems with a bipartite graph topology. Sci. China Inf. Sci. 2014, 57, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Shoham, Y.; Leyton-Brown, K. Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Zhu, M.; Martínez, S. Distributed coverage games for energy-aware mobile sensor networks. SIAM J. Control Optim. 2013, 51, 1–27. [Google Scholar] [CrossRef]
- Sengupta, S.; Kambhampati, S. Multi-agent reinforcement learning in bayesian stackelberg markov games for adaptive moving target defense. arXiv 2020, arXiv:2007.10457. [Google Scholar]
- Sun, C.; Wang, X.; Liu, J. Evolutionary game theoretic approach for optimal resource allocation in multi-agent systems. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 5588–5592. [Google Scholar]
- Yan, B.; Shi, P.; Lim, C.C.; Shi, Z. Optimal robust formation control for heterogeneous multi-agent systems based on reinforcement learning. Int. J. Robust Nonlinear Control 2021, 32, 2683–2704. [Google Scholar] [CrossRef]
- Wai, H.T.; Yang, Z.; Wang, Z.; Hong, M. Multi-agent reinforcement learning via double averaging primal-dual optimization. arXiv 2018, arXiv:1806.00877. [Google Scholar]
- Jian, L.; Zhao, Y.; Hu, J.; Li, P. Distributed inexact consensus-based ADMM method for multi-agent unconstrained optimization problem. IEEE Access 2019, 7, 79311–79319. [Google Scholar] [CrossRef]
- Kapoor, S. Multi-agent reinforcement learning: A report on challenges and approaches. arXiv 2018, arXiv:1807.09427. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Decentralized multi-agent reinforcement learning with networked agents: Recent advances. arXiv 2019, arXiv:1912.03821. [Google Scholar] [CrossRef]
- Papoudakis, G.; Christianos, F.; Rahman, A.; Albrecht, S.V. Dealing with non-stationarity in multi-agent deep reinforcement learning. arXiv 2019, arXiv:1906.04737. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Cham, Switzerland, 2021; pp. 321–384. [Google Scholar]
- Du, W.; Ding, S. A survey on multi-agent deep reinforcement learning: From the perspective of challenges and applications. Artif. Intell. Rev. 2021, 54, 3215–3238. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 1928–1937. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Lee, L.C.; Nwana, H.S.; Ndumu, D.T.; De Wilde, P. The stability, scalability and performance of multi-agent systems. BT Technol. J. 1998, 16, 94–103. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Sun, C.; Yu, Y. Fixed-time consensus of multi-agent systems with input delay and uncertain disturbances via event-triggered control. Inf. Sci. 2019, 480, 261–272. [Google Scholar] [CrossRef]
- Chli, M.; De Wilde, P.; Goossenaerts, J.; Abramov, V.; Szirbik, N.; Correia, L.; Mariano, P.; Ribeiro, R. Stability of multi-agent systems. In Proceedings of the SMC’03 Conference Proceedings, 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme-System Security and Assurance (Cat. No. 03CH37483), Washington, DC, USA, 8 October 2003; Volume 1, pp. 551–556. [Google Scholar]
- Maadani, M.; Butcher, E.A. Consensus stability in multi-agent systems with periodically switched communication topology using Floquet theory. Trans. Inst. Meas. Control 2021, 43, 1239–1254. [Google Scholar] [CrossRef]
- Miao, G.; Xu, S.; Zou, Y. Consentability for high-order multi-agent systems under noise environment and time delays. J. Frankl. Inst. 2013, 350, 244–257. [Google Scholar] [CrossRef]
- Wang, B.; Fang, X.; Zhao, Y. Stability Analysis of Cooperative Control for Heterogeneous Multi-agent Systems with Nonlinear Dynamics. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 13–15 February 2019; pp. 1446–1453. [Google Scholar]
- Liu, Y.; Min, H.; Wang, S.; Liu, Z.; Liao, S. Distributed consensus of a class of networked heterogeneous multi-agent systems. J. Frankl. Inst. 2014, 351, 1700–1716. [Google Scholar] [CrossRef]
- Sun, X.; Cassandras, C.G.; Meng, X. Exploiting submodularity to quantify near-optimality in multi-agent coverage problems. Automatica 2019, 100, 349–359. [Google Scholar] [CrossRef]
- Katsuura, H.; Fujisaki, Y. Optimality of consensus protocols for multi-agent systems with interaction. In Proceedings of the 2014 IEEE International Symposium on Intelligent Control (ISIC), Juan Les Pins, France, 8–10 October 2014; pp. 282–285. [Google Scholar]
- Yang, X.; Wang, J.; Tan, Y. Robustness analysis of leader–follower consensus for multi-agent systems characterized by double integrators. Syst. Control Lett. 2012, 61, 1103–1115. [Google Scholar] [CrossRef]
- Wang, G.; Xu, M.; Wu, Y.; Zheng, N.; Xu, J.; Qiao, T. Using machine learning for determining network robustness of multi-agent systems under attacks. In Pacific Rim International Conference on Artificial Intelligence; Springer: Cham, Switzerland, 2018; pp. 491–498. [Google Scholar]
- Baldoni, M.; Baroglio, C.; Micalizio, R. Fragility and Robustness in Multiagent Systems. In International Workshop on Engineering Multi-Agent Systems; Springer: Cham, Switzerland, 2020; pp. 61–77. [Google Scholar]
- Tian, Y.P.; Liu, C.L. Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations. Automatica 2009, 45, 1347–1353. [Google Scholar] [CrossRef]
- Münz, U.; Papachristodoulou, A.; Allgöwer, F. Delay robustness in consensus problems. Automatica 2010, 46, 1252–1265. [Google Scholar] [CrossRef]
- Trentelman, H.L.; Takaba, K.; Monshizadeh, N. Robust synchronization of uncertain linear multi-agent systems. IEEE Trans. Autom. Control 2013, 58, 1511–1523. [Google Scholar] [CrossRef] [Green Version]
- Minsky, N.H.; Murata, T. On manageability and robustness of open multi-agent systems. In International Workshop on Software Engineering for Large-Scale Multi-Agent Systems; Springer: Heidelberg, Germany, 2003; pp. 189–206. [Google Scholar]
- Kim, J.; Yang, J.; Shim, H.; Kim, J.S. Robustness of synchronization in heterogeneous multi-agent systems. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3821–3826. [Google Scholar]
- Zelazo, D.; Bürger, M. On the robustness of uncertain consensus networks. IEEE Trans. Control Netw. Syst. 2015, 4, 170–178. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Feng, G.; Shi, Y.; Srinivasan, D. Physical safety and cyber security analysis of multi-agent systems: A survey of recent advances. IEEE/CAA J. Autom. Sin. 2021, 8, 319–333. [Google Scholar] [CrossRef]
- Jung, Y.; Kim, M.; Masoumzadeh, A.; Joshi, J.B. A survey of security issue in multi-agent systems. Artif. Intell. Rev. 2012, 37, 239–260. [Google Scholar] [CrossRef] [Green Version]
- Chevalier-Boisvert, M.; Willems, L.; Pal, S. Minimalistic Gridworld Environment for OpenAI Gym. 2018. Available online: https://github.com/maximecb/gym-minigrid (accessed on 10 January 2022).
- Mezgebe, T.T.; Demesure, G.; El Haouzi, H.B.; Pannequin, R.; Thomas, A. CoMM: A consensus algorithm for multi-agent-based manufacturing system to deal with perturbation. Int. J. Adv. Manuf. Technol. 2019, 105, 3911–3926. [Google Scholar] [CrossRef]
- Foerster, J.N.; Assael, Y.M.; De Freitas, N.; Whiteson, S. Learning to communicate with deep multi-agent reinforcement learning. arXiv 2016, arXiv:1605.06676. [Google Scholar]
- Du, Y.; Wang, S.; Guo, X.; Cao, H.; Hu, S.; Jiang, J.; Varala, A.; Angirekula, A.; Zhao, L. GraphGT: Machine Learning Datasets for Graph Generation and Transformation. In Proceedings of the Thirty-Fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), Virtual, 6–14 December 2021. [Google Scholar]
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection; SNAP: Santa Monica, CA, USA, 2014. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nezamoddini, N.; Gholami, A. A Survey of Adaptive Multi-Agent Networks and Their Applications in Smart Cities. Smart Cities 2022, 5, 318-347. https://doi.org/10.3390/smartcities5010019
Nezamoddini N, Gholami A. A Survey of Adaptive Multi-Agent Networks and Their Applications in Smart Cities. Smart Cities. 2022; 5(1):318-347. https://doi.org/10.3390/smartcities5010019
Chicago/Turabian StyleNezamoddini, Nasim, and Amirhosein Gholami. 2022. "A Survey of Adaptive Multi-Agent Networks and Their Applications in Smart Cities" Smart Cities 5, no. 1: 318-347. https://doi.org/10.3390/smartcities5010019
APA StyleNezamoddini, N., & Gholami, A. (2022). A Survey of Adaptive Multi-Agent Networks and Their Applications in Smart Cities. Smart Cities, 5(1), 318-347. https://doi.org/10.3390/smartcities5010019





