Influence of Embedded Charging Units Characteristics on Long-Term Structural Behavior of E-Roads
Abstract
:1. Introduction
- Optimization of void CU material, shape, and dimension, considering a 2D Finite Element approach and typical material characteristics from scientific literature;
- Fatigue resistance of e-road_void CU, considering some of the optimized void CU geometries. This part is separated into two steps: the theoretical fatigue assessment, which allows to calculate the critical load repetitions leading to pavement failure, and the case study of Viale Forlanini in Milan, which allows to determine the pavement DI under specific traffic conditions;
- Rutting resistance of e-road_void CU, considering some of the optimized void CU geometries. In line with the previous one, also this part is divided in two steps: the theoretical rutting assessment, which allows to calculate the critical load cycles leading to rut an e-road pavement for a particular Rut Depth (RD) and the case study of Viale Forlanini in Milan, which allows to determine the pavement RD under specific traffic conditions.
2. Materials and Methods
2.1. Optimization of Void CU Material, Shape and Dimension
- Void CU_R1: this is the simplest geometry, showing a rectangular cavity (R1), as studied in previous Author’s research [2];
- Void CU_R2: this geometry has a vertical cavity partition that leads to two rectangular cavities (R2);
- Void CU_C4: this geometry is characterized by four circular cavities (C4) equally distributed along CU horizontal axis;
- Void CU_C6: this geometry is characterized by six circular cavities (C6) equally distributed along CU horizontal axis.
2.2. Methodology
2.2.1. Fatigue
- Theoretical assessment: since the actual traffic is unknown, Miner’s law cannot be applied in a traditional manner. Considering that, theoretically, fatigue cracking appears at DI equal to 1, it is possible to calculate the number of traffic repetitions that leads to that damage value.
- Case study: the actual traffic in Viale Forlanini (Milan) is available, therefore, Miner’s law can be used to calculate pavement DI. Two traffic conditions are examined, as explained in [19]: traffic on one lane—conservative assumption—(5.75 × 107 ESAL) and traffic equally distributed on two lanes (2.88 × 107 ESAL).
2.2.2. Rutting
- Four e-road cross-sectional geometries are analyzed: R1_35, R2_35, C4_33, and C6_33;
- The characteristics of each material are listed below:
- Three load positions are examined: centered on CU, CU edge, and CU center.
- Theoretical assessment: since the actual traffic is unknown, RD cannot be calculated. Therefore, the aim of this part is the identification of traffic repetition numbers that lead to rut a pavement for a defined depth equal to 1.5 cm [12,13,14]. A spreadsheet solver is developed to calculate those critical cycle numbers.
- Case study: the actual traffic in Viale Forlanini (Milan) is available, therefore, it is possible to calculate the RD. As shown in [19], two traffic conditions are studied: total traffic vehicles on one or two lanes.
3. Results and Discussion
3.1. Theoretical Assessment Results
3.2. Case Study Results
- R2_35 rut depth decreases 0.7% (centered on CU) and 6.1% (CU edge) with respect to the circular cavities outcomes;
- R2_35 rut depth increases 37.4% (CU center) with respect to the circular cavities value.
- Fatigue Damage Index: DIFatigue = DI, and
- Rutting Damage Index: DIRutting = RD/1.5 cm
4. Conclusions
- Several CU geometries are suggested to provide the electronic field specialists with different alternatives for satisfying electrical technology needs, while ensuring long-lasting pavement structural performance.
- Among the investigated CU geometries, both rectangular and circular cavities can be used for electrical technologies accommodation; among the others, R2_35 (two rectangular cavities, 295 mm in width and 80 mm in heigh each, 47,200 mm2 of total area) and C6_33 (six circular cavities, 100 mm in diameter each, 47,124 mm2 of total area) maximize CU cavity area.
- Although R2_35 and C6_33 are characterized by the same cavity area, the obtained results are really different with better outcomes for the rectangular cavities. This means that the CU cavity shape affects the final outcomes. Therefore, both shape and dimension are essential to assess the void CU structural behavior.
- By comparing fatigue and rutting results, it is possible to note that the critical phenomenon is fatigue. In fact, the theoretical assessment demonstrates that the numbers of critical load cycles in fatigue are lower (about three order of magnitude) than the traffic repetitions computed for rutting.
- R2_35 shows different fatigue (the best one) and rutting (the worst one) behaviors when the load is on CU center. Probably, these results can be attributed to the high vertical strains recorded in the wearing course during rutting assessment.
- Load positions affect the theoretical results. In fact, when the load is centered on CU or on CU center, fatigue/rutting results are quite similar under the same CU geometry. The only exception is for rutting of R2_35, which is characterized by high difference between results (that are obtained considering the above load positions). For all geometries and considering both phenomena (except for R2_35-rutting), the most critical load position is load along CU edge.
- For both phenomena, the configuration described by F6_33 and load along CU edge leads to the lower results.
- The case study results corroborate the outcomes of the theoretical part, also in presence of the most conservative assumption of traffic (on one lane).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Commission. European Alternative Fuels Observatory. Available online: https://alternative-fuels-observatory.ec.europa.eu/transport-mode/road/european-union-eu27/country-comparison (accessed on 17 June 2022).
- Nodari, C.; Crispino, M.; Pernetti, M.; Toraldo, E. Structural Analysis of Bituminous Road Pavements Embedding Charging Units for Electric Vehicles. In Proceedings of the Computational Science and Its Applications—ICCSA 2021: 21st International Conference, Cagliari, Italy, 13–16 September 2021; Volume 1, pp. 149–162. [Google Scholar]
- Mahmoudzadeh Andwari, A.; Pesiridis, A.; Rajoo, S.; Martinez-Botas, R.; Esfahanian, V. A Review of Battery Electric Vehicle Technology and Readiness Levels. Renew. Sustain. Energy Rev. 2017, 78, 414–430. [Google Scholar] [CrossRef]
- Gill, J.S.; Bhavsar, P.; Chowdhury, M.; Johnson, J.; Taiber, J.; Fries, R. Infrastructure Cost Issues Related to Inductively Coupled Power Transfer for Electric Vehicles. Procedia Comput. Sci. 2014, 32, 545–552. [Google Scholar] [CrossRef] [Green Version]
- Ajanovic, A.; Haas, R. Dissemination of Electric Vehicles in Urban Areas: Major Factors for Success. Energy 2016, 115, 1451–1458. [Google Scholar] [CrossRef]
- Chabot, A.; Deep, P. 2D Multilayer Solution for an Electrified Road with a Built-in Charging Box. Road Mater. Pavement Des. 2019, 20, S590–S603. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Balieu, R.; Córdoba, E.; Kringos, N. Towards an Understanding of the Structural Performance of Future Electrified Roads: A Finite Element Simulation Study. Int. J. Pavement Eng. 2019, 20, 204–215. [Google Scholar] [CrossRef]
- Marghani, A.; Wilson, D.; Larkin, T. Performance of Inductive Power Transfer-Based Pavements of Electrified Roads. In Proceedings of the 2019 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), London, UK, 18–21 June 2019; pp. 196–201. [Google Scholar] [CrossRef]
- Soares, L.; Wang, H. A Study on Renewed Perspectives of Electrified Road for Wireless Power Transfer of Electric Vehicles. Renew. Sustain. Energy Rev. 2022, 158, 112110. [Google Scholar] [CrossRef]
- Ara, Inc. Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures—Appendix II-1; National Cooperative Highway Research Program, Transportation Research Board, National Research Council: Champaign, IL, USA, 2004. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). Mechanistic-Empirical Pavement Design Guide—A Manual of Practice (MEPDG-2); American Association of State Highway and Transportation Officials: Washington, DC, USA, 2015; ISBN 9781560515975. [Google Scholar]
- Lister, N.W.; Addis, R.R. Field Observations of Rutting and Their Practical Implications. Transp. Res. Rec. 1977. Available online: https://onlinepubs.trb.org/Onlinepubs/trr/1977/640/640-004.pdf (accessed on 27 May 2022).
- D6433–20; Standard Practice for Roads and Parking Lots Pavement Condition Index Surveys. ASTM International: West Conshohocken, PA, USA, 2020.
- Direzione Generale Infrastrutture e Mobilità—Regione Lombardia Catalogo Dei Dissesti Delle Pavimentazioni Stradali 2005. Available online: https://docplayer.it/3761481-Catalogo-dei-dissesti-delle-pavimentazioni-stradali.html (accessed on 17 June 2022).
- Veverka, V. Raming van de Spoordiepte Bij Wegen Met Een Bitumineuze Verhanding. Wegentechniek 1979, 24, 25–45. [Google Scholar]
- Monismith, C.L. Analytically Based Asphalt Pavement Design and Rehabilitation: Theory to Practice, 1962–1992. Transp. Res. Rec. 1992, 1354, 5–26. [Google Scholar]
- EN 206-1; Concrete—Part 1: Specification, Performance, Production and Conformity, European Commission. NSAI: Dublin, Ireland, 2006.
- Ministero delle Infrastrutture e dei Trasporti. Aggiornamento Delle “Norme Tecniche per Le Costruzioni”; 2018. Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 27 May 2022).
- Nodari, C.; Crispino, M.; Toraldo, E. Fatigue Effects of Embedding Electric Vehicles Charging Units into Electrified Road. Case Stud. Constr. Mater. 2022, 16, e00848. [Google Scholar] [CrossRef]
- Nodari, C.; Crispino, M.; Toraldo, E. Laboratory Investigation on the Use of Recycled Materials in Bituminous Mixtures for Dense-Graded Wearing Course. Case Stud. Constr. Mater. 2021, 15, e00556. [Google Scholar] [CrossRef]
- Nodari, C.; Crispino, M.; Toraldo, E. Bituminous Mixtures with High Environmental Compatibility: Laboratory Investigation on the Use of Reclaimed Asphalt and Steel Slag Aggregates. Lect. Notes Civ. Eng. 2020, 76, 433–442. [Google Scholar] [CrossRef]







| Concrete Characteristics | |||||
|---|---|---|---|---|---|
| Bulk Density [N/m3] | Young’s Modulus [N/mm2] | Poisson’s Ratio [-] | Failure Tensile Stress [N/mm2] | ||
| Compressive strength classes of concrete | C20/25 | 23,000 | 25,000 | 0.20 | 2.21 |
| C30/37 | 33,000 | 2.90 | |||
| C40/45 | 35,000 | 3.51 | |||
| Concrete Young’s modulus [N/mm2] | ||||||
| 25,000 | 33,000 | 35,000 | ||||
| CU geometry | 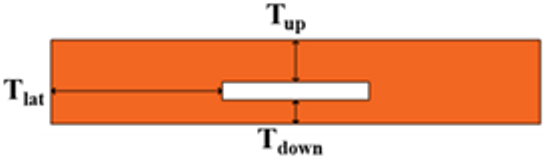 | Thickness [mm] | Up | 70 | 60 | 50 |
| Down | 40 | 40 | 40 | |||
| Lateral | 280 | 280 | 280 | |||
| Cavity dimension [mm] | 240 × 30 | 240 × 40 | 240 × 50 | |||
| Cavity area [mm2] | 7200 | 9600 | 12,000 | |||
| ID | R1_25 | R1_33 | R1_35 | |||
 | Thickness [mm] | Up | 20 | 20 | 20 | |
| Down | 40 | 40 | 40 | |||
| Lateral | 90 | 80 | 70 | |||
| Cavity dimension [mm] | 265 × 80 | 280 × 80 | 295 × 80 | |||
| Cavity area [mm2] | 42,400 | 44,800 | 47,200 | |||
| ID | R2_25 | R2_33 | R2_35 | |||
 | Thickness [mm] | Up | 30 | 20 | 20 | |
| Down | 30 | 20 | 20 | |||
| Lateral | 96 | 80 | 80 | |||
| Cavity dimension [mm] | 80 × 80 | 100 × 100 | 100 × 100 | |||
| Cavity area [mm2] | 20,106 | 31,416 | 31,416 | |||
| ID | C4_25 | C4_33 | C4_35 | |||
 | Thickness [mm] | Up | 30 | 20 | 20 | |
| Down | 30 | 20 | 20 | |||
| Lateral | 46 | 29 | 29 | |||
| Cavity dimension [mm] | 80 × 80 | 100 × 100 | 100 × 100 | |||
| Cavity area [mm2] | 30,159 | 47,124 | 47,124 | |||
| ID | C6_25 | C6_33 | C6_35 | |||
| Cross-Sectional Geometries | |||||
|---|---|---|---|---|---|
| Void CU_R1_35 | Void CU_R2_35 | Void CU_C4_33 | Void CU_C6_33 | ||
| Load centered on CU | σyy |  |  |  |  |
| σxx |  |  |  | 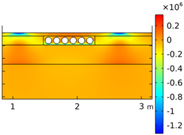 | |
| Load on CU edge | σyy |  |  | 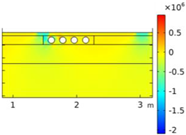 | 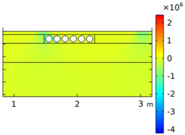 |
| σxx | 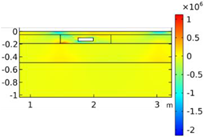 |  |  |  | |
| Load on CU center | σyy |  |  | 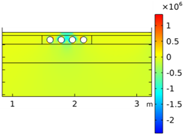 |  |
| σxx | 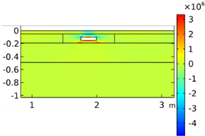 |  |  | 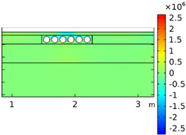 | |
| Bulk Density [N/mm3] | Young’s Modulus [N/mm2] | |||||||
|---|---|---|---|---|---|---|---|---|
| Winter | Spring/Autumn | Summer | ||||||
| Theoretical | Case Study | Theoretical E + 50% | Case Study 8 °C | Theoretical | Case Study 21 °C | Theoretical E − 50% | Case Study 34 °C | |
| Wearing Course | 24,000 | 24,240 | 8250 | 17,502 | 5500 | 8092 | 2750 | 2822 |
| Binder Course | 23,500 | 23,970 | 5250 | 17,242 | 3500 | 8610 | 1750 | 3363 |
| Theoretical | Case Study | |
|---|---|---|
| Maximum horizontal tensile strains εt [-] | According to geometries, load positions and temperatures | |
| Asphalt concrete Young’s modulus E [N/mm2] | According to Table 4 | |
| Binder content Vb [%] | 5.00 | 4.80 |
| Air void content Va [%] | 4.00 | 3.85 |
| HMA total thickness HHMA [m] | 0.19 | 0.19 |
| n [ESAL] Corresponding to DI = 1 | CU Geometries | ||||
|---|---|---|---|---|---|
| R1_35 | R2_35 | C4_33 | C6_33 | ||
| Load positions | Centered on CU | 3.83 × 108 | 4.19 × 108 | 4.45 × 108 | 4.11 × 108 |
| CU edge | 3.05 × 108 | 3.85 × 108 | 5.02 × 107 | 1.58 × 107 | |
| CU center | 4.38 × 108 | 4.46 × 108 | 4.23 × 108 | 3.88 × 108 | |
| Critical Load Cycles n [ESAL] | Cavity Area [m2] | ||
|---|---|---|---|
| Cross-sectional geometry | e-road_solid CU_25 | 2.46 × 108 | 0.0 |
| e-road_ void CU_R1_25 | 2.22 × 108 | 7.2 × 10−3 | |
| e-road_void CU_R1_35 | 3.05 × 108 | 12.0 × 10−3 | |
| e-road_ void CU_R2_35 | 3.85 × 108 | 47.2 × 10−3 | |
| e-road_ void CU_C4_33 | 5.02 × 107 | 31.4 × 10−3 | |
| e-road_ void CU_C6_33 | 1.58 × 107 | 47.1 × 10−3 |
| n [ESAL] Leading to RD = 1.5 cm | CU Geometries | ||||
|---|---|---|---|---|---|
| R1_35 | R2_35 | C4_33 | C6_33 | ||
| Load positions | Centered on CU | 1.22 × 1011 | 1.31 × 1011 | 1.30 × 1011 | 1.28 × 1011 |
| CU edge | 1.07 × 1011 | 5.92 × 1010 | 4.84 × 1010 | 2.91 × 1010 | |
| CU center | 1.28 × 1011 | 3.56 × 1010 | 1.26 × 1011 | 1.09 × 1011 | |
| Damage Index [-] | CU Geometries | |||||
|---|---|---|---|---|---|---|
| R1_35 | R2_35 | C4_33 | C6_33 | |||
| Load positions and traffic conditions | Centered on CU | One lane | 0.34 | 0.31 | 0.29 | 0.31 |
| Two lanes | 0.17 | 0.16 | 0.14 | 0.15 | ||
| CU edge | One lane | 0.40 | 0.35 | 0.86 | 2.79 | |
| Two lanes | 0.20 | 0.17 | 0.43 | 1.39 | ||
| CU center | One lane | 0.29 | 0.29 | 0.31 | 0.34 | |
| Two lanes | 0.14 | 0.15 | 0.15 | 0.17 | ||
| Rut Depth [cm] | CU Geometries | |||||
|---|---|---|---|---|---|---|
| R1_35 | R2_35 | C4_33 | C6_33 | |||
| Load positions and traffic conditions | Centered on CU | One lane | 0.145 | 0.142 | 0.143 | 0.143 |
| Two lanes | 0.123 | 0.120 | 0.121 | 0.121 | ||
| CU edge | One lane | 0.151 | 0.183 | 0.169 | 0.195 | |
| Two lanes | 0.127 | 0.154 | 0.143 | 0.165 | ||
| CU center | One lane | 0.142 | 0.224 | 0.154 | 0.163 | |
| Two lanes | 0.121 | 0.190 | 0.131 | 0.138 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nodari, C.; Ketabdari, M.; Crispino, M.; Toraldo, E. Influence of Embedded Charging Units Characteristics on Long-Term Structural Behavior of E-Roads. Smart Cities 2022, 5, 756-770. https://doi.org/10.3390/smartcities5030039
Nodari C, Ketabdari M, Crispino M, Toraldo E. Influence of Embedded Charging Units Characteristics on Long-Term Structural Behavior of E-Roads. Smart Cities. 2022; 5(3):756-770. https://doi.org/10.3390/smartcities5030039
Chicago/Turabian StyleNodari, Claudia, Misagh Ketabdari, Maurizio Crispino, and Emanuele Toraldo. 2022. "Influence of Embedded Charging Units Characteristics on Long-Term Structural Behavior of E-Roads" Smart Cities 5, no. 3: 756-770. https://doi.org/10.3390/smartcities5030039
APA StyleNodari, C., Ketabdari, M., Crispino, M., & Toraldo, E. (2022). Influence of Embedded Charging Units Characteristics on Long-Term Structural Behavior of E-Roads. Smart Cities, 5(3), 756-770. https://doi.org/10.3390/smartcities5030039








