Prediction and Evaluation of Electricity Price in Restructured Power Systems Using Gaussian Process Time Series Modeling
Abstract
:1. Introduction
1.1. Motivation
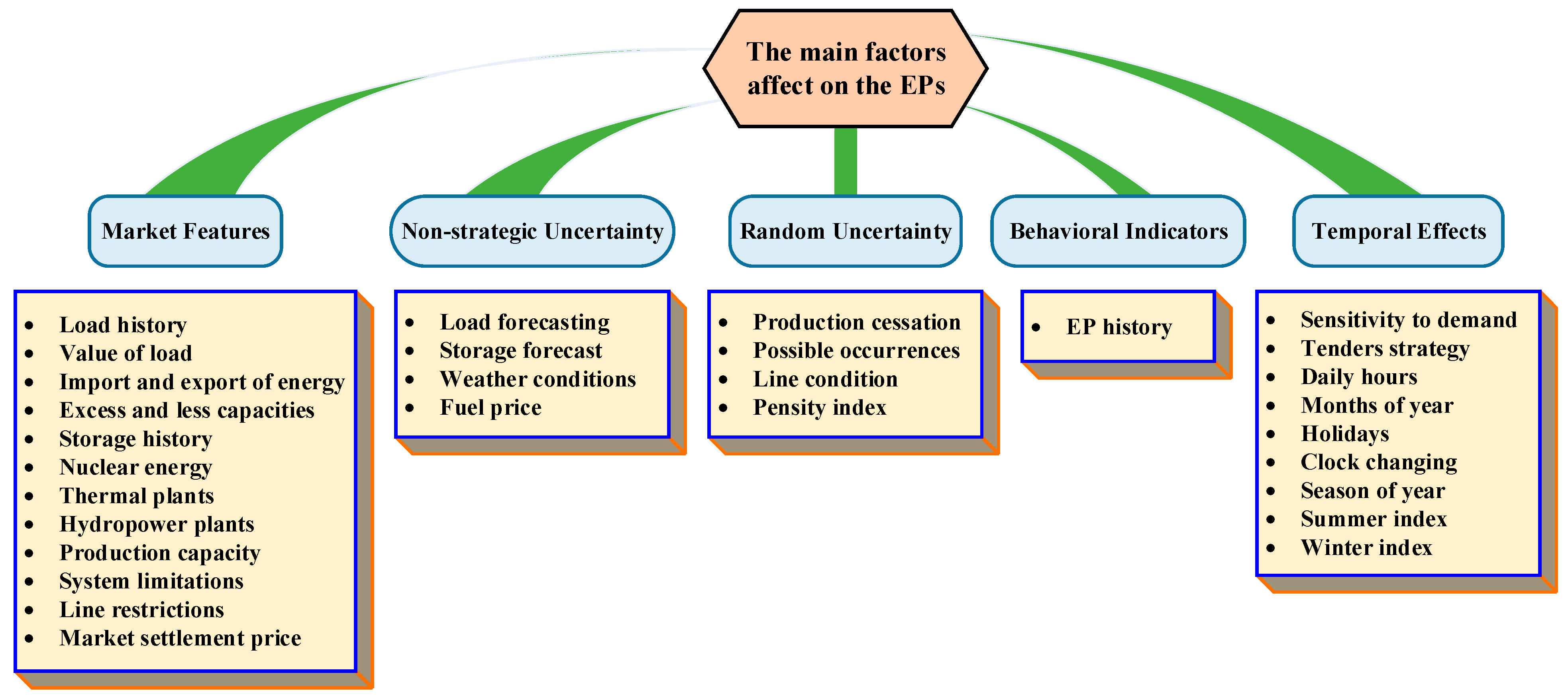
1.2. Related Works
- WT decomposition models: These models can decompose the main data of the problem into sub-data that contain various frequencies. Therefore, the outputs with low errors are extracted in the time domain. However, the WT model has a weakness as it needs more prior data for various decomposition levels [1]. Additionally, this model has few applications because it is a non-compatible approach [31].
- Singular Spectrum Analysis (SSA): this method eliminates the noises from the time series data [32], but its parameters are difficult to set or optimize. In other words, when the each of parameters was modified, the precision of the forecasting changed.
- Empirical Mode Decomposition (EMD): this algorithm in the original mode needs low hyper-parameters (HPs) that can find the local oscillations in the main data [33].
- Variational Mode Decomposition (VMD): this method is better than the three previous methods because of low data mining, easy modification of parameters, and better findings in the local oscillations, as reported in various studies [1,9,34]. However, this method cannot obtain acceptable accuracy in forecasting.
1.3. Contributions
- Using the robust method as the GP adapted to the time series to increase the accuracy of EP forecasting in a restructured system, which has not been accomplished before. The proposed method is based on the Gaussian distribution and can overcome to complicated problems, such as the prediction of wind speed, weather conditions, and electricity loads. In this paper, we used this method for EP forecasting.
- Using various GP models, including dynamic, static, direct, and indirect, and their combinations, to evaluate the models. The proposed models in the electricity markets of Spain and the United States (US) are simulated and examined in different seasons for a full investigation of the proposed method.
- Different covariance functions (CFs) are used to find the best one, unlike the previous papers, which used CF singularly. Finally, all models are validated using a comparison of the performance evaluation metrics in terms of accuracy and error.
- The results show that the best method is the dynamic indirect GP, which has the highest accuracy in comparison with the other methods. The proposed method is also compared to SVM and its accuracy is shown.
1.4. Paper Organization
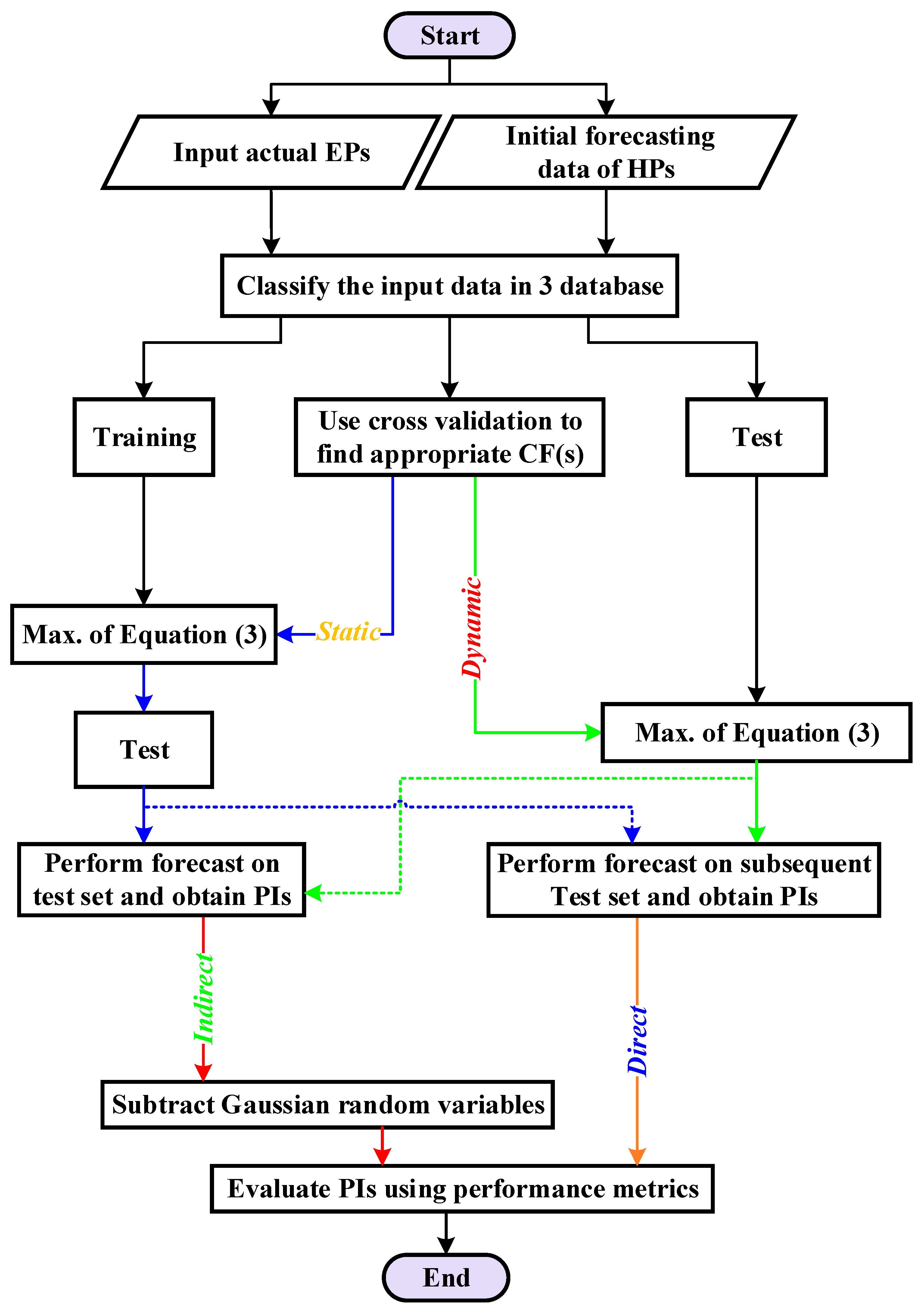
2. Methodology
2.1. The Gaussian Processes Models
2.2. GP for Time Series Modeling
2.3. The CFs for Time Series
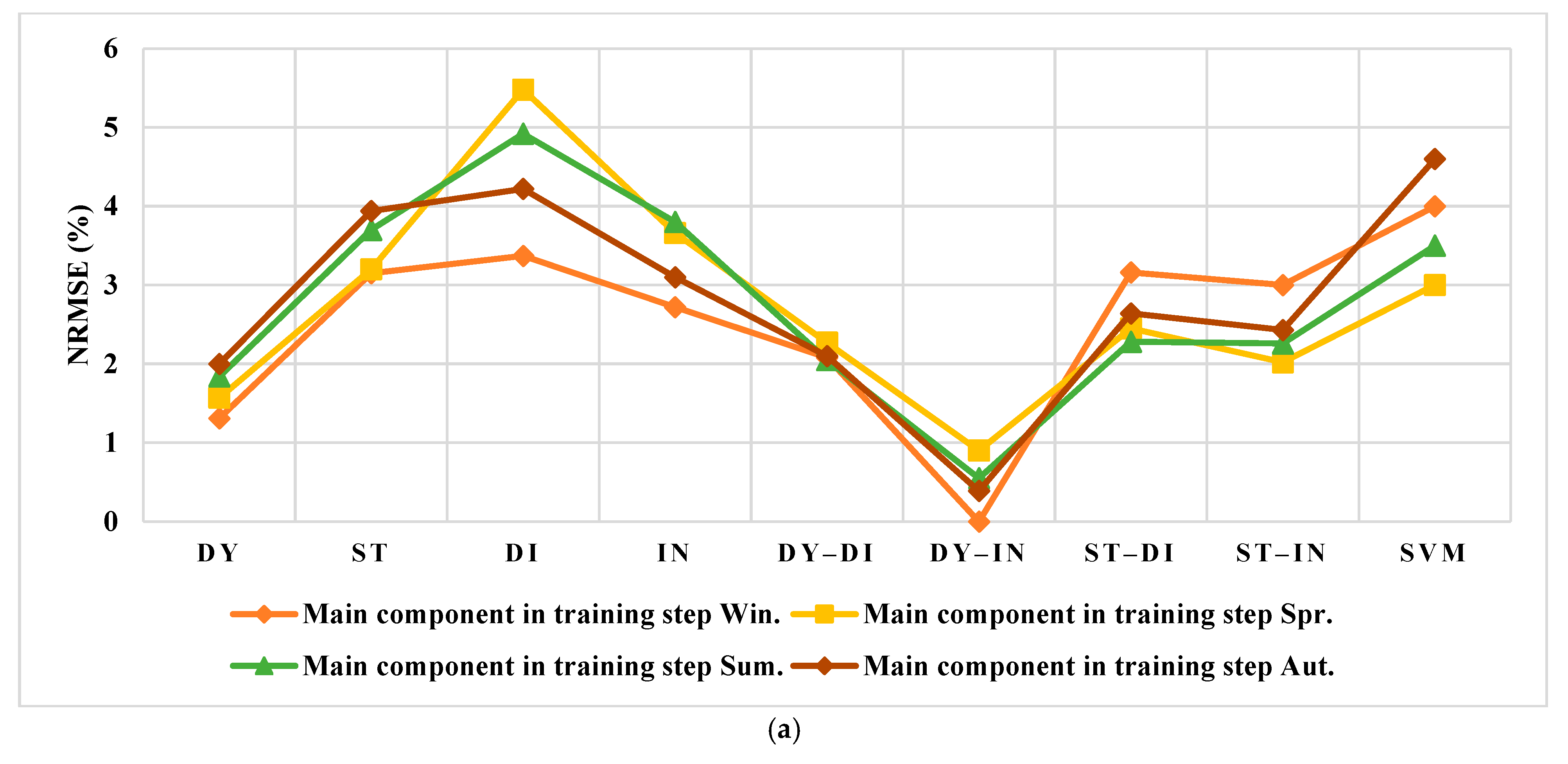
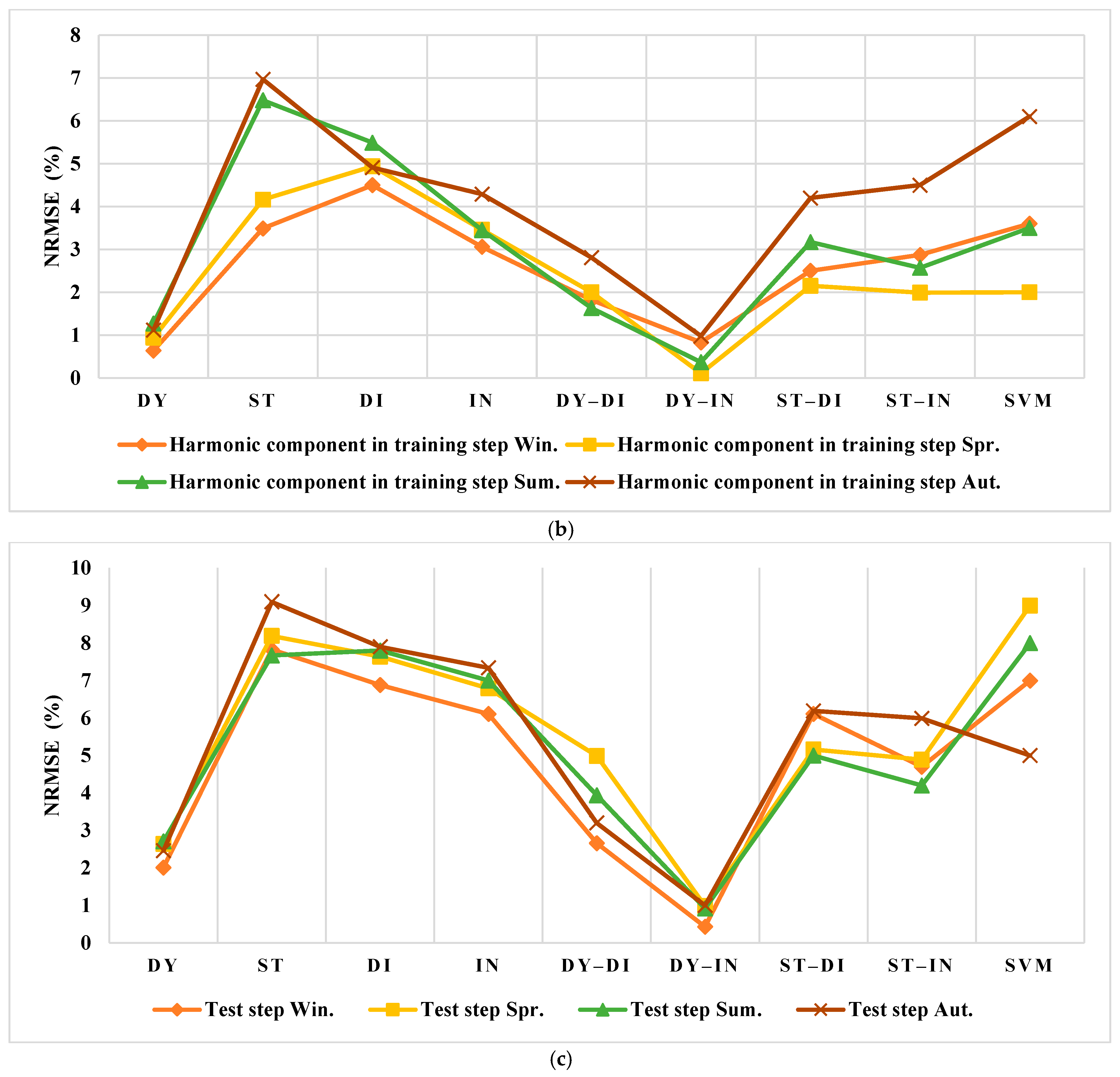
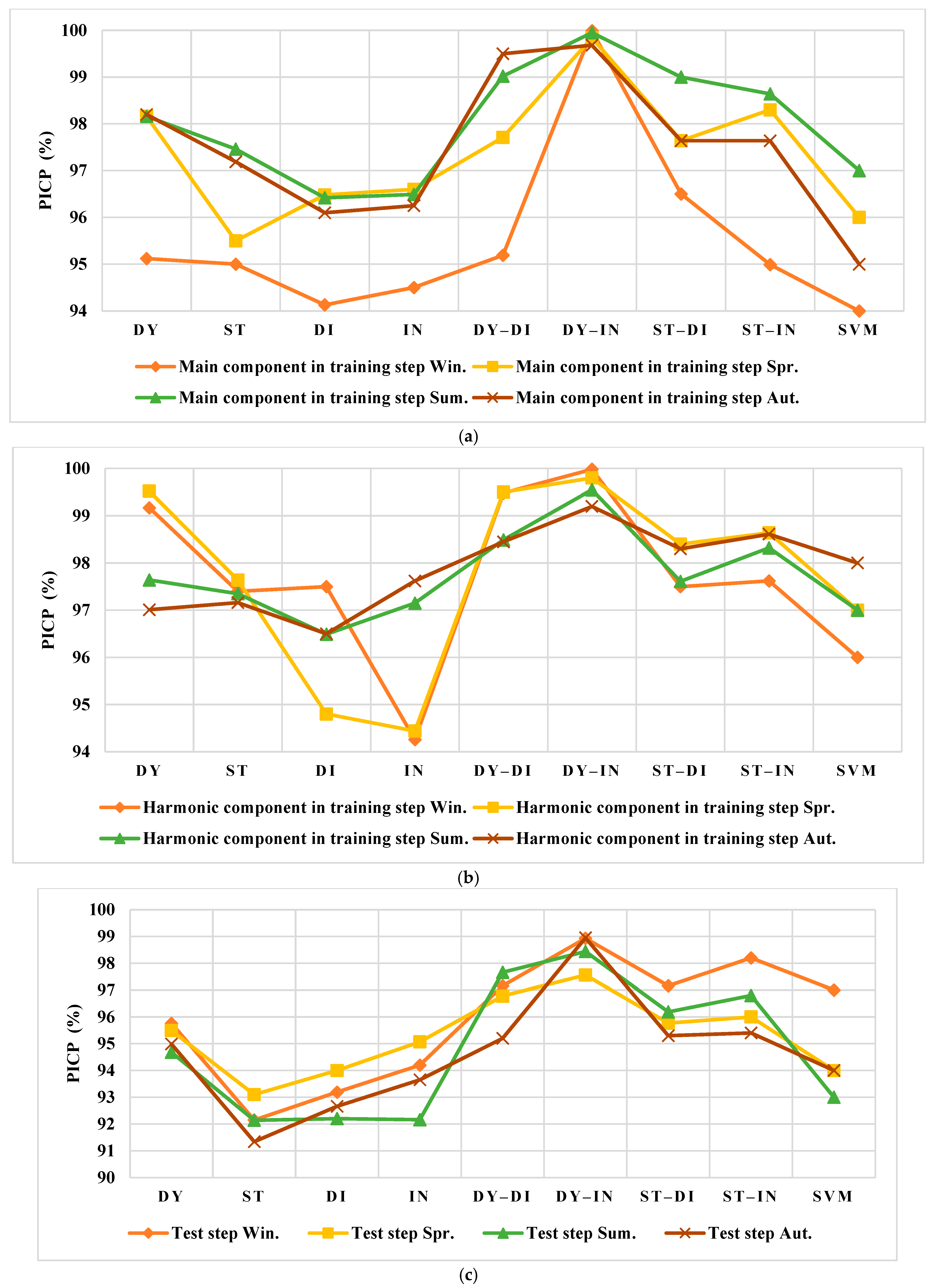
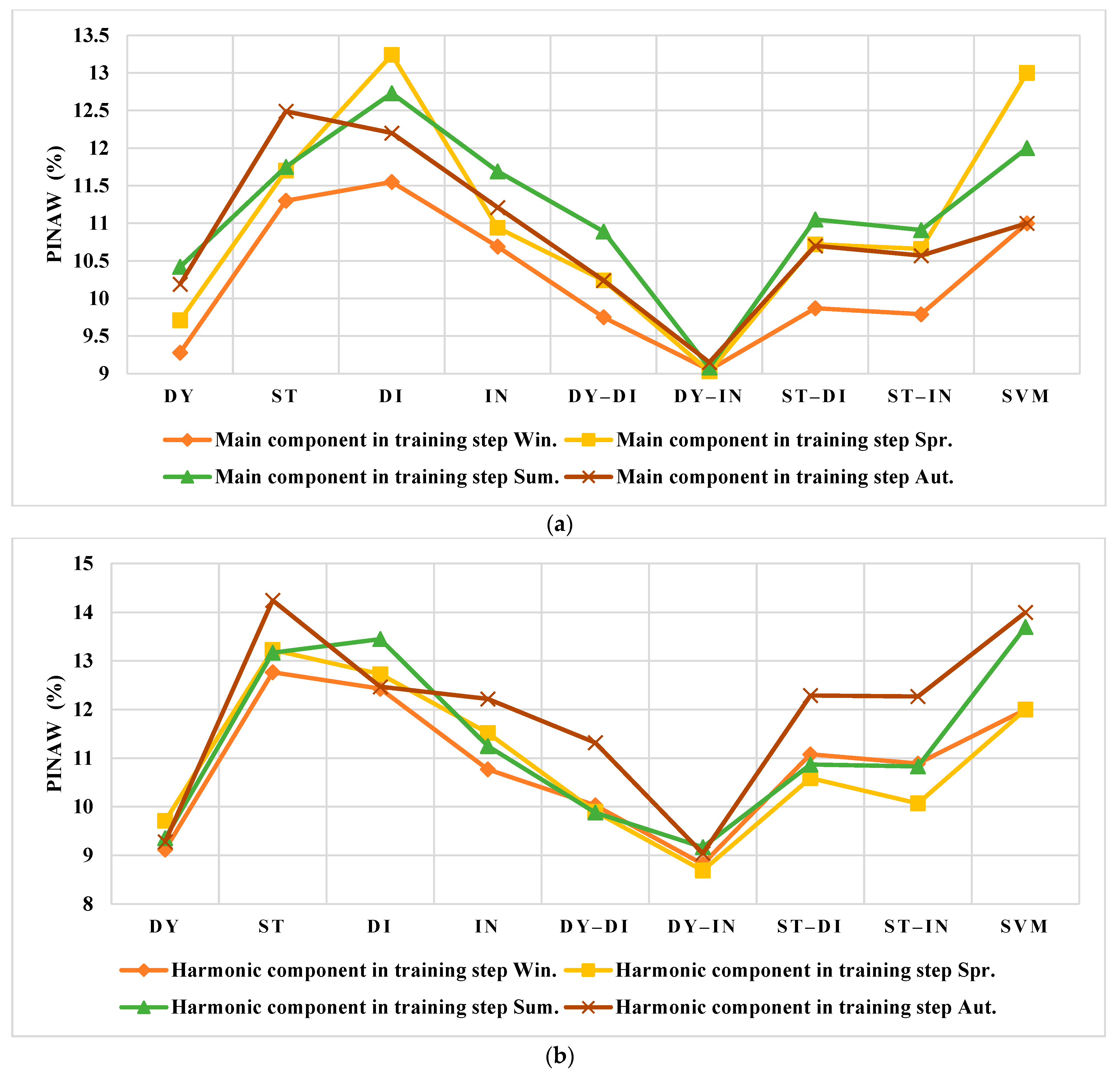
3. Results
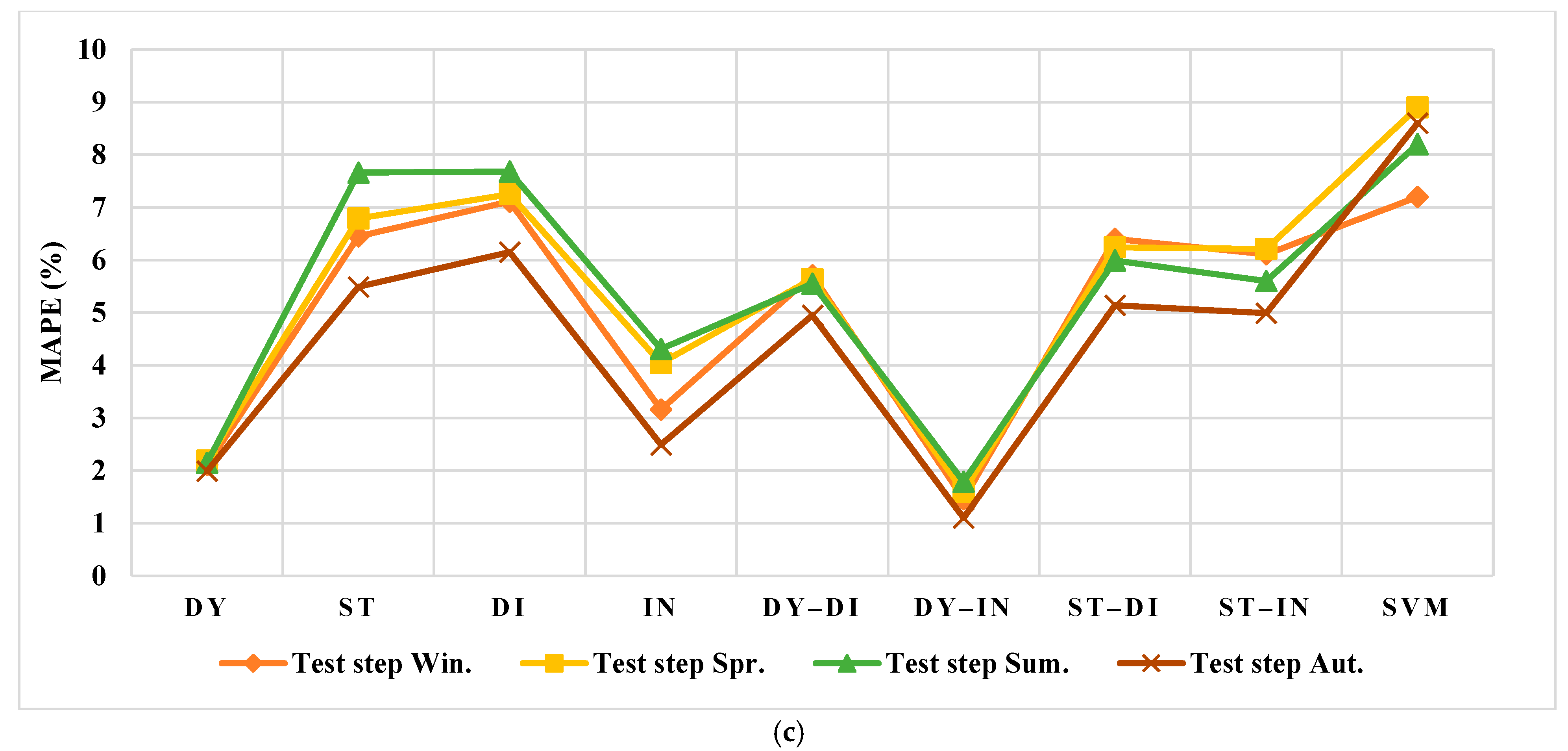
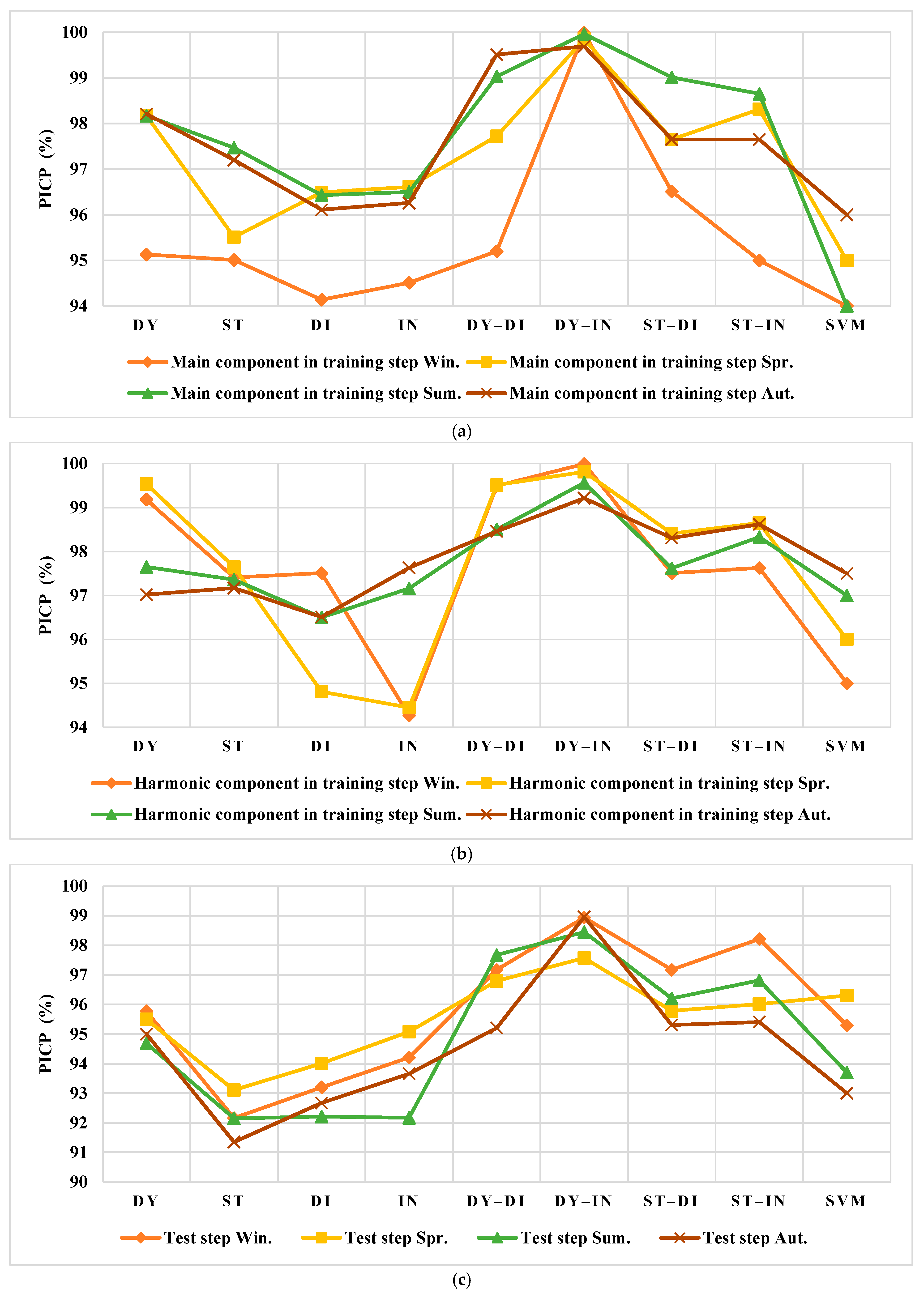
3.1. Performance Metrics
3.2. Data
3.2.1. The Spanish Electricity Market
3.2.2. The US Electricity Market
3.2.3. Data Analysis
- The EP decreases at the beginning of the day and increases at night;
- On different days of each week, the EP is different and declines towards the weekend;
- The price in the early hours of midnight on weekdays is low. As daylight approaches, the EP increases, and in the middle of the day it reaches the maximum value. Therefore, it will be more useful if the main power system is divided into several subsystems to enhance the model’s performance;
- The EP on holidays is lower than on weekdays, due to lower consumption from large industrial factories.
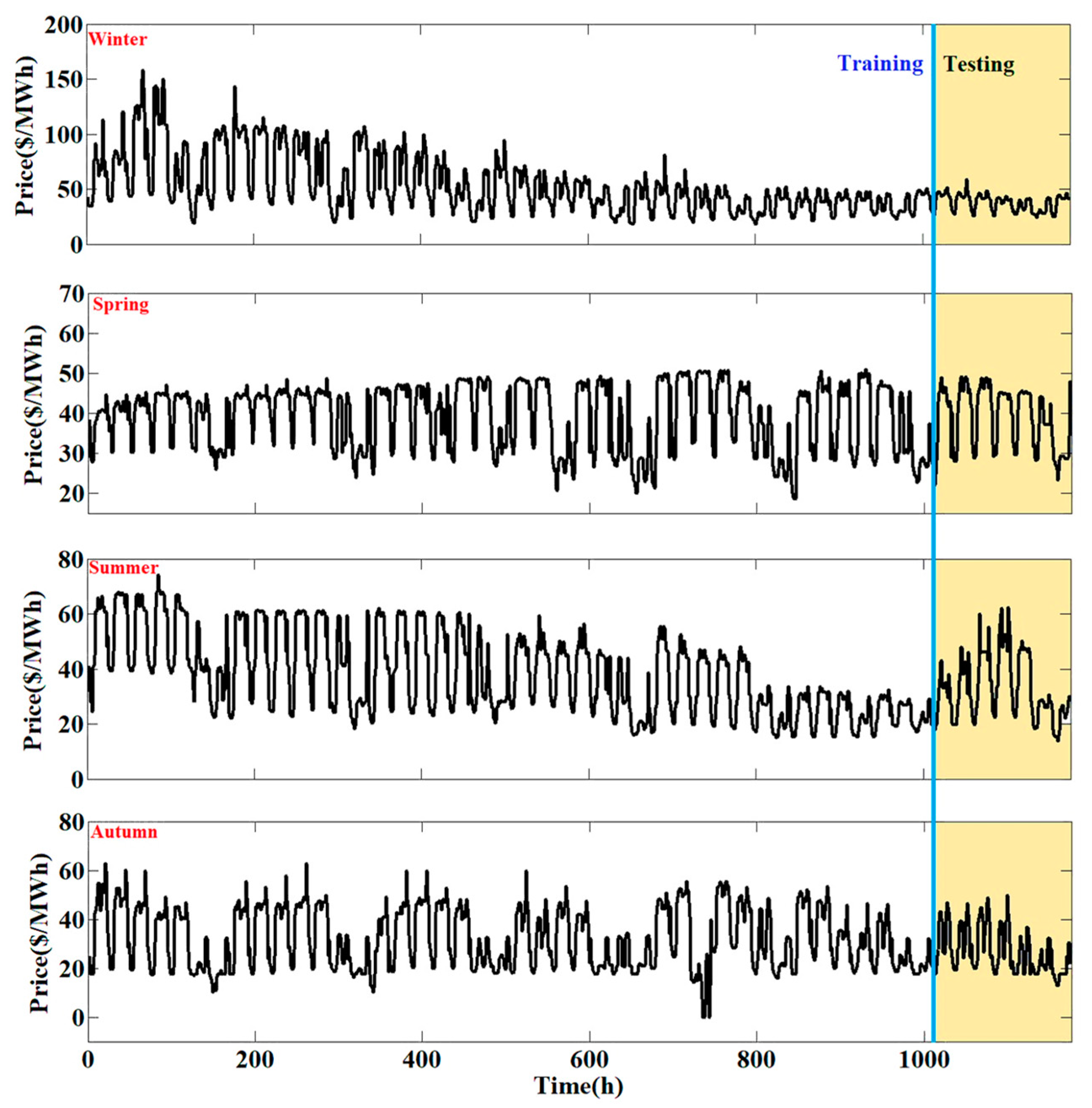
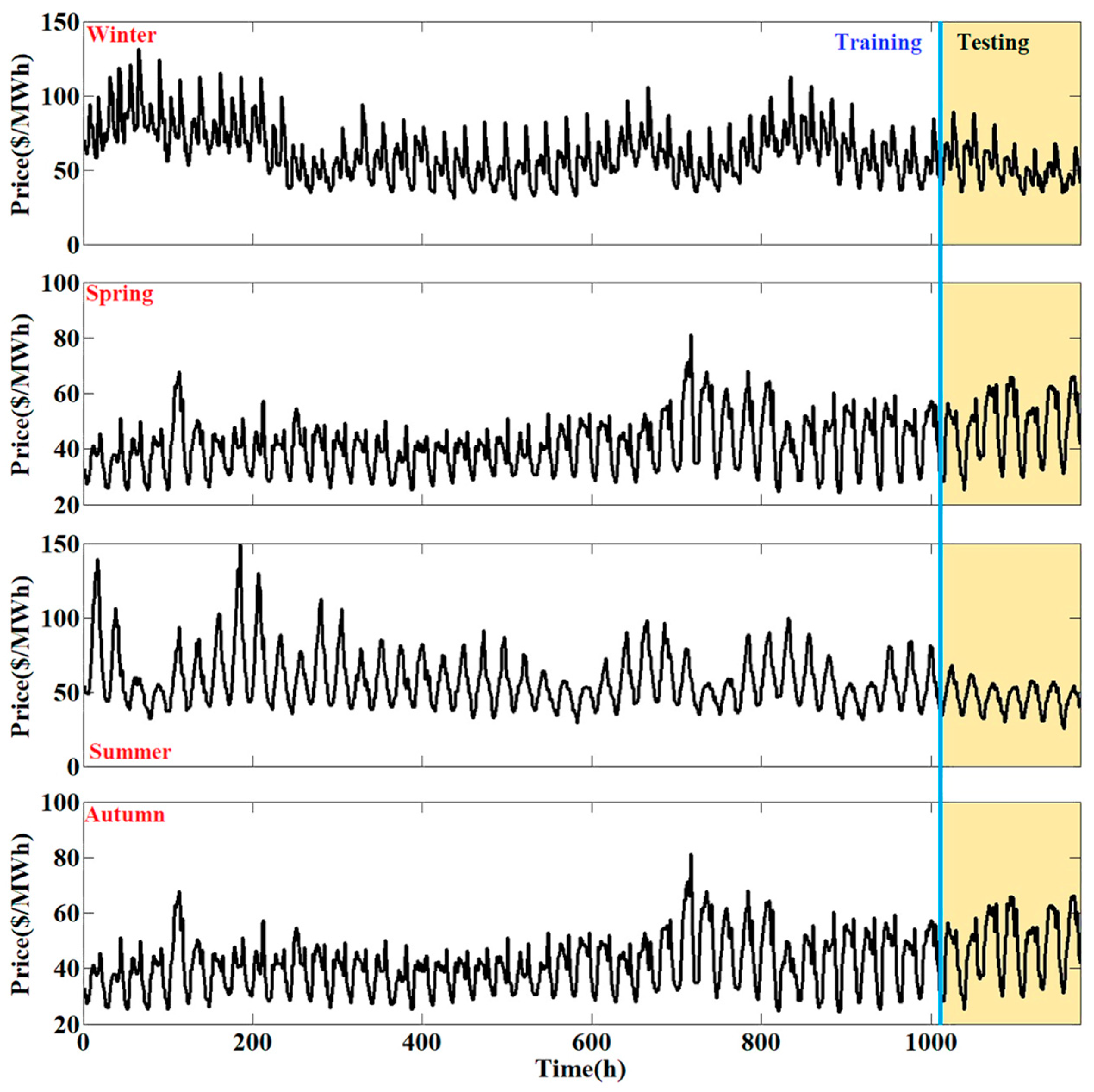
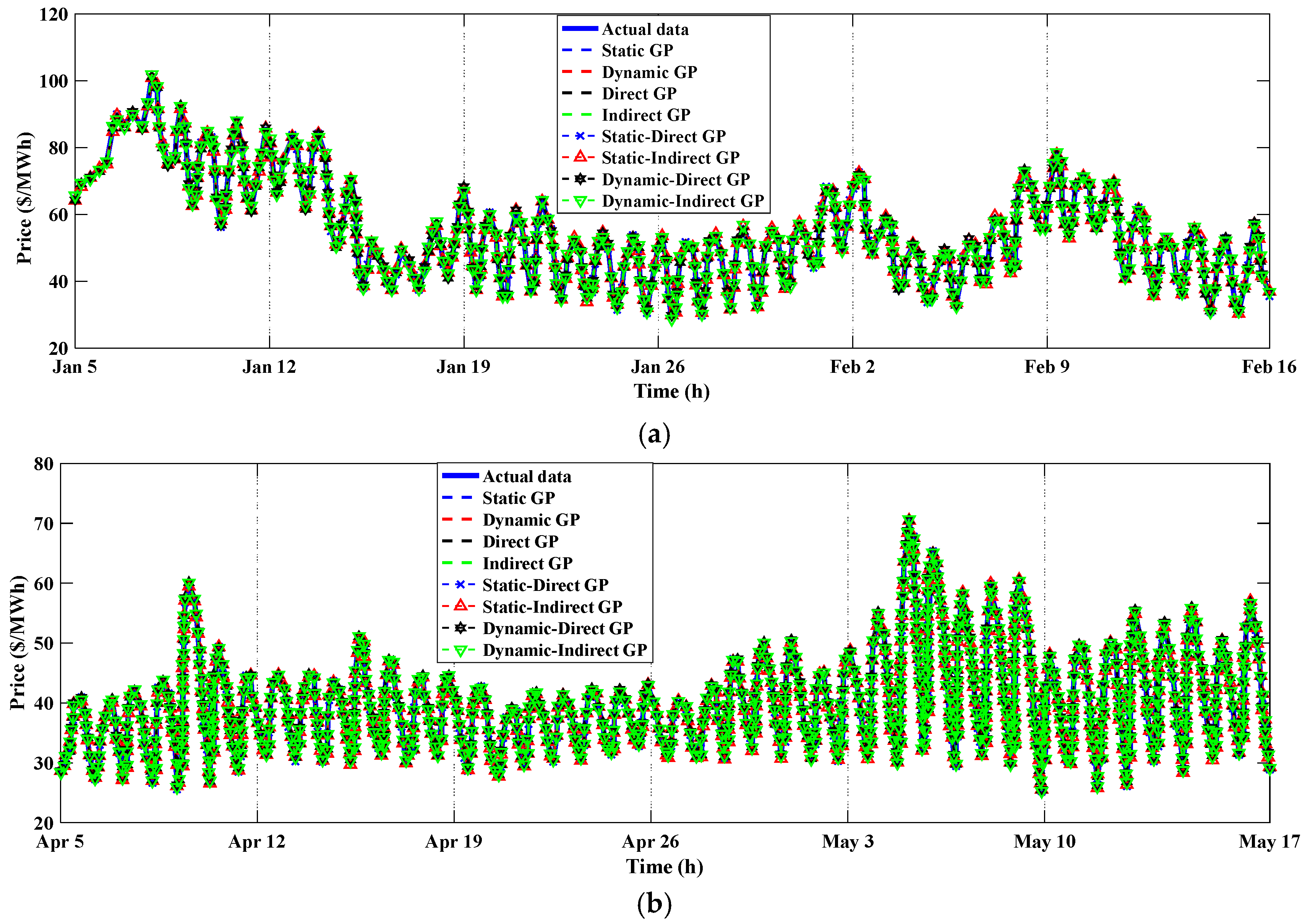
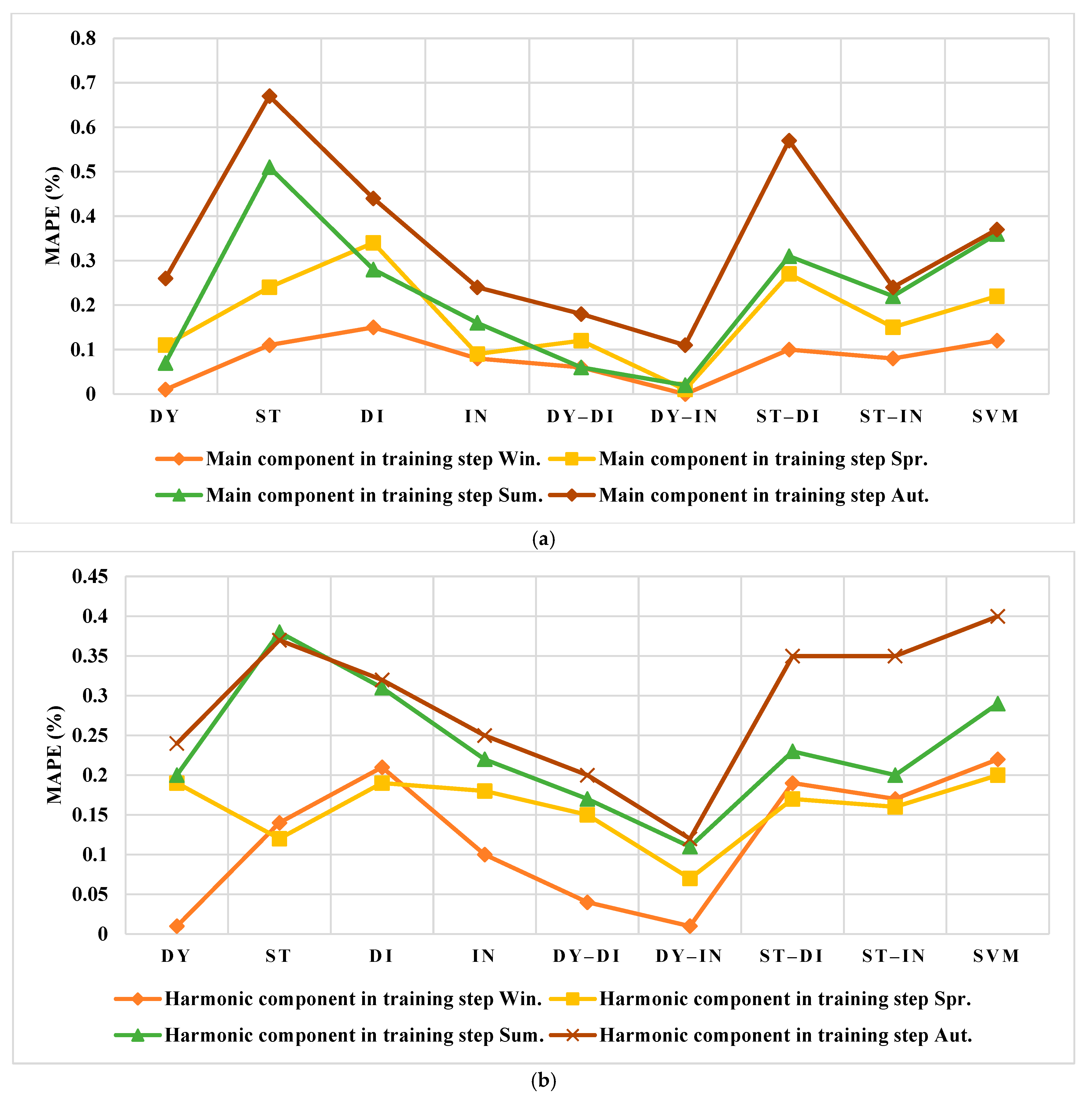
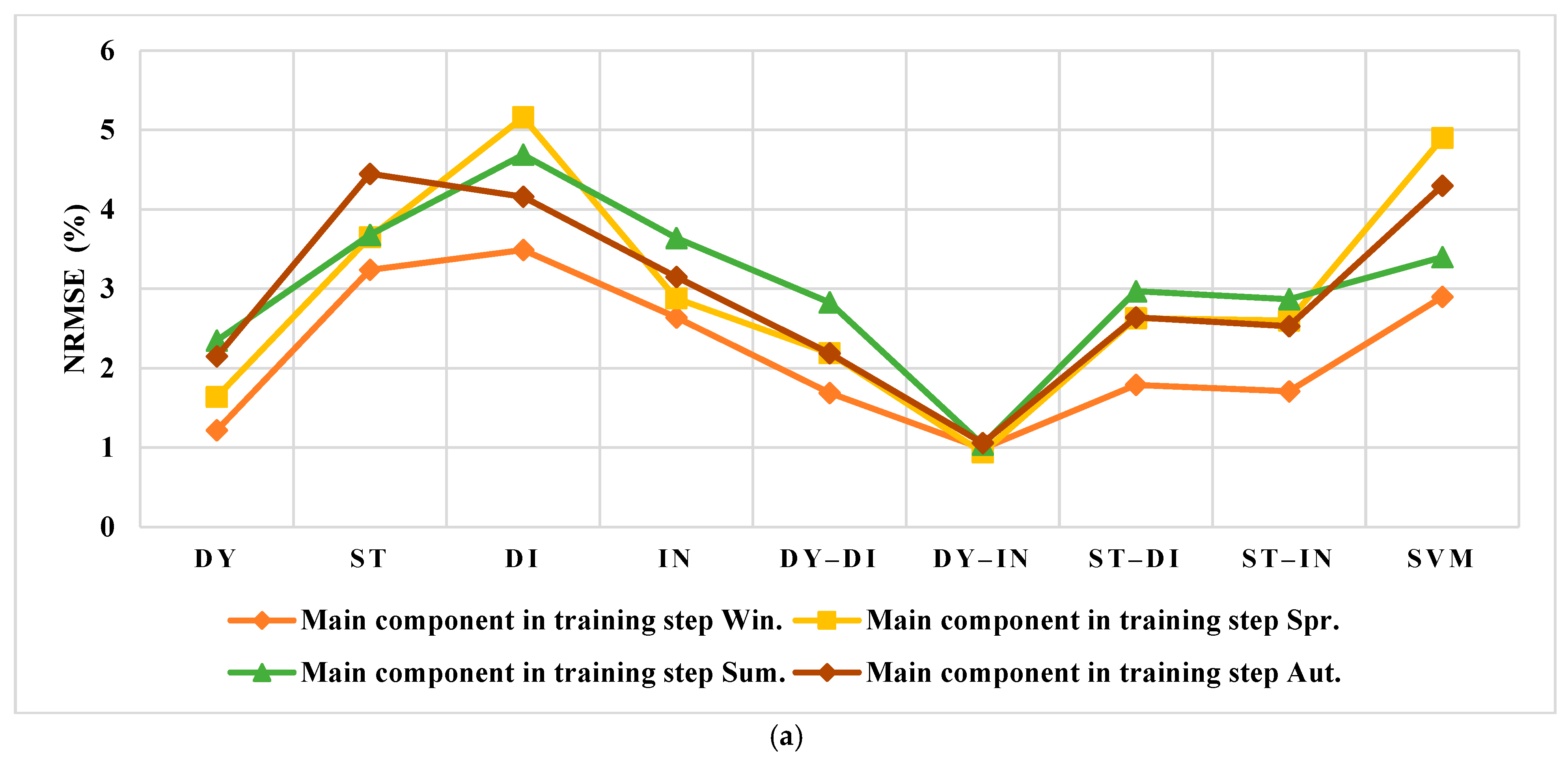
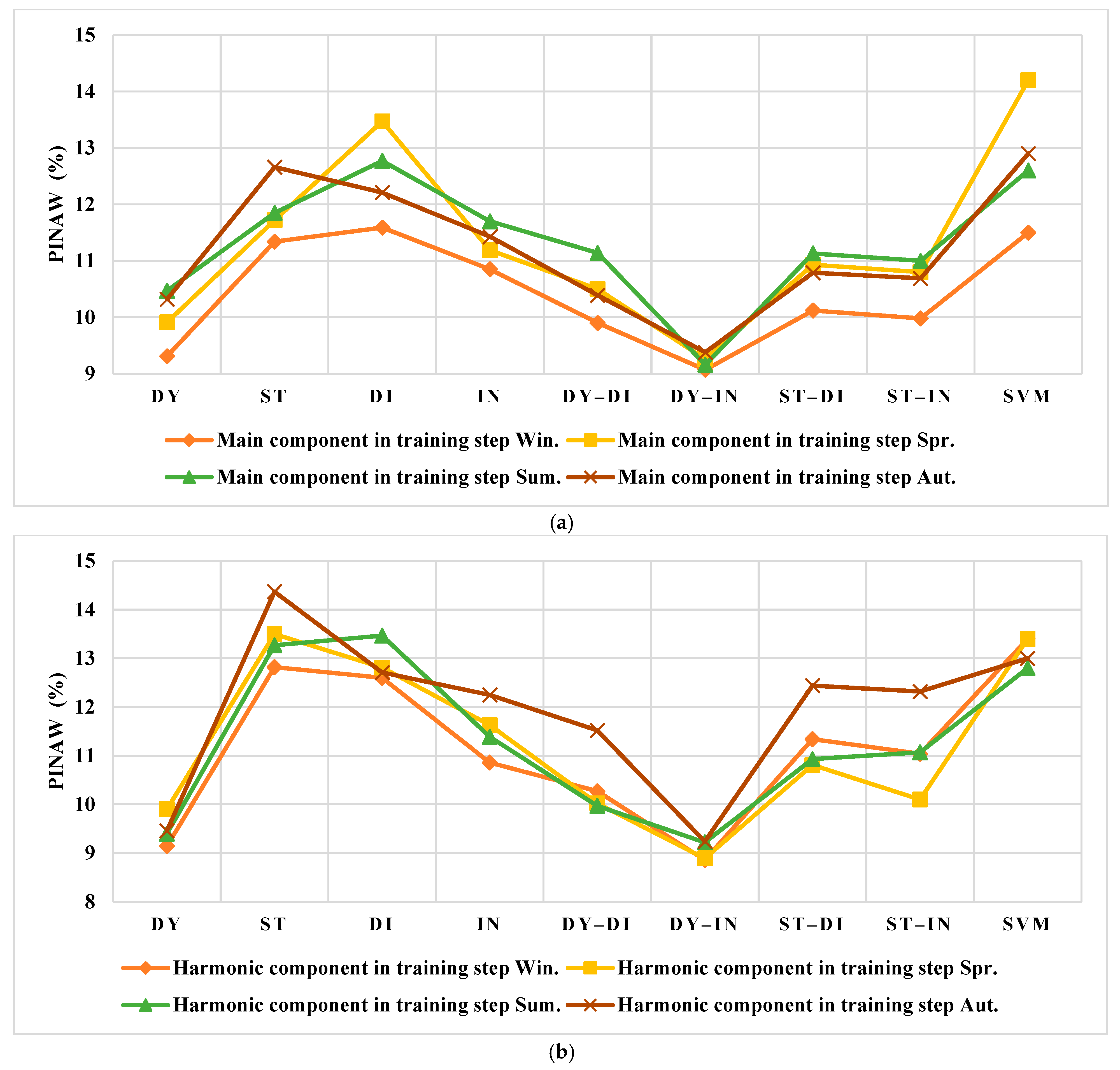
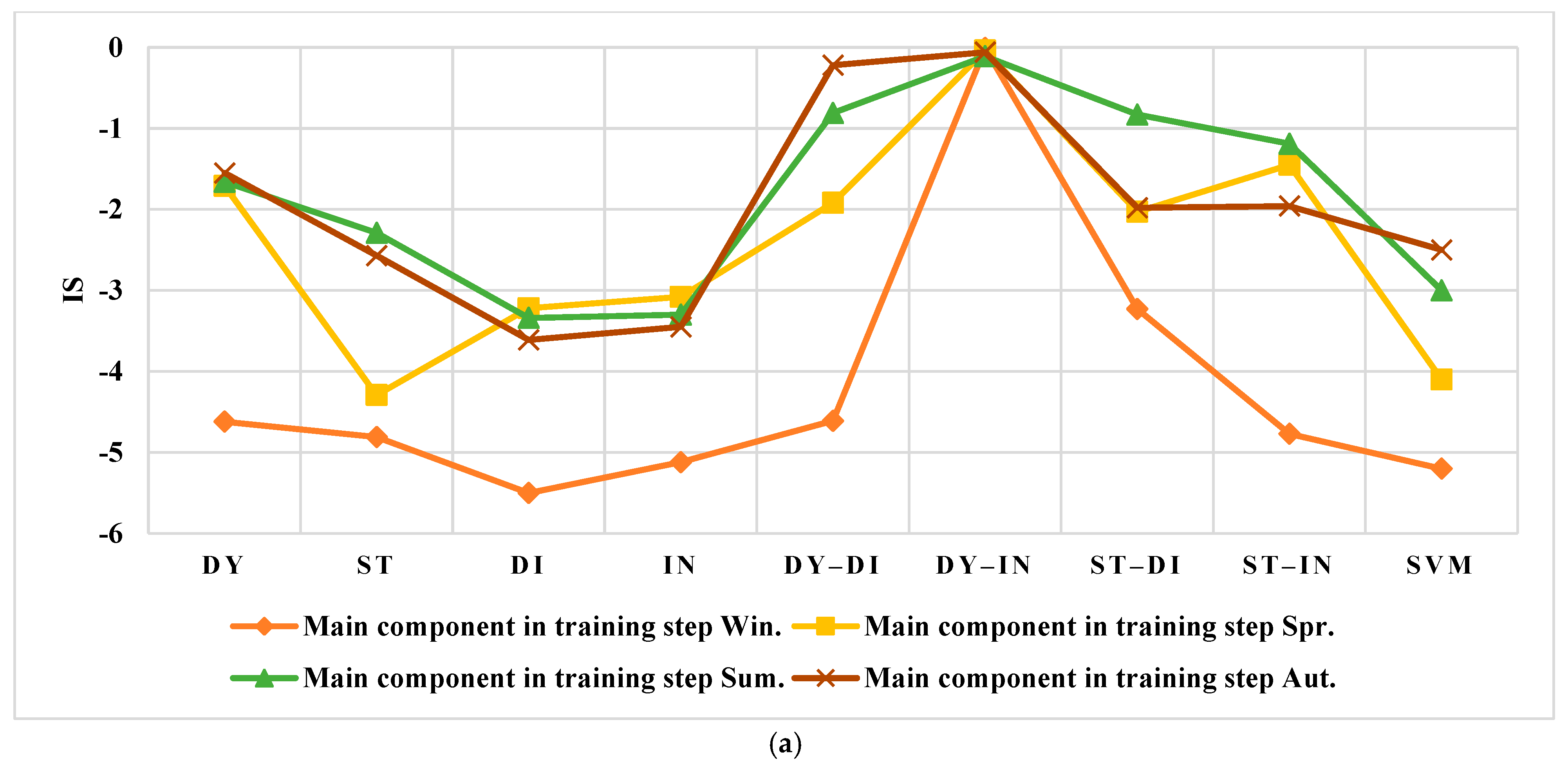
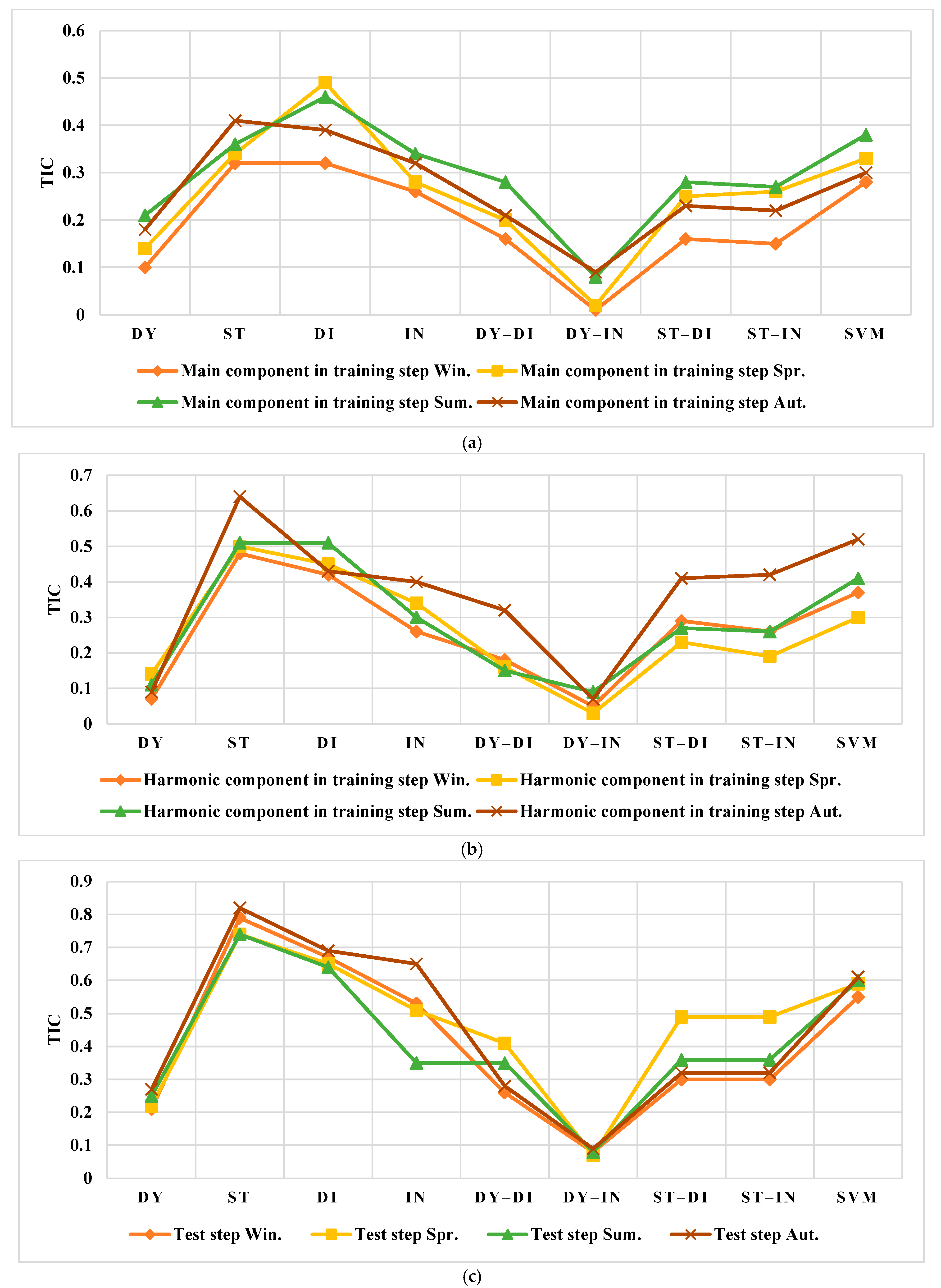
3.3. The Forecasting of the Training Data
3.3.1. The Spanish Electricity Market
3.3.2. The US Electricity Market
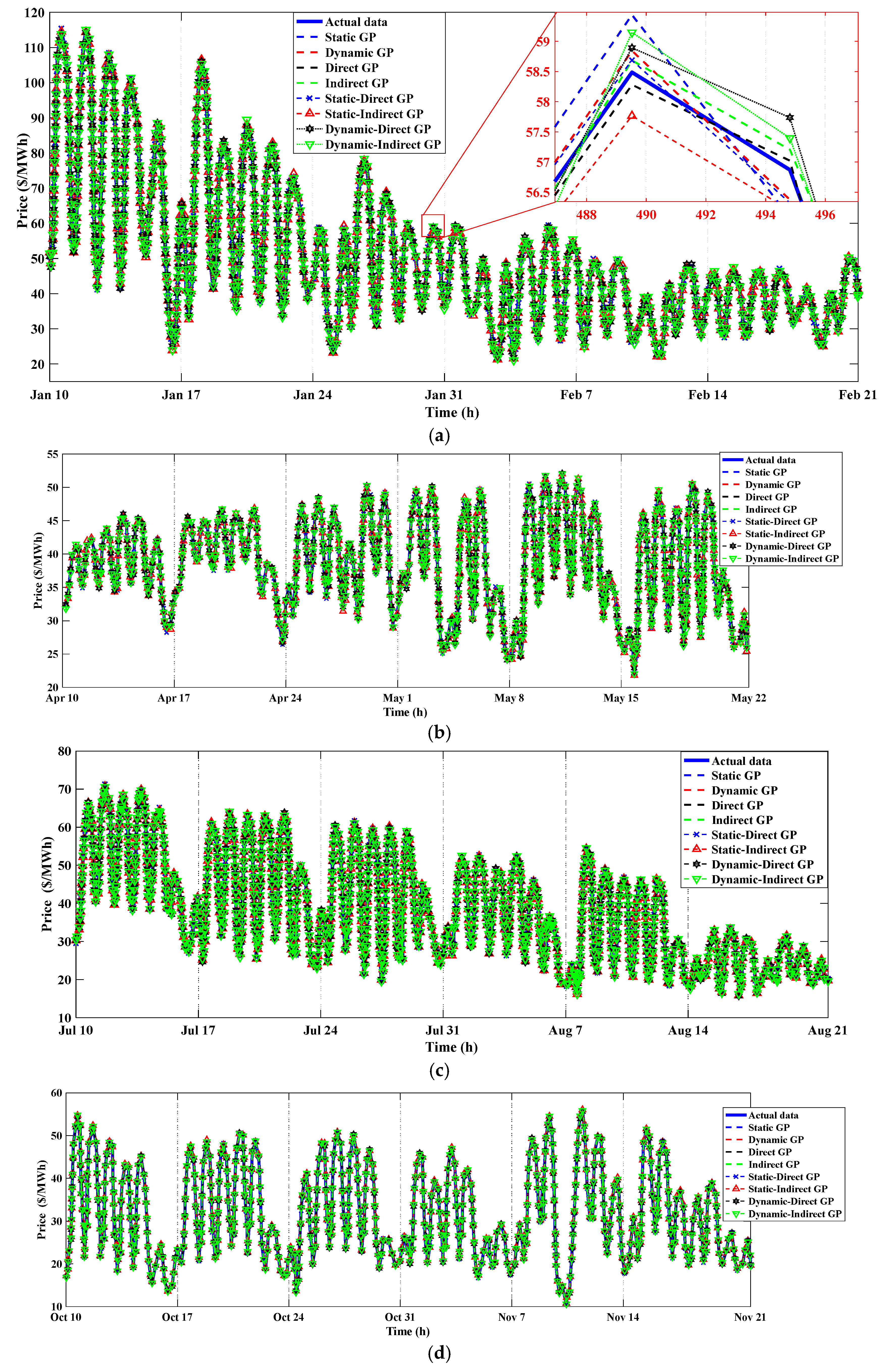
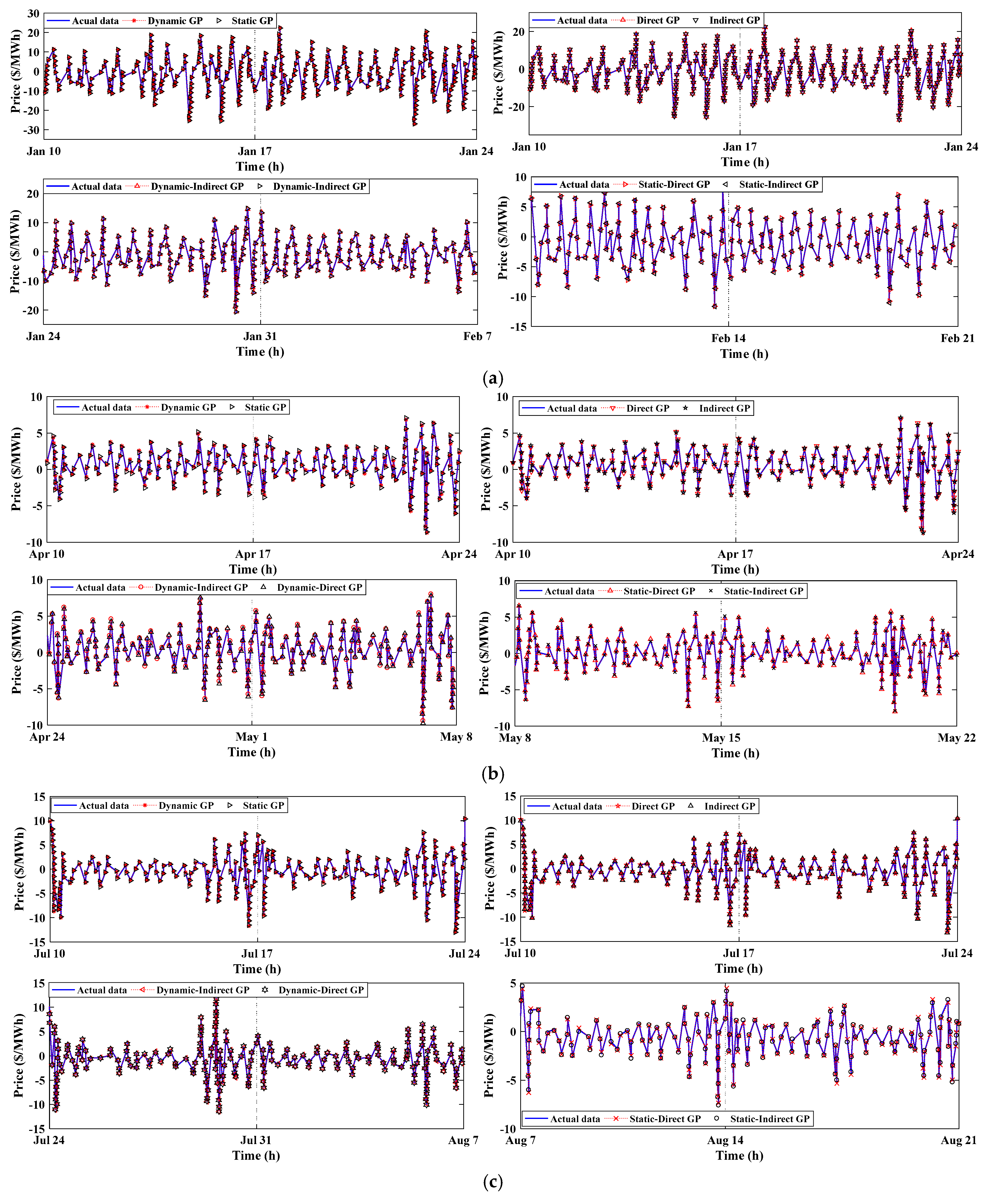
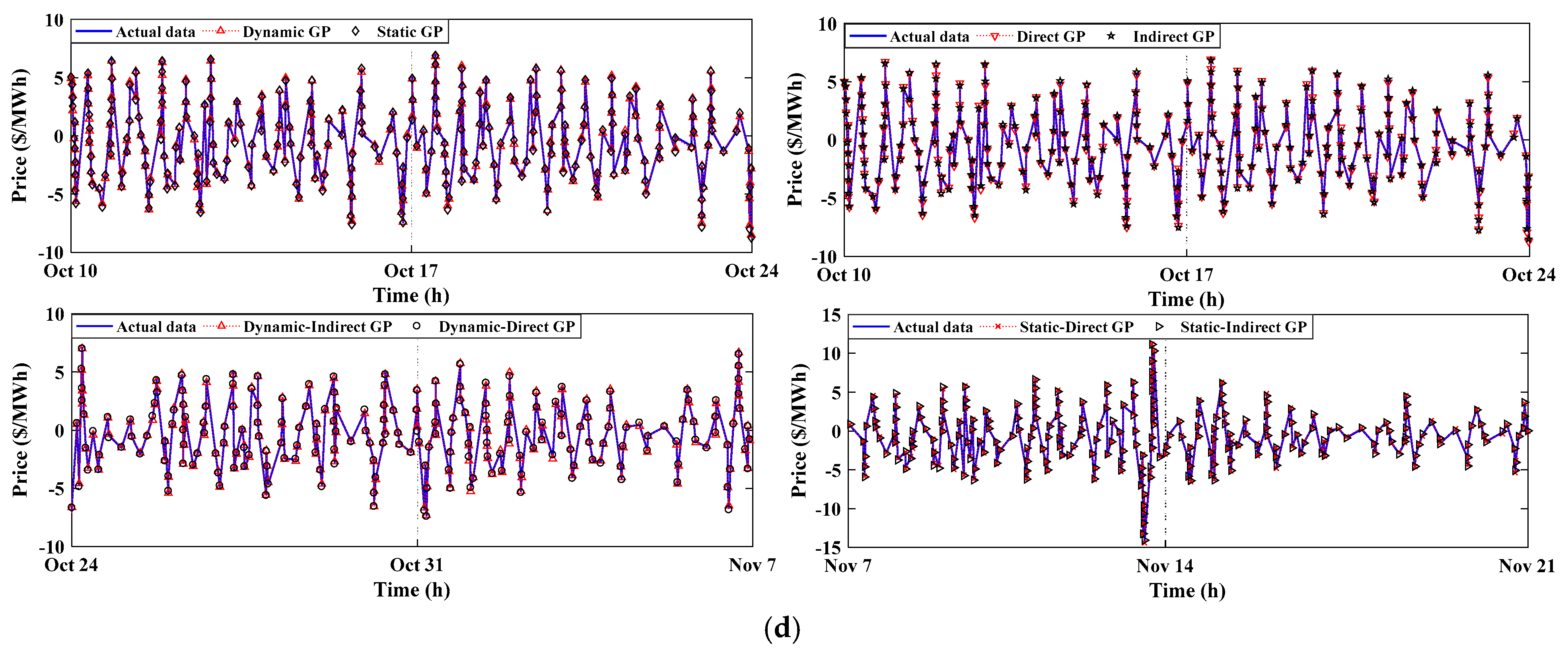
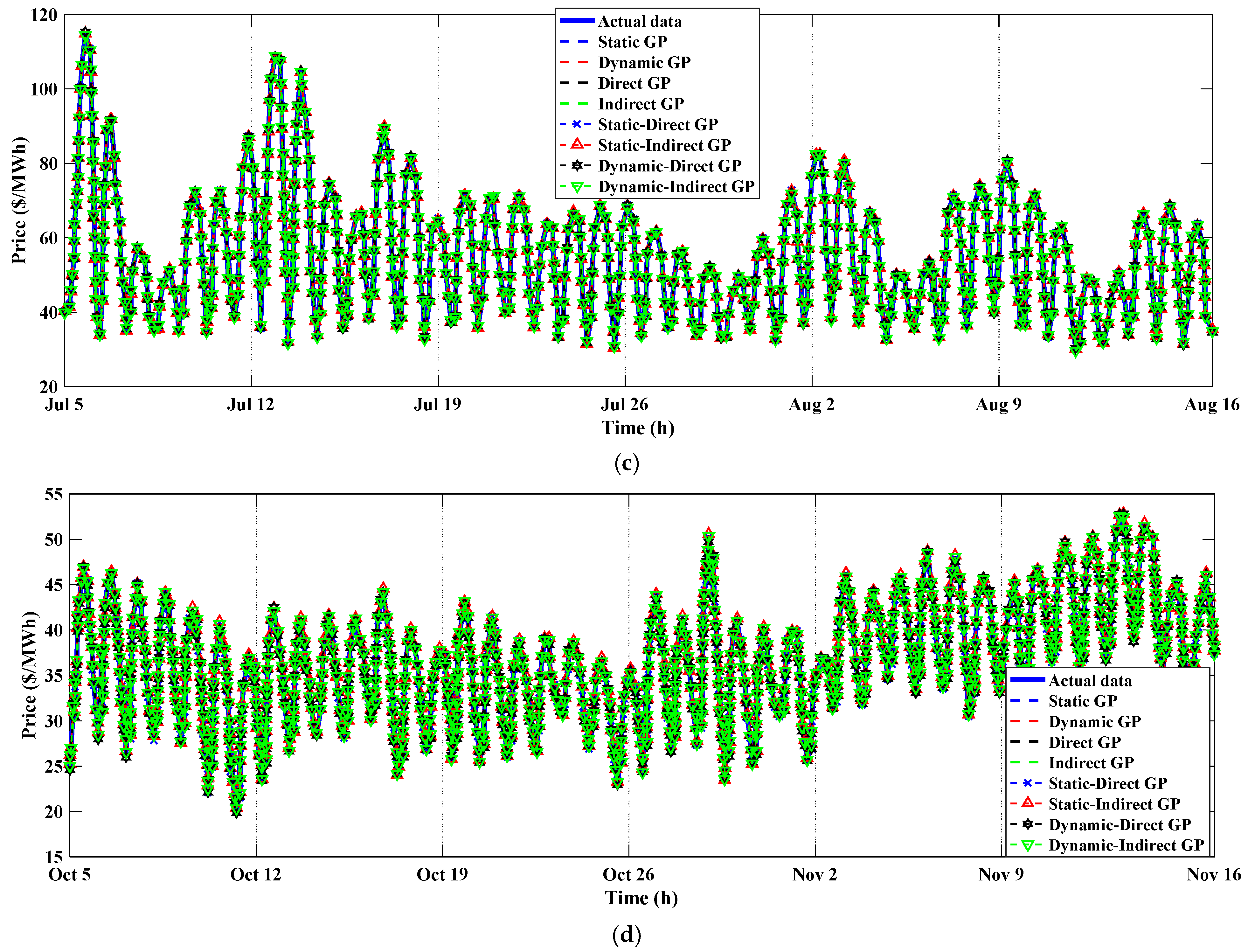
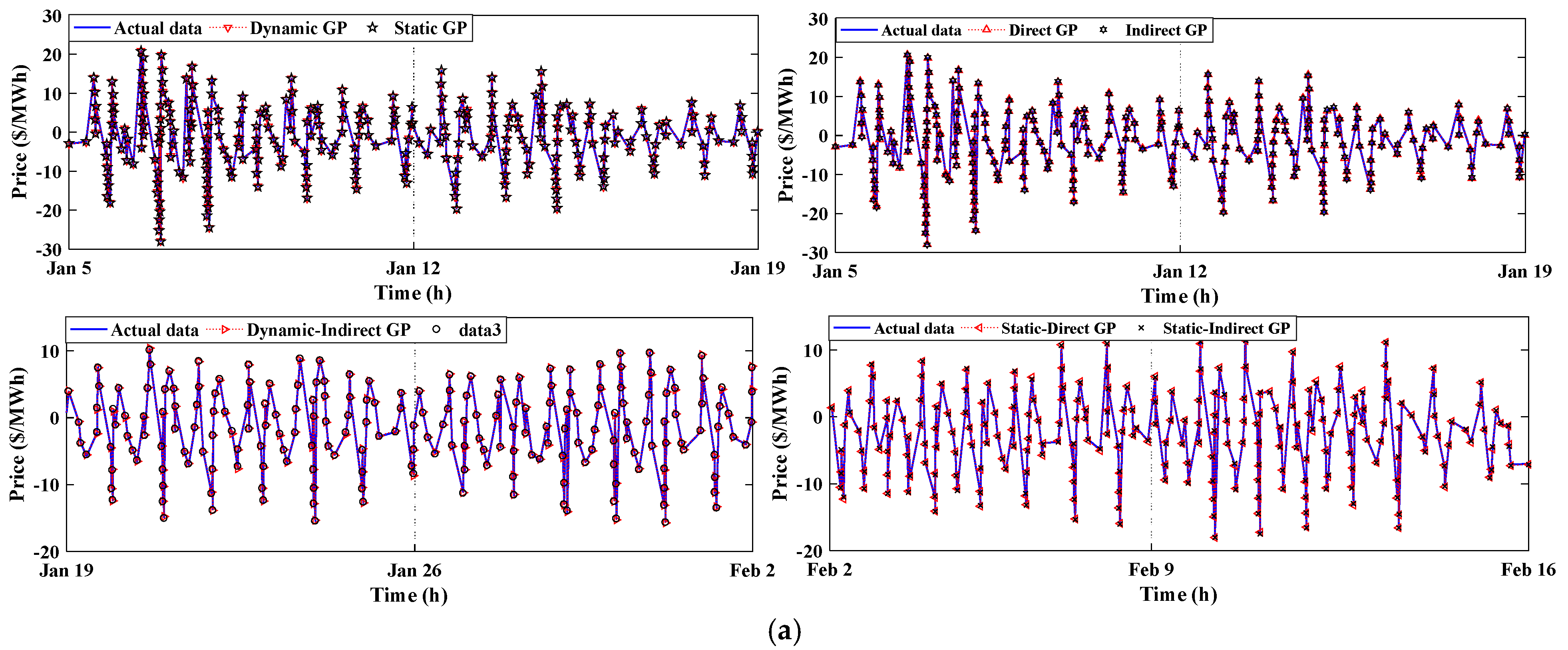
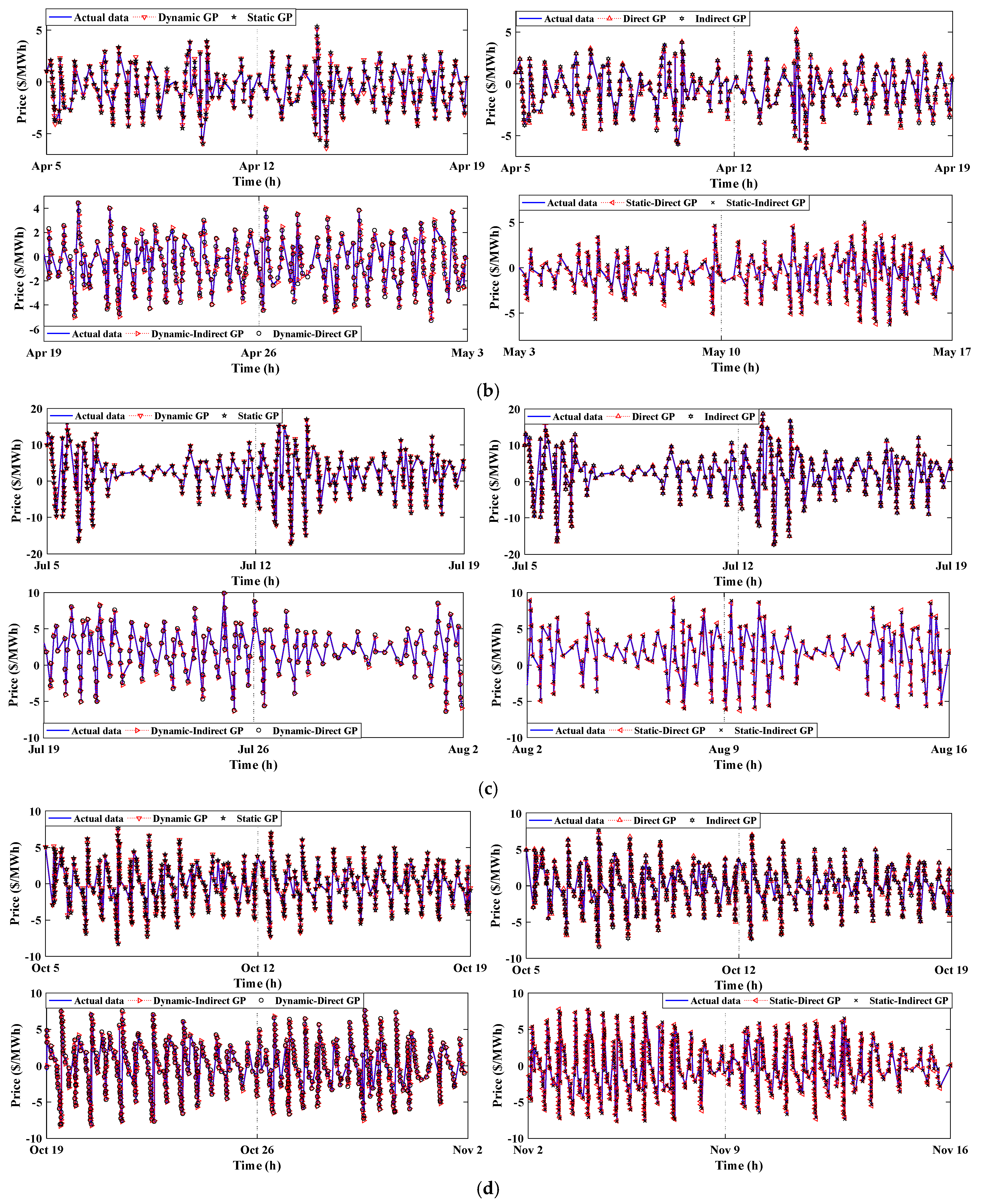
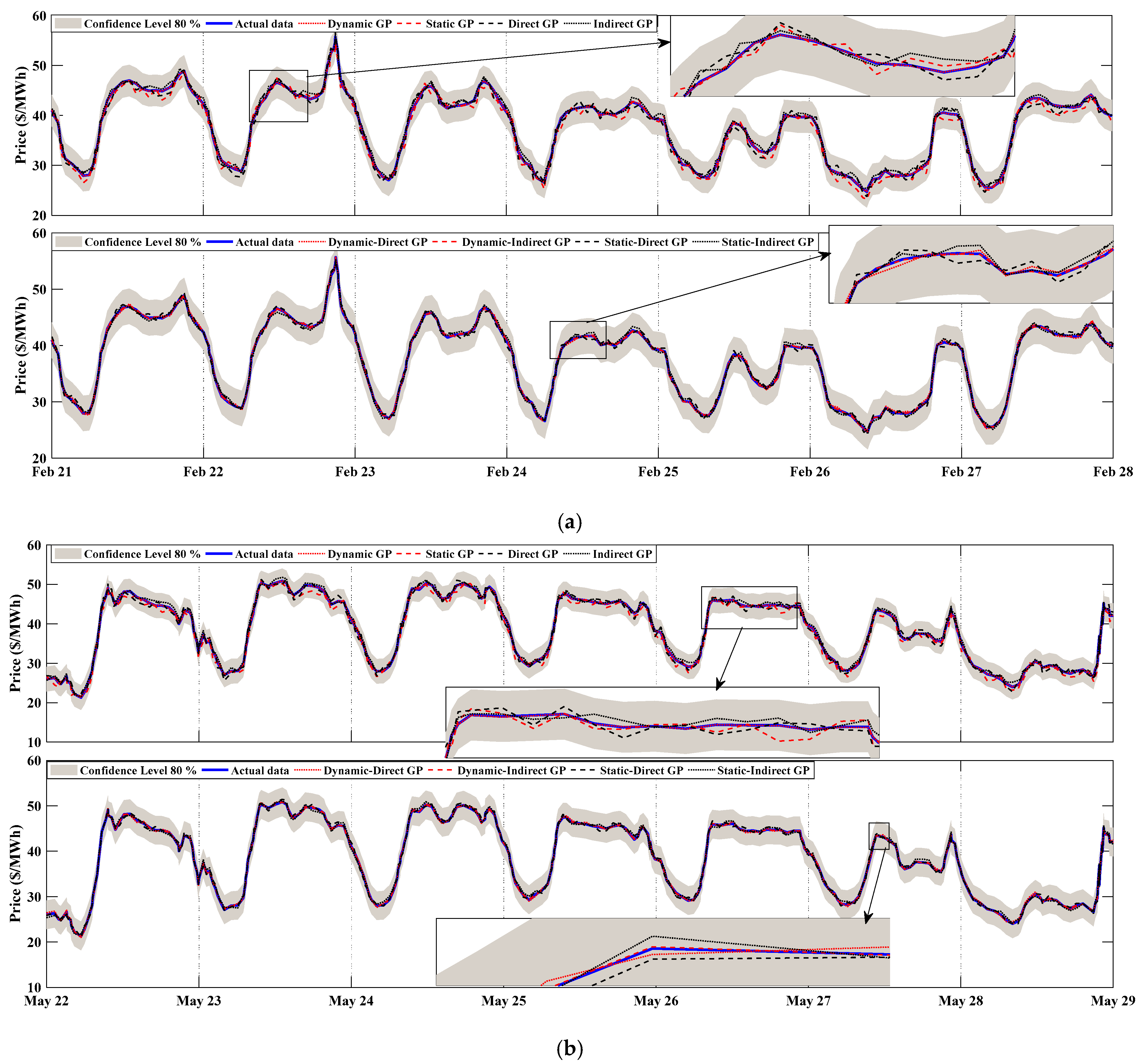
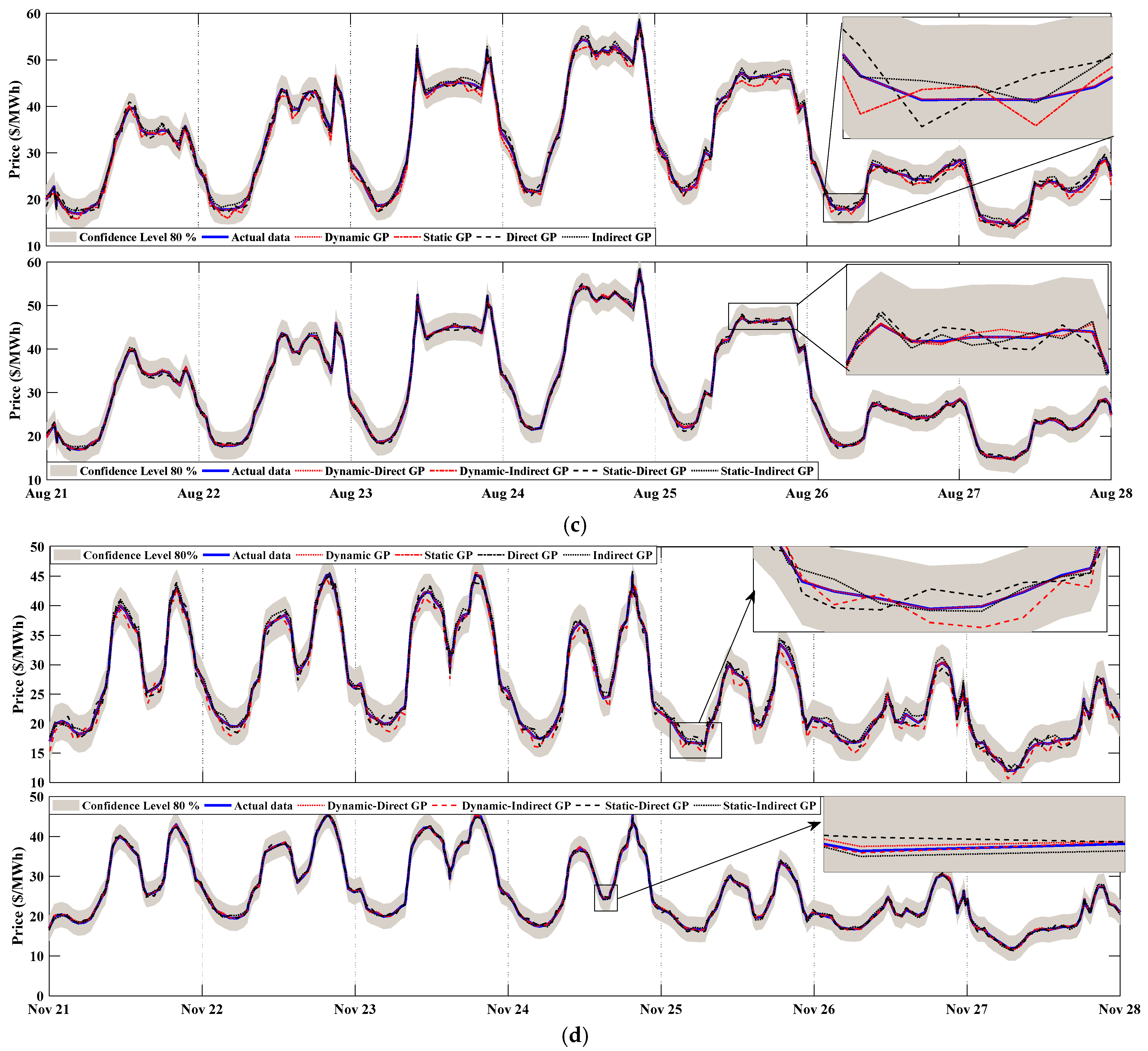
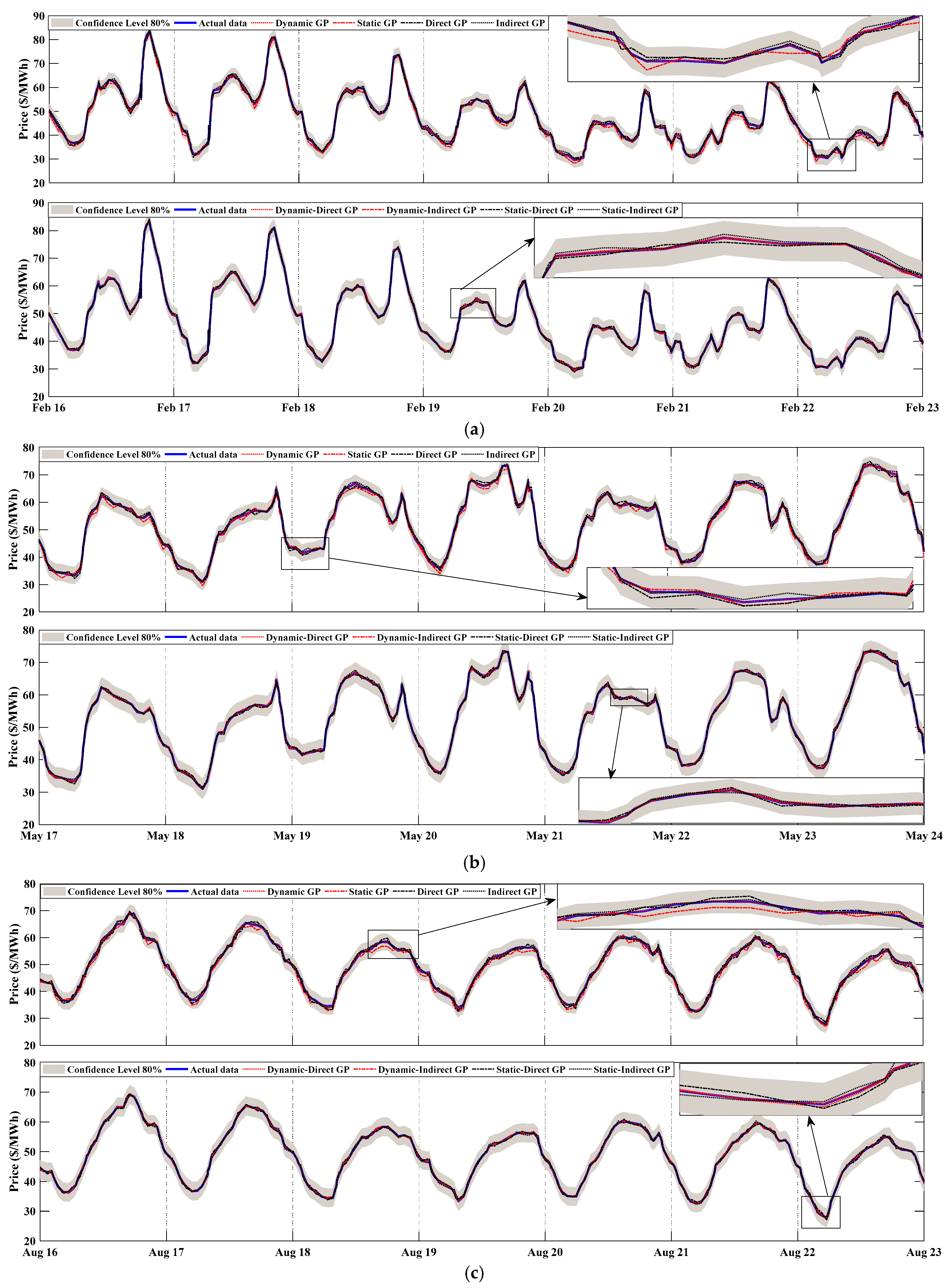
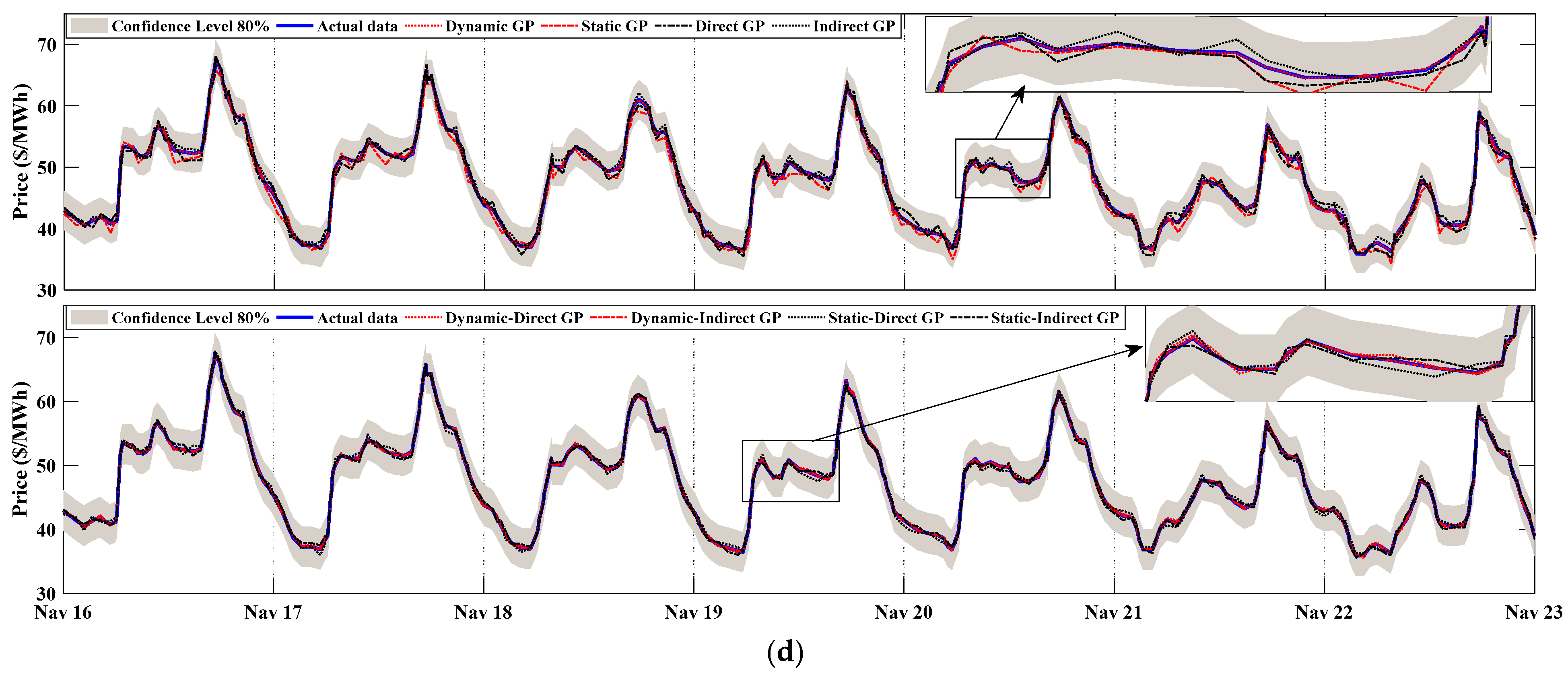
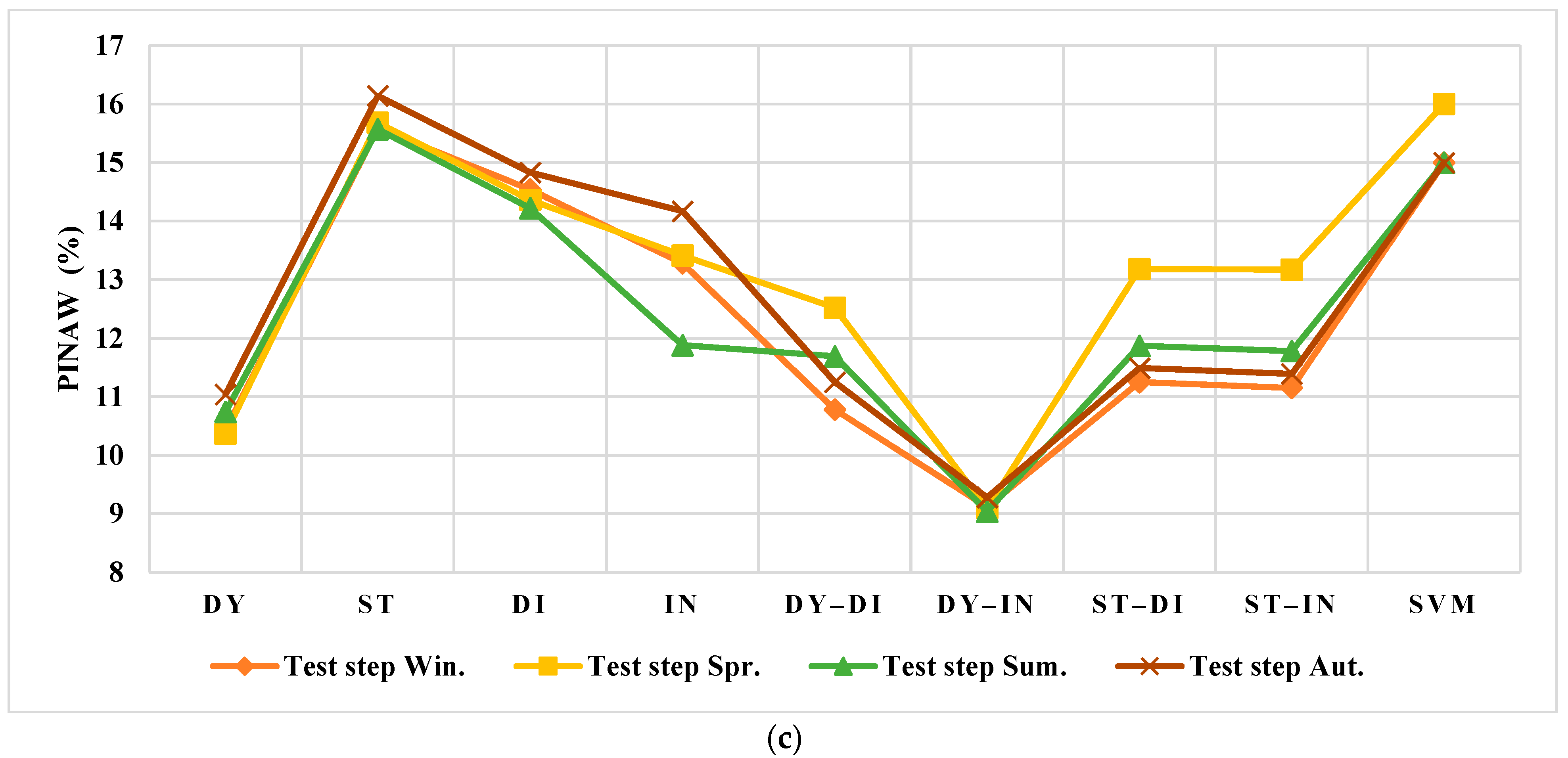
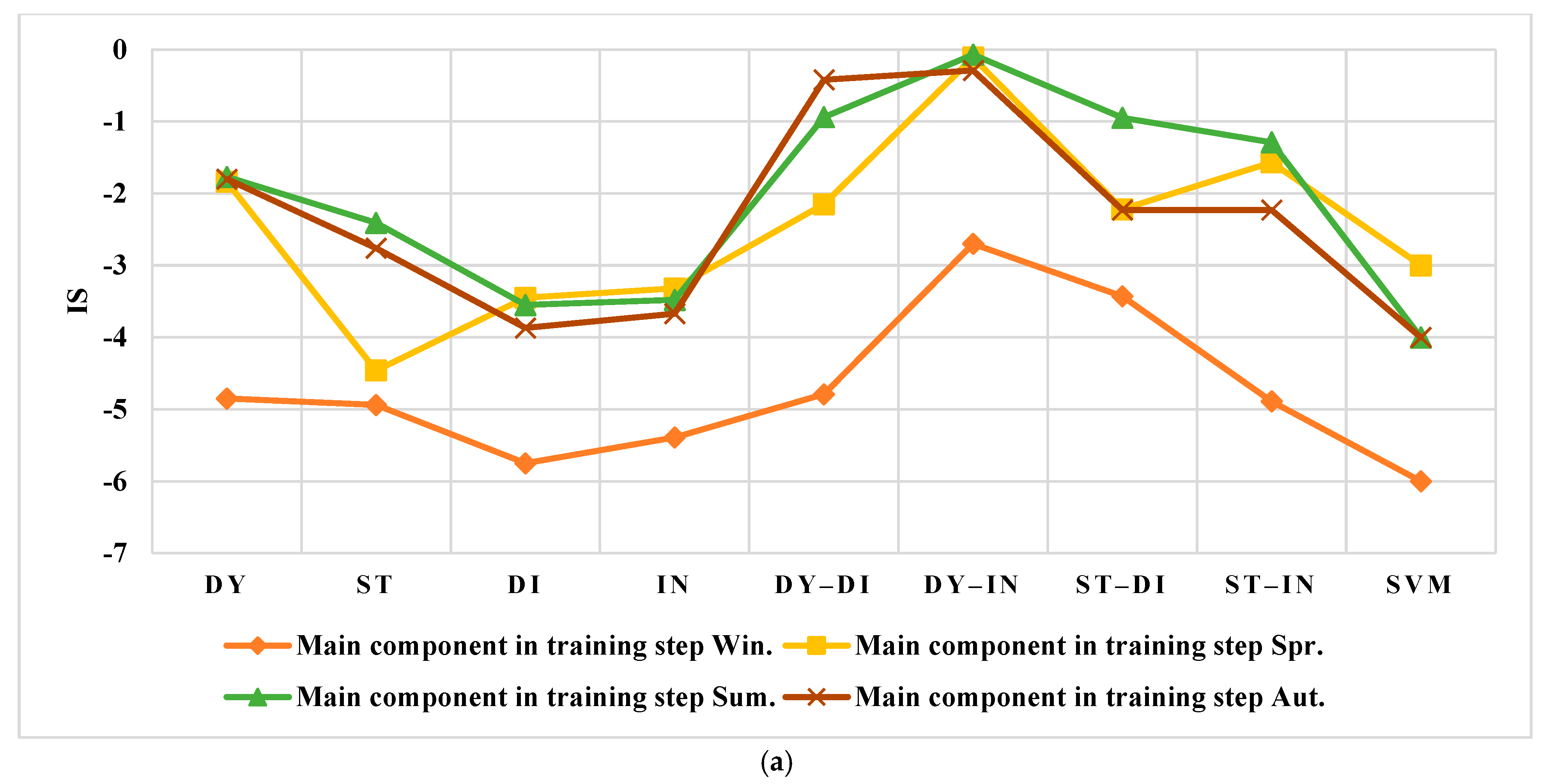
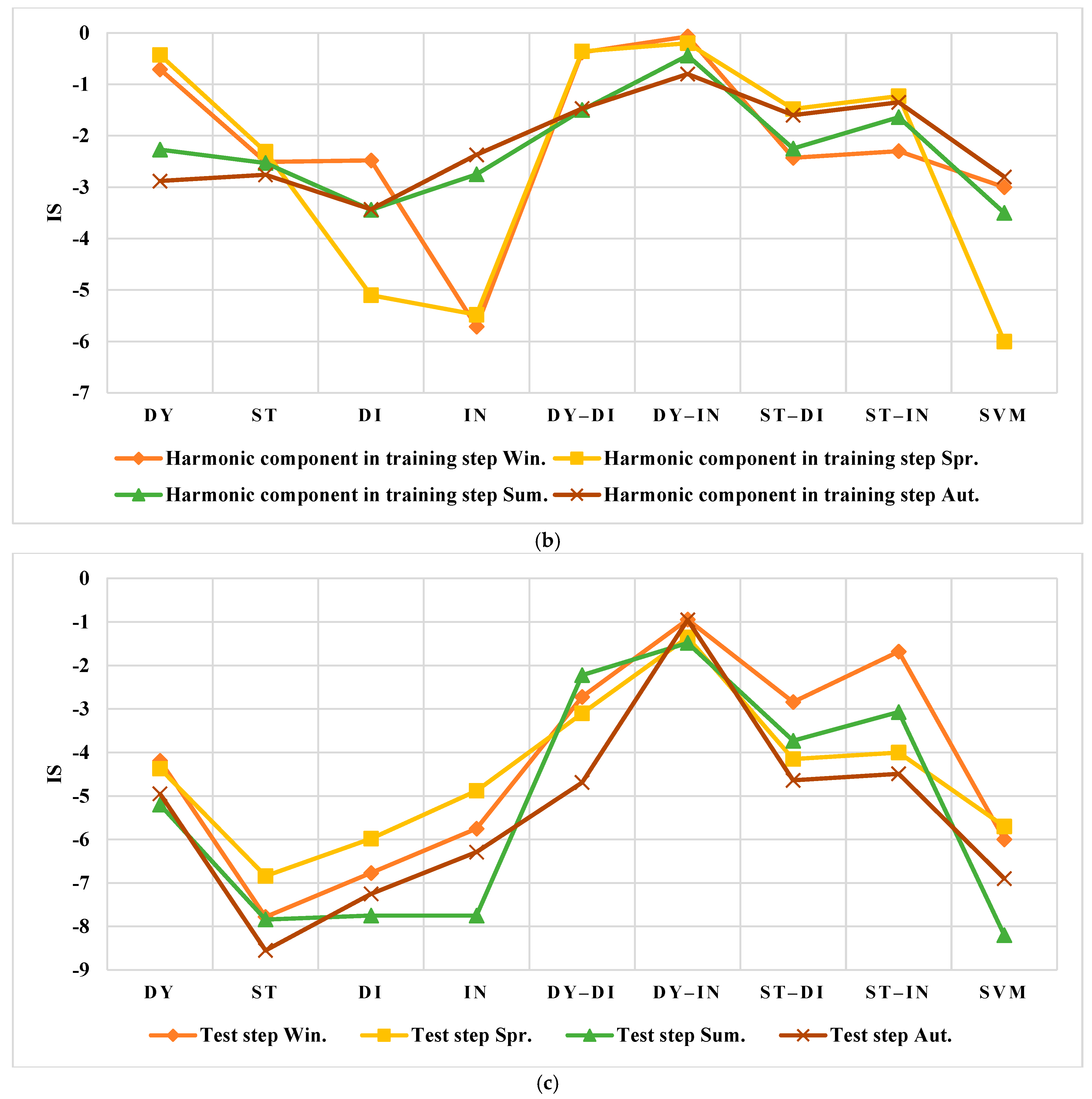
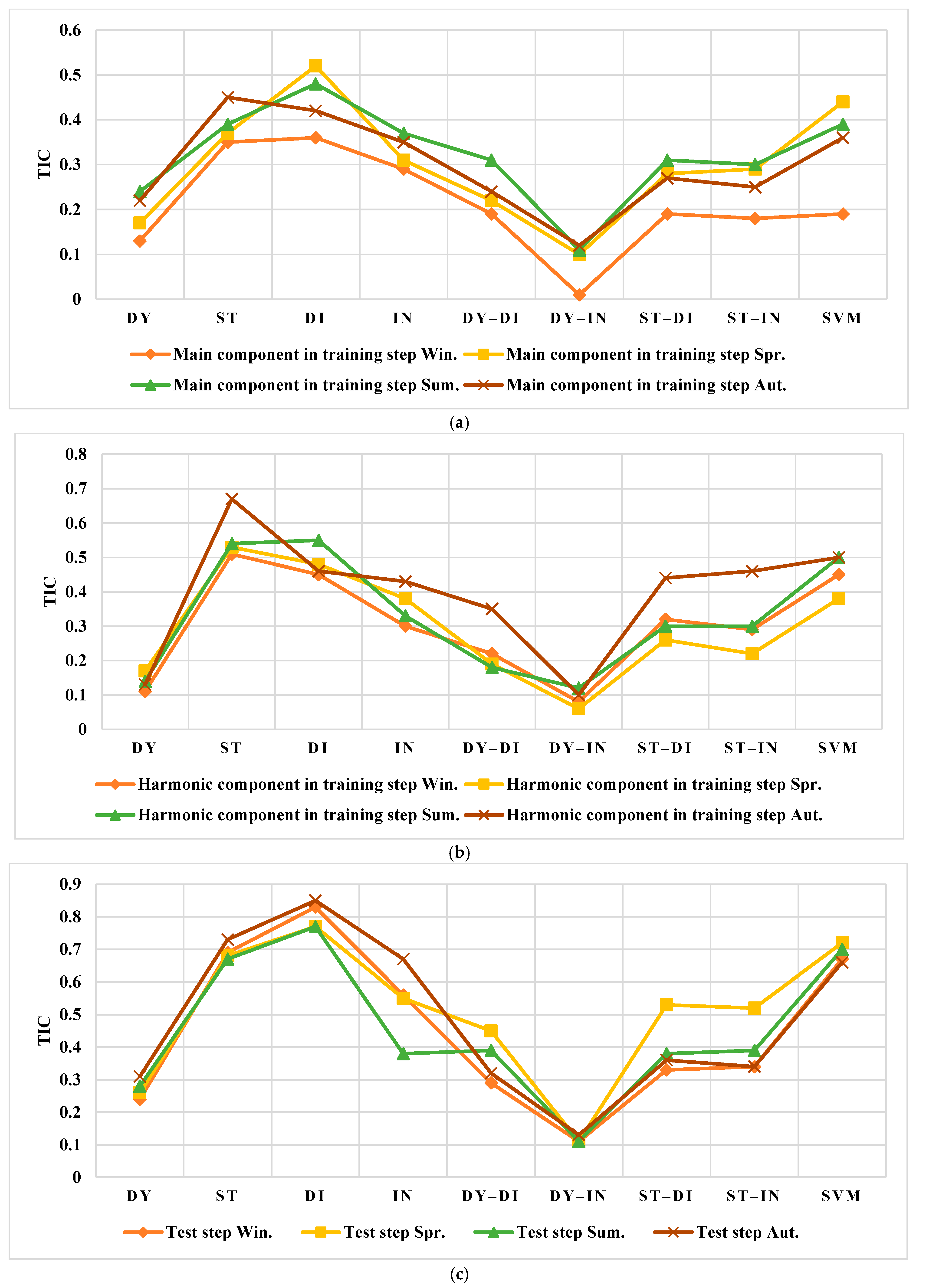
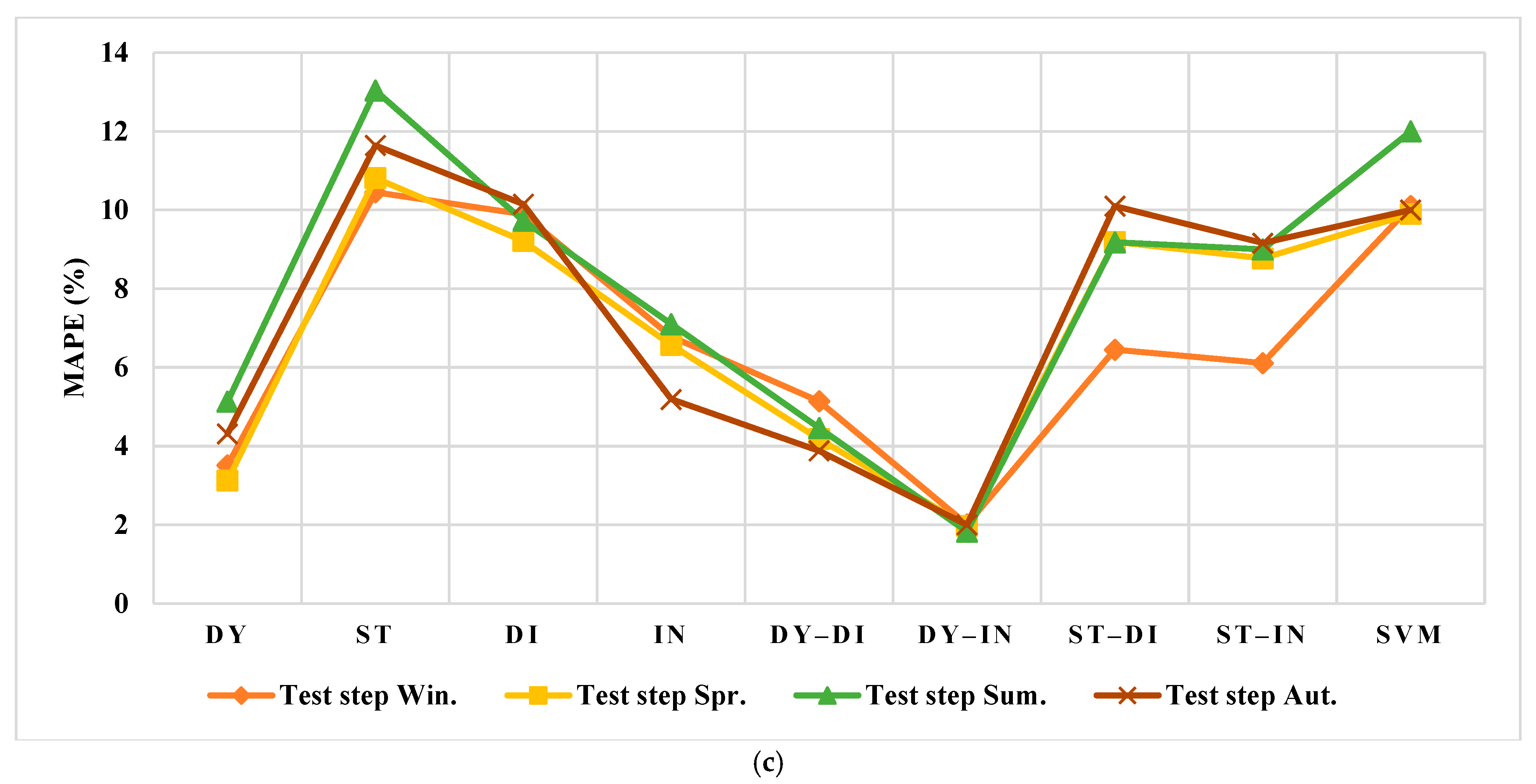
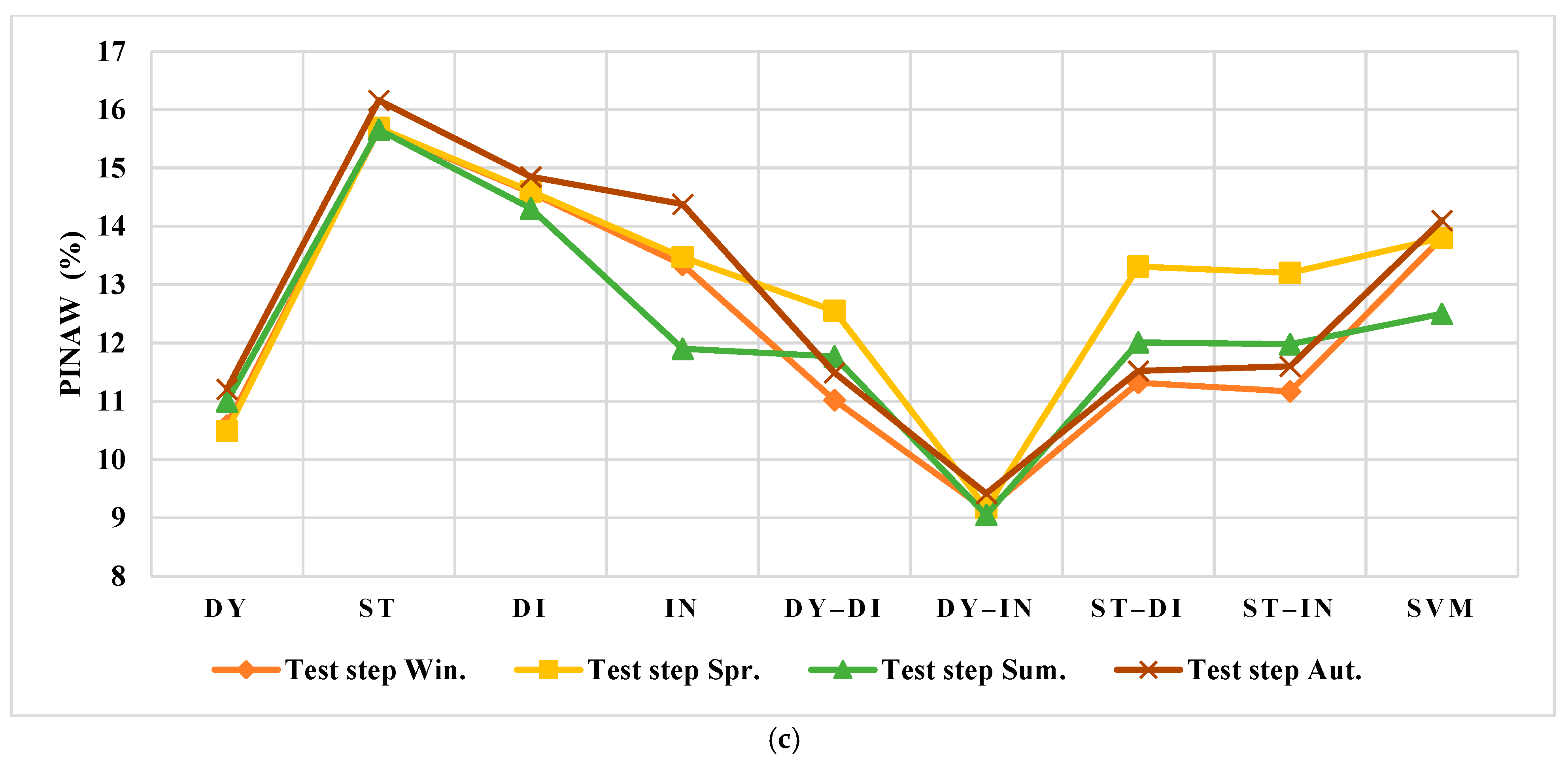
3.4. The Forecasting of the Testing Data
3.4.1. The Spanish Electricity Market
3.4.2. The US Electricity Market
4. Discussion
4.1. Results Evaluation of Spain
4.2. Results Evaluation of the US
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, W.; Wang, J.; Niu, T.; Du, P. A novel system for multi-step electricity price forecasting for electricity market management. Appl. Soft Comput. 2019, 88, 106029. [Google Scholar] [CrossRef]
- Seyed Shenava, S.J.; Dejamkhooy, A.; JavanAjdadi, K. Short-term Electric Load Forecasting Using Grey Models by Considering Demand Response. Comput. Intell. Electr. Eng. 2018, 8, 1–16. [Google Scholar]
- Ahmadpour, A.; Mokaramian, E.; Anderson, S. The effects of the renewable energies penetration on the surplus welfare under energy policy. Renew. Energy 2020, 164, 1171–1182. [Google Scholar] [CrossRef]
- Huang, C.J.; Shen, Y.; Chen, Y.H.; Chen, H.C. A novel hybrid deep neural network model for short-term electricity price forecasting. Int. J. Energy Res. 2021, 45, 2511–2532. [Google Scholar] [CrossRef]
- Amjady, N.; Daraeepour, A. Design of input vector for day-ahead price forecasting of electricity markets. Expert Syst. Appl. 2009, 36, 12281–12294. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, C.; Zhu, Z. Inter-hours rolling scheduling of behind-the-meter storage operating systems using electricity price forecasting based on deep convolutional neural network. Int. J. Electr. Power Energy Syst. 2020, 125, 106499. [Google Scholar] [CrossRef]
- Golmohamadi, H.; Larsen, K.G.; Jensen, P.G.; Hasrat, I.R. Optimization of power-to-heat flexibility for residential buildings in response to day-ahead electricity price. Energy Build. 2021, 232, 110665. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Wang, J.; Yang, W.; Du, P.; Niu, T. Outlier-robust hybrid electricity price forecasting model for electricity market management. J. Clean. Prod. 2020, 249, 119318. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, C.; Nokleby, M.; Miller, C.J. Improving short-term electricity price forecasting using day-ahead LMP with ARIMA models. In 2017 IEEE Power & Energy Society General Meeting; IEEE: New York, NY, USA, 2017; pp. 1–5. [Google Scholar]
- Kumar, V.; Singh, N.; Singh, D.K.; Mohanty, S.R. Short-Term Electricity Price Forecasting Using Hybrid SARIMA and GJR-GARCH Model. In Networking Communication and Data Knowledge Engineering; Springer: Singapore, 2017; pp. 299–310. [Google Scholar]
- Marín, J.B.; Orozco, E.T.; Velilla, E. Forecasting electricity price in Colombia: A comparison between neural network, ARMA process and hybrid models. Int. J. Energy Econ. Policy 2018, 8, 97. [Google Scholar]
- Brusaferri, A.; Matteucci, M.; Portolani, P.; Vitali, A. Bayesian deep learning based method for probabilistic forecast of day-ahead electricity prices. Appl. Energy 2019, 250, 1158–1175. [Google Scholar] [CrossRef]
- Kavaklioglu, K. Principal components based robust vector autoregression prediction of Turkey’s electricity consumption. Energy Syst. 2019, 10, 889–910. [Google Scholar] [CrossRef]
- Korir, E.K.; Aduda, J.; Mageto, T. Forecasting Electricity Prices Using Ensemble Kalman Filter. J. Stat. Econometr. Methods 2020, 9, 27–45. [Google Scholar]
- Singh, S.; Hussain, S.; Bazaz, M.A. Short term load forecasting using artificial neural network. In 2017 Fourth International Conference on Image Information Processing (ICIIP); IEEE: Piscataway, NJ, USA; pp. 1–5.
- Alshejari, A.; Kodogiannis, V.S. Electricity price forecasting using asymmetric fuzzy neural network systems. In 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE); IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity Price Forecasting Using Recurrent Neural Networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef] [Green Version]
- Marcjasz, G.; Lago, J.; Weron, R. Neural networks in day-ahead electricity price forecasting: Single vs. multiple outputs. multiple outputs. arXiv 2020, preprint. [Google Scholar] [CrossRef]
- Heydari, A.; Nezhad, M.M.; Pirshayan, E.; Garcia, D.A.; Keynia, F.; De Santoli, L. Short-term electricity price and load forecasting in isolated power grids based on composite neural network and gravitational search optimization algorithm. Appl. Energy 2020, 277, 115503. [Google Scholar] [CrossRef]
- Bisoi, R.; Dash, P.K.; Das, P.P. Short-term electricity price forecasting and classification in smart grids using optimized multikernel extreme learning machine. Neural Comput. Appl. 2018, 32, 1457–1480. [Google Scholar] [CrossRef]
- Yan, X.; Chowdhury, N.A. Mid-term electricity market clearing price forecasting: A multiple SVM approach. Int. J. Electr. Power Energy Syst. 2014, 58, 206–214. [Google Scholar] [CrossRef]
- Kuo, P.-H.; Huang, C.-J. An Electricity Price Forecasting Model by Hybrid Structured Deep Neural Networks. Sustainability 2018, 10, 1280. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Xu, C.; Zhang, Y.; Guo, S.; Zomaya, A.Y. Robust Big Data Analytics for Electricity Price Forecasting in the Smart Grid. IEEE Trans. Big Data 2017, 5, 34–45. [Google Scholar] [CrossRef]
- Shayeghi, H.; Ghasemi, A. Day-ahead electricity prices forecasting by a modified CGSA technique and hybrid WT in LSSVM based scheme. Energy Convers. Manag. 2013, 74, 482–491. [Google Scholar] [CrossRef]
- Shrivastava, N.A.; Panigrahi, B.K. A hybrid wavelet-ELM based short term price forecasting for electricity markets. Int. J. Electr. Power Energy Syst. 2014, 55, 41–50. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, Z.; Li, C. A Novel Hybrid Forecasting Method Using GRNN Combined with Wavelet Transform and a GARCH Model. Energy Sources Part B Econ. Plan. Policy 2015, 10, 418–426. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Tian, X.; Fang, S.; Cheng, Y.; Chang, Y.; Liu, H. Short-term wind power forecasting using the hybrid model of improved variational mode decomposition and Correntropy Long Short -term memory neural network. Energy 2020, 214, 118980. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.; Yang, W.; Niu, T. A novel hybrid model for short-term wind power forecasting. Appl. Soft Comput. 2019, 80, 93–106. [Google Scholar] [CrossRef]
- Shang, Z.; He, Z.; Song, Y.; Yang, Y.; Li, L.; Chen, Y. A Novel Combined Model for Short-Term Electric Load Forecasting Based on Whale Optimization Algorithm. Neural Process. Lett. 2020, 52, 1207–1232. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C. Data processing strategies in wind energy forecasting models and applications: A comprehensive review. Appl. Energy 2019, 249, 392–408. [Google Scholar] [CrossRef]
- Ma, X.; Jin, Y.; Dong, Q. A generalized dynamic fuzzy neural network based on singular spectrum analysis optimized by brain storm optimization for short-term wind speed forecasting. Appl. Soft Comput. 2017, 54, 296–312. [Google Scholar] [CrossRef]
- Qian, Z.; Pei, Y.; Zareipour, H.; Chen, N. A review and discussion of decomposition-based hybrid models for wind energy forecasting applications. Appl. Energy 2018, 235, 939–953. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Lu, H.; Niu, T.; Du, P. Hybrid wind energy forecasting and analysis system based on divide and conquer scheme: A case study in China. J. Clean. Prod. 2019, 222, 942–959. [Google Scholar] [CrossRef] [Green Version]
- van der Meer, D.; Shepero, M.; Svensson, A.; Widén, J.; Munkhammar, J. Probabilistic forecasting of electricity consumption, photovoltaic power generation and net demand of an individual building using Gaussian Processes. Appl. Energy 2018, 213, 195–207. [Google Scholar] [CrossRef]
- Ahmadpour, A.; Farkoush, S.G. Gaussian models for probabilistic and deterministic Wind Power Prediction: Wind farm and regional. Int. J. Hydrogen Energy 2020, 45, 27779–27791. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casanova-Mateo, C.; Muñoz-Marí, J.; Camps-Valls, G. Prediction of daily global solar irradiation using temporal Gaussian processes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1936–1940. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J.; Cheng, Y.; Ni, Q.; Wang, S. Short-Term Solar Power Forecasting Based on Weighted Gaussian Process Regression. IEEE Trans. Ind. Electron. 2017, 65, 300–308. [Google Scholar] [CrossRef]
- Aggarwal, S.K.; Saini, L.M.; Kumar, A. Electricity price forecasting in deregulated markets: A review and evaluation. Int. J. Electr. Power Energy Syst. 2009, 31, 13–22. [Google Scholar] [CrossRef]
- Verdoolaege, G.; Scheunders, P. On the Geometry of Multivariate Generalized Gaussian Models. J. Math. Imaging Vis. 2011, 43, 180–193. [Google Scholar] [CrossRef]
- Spanish Electricity Market Website. Available online: https://www.omie.es/en (accessed on 23 April 2021).
- New York’s Electricity Market Website. Available online: https://www.nyiso.com/ (accessed on 25 April 2021).



| Input Period | Period for Forecasting | Season |
|---|---|---|
| 10 January to 20 February | 21 to 27 February | Winter |
| 10 April to 21 May | 22 to 28 May | Spring |
| 10 July to 20 August | 21 to 27 August | Summer |
| 10 October to 20 November | 21 to 27 November | Autumn |
| Input Period | Period for Forecasting | Season |
|---|---|---|
| 5 January to 15 February | 16 to 22 February | Winter |
| 5 April to 16 May | 17 to 23 May | Spring |
| 5 July to 15 August | 16 to 22 August | Summer |
| 5 October to 15 November | 16 to 22 November | Autumn |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dejamkhooy, A.; Ahmadpour, A. Prediction and Evaluation of Electricity Price in Restructured Power Systems Using Gaussian Process Time Series Modeling. Smart Cities 2022, 5, 889-923. https://doi.org/10.3390/smartcities5030045
Dejamkhooy A, Ahmadpour A. Prediction and Evaluation of Electricity Price in Restructured Power Systems Using Gaussian Process Time Series Modeling. Smart Cities. 2022; 5(3):889-923. https://doi.org/10.3390/smartcities5030045
Chicago/Turabian StyleDejamkhooy, Abdolmajid, and Ali Ahmadpour. 2022. "Prediction and Evaluation of Electricity Price in Restructured Power Systems Using Gaussian Process Time Series Modeling" Smart Cities 5, no. 3: 889-923. https://doi.org/10.3390/smartcities5030045
APA StyleDejamkhooy, A., & Ahmadpour, A. (2022). Prediction and Evaluation of Electricity Price in Restructured Power Systems Using Gaussian Process Time Series Modeling. Smart Cities, 5(3), 889-923. https://doi.org/10.3390/smartcities5030045






