Modeling Strategic Interventions to Increase Attendance at Youth Community Centers
Highlights
- The research utilizes advanced gravitational Huff models to predict attendance at BCYF community centers.
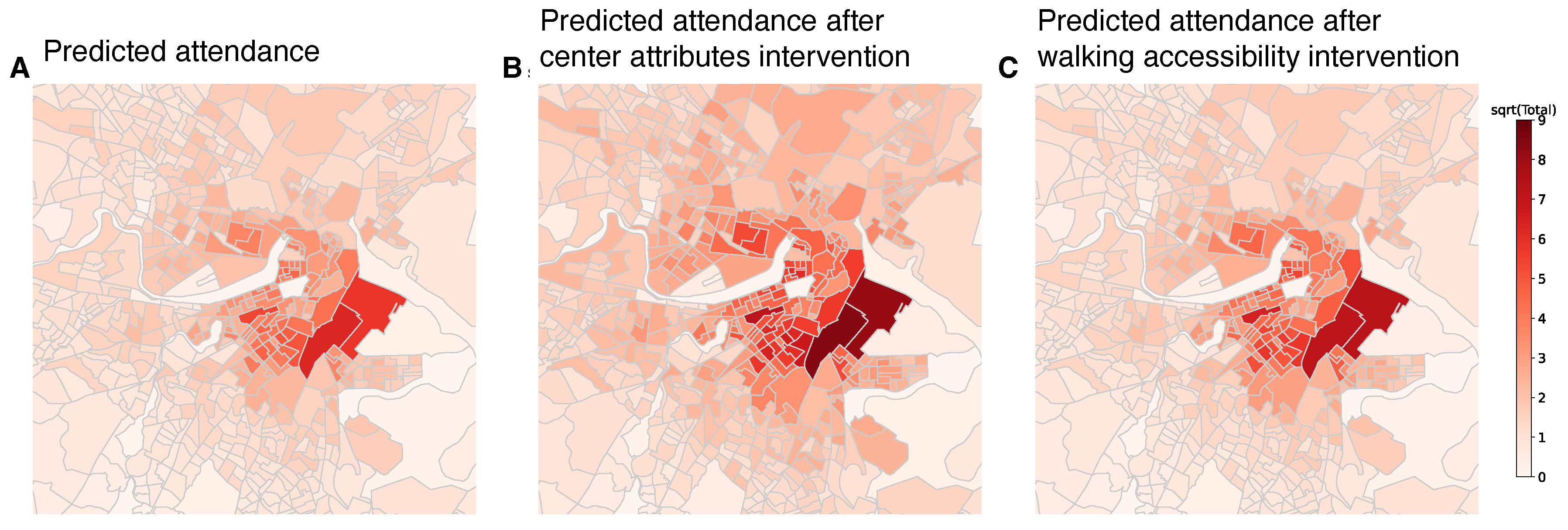
- The research also explores interventions focusing on improving center attributes and fostering walking accessibility at the BCYF community centers.
- The results demonstrate that increasing educational and recreational offerings is the most cost-effective way to increase attendance.
- The developed tool provides data-driven insights for optimizing community center resources to effectively serve underserved populations.
Abstract
:1. Introduction
2. Methodology
2.1. Data
2.2. Models
3. Optimization of the Model
4. Interventions
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Massachusetts Department of Elementary and Secondary Education. 21st Century Community Learning Centers (CCLC) Grant Program, Summer Reports. Available online: https://www.doe.mass.edu/21cclc/ (accessed on 21 January 2024).
- Afterschool Alliance. What Does the Research Say about 21st Century Community Learning Centers? Available online: http://afterschoolalliance.org//documents/What_Does_the_Research_Say_About_21stCCLC.pdf (accessed on 21 January 2024).
- City of Boston. Boston Centers for Youth and Families. Available online: https://www.boston.gov/departments/boston-centers-youth-families (accessed on 16 January 2024).
- Huff, D.L. Parameter Estimation in the Huff Model; Esri, ArcUser: Redlands, CA, USA, 2003; pp. 34–36. [Google Scholar]
- Sevtsuk, A.; Kalvo, R. Patronage of urban commercial clusters: A network-based extension of the huff model for balancing location and size. Environ. Plan. Urban Anal. City Sci. 2018, 45, 508–528. [Google Scholar] [CrossRef]
- Gibbs, R.J. Principles of Urban Retail Planning and Development; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Doorley, R.; Noyman, A.; Sakai, Y.; Larson, K. What’s your mocho? real-time mode choice prediction using discrete choice models and a hci platform. In Proceedings of the UrbComp’19, London, UK, 11–13 September 2019. [Google Scholar]
- Antonelli, D.; Azzato, S.; Elkatsha, M.; Defrain, E.-M.; Pastor, A.; Larson, K. Predicting behavioral changes as a result of land-use modifications in auto-centric communities: Data driven discrete mode choice modeling for dallas TX. In SUPTM 2024; Universidad Politécnica de Cartagena: Cartagena, Colombia, 2023. [Google Scholar]
- Wang, W.; Zhou, Z.; Chen, J.; Cheng, W.; Chen, J. Analysis of location selection of public service facilities based on urban land accessibility. Int. J. Environ. Res. Public Health 2021, 18, 516. [Google Scholar] [CrossRef] [PubMed]
- Talen, E.; Anselin, L. Assessing spatial equity: An evaluation of measures of accessibility to public playgrounds. Environ. Plan. A Econ. Space 1998, 30, 595–613. [Google Scholar] [CrossRef]
- Hodgart, R.L. Optimizing access to public services: A review of problems, models and methods of locating central facilities. Prog. Hum. Geogr. 1978, 2, 17–48. [Google Scholar] [CrossRef]
- Sui, J.; Zhang, G.; Lin, T.; Hamm, N.A.S.; Li, C.; Wu, X. Quantitative evaluation of spatial accessibility of various urban medical services based on big data of outpatient appointments. Int. J. Environ. Res. Public Health 2023, 20, 5050. [Google Scholar] [CrossRef] [PubMed]
- Alonso, L.; Zhang, Y.R.; Grignard, A.; Noyman, A.; Sakai, Y.; Doorley, R.; Larson, K. Cityscope: A data-driven interactive simulation tool for urban design. use case volpe. In Unifying Themes in Complex Systems IX: Proceedings of the Ninth International Conference on Complex Systems 9; Springer: Cham, Switzerland, 2018; pp. 253–261. [Google Scholar]
- Grignard, A.; Alonso, L.; Taillandier, P.; Gaudou, B.; Nguyen-Huu, T.; Gruel, W.; Larson, K. The impact of new mobility modes on a city: A generic approach using abm. In Unifying Themes in Complex Systems IX: Proceedings of the Ninth International Conference on Complex Systems 9; Springer: Cham, Switzerland, 2018; pp. 272–280. [Google Scholar]
- Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.; Simini, F.; Tomasini, M. Human mobility: Models and applications. Phys. Rep. 2018, 734, 1–74. [Google Scholar] [CrossRef]
- Simons, D.; Bourdeaudhuij, I.; Clarys, P.; Geus, B.; Vandelanotte, C.; Cauwenberg, J.; Deforche, B. Choice of transport mode in emerging adulthood: Differences between secondary school students, studying young adults and working young adults and relations with gender, ses and living environment. Transp. Res. Part-Policy Pract. 2017, 103, 172–184. [Google Scholar] [CrossRef]
- Grignard, A.; Macià, N.; Pastor, L.A.; Noyman, A.; Zhang, Y.; Larson, K. Cityscope andorra: A multi-level interactive and tangible agent-based visualization. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 1939–1940. [Google Scholar]
- United States Census Bureau. 2015–2019 American Community Survey 5-Year Estimates. 2021. Available online: https://www.census.gov/programs-surveys/acs (accessed on 16 January 2024).
- Ibargoyen, T.M.; Barrenechea, P.; Elkatsha, M.; Pastor, L.A.; Larson, a.K. A methodology to quantify demands and space requirements of amenities and services for a given community. Use case: Volpe development, kendall sq. In SUPTM 2024; Universidad Politécnica de Cartagena: Cartagena, Colombia, 2023. [Google Scholar]
- Hidalgo, C.A.; Castañer, E.; Sevtsuk, A. The amenity mix of urban neighborhoods. Habitat Int. 2020, 106, 102205. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]

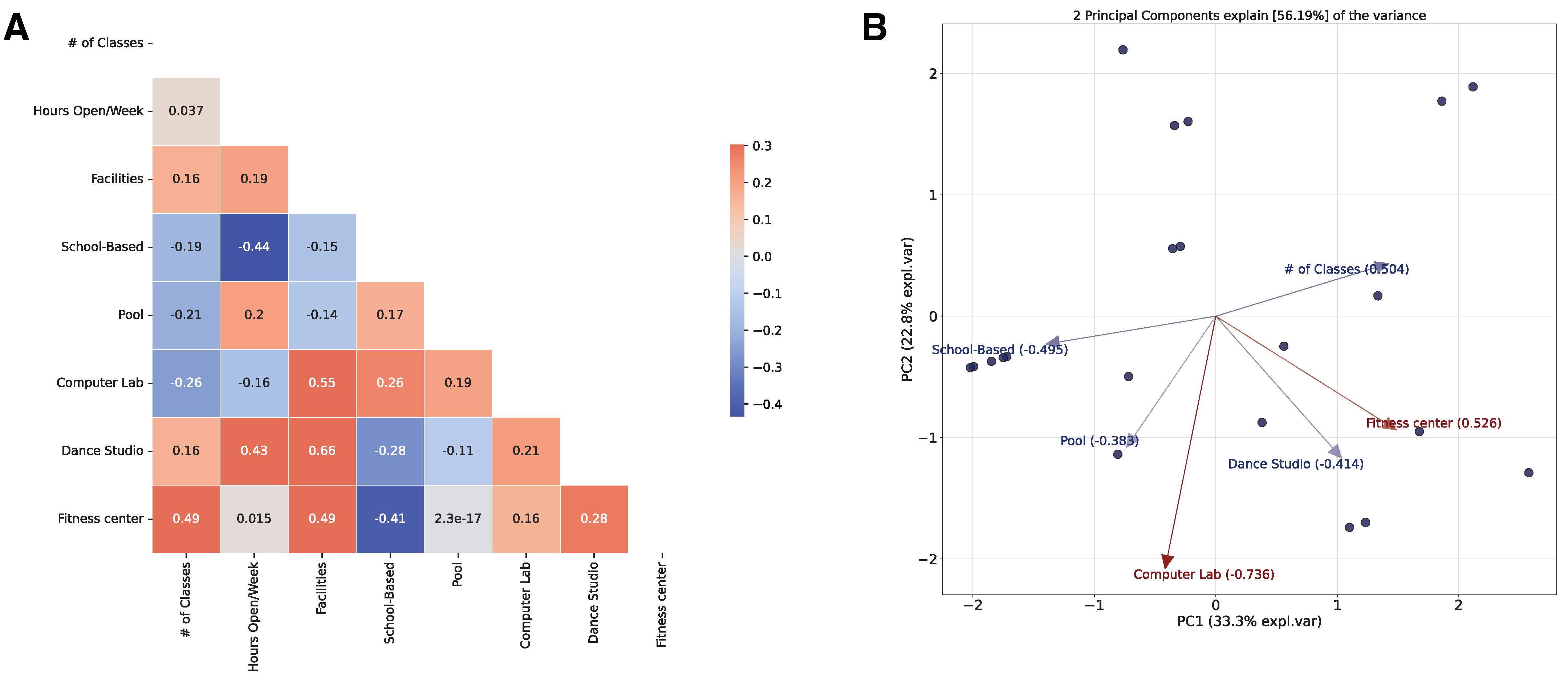


| Community Center | # of Classes | Hours Open/Week | Facilities | School-Based | Pool | Computer Lab | Dance Studio | Fitness Center |
|---|---|---|---|---|---|---|---|---|
| Quincy | 84 | 58 | 6 | 1 | 1 | 1 | 1 | 0 |
| Blackstone | 21 | 58 | 11 | 1 | 0 | 1 | 1 | 0 |
| Nazzaro | 183 | 60 | 8 | 0 | 0 | 0 | 0 | 1 |
| Condon | 22 | 58 | 6 | 1 | 1 | 1 | 0 | 0 |
| Tobin | 61 | 73 | 10 | 0 | 0 | 1 | 1 | 1 |
| Mason Pool | 82 | 66 | 2 | 0 | 1 | 0 | 0 | 0 |
| Charlestown | 59 | 40 | 6 | 0 | 1 | 1 | 0 | 1 |
| Tynan | 73 | 50 | 4 | 1 | 0 | 0 | 0 | 0 |
| Curley | 54 | 78.5 | 9 | 0 | 1 | 1 | 1 | 1 |
| Paris Street | 73 | 68 | 12 | 0 | 1 | 1 | 1 | 1 |
| Hennigan | 61 | 70 | 6 | 1 | 1 | 1 | 0 | 0 |
| Curtis Hall | 266 | 78 | 13 | 0 | 1 | 1 | 1 | 1 |
| Holland | 18 | 58 | 8 | 1 | 1 | 1 | 0 | 0 |
| Marshall | 43 | 50 | 4 | 1 | 1 | 1 | 0 | 0 |
| Perkins | 57 | 68 | 8 | 1 | 1 | 1 | 0 | 0 |
| Gallivan | 47 | 68 | 6 | 0 | 0 | 1 | 0 | 0 |
| Menino | 38 | 55 | 6 | 0 | 0 | 1 | 0 | 0 |
| Flaherty Pool | 66 | 78 | 2 | 0 | 1 | 0 | 0 | 0 |
| Roche | 198 | 73 | 5 | 0 | 0 | 0 | 1 | 0 |
| Hyde Park | 61 | 60 | 12 | 0 | 0 | 1 | 1 | 0 |
| Ohrenberger | 264 | 40 | 7 | 1 | 0 | 1 | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moro-Araujo, A.; Alonso Pastor, L.; Larson, K. Modeling Strategic Interventions to Increase Attendance at Youth Community Centers. Smart Cities 2024, 7, 1878-1887. https://doi.org/10.3390/smartcities7040073
Moro-Araujo A, Alonso Pastor L, Larson K. Modeling Strategic Interventions to Increase Attendance at Youth Community Centers. Smart Cities. 2024; 7(4):1878-1887. https://doi.org/10.3390/smartcities7040073
Chicago/Turabian StyleMoro-Araujo, Alejandro, Luis Alonso Pastor, and Kent Larson. 2024. "Modeling Strategic Interventions to Increase Attendance at Youth Community Centers" Smart Cities 7, no. 4: 1878-1887. https://doi.org/10.3390/smartcities7040073
APA StyleMoro-Araujo, A., Alonso Pastor, L., & Larson, K. (2024). Modeling Strategic Interventions to Increase Attendance at Youth Community Centers. Smart Cities, 7(4), 1878-1887. https://doi.org/10.3390/smartcities7040073





