Stochastic Scheduling of Grid-Connected Smart Energy Hubs Participating in the Day-Ahead Energy, Reactive Power and Reserve Markets

Highlights

What are the main findings?

• The presented smart energy hub (EH) operation enhances the economic and flexibility status of EHs while improving energy network performance.
• Utilization of the bi-level optimization is able to improve energy losses, voltage and temperature drops significantly.

What are the implications of the main findings?

• The integration of energy hubs with flexible operation models enhances the economic and operational performance of energy networks, making them more resilient and efficient.
• The proposed scheme can be a valuable tool for energy market participants, providing a strategic advantage in maximizing profits while maintaining optimal grid performance under uncertainty.

Abstract

An Energy Hub (EH) is able to manage several types of energy at the same time by aggregating resources, storage devices, and responsive loads. Therefore, it is expected that energy efficiency is high. Hence, the optimal operation for smart EHs in energy (gas, electrical, and thermal) networks is discussed in this study based on their contribution to reactive power, the energy market, and day-ahead reservations. This scheme is presented in a smart bi-level optimization. In the upper level, the equations of linearized optimal power flow are used to minimize energy losses in the presented energy networks. The lower level considers the maximization of profits of smart EHs in the mentioned markets; it is based on the EH operational model of resource, responsive load, and storage devices, as well as the formulation of the reserve and flexible constraints. This paper uses the “Karush–Kuhn–Tucker” method for single-level model extraction. An “unscented transformation technique” is then applied in order to model the uncertainties associated with energy price, renewable energy, load, and energy consumed in mobile storage. The participation of hubs in the mentioned markets to improve their economic status and the technical status of the networks, modeling of the flexibility of the hubs, and using the unscented transformation method to model uncertainties are the innovations of this article. Finally, the extracted numerical results indicate the proposed model’s potential to improve EHs’ economic and flexibility status and the energy network’s performance compared to their load flow studies. As a result, energy loss, voltage, and temperature drop as operation indices are improved by 14.5%, 48.2%, and 46.2% compared to the load flow studies, in the case of 100% EH flexibility and their optimal economic situation extraction.

1. Introduction

1.1. Motivation

An energy hub (EH) is an aggregator and coordinating framework for resources, storage, and responsive loads, along with demand response programs (DRPs), which are able to operate in both power transmission and energy storage modes [1]. An EH manages different energy sources, including thermal, electrical, and gas, simultaneously, so it has suitable ability to improve energy efficiency [1]. Furthermore, EHs are typically equipped with environmentally friendly elements, including renewable energy sources (RESs) and non-RESs, such as combined heat and power (CHP), which make them an appropriate solution for minimizing the environmental impacts associated with uncontrolled fossil fuel consumption [2]. However, this causes them not to have control over the resources in their produced energy, which will further reduce the flexibility of EHs [3]. For example, thanks to low operating costs and low emissions, RESs generally inject an active power equal to their maximum output active power into the EH in proportion to the weather conditions. As a result of uncertainty in active power, the operation results of day-ahead (DA) and real-time (RT) are not the same. Thus, RT operation might not achieve the balance between production and consumption for EHs with only RESs, which is considered low flexibility for an EH. [3]. Similar problems arise with CHP’s thermal power, as it is reliant on active power and cannot be controlled independently. This issue may result in a low level of flexibility in the thermal section [4]. Storage and responsive loads have been proposed as energy-controllable elements to improve EH flexibility [3,4]. On the other hand, an EH is able to transmit power and store energy. Therefore, it is predicted that by participating in the energy market and ancillary services, it can achieve optimal financial benefits for resources, storage, and responsive loads. However, these cases depend on the establishment of a smart energy management system for EHs, and according to this, the appropriate technical and economic capabilities for EHs and energy networks can be achieved [5].

1.2. Literature Review

The energy management of EHs in various energy networks has been the subject of various studies. Considering the uncertainty of thermal/electric loads and wind generation, [6] develops a robust framework for microgrid operation in the gas network. Using the constraint generation and column (CG&C) method, the proposed model is linearized and solved. Using a min–max objective function, the unit commitment cost is minimized in the master problem, while the dispatch cost of worst-case uncertainties is developed in the subproblem. In addition, the balance of degree of robustness and operational expenses is adjusted by means of polyhedral uncertainties, which are defined through uncertainty parameters. A stochastic framework based on natural gas, biomass, electricity, and thermal energy is presented in [7] for the optimal operation of a novel EH with multiple energy converters and electrical storage. Within systems of multiple energies, this scheme has the role of a bidding technique for smart elements. In [7], scenario-based stochastic optimization (SBSO) is utilized to model uncertainties in solar radiation, the market price of energy, and wind speed [7]. Based on wind power’s penetration, [8] presents a regional power grid and a structure for determining grid-connected EHs’ optimal operation. The optimization problem aims to address several primary challenges that have yet to be adequately addressed, such as the rate of emissions and amounts of renewable energy curtailed as well as total operating costs. Uncertainty in wind power is accurately modeled using a robust model based on information-gap decision theory (IGDT). In [9], the hub is utilized as a framework for coordination between the distributed generation (DG) and energy storage system (ESS) with respect to the energy management of EHs connected to energy networks. According to the proposed scheme, the total operating cost of the energy networks is minimized through a deterministic model with respect to the EH constraints. In order to model the uncertainty, an adaptive robust optimization method is applied using a hybrid metaheuristic algorithm based on the non-convexity and nonlinearity of the proposed problem. To model the aspects of planning and operation of the system, [10] develops an optimal EH including various RES types, considering storage systems of thermal energy and electricity. Additionally, by considering the stochastic nature of PV and wind, multi-energy systems’ optimal scheduling and planning are modeled. Aiming to minimize the total cost of EHs and based on Quantum Particle Swarm Optimization (QPSO), a robust technique is applied to solve this model. Taking into account RESs’ high penetration and aiming at the operation of renewable systems and private EH systems collaboratively, a decision-making structure based on privacy preserving is presented in [11]. Based on different entities’ private ownership, the presented scheme is solved by applying Benders’ decomposition algorithm (BDA) and is established according to a decentralized robust and stochastic bi-level method. The study’s main goals are to reduce renewable energy constraints and to reduce the entities’ operating expenses. A market optimization participation method in a virtual energy hub including industrial energy hubs and consumers is developed in [12]. Based on power grid operational limits, a two-stage robust stochastic optimization scheme is developed in [12] to compensate for operational risks of uncertainties and minimize the virtual energy hub operation expenses. To achieve this goal, transactive energy management and demand response programs are considered as enhanced ancillary services in the optimization problem. The industrial and technical operation of a combined scheme incorporating a photovoltaic system coupled with an electric vehicle parking lot and a storage system is presented in [13]. Moreover, a three-level cooperative control system is developed to schedule the economic operation and reactive and active power flows of the virtual energy hub. For electric power generation using thermal power, EH uses a new technology (organic Rankine cycle) and a flexible load (seawater desalination systems using reverse osmosis units) [14]. Furthermore, a battery interchange station and an electric vehicle parking lot are presented as a suitable means of interaction with electric vehicles. A fuel cell and hydrogen tank serve as a balance between hydrogen consumption and production, and electric power is utilized by the electrolyzer to supply the required hydrogen. IGDT and method-based scenario generation are utilized in uncertainty modeling. Based on day-ahead (DA) markets hub cooperation, [15] develops a unified approach to EHs’ energy management in various networks. During the process, aiming at DA market profit maximization based on hubs and linear network restrictions, unified energy management based on a linear objective function is considered. Ref. [16] proposes a novel flexibilization service for the distribution system exploiting the capabilities of renewable energy communities through the concept of Virtual Islanding operation. This new paradigm can ease the sustainable energy transition of distribution systems, making them keener to accommodate larger shares of renewable sources in the grid. The work in [17] analyzed common architectures and protocols commonly used to build smart energy communities, evaluating the attack surfaces and possible vulnerabilities. This work also discusses some solutions which can be employed to mitigate the risk, and highlights current gaps in the state of the art. Ref. [18] aims to propose a novel evolving framework for optimal energy flow (OEF) of an electricity, heat, and gas integrating system, taking into account flexible heat and electricity demand. To this end, a switching approach between input energy carriers has been introduced to combine the traditional demand response with demand-side energy supply management. Switching between the feeding energy carriers could change how power is supplied to the end users and thus would affect the total cost of the grid. Finally,

Table 1. Recent research work taxonomy.

Ref.	Market Model			Uncertainty Modeling	Flexibility Model
	Energy	Reactive Power	Reserve Regulation
[6]	No	No	No	Robust optimization	No
[7]	Yes	No	No	SBSO	No
[8]	No	No	No	IGDT	No
[9]	No	No	No	Robust optimization	No
[10]	No	No	No	Robust optimization	No
[11]	No	No	No	Robust stochastic optimization	No
[12]	Yes	No	No	Robust stochastic optimization	No
[13]	No	No	No	SBSO	No
[14]	No	No	No	IGDT	No
[15]	Yes	No	No	SBSO	No
[16]	No	No	No	-	Yes
[17]	No	No	No	-	No
[18]	No	No	No	-	No
PM	Yes	Yes	Yes	Unscented transformation (UT) method	Yes

PM: Proposed model.

summarizes the literature.

1.3. Research Gaps

The following research gaps are identified in the grid-connected EH field, considering the research background and Table 1 discussed in the previous section:

• EHs are typically operated on a cost-based model in most studies. However, EHs are able to transfer power and store energy [1]. Therefore, they are expected to be able to extract favorable financial benefits from energy and ancillary services markets (such as active and reactive power) for resources, responsive loads, and storage. In some research, EHs have been analyzed according to their operation model in proportion to the energy market; however, their participation in ancillary services has been less discussed [7,12,15].
• Market participation and energy management of grid-connected smart EHs are types of operational issues. The operation step for this issue is generally under an hour [9,15]. Thus, to solve the problem, a short computational time is particularly important [15]. This is accomplished in cases of low-volume data and simple formulation of the problem. In addition, the aforementioned problem has a high number of uncertainty parameters, including loads, energy prices, EVs, and renewable power. In some research, such as [7,11,13,15], the SBSO method has been considered for modeling. As a result of these uncertainties, a large number of scenarios must be considered. Nevertheless, the volume of the problem data and the computational time increase. Some studies have used robust optimization for uncertainty modeling to solve this issue [6,8,9,10,14], which includes only one scenario. However, calculating some indices, such as flexibility, requires examining different states related to uncertainty parameters, like renewable power. This is not achieved through robust optimization. To overcome this research gap, using stochastic optimization based on methods with a minimum number of scenarios such as unscented transformation (UT) is necessary, which has been less discussed in the literature.
• An EH is less flexible due to the presence of RESs and CHP [3,4]. To compensate, most research discusses flexible resource utilization, including responsive loads and storage [6,7,8,9,10,11,12,13,14,15]. However, the improvement of an EH’s flexibility depends on its optimal energy management by considering the number of flexible indices. This issue can be established only by considering a flexible model with respect to the grid-connected smart EH energy management issue, which has been discussed less in the literature, such as [16].

1.4. Contributions

Based on Figure 1, this paper addresses the first and third research gaps by examining grid-connected flexible EH operations participating in markets of energy, DA reservation, and reactive power. The energy hub is a means of aggregating and coordinating resources, storage devices, and responsive loads, which can be used to transfer and store different energies such as electricity, heat, and gas. Hence, it involves high efficiency. Thermal, gas, and electrical networks are also connected to the EH. In this scheme, the mentioned EHs are a coordinating system including RESs, CHP, boiler, thermal energy storage (TES), static electrical energy storage (EES) (battery), and mobile EES (electric vehicle (EV) aggregation), and demand response programs (DRP). As shown in Figure 1, EH operators are in bidirectional coordination with the operators of storage, resources, and responsive loads in the proposed energy management system (EMS). EH operators are also in bidirectional coordination to establish optimal operation in energy networks. A bi-level optimization approach is used in the following explanation of the proposed plan. The objective function of the upper level problem is to minimize energy losses in the networks mentioned. Additionally, the linearized optimal power flow for this network is also included. The objective function of the lower level problem is to maximize the EH profits in the aforementioned markets. It is also based on the operational formulation of the EH, including sources, storage, responsive loads, the reservation model, and the EH’s flexibility limitations. By using the Karush–Kuhn–Tucker (KKT) method, the proposed problem can be solved using conventional solvers. This scheme also includes the uncertainties of loads, renewable power, energy prices, and EH aggregation parameters. Thus, the UT technique is used in this article to address the second research gap. This method provides a smaller number of scenarios compared to other stochastic optimization methods [19]. Finally, the innovations in this scheme are as follows:

• The operation of grid-connected EHs in energy networks, considering their simultaneous participation in reserve, reactive, and energy markets in order to improve the economic status of hubs and the operational status of the network simultaneously.
• Providing flexible constraint formulation in the proposed scheme in order to access an EH with high flexibility with respect to the uncertainties of renewable resources.
• Utilizing the UT technique to simultaneously carry out uncertainty modeling of the energy price, EV’ aggregation parameters, loads, and renewable power to reduce the volume of problem data and increase problem convergence rates under the goals of the operators.

1.5. Paper Organization

The following is a summary of the rest of the paper: the formulation of the proposed scheme in proportion to its methods of uncertainty modeling is provided in the Section 2. The extraction of a single-level model based on KKT for the proposed scheme is presented in the Section 3. Finally, Section 4 and Section 5 discuss the numerical results and conclusions, respectively.

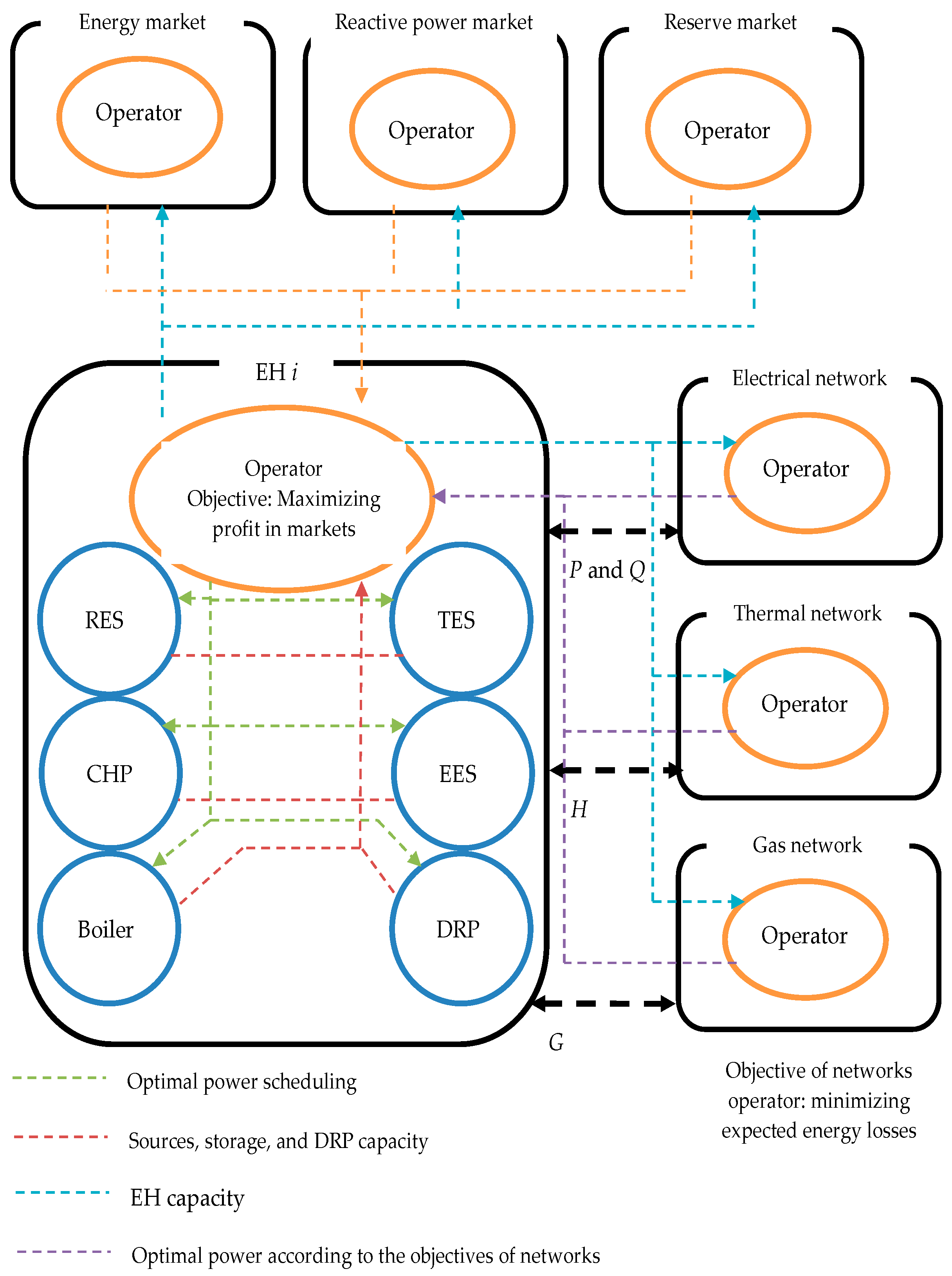
2. Energy Network Operation Considering EHs Participating in the Markets

2.1. Proposed Scheme Formulation

This section discusses the energy management formulation for energy networks (gas, thermal, and electricity) considering the concurrent participation of hubs in reactive, reserve, and energy markets. It is considered as a bi-level optimization; the optimal operation of the mentioned networks with the aim of energy loss minimization is modeled in the upper level. With respect to the EH, the lower level refers to the operational model of storage, resources, and responsive loads in order to maximize profit. Accordingly, this problem can be expressed as follows.

(A)

Upper level problem

-

Objective function: The objective function in Equation (1) is equal to minimizing expected energy losses (EELs) in three networks: electrical (first part), thermal (second part), and gas (third part). Hence, the difference between the produced energy (by distribution substation and EH) and the consumed energy due to passive loads of the network is considered an energy loss in a network [4]. However, in modeling the problem, it is assumed that EHs are producers. In this case, if the gas, thermal, reactive, and active power have a positive (negative) value, then it will be a producer (consumer). In this equation, P^ES, H^HS, and G^GS are the active power of the electrical station, thermal power of the heat post, and gas power of the gas station, respectively. P^ED, H^HD, and G^GD are the active, thermal, and gas load, respectively. P^EH, H^EH, and G^EH are the active, thermal, and gas power of the i-th EH in hour t and scenario w.

$$\min \hspace{1em}\hspace{1em}EEL=\left\{\begin{array}{l}{\displaystyle \sum _{e,t,w}{\pi }_w\left(P_{e,t,w}^{ES}-P_{e,t,w}^{ED}+{\displaystyle \sum _i{I}_{e,i}^E{P}_{i,t,w}^{EH}}\right)}+{\displaystyle \sum _{h,t,w}{\pi }_w\left(H_{h,t,w}^{HS}-H_{h,t,w}^{HD}+{\displaystyle \sum _i{I}_{h,i}^H{H}_{i,t,w}^{EH}}\right)}\\ +{\displaystyle \sum _{g,t,w}{\pi }_w\left(G_{g,t,w}^{GS}-G_{g,t,w}^{GD}+{\displaystyle \sum _i{I}_{g,i}^G{G}_{i,t,w}^{EH}}\right)}\end{array}\right\}$$

(1)

-

Model of energy networks: A linearized optimal power flow equation in an electrical, gas, or thermal network is the basis of Equations (2)–(21). Constraints (2)–(5) represent linearized equations of power flow in electrical networks, which describe the balance of active and reactive power in electrical buses [20,21,22,23,24] and active and reactive power flows in electrical distribution lines, respectively [5,25]. Thermal network power flow Equations (6) and (7) represent the balance of thermal power in the thermal node and also the thermal power flow through the thermal pipe, respectively [1,2]. Relations (8)–(12) also represent the linearized power flow constraints of the gas networks [2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Constraint (8) refers to the balance of the gas power in gas nodes. Constraints (9)–(12) represent the linearized power flow model through the gas pipe [15]. Electrical, thermal, and gas network operation constraints are expressed in (13)–(15) [25,26], (16)–(18) [1,2], and (19)–(21) [14,15], respectively. These constraints for the electrical networks (thermal/gas) refer to the voltage deviation limitation (temperature/pressure) and apparent power (thermal/gas) flow through the line and substation, respectively.

$$P_{e,t,w}^{ES}+{\displaystyle \sum _i{I}_{e,i}^E{P}_{i,t,w}^{EH}}-{\displaystyle \sum _m{J}_{e,m}^E{P}_{e,m,t,w}^{EL}=P_{e,t,w}^{ED}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,t,w$$

(2)

$$Q_{e,t,w}^{ES}+{\displaystyle \sum _i{I}_{e,i}^E{Q}_{i,t,w}^{EH}}-{\displaystyle \sum _m{J}_{e,m}^E{Q}_{e,m,t,w}^{EL}=Q_{e,t,w}^{ED}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,t,w$$

(3)

$$P_{e,m,t,w}^{EL}=G_{e,m}^{EL}\left(\Delta V_{e,t,w}-\Delta V_{m,t,w}\right)-B_{e,m}^{EL}\left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,m,t,w$$

(4)

$$Q_{e,m,t,w}^{EL}=-B_{e,m}^{EL}\left(\Delta V_{e,t,w}-\Delta V_{m,t,w}\right)-G_{e,m}^{EL}\left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,m,t,w$$

(5)

$$H_{h,t,w}^{HS}+{\displaystyle \sum _i{I}_{h,i}^H{H}_{i,t,w}^{EH}}-{\displaystyle \sum _m{J}_{h,m}^H{H}_{h,m,t,w}^{HL}=H_{h,t,w}^{HD}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall h,t,w$$

(6)

$$H_{h,m,t,w}^{HL}={\vartheta }_{h,m}\left(T_{h,t,w}-T_{m,t,w}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall h,m,t,w$$

(7)

$$G_{g,t,w}^{GS}+{\displaystyle \sum _i{I}_{g,i}^G{G}_{i,t,w}^{EH}}-{\displaystyle \sum _m{J}_{g,m}^G{G}_{g,m,t,w}^{GL}=G_{g,t,w}^{GD}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,t,w$$

(8)

$$G_{g,m,t,w}^{GL}={\omega }_{g,m}sign\left({\xi }_{g,t,w},{\xi }_{m,t,w}\right){\phi }_{g,m,t,w}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,m,t,w$$

(9)

$${\xi }_{g,t,w}=\underset{¯}{\xi }+{\displaystyle \sum _k\Delta {\xi }_{g,t,w,k}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,t,w$$

(10)

$${\phi }_{g,m,t,w}={\displaystyle \sum _k\Delta {\phi }_{g,m,t,w,k}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,m,t,w$$

(11)

$$\Delta {\phi }_{g,m,t,w,k}={\displaystyle \frac{l{s}_k^{\xi }}{l{s}_k^{\phi }}}sign\left({\xi }_{g,t,w},{\xi }_{m,t,w}\right)\left(\Delta {\xi }_{g,t,w,k}-\Delta {\xi }_{m,t,w,k}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,m,t,w,k$$

(12)

$$\underset{¯}{V}-1\le \Delta V_{e,t,w}\le \overline{V}-1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,t,w\hspace{0.17em}$$

(13)

$$P_{e,m,t,w}^{EL}\cos \left(s\times \Delta \theta \right)+Q_{e,m,t,w}^{EL}\sin \left(s\times \Delta \theta \right)\le {\overline{S}}_{e,m}^{EL}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,m,t,w,s$$

(14)

$$P_{e,t,w}^{ES}\cos \left(s\times \Delta \theta \right)+Q_{e,t,w}^{ES}\sin \left(s\times \Delta \theta \right)\le {\overline{S}}_e^{ES}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e=o,t,w,s$$

(15)

$$\underset{¯}{T}\le T_{h,t,w}\le \overline{T}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall h,t,w\hspace{0.17em}$$

(16)

$$-{\overline{H}}_{h,m}^{HL}\le H_{h,m,t,w}^{HL}\le {\overline{H}}_{h,m}^{HL}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall h,m,t,w$$

(17)

$$-{\overline{H}}_h^{HS}\le H_{h,t,w}^{HS}\le {\overline{H}}_h^{HS}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall h=o,t,w$$

(18)

$$\underset{¯}{\xi }\le {\xi }_{g,t,w}\le \overline{\xi }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,t,w\hspace{0.17em}$$

(19)

$$-{\overline{G}}_{g,m}^{GL}\le G_{g,m,t,w}^{GL}\le {\overline{G}}_{g,m}^{GL}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,m,t,w$$

(20)

$$-{\overline{G}}_g^{GS}\le G_{g,t,w}^{GS}\le {\overline{G}}_g^{GS}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g=o,t,w$$

(21)

In fact, constraints (4) and (5) have a nonlinear format, respectively, as follows [25]:

$$P_{e,m,t,w}^{EL}=G_{e,m}^{EL}{\left(V_{e,t,w}\right)}^2-V_{e,t,w}{V}_{m,t,w}\left\{G_{e,m}^{EL}\cos \left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)+B_{e,m}^{EL}\sin \left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)\right\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,m,t,w$$

(22)

$$Q_{e,m,t,w}^{EL}=-B_{e,m}^{EL}{\left(V_{e,t,w}\right)}^2+V_{e,t,w}{V}_{m,t,w}\left\{B_{e,m}^{EL}\cos \left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)-G_{e,m}^{EL}\sin \left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)\right\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall e,m,t,w$$

(23)

Based on the result of [25], the voltage angle deviation between the distribution line’s starting and ending buses is less than 6 degrees in the electrical distribution networks, and the voltage magnitude should also be maintained at more than 0.9 and less than 1.1 per unit [5]. Therefore, the expressions $\cos \left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)$ and $\cos \left({\sigma }_{e,t,w}-{\sigma }_{m,t,w}\right)$ are approximated to 1, respectively. The voltage magnitude (V) can also be considered as V = 1 + ΔV, in which the amount of voltage deviation is much less than 1 per unit. Now, under these conditions, and ignoring the small values of ΔV², ΔV_e, ΔV_m, and ΔV × (σ_e − σ_m), the linearized relations (4) and (5) are obtained for nonlinear constraints (53) and (54) [5,25].

In fact, Equation (9) has a nonlinear relation, as in Equation (24) [2]:

$$G_{g,m,t,w}^{GL}={\omega }_{g,m}sign\left({\xi }_{g,t,w},{\xi }_{m,t,w}\right)\sqrt{\left({\xi }_{g,t,w},{\xi }_{m,t,w}\right)\left({\left({\xi }_{g,t,w}\right)}^2-{\left({\xi }_{m,t,w}\right)}^2\right)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,m,t,w$$

(24)

For its linearization, this relation was first written as (9), where φ as an auxiliary variable is calculated through relation (25):

$${\left({\phi }_{g,m,t,w}\right)}^2=sign\left({\xi }_{g,t,w},{\xi }_{m,t,w}\right)\left({\left({\xi }_{g,t,w}\right)}^2-{\left({\xi }_{m,t,w}\right)}^2\right)$$

(25)

In this article, the linear piece linearization method has been used to linearize this relation [2,15]. In this technique, based on the pressure deviation (Δξ) with a value much less than ξ, the pressure variable (ξ) is expressed as a relation (10). This is the case for φ in Equation (11). In this technique, the expressions ξ² and φ² are expressed as ${\xi }^2={\left(\underset{¯}{\xi }\right)}^2+{\displaystyle \sum _{k}l{s}_k^{\xi }\Delta {\xi }_k}$ and ${\phi }^2={\displaystyle \sum _{k}l{s}_k^{\phi }\Delta {\phi }_k}$, respectively, where ls^ξ and ls^φ represent the linear piece slope for ξ and φ, respectively. Considering these cases, the linearized relation ${\left({\phi }_{g,m,t,w}\right)}^2=sign\left({\xi }_{g,t,w},{\xi }_{m,t,w}\right)\left({\left({\xi }_{g,t,w}\right)}^2-{\left({\xi }_{m,t,w}\right)}^2\right)$ is expressed as (12) [2,15].

It has to be noted that the voltage constraint is expressed in operational problems as $\underset{¯}{V}\le V_{e,t,w}\le \overline{V}\hspace{0.17em}$ [26]. However, since the voltage deviation variable has been used in the proposed problem, constraint (13) replaces the voltage magnitude constraint [25]. The limitation of apparent power flow through a line or distribution substation (14)–(15), is modeled in coordinates PQ as a circular plane with the origin point at the center and radius S, i.e., $\sqrt{P^2+Q^2}\le S\hspace{0.17em}$. This article approximates the circular plane as a regular polygonal plane [19]. In this plane, on each side of the equation (s) is linear, i.e., $P\cos \left(s\times \Delta \theta \right)+Q\sin \left(s\times \Delta \theta \right)=S\hspace{0.17em}$. Δθ represents the angle deviation and is equal to 360/n_S. Then, n_S represents the total number of sides in the new plane; therefore, s is selected from {1, 2, …, n_S}. Finally, from each side, a square plane is extracted as $P\cos \left(s\times \Delta \theta \right)+Q\sin \left(s\times \Delta \theta \right)\le S\hspace{0.17em}$, and its repetition for the set {1, 2, …, n_S} results in the extraction of a plane in regular polygon form [27].

(B)

Lower level problem

This section refers to the operational model of storage, responsive load, and resource in the EH, which considers market participation in reactive power, energy, and reserve.

-

Objective function: The objective function in relation (26) maximizes the expected profit of EHs in the energy market (the first line of the relation), reactive power market (the second line of the relation), and reserve power market (the third line of the relation). There are reserve and energy markets for three sections, including electricity, thermal, and gas. The positive sign (or negative sign) of power in each equation section represents the profit (or cost) in that section. In other words, relationship (26) simultaneously calculates the profit or cost of hubs in different markets. In this regard, the reserve and reactive power variables of hubs are positive. Therefore, the relationship (26) in the market of reactive power and reservation for hubs is profitable. In the energy market, if the active power of hubs is positive, that profit is obtained for the hubs in this market. But if the active power of hubs is negative, the hubs have a cost in the energy market. Therefore, if Profit had a positive value, then hubs have profits in all markets. Otherwise, they have a cost.

$$\begin{array}{l}{P}^{EH},Q^{EH},G^{EH},H^{EH}\in \arg \left\{\max \hspace{1em}\hspace{0.17em}\mathrm{Profit}={\displaystyle \sum _{i,t,w}\left({\lambda }_{t,w}^E{P}_{i,t,w}^{EH}+{\lambda }_{t,w}^H{H}_{i,t,w}^{EH}+{\lambda }_{t,w}^G{G}_{i,t,w}^{EH}\right)}\right.\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _{i,t,w}{\lambda }_{t,w}^E{K}_Q{Q}_{i,t,w}^{EH}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _{i,t,w}\left({\lambda }_{t,w}^{ER}E{R}_{i,t,w}^{EH}+{\lambda }_{t,w}^{HR}H{R}_{i,t,w}^{EH}+{\lambda }_{t,w}^{GR}G{R}_{i,t,w}^{EH}\right)}\end{array}$$

(26)

-

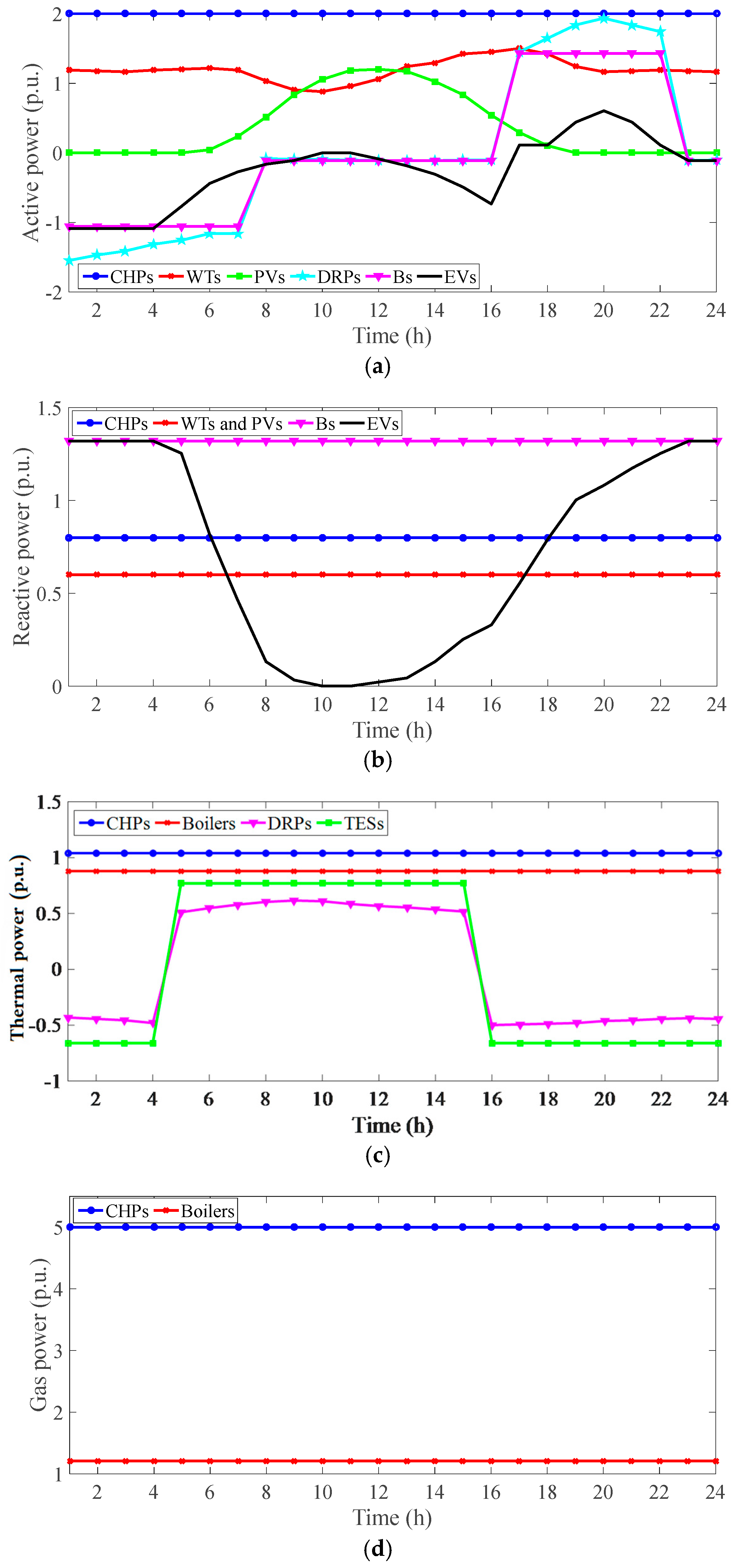
Power balance model of EHs: Relations (27)–(30) represent the power balances of active power, reactive power, thermal, and gas in an EH. CHP, RESs, storage, and responsive loads can control EH active power based on (23). CHP, RESs, and EES play a role in reactive control. CHP, boiler, and responsive loads are used for reactive power control in an EH. In gas power control, the boiler and CHP play a role in gas energy consumption; however, the responsive load can act in production/consumption mode.

$$P_{i,t,w}^{EH}+E{R}_{i,t,w}^{EH}=P_{i,t,w}^C+P_{i,t,w}^R+P_{i,t,w}^D+\left(P_{i,t,w}^{DCH}-P_{i,t,w}^{CH}\right)-P_{i,t,w}^{ED}:{\gamma }_{i,t,w}^p\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(27)

$$Q_{i,t,w}^{EH}=Q_{i,t,w}^C+Q_{i,t,w}^R+Q_{i,t,w}^E-Q_{i,t,w}^{ED}:{\gamma }_{i,t,w}^q\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(28)

$$H_{i,t,w}^{EH}+H{R}_{i,t,w}^{EH}=H_{i,t,w}^C+H_{i,t,w}^B+H_{i,t,w}^D+\left(H_{i,t,w}^{DCH}-H_{i,t,w}^{CH}\right)-H_{i,t,w}^{HD}:{\gamma }_{i,t,w}^h\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(29)

$$G_{i,t,w}^{EH}+G{R}_{i,t,w}^{EH}=G_{i,t,w}^D-G_{i,t,w}^C-G_{i,t,w}^B-G_{i,t,w}^{GD}:{\gamma }_{i,t,w}^g\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(30)

-

CHP model: The CHP operational constraints are presented in (31)–(34) [4], which refer to thermal and gas power [28,29,30], and also the power constraints of active and reactive power in CHP, respectively.

$$H_{i,t,w}^C=P_{i,t,w}^C{\displaystyle \frac{\left(1-{\eta }^T-{\eta }^L\right){\eta }^H}{{\eta }^T}}:{\gamma }_{i,t,w}^{hc}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(31)

$$G_{i,t,w}^C={\displaystyle \frac{1}{{\eta }^T}}{P}_{i,t,w}^C:{\gamma }_{i,t,w}^{gc}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(32)

$${\underset{¯}{P}}_i^C\le P_{i,t,w}^C\le {\overline{P}}_i^C:{\underset{¯}{\mu }}_{i,t,w}^{pc},{\overline{\mu }}_{i,t,w}^{pc}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(33)

$${\underset{¯}{Q}}_i^C\le Q_{i,t,w}^C\le {\overline{Q}}_i^C:{\underset{¯}{\mu }}_{i,t,w}^{qc},{\overline{\mu }}_{i,t,w}^{qc}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(34)

-

Boiler model: The boiler operation model is represented in (35)–(36) [15]. The input gas amount is calculated in (35), and the output thermal power limitation is expressed in (36).

$$G_{i,t,w}^B={\displaystyle \frac{1}{{\eta }^B}}{H}_{i,t,w}^B:{\gamma }_{i,t,w}^{gb}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(35)

$${\underset{¯}{H}}_i^B\le H_{i,t,w}^B\le {\overline{H}}_i^B:{\underset{¯}{\mu }}_{i,t,w}^{hb},{\overline{\mu }}_{i,t,w}^{hb}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(36)

-

RES model: It should be noted that, generally, the amount of active power in an RES is a parameter [31,32,33,34,35]; however, its reactive power can be controlled by an electric power converter [25]. The active power of the RES is constant [36,37,38,39]. Hence, Equation (37) is taken into consideration for the RES, which refers to the RES’s reactive power constraints.

$${\underset{¯}{Q}}_i^R\le Q_{i,t,w}^R\le {\overline{Q}}_i^R:{\underset{¯}{\mu }}_{i,t,w}^{qr},{\overline{\mu }}_{i,t,w}^{qr}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(37)

-

EES model: The operation model of EES is described in (38)–(41) [40], which refer to the limitations of the charge and discharge rates [41,42,43,44], stored energy, and reactive power, respectively. EES devices such as batteries and EVs are connected to the network by a DC/AC converter. These converters are able to control reactive power using IGBT switches [45,46]. Additionally, in other forms of EES, like compressed air energy storage (CAES), the synchronous generator is also capable of controlling reactive power. As another point, relations (38)–(41) can be used for the aggregation of EVs, with the difference that the parameters CR^EES, DR^EES, EI, $\underset{¯}{E}$, $\overline{E}$, ${\underset{¯}{Q}}^E$, and ${\overline{Q}}^E$ depend on the number and the type of EVs [5,25]. Hence, the indexes of time (t) and scenario (w) are used for these parameters. The right-side unequal expression of constraint (40) is also converted to the equal expression because in the operation model of EVs, $\overline{E}$ represents the energy consumption of EVs during travel, which must be provided [5,25].

$$0\le P_{i,t,w}^{CH}\le \hspace{0.17em}C{R}_i^{EES}:{\underset{¯}{\mu }}_{i,t,w}^{ec},{\overline{\mu }}_{i,t,w}^{ec}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(38)

$$0\le P_{i,t,w}^{DCH}\le \hspace{0.17em}D{R}_i^{EES}:{\underset{¯}{\mu }}_{i,t,w}^{ed},{\overline{\mu }}_{i,t,w}^{ed}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(39)

$${\underset{¯}{E}}_i\le E{I}_i+{\displaystyle \sum _{t=1}^{\tau }\left({\eta }^{CH}{P}_{i,\tau ,w}^{CH}-\frac{1}{{\eta }^{DCH}}{P}_{i,\tau ,w}^{DCH}\right)}\le {\overline{E}}_i:{\underset{¯}{\mu }}_{i,t,w}^{ees},{\overline{\mu }}_{i,t,w}^{ees}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(40)

$${\underset{¯}{Q}}_i^E\le Q_{i,t,w}^E\le {\overline{Q}}_i^E:{\underset{¯}{\mu }}_{i,t,w}^{qe},{\overline{\mu }}_{i,t,w}^{qe}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(41)

-

TES model: The limitations of charge and discharge rate and stored energy in thermal energy storage (TES) are described in (42)–(44) as the operation model of TES [4].

$$0\le H_{i,t,w}^{CH}\le \hspace{0.17em}C{R}_i^{TES}:{\underset{¯}{\mu }}_{i,t,w}^{tc},{\overline{\mu }}_{i,t,w}^{tc}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(42)

$$0\le H_{i,t,w}^{DCH}\le \hspace{0.17em}D{R}_i^{TES}:{\underset{¯}{\mu }}_{i,t,w}^{td},{\overline{\mu }}_{i,t,w}^{td}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(43)

$${\underset{¯}{E}}_i\le E{I}_i+{\displaystyle \sum _{t=1}^{\tau }\left({\eta }^{CH}{H}_{i,\tau ,w}^{CH}-\frac{1}{{\eta }^{DCH}}{H}_{i,\tau ,w}^{DCH}\right)}\le {\overline{E}}_i:{\underset{¯}{\mu }}_{i,t,w}^{tes},{\overline{\mu }}_{i,t,w}^{tes}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(44)

-

DRP model: The DRP formulation for electrical, thermal, and gas consumers is expressed in (45)–(46). This model is based on the price and incentive method [5]. Therefore, if the energy price is high (low), consumers will reduce (increase) their energy consumption, and all the reduced energy must be provided in cheap energy price hours [5]. Therefore, this leads to an increase in the profits of EHs based on Equation (1). Thus, constraint (45) indicates the power control range of active, thermal, and gas in DRP, while (46) ensures that the total decreased energy in expensive energy hours is supplied in cheap energy hours.

$$\begin{array}{l}-{\beta }_i{P}_{i,t,w}^{ED}(H_{i,t,w}^{ED}\hspace{0.17em}\mathrm{or}\hspace{0.17em}{G}_{i,t,w}^{ED})\le P_{i,t,w}^D(H_{i,t,w}^D\hspace{0.17em}\mathrm{or}\hspace{0.17em}{G}_{i,t,w}^D)\le {\beta }_i{P}_{i,t,w}^{ED}(H_{i,t,w}^{ED}\hspace{0.17em}\mathrm{or}\hspace{0.17em}{G}_{i,t,w}^{ED}):{\underset{¯}{\mu }}_{i,t,w}^{pd}({\underset{¯}{\mu }}_{i,t,w}^{hd}\hspace{0.17em}\mathrm{or}\hspace{0.17em}{\underset{¯}{\mu }}_{i,t,w}^{gd}),{\overline{\mu }}_{i,t,w}^{pd}({\overline{\mu }}_{i,t,w}^{hd}\hspace{0.17em}\mathrm{or}\hspace{0.17em}{\overline{\mu }}_{i,t,w}^{gd})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall i,t,w\end{array}$$

(45)

$${\displaystyle \sum _t{P}_{i,t,w}^D(H_{i,t,w}^D\hspace{0.17em}\mathrm{or}\hspace{0.17em}{G}_{i,t,w}^D)}=0:{\gamma }_{i,w}^{pd}({\gamma }_{i,w}^{hd}\hspace{0.17em}\mathrm{or}\hspace{0.17em}{\gamma }_{i,w}^{gd})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,w$$

(46)

-

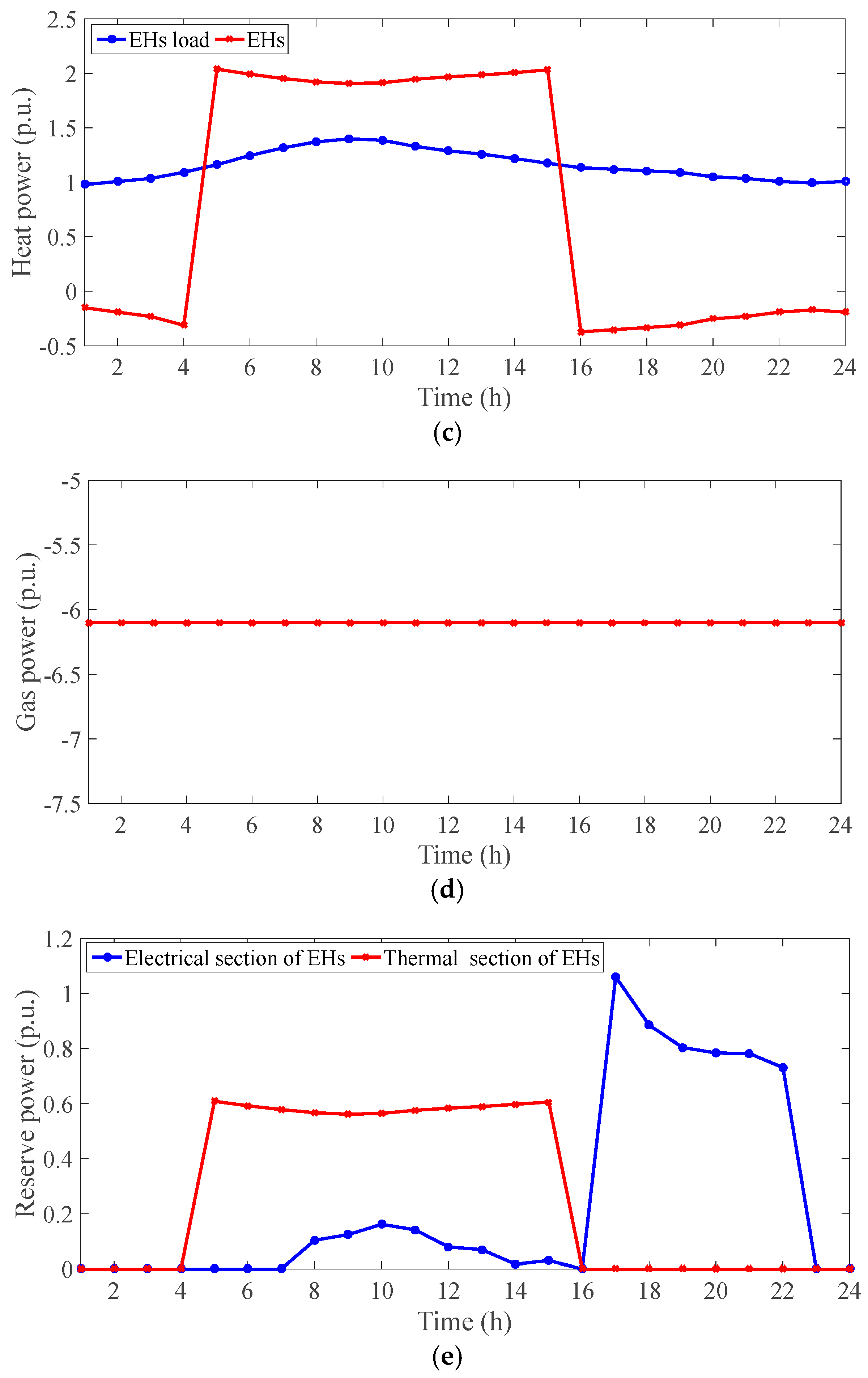
Reserve model of EHs: Constraint (47) can also be used to calculate the reserve amount of electrical, thermal, and gas power. It is noted that the difference between the consumed active power of the loads and the generated active power by storage, sources, and responsive loads is injected into the network as P^EH or reserved in the EH as ER^EH. This is true for the thermal and gas sections in relations (29)–(30). There is always a positive value for reserve power, as stated in constraint (47) [47].

$$E{R}_{i,t,w}^{EH},H{R}_{i,t,w}^{EH},G{R}_{i,t,w}^{EH}\ge 0\hspace{0.17em}:{\underset{¯}{\mu }}_{i,t,w}^{er},{\underset{¯}{\mu }}_{i,t,w}^{hr},{\underset{¯}{\mu }}_{i,t,w}^{gr}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(47)

-

Flexibility model of EHs: Constraint (48) describes the flexibility of EHs in the thermal and electrical sections. In this constraint, 100% flexibility is achieved if ΔF tend to zero. According to the generated active power uncertainty of RESs, there will be different values for active power in different scenarios. Therefore, flexible sources, including responsive loads, non-renewable resources, and storage in the EH, are able to overcome the fluctuation of power produced by RESs through active power control. As a result, this enables EHs to achieve high flexibility through a certain amount of active power injection into each scenario [48]. Formulation (48) can be used to address this issue. CHP thermal power (relation 27) depends on the active power in the thermal section. Therefore, independent control is not applicable to it. In the case of CHP’s active power changes to compensate for RES active power, thermal power changes occur in the EH. CHP’s thermal power fluctuation can be compensated for by TES, responsive load, and boiler, which leads to the injection of a certain amount of thermal power into the network by the EH in different scenarios. This will result in the improved flexibility of the EH’s thermal section, and the mathematical model (48) can be used to access it. Finally, variables γ and μ represent Lagrangian multipliers.

$$-\Delta F\le P_{i,t,w}^{EH}-P_{i,t,w=1}^{EH}(\mathrm{or}\hspace{0.17em}{H}_{i,t,w}^{EH}-H_{i,t,w=1}^{EH})\le \Delta F:{\underset{¯}{\mu }}_{i,t,w}^{fe},{\overline{\mu }}_{i,t,w}^{fe}(\mathrm{or}\hspace{0.17em}{\underset{¯}{\mu }}_{i,t,w}^{fh},{\overline{\mu }}_{i,t,w}^{fh})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(48)

2.2. Uncertainty Modeling Based on UT

Uncertainty parameters include load (P^ED, Q^ED, H^HD, G^GD), market prices (λ^E, λ^H, λ^G, λ^ER, λ^HR, λ^GR), renewable power P^R, and the aggregation parameters of EVs (CR^EES, DR^EES, EI, ${\overline{Q}}^E$, $\underset{¯}{E}$, $\overline{E}$, ${\underset{¯}{Q}}^E$). In this article, uncertainties are modeled using stochastic programming.

In comparison with other methods, based on the shorter time of convergence and computation, UT is considered an efficient method [19]. Moreover, the model simplification is not based on mathematical assumptions, contrary to analytical methods. This method is included in this work for uncertainty modeling; furthermore, this method is suitable and reliable for coping with probability distribution function estimation and nonlinear transitions [16]. The input uncertain parameters (U) are developed through n = 18. Based on n =18, 2n + 1 scenarios (i.e., 37 scenarios) are generated. Consequently, based on the small scenario number, no scenario reduction strategy is required to reduce the time of computation. This approach’s formulation has been extensively presented in [19].

Suppose y = f(x) is a nonlinear stochastic problem with uncertainty including two uncertain variables, y ∈ R^r (the vector of uncertain output with r elements) and x ∈ Rⁿ (the vector of uncertain input with the values of covariance and mean, σ_x and μ_x, respectively). The covariance of uncertain variables is expressed by non-symmetric matrix inputs, while the variance of uncertain parameters is given by symmetric matrix inputs. The covariance and mean parameters (σ_y and μ_y) are found by means of the UT technique [19]:

• Step 1: 2n + 1 scenarios are taken from the uncertain entries:

$$x_0={\mu }_x$$

(49)

$$x_{\varpi }={\mu }_x+\sqrt{{\displaystyle \frac{n}{1-W^0}}{\sigma }_x}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \varpi =1,2,\cdots ,n$$

(50)

$$x_{\varpi }={\mu }_x-\sqrt{{\displaystyle \frac{n}{1-W^0}}{\sigma }_x}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \varpi =n+1,n+2,\cdots ,2n$$

(51)

where W⁰ represents the mean value weight (μ_x).

• Step 2: The scenario weight factor evaluation:

$$W^0=W^0$$

(52)

$$W_{\varpi }={\displaystyle \frac{1-W^0}{2n}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \varpi =1,2,\cdots ,n$$

(53)

$$W_{\varpi +n}={\displaystyle \frac{1-W^0}{2n}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \varpi +n=n+1,n+2,\cdots ,2n$$

(54)

$${\displaystyle \sum _{\varpi =1}^n{W}_{\varpi }}=1$$

(55)

• Step 3: Output parameter determination based on (56) and scenario 2n + 1 indicate the nonlinear function:

$$y_{\varpi }=f(x_{\varpi })$$

(56)

• Step 4: Output parameter ν evaluation, including mean and covariance (μ_y and σ_y, respectively):

$${\mu }_y={\displaystyle \sum _{\varpi =1}^n{W}_{\varpi }{\nu }_{\varpi }}$$

(57)

$${\sigma }_y={\displaystyle \sum _{\varpi =1}^n{W}_{\varpi }\left({\nu }_{\varpi }-{\mu }_y\right)}-{\left({\nu }_{\varpi }-{\mu }_y\right)}^T$$

(58)

3. The Extraction of a Single-Level Formulation

To solve formulations (1)–(21) and (26)–(48) as a bi-level problem using a conventional solver, a single-level model is extracted [49]. In this article, this purpose is achieved through the KKT method. In mathematical optimization, the KKT conditions are first derivative tests (sometimes called first-order necessary conditions) for a solution in nonlinear programming to be optimal, provided that some regularity conditions are satisfied. Allowing inequality constraints, the KKT approach to nonlinear programming generalizes the method of Lagrange multipliers, which allows only equality constraints. Similarly to the Lagrange approach, the constrained maximization (minimization) problem is rewritten as a Lagrange function whose optimal point is a global maximum or minimum over the domain of the choice variables and a global minimum (maximum) over the multipliers [49]. The KKT constraint is derived from the lower level problem in this method, while the upper level problem is equivalent to the single-level model [49]. To extract the KKT constraints, the sum of the objective function and the penalty function of the lower level constraints is first calculated as the Lagrange (L) function of the low-level problem [49]. The penalty functions for the equal (a = b) and unequal (a ≤ b) constraints are γ.(b − a) and μ.max(0, a − b), respectively. The variables γ ∈ (−∞, +∞) and μ ≥ 0 represent Lagrangian multipliers [50]. The KKT constraint is obtained by equalizing the Lagrange function’s derivative to the "lower-level variable and lagrangian multipliers" with zero [49]. As a result, the proposed scheme can be expressed as a single-level formulation as follows:

$$\min \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}EEL=\left\{\begin{array}{l}{\displaystyle \sum _{e,t,w}{\pi }_w\left(P_{e,t,w}^{ES}-P_{e,t,w}^{ED}+{\displaystyle \sum _i{I}_{e,i}^E{P}_{i,t,w}^{EH}}\right)}+{\displaystyle \sum _{h,t,w}{\pi }_w\left(H_{h,t,w}^{HS}-H_{h,t,w}^{HD}+{\displaystyle \sum _i{I}_{h,i}^H{H}_{i,t,w}^{EH}}\right)}\\ +{\displaystyle \sum _{g,t,w}{\pi }_w\left(G_{g,t,w}^{GS}-G_{g,t,w}^{GD}+{\displaystyle \sum _i{I}_{g,i}^G{G}_{i,t,w}^{EH}}\right)}\end{array}\right\}$$

(59)

subject to the following:

Constraints (2)–(21)

(60)

Constraints (27)–(48): ∂L/∂γ = 0 and ∂L/∂μ = 0

(61)

μ.(a − b) = 0: ∂L/∂μ = 0 for inequality constraints in the lower level model (26)–(48)

(62)

∂L/∂p = 0   p is all primal variables of the lower level model (26)–(48)

(63)

$$\gamma \in \left(-\infty ,+\infty \right),\mu \ge 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,t,w$$

(64)

According to (59), the objective function of the single-level model of the proposed scheme is equal to the objective function of the upper level problem in relation (1). The upper level problem’s constraints are also used in this new problem, which is stated in constraint (60). Equations (61)–(64) include the KKT model of the lower level problem (26)–(48).

It is noteworthy that equalizing the Lagrange function’s derivative to Lagrangian multipliers with zero (i.e., ${\displaystyle \frac{\partial L}{\partial \gamma }}=0$) leads to the extraction of the equal constraint in the lower problem [49]. ${\displaystyle \frac{\partial L}{\partial \mu }}=0$ (μ represents the Lagrangian multiplier for the unequal constraint) also leads to the extraction of the two types of equations (known as the first and second conditions of KKT). ${\displaystyle \frac{\partial L}{\partial \mu }}=0$ leads to the unequal constraint extraction of the lower problem in the first condition of KKT. In the second condition of KKT, $\mu .(a-b)=0$ is obtained from ${\displaystyle \frac{\partial L}{\partial \mu }}=0$ [49]. The corresponding constraints to ${\displaystyle \frac{\partial L}{\partial \gamma }}=0$ and the first condition of KKT are stated in (61). Constraint (62) is obtained from the second condition of KKT. Relation (63) is also equal to the constraints of KKT, which have been obtained by equalizing the Lagrange function’s derivative to the lower level variable’s problem with zero. Finally, relation (64) refers to the Lagrangian multiplier limitation. In addition, $\mu .(a-b)=0$ in constraint (63) is nonlinear. Then, using the BIG-M method [49], two constraints $-M(1-z)\le a-b\le M(1-z)$ and $-M\times z\le \mu \le M\times z$ are used for the mentioned nonlinear constraint. In these constraints, M is a large constant such as 10⁶, and z is a binary variable.

The proposed scheme is an optimization model. This model includes an objective function [51,52,53,54,55]. In this function, the min or max value of a factor is obtained [56,57,58,59]. This problem is based on the different constraints [60,61,62]. Constraints contain equality and inequality formulations [63,64,65,66]. To apply the optimization model to the network, the system needs smart devices [67,68,69].

4. Numerical Results

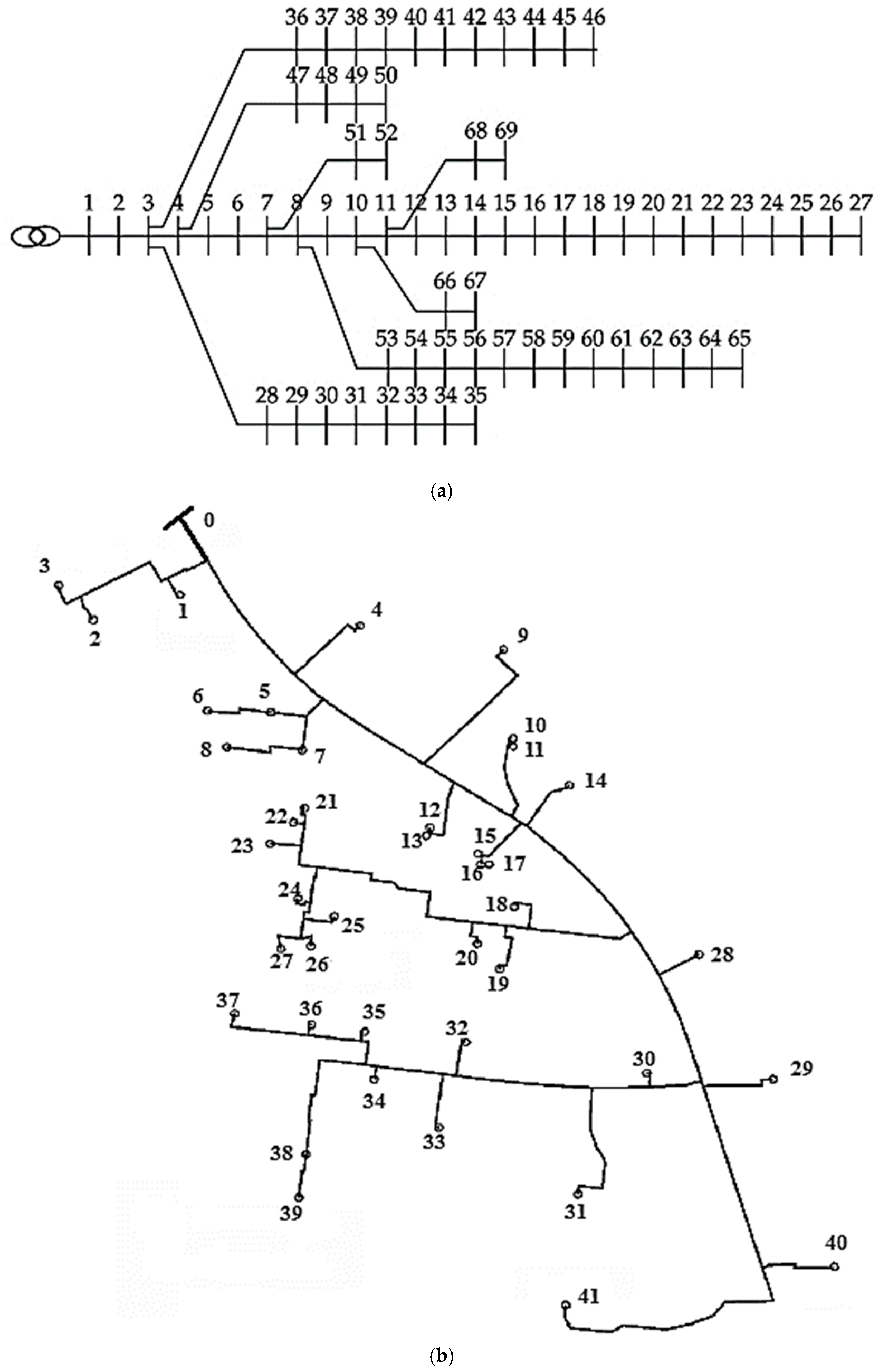
4.1. Problem Data

This section applies the proposed optimization scheme to a test system in Figure 2 that comprises three networks: an IEEE 69-bus electrical distribution network [4], a gas system that includes four nodes [15], and a Naestved 42-node thermal network [70]. Thermal, gas, and electrical networks have a base power of 1 MW, 1 MW, and 1 MVA, respectively. Ten bar, 373.15 K, and 12.66 KV are the base pressure, temperature, and voltage of the system. Zero, 1, and 1 are the slack buses in thermal, gas, and electrical networks, respectively; 1.1 and 0.9 per unit are the upper and lower limits of these variables [71,72,73,74,75,76]. Refs [4,15,70] present the aforementioned network data, including peak load, lines, and substations. In the electrical network, the peak reactive and active loads are 2.694 MVAr and 3.791 MW, respectively, while in the thermal network, the thermal peak load is 6 MW [70]. In EHs, gas energy is assumed to be supplied by the gas network only for CHP systems and boilers; therefore, the value of the passive gas load is zero. According to the curve presented in [15], each network’s hourly load data are calculated by multiplying the load factor curves and peak load. Based on the various network energy prices presented in [15], for the hours 23:00–08:00, 08:00–17:00, and 17:00–23:00, the prices of energy in the electrical network are 17.60 USD/MWh, 33 USD/MWh, and 26.40 USD/MWh, respectively. The prices in the thermal network for the hours 16:00–04:00 and 04:00–16:00 are 15 USD/MWh and 22 USD/MWh, and in the gas network for the hours 05:00–22:00 and 22:00–05:00 are 18 USD/MWh and 12 USD/MWh, respectively. Each network has a reserve price that is the same as its energy price. K_Q is also equivalent to 0.08, based on [25]. Figure 1 illustrates a system containing 8 EHs, and

Table 2. EH data.

EH	Location (e, h, g)	Source	ESS	DRP	PED (MW)	QED (MVAr)	HHD (MW)	GGD (MW)
1	6, -, -	PV, WT	B, EVs	Electrical	0.6	0.3	0	0
2	13, -, -	PV, WT	B, EVs	Electrical	0.4	0.2	0	0
3	23, -, -	PV, WT	B, EVs	Electrical	0.6	0.3	0	0
4	26, -, -	PV, WT	B, EVs	Electrical	0.4	0.2	0	0
5	17, 5, 2	CHP, boiler, PV, WT	TES, B, EVs	Electrical and thermal	0.8	0.4	0.4	0
6	31, 11, 4	CHP, boiler, PV, WT	TES, B, EVs	Electrical and thermal	0.8	0.4	0.4	0
7	21, 2, 3	CHP, boiler	TES	Thermal	0.4	0.2	0.3	0
8	10, 8, 3	CHP, boiler	TES	Thermal	0.4	0.2	0.3	0

reports its peak load, different network placements, and elements. Based on Table 2, RESs in EHs 1–6 consist of wind turbines (WTs) and photovoltaics (PV). RES peak active power for PV and WTs is 0.25 MW and 0.2 MW, respectively. As presented in [5], the daily profile of the active power generated by these sources can be calculated by multiplying the daily power generation curve by the active peak power [77,78,79,80,81]. Additionally, each of these sources can regulate its reactive power within the range of −0.1 MVAr to 0.1 MVAr. The DRP scheme is assumed to be available to 40% of EH consumers. EHs 1–6 consist of two types of static (battery type (B)) and mobile (aggregation of EVs) EES. In each of these EHs, 80 electric vehicles are assumed. By multiplying the daily penetration rate curve [5] by the total number of EVs, the number of EVs connected to the EH per hour can be calculated. The rate of discharge/charge, energy consumption, the capacity of charge, and other factors such as EV characteristics are reported in [5,25]. In the above-mentioned EHs, a 1.5 MWh battery with a 90% efficiency has been used. The initial and minimum storable energy of this battery are both 0.2 MW, and the rate of discharge and charge for this battery is 0.8 MW/h [15]. The battery charger can also adjust its reactive power within the range of −0.2 MVAr to 0.2 MVAr. There are similar specifications for TES, with the exception of its 80 percent charge and discharge efficiency. There is a capacity (maximum thermal power) of 0.4 MW and efficiency of 80% for boilers in EHs 5–8. The maximum (minimum) reactive, active, and thermal power of CHP in EHs, are 0.2 MVAr, 0.5 MW, and 0.3 MW (−0.2 MVAr, 0 MW, and 0 MW) respectively. The efficiency of thermal power, losses, and the turbine in CHP are 40%, 8%, and 40%, respectively [4]. Lastly, a 10% standard deviation is assumed for uncertainty parameters, and a 0.05 flexibility tolerance is designated in order to achieve flexible EHs.

4.2. Results

With the GAMS optimization software (version 45.7.0) [82], the proposed scheme was simulated based on the data in Section 4.1 [82]. GAMS version 15.2 is used in this paper, and the simulation was done on a Dell Laptop with RAM 12, Core i7-10850H, and Intel UHD Graphics. Thus, the following numerical results are reported for the various case studies.

(A)

Appropriate solution algorithm extraction

In

Table 3. Proposed scheme convergence status based on the various solvers in ΔF = 0.05 p.u.

Model	Solver	UT Method (39 Scenarios)				SBSO-Based KWM and KM (80 Scenarios)
		EEL (MWh)	Profit (USD)	CI	CT (min)	EEL (MWh)	Profit (USD)	CI	CT (min)
NLP	IPOPT	6.73	3253.40	1469	47.3	6.73	3253.60	1894	65.5
	CONOPT	6.91	3089.50	1722	54.8	6.92	3089.90	2347	75.2
	MINOS	7.17	2845.80	2046	65.5	Infeasible
	LGO	Infeasible				Infeasible
LP	CPLEX	6.58	3405.70	46	2.2	6.58	3405.90	63	3.1
	OSL	6.58	3405.70	82	3.6	6.58	3405.90	105	5.2
	CBC	6.58	3405.70	65	2.9	6.58	3405.90	87	4.4

, the convergence status of the proposed scheme in nonlinear programming (NLP) and linear programming (LP) based on uncertainty modeling using UT and SBSO for a flexibility tolerance of 0.05 per unit is presented. It has to be noted that the nonlinear model of relations (4), (5), (9), (13)–(14), and (90)–(126) has been used in the NLP model. Due to the convexity of the lower level problem, the KKT method is applicable. In SBSO [15], the roulette wheel mechanism (RWM) first generates a large number of scenarios (here 2000 scenarios). In each scenario, the value of the uncertainty parameters is determined based on the mean value and standard deviation. Then, the probability of the selected value is calculated for the uncertainty parameters in each scenario. To calculate the probability value of the energy price, load, renewable power of solar/wind, and EV parameters, the normal probability distribution function (PDF), Weibull/Beta, and Riley distributions are used [3,5,15]. Multiplying the probability of the uncertainty parameters is equal to the probability of each scenario. Therefore, the Kantorovich method (KM) [15] as a technique of scenario reduction selects a certain number of generated scenarios that are close to each other and applies them to the problem. In this section, KM applies 80 scenarios to the problem to access the optimal and safe solution. In the following, IPOPT, CONOPT, MINOS, and LGO solvers [82] are used to solve the proposed NLP problem. Based on Table 3, the optimal solution cannot be extracted by the LGO solver in UT, which requires 39 scenarios. In SBSO, where the number of scenarios has increased to 80, the LGO and MINOS solvers are not able to solve the problem. In addition, the answers obtained in IPOPT and CONOPT are different. IPOPT has the best solution among these two solvers because it has the lowest EEL and the highest profit. It also has low computational time (CT) and low convergence iteration (CI), especially in UT due to the lower number of scenarios. Therefore, considering these conditions, IPOPT has the best conditions for NLP in the proposed scheme. Then, CPLEX, OSL, and CBC solvers [82] are used to solve the proposed LP problem [82]. According to Table 3, it is evident that the optimal solution obtained by the three solvers mentioned is the same. Thus, EEL and profit are equal to 6.58 MWh and USD 3405.70, respectively. These solvers differ only in CT and CI values. The lowest (and highest) CI and CT were obtained in CPLEX (OSL). Therefore, in solving the proposed LP problem, it can be stated that CPLEX has the best conditions. It is noteworthy that the executive step is generally low [5] in operational problems, for example, around an hour. Therefore, the low computational time is important in solving the operation problem. In this article, this issue has been addressed by linearizing the proposed scheme and modeling the uncertainties with UT. So, in the nonlinear model and SBSO, the computational time is around 65.5 min; however, in the UT and linear model, it is around 2.2 min.

In the LP model (CPLEX solver), the problem variables computational error compared to the real model of NLP (IPOPT solver) has been evaluated for ΔF = 0.05 p.u. Based on this table, it is evident that the computational error for active and reactive power is 2.4%, and that it is around 0.9% for gas power. This value for voltage and pressure is around 0.45% and 0.1%, respectively. According to Section 2, LP and NLP models have the same optimal power flow equations for the thermal network, so its variables have no computational error. Finally, based on Table 3 and

Table 4. Computational error of various variables in the LP model compared to the NLP model in ΔF = 0.05 p.u.

Model	LP	NLP	Calculation Error (%)
Solver	CPLEX	IPOPT
PES in electrical peak load hour (p.u.)	2.18	2.23	2.24
QES in electrical peak load hour (p.u.)	1.60	1.64	2.44
HHS in thermal peak load hour (p.u.)	3.87	3.87	0
Maximum value of GGS (p.u.)	12.34	12.45	0.88
Mean value of V (p.u.)	0.962	0.958	0.42
Mean value of σ (rad)	−0.01406861	−0.014	0.49
Mean value of T (p.u.)	0.947	0.947	0
Mean value of ξ (p.u.)	0.964	0.963	0.10

, the calculation error is low and can be removed; therefore, a unique optimal solution can be obtained by a linear model, while this issue is not available in a nonlinear model.

(B)

EH performance evaluation

For ΔF = 0.05 p.u., Figure 3 and Figure 4 display daily performance curves for EHs and their elements. The expectation daily curve for reactive, active, gas, and thermal power from storage devices, sources, and responsive loads is represented in Figure 3. According to Figure 3a, the RESs inject the maximum producible active power into the EHs in accordance with the weather conditions at all hours. According to [5], the generation rate for photovoltaic power is 1 at 12:00 and zero at 19:00–05:00. Moreover, based on Section 4.1, there are six photovoltaic plants, whose capacity is 0.2 p.u. Therefore, photovoltaic plants do not generate active power during 19:00–05:00, and at 12:00 the active power is equal to 1.2 p.u. This is also true for wind turbines. According to Section 4.1, since the price of electricity and heat is higher than the price of gas energy in all operating hours, based on Figure 3a, this has led to a high active power injection by CHP systems into the EHs. A maximum active power of 0.5 p.u. is generated by each CHP system according to Section 4.1. Therefore, they inject a maximum active power of 2 p.u into EHs. Batteries and DRP are in charge mode in off-peak and mid-peak hours (23:00–16:00), and they are discharged in peak electricity hours (16:00–23:00). In the case of EVs, they receive the required energy for traveling from the grid between 23:00 and 07:00, when the price of electrical energy is the cheapest, and during these hours they receive high active power from EHs based on Figure 3a. From 12:00 to 16:00, they are in charging mode, until electrical load peak hours when they inject their stored battery energy into the EHs. In the energy market, this operation of the different elements corresponds to maximizing the EHs’ profit. Due to RES uncertainty, they could lose flexibility at any hour due to their active power generation in all operating hours, based on Figure 3a. Therefore, according to Figure 3a, flexible sources such as EVs, batteries, DRP, and CHP systems are operational during all operation hours.

The expected daily curve of reactive power for CHP, batteries, EVs, and RESs is shown in Figure 3b. According to Equation (22), an incentive for providing reactive power services in the market of the proposed scheme has been considered; thus, these elements try to inject their maximum reactive power into EHs or electrical networks during all operating hours. For example, the maximum capacity of photovoltaic plants to control reactive power is equal to 0.1 p.u., and according to Section 4.1, there are six photovoltaic plants. Hence, they inject a total reactive power of 0.6 p.u. into EHs. The reactive power produced by EVs is proportional to their number and type. Since a number of different types of EVs are connected to the EHs at any time, their total reactive power changes with time. Figure 3c shows the expected daily thermal curves for CHPs, boilers, TESs, and DRPs. According to Equation (27), the CHP thermal power is its active power coefficient, and the value of CHP active power is constant in all operation hours based on Figure 3c. Therefore, Figure 3c depicts the CHP thermal power during all operation hours with a constant value. Regarding boiler operation, it is noteworthy that the thermal energy price during all simulation hours is higher than the gas energy price, according to Section 4.1. Therefore, in order to maximize profit, they inject their maximum thermal power into EHs. During the hours of cheap thermal energy (16:00–04:00), thermal DRPs and TES systems are in charging mode, while in other operation hours they are in discharge mode. In the market for thermal energy, this type of operation of the mentioned elements maximizes EH profit. In addition, the thermal power of CHP has a value at all hours; therefore, there is a possibility of the thermal share’s flexibility being reduced. To compensate for this, flexible sources such as thermal boilers, TES, and DRPs are always on. Finally, the expected daily gas power curve of CHP systems and boilers is presented in Figure 3d. Based on Equations (28) and (32), the gas power of the CHP and boiler is a factor of active and thermal power, respectively. Since the active and thermal power of the CHP and boiler are constant at all hours, their gas power is constant for all operating hours, according to Figure 4d.

The active, reactive, thermal, and gas power expected daily curve of EHs is represented in Figure 4. These expressions are calculable from Equations (23)–(26). Based on these equations, the difference between the generated power of resources, storage devices in discharge mode, and responsive load, as well as the power consumption of load, storage devices in charge mode, and responsive load, is equal to the total active and reserve power of EHs. This is also true for the thermal and gas sections. The EHs’ reactive power is equal to the difference between the generated power of resources and storage and the power consumption of passive loads. The active, reactive, thermal, and gas loads expected daily curve is presented in Figure 4. According to these curves and Figure 3, the active, reactive, thermal, and gas power expected daily curves of EHs are proportional to Figure 4a to Figure 4d, respectively. According to these figures, EHs are active power consumers during 23:00–07:00 because, according to Figure 3a, electric batteries, DRPs, and EVs work in charging mode at these hours. According to Figure 3a, they act as producers during other times because of the high level of active power generation related to storage, responsive loads, and resources. EHs generate reactive power at all hours. EHs are thermal energy consumers during 16:00–04:00 because thermal DRPs and TES systems receive power from the grid during these hours, according to Figure 3c. However, the responsive loads, sources, and storage are in a thermal power-generating mode at other hours, and then EHs are thermal energy generators during these hours. According to Section 4.1, the gas network and EHs do not have gas loads. Therefore, they do not have responsive load capability. Therefore, EHs are always in consumer mode at all hours since they only have consumers, which are the CHP and boiler.

Finally, Figure 4e represents the EHs’ thermal and electrical reserve power expected daily curve. Based on Figure 4e, EHs can have electric and thermal reserve power when they are in producer mode.

Table 5. The expected profit of EHs in different proposed markets for different amounts of flexibility tolerance.

DA Market	Flexibility Tolerance (p.u.)
	0	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40
Energy	2095.4	2180.6	2224.1	2245.9	2259.8	2268.9	2273.4	2275.1	2275.1
Reactive power	154.3	154.3	154.3	154.3	154.3	154.3	154.3	154.3	154.3
Reserve	1503.2	1526.7	1538.3	1548.9	1553.7	1555.9	1557.1	1557.8	1557.8
Total	3752.9	3861.6	3916.7	3949.1	3967.8	3979.1	3984.8	3987.2	3987.2

reports EHs’ profit expectation in the markets of energy, reactive, and reserve power using different flexibility tolerances. This table indicates that profitability for EHs in the reserve and energy markets increases with increased flexibility tolerance. Because of these conditions, the importance of constraints (51) and (52) and flexibility constraints decreases in the proposed problem. Therefore, the performance of EHs and their elements will be in proportion to their profit maximization. For example, by reducing the importance of flexibility, electric batteries and DRPs can be turned off from 08:00 to 17:00 and 17:00 to 23:00 when the price of electricity is higher than the hours from 23:00 to 08:00. Therefore, they consume energy only during the cheapest hours of electricity (23:00–08:00). This will increase the profits of EHs. Table 5 indicates that there is no flexibility tolerance in EH profits in the reactive power market. Therefore, the flexibility in EHs does not affect the profitability of EHs in the reactive power market and only reduces the profitability of EHs in the reserve and energy markets.

(C)

Evaluation of the operation status of the energy networks

To evaluate the proposed scheme feasibility, two study cases have been reviewed here:

• Power flow analysis
• Proposed scheme

The results of this section are presented in

Table 6. The operation indices status for various study cases and different flexibility tolerance.

Index		Case I	Case II
			ΔF = 0	ΔF = 0.05 p.u.	ΔF = 0.1 p.u.
EEL (MWh)	Electrical network	3.28	2.34	2.32	2.29
	Thermal network	4.47	3.17	3.15	3.12
	Gas network	0	1.12	1.11	1.10
	Total	7.75	6.63	6.58	6.51
MVD (p.u.)		0.092	0.047	0.046	0.044
MTD (p.u.)		0.107	0.058	0.057	0.055
MPD (p.u.)		0	0.039	0.038	0.038
MOV (p.u.)		0	0.012	0.012	0.013
MOT (p.u.)		0	0.015	0.016	0.017
MOP (p.u.)		0	0	0	0

. The operation indices compared are maximum pressure drop (MPD), maximum overtemperature (MOT), maximum overpressure (MOP), maximum temperature drop (MTD), maximum voltage drop (MVD), maximum overvoltage (MOV), and expected energy losses (EELs). For different flexibility tolerances, values of the operating indices are presented in Case II. According to Table 6, for 100% flexibility (ΔF = 0), the proposed scheme is able to reduce EELs in both thermal and electrical networks by around 28.7% and 29.1%, respectively, compared to case I. However, compared to case I, EEL has increased by around 1.12 MWh in the gas network. However, under these conditions, EEL in all energy networks has decreased by around 14.5% in the proposed scheme compared to case I. Compared to case I and for 100% flexibility, the proposed scheme, considering an EH’s optimal power management, is able to improve MVD and MTD by 49% and 46%, respectively. However, these conditions are associated with pressure drop, overvoltage, and temperature. Considering Table 6, they have a maximum value less than their allowable value, i.e., 0.1 p.u. (1.1−1 or 1−0.09). Finally, based on Table 6, it is evident that the operation index status improves with increasing ΔF. In other words, EHs are mostly responsible for the improvement of the energy network’s operation.

5. Conclusions

In the presence of smart energy hubs, the operation of thermal, gas, and electrical networks, considered in relation to their presence in the markets of energy, reserve, and day-ahead reactive power, was discussed in this paper. A scheme based on bi-level optimization was used to model the plan. In energy networks, the upper level outlines the minimization of energy loss based on the equations of linearized optimal power flow. Based on reserves, flexible EHs, and operational constraints, the lower level formulated the maximization of profit for EHs in the market. Therefore, a single-level model was extracted using the KKT method, and to model renewable power, energy price, mobile storage parameters, and load uncertainties, the UT method was applied. Based on the numerical results, a unique solution can be extracted by a linear model of solvers, while a nonlinear model cannot. As compared to other linear and nonlinear solvers, the CPLEX solver has a shorter computation time in the proposed linearized model. Furthermore, the UT method involves fewer scenarios than SBSO, which increases the convergence speed of problem-solving. Therefore, by extracting the optimal timing for the EHs’ power, it was clear that, in comparison to the load flow studies of the grid, the proposed plan was capable of improving the operation indices, including the maximum drop of temperature and voltage and energy losses, by 46%, 49%, and 14.5%, respectively, in the EHs’ flexible condition of 100%. This condition also leads to a pressure drop, overvoltage, and overheating under their allowable value, i.e., 0.1 p.u. Increasing flexibility in the proposed scheme decreases the improvement rate of operation indices and reduces the EHs’ profit in the markets of energy and reserve. Therefore, the advantages of this plan include modeling the flexibility of hubs, modeling uncertainties with UT, and the participation of hubs in the mentioned markets.