Development of a Delivery Time-Period Selection Model for Urban Freight Using GPS Data
Abstract
Highlights
- Shipment delivery time is not only affected by the type of goods but also by the receiver function, shipment size, shipment distance, and zoning type of the receiver’s location.
- The proposed modeling approach using GPS data can be used to replicate the heterogeneity of shipment delivery time.
- Understanding various observable characteristics of receivers and shipments leads to infer time of day delivery demand distribution.
- Readily available GPS data can be used to develop a simulation model of delivery times for urban freight analysis.
Abstract
1. Introduction
2. Literature Review
2.1. Selection Modeling of Delivery Time or Departure Time
2.2. Agent-Based Urban Freight Simulators
2.3. Research Gap
3. Data
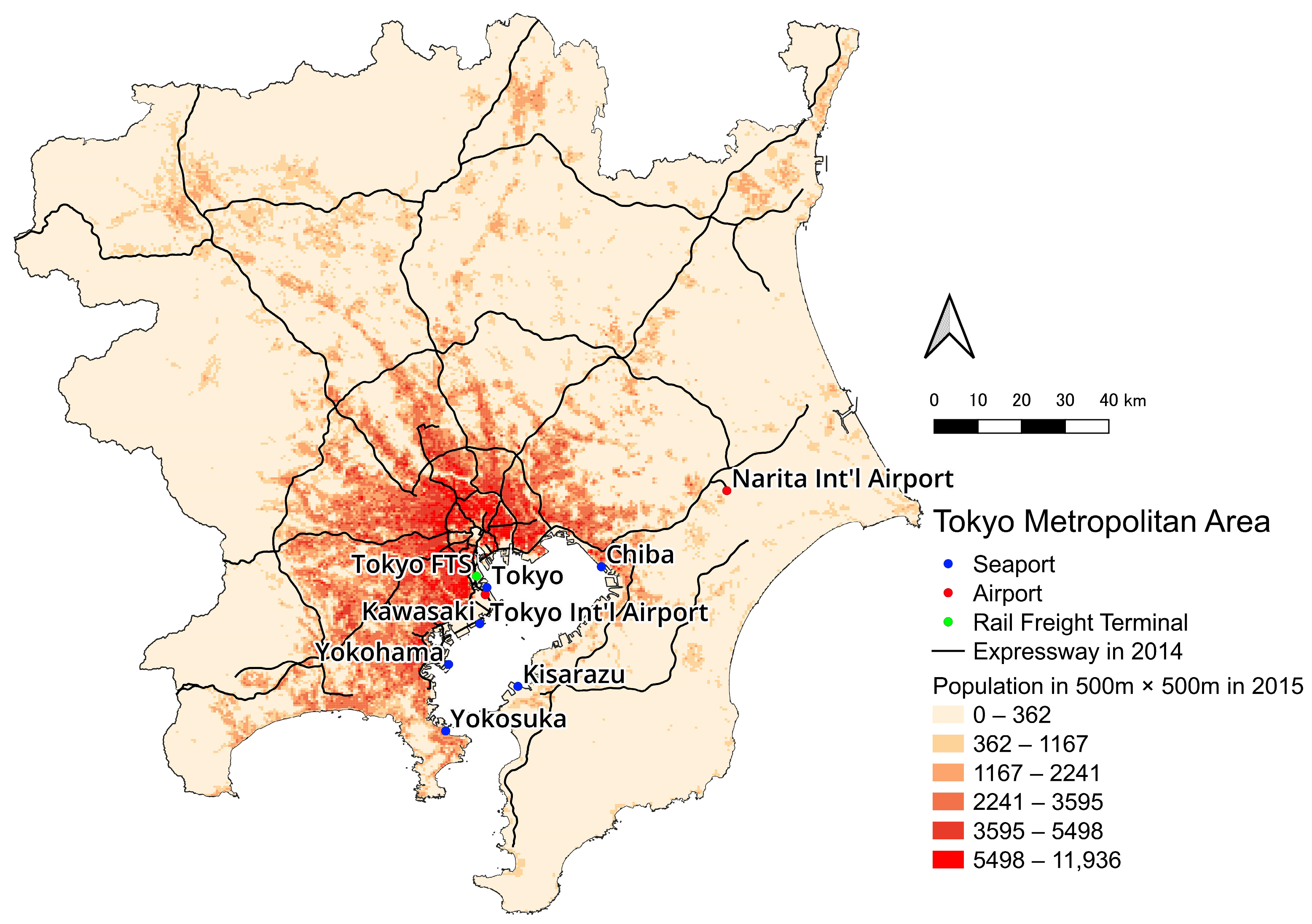
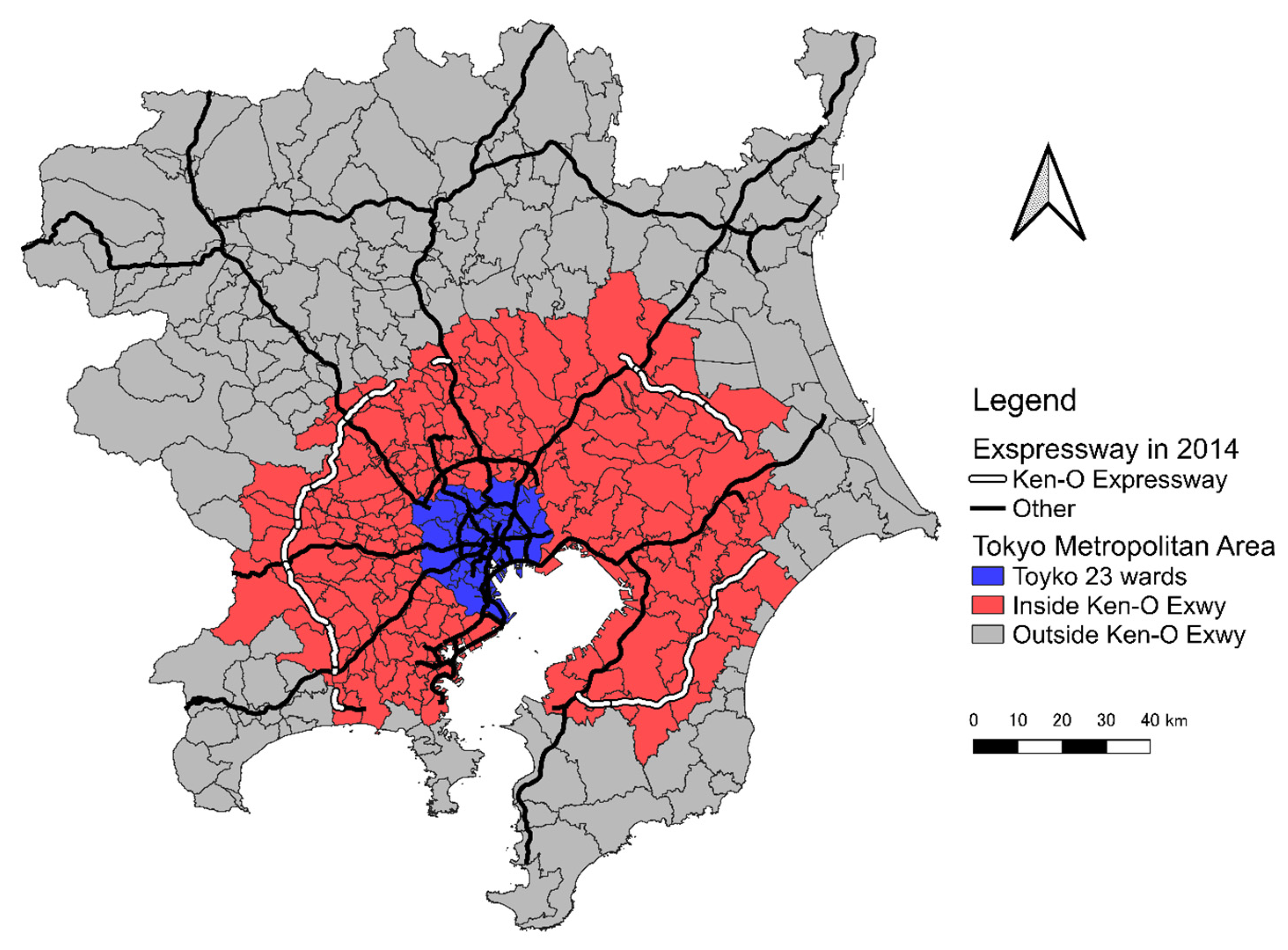
3.1. Study Area
3.2. GPS Data
3.3. Tours and Shipments
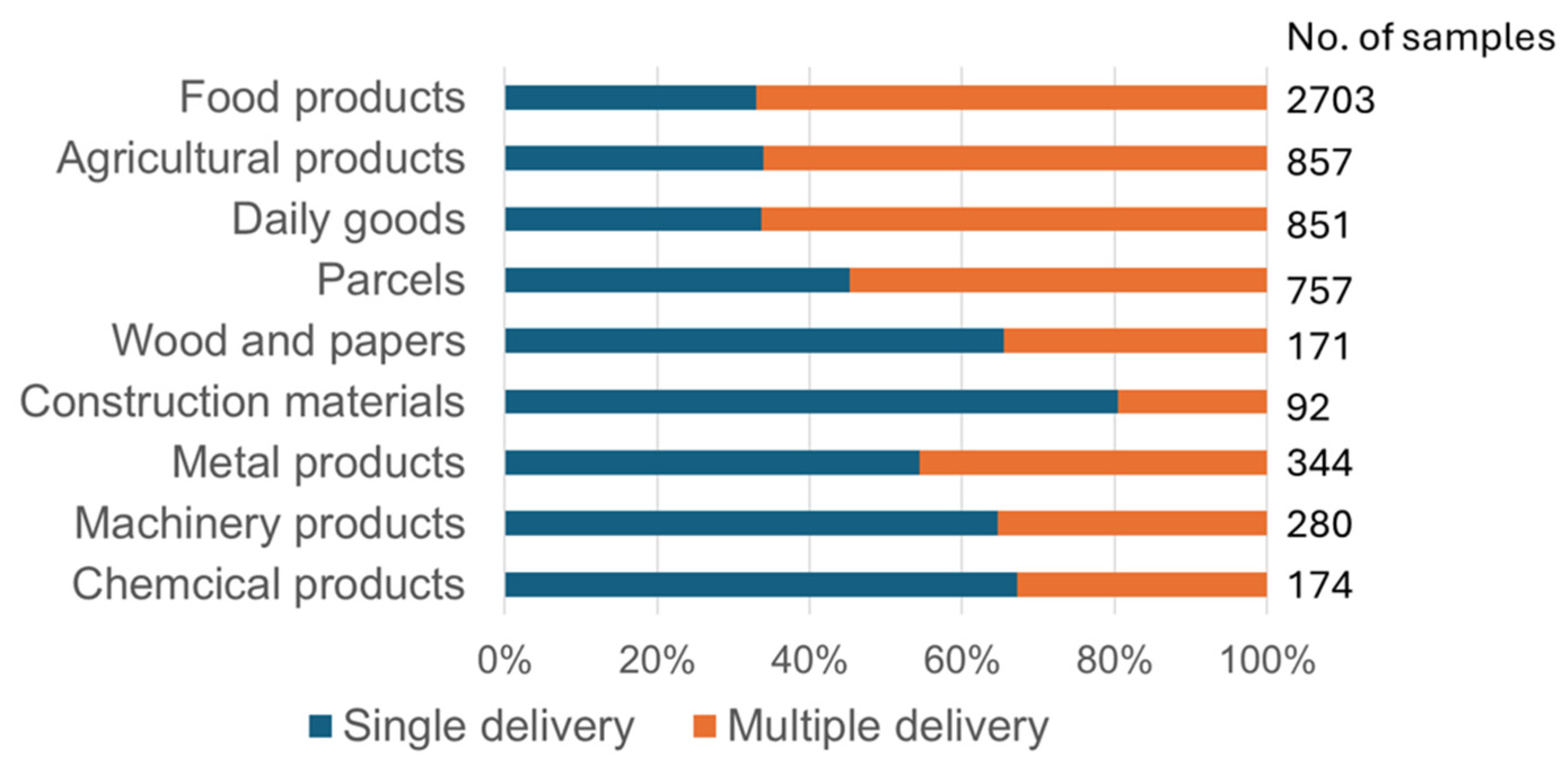
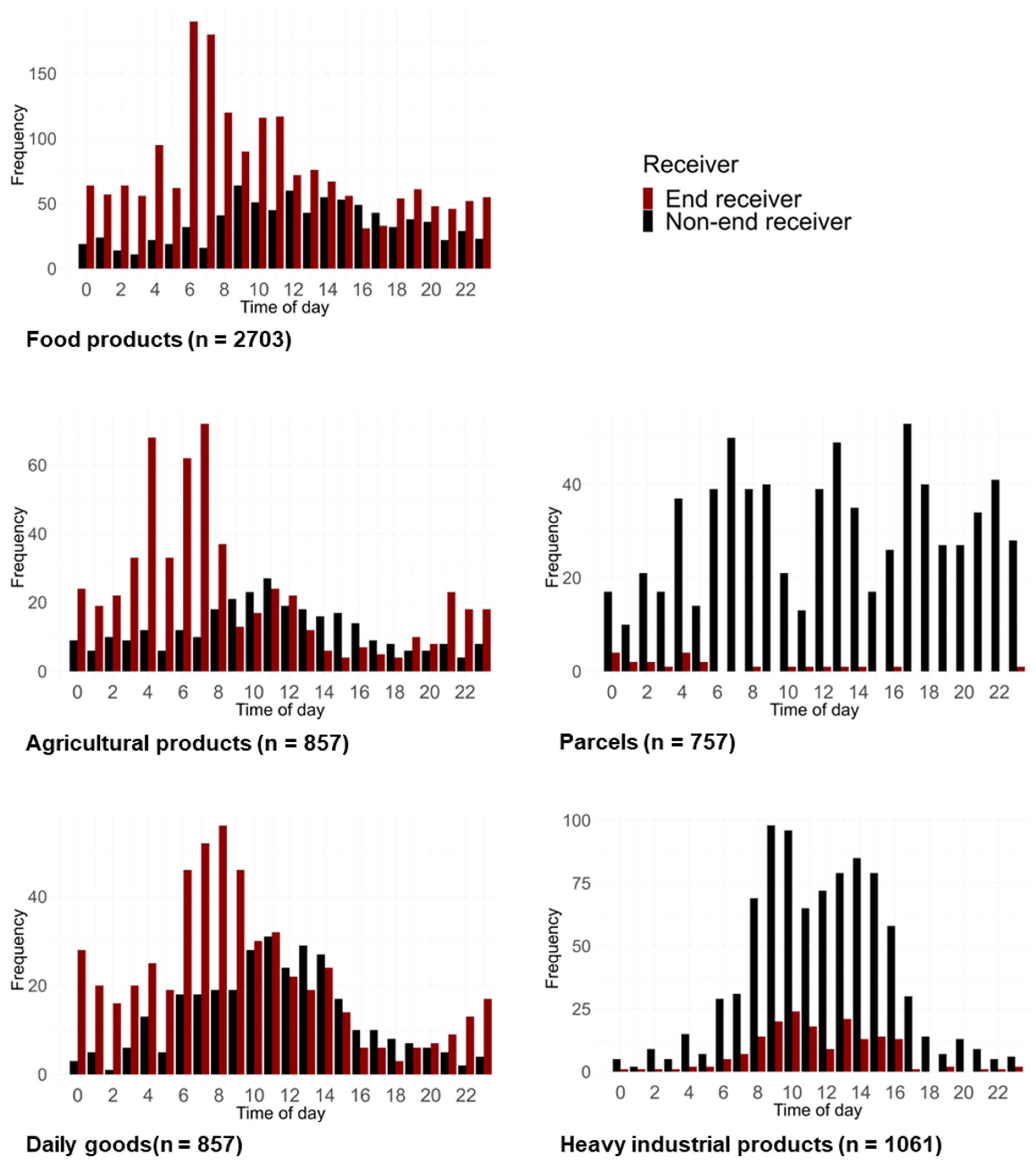
3.4. Goods Type
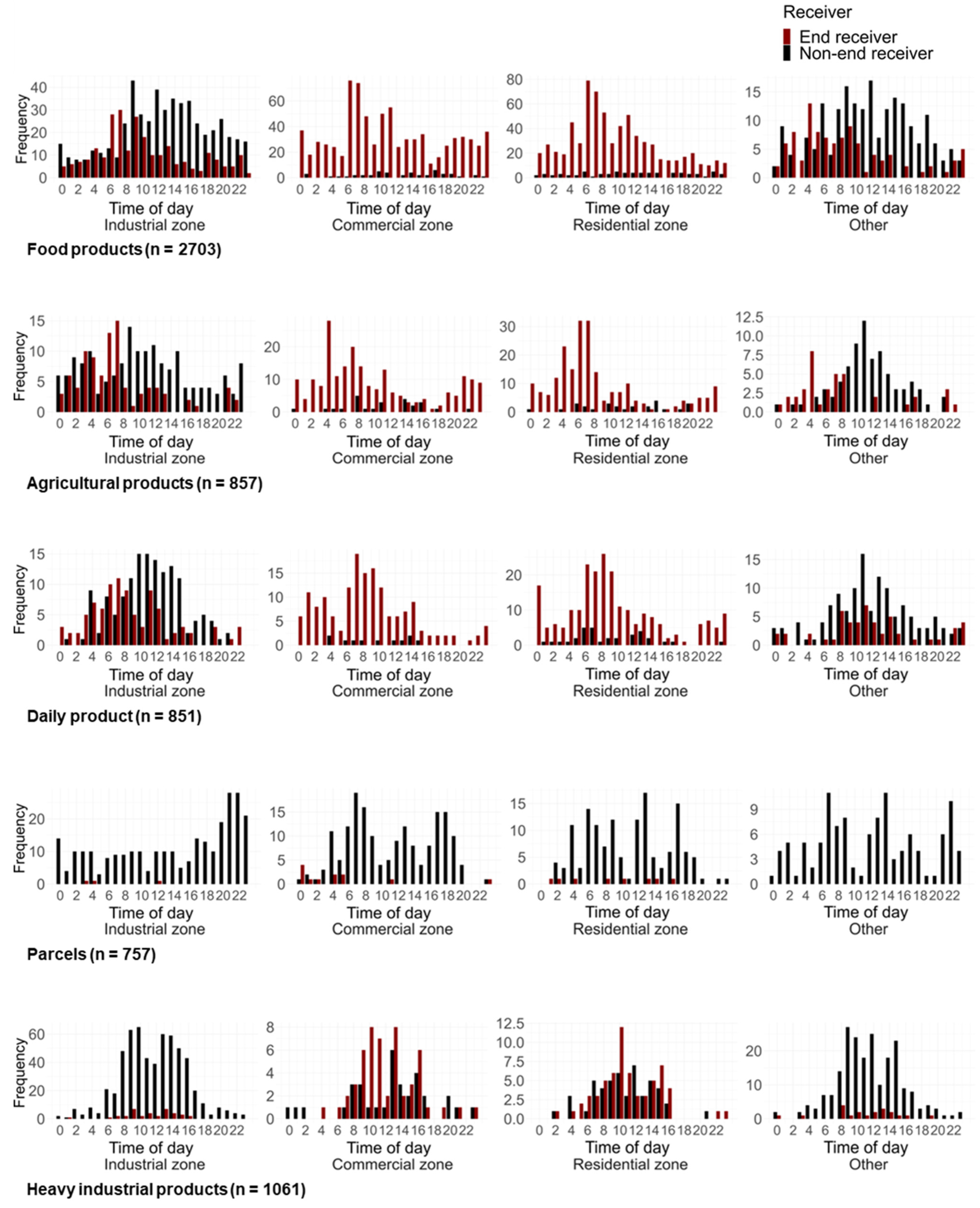
3.5. Zoning Type of Destination
3.6. Pseudo-Shipment Size
4. Method: Model Description
5. Results
6. Additional Analysis: Demonstrative Application
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holguín-Veras, J.; Leal, J.A.; Sánchez-Diaz, I.; Browne, M.; Wojtowicz, J. State of the art and practice of urban freight management: Part I: Infrastructure, vehicle-related, and traffic operations. Transp. Res. Part A Policy Pract. 2020, 137, 360–382. [Google Scholar] [CrossRef]
- De Jong, G.; Kouwenhoven, M.; Ruijs, K.; van Houwe, P.; Borremans, D. A time-period choice model for road freight transport in Flanders based on stated preference data. Transp. Res. Part E Logist. Transp. Rev. 2016, 86, 20–31. [Google Scholar] [CrossRef]
- Sakai, T.; Alho, A.R.; Bhavathrathan, B.K.; Dalla Chiara, G.; Gopalakrishnan, R.; Jing, P.; Ben-Akiva, M. SimMobility Freight: An agent-based urban freight simulator for evaluating logistics solutions. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 102017. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. Urban freight demand forecasting: A mixed quantity/delivery/vehicle-based model. Transp. Res. Part E Logist. Transp. Rev. 2014, 65, 84–98. [Google Scholar] [CrossRef]
- Hunt, J.D.; Stefan, K.J. Tour-based microsimulation of urban commercial movements. Transp. Res. Part B Methodol. 2007, 41, 981–1013. [Google Scholar] [CrossRef]
- Nadi, A.; Yorke-Smith, N.; Snelder, M.; Van Lint, J.W.C.; Tavasszy, L. Data-driven preference-based routing and scheduling for activity-based freight transport modelling. Transp. Res. Part C Emerg. Technol. 2024, 158, 104413. [Google Scholar] [CrossRef]
- De Bok, M.; Tavasszy, L. An empirical agent-based simulation system for urban goods transport (MASS-GT). Procedia Comput. Sci. 2018, 130, 126–133. [Google Scholar] [CrossRef]
- Oka, H.; Hagino, Y.; Kenmochi, T.; Tani, R.; Nishi, R.; Endo, K.; Fukuda, D. Predicting travel pattern changes of freight trucks in the Tokyo Metropolitan area based on the latest large-scale urban freight survey and route choice modeling. Transp. Res. Part E Logist. Transp. Rev. 2019, 129, 305–324. [Google Scholar] [CrossRef]
- Tok, A.; Hyun, K.; Hernandez, S.; Jeong, K.; Sun, Y.; Rindt, C.; Ritchie, S.G. Truck Activity Monitoring System for Freight Transportation Analysis. Transp. Res. Rec. 2017, 2610, 97–107. [Google Scholar] [CrossRef]
- Ben-Akiva, M.E.; Toledo, T.; Santos, J.; Cox, N.; Zhao, F.; Lee, Y.J.; Marzano, V. Freight data collection using GPS and web-based surveys: Insights from US truck drivers’ survey and perspectives for urban freight. Case Stud. Transp. Policy 2016, 4, 38–44. [Google Scholar] [CrossRef]
- Stefan, K.J.; McMillan, J.D.P.; Hunt, J.D. Urban commercial vehicle movement model for Calgary, Alberta, Canada. Transp. Res. Rec. 2005, 1921, 1–10. [Google Scholar] [CrossRef]
- Khan, M.; Machemehl, R. Commercial vehicles time of day choice behavior in urban areas. Transp. Res. Part A Policy Pract. 2017, 102, 68–83. [Google Scholar] [CrossRef]
- Nadi, A.; Tavasszy, L.; van Lint, J.W.C.; Snelder, M. Spatial and Temporal Characteristics of Freight Tours: A Data-Driven Exploratory Analysis. arXiv 2023, arXiv:2311.15287. [Google Scholar]
- Holguín-Veras, J.; Silas, M.; Polimeni, J.; Cruz, B. An Investigation on the Effectiveness of Joint Receiver–Carrier Policies to Increase Truck Traffic in the Off-peak Hours. Part I: The Behavior of Receivers. Netw. Spat. Econ. 2007, 7, 277–295. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Silas, M.; Polimeni, J.; Cruz, B. An Investigation on the Effectiveness of Joint Receiver–Carrier Policies to Increase Truck Traffic in the Off-peak Hours: Part II: The Behavior of Carriers. Netw. Spat. Econ. 2008, 8, 327–354. [Google Scholar] [CrossRef]
- Silas, M.A.; Holguín-Veras, J. Behavioral microsimulation formulation for analysis and design of off-hour delivery policies in urban areas. Transp. Res. Rec. 2009, 2097, 43–50. [Google Scholar] [CrossRef]
- Mepparambath, R.M.; Cheah, L.; Zegras, P.C.; Alho, A.R.; Sakai, T. Evaluating the impact of urban consolidation center and off-hour deliveries on freight flows to a retail district using agent-based simulation. Transp. Res. Rec. 2023, 2677, 264–281. [Google Scholar] [CrossRef]
- Stinson, M.; Mohammadian, A.K. Introducing CRISTAL: A model of collaborative, informed, strategic trade agents with logistics. Transp. Res. Interdiscip. Perspect. 2022, 13, 100539. [Google Scholar] [CrossRef]
- Transport Planning Commission of the Tokyo Metropolitan Region. The 2013 Tokyo Metropolitan Freight Survey. Available online: https://www.tokyo-pt.jp/pd/02 (accessed on 7 November 2024).
- Isuzu Motors Limited. Mimamori. Available online: https://www.isuzu.co.jp/cv/cost/mimamori/ (accessed on 26 January 2025).
- Romano Alho, A.; Sakai, T.; Chua, M.H.; Jeong, K.; Jing, P.; Ben-Akiva, M. Exploring algorithms for revealing freight vehicle tours, tour-types, and tour-chain-types from GPS vehicle traces and stop activity data. J. Big Data Anal. Transp. 2019, 1, 175–190. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, Transport and Tourism. The List of Vehicle Fuel Consumption 2015. Available online: https://www.mlit.go.jp/jidosha/jidosha_fr10_000024.html (accessed on 7 November 2024).
- Yamato Transport Co., Ltd. Yamato Holdings’ Haneda Chronogate. Available online: https://www.yamato-hd.co.jp/facilities/en/haneda-chronogate/ (accessed on 26 January 2025).
- Google. Google Map. Available online: https://www.google.com/maps (accessed on 7 November 2024).
- Ministry of Land, Infrastructure, Transport and Tourism. Denshikokudo Web System. Available online: https://maps.gsi.go.jp/#5/36.104611/140.084556/&base=std&ls=std&disp=1&vs=c1g1j0h0k0l0u0t0z0r0s0m0f1 (accessed on 7 November 2024).
- Ministry of Land, Infrastructure, Transport and Tourism. National Land Numerical Information (Zoning Data). Available online: https://nlftp.mlit.go.jp/ksj/gml/datalist/KsjTmplt-A29.html (accessed on 7 November 2024).
- Ministry of Land, Infrastructure, Transport and Tourism. National Land Numerical Information (Urban Area Data). Available online: https://nlftp.mlit.go.jp/ksj/gml/datalist/KsjTmplt-A09.html (accessed on 7 November 2024).
- Ministry of Land, Infrastructure, Transport and Tourism. The Survey on Motor Vehicle Transport 2014. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00600330&kikan=00600&tstat=000001078083&cycle=8&year=20141&month=0&result_back=1&result_page=1&tclass1val=0 (accessed on 7 November 2024).
- Ministry of Economy, Trade and Industry. 2021 Economic Census. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00200553&tstat=000001145590&cycle=0&tclass1=000001145649&tclass2=000001145668&tclass3=000001161869&tclass4=000001161887&cycle_facet=tclass1%3Atclass2%3Atclass3&tclass5val=0 (accessed on 7 November 2024).
- Holguín-Veras, J.; Wang, Q.; Xu, N.; Ozbay, K.; Cetin, M.; Polimeni, J. The impacts of time of day pricing on the behavior of freight carriers in a congested urban area: Implications to road pricing. Transp. Res. Part A Policy Pract. 2006, 40, 744–766. [Google Scholar] [CrossRef]
- Holguín-Veras, J. Necessary conditions for off-hour deliveries and the effectiveness of urban freight road pricing and alternative financial policies in competitive markets. Transp. Res. Part A Policy Pract. 2008, 42, 392–413. [Google Scholar] [CrossRef]


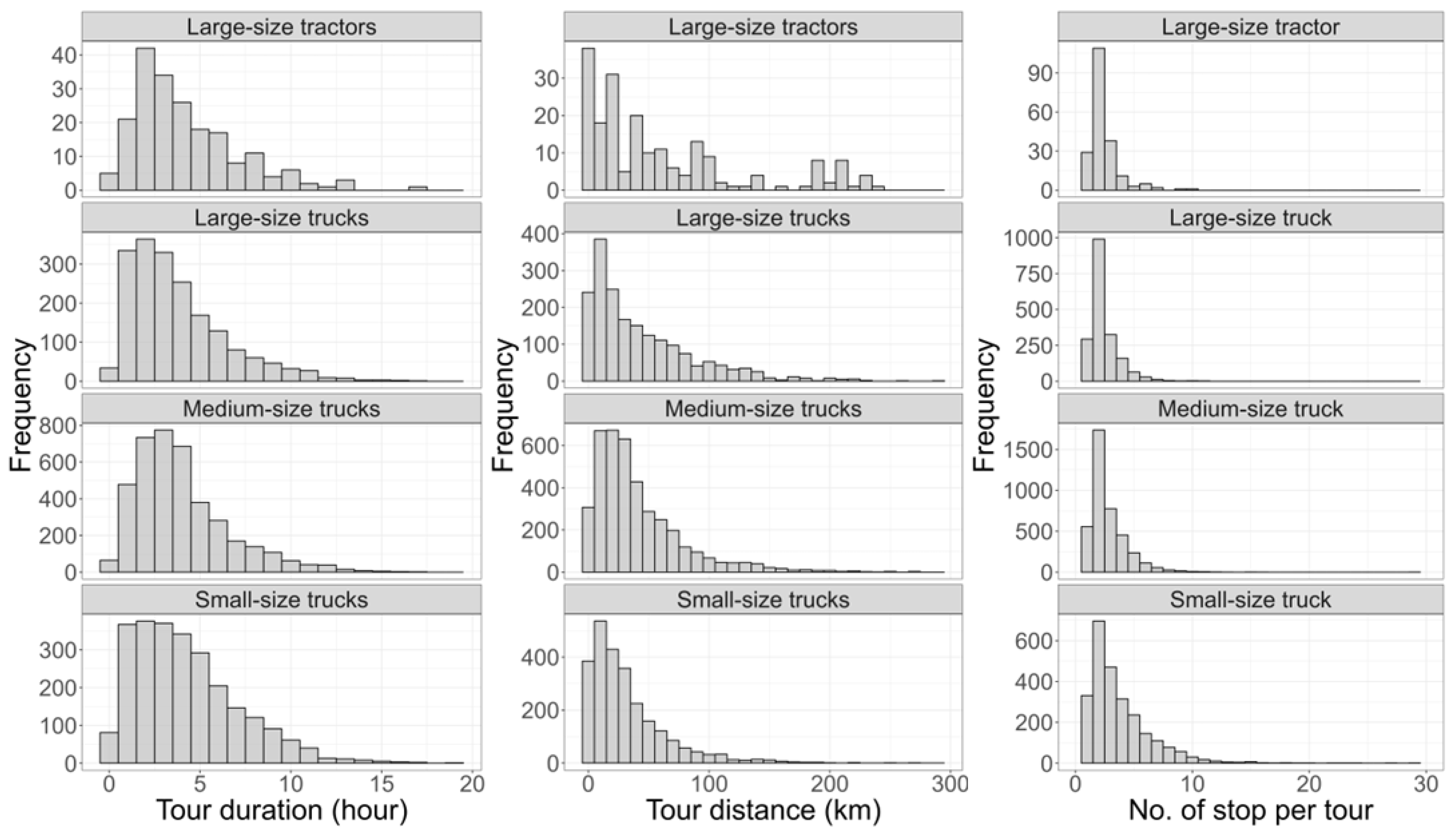
| Large Tractor | Large Truck | Medium Truck | Small Truck | |
|---|---|---|---|---|
| No. of vehicles | 528 | 5518 | 12,324 | 8860 |
| No. of tours | 199 | 1886 | 3991 | 2535 |
| No. of pseudo shipments | 114 | 1243 | 2956 | 1916 |
| Variables | Definition | Notation |
|---|---|---|
| Delivery time period | Goods delivery time period (categorical variable)
| |
| ln (Shipment distance) | Euclidean distance from base to destination. Log-transformed and then standardized to mean 0 standard deviation 1. | ln_dist |
| ln (Shipment size) | Pseudo-shipment size. Log-transformed and then standardized to mean 0 standard deviation 1. | ln_size |
| End receiver | A dummy variable. 1 if shipment is to an end receiver; 0 otherwise. | |
| Zoning type | Dummy variables. 1 if shipment destination is in a specific zoning type (below); 0 otherwise.
| (residential zone) (industrial zone) (other) |
| Goods type | Dummy variables. 1 if goods type is a specific goods type (below); 0 otherwise.
| (chemical) (machinery) (metal) |
| Afternoon | Night | Late at Night | Early Morning | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. |
| Constant | 0.188 | 0.212 | 0.870 ** | 0.205 | 0.232 | 0.215 | −0.186 | 0.198 |
| ln_dist | −0.047 | 0.060 | 0.267 ** | 0.064 | 0.466 ** | 0.072 | 0.208 ** | 0.061 |
| ln_size | 0.273 ** | 0.081 | −0.192 * | 0.078 | −0.548 ** | 0.078 | −0.178 * | 0.069 |
| −0.280 | 0.189 | −0.889 ** | 0.191 | −0.354. | 0.202 | 0.690 ** | 0.181 | |
| −0.064 | 0.177 | −0.387 * | 0.177 | −0.087 | 0.171 | 0.299 * | 0.150 | |
| −0.169 | 0.203 | −0.341. | 0.200 | −0.268 | 0.205 | 0.037 | 0.181 | |
| −0.248 | 0.255 | −0.586 * | 0.256 | −0.136 | 0.257 | 0.349 | 0.227 | |
| Null log-likelihood | −4291 | |||||||
| Maximum log-likelihood | −4090 | |||||||
| Rho-squared | 0.047 | |||||||
| No. of samples | 2703 | |||||||
| Afternoon | Night | Late at Night | Early Morning | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. |
| Constant | −0.264 | 0.376 | −0.090 | 0.372 | −0.843 * | 0.361 | −0.546. | 0.326 |
| ln_dist | 0.034 | 0.117 | 0.370 ** | 0.129 | 0.319 ** | 0.120 | 0.204. | 0.107 |
| ln_size | 0.068 | 0.158 | −0.344 * | 0.152 | −0.475 ** | 0.136 | −0.145 | 0.126 |
| −0.111 | 0.335 | 0.022 | 0.345 | 1.296 ** | 0.320 | 1.791 ** | 0.291 | |
| 0.347 | 0.402 | 0.105 | 0.387 | 0.438 | 0.346 | 0.680 * | 0.312 | |
| 0.273 | 0.406 | −0.035 | 0.411 | 1.065 ** | 0.367 | 0.641. | 0.338 | |
| 0.182 | 0.437 | −0.108 | 0.446 | −0.250 | 0.460 | 0.156 | 0.381 | |
| Null log-likelihood | −1290 | |||||||
| Maximum log-likelihood | −1199 | |||||||
| Rho-squared | 0.070 | |||||||
| No. of samples | 857 | |||||||
| Afternoon | Night | Late at Night | Early Morning | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. |
| Constant | 0.365 | 0.376 | −1.114 * | 0.372 | −1.147 ** | 0.361 | 0.097 | 0.326 |
| ln_dist | −0.109 | 0.117 | 0.184 | 0.129 | 0.442 ** | 0.120 | 0.166 | 0.107 |
| ln_size | 0.022 | 0.158 | 0.568 ** | 0.152 | 0.460 ** | 0.136 | 0.402 ** | 0.126 |
| −0.570. | 0.335 | 0.077 | 0.345 | 1.620 ** | 0.320 | 0.741 ** | 0.291 | |
| −0.089 | 0.402 | 0.324 | 0.387 | −0.212 | 0.346 | 0.145 | 0.312 | |
| −0.164 | 0.406 | 0.019 | 0.411 | −1.080 ** | 0.367 | −0.247 | 0.338 | |
| −0.281 | 0.437 | 0.332 | 0.446 | −0.220 | 0.460 | −0.825 * | 0.381 | |
| Null log-likelihood | −1312 | |||||||
| Maximum log-likelihood | −1233 | |||||||
| Rho-squared | 0.060 | |||||||
| No. of samples | 851 | |||||||
| Afternoon | Night | Late at Night | Early Morning | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. |
| Constant | 0.868 ** | 0.376 | 1.518 ** | 0.372 | −0.003 | 0.361 | 1.653 ** | 0.326 |
| ln_dist | 0.042 | 0.117 | 0.189 | 0.129 | 0.649 ** | 0.120 | 0.218 | 0.107 |
| ln_size | 0.316 * | 0.158 | 0.706 ** | 0.152 | 1.270 ** | 0.136 | 0.660 ** | 0.126 |
| 0.414 | 0.335 | 0.035 | 0.345 | 5.506 ** | 0.320 | 1.774 * | 0.291 | |
| −0.007 | 0.402 | −0.694. | 0.387 | −0.767 | 0.346 | −0.583 | 0.312 | |
| −0.428 | 0.406 | −0.259 | 0.411 | 0.825. | 0.367 | −1.201 ** | 0.338 | |
| 0.022 | 0.437 | −0.943. | 0.446 | 0.077 | 0.460 | −0.854. | 0.381 | |
| Null log-likelihood | −1182 | |||||||
| Maximum log-likelihood | −1082 | |||||||
| Rho-squared | 0.085 | |||||||
| No. of samples | 757 | |||||||
| Afternoon | Night | Late at Night | Early Morning | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. | Coef. | S.E. |
| Constant | 0.001 | 0.161 | −1.276 ** | 0.245 | −1.908 ** | 0.319 | −0.554 ** | 0.189 |
| ln_dist | −0.016 | 0.078 | 0.117 | 0.101 | 0.360 * | 0.176 | 0.274 ** | 0.097 |
| ln_size | 0.074 | 0.082 | 0.257 * | 0.114 | 0.515 * | 0.205 | 0.221 * | 0.103 |
| −0.208 | 0.223 | −0.318 | 0.325 | 0.192 | 0.476 | 0.023 | 0.270 | |
| 0.083 | 0.247 | 0.374 | 0.345 | −1.314 * | 0.664 | −0.062 | 0.287 | |
| 0.429 * | 0.218 | 0.986 ** | 0.301 | 0.169 | 0.410 | 0.107 | 0.261 | |
| 0.201 | 0.203 | 0.623 * | 0.293 | −0.833. | 0.489 | −0.173 | 0.249 | |
| Null log-likelihood | −1514 | |||||||
| Maximum log-likelihood | −1485 | |||||||
| Rho-squared | 0.019 | |||||||
| No. of samples | 1061 | |||||||
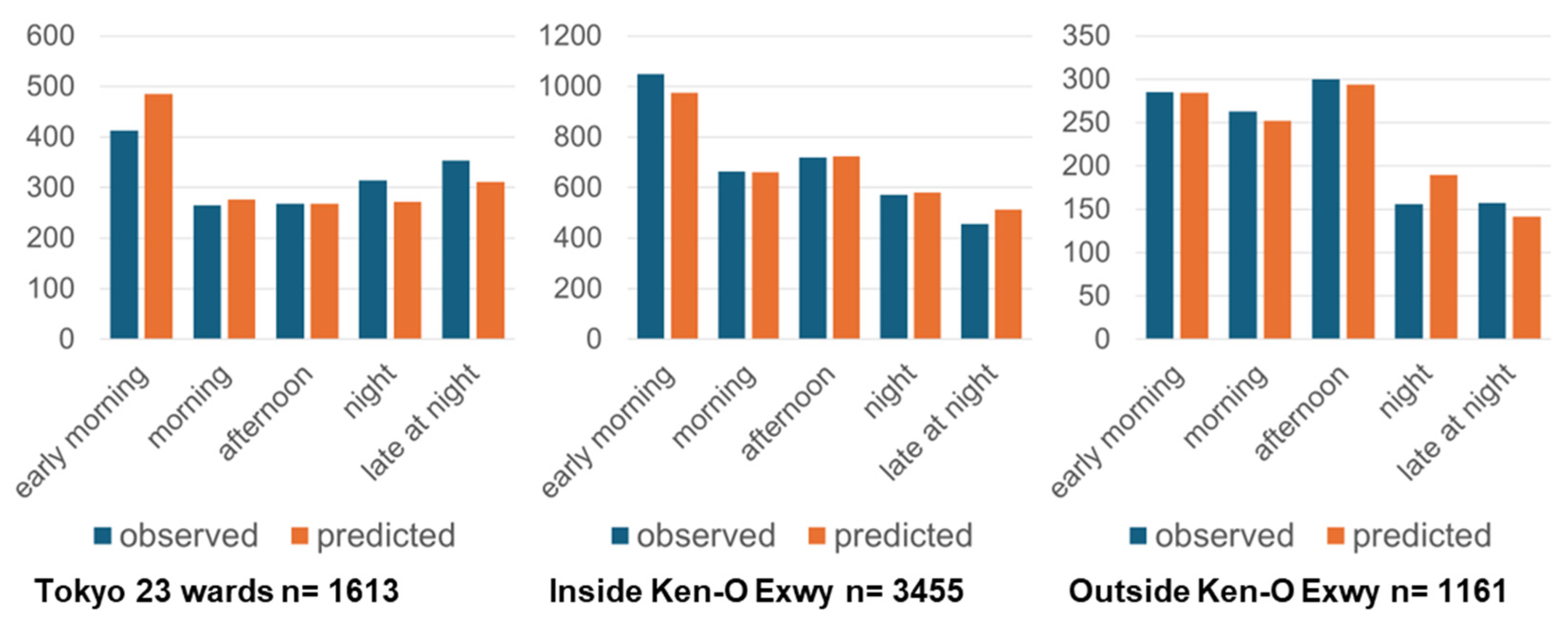
| Tokyo 23 Wards | Inside Ken-O Exwy | Outside Ken-O Exwy | ||||
|---|---|---|---|---|---|---|
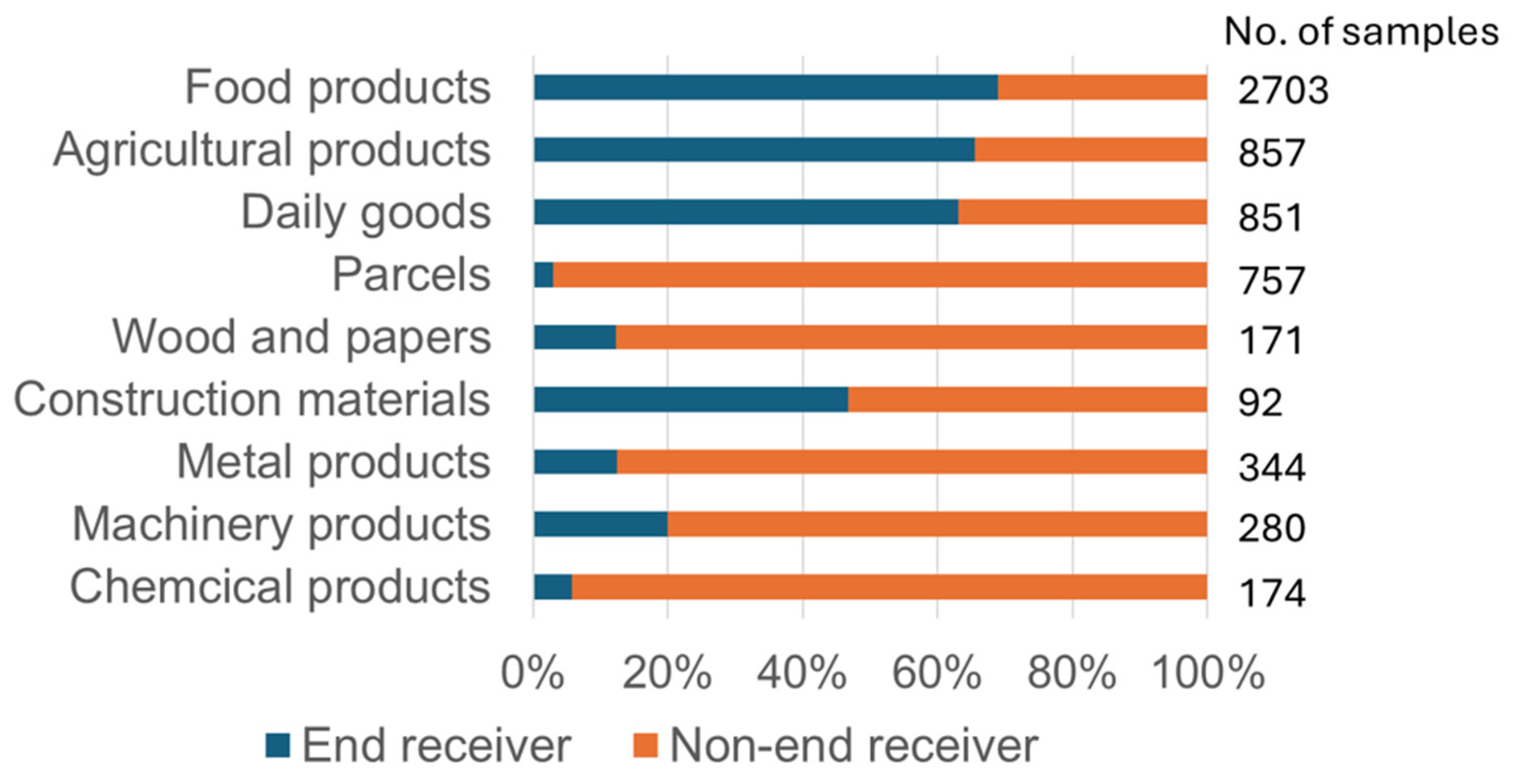
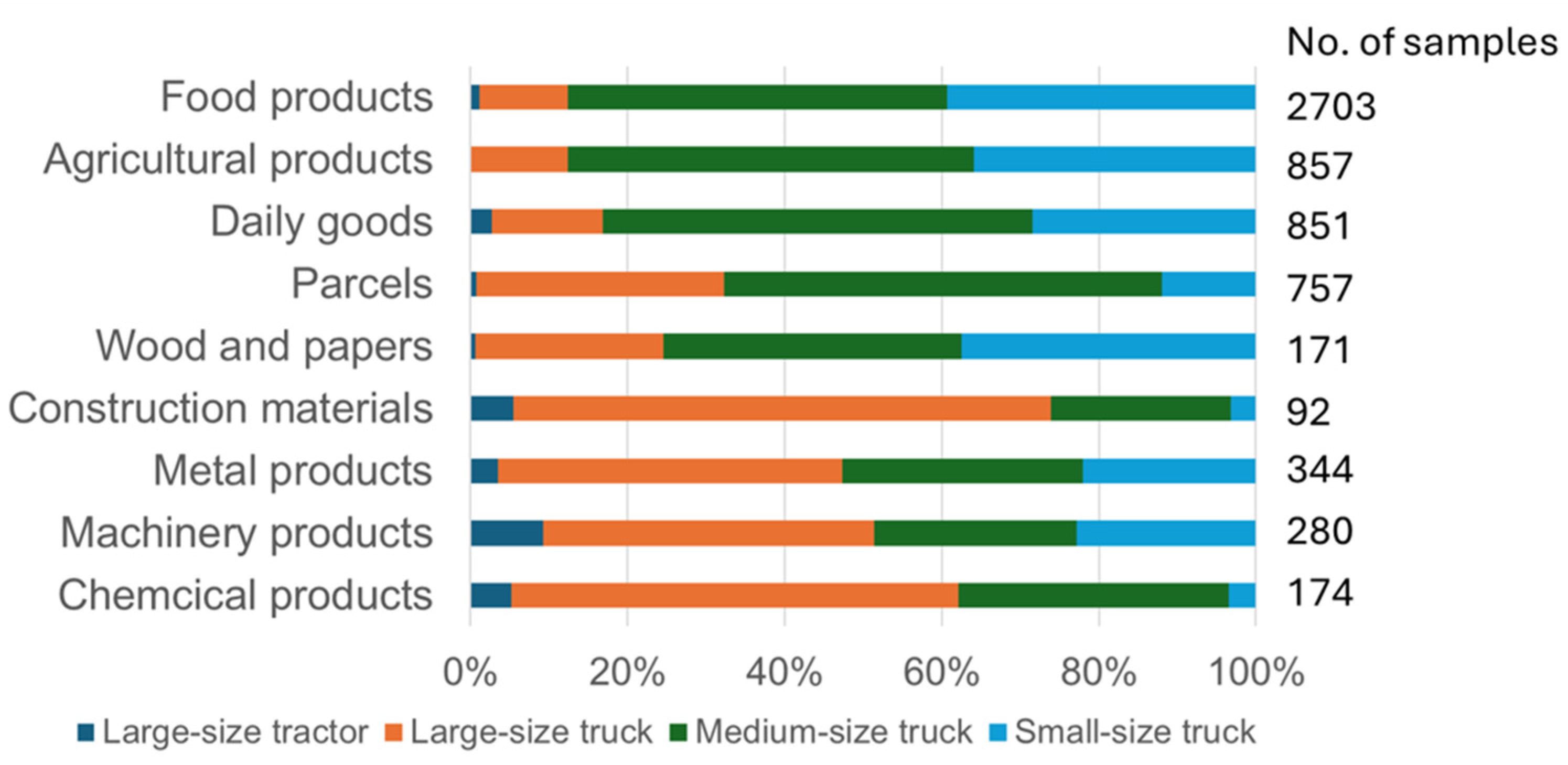
| Goods Type | End Receiver | Non-End Receiver | End Receiver | Non-End Receiver | End Receiver | Non-End Receiver |
| Food products | 757 | 56 | 935 | 608 | 170 | 177 |
| (65.6%) | (12.2%) | (57.3%) | (33.4%) | (46.1%) | (22.3%) | |
| Agricultural products | 165 | 30 | 319 | 178 | 77 | 88 |
| (14.3%) | (6.5%) | (19.5%) | (9.8%) | (20.9%) | (11.1%) | |
| Daily goods | 142 | 32 | 293 | 211 | 101 | 72 |
| (12.3%) | (7.0%) | (18.0%) | (11.6%) | (27.4%) | (9.1%) | |
| Parcels | 16 | 277 | 6 | 372 | 1 | 85 |
| (1.4%) | (60.3%) | (0.4%) | (20.4%) | (0.3%) | (10.7%) | |
| Heavy industrial products | 74 | 64 | 79 | 454 | 20 | 370 |
| (6.4%) | (13.9%) | (4.8%) | (24.9%) | (5.4%) | (46.7%) | |
| Total | 1154 | 459 | 1632 | 1823 | 369 | 792 |
| (100%) | (100%) | (100%) | (100%) | (100%) | (100%) | |
| Tokyo 23 Wards | Inside Ken-O Exwy | Outside Ken-O Exwy | ||||
|---|---|---|---|---|---|---|
| Observed | Predicted | Observed | Predicted | Observed | Predicted | |
| early morning | 412 | 485.0 | 1048 | 975.2 | 285 | 284.3 |
| (25.5%) | (30.1%) | (30.3%) | (28.2%) | (24.5%) | (24.5%) | |
| morning | 265 | 276.8 | 663 | 661.7 | 263 | 251.9 |
| (16.4%) | (17.2%) | (19.2%) | (19.2%) | (22.7%) | (21.7%) | |
| afternoon | 268 | 268.6 | 719 | 724.1 | 300 | 293.8 |
| (16.6%) | (16.7%) | (20.8%) | (21.0%) | (25.8%) | (25.3%) | |
| night | 314 | 271.9 | 570 | 580.6 | 156 | 189.2 |
| (19.5%) | (16.9%) | (16.5%) | (16.8%) | (13.4%) | (16.3%) | |
| late at night | 354 | 310.6 | 455 | 513.5 | 157 | 141.8 |
| (21.9%) | (19.3%) | (13.2%) | (14.9%) | (13.5%) | (12.2%) | |
| Total | 1613 | 1613 | 3455 | 3455 | 1161 | 1161 |
| (100%) | (100%) | (100%) | (100%) | (100%) | (100%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodera, R.; Sakai, T.; Hyodo, T. Development of a Delivery Time-Period Selection Model for Urban Freight Using GPS Data. Smart Cities 2025, 8, 31. https://doi.org/10.3390/smartcities8010031
Kodera R, Sakai T, Hyodo T. Development of a Delivery Time-Period Selection Model for Urban Freight Using GPS Data. Smart Cities. 2025; 8(1):31. https://doi.org/10.3390/smartcities8010031
Chicago/Turabian StyleKodera, Ryota, Takanori Sakai, and Tetsuro Hyodo. 2025. "Development of a Delivery Time-Period Selection Model for Urban Freight Using GPS Data" Smart Cities 8, no. 1: 31. https://doi.org/10.3390/smartcities8010031
APA StyleKodera, R., Sakai, T., & Hyodo, T. (2025). Development of a Delivery Time-Period Selection Model for Urban Freight Using GPS Data. Smart Cities, 8(1), 31. https://doi.org/10.3390/smartcities8010031





