Fifteen Years of Continuous High-Resolution Borehole Strainmeter Measurements in Eastern Taiwan: An Overview and Perspectives
Abstract
:1. Introduction
2. Instrumentation Design and Basic Processing
2.1. Sacks–Evertson Sensor: Details and Installation
2.2. Sensor Calibration and Orientation
2.3. Strainmeter Response to Atmospheric Pressure Variations
3. Borehole Strainmeter Observations in Eastern Taiwan
3.1. Earthquake Source Modeling: The 2013 Ruisui Earthquake
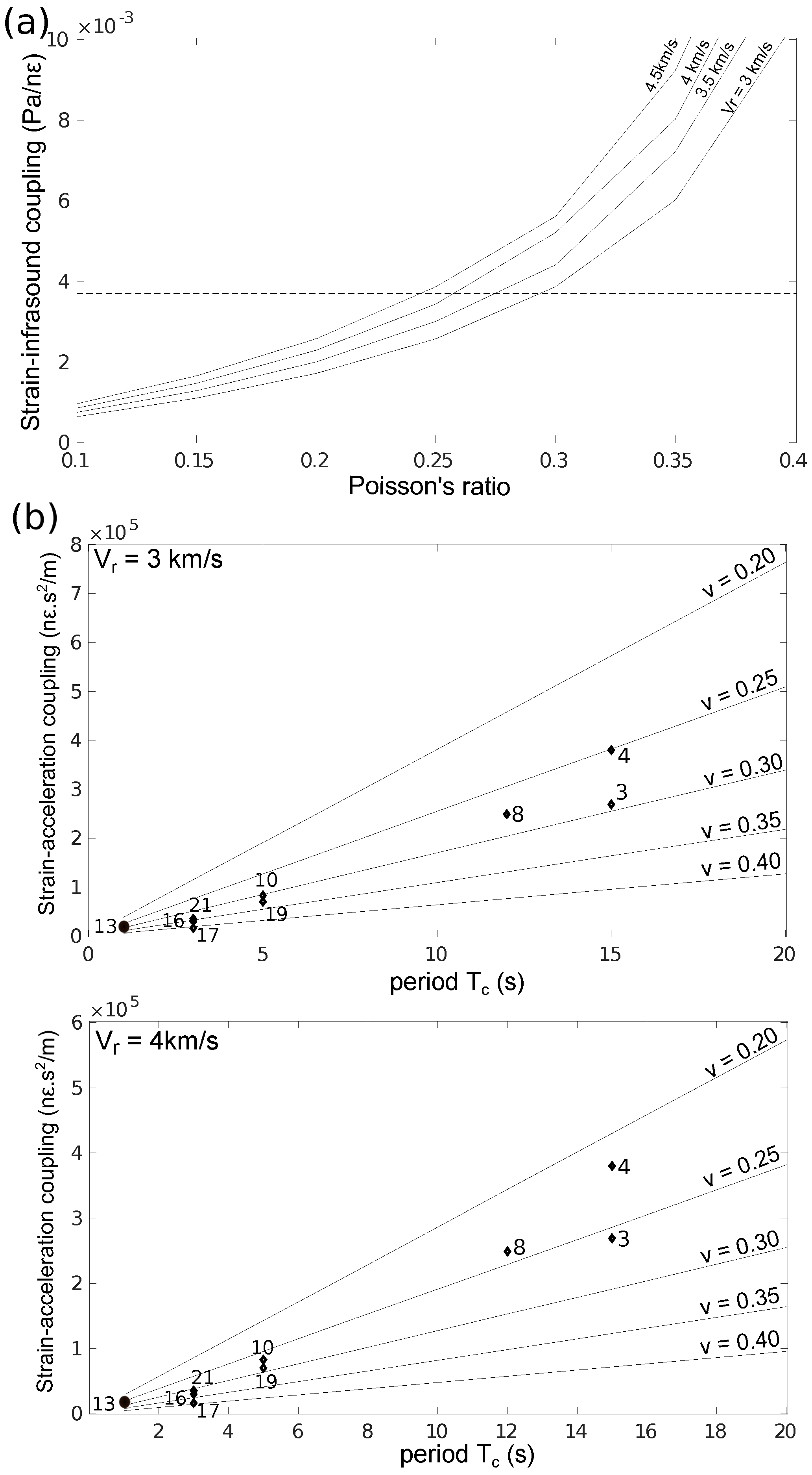
3.2. Strain-Infrasound Coupling: Observation and Theory
3.3. Evidence for Aseismic Deformation in the LV
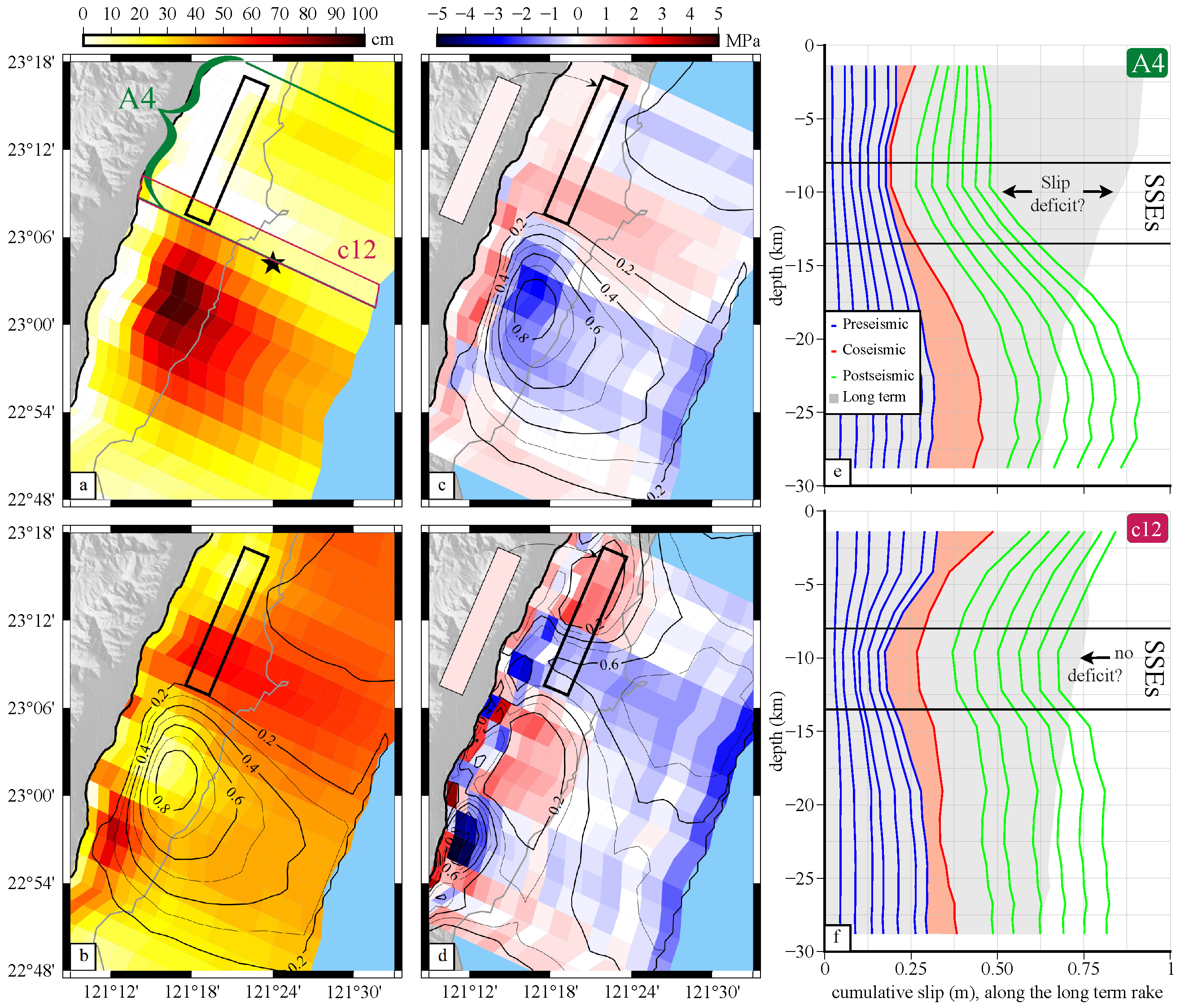
3.3.1. Detection and Characterization of SSEs
3.3.2. Afterslip Detected during Small Earthquakes ()
3.4. Ground Deformation Detected during Tropical Cyclones
4. Future Perspectives
4.1. Hydrological Modulation of Crustal Strain, Seismicity and Aseismic Slip
4.2. Quantification of the Mass of Sediment Removed by Landslides
4.3. Rapid Moment Magnitude Estimate and Implications for EEW Systems
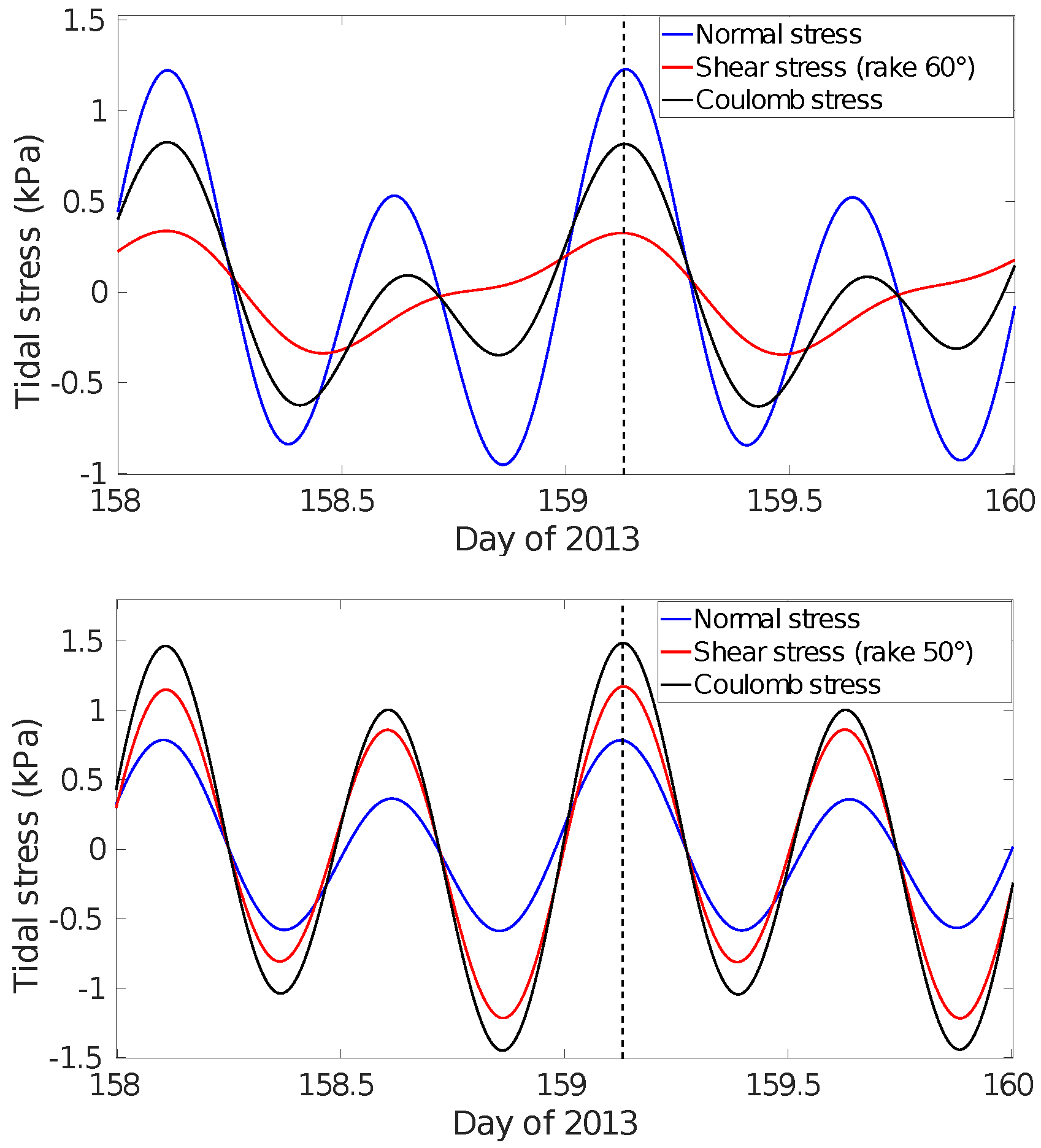
4.4. Tidal Variations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite System |
| LV | Longitudinal Valley |
| LVF | Longitudinal Valley Fault |
| SSE | Slow Slip Event |
| InSAR | Interferometric Synthetic Aperture Radar |
| EEW | Earthquake early warning |
References
- Johnston, M.J.S.; Linde, A.T. Implications of crustal strain during conventional, slow, and silent earthquakes. In International Handbook of Earthquake and Engineering Seismology, Volume 81, Part A; Lee, W.H.K., Kanamori, H., Jennings, P.C., Kisslinger, C., Eds.; Academic Press: Cambridge, MA, USA, 2002; pp. 589–605. [Google Scholar]
- Hsu, Y.J.; Yu, S.B.; Loveless, J.P.; Bacolcol, T.; Solidum, R.; Luis, A., Jr.; Pelicano, A.; Woessner, J. Interseismic deformation and moment deficit along the Manila subduction zone and the Philippine Fault system. J. Geophys. Res. Solid Earth 2016, 121, 7639–7665. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.B.; Chen, H.Y.; Kuo, L.C. Velocity field of GPS stations in the Taiwan area. Tectonophysics 1997, 274, 41–59. [Google Scholar] [CrossRef]
- Thomas, M.Y.; Avouac, J.P.; Champenois, J.; Lee, J.C.; Kuo, L.C. Spatiotemporal evolution of seismic and aseismic slip on the Longitudinal Valley Fault, Taiwan. J. Geophys. Res. Solid Earth 2014, 119, 5114–5139. [Google Scholar] [CrossRef] [Green Version]
- Canitano, A.; Gonzalez-Huizar, H.; Hsu, Y.J.; Lee, H.M.; Linde, A.T.; Sacks, S. Testing the influence of static and dynamic stress perturbations on the occurrence of a shallow, slow slip event in eastern Taiwan. J. Geophys. Res. Solid Earth 2019, 124, 3073–3087. [Google Scholar] [CrossRef]
- Canitano, A.; Godano, M.; Thomas, M.Y. Inherited state of stress as a key factor controlling slip and slip mode: Inference from the study of a slow slip event in the Longitudinal Valley, Taiwan. Geophys. Res. Lett. 2021, 48, e2020GL090278. [Google Scholar] [CrossRef]
- Sacks, S.; Suyehiro, S.; Evertson, D.W.; Yamagishi, Y. Sacks–Evertson strainmeter, its installation in Japan and some preliminary results concerning strain steps. Paper Meteorol. Geophys. 1971, 22, 195–208. [Google Scholar] [CrossRef] [Green Version]
- Ágústsson, K.; Linde, A.T.; Stefánsson, R.; Sacks, S. Strain changes for the 1987 Vatnafjöll earthquake in south Iceland and possible magmatic triggering. J. Geophys. Res. 1999, 104, 1151–1161. [Google Scholar] [CrossRef]
- Langbein, J. Borehole strainmeter measurements spanning the 2014 Mw 6.0 South Napa Earthquake, California: The effect from instrument calibration. J. Geophys. Res. 2015, 120, 7190–7202. [Google Scholar] [CrossRef] [Green Version]
- Canitano, A.; Bernard, P.; Linde, A.T.; Sacks, S. Analysis of signals of a borehole strainmeter in the western rift of Corinth. J. Geod. Sci. 2013, 3, 63–76. [Google Scholar] [CrossRef]
- Canitano, A.; Bernard, P.; Linde, A.T.; Sacks, S.; Boudin, F. Correcting high-resolution borehole strainmeter data from complex external influences and partial-solid coupling: The case of Trizonia, Rift of Corinth (Greece). Pure Appl. Geophys. 2014, 171, 1769–1790. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini, L.; Linde, A.T.; Sacks, I.S.; Scarpa, R.; Romano, P. Horizontal crack in a layered structure satisfies deformation for the 2004–2006 uplift of Campi Flegrei. Geophys. Res. Lett. 2007, 34, L22313. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini; Scarpa, R.; Bilham, R.; Linde, A.T.; Sacks, I.S. Abrupt magma chamber contraction and micro- seismicity at Campi Flegrei, Italy: Cause and effect determined from strainmeters and tiltmeters. J. Geophys. Res. Solid Earth 2015, 120, 5467–5478. [Google Scholar] [CrossRef] [Green Version]
- Giudicepietro, F.; López, C.; Macedonio, G.; Alparone, S.; Bianco, F.; Calvari, S.; De Cesare, W.; Delle Donne, D.; Di Lieto, B.; Esposito, A.M.; et al. Geophysical precursors of the July–August 2019 paroxysmal eruptive phase and their implications for Stromboli volcano (Italy) monitoring. Sci. Rep. 2020, 10, 10296. [Google Scholar] [CrossRef]
- Di Lieto, B.; Romano, P.; Scarpa, R.; Linde, A.T. Strain signals before and during paroxysmal activity at Stromboli volcano, Italy. Geophys. Res. Lett. 2020, 47, e2020GL088521. [Google Scholar] [CrossRef]
- Linde, A.T.; Ágústsson, K.; Sacks, S.; Stefánsson, R. Mechanism of the 1991 eruption of Hekla from continuous borehole strain monitoring. Nature 1993, 365, 737–740. [Google Scholar] [CrossRef]
- Bonaccorso, A.; Linde, A.; Currenti, G.; Sacks, S.; Sicali, A. The borehole dilatometer network of Mount Etna: A powerful tool to detect and infer volcano dynamics. J. Geophys. Res. Solid Earth 2016, 121, 4655–4669. [Google Scholar] [CrossRef] [Green Version]
- Canitano, A.; Hsu, Y.J.; Lee, H.M.; Linde, A.T.; Sacks, S. Near-field strain observations of the October 2013 Ruisui, Taiwan, earthquake: Source parameters and limits of very short-term strain detection. Earth Planets Space 2015, 67, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Canitano, A.; Godano, M.; Hsu, Y.J.; Lee, H.M.; Linde, A.T.; Sacks, S. Seismicity controlled by a frictional afterslip during a small-magnitude seismic sequence (ML < 5) on the Chihshang Fault, Taiwan. J. Geophys. Res. Solid Earth 2018, 123, 2003–2018. [Google Scholar]
- Liu, C.C.; Linde, A.T.; Sacks, I.S. Slow earthquakes triggered by typhoons. Nature 2009, 459, 833–836. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Chang, Y.S.; Liu, C.C.; Lee, H.M.; Linde, A.T.; Sacks, S.; Kitagawa, G.; Chen, Y.G. Revisiting borehole strain, typhoons, and slow earthquakes using quantitative estimates of precipitation-induced strain changes. J. Geophys. Res. Solid Earth 2015, 120, 4556–4571. [Google Scholar] [CrossRef]
- Mouyen, M.; Canitano, A.; Chao, B.F.; Hsu, Y.J.; Steer, P.; Longuevergne, L.; Boy, J.P. Typhoon-induced ground deformation. Geophys. Res. Lett. 2017, 44, 11,004–11,011. [Google Scholar] [CrossRef] [Green Version]
- Benioff, H. A linear strain seismograph. Bull. Seismol. Soc. Am. 1935, 25, 283–309. [Google Scholar] [CrossRef]
- Roeloffs, E.A.; Linde, A.T. Borehole observations and continuous strain and fluid pressure. In Volcano Deformation Geodetic Measurments Techniques; Dzurisin, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 305–322. [Google Scholar]
- Hart, R.H.G.; Galdwin, M.T.; Gwyther, R.L.; Agnew, D.C.; Wyatt, F.K. Tidal calibration of borehole strain meters: Removing the effects of small-scale inhomogeneity. J. Geophys. Res. 1996, 101, 25553–25571. [Google Scholar] [CrossRef]
- Matsumoto, K.; Sato, T.; Takanezawa, T.; Ooe, M. GOTIC2: A program for computation of Oceanic Tidal Loading effect. J. Geod. Soc. Jpn 2001, 47, 243–248. [Google Scholar]
- Roeloffs, E.A. Tidal calibration of plate boundary observatory borehole strainmeters: Roles of vertical and shear coupling. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Hodgkinson, K.; Langbein, J.; Henderson, B.; Mencin, D.; Borsa, A. Tidal calibration of Plate Boundary Observatory borehole strainmeters. J. Geophys. Res. 2013, 118, 447–458. [Google Scholar] [CrossRef]
- Canitano, A.; Hsu, Y.J.; Lee, H.M.; Linde, A.T.; Sacks, S. Calibration for the shear strain of 3-component borehole strainmeters in eastern Taiwan through Earth and ocean tidal waveform modeling. J. Geodesy 2018, 92, 223–240. [Google Scholar] [CrossRef]
- Langbein, J. Effect of error in theoretical Earth tide on calibration of borehole strainmeters. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Currenti, G.; Zuccarello, L.; Bonaccorso, A.; Sicali, A. Borehole volumetric strainmeter calibration from a nearby seismic broadband array at Etna Volcano. J. Geophys. Res. Solid Earth 2017, 122, 7729–7738. [Google Scholar] [CrossRef]
- Tamura, Y.; Sato, T.; Ooe, M.; Ishiguro, M. A procedure for tidal analysis with a Bayesian information criterion. Geophys. J. Int. 1991, 104, 507–516. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Mavroeidis, G.P.; Ashoory, M. Comparison of observed and synthetic near-fault dynamic ground strains and rotations from the 2004 Mw 6.0 Parkfield, California, earthquake. Bull. Seismol. Soc. Am. 2018, 108, 1240–1256. [Google Scholar] [CrossRef]
- Canitano, A.; Hsu, Y.J.; Lee, H.M.; Linde, A.T.; Sacks, S. A first modeling of dynamic and static crustal strain field from near-field dilatation measurements: Example of the 2013 Mw 6.2 Ruisui earthquake, Taiwan. J. Geodesy 2017, 91, 1–8. [Google Scholar] [CrossRef]
- Vidale, J.; Goes, S.; Richards, P.G. Near-field deformation seen on distant broadband seismograms. Geophys. Res. Lett. 1995, 22, 1–4. [Google Scholar] [CrossRef]
- Yu, Z.; Hattori, K.; Zhu, K.; Fan, M.; Marchetti, D.; He, X.; Chi, C. Evaluation of pre-earthquake anomalies of borehole strain network by using receiver operating characteristic curve. Remote Sens. 2021, 13, 515. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini, L. Limits on earthquake nucleation and other pre-seismic phenomena from continuous strain in the near field of the 2009 L’Aquila earthquake. Geophys. Res. Lett. 2010, 37, L10307. [Google Scholar] [CrossRef]
- Sacks, I.S.; Snoke, J.A.; Evans, R.; King, G.; Beavan, J. Single-site phase velocity measurement. Geophys. J. Int. 1976, 46, 253–258. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Amoruso, A.; Crescentini, L.; Boschi, E. Long-period toroidal earth free oscillations from the great Sumatra-Andaman earthquake observed by paired laser extensometers in Gran Sasso, Italy. Geophys. J. Int. 2008, 173, 887–905. [Google Scholar] [CrossRef] [Green Version]
- Canitano, A. Observation and theory of strain-infrasound coupling during ground-coupled infrasound generated by Rayleigh waves in the Longitudinal Valley (Taiwan). Bull. Seismol. Soc. Am. 2020, 110, 2991–3003. [Google Scholar] [CrossRef]
- Young, J.M.; Greene, G.E. Anomalous infrasound generated by the Alaskan earthquake of 28 March 1964. J. Acoust. Soc. Am. 1984, 71, 334–339. [Google Scholar] [CrossRef]
- Le Pichon, A.; Mialle, P.; Guilbert, J.; Vergoz, J. Multistation infrasonic observations of the Chilean earthquake of 2005 June 13. Geophys. J. Int. 2006, 167, 838–844. [Google Scholar] [CrossRef] [Green Version]
- Marchetti, E.; Lacanna, G.; Le Pichon, A.; Piccinini, D.; Ripepe, M. Evidence of large infrasonic radiation induced by earthquake interaction with alluvial sediments. Seismol. Res. Lett. 2016, 87, 678–684. [Google Scholar] [CrossRef]
- Watada, S.; Kunugi, T.; Hirata, K.; Sugioka, H.; Nishida, K.; Sekiguchi, S.; Oikawa, J.; Tsuji, Y.; Kanamori, H. Atmospheric pressure change associated with the 2003 Tokachi-Oki earthquake. Geophys. Res. Lett. 2006, 33, L24306. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Gomberg, J. An integrated perspective of the continuum between earthquakes and slow-slip phenomena. Nat. Geosci. 2010, 3, 599–607. [Google Scholar] [CrossRef]
- Sacks, I.S.; Suyehiro, S.; Linde, A.T.; Snoke, J.A. Slow earthquakes and stress redistribution. Nature 1978, 275, 599–602. [Google Scholar] [CrossRef]
- Sacks, I.S.; Suyehiro, S.; Linde, A.T.; Snoke, J.A. Stress redistribution and slow earthquakes. Tectonophysics 1982, 81, 311–318. [Google Scholar] [CrossRef]
- Gualandi, A.; Nichele, C.; Serpelloni, E.; Chiaraluce, L.; Latorre, D.; Belardinelli, M.E.; Avouac, J.P. Aseismic deformation associated with an earthquake swarm in the northern Apennines (Italy). Geophys. Res. Lett. 2017, 44, 7706–7714. [Google Scholar] [CrossRef] [Green Version]
- Beroza, G.C.; Ide, S. Slow earthquakes and nonvolcanic tremors. Annu. Rev. Earth Planet. Sci. 2011, 39, 271–296. [Google Scholar] [CrossRef] [Green Version]
- Bürgmann, R. The geophysics, geology and mechanics of slow fault slip. Earth Planet. Sci. Lett. 2018, 495, 112–134. [Google Scholar] [CrossRef] [Green Version]
- Di Lieto, B.; Romano, P.; Bilham, R.; Scarpa, R. Aseismic strain episodes at Campi Flegrei Caldera, Italy. Adv. Geosci. 2021, 52, 119–129. [Google Scholar] [CrossRef]
- Linde, A.T.; Gladwin, M.T.; Johnston, M.J.S.; Gwyther, R.L.; Bilham, R.G. A slow earthquake sequence on the San Andreas fault. Nature 1996, 383, 65–68. [Google Scholar] [CrossRef]
- Martínez-Garzón, P.; Bohnhoff, M.; Mencin, D.; Kwiatek, G.; Dresen, G.; Hodgkinson, K.; Nurlu, M.; Tuba, K.F.; Feyiz, K.R. Slow strain release along the eastern Marmara region offshore Istanbul in conjunction with enhanced local seismic moment release. Earth Planet. Sci. Lett. 2019, 510, 209–218. [Google Scholar] [CrossRef]
- Hawthorne, J.C.; Rubin, A.M. Tidal modulation of slow slip in Cascadia. J. Geophys. Res. 2010, 115, B09406. [Google Scholar] [CrossRef]
- Araki, E.; Saffer, D.M.; Kopf, A.J.; Wallace, L.M.; Kimura, T.; Machida, Y.; Ide, S.; Davis, E.; IODP Expedition 365 shipboard scientists. Recurring and triggered slow-slip events near the trench at the Nankai Trough subduction megathrust. Science 2017, 356, 1157–1160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Itaba, S.; Ando, R. A slow slip event triggered by teleseismic surface waves. Geophys. Res. Lett. 2011, 38, L21306. [Google Scholar] [CrossRef]
- Wallace, L.; Bartlow, N.; Fry, B. Quake clamps down on slow slip. Geophys. Res. Lett. 2014, 41, 8840–8846. [Google Scholar] [CrossRef]
- Segou, M.; Parsons, T. The role of seismic and slow slip events in triggering the 2018 M7.1 Anchorage earthquake in the South-central Alaska subduction zone. Geophys. Res. Lett. 2020, 47, e2019GL086640. [Google Scholar] [CrossRef]
- Marone, C.J.; Scholz, C.H.; Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. 1991, 96, 8441–8452. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.P. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. 2004, 109, B07409. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Simons, M.; Avouac, J.P.; Galetzka, J.; Sieh, K.; Chlieh, M.; Natawidjaja, D.; Prawirodirdjo, L.; Bock, Y. Frictional afterslip following the 2005 Nias-Simeulue earthquake, Sumatra. Science 2006, 312, 1921–1926. [Google Scholar] [CrossRef] [PubMed]
- Freed, A.M. Afterslip (and only afterslip) following the 2004 Parkfield, California, earthquake. Geophys. Res. Lett. 2007, 34, L06312. [Google Scholar] [CrossRef] [Green Version]
- Fatahi, H.; Amelung, F.; Chaussard, E.; Wdowinski, S. Coseismic and postseismic deformation due to the 2007 M5.5 Ghazaband fault earthquake, Balochistan, Pakistan. Geophys. Res. Lett. 2015, 42, 3305–3312. [Google Scholar]
- Hawthorne, J.C.; Simons, M.; Ampuero, J.P. Estimates of aseismic slip associated with small earthquakes near San Juan Bautista, CA. J. Geophys. Res. Solid Earth 2016, 121, 8254–8275. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Yu, S.B.; Chen, H.Y. Coseismic and postseismic deformation associated with the 2003 Chengkung, Taiwan, earthquake. Geophys. J. Int. 2009, 176, 420–430. [Google Scholar] [CrossRef] [Green Version]
- Tu, J.T.; Chou, C.; Chu, P.S. The abrupt shift of typhoon activity in the vicinity of Taiwan and its association with western North Pacific-East Asian climate change. J. Clim. 2009, 22, 3617–3628. [Google Scholar] [CrossRef]
- Naval Oceanography Portal. Available online: https://www.metoc.navy.mil/jtwc/jtwc.html?western-pacific (accessed on 12 May 2021).
- Bettinelli, P.; Avouac, J.P.; Flouzat, M.; Bollinger, L.; Ramilien, G.; Rajaure, S.; Sapkota, S. Seasonal variations of seismicity and geodetic strain in the Himalaya induced by surface hydrology. Earth Planet. Sci. Lett. 2008, 266, 332–344. [Google Scholar] [CrossRef]
- Craig, T.J.; Chanard, K.; Calais, E. Hydrologically-driven crustal stresses and seismicity in the New Madrid Seismic Zone. Nat. Commun. 2017, 8, 2143. [Google Scholar] [CrossRef] [Green Version]
- Johnson, C.W.; Fu, Y.; Bürgmann, R. Seasonal water storage, stress modulation, and California seismicity. Science 2017, 356, 1161–1164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Argus, D.F.; Yu, F.; Landerer, F.W. Seasonal variation in total water storage in California inferred fron GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Fu, Y.; Bürgmann, R.; Hsu, S.Y.; Lin, C.C.; Tang, C.H.; Wu, Y.M. Assessing seasonal and interannual water storage variations in Taiwan using geodetic and hydrological data. Earth Planet. Sci. Lett. 2020, 500, 116532. [Google Scholar] [CrossRef]
- Hsu, Y.J.; Kao, H.; Bürgmann, R.; Lee, Y.T.; Huang, H.H.; Hsu, Y.F.; Wu, Y.M.; Zhuang, J. Synchronized and asynchronous modulation of seismicity by hydrological loading: A case study in Taiwan. Sci. Adv. 2021, 7, eabf7282. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Plan. Int. 2014, 25, 297–356. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Wech, A.; Kao, H.; Bürgmann, R. Annual modulation of non-volcanic tremor in northern Cascadia. J. Geophys. Res. Solid Earth 2013, 118, 2445–2459. [Google Scholar] [CrossRef]
- Beeler, N.; Lockner, D. Why earthquakes correlate weakly with the solid Earth tides: Effects of periodic stress on the rate and probability of earthquake occurrence. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Ader, T.; Lapusta, N.; Avouac, J.P.; Ampuero, J.P. Response of rate-and-state seismogenic faults to harmonic shear-stress perturbations. Geophys. J. Int. 2014, 198, 385–413. [Google Scholar] [CrossRef] [Green Version]
- Hovius, N.; Meunier, P.; Lin, C.W.W.; Chen, H.; Chen, Y.G.G.; Dadson, S.; Horng, M.J.J.; Lines, M. Prolonged seismically induced erosion and the mass balance of a large earthquake. Earth Planet. Sci. Lett. 2011, 304, 347–355. [Google Scholar] [CrossRef]
- Tsou, C.Y.; Feng, Z.Y.; Chigira, M. Catastrophic landslide induced by Typhoon Morakot, Shiaolin, Taiwan. Geomorphology 2011, 127, 166–178. [Google Scholar] [CrossRef] [Green Version]
- Steer, P.; Jeandet, L.; Cubas, N.; Marc, O.; Meunier, P.; Simoes, M.; Cattin, R.; Shyu, J.B.H.; Mouyen, M.; Liang, W.T.; et al. Earthquake statistics changed by typhoon-driven erosion. Sci. Rep. 2020, 10, 10899. [Google Scholar] [CrossRef] [PubMed]
- Steer, P.; Simoes, M.; Cattin, R.; Shyu, J.B.H. Erosion influences the seismicity of active thrust faults. Nat. Commun. 2014, 5, 5564. [Google Scholar] [CrossRef] [Green Version]
- Farghal, N.; Barbour, A.; Langbein, J. The potential of using dynamic strains in earthquake early warning applications. Seismol. Res. Lett. 2020, 91, 2817–2827. [Google Scholar] [CrossRef]
- Melgar, D.; Bock, Y.; Sanchez, D.; Crowell, B.W. On robust and reliable automated baseline corrections for strong motion seismology. J. Geophys. Res. 2013, 118, 1177–1187. [Google Scholar] [CrossRef]
- Melgar, D.; Melbourne, T.; Crowell, B.; Geng, J.; Szeliga, W.; Scrivner, C.; Santillan, M.; Goldberg, D. Real-time high rate GNSS displacements: Performance demonstration during the 2019 Ridgecrest, California, earthquakes. Seismol. Res. Lett. 2019. [Google Scholar] [CrossRef]
- Barbour, A.J.; Langbein, J.O.; Farghal, N.S. Earthquake magnitudes from dynamic strain. Bull. Seismol. Soc. Am. 2021. [Google Scholar] [CrossRef]
- Wu, Y.M.; Kanamori, H. Experiment on an onsite early warning method for the Taiwan Early Warning System. Bull. Seismol. Soc. Am. 2005, 95, 347–353. [Google Scholar] [CrossRef] [Green Version]
- Meurers, B.; Van Camp, M.; Francis, O.; Pálinkáš, V. Temporal variation of tidal parameters in superconducting gravimeter time-series. Geophys. J. Int. 2016, 205, 284–300. [Google Scholar] [CrossRef] [Green Version]
- Calvo, M.; Hinderer, J.; Rosat, S.; Legros, H.; Boy, J.P.; Ducarme, B.; Zürn, W. Time stability of spring and superconducting gravimeters through the analysis of very long gravity records. J. Geodyn. 2014, 80. [Google Scholar] [CrossRef]
- Beaumont, C.; Berger, J. Earthquake prediction: Modification of the Earth tide tilts and strains by dilatancy. J. R. Astron. Soc. 1974, 39, 111–121. [Google Scholar] [CrossRef]
















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canitano, A.; Mouyen, M.; Hsu, Y.-J.; Linde, A.; Sacks, S.; Lee, H.-M. Fifteen Years of Continuous High-Resolution Borehole Strainmeter Measurements in Eastern Taiwan: An Overview and Perspectives. GeoHazards 2021, 2, 172-195. https://doi.org/10.3390/geohazards2030010
Canitano A, Mouyen M, Hsu Y-J, Linde A, Sacks S, Lee H-M. Fifteen Years of Continuous High-Resolution Borehole Strainmeter Measurements in Eastern Taiwan: An Overview and Perspectives. GeoHazards. 2021; 2(3):172-195. https://doi.org/10.3390/geohazards2030010
Chicago/Turabian StyleCanitano, Alexandre, Maxime Mouyen, Ya-Ju Hsu, Alan Linde, Selwyn Sacks, and Hsin-Ming Lee. 2021. "Fifteen Years of Continuous High-Resolution Borehole Strainmeter Measurements in Eastern Taiwan: An Overview and Perspectives" GeoHazards 2, no. 3: 172-195. https://doi.org/10.3390/geohazards2030010
APA StyleCanitano, A., Mouyen, M., Hsu, Y.-J., Linde, A., Sacks, S., & Lee, H.-M. (2021). Fifteen Years of Continuous High-Resolution Borehole Strainmeter Measurements in Eastern Taiwan: An Overview and Perspectives. GeoHazards, 2(3), 172-195. https://doi.org/10.3390/geohazards2030010





