Reduction of Bias and Uncertainty in Regional Seismic Site Amplification Factors for Seismic Hazard and Risk Analysis
Abstract
:1. Introduction
2. Methodology of Equivalent Linear 1-D Analysis
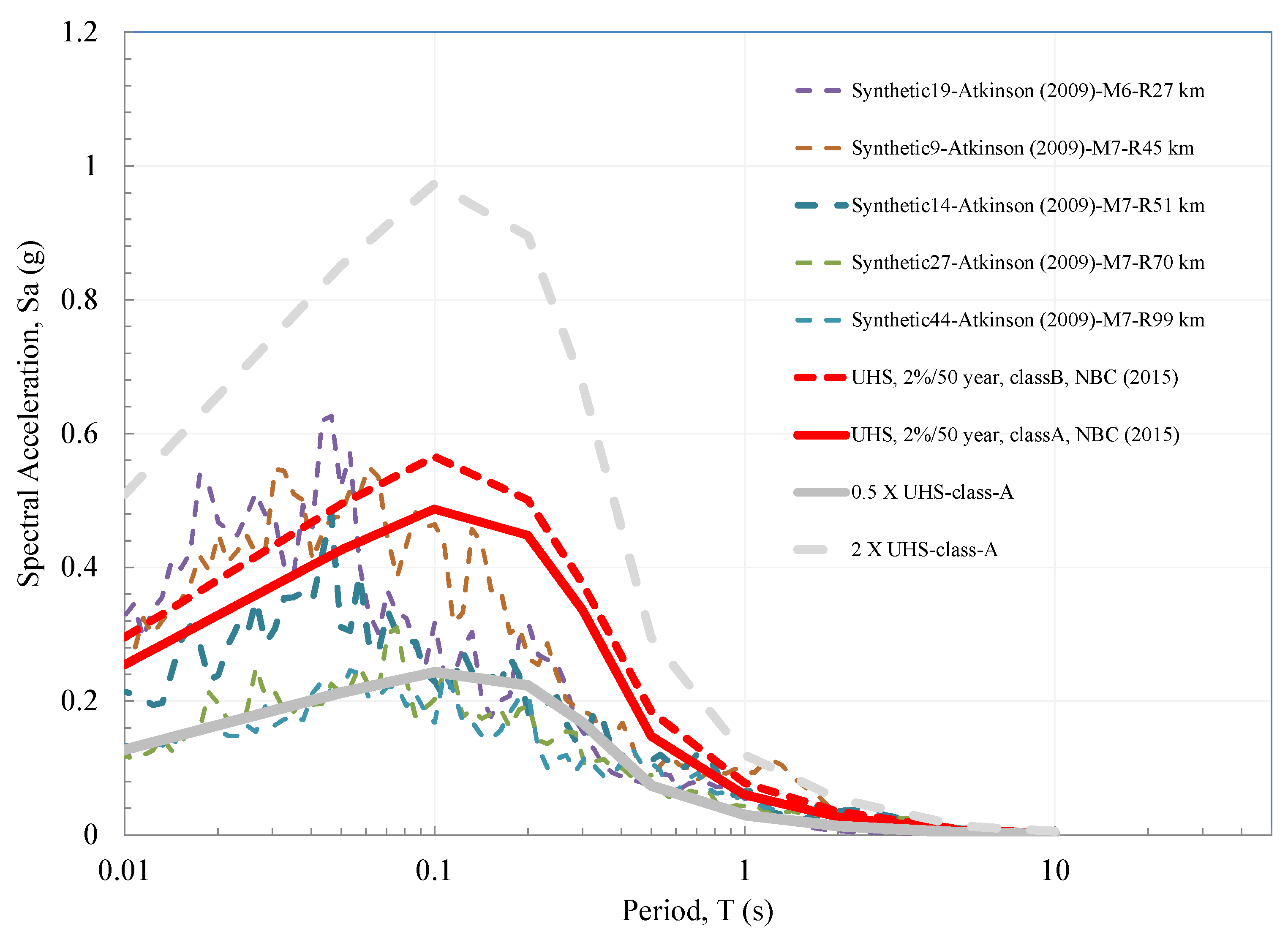
2.1. Selection of Input Rock Ground Motions
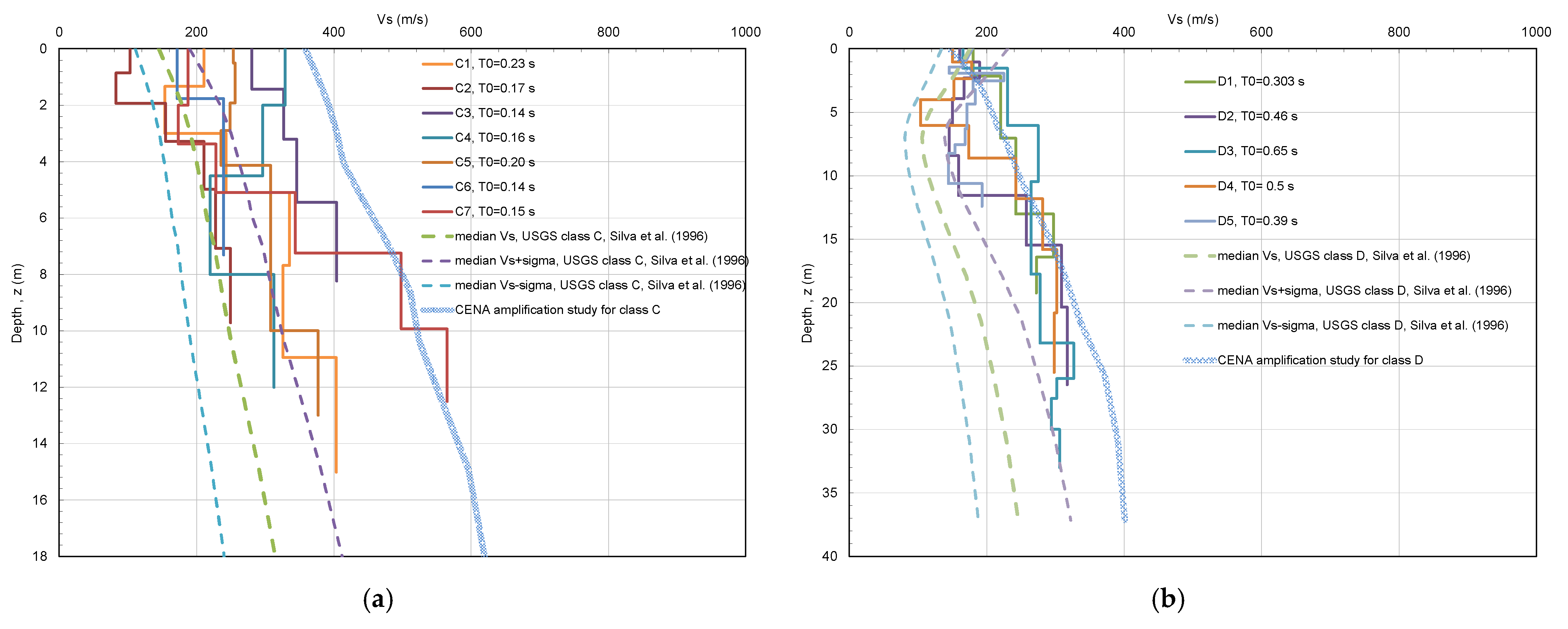
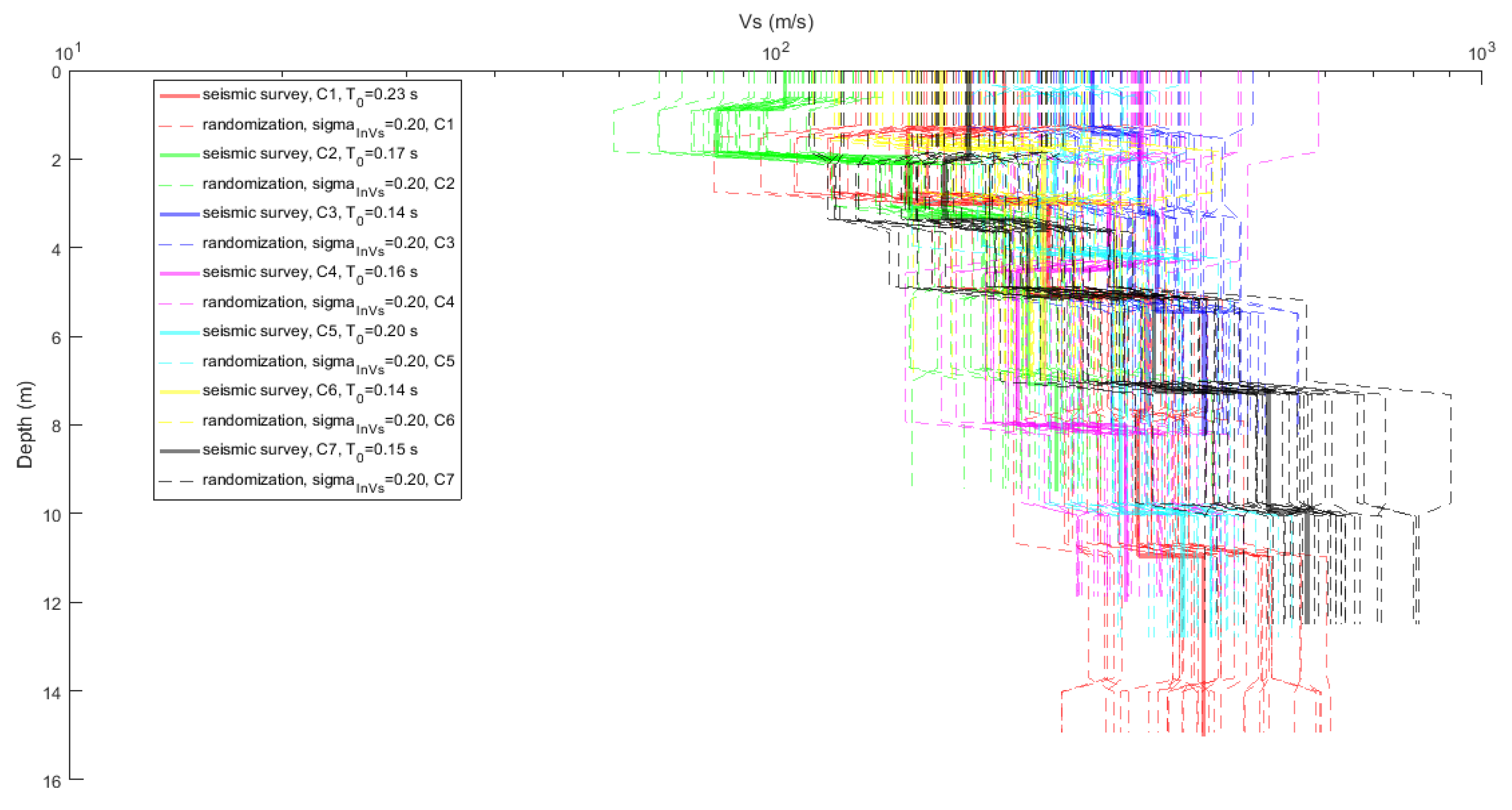
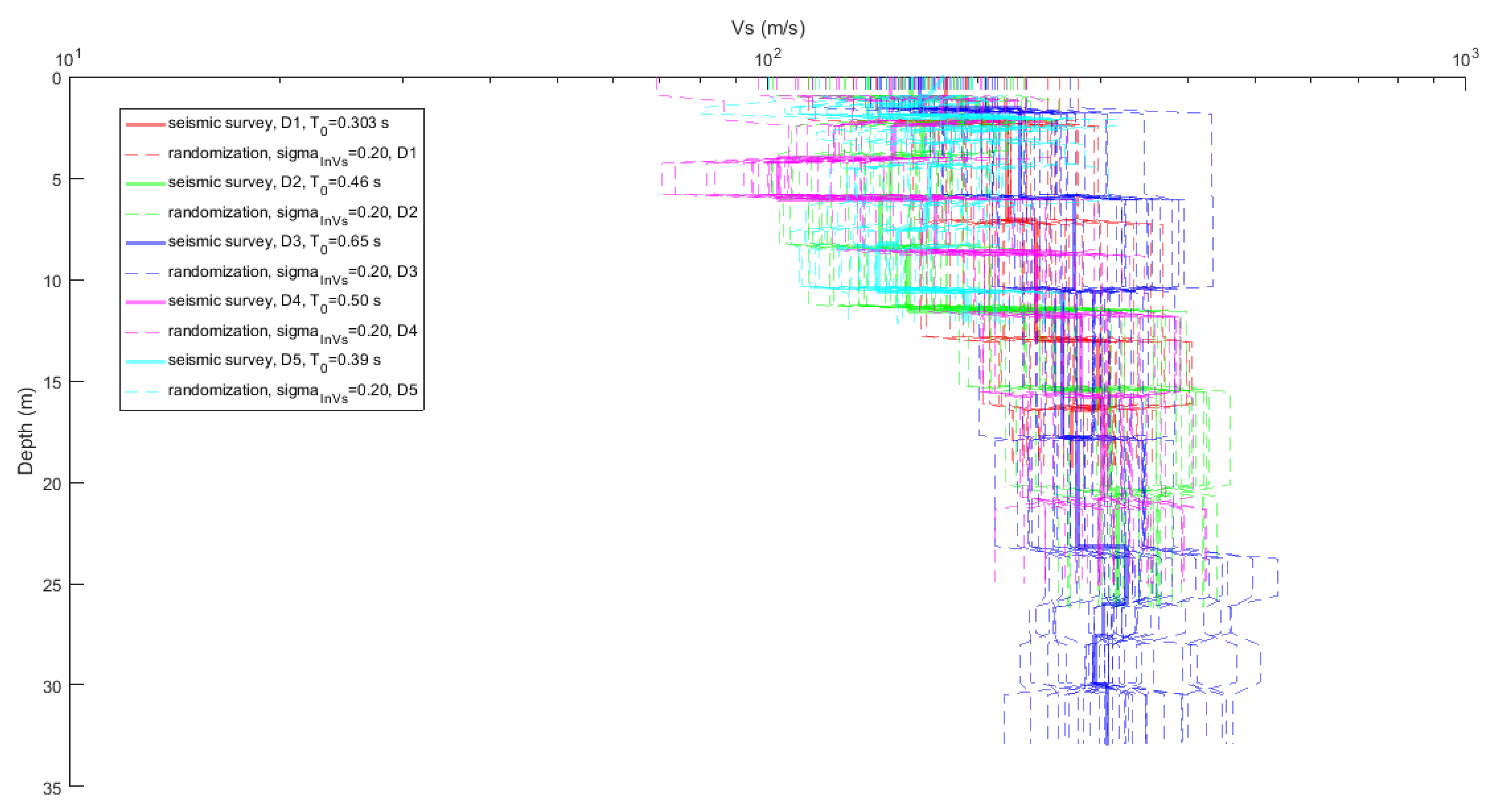
2.2. Randomization of Vs Profiles Obtained from Seismic Surveys
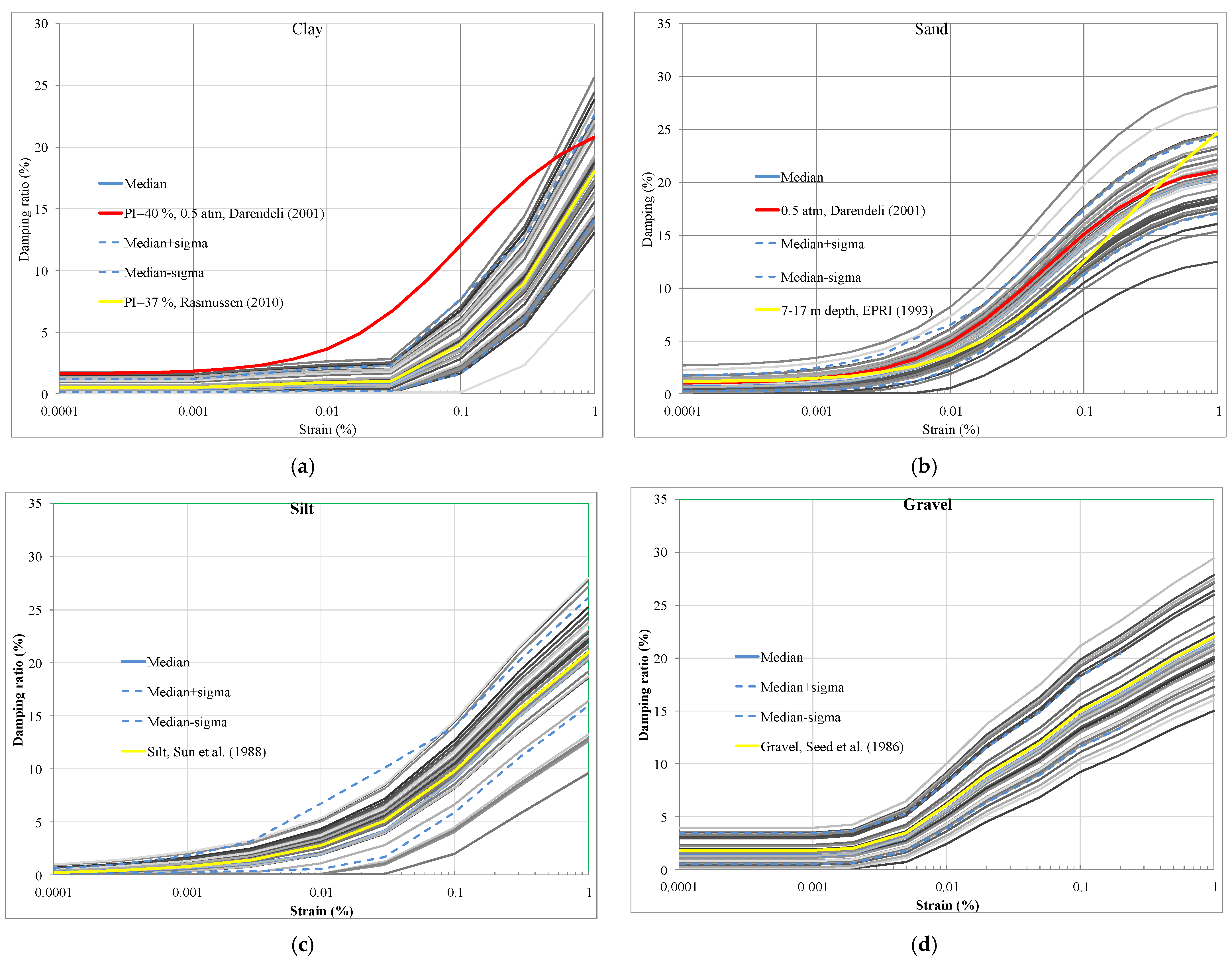
2.3. Randomization of G/Gmax and Damping Ratios Curves
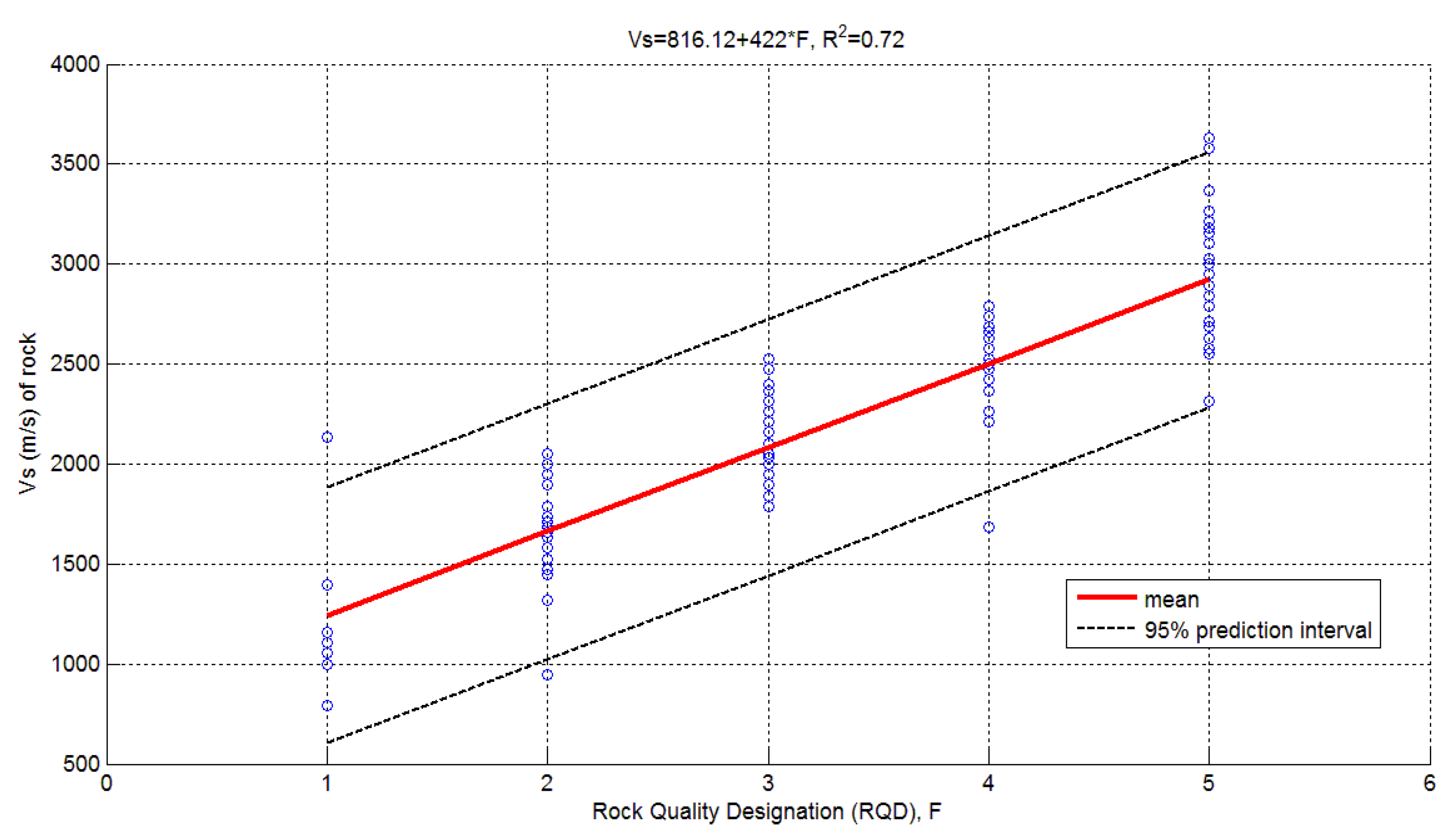
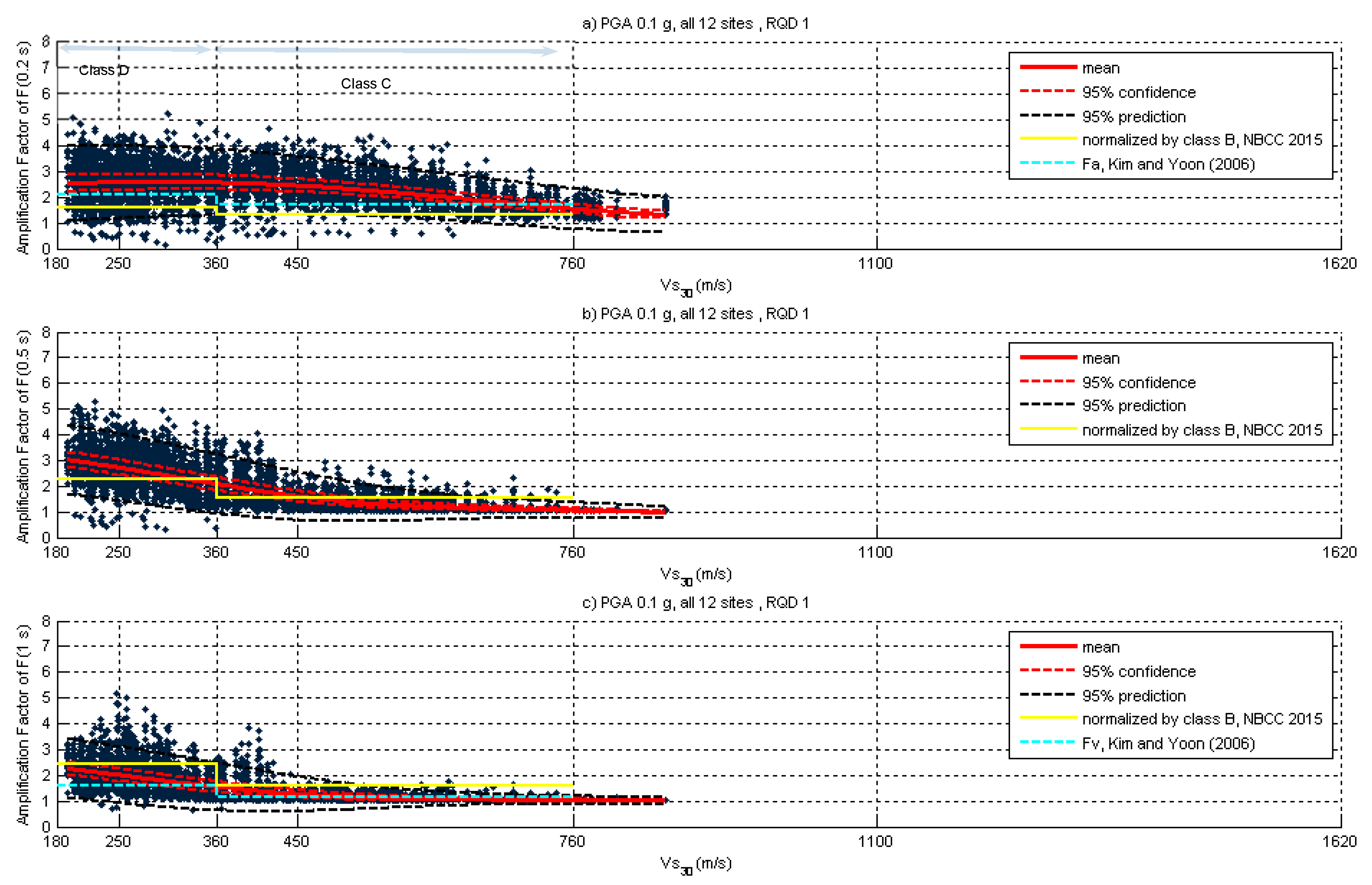
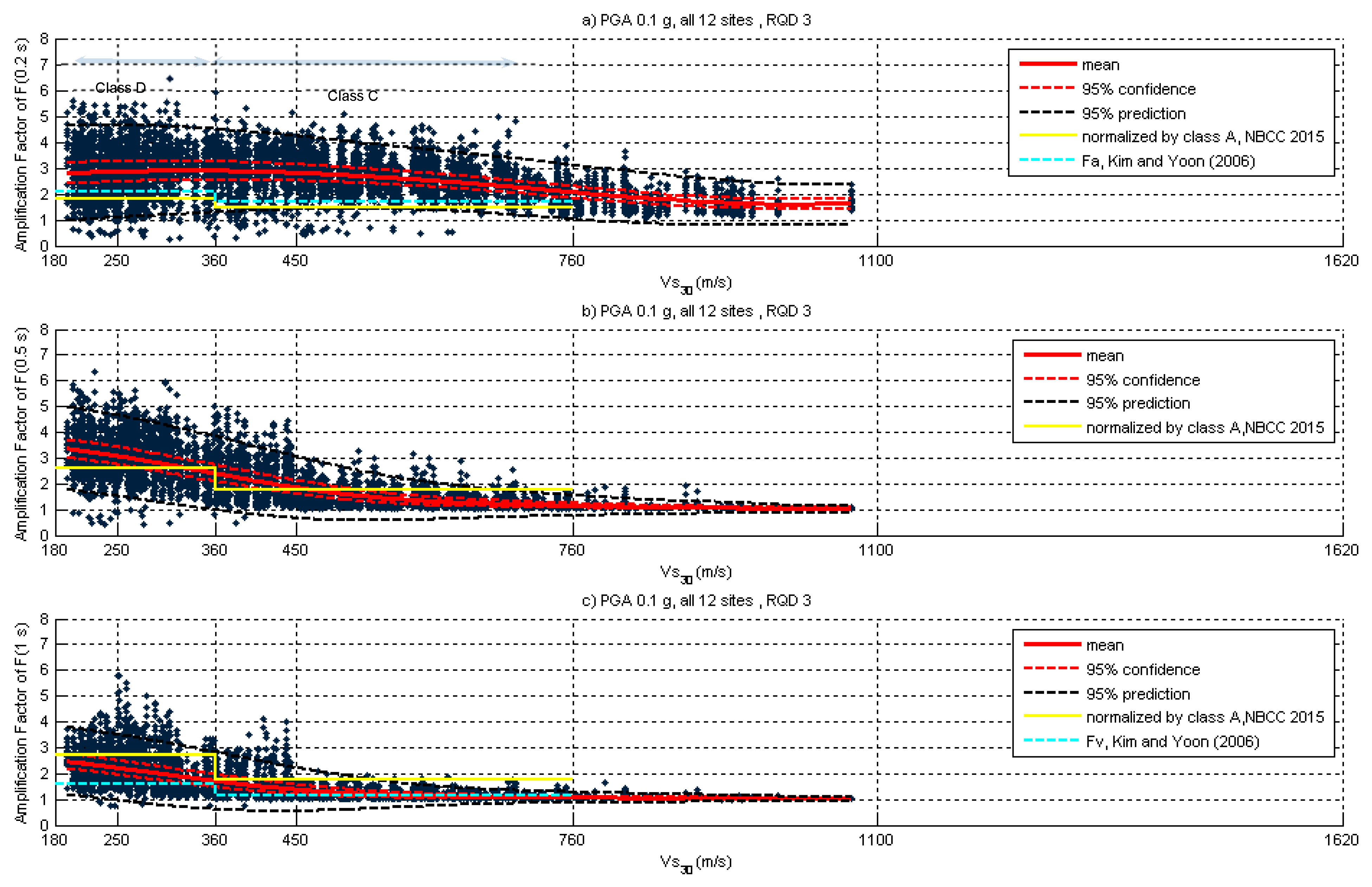
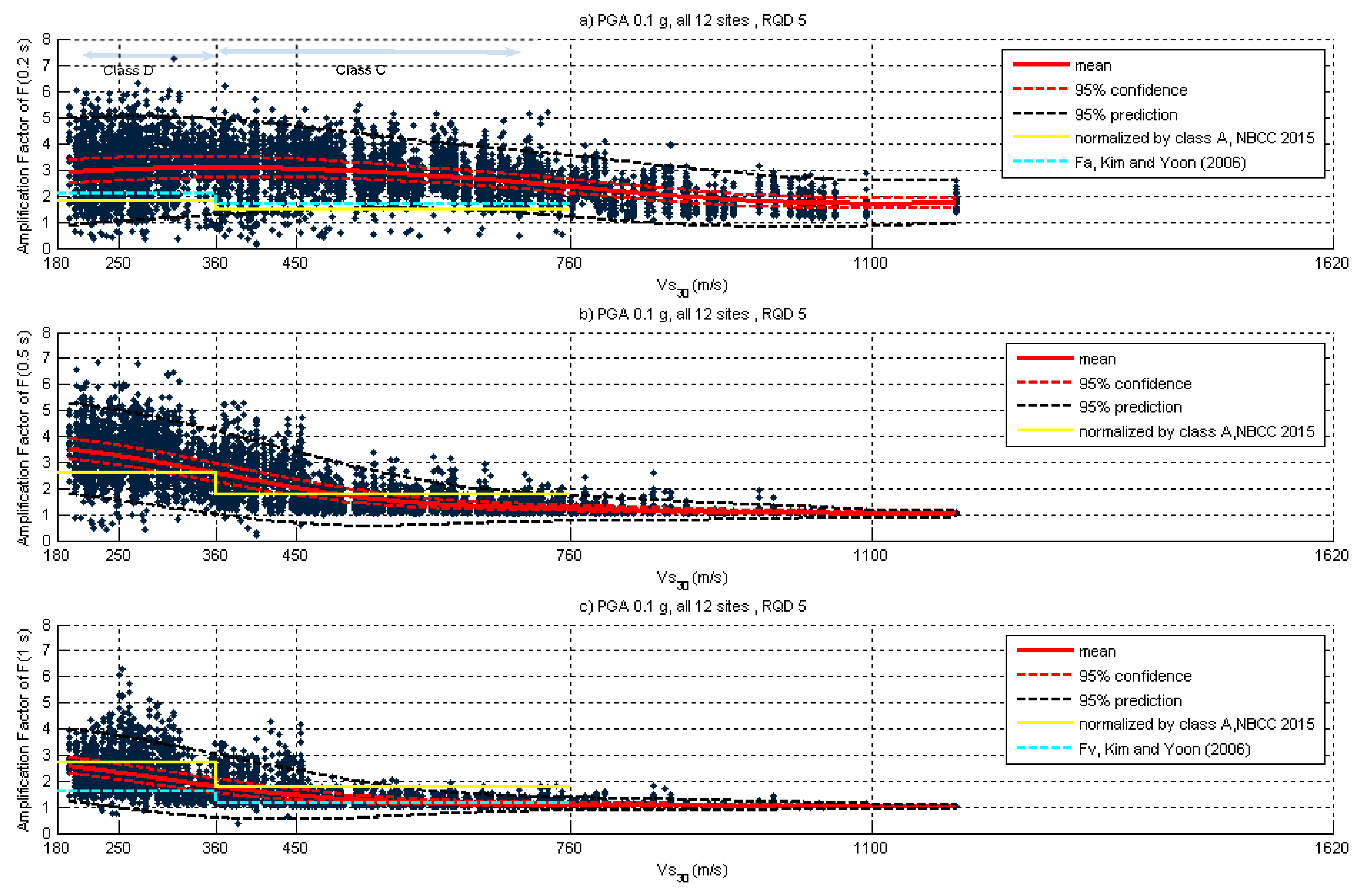
2.4. Relationship between Bedrock Vs versus Rock Quality Designation (RQD)
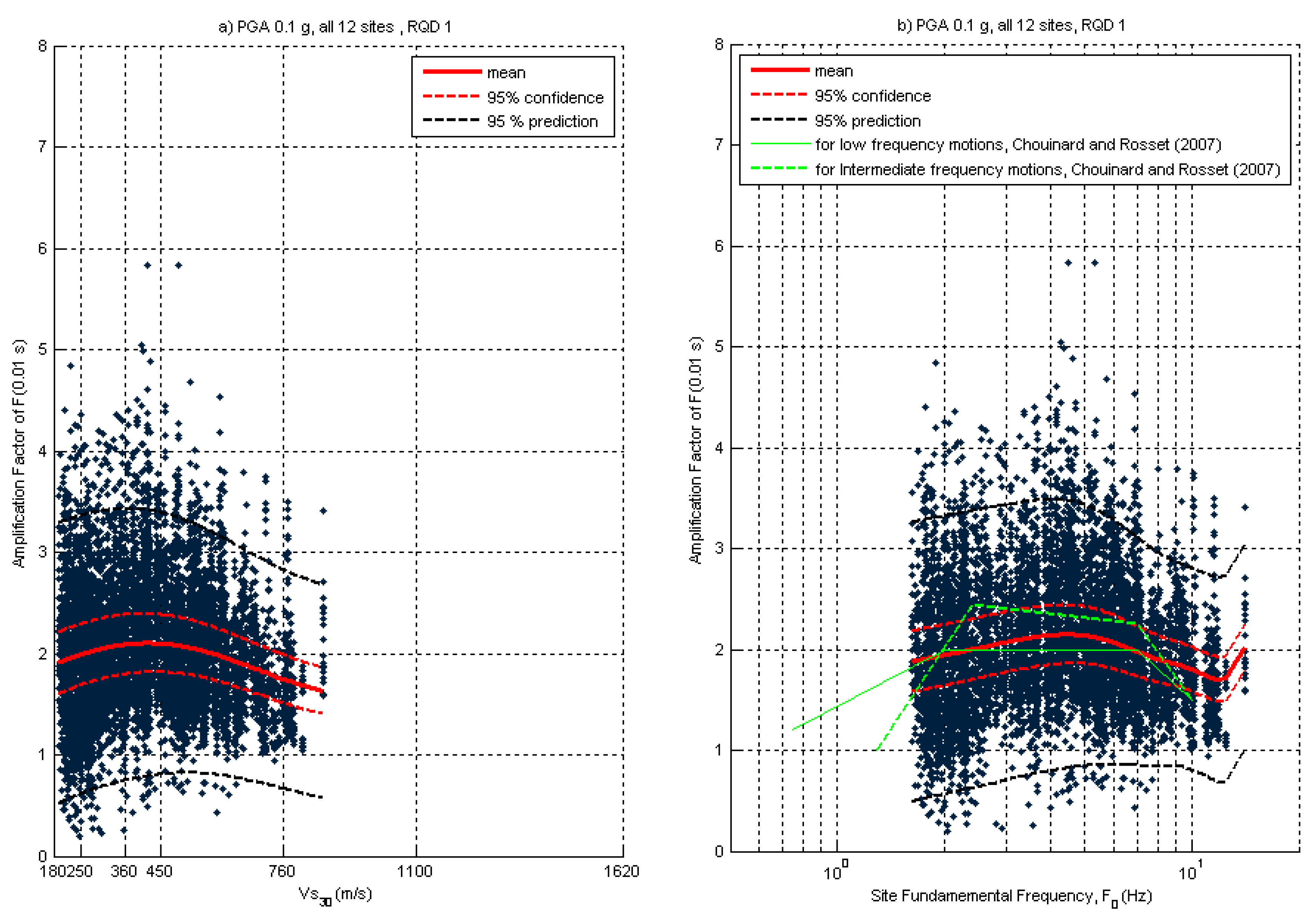
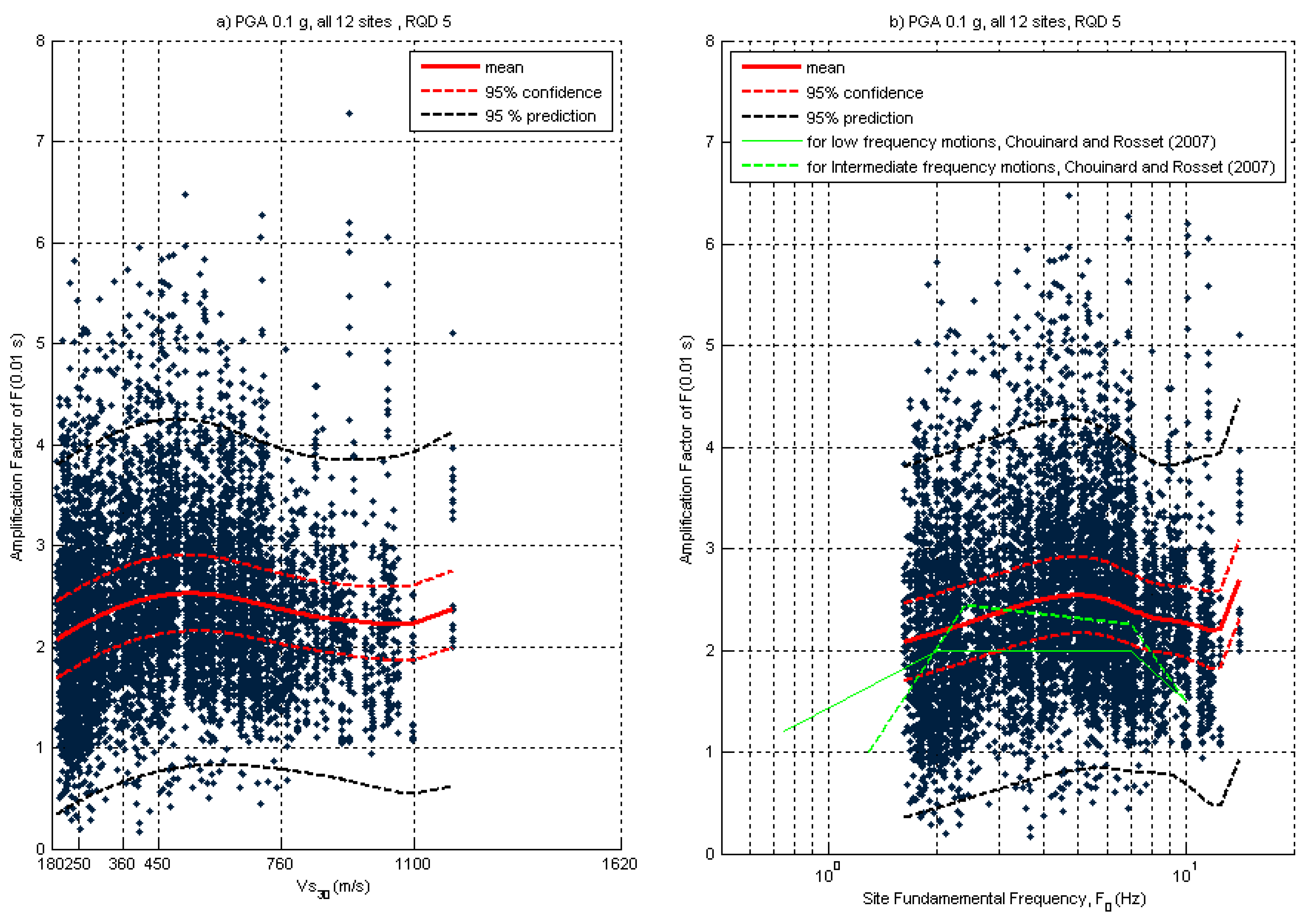
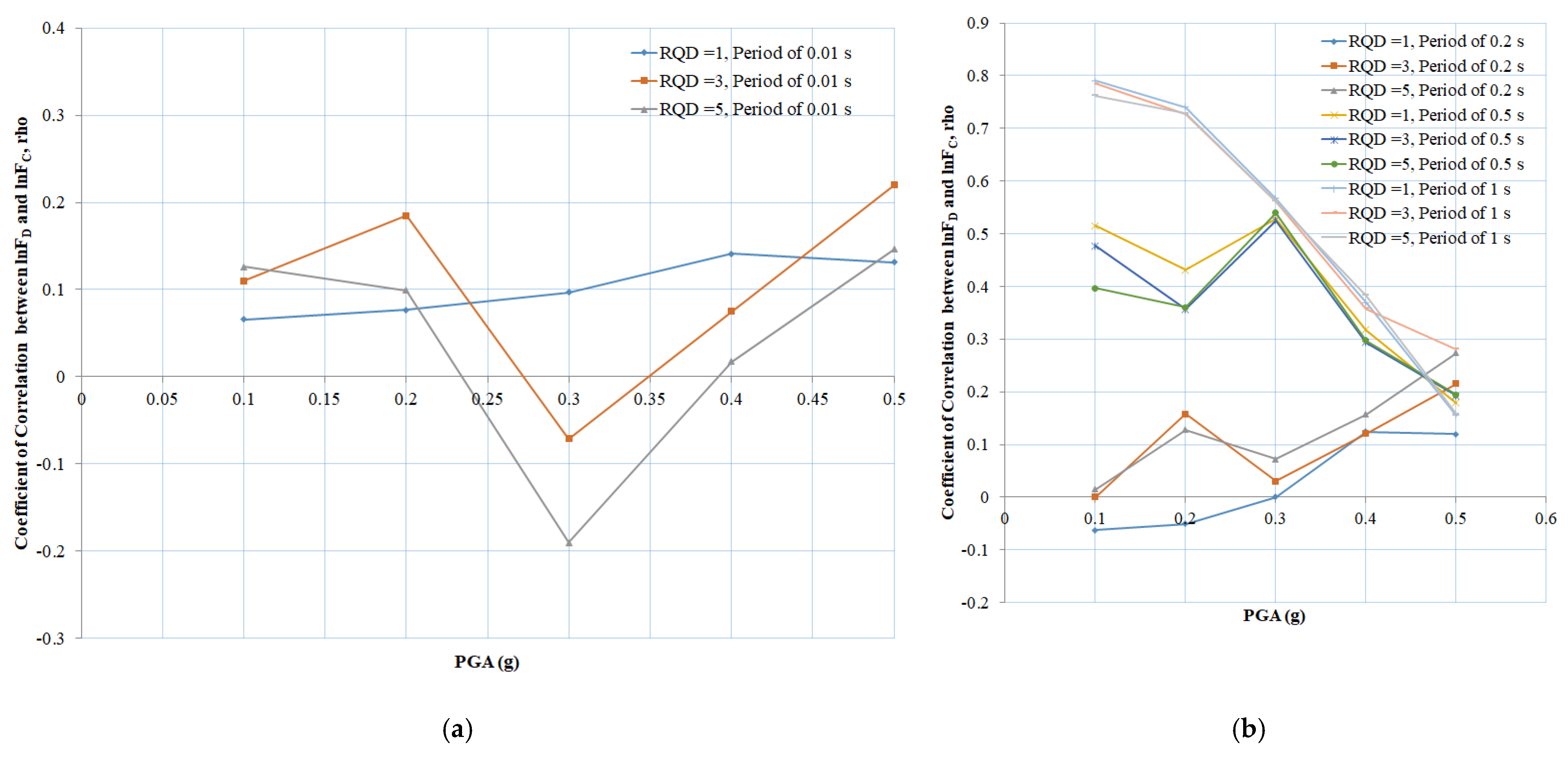
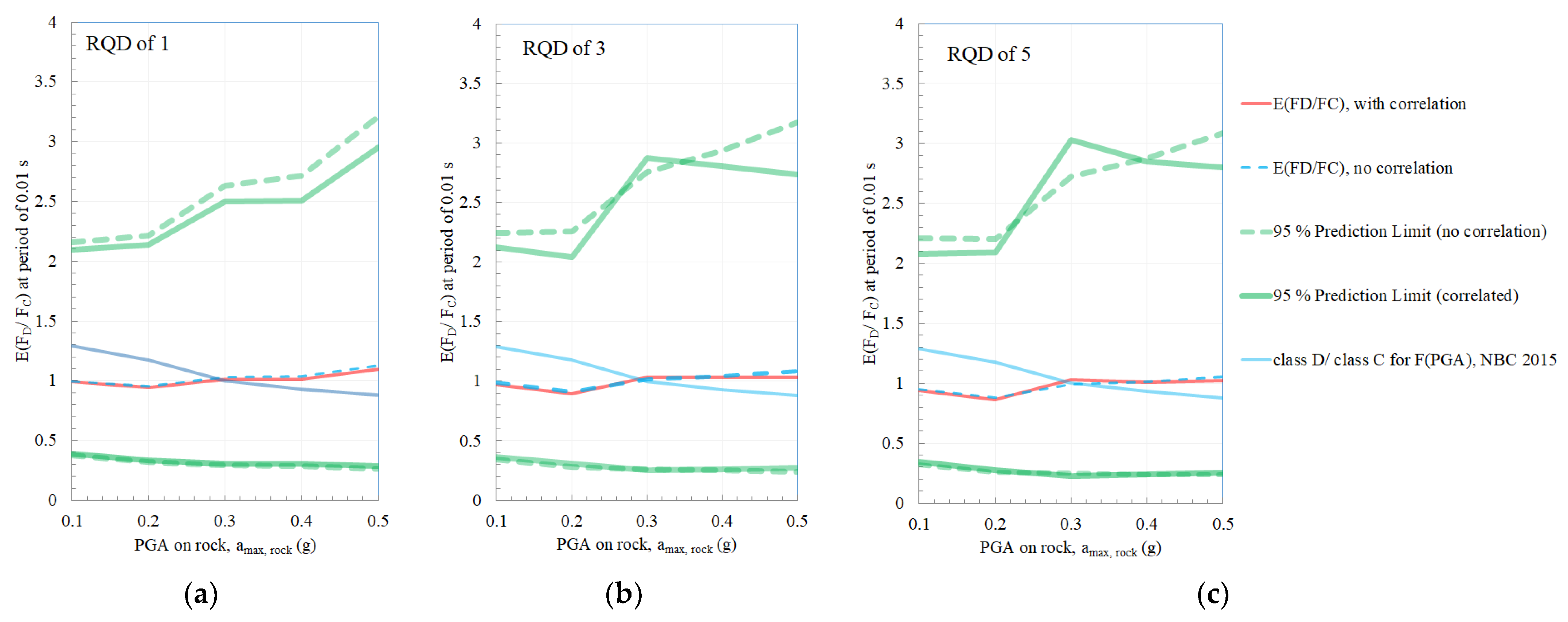
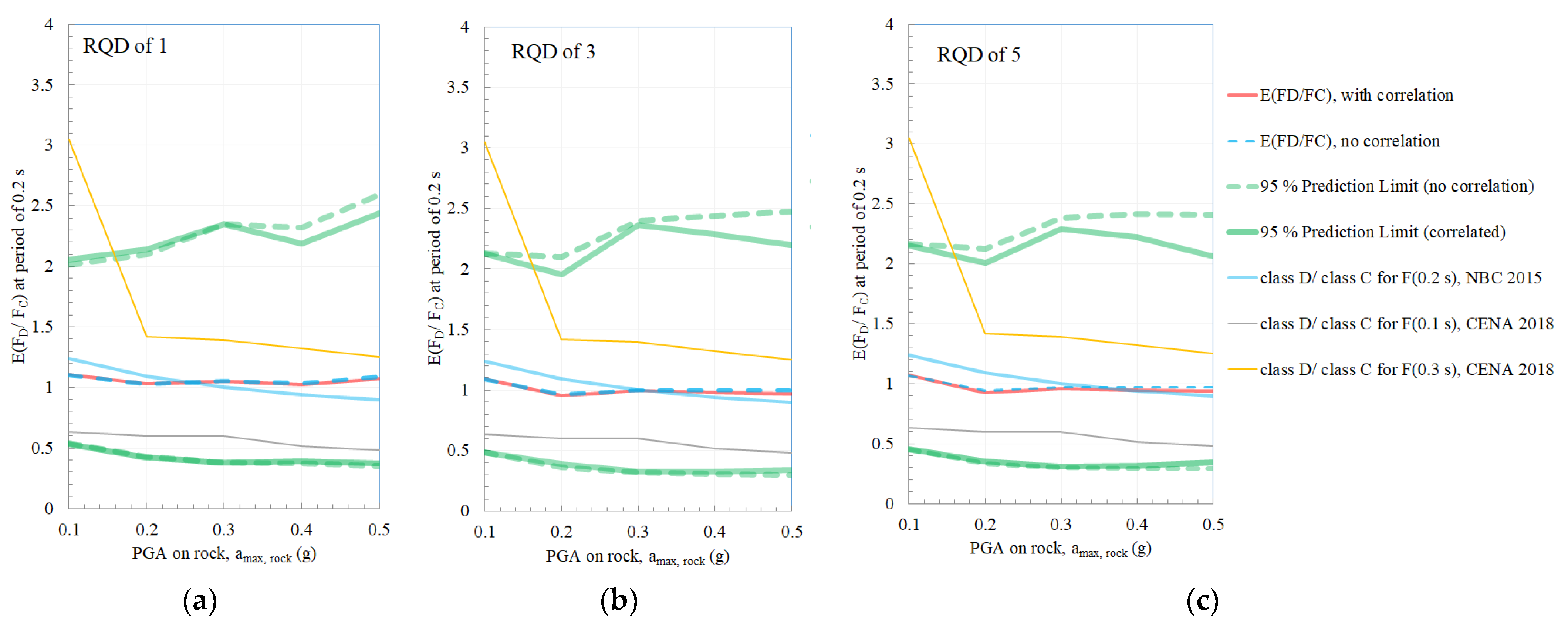
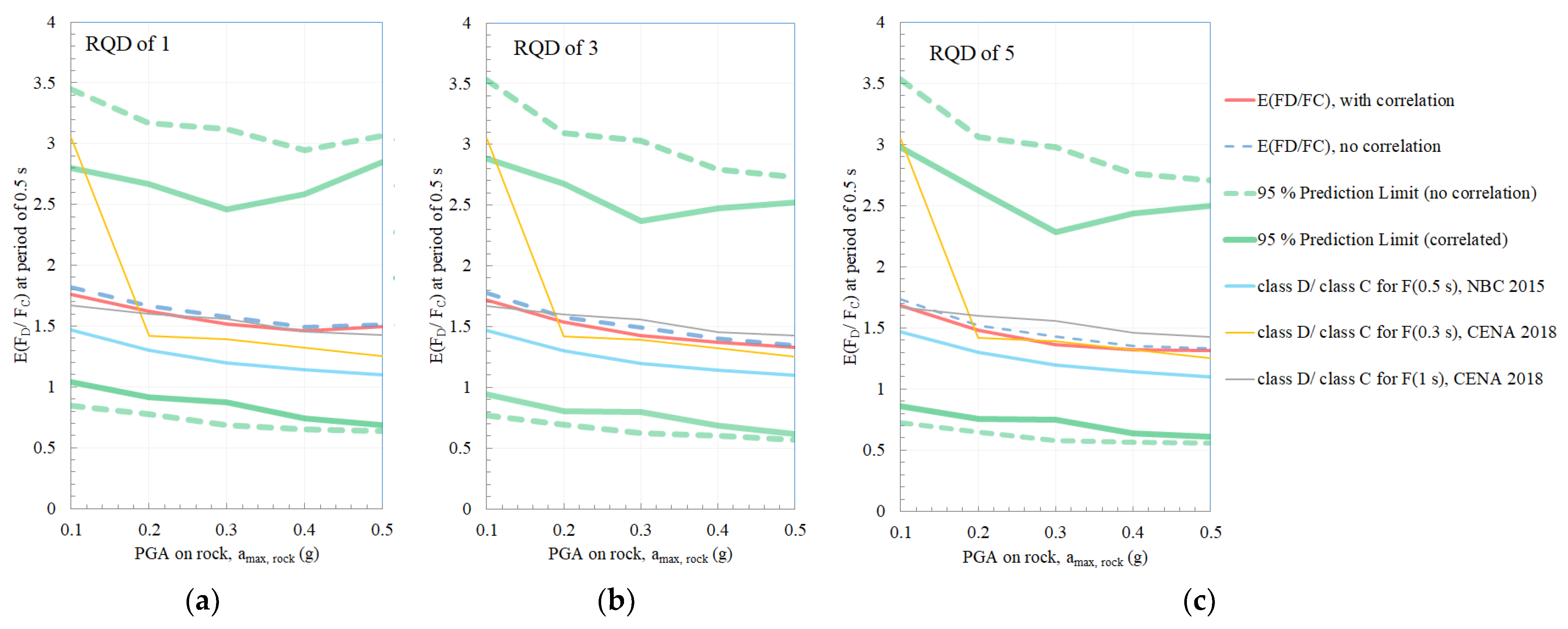
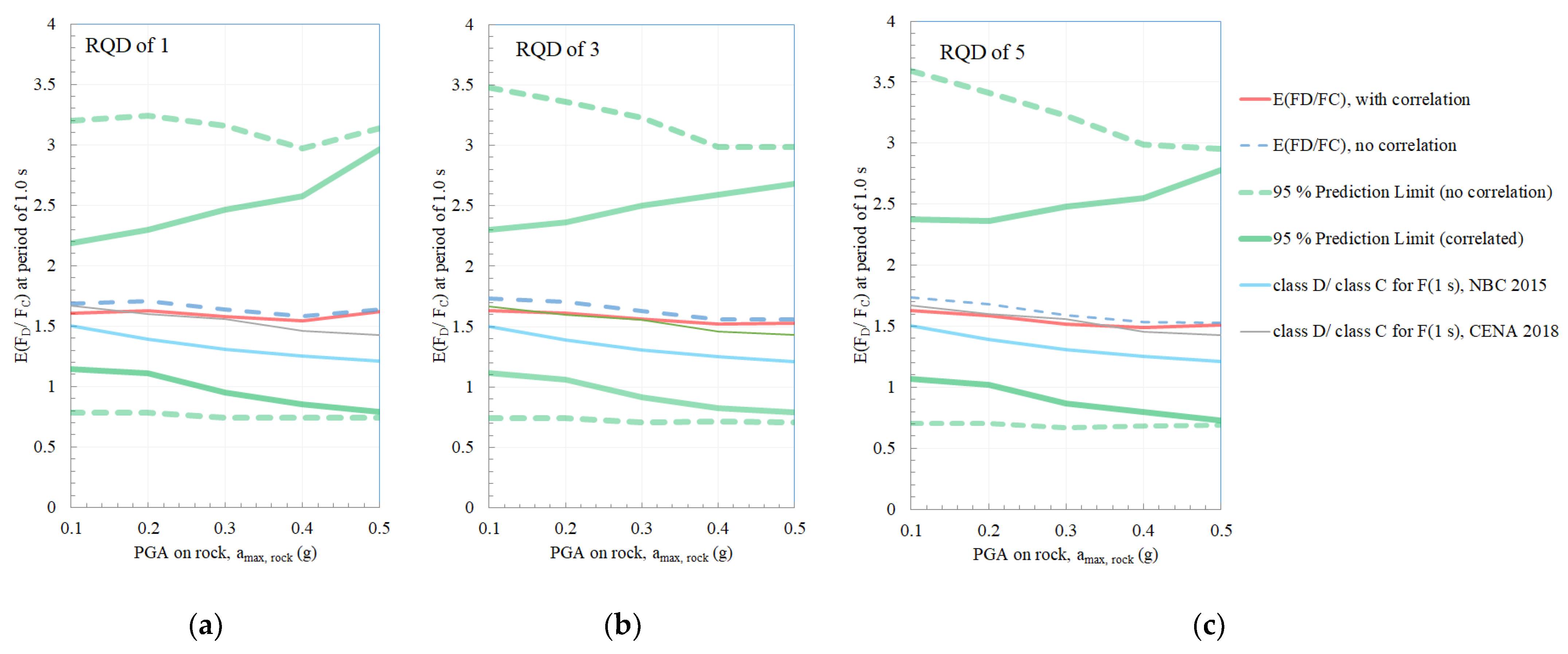
3. Site Amplification Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lamontagne, M. Description and Analysis of the Earthquake Damage in the Quebec City Region between 1608 and 2008. Seism. Res. Lett. 2009, 80, 514–524. [Google Scholar] [CrossRef]
- Mitchell, D.; Tinawi, R.; Law, T. Damage caused by the 25 November 1988, Saguenay earthquake. Can. J. Civ. Eng. 1990, 17, 338–365. [Google Scholar] [CrossRef]
- Chouinard, L.; Rosset, P. On the Use of Single Station Ambient Noise Techniques for Microzonation Purposes: The Case of Montreal. In Shear Wave Velocity Measurement Guidelines for Canadian Seismic Site Characterization in Soil and Rock; Hunter, J.A., Crow, H.L., Eds.; Geological Survey of Canada: Ottawa, ON, Canada, 2012; pp. 85–93. [Google Scholar]
- Rosset, P.; Chouinard, L.E. Characterization of site effects in Montreal, Canada. Nat. Hazards 2008, 48, 295–308. [Google Scholar] [CrossRef]
- Rosset, P.; Bour-Belvaux, M.; Chouinard, L. Estimation and Comparison of Vs30; Microzonation Maps for Montreal Using Multiple Sources of Information. Bull. Earthq. Eng. 2015, 13, 2225–2239. [Google Scholar] [CrossRef]
- Choi, Y.; Stewart, J.P. Nonlinear Site Amplification as Function of 30 m Shear Wave Velocity. Earthq. Spectra 2005, 21, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Ordonez, G.A. SHAKE 2000. A Computer Program for the I-D Analysis of Geotechnical Earthquake Engineering Problems; University of California: Los Angeles, CA, USA, 2000. [Google Scholar]
- Kottke, A.R.; Rathje, E.M. Technical Manual for Strata; PEER: Saint Paul, MN, USA, 2008. [Google Scholar]
- Aaqib, M.; Sadiq, S.; Park, D.; Hashash, Y.M.A.; Pehlivan, M. Importance of Implied Strength Correction for 1D Site Response at Shallow Sites at a Moderate to Low Seismicity Region. In Geotechnical Earthquake Engineering and Soil Dynamics V: Seismic Hazard Analysis, Earthquake Ground Motions, and Regional-Scale Assessment; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 445–453. [Google Scholar] [CrossRef]
- Ciancimino, A.; Fotia, S.; Lanzob, G. Stochastic analysis of seismic ground response for site classification methods verifica-tion. Soil Dynamics and Earthquake Engineering. Soil Dyn. Earthq. Eng. 2018, 111, 169–183. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Harmon, J.; Ilhan, O.; Stewart, J.P.; Rathje, E.M.; Campbell, K.W.; Silva, W.J.; Goulet, C.A. Modelling of Site Amplification via Large Scale Nonlinear Simulations with Applications to North America. In Geotechnical Earthquake Engineering and Soil Dynamics V: Seismic Hazard Analysis, Earthquake Ground Motions, and Regional-Scale Assessment; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 523–537. [Google Scholar] [CrossRef]
- Harmon, J.; Hashash, Y.M.A.; Stewart, J.P.; Rathje, E.M.; Campbell, K.W.; Silva, W.J.; Xu, B.; Musgrove, M.; Ilhan, O. Site Amplification Functions for Central and Eastern North America—Part I: Simulation Data Set Development. Earthq. Spectra 2019, 35, 787–814. [Google Scholar] [CrossRef]
- Sextos, A.; De Risi, R.; Pagliaroli, A.; Foti, S.; Passeri, F.; Ausilio, E.; Cairo, R.; Capatti, M.C.; Chiabrando, F.; Chiaradonna, A.; et al. Local Site Effects and Incremental Damage of Buildings during the 2016 Central Italy Earthquake Sequence. Earthq. Spectra 2018, 34, 1639–1669. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Marek, A.; Bommer, J.J.; Youngs, R.R.; Crespo, M.J.; Stafford, P.J.; Bahrampouri, M. Capturing epistemic uncertainty in site response. Earthq. Spectra 2020, 37, 921–936. [Google Scholar] [CrossRef]
- Falcone, G.; Boldini, D.; Martelli, L.; Amorosi, A. Quantifying local seismic amplification from regional charts and site specific numerical analyses: A case study. Bull. Earthq. Eng. 2019, 18, 77–107. [Google Scholar] [CrossRef]
- Falcone, G.; Acunzo, G.; Mendicelli, A.; Mori, F.; Naso, G.; Peronace, E.; Porchia, A.; Romagnoli, G.; Tarquini, E.; Moscatelli, M. Seismic amplification maps of Italy based on site-specific microzonation dataset and one-dimensional numerical ap-proach. Eng. Geol. 2021, 289, 106170. [Google Scholar] [CrossRef]
- Stambouli, A.B.; Zendagui, D.; Bard, P.-Y.; Derras, B. Deriving amplification factors from simple site parameters using generalized regression neural networks: Implications for relevant site proxies. Earth Planets Space 2017, 69, 99. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.; Pilz, M.; Cotton, F. Which is a better proxy, site period or depth to bedrock, in modelling linear site response in addition to the average shear-wave velocity? Bull. Earthq. Eng. 2019, 18, 797–820. [Google Scholar] [CrossRef]
- Gobbi, S.; Lenti, L.; Santisi d’Avila, M.P.; Semblat, J.-F.; Reiffsteck, P. Influence of the variability of soil profile properties on weak and strong seismic response. Soil Dyn. Earthq. Eng. 2020, 135, 106200. [Google Scholar] [CrossRef]
- Fayjaloun, R.; Negulescu, C.; Roullé, A.; Auclair, S.; Gehl, P.; Faravelli, M. Sensitivity of Earthquake Damage Estimation to the Input Data (Soil Characterization Maps and Building Exposure): Case Study in the Luchon Valley, France. Geosciences 2021, 11, 249. [Google Scholar] [CrossRef]
- Régnier, J.; Bonilla, L.F.; Bard, P.; Bertrand, E.; Hollender, F.; Kawase, H.; Sicilia, D.; Arduino, P.; Amorosi, A.; Asimaki, D.; et al. International Benchmark on Numerical Simulations for 1D, Nonlinear Site Response (PRENOLIN): Verification Phase Based on Canonical Cases. Bull. Seismol. Soc. Am. 2016, 106, 2112–2135. [Google Scholar] [CrossRef]
- Régnier, J.; Bonilla, L.; Bard, P.; Bertrand, E.; Hollender, F.; Kawase, H.; Verrucci, L. PRENOLIN: International Benchmark on 1D Nonlinear Site-Response Analysis—Validation Phase Exercise. Bull. Seismol. Soc. Am. 2018, 108, 876–900. [Google Scholar] [CrossRef]
- Stewart, J.P.; Afshari, K. Epistemic Uncertainty in Site Response as Derived from One-Dimensional Ground Response Analyses. J. Geotech. Geoenviron. Eng. 2020, 147, 04020146. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Soil Moduli and Damping Factors for Dynamic Response Analyses; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1970. [Google Scholar]
- Seed, H.B.; Wong, R.T.; Idriss, I.M.; Tokimatsu, K. Moduli and Damping Factors for Dynamic Analyses of Cohesionless Soils. J. Geotech. Eng. 1986, 112, 1016–1032. [Google Scholar] [CrossRef]
- Sun, J.I.; Golesorkhi, R.; Seed, H.B. Dynamic Moduli and Damping Ratios for Cohesive Soils; Report No UCB/EERC-88/15; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1988. [Google Scholar]
- Cao, Y.L.; Rainer, J.H.; Chidiac, S.E. Études Sismiques au Poste Port-Alfred Region du Saguenay; National Research Council Canada Report to Hydro-Quebec: Ottawa, ON, Canada, 1992; Volume 1, pp. 1–113. [Google Scholar]
- EPRI, E.P.R.I. Guidelines for Determining Design Basis Ground Motions; Report TR-102293; EPRI: Palo Alto, CA, USA, 1993. [Google Scholar]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2001. [Google Scholar]
- Rasmussen, K.K. An Investigation of Monotonic and Cyclic Behavior of Leda Clay. Master’s Thesis, The University of Western Ontario, London, ON, Canada, 2012. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Hoboken, NJ, USA, 1996; ISBN 10 0133749436. [Google Scholar]
- Luzi, L.; Puglia, R.; Russo, E.; Orfeus, W. Engineering Strong Motion Database; Version 1.0; Istituto Nazionale di Geof-isica e Vulcanologia, Observatories & Research Facilities for European Seismology: GA De Bilt, The Netherlands, 2016. [CrossRef]
- Atkinson, G.M. Earthquake time histories compatible with the 2005 National building code of Canada uniform hazard spectrum. Can. J. Civ. Eng. 2009, 36, 991–1000. [Google Scholar] [CrossRef]
- Prest, V.K.; Hode-Keyser, J. Geology and Engineering Characteristics of Surficial Deposits; Montreal Island and Vicinity: Montreal, QC, Canada, 1977. [Google Scholar] [CrossRef]
- Talukder, M.K.; Chouinard, L. Probabilistic methods for the estimation of seismic Fa and Fv maps—Application to Montreal. Bull. Earthq. Eng. 2015, 14, 345–372. [Google Scholar] [CrossRef]
- Silva, W.J.; Abrahamson, N.; Toro, G.; Costantino, C. Description and Validation of the Stochastic Ground Motion Model; Brookhaven National Laboratory, Associated Universities Inc.: Upton, NY, USA, 1996. [Google Scholar]
- Darragh, B.; Silva, W. Development of Amplification Factors (5% Damped Response Spectra) For NEHRP Categories in CENA. In Proceedings of the Conference Call on Seismic Site Amplification in Central and Eastern North America, PEER, Berkeley, CA, USA, 7–10 February 2016. [Google Scholar]
- Boyer, L. Geology of Montreal, Province of Quebec, Canada. Bull. Assoc. Eng. Geol. 1985, 22, 329–394. [Google Scholar] [CrossRef]
- Aboye, S.A.; Andrus, R.D.; Ravichandran, N.; Bhuiyan, A.H.; Harman, N. Seismic Site Factors and Design Response Spectra Based on Conditions in Charleston, South Carolina. Earthq. Spectra 2015, 31, 723–744. [Google Scholar] [CrossRef]
- Kamai, R.; Abrahamson, N.A.; Silva, W.J. Nonlinear Horizontal Site Amplification for Constraining the NGA-West2 GMPEs. Earthq. Spectra 2014, 30, 1223–1240. [Google Scholar] [CrossRef]
- Rathje, E.M.; Kottke, A.R.; Trent, W.L. Influence of Input Motion and Site Property Variabilities on Seismic Site Response Analysis. J. Geotech. Geoenviron. Eng. 2010, 136, 607–619. [Google Scholar] [CrossRef]
- Hashash, Y.; Moon, S. Site Amplification Factors for Deep Deposits and Their Application in Seismic Hazard Analysis for Central U.S.; University of Illinois at Urbana-Champaign: Urbana, IL, USA; Champaign, IL, USA, 2011. [Google Scholar]
- Deere, D.E.; Deere, W.D. The Rock Quality Designation Index in Practice. In Rock Classification Systems for Engineering Purposes; ASTM STP 984; American Society for Testing and Materials: West Conshohocken, PA, USA, 1988; pp. 91–101. [Google Scholar]
- Falcone, G.; Romagnoli, G.; Naso, G.; Mori, F.; Peronace, E.; Moscatelli, M. Effect of bedrock stiffness and thickness on numerical simulation of seismic site response. Italian case studies. Soil Dyn. Earthq. Eng. 2020, 139, 106361. [Google Scholar] [CrossRef]
- Rosenblueth, E. Point estimates for probability moment. Proc. Natl. Acad. Sci. USA 1975, 72, 3812–3814. [Google Scholar] [CrossRef] [Green Version]
- Rosenblueth, E. Two-point estimates in probabilities. Appl. Math. Model. 1981, 5, 329–335. [Google Scholar] [CrossRef]
- Talukder, M.K. Seismic Site Effects for the Island of Montreal. Ph.D. Thesis, McGill University, Montréal, QC, Canada, 2018. [Google Scholar]
- Chouinard, L.; Rosset, P. Seismic site effects and seismic risk in the Montreal urban area. The influence of marine clays. In Proceedings of the Ninth Canadian Conference on Earthquake Engineering, Ottawa, ON, Canada, 26–29 June 2007; pp. 26–29. [Google Scholar]
- Tempa, K.; Sarkar, R.; Dikshit, A.; Pradhan, B.; Simonelli, A.; Acharya, S.; Alamri, A. Parametric Study of Local Site Response for Bedrock Ground Motion to Earthquake in Phuentsholing, Bhutan. Sustainability 2020, 12, 5273. [Google Scholar] [CrossRef]
- Sun, C.-G.; Kim, H.-S.; Cho, H.-I. Geo-Proxy-Based Site Classification for Regional Zonation of Seismic Site Effects in South Korea. Appl. Sci. 2018, 8, 314. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.-S.; Sun, C.-G.; Cho, H.-I. Geospatial Assessment of the Post-Earthquake Hazard of the 2017 Pohang Earthquake Considering Seismic Site Effects. ISPRS Int. J. Geo-Inf. 2018, 7, 375. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.-S.; Sun, C.-G.; Kim, M.; Cho, H.-I.; Lee, M.-G. GIS-Based Optimum Geospatial Characterization for Seismic Site Effect Assessment in an Inland Urban Area, South Korea. Appl. Sci. 2020, 10, 7443. [Google Scholar] [CrossRef]
- Chieffo, N.; Formisano, A. Induced Seismic-Site Effects on the Vulnerability Assessment of a Historical Centre in the Molise Region of Italy: Analysis Method and Real Behaviour Calibration Based on 2002 Earthquake. Geosciences 2020, 10, 21. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.S.; Yoon, J.K. Development of new site classification system for the regions of shallow bedrock in Korea. J. Earthq. Eng. 2006, 10, 331–358. [Google Scholar] [CrossRef]
- Akkar, S.; Sandıkkaya, M.A.; Bommer, J.J. Empirical ground-motion models for point- and extended-source crustal earth-quake scenarios in Europe and the Middle East. Bull. Earthq. Eng. 2014, 12, 359–387. [Google Scholar] [CrossRef] [Green Version]
- Bindi, D.; Massa, M.; Luzi, L.; Ameri, G.; Pacor, F.; Puglia, R.; Augliera, P. Pan-European ground-motion prediction equa-tions for the average horizontal component of PGA, PGV, and 5%-damped PSA at spectral periods up to 3.0 s using the RESORCE dataset. Bull. Earthq. Eng. 2014, 12, 391–430. [Google Scholar] [CrossRef] [Green Version]
- Kotha, S.; Weatherill, G.; Bindi, D.; Cotton, F. A Regionally-Adaptable Ground-Motion Model for Shallow Crustal Earth-quakes in Europe. Bull. Earthq. Eng. 2020, 18, 4091–4125. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Harmon, J.A.; Ilhan, O. Recommendation for Ergodic Nonlinear Site Amplification in Central and Eastern North America; PEER Report No. 2017/05; University of California: Berkeley, CA, USA, 2017. [Google Scholar]
- Stewart, J.P.; Parker, G.A.; Harmon, J.A.; Atkinson, G.M.; Boore, D.M.; Darragh, R.B.; Silva, W.J.; Hashash, Y.M.A. Expert Panel Recommendations for Ergodic Site Amplification in Central and Eastern North America; PEER Report No. 2017/04; University of California: Berkeley, CA, USA, 2017. [Google Scholar]





| Input Motion | Year | Earthquake Mechanism | Site Class | PGA (g) | Moment Magnitude | Epicentral Distance (km) |
|---|---|---|---|---|---|---|
| Irpinia, Italy | 1980 | Normal Faulting | B | 0.080 | 6.9 | 28 |
| Morgan Hil, Gilroy | 1984 | Strike-slip | A | 0.100 | 6.19 | 15 |
| Saguenay (Chicoutimi) | 1988 | Strike-slip | A | 0.130 | 5.7 | 30 |
| Saguenay (St-Andrea) | 1988 | Strike-slip | A | 0.160 | 5.7 | 70 |
| Saguenay (La Malbaie) | 1988 | Strike-slip | A | 0.170 | 5.7 | 95 |
| Southern Iran | 1990 | Strike-slip | B | 0.160 | 6.2 | 18 |
| Greece | 1990 | Normal Faulting | B | 0.120 | 5.9 | 19 |
| Western Iran | 1990 | Strike-slip | B | 0.130 | 7.4 | 85 |
| Basilicata, Italy | 1998 | Normal Faulting | B | 0.160 | 5.6 | 18 |
| Kocaeli, Turkey | 1999 | Strike-slip | B | 0.26 | 7.51 | 11 |
| Tottori, Japan | 2000 | Strike-slip | B | 0.130 | 6.61 | 15 |
| Presbytere, Martinique | 2007 | Normal Faulting | B | 0.160 | 7.4 | 69 |
| Guadeloupe | 2007 | Normal Faulting | B | 0.080 | 7.4 | 144 |
| Goudeloupe, France | 2007 | Strike-slip | B | 0.110 | 7.4 | 167 |
| Lipari, Italy | 2010 | Strike-slip | B | 0.32 | 4.7 | 12 |
| Synthetic-44 | N/A | Strike-slip | A | 0.133 | 7 | 99 |
| Synthetic-27 * | N/A | Strike-slip | A | 0.120 | 7 | 70 |
| Synthetic-9 * | N/A | Strike-slip | A | 0.280 | 7 | 45 |
| Synthetic-14 * | N/A | Strike-slip | A | 0.210 | 7 | 51 |
| Synthetic-19 * | N/A | Strike-slip | A | 0.330 | 6 | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talukder, M.K.; Rosset, P.; Chouinard, L. Reduction of Bias and Uncertainty in Regional Seismic Site Amplification Factors for Seismic Hazard and Risk Analysis. GeoHazards 2021, 2, 277-301. https://doi.org/10.3390/geohazards2030015
Talukder MK, Rosset P, Chouinard L. Reduction of Bias and Uncertainty in Regional Seismic Site Amplification Factors for Seismic Hazard and Risk Analysis. GeoHazards. 2021; 2(3):277-301. https://doi.org/10.3390/geohazards2030015
Chicago/Turabian StyleTalukder, Mohammad Kamruzzaman, Philippe Rosset, and Luc Chouinard. 2021. "Reduction of Bias and Uncertainty in Regional Seismic Site Amplification Factors for Seismic Hazard and Risk Analysis" GeoHazards 2, no. 3: 277-301. https://doi.org/10.3390/geohazards2030015
APA StyleTalukder, M. K., Rosset, P., & Chouinard, L. (2021). Reduction of Bias and Uncertainty in Regional Seismic Site Amplification Factors for Seismic Hazard and Risk Analysis. GeoHazards, 2(3), 277-301. https://doi.org/10.3390/geohazards2030015







