Analysis of Faster-Than-Real-Time (FTRT) Tsunami Simulations for the Spanish Tsunami Warning System for the Atlantic
by
, , , ,
Beatriz Gaite
1,*
,
Jorge Macías
2
,
Juan Vicente Cantavella
1,
Carlos Sánchez-Linares
2,
Carlos González
1 and
Luis Carlos Puertas
1 1
National Geographic Institute of Spain (IGN), E-28003 Madrid, Spain
2
Departamento de Análisis Matemático, Estadística e Investigación Operativa y Matemática Aplicada, Facultad de Ciencias, Universidad de Málaga, Campus de Teatinos, 29010 Málaga, Spain
*
Author to whom correspondence should be addressed.
GeoHazards 2022, 3(3), 371-394; https://doi.org/10.3390/geohazards3030019
Submission received: 1 March 2022
/
Revised: 1 June 2022
/
Accepted: 27 June 2022
/
Published: 1 July 2022
(This article belongs to the Special Issue Modelling and Numerical Simulation of Tsunami)
Abstract
:Real-time local tsunami warnings embody uncertainty from unknowns in the source definition within the first minutes after the tsunami generates. In general, Tsunami Warning Systems (TWS) provide a quick estimate for tsunami action from deterministic simulations of a single event. In this study, variability in tsunami source parameters has been included by running 135 tsunami simulations; besides this, four different computational domains in the northeastern Atlantic ocean have been considered, resulting in 540 simulations associated with a single event. This was done for tsunamis generated by earthquakes in the Gulf of Cadiz with impact in the western Iberian peninsula and the Canary Islands. A first answer is provided after one minute, and 7 min are required to perform all the simulations in the four computational domains. The fast computation allows alert levels all along the coast to be incorporated into the Spanish National Tsunami Early Warning System. The main findings are that the use of a set of scenarios that account for the uncertainty in source parameters can produce higher tsunami warnings in certain coastal areas than those obtained from a single deterministic reference scenario. Therefore, this work shows that considering uncertainties in tsunami source parameters helps to avoid possible tsunami warning level underestimations. Furthermore, this study demonstrates that this is possible to do in real time in an actual TWS with the use of high-performance computing resources.
1. Introduction
Currently, several Tsunami Warning Systems (TWS) warn coastal areas of tsunamis in different regions (e.g., JMA in Japan, PTWS in the Pacific ocean, CARIBE-EWS in the Caribbean, NEAMTWS in the northeastern Atlantic and Mediterranean and connected seas). They forecast the impact of tsunamis to warn the population before the tsunami arrives. Great efforts and progress are being made in TWS to avoid unnecessary evacuations [1] and to improve tsunami warning level estimations [2]. Tsunami warning requires in-depth knowledge of the phenomenon, covering generation, propagation, and coastal impact. However, there are several unknowns and uncertainties mainly related to the source of tsunamis. This lack of knowledge is greater in regions with slow tectonic activity, where the occurrence of tsunamis is infrequent. This is the case of the northeastern Atlantic ocean. Despite this, the occurrence of a few tens of tsunamis is well known [3,4,5]. Ninety percent were caused by earthquakes, and some of them caused damage. The most catastrophic tsunami occurred in 1755, generated by a magnitude 8.5 [6,7,8] earthquake offshore southwest of the Iberian peninsula (a recent study points to a magnitude between 7.2 and 8.2 [9]), generating more than 1000 fatalities in Spain alone and having effects on far coasts within the basin [10,11].
Within the first minutes after the tsunami warning system is triggered, there is a lack of source parameter information. Uncertainties on tsunami source parameters might lead to varying tsunami maximum height and spatial patterns [12]. There are several approaches to overcome this lack of information that widely used in TWS in order to emit a tsunami early warning (e.g., Decision Matrices (DM) [13], precomputed tsunami propagation synthetics [12,14]). Several advances in fast source estimation [15,16,17,18], deep-sea data, innovative sensors, and methods to detect the tsunami and unveil its source [19,20,21] contribute to improving the accuracy and reducing the time to emit the tsunami warning. However, to account for the uncertainties of the tsunami warning, recent research efforts are in the direction of probabilistic tsunami forecasting (PTF) early warning [22], relying on high-performance computing. This scheme surpasses the deterministic approach and deals with uncertainties to be able to link the alert levels to the desired level of conservatism. The approach presented in this study is similar to PTF, as it considers source uncertainties and is able to decide the level of conservatism. However, input scenarios are limited to the range of estimated uncertainty of each source parameter based on geologic information of the region in order to be able to compute faster-than-real-time local tsunami warning forecasts, making use of high-performance supercomputing resources.
In the Spanish Tsunami Warning System (TWS), a tsunami propagation simulation of one scenario requires about 1 min of computation running in two Tesla V100 GPUs (Graphics Processing Units). This is a reasonable computing time that allows the use of numerical simulations to generate tsunami alert messages to warn the coastal population. In these messages, alert levels based on estimated tsunami wave heights are used. However, there are several unknowns that can influence the estimated tsunami warning level. In this study, the results from a live demo carried out in the framework of the ChEESE project (Centre of Excellence for Exascale in Solid Earth, on 22 November 2021 [23,24] are analyzed. In this live demo, 135 scenarios in four different computational domains at three different numerical resolutions using 270 NVIDIA V100 GPUs from CINECA (the Italian Supercomputing Center) were simulated. The aim of the live exercise was to obtain tsunami alert levels in real time, but also to include uncertainties in input parameters.
2. Materials and Methods
2.1. Tectonic Context
The live demo simulations were framed in the Southwest Iberian Margin (SWIM) in the outer part of the Gulf of Cadiz, at the eastern edge of the Atlantic ocean, close to the boundary of the Eurasia and Africa plates. Tsunamis that have affected the Spanish coast are mainly generated by earthquakes along the Eurasia-Africa plate border [4,25]. The most catastrophic one happened in the Atlantic ocean, southwest of the Iberian peninsula, in 1755. It devastated main coastal cities such as Lisbon and Cadiz with maximum heights larger than 10 m, and it caused more than 1000 fatalities in Spain alone [6,7,8,9]. There is still controversy about its source location and cause, despite numerous research studies [26,27]. Only a few other tsunamis originating in the Atlantic region have affected surrounding coasts, although with much less severity than the oceanic-basin impact of the tsunami of 1755. The IGN catalogue of tsunamis that have affected the Spanish coasts comprises three other tsunamis in the SWIM that occurred in 1761, 1969, and 1975 (Figure 1). The origin of these tsunamis is attributed to earthquakes of magnitudes 8.5 [28], 7.8 [29,30], and 7.8, respectively [25].
Seismicity distribution [31] in this region suggests that the Eurasia-Africa plate boundary is reflected in a fault system distributed in an east-west 100–150 km wide band. The slow northwest-southeast direction convergence (3.8–5.6 mm/y) [32] of this diffuse margin [33] is carried out by a series of thrust and strike-slip faults [34]. Seismicity reaching in some cases 50–60 km reveals fragile behavior up to the upper mantle without a clear subduction zone, implying an old and cold oceanic lithosphere.
![Geohazards 03 00019 g001]()
Figure 1.
Seismicity of the Southwest Iberian Margin and the Gulf of Cadiz. Historical and instrumental earthquakes (circles) [31]. Tsunami sources in the catalogue of the Spanish TWS [25] are labelled indicating their year of occurrence. Blue stars indicate the reference scenario locations of the synthetics computed in this study (Table A1). Faults used in the Spanish TWS database are denoted as blue lines [35]. HF indicates the Horseshoe trace fault location. Bathymetry comes from EMODNET and topography from the Digital Terrain Model 200 [36] and SRTM [37].
Figure 1.
Seismicity of the Southwest Iberian Margin and the Gulf of Cadiz. Historical and instrumental earthquakes (circles) [31]. Tsunami sources in the catalogue of the Spanish TWS [25] are labelled indicating their year of occurrence. Blue stars indicate the reference scenario locations of the synthetics computed in this study (Table A1). Faults used in the Spanish TWS database are denoted as blue lines [35]. HF indicates the Horseshoe trace fault location. Bathymetry comes from EMODNET and topography from the Digital Terrain Model 200 [36] and SRTM [37].
Recent seismic studies are revealing the evolution and the structure of the main offshore tectonic structures in this area and their implications for seismic and tsunami hazards [28,34]. This results in fundamental information to update and diminish the uncertainties in potential tsunamigenic sources that play an important role in tsunami warning forecasts.
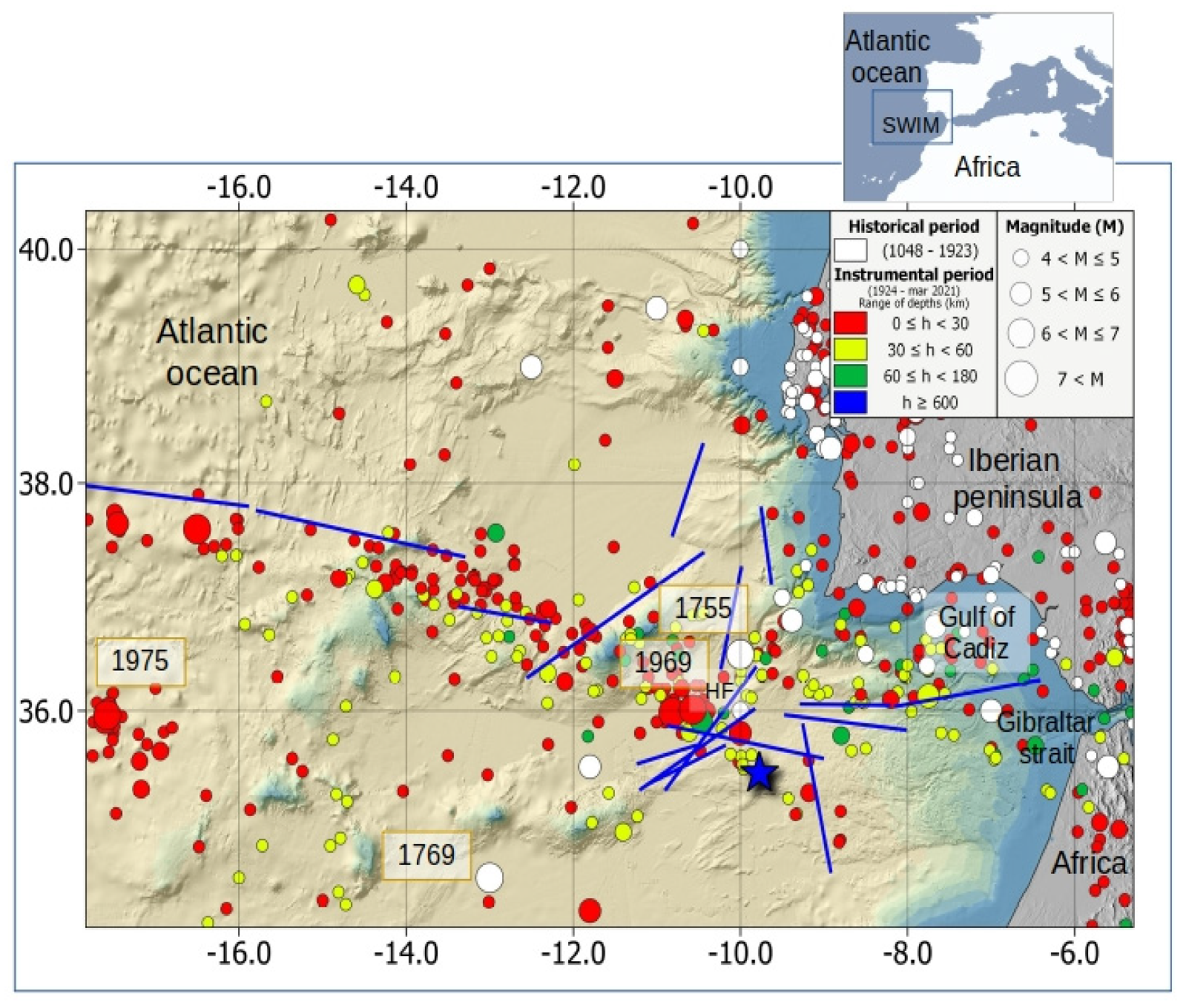
2.2. Tsunami Warning System of Spain
The Spanish TWS has been in operation since 2015 at the National Geographic Institute (IGN). IGN disseminates tsunami alert messages of tsunamis that may affect Spanish coasts to the Spanish Civil Protection [25]. The tsunami warning is issued within the first five minutes after the origin time of an earthquake that activates the TWS; this triggering is based on its magnitude and hypocentral coordinates. The tsunami alert level is based on decision matrices adapted from those proposed by the UNESCO Intergovernmental Oceanographic Commission (IOC)—Intergovernmental Coordination Group (ICG) for the Tsunami Early Warning and Mitigation System in the North-Eastern Atlantic, the Mediterranean and Connected Seas (NEAMTWS) [38,39,40,41]; precomputed scenarios [42,43,44], real-time simulations, and real-time sea level measures from tide-gauges at coastal locations. The IGN receives continuous real-time sea level data from different national and international institutions, namely, Spanish Ports of the State, Balearic Islands Observing and Forecasting System (SOCIB), Joint Research Centre (JRC), CENtre d’ALerte aux Tsunamis (CENALT), Instituto Português do Mar e da Atmosfera (IPMA), and IGN itself.
Decision matrices are based on earthquake magnitude and hypocentral location, and are generally a conservative estimation of expected tsunami warning levels [13,22,40,41]. Besides, they do not consider source parameters that can influence the tsunami’s coastal impact. The use of precomputed scenarios aims to overcome the limits established by decision matrices regarding the role of tsunami source parameter information in actual tsunami impact. Despite this, this methodology still has some limitations, such as the unavoidable discretization of the possible source parameters and the need to be updated to new fault information or changes in forecast points. Real-time tsunami computations can be better adjusted to actual tsunami source parameters insofar as there is some knowledge about them within the first minutes after the earthquake. This allows computing in real-time (in very few minutes) and the dissemination of the alert to coastal populations in a very short time. Actual real-time observations may be thought to be the best method of producing accurate tsunami impact estimates, as they measure the real event. However, the measuring instruments for tsunamis in this region are mainly located close to the coast, in harbors. This means that there is not enough time to warn the populations of these areas before the tsunami hits the coast. Summarizing, there is not a best way to forecast the tsunami warning level, and TWSs are usually based on a combination of the methods described here [38,41,45], which is the case for the Spanish TWS.
The alert levels used in the Spanish TWS are the same as those proposed by NEAMTWS [38]. They are divided into three levels based on the estimated maximum height of the tsunami wave at coastal areas or the equivalent run-up (Table 1). The tsunami alert level is determined for each predefined coastal segment and is taken as the maximum alert level estimated in the forecast points (FCP) of each segment. Figure 2 shows the distribution of alert coastal zones for a tsunami that might affect the Spanish coasts.
Real-time tsunami propagation synthetics in the TWS of Spain are computed using the Tsunami-HySEA model [46,47,48] using GPU parallel computing with two nodes and two NVidia V100 GPUs. The bathymetric domain and simulated time depends on the earthquake location in the Atlantic ocean or in the Mediterranean sea regarding its distance from the Spanish coasts. Therefore, the number of volumes and time of computation depends also on the earthquake location, ranging from less than one minute for a tsunami source in the western Mediterranean to 14 min when its origin is in the Caribbean. For a tsunami originating from an earthquake located in the eastern Atlantic, the time to simulate 8 h of tsunami propagation is less than 3 min (Table 2), a time short enough to create a useful tsunami alert message and to disseminate it to Civil Protection. The lack of information about the tsunami source parameters is overcome by selecting the fault parameters from those of the closest mapped fault area from the IGN fault database [35]. This database is a compilation of mapped faults from literature [42,43,49] and publicly available fault databases [50]. Each fault in the database is associated with a magnitude-scale relationship according to the region and its fault mechanism, allowing an estimation of the rupture area based on the magnitude of the earthquake [35]. Despite efforts to obtain the most accurate source parameters, there is a wide range of uncertainties in the estimation of location, magnitude, dip, strike, and rupture source direction. However, source parameter variability cannot be considered in tsunami real time synthetics because computing time would too long to be useful in real-time local tsunami warnings.
2.3. Design of the Scenarios for PD2 ChEESE Live Demo
The live demo was designed to verify whether considering uncertainties in tsunami source parameters can be useful for generating local tsunami warnings in two aspects. The first aspect is in terms of obtaining useful additional information compared to a deterministic approach. The second is in terms of computing time, which must be short enough to warn coastal populations before the tsunami arrives. In this approach, uncertainty in the seismic tsunami source is addressed using a set of equally probable scenarios, taking into account the unknowns and uncertainties of earthquake source parameters within the first few minutes after earthquake origin time. The reference scenario is a magnitude Mw 7.8 located in the vicinity of the Gulf of Cadiz (Appendix A Table A1) with coordinates −9.772°, 35.442°. Then, following the automatic process implemented in the Spanish TWS [35], the estimated source parameters are strike 39°, dip 35°, rake 90°, and slip 2.76 m, and the rupture size is 61 km length and 51 km width.
Then, 135 modified sources are automatically generated from the reference scenario to consider uncertainties in magnitude, strike, dip, and rupture direction source parameters (Table A1). The range of parameter variation was selected from typical uncertainties in earthquake magnitude (±0.2). Strike and dip errors were chosen greater than common values for the Atlantic Quaternary active faults compilation in the QAFI v.3 database [50], as ±15° and ±20°, respectively. Uncertainties related to the direction of the rupture propagation were also considered. With a single scenario, it is usually assumed that the hypocenter is located in the center of the rupture area. In this live demo, four additional situations in which the hypocenter was close to each of the rectangular rupture area corners were also considered. This is equivalent to considering that the hypocenter has an uncertainty of half the length and width of the rupture area, which is greater than the actual hypocentral location uncertainty. That is, the center of the rupture can be located at each corner of the rupture area of the reference scenario (Figure 3). The assumed error in the direction of the rupture depends on the estimated rupture size and, therefore, on the magnitude of the earthquake, ranging in this case from 30 to 42 km. Then, from the reference scenario, which is assumed to have its hypocenter in the center of the rupture area, four scenarios are generated by changing the location of the hypocenter to half the width and half the length of the rupture within the fault-associated plane. Performing this along and perpendicularly to the strike in both directions, four scenarios are obtained from the initial one at the edges of the reference-scenario rupture area (Figure 3). The coordinates of the hypocenters for these scenarios are computed automatically and this step is performed for the three magnitudes considered. The average distance of the generated hypocenters to the reference scenario hypocenter is about 37 km, greater than location uncertainty, which in this area and with an automatic solution obtained a few minutes after the origin time could be around 10 km. The distances considered in this study to take into account the uncertainty on slip distribution are in the range of the difference between hypocentral location and maximum slip from finite rupture source models for great earthquakes [51].
Besides considering 135 scenarios for addressing the uncertainty in the source, these 135 scenarios are also simulated at four different computational domains using three different numerical resolutions (Table 2). The objective is to check eventual alert level variations when increasing the bathymetry and numerical resolution. All the simulations, in the global or reduced domains with coarser or finer resolutions, must mandatorily be performed in only a few minutes. Bathymetry of the four domains comes from EMODNET data that has been merged, degraded to the desired resolution, and converted to the GRD format using GDAL library [52], GMT [53], QGIS [54], and R [55].
The computations of the 540 simulations have been performed using Tsunami-HySEA code [46,47,48] on GPUs using 68 nodes/272 NVIDIA V100 GPUs from a Marconi100 machine at CINECA supercomputing center (Table 2). These 540 simulations were done during a live demo that took place on 22 November 2021 [23,24]. During the live demo, first, IGN sent the list containing the 135 scenarios to be simulated to the University of Malaga (UMA); then, UMA launched the simulations in the Marconi100 machine using predefined scripts and the IGN list of scenarios in the four computational domains. This second step was completely automatized. The results of the 540 simulations were computed in seven minutes and a first estimate of the hazard in the closer coastal areas of Huelva and Cádiz was provided in one minute.
Then, sea surface time series were extracted from the numerical simulation at 293 FCP along western Atlantic coast and located as close to isobath 50 m as possible (Figure 3). FCPs along the Spanish coast contribute to estimating tsunami alert levels by the Spanish NTWC (National Tsunami Warning Centre). The alert level is computed from the largest synthetic maximum height at FCPs belonging to the same warning region. The synthetic maximum height at 1 m isobath is computed from offshore to the coast by multiplying by the Green coefficient [56], c:
where h is the water column depth in meters at the location where the tsunami height has been computed, in this case, 50 m. h0 is the water column depth where the tsunami height is going to be estimated, in this case, 1 m. Green’s law provides a fast approximation of the wave height as close as possible to the coast.
c = (h/h0)1/4
In this study, the alert level at each FCP is generated considering first the maximum water height computed at each FCPs for each simulation, and then the 90th percentile of these values through the 135 computed scenarios. Afterwards, an alert level for each coastal segment defined in the Spanish NTWC (Table 1) is computed from the maximum of the FCP alert levels belonging to that segment (Figure 2).
3. Results and Discussion
The reference scenario was a magnitude Mw 7.8 earthquake with an epicenter located at 9.772° W, 35.442° N, and 50 km depth. Its fault parameters were selected from the closest mapped fault from the IGN fault database. In this particular case, the strike is 39° and the dip is 35°. Fault rupture size is computed from earthquake magnitude and the relationship for reverse faults in the Gulf of Cadiz from [43]. The list of scenarios simulated is provided in Table A1.
The simulation of the 135 scenarios computed in four different computational domains in three numerical resolutions, that is, 540 simulations of 4 h tsunami propagation, were performed in 7 min using 270 Tesla V100 GPUs at CINECA. For most of the cases foreseen in the Atlantic that may affect the Spanish coasts, this time is short enough to be able to adopt preventive measures against the impact of the tsunami. In any case, a first estimate is provided within one minute.
3.1. Maximum Height and Arrival Time Variability
Results from the ATL domain reached 2.5 m for the maximum height and 240 min for the arrival time when all FCPs and scenarios were considered (Figure 4). The standard deviation ranged from 0 to 0.5 m for the maximum height and from 0 to 100 min for the arrival time. The geographic distribution of FCPs with more variability differed from tsunami maximum height and arrival time results (Figure 4e,f). FCPs that show larger variability in maximum height were located along the closest coastal segments to the tsunami source, at the southwest of the Iberian peninsula, west of Africa, and north of the Canary Islands. On the contrary, FCPs with larger arrival time standard deviation are located far away from the sources, at the northern Atlantic coast, the Mediterranean, and the southern Canary Islands coasts. This is probably because the tsunami effect is low at these locations and its arrival time estimation is more difficult to precisely define.
3.2. Source Parameter Uncertainty Contribution
To compare the sensitivity to each source parameter, the largest differences at each FCP for scenarios with all but one of the source parameters considered fixed are computed. In this way, 162 cases of scenario subsets with varying location, magnitude, strike, or dip, and the rest of parameters remaining fixed, are considered. Therefore, 45 subsets of scenarios or cases of either the magnitude, dip, or strike parameter free (Table A2, Table A3 and Table A4) are obtained, and 27 subsets of scenarios with the rupture location parameter free are obtained (Table A5).
The largest difference in maximum height and arrival time at each FCP for each case where only one parameter (strike, dip, magnitude, or location) varies at a time are computed. The maximum difference in each FCP is normalized by dividing by the reference scenario value at this FCP i:
where diffij denotes the normalized greatest difference of value v at FCP i and case j, with j being one of the 162 possible cases. max(vij) is the largest value and min(vij) is the lowest value at FCP i and case j. vi0 is the value of the reference scenario at FCP I and v refers to the maximum height or arrival time.
diffij = (max(vij) − min(vij))/vi0
The mean of the normalized largest maximum height and arrival time differences for all FCPs and cases varying one of the four source parameters shows that the greatest differences are obtained by varying the magnitude (Table 3).
This result is observed in the examples presented in Figure 5 and Figure 6 depicting maximum height differences in each FCP for four cases as close as possible to the scenario of reference. Values behave depending on the parameter that is kept free. Mean differences from every FCP for cases varying the strike are lower (~0.03–0.4 m) than for cases varying the dip (~0.1–0.8 m). The mean largest differences of hmax varying the dip and strike are far lower than when varying location (~0.2–1.1 m) or magnitude (~0.7–1.5 m); with this latter parameter, the largest differences are obtained. Maximum differences for each case show the same behavior as the mean differences with each parameter (Figure 5). When varying location, the mean and largest differences duplicate their value when increasing the magnitude. For example, the mean hmax differences are 0.8, 1.5, and 3 m for magnitude values M0 − 0.2, M0, and M0 + 0.2, respectively. Maximum differences ~1 m of mean difference are obtained with M0 + 0.2 (mU case) and dip dip0 + 20° (dU case). When varying the magnitude, the highest differences are obtained with mean values greater than 0.6 m in all cases. These height differences depend on the dip and location values. Differences increase when the dip changes from 35° to 55°, increasing the mean difference by 0.1 m. Regarding the location, the highest mean differences (>1.1 m) are obtained in CC, W, and N locations (i.e., for radial rupture propagation or towards the surface) for any strike and dip. This result, is probably influenced by the hypocenter depth because, at CC, W, and N locations, the hypocenter is shallower, at depths of 50 km, 34 km, and 34 km, respectively, than at the E and S locations. where the hypocenter is located at a depth of 66 km.
Varying the magnitude seems to affect all FCPs similarly up to a certain distance, as expected (Figure 5c and Figure 6c). However, varying the location affects some FCPs more than others (Figure 5d and Figure 6d). Surprisingly, there are some FCPs distant from the source that are affected similarly to the FCPs in the vicinity, probably because of their relative position to the coast and/or the coastal orientation relative to the tsunami source location.
3.3. Alert Levels Variation
The tsunami alert levels obtained from the set of 135 scenarios are higher than when only the reference scenario is considered, and are lower than when using the decision matrix, in most areas (Figure 7). The difference depends on the statistical parameter selected when computing the alert levels. For example, alert levels from the mean maximum amplitude from all scenarios are quite similar to the levels obtained with the reference model, with the exception of one alert zone. However, computing alert levels from the 90th percentile or the maximum of maximum amplitudes from all scenarios clearly increases the alert levels in several coastal areas from INFORMATION to ADVISORY and from ADVISORY to WATCH. The zones that experience most changes are the northwest coast of the Iberian peninsula, the Canary Islands, and even the westernmost zone of the Mediterranean coast of the Iberian peninsula (Figure 7). These results confirm that DM tsunami warnings are conservative in favor of reducing incorrect warnings, which has already been discussed in previous studies [13,22,40,41]. It is also shown that considering the maximum height from all the scenarios has similar effects, but does not generate the same tsunami warning level distribution as the DM. In this case, the tsunami warning levels might vary because the bathymetry and coastal geometry are considered when computing the tsunami propagation synthetics, while these are not taken into account when using DM. Similar results are obtained when computing the alert levels with the reference model and the mean maximum height from the set of scenarios. This similarity is not surprising because the reference model is an average of the parameters of the scenarios considered. Then, the 90th percentile of the tsunami maximum height obtains higher tsunami warning levels in specific regions. This result shows that computing a set of scenarios and obtaining the tsunami alert level from the 90th percentile of the maximum height from all the scenarios might increase the alert level computed from a single scenario. Furthermore, the approach of this study allows decision-makers to choose the level of desired conservatism and to have an estimation of the uncertainties in the tsunami alert level forecast, similar to PTF results from [22]. However, one of the handicaps of the presented method is that it relies on previous tectonic knowledge about fault parameters in the region. In the case that the tsunami source occurs in an area where there is a lack of fault parameter information, the tsunami forecast using this methodology would be uncertain. Other improvements can made to obtain more accurate tsunami alert forecasts, beyond completing and updating the fault database with new research. One possible improvement is to consider a more complex amplification factor to increase the accuracy on maximum height estimations close to the coast, instead of using Green’s law. Another is to reproduce this study with tsunami source parameters of past tsunamis to compare the different levels obtained from tsunami warnings with tsunami height measures.
3.4. Role of the Computational Domain Resolution
Although the demo had restricted dedicated access to 270 GPUs, for the sake of efficiency and to reduce the overall computing time, the approach was not to compute in multi-GPU mode. Instead, every single simulation was performed with a single GPU. Then, depending on the size of the numerical problem to be solved (in Table 2), which, in its turn, depends on the extension of the computational domain and the mesh resolution, the time-to-solution varied from 1 min to 7 min. More precisely, in the present case, for the mesh ATL at ½ arcmin and composed by 4,536,000 volumes, the computing time for the 4 h simulation was 1 min; for the GCN and GCIC domains at ¼ arcmin resolution and 7,948,800 and 8,553,600 volumes, respectively, it was 3 min; and for the GC domain at ⅛ arcmin resolution and 9,331,200 volumes, it was 7 min. See Figure 2c for the spatial extent of the meshes.
Maximum heights obtained at different resolutions differ at some FCPs, and the differences are about 10−1 m (Figure S1). However, these differences are large enough to increase the tsunami alert level in some coastal regions (Figure 8). The alert level is computed for specific warning segments along the Spanish coast based on the largest maximum height of the FCPs belonging to each segment. In this study, the maximum height at each FCPs was computed as the 90th percentile of the maximum height from the 135 scenarios. Tsunami warning level results (Figure 8) show few changes in alert levels when increasing the resolution of the computational domain. They change only in two warning segments close to the strait that separates the Iberian peninsula and Africa (Figure 2), in the westernmost part of the Mediterranean. One segment changes level from INFORMATION to ADVISORY, while another segment changes level from ADVISORY to INFORMATION when domain resolution is refined from ½ arcmin to ¼ arcmin, and both segments stay at ADVISORY when the resolution domain is refined to ⅛ arcmin. These small variations in the maximum height and, therefore, in the tsunami alert level, might be in part due to the resolution of computational domains playing an important role because of the narrow distance between coasts (e.g., at Gibraltar Strait ) and the shallow and heterogeneous bathymetry in the area (Figure 1). Tsunami alert levels maintain the same levels at the rest of the segments in the Iberian peninsula and the Canary Islands when the domain resolution is refined from ½ arcmin to ¼ arcmin and to ⅛ arcmin.
Tsunami arrival differences obtained from different resolution domains are less than 2 min for the majority of FCPs. The greatest differences are observed at FCPs far from the source and with maximum tsunami height lower than 0.2 m. Therefore, the observed arrival time differences considering finer resolution computational domains will not significantly affect the tsunami warning. The same behavior for arrival time forecasts is observed using different resolution domains, this may be due in part because the arrival times are computed at isobath 50 m FCPs and, therefore, variations in high–resolution bathymetric details close to the coast do not affect TW arrival time results. The differences in the tsunami warning levels that are obtained when using finer resolution discretizations are small; these differences could increase if the maximum height of the tsunami and the arrival times were calculated in FCPs closest to the coasts, where shoaling effects should be considered.
4. Conclusions
The live demo for Faster-Than-Real-Time (FTRT) tsunami simulations conducted under the ChEESE project provided a set of data worth analyzing, in order to assess the potential benefits and performance of the proposed technology for the Spanish NTWC. The computing time achieved for 135 scenarios in the Atlantic area, in four different spatial domains with three different numerical resolutions, was 7 min. This computing time is short enough to allow preventive measures to be taken against the impact of the tsunami, and is achievable if 270 GPUs are available for computing in case of an event. Furthermore, a first estimate is obtained after just one minute. Carrying out this experiment at NTWCs in real time implies agreements with supercomputing centers to be able to access their resources immediately when the tsunami alert is triggered (in the detection phase).
The results of this experiment show that tsunami alert levels are sensitive to variations in source parameters, of which there is a lack of knowledge within the first few minutes after the tsunami alert is triggered. Therefore, assuming alert levels computed from a single scenario with considerable uncertainties may lead to incorrect warnings and underestimations of the tsunami hazard in some coastal areas. In addition, this methodology provides the capacity to set the desired level of conservatism in the warnings, as the decision-maker can choose to work with the most hazardous scenario, the mean from all the considered scenarios, or with a fixed percentile. From this study, the results show that variation of the dip parameter has more influences than the strike parameter on the maximum heights computed. This behavior may be due to the specific geographical conditions of the reference scenario or to the range of variation considered, that is, ±20° for dip and ±15° for strike. Shallow depths and large magnitudes appear to make scenarios more sensitive to strike, dip, and location variations. It is probable that a different reference scenario defined by a different set of Okada parameters than those considered in this study could generate a different dependency of the tsunami alert level on the parameters than the relations found in this demo.
It is also found that domain resolution affects the generated alert level. In this case, the alert level increases at two coastal regions with increasing domain resolution. The warning differences obtained from increasing the computational domain resolution are lower than those ones from source parameter variation. This result implies that, in case of limited computational resources, an alternative could be not to consider finer numerical resolutions.
The results from this live demo show that the alert levels can change when considering scenarios that vary in the range within the uncertainties of the source parameters. However, the results of the sensitivity of the alert levels to the variation of each parameter are specific to this study and how it was designed. More specifically, it depends on the range of variation of the source parameter and the relative geographic distribution of the FCPs in relation to the direction of the rupture. Although the results are specific to this experiment, the computation of the tsunami alert levels considering several scenarios to account for the uncertainties in the source parameters, with analogous methodologies to the one proposed here, should be considered by TWS as step forward to producing tsunami forecast warnings that include variability. This is now possible thanks to pre-exascale computational resources.
The method presented in this study generates tsunami alert warnings that consider the uncertainty in source parameters within the first minutes after earthquake origin time. The computation time (7 min) of all scenarios is fast enough to be useful to near-source tsunami early warning. Obtaining the results within this time is possible under agreements between tsunami warning centers and supercomputing centers. The results of this study are similar to previous works on probabilistic tsunami forecast, but were obtained using a simpler methodology. However, results from the present study are specific to the considered scenarios, finite source slip distribution, and the approach to computing the maximum tsunami height at the coast. Some of the limits of this study can be overcome by considering a more complex finite source slip distribution. Furthermore, results from tsunami warning estimations can be improved by considering more complex approaches for computing maximum tsunami heights at the coast or by computing fast source determination. Future work includes carrying out the same real-time exercise using a recent historical tsunami that has affected the Spanish coast as the reference scenario in order to be able to compare the forecast with tide-gauge measurements.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geohazards3030019/s1, Figure S1: Comparison of maximum heights at FPCs of scenario of reference computing tsunami propagation with different resolution domains. (a,c,e) ATL at 1/2 arcmin (b,f) GCIC at 1/4 arcmin, and (d) GC at 1/8 arcmin.
Author Contributions
Conceptualization, J.M., B.G. and J.V.C.; methodology, J.M., B.G. and J.V.C.; workflow implementation, C.S.-L.; formal analysis, B.G.; data curation, B.G. and C.S.-L.; writing—original draft preparation, B.G.; writing—review and editing, B.G., J.M., C.S.-L. and J.V.C.; visualization, B.G., C.S.-L., C.G. and L.C.P.; supervision, J.M.; project administration, J.M.; funding acquisition, J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the European Union’s Horizon 2020 Research and Innovation Program under grant agreement No. 823844 (ChEESE Centre of Excellence, www.cheese-coe.eu, accessed on 27 June 2022) and by the Spanish Government-FEDER funded project MEGAFLOW (RTI2018-096064-B-C21).
Data Availability Statement
All the data generated and analyzed by this study can be found at Sánchez Linares, Carlos (2022), “Faster Than Real Time (FTRT) tsunami simulations for the Spanish Tsunami Warning System for the Atlantic. Live Demo ChEESE.”, Mendeley Data, V1, doi: 10.17632/cpgf3c5dtx.1, https://data.mendeley.com/datasets/cpgf3c5dtx/1 (accessed on 27 June 2022).
Acknowledgments
Authors are grateful to CINECA for providing us with the numerical resources for performing the live demo and the numerical results generated in the present work. Special thanks to Piero Lanucara and Silvia Giuliani. The bathymetric metadata and digital terrain model data products have been derived from the EMODnet Bathymetry portal—http://www.emodnet-bathymetry.eu, accessed on 27 February 2022. The authors thank the reviewers’ useful comments that helped to improve this manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
Table A1.
List of scenarios and input source parameters to the Tsunami-HySEA model used to compute the results of this study.
Table A1.
List of scenarios and input source parameters to the Tsunami-HySEA model used to compute the results of this study.
| SCENARIO ID | Longitude (°) | Latitude (°) | Depth (km) | Length (km) | Width (km) | Strike (°) | Dip (°) | Rake (°) | Slip (m) |
|---|---|---|---|---|---|---|---|---|---|
| CCmCsCdC * | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 39 | 35 | 90 | 2.76 |
| CCmCsDdC | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 24 | 35 | 90 | 2.76 |
| CCmCsUdC | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 54 | 35 | 90 | 2.76 |
| CCmCsCdD | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 39 | 15 | 90 | 2.76 |
| CCmCsDdD | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 24 | 15 | 90 | 2.76 |
| CCmCsUdD | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 54 | 15 | 90 | 2.76 |
| CCmCsCdU | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 39 | 55 | 90 | 2.76 |
| CCmCsDdU | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 24 | 55 | 90 | 2.76 |
| CCmCsUdU | −9.772 | 35.442 | 50 | 61.332 | 51.11 | 54 | 55 | 90 | 2.76 |
| CCmDsCdC | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 39 | 35 | 90 | 2.19 |
| CCmDsDdC | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 24 | 35 | 90 | 2.19 |
| CCmDsUdC | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 54 | 35 | 90 | 2.19 |
| CCmDsCdD | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 39 | 15 | 90 | 2.19 |
| CCmDsDdD | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 24 | 15 | 90 | 2.19 |
| CCmDsUdD | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 54 | 15 | 90 | 2.19 |
| CCmDsCdU | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 39 | 55 | 90 | 2.19 |
| CCmDsDdU | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 24 | 55 | 90 | 2.19 |
| CCmDsUdU | −9.772 | 35.442 | 50 | 48.718 | 40.598 | 54 | 55 | 90 | 2.19 |
| CCmUsCdC | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 39 | 35 | 90 | 3.47 |
| CCmUsDdC | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 24 | 35 | 90 | 3.47 |
| CCmUsUdC | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 54 | 35 | 90 | 3.47 |
| CCmUsCdD | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 39 | 15 | 90 | 3.47 |
| CCmUsDdD | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 24 | 15 | 90 | 3.47 |
| CCmUsUdD | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 54 | 15 | 90 | 3.47 |
| CCmUsCdU | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 39 | 55 | 90 | 3.47 |
| CCmUsDdU | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 24 | 55 | 90 | 3.47 |
| CCmUsUdU | −9.772 | 35.442 | 50 | 77.212 | 64.343 | 54 | 55 | 90 | 3.47 |
| EmCsCdC | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 39 | 35 | 90 | 2.76 |
| EmCsDdC | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 24 | 35 | 90 | 2.76 |
| EmCsUdC | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 54 | 35 | 90 | 2.76 |
| EmCsCdD | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 39 | 15 | 90 | 2.76 |
| EmCsDdD | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 24 | 15 | 90 | 2.76 |
| EmCsUdD | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 54 | 15 | 90 | 2.76 |
| EmCsCdU | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 39 | 55 | 90 | 2.76 |
| EmCsDdU | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 24 | 55 | 90 | 2.76 |
| EmCsUdU | −9.39 | 35.56 | 64 | 61.332 | 51.11 | 54 | 55 | 90 | 2.76 |
| EmDsCdC | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 39 | 35 | 90 | 2.19 |
| EmDsDdC | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 24 | 35 | 90 | 2.19 |
| EmDsUdC | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 54 | 35 | 90 | 2.19 |
| EmDsCdD | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 39 | 15 | 90 | 2.19 |
| EmDsDdD | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 24 | 15 | 90 | 2.19 |
| EmDsUdD | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 54 | 15 | 90 | 2.19 |
| EmDsCdU | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 39 | 55 | 90 | 2.19 |
| EmDsDdU | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 24 | 55 | 90 | 2.19 |
| EmDsUdU | −9.47 | 35.53 | 61.5 | 48.718 | 40.598 | 54 | 55 | 90 | 2.19 |
| EmUsCdC | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 39 | 35 | 90 | 3.47 |
| EmUsDdC | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 24 | 35 | 90 | 3.47 |
| EmUsUdC | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 54 | 35 | 90 | 3.47 |
| EmUsCdD | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 39 | 15 | 90 | 3.47 |
| EmUsDdD | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 24 | 15 | 90 | 3.47 |
| EmUsUdD | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 54 | 15 | 90 | 3.47 |
| EmUsCdU | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 39 | 55 | 90 | 3.47 |
| EmUsDdU | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 24 | 55 | 90 | 3.47 |
| EmUsUdU | −9.36 | 35.56 | 66 | 77.212 | 64.343 | 54 | 55 | 90 | 3.47 |
| SmCsCdC | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 39 | 35 | 90 | 2.76 |
| SmCsDdC | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 24 | 35 | 90 | 2.76 |
| SmCsUdC | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 54 | 35 | 90 | 2.76 |
| SmCsCdD | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 39 | 15 | 90 | 2.76 |
| SmCsDdD | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 24 | 15 | 90 | 2.76 |
| SmCsUdD | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 54 | 15 | 90 | 2.76 |
| SmCsCdU | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 39 | 55 | 90 | 2.76 |
| SmCsDdU | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 24 | 55 | 90 | 2.76 |
| SmCsUdU | −9.78 | 35.12 | 64 | 61.332 | 51.11 | 54 | 55 | 90 | 2.76 |
| SmDsCdC | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 39 | 35 | 90 | 2.19 |
| SmDsDdC | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 24 | 35 | 90 | 2.19 |
| SmDsUdC | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 54 | 35 | 90 | 2.19 |
| SmDsCdD | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 39 | 15 | 90 | 2.19 |
| SmDsDdD | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 24 | 15 | 90 | 2.19 |
| SmDsUdD | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 54 | 15 | 90 | 2.19 |
| SmDsCdU | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 39 | 55 | 90 | 2.19 |
| SmDsDdU | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 24 | 55 | 90 | 2.19 |
| SmDsUdU | −9.78 | 35.18 | 61.5 | 48.718 | 40.598 | 54 | 55 | 90 | 2.19 |
| SmUsCdC | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 39 | 35 | 90 | 3.47 |
| SmUsDdC | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 24 | 35 | 90 | 3.47 |
| SmUsUdC | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 54 | 35 | 90 | 3.47 |
| SmUsCdD | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 39 | 15 | 90 | 3.47 |
| SmUsDdD | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 24 | 15 | 90 | 3.47 |
| SmUsUdD | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 54 | 15 | 90 | 3.47 |
| SmUsCdU | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 39 | 55 | 90 | 3.47 |
| SmUsDdU | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 24 | 55 | 90 | 3.47 |
| SmUsUdU | −9.77 | 35.09 | 66 | 77.212 | 64.343 | 54 | 55 | 90 | 3.47 |
| WmCsCdC | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 39 | 35 | 90 | 2.76 |
| WmCsDdC | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 24 | 35 | 90 | 2.76 |
| WmCsUdC | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 54 | 35 | 90 | 2.76 |
| WmCsCdD | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 39 | 15 | 90 | 2.76 |
| WmCsDdD | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 24 | 15 | 90 | 2.76 |
| WmCsUdD | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 54 | 15 | 90 | 2.76 |
| WmCsCdU | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 39 | 55 | 90 | 2.76 |
| WmCsDdU | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 24 | 55 | 90 | 2.76 |
| WmCsUdU | −9.77 | 35.77 | 36 | 61.332 | 51.11 | 54 | 55 | 90 | 2.76 |
| WmDsCdC | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 39 | 35 | 90 | 2.19 |
| WmDsDdC | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 24 | 35 | 90 | 2.19 |
| WmDsUdC | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 54 | 35 | 90 | 2.19 |
| WmDsCdD | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 39 | 15 | 90 | 2.19 |
| WmDsDdD | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 24 | 15 | 90 | 2.19 |
| WmDsUdD | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 54 | 15 | 90 | 2.19 |
| WmDsCdU | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 39 | 55 | 90 | 2.19 |
| WmDsDdU | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 24 | 55 | 90 | 2.19 |
| WmDsUdU | −9.77 | 35.7 | 38.5 | 48.718 | 40.598 | 54 | 55 | 90 | 2.19 |
| WmUsCdC | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 39 | 35 | 90 | 3.47 |
| WmUsDdC | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 24 | 35 | 90 | 3.47 |
| WmUsUdC | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 54 | 35 | 90 | 3.47 |
| WmUsCdD | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 39 | 15 | 90 | 3.47 |
| WmUsDdD | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 24 | 15 | 90 | 3.47 |
| WmUsUdD | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 54 | 15 | 90 | 3.47 |
| WmUsCdU | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 39 | 55 | 90 | 3.47 |
| WmUsDdU | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 24 | 55 | 90 | 3.47 |
| WmUsUdU | −9.77 | 35.79 | 34 | 77.212 | 64.343 | 54 | 55 | 90 | 3.47 |
| NmCsCdC | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 39 | 35 | 90 | 2.76 |
| NmCsDdC | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 24 | 35 | 90 | 2.76 |
| NmCsUdC | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 54 | 35 | 90 | 2.76 |
| NmCsCdD | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 39 | 15 | 90 | 2.76 |
| NmCsDdD | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 24 | 15 | 90 | 2.76 |
| NmCsUdD | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 54 | 15 | 90 | 2.76 |
| NmCsCdU | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 39 | 55 | 90 | 2.76 |
| NmCsDdU | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 24 | 55 | 90 | 2.76 |
| NmCsUdU | −10.14 | 35.33 | 36 | 61.332 | 51.11 | 54 | 55 | 90 | 2.76 |
| NmDsCdC | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 39 | 35 | 90 | 2.19 |
| NmDsDdC | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 24 | 35 | 90 | 2.19 |
| NmDsUdC | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 54 | 35 | 90 | 2.19 |
| NmDsCdD | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 39 | 15 | 90 | 2.19 |
| NmDsDdD | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 24 | 15 | 90 | 2.19 |
| NmDsUdD | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 54 | 15 | 90 | 2.19 |
| NmDsCdU | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 39 | 55 | 90 | 2.19 |
| NmDsDdU | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 24 | 55 | 90 | 2.19 |
| NmDsUdU | −10.07 | 35.35 | 38.5 | 48.718 | 40.598 | 54 | 55 | 90 | 2.19 |
| NmUsCdC | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 39 | 35 | 90 | 3.47 |
| NmUsDdC | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 24 | 35 | 90 | 3.47 |
| NmUsUdC | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 54 | 35 | 90 | 3.47 |
| NmUsCdD | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 39 | 15 | 90 | 3.47 |
| NmUsDdD | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 24 | 15 | 90 | 3.47 |
| NmUsUdD | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 54 | 15 | 90 | 3.47 |
| NmUsCdU | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 39 | 55 | 90 | 3.47 |
| NmUsDdU | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 24 | 55 | 90 | 3.47 |
| NmUsUdU | −10.18 | 35.32 | 34 | 77.212 | 64.343 | 54 | 55 | 90 | 3.47 |
* Scenario of reference.
Table A2.
Mean normalized difference of maximum height and of arrival time for scenarios with varying strike.
Table A2.
Mean normalized difference of maximum height and of arrival time for scenarios with varying strike.
| Free Parameter: Magnitude | Normalized Difference of Maximum Height (m) | Normalized Difference of Arrival Time (s) | ||
|---|---|---|---|---|
| Name of Case | Mean | STD | Mean | STD |
| ‘CCmCsXdC_ATL_1_2’ | 0.101 | 0.081 | 1.370 | 16.000 |
| ‘CCmCsXdD_ATL_1_2’ | 0.174 | 0.138 | 0.115 | 0.000 |
| ‘CCmCsXdU_ATL_1_2’ | 0.122 | 0.098 | 2.091 | 18.000 |
| ‘CCmDsXdC_ATL_1_2’ | 0.052 | 0.042 | 0.054 | 0.000 |
| ‘CCmDsXdD_ATL_1_2’ | 0.094 | 0.074 | 0.165 | 0.000 |
| ‘CCmDsXdU_ATL_1_2’ | 0.060 | 0.046 | 0.055 | 0.000 |
| ‘CCmUsXdC_ATL_1_2’ | 0.192 | 0.155 | 1.092 | 11.000 |
| ‘CCmUsXdD_ATL_1_2’ | 0.311 | 0.251 | 1.969 | 16.000 |
| ‘CCmUsXdU_ATL_1_2’ | 0.248 | 0.217 | 3.111 | 20.000 |
| ‘EmCsXdC_ATL_1_2’ | 0.079 | 0.066 | 0.060 | 0.000 |
| ‘EmCsXdD_ATL_1_2’ | 0.142 | 0.138 | 0.816 | 10.000 |
| ‘EmCsXdU_ATL_1_2’ | 0.101 | 0.075 | 0.098 | 1.000 |
| ‘EmDsXdC_ATL_1_2’ | 0.041 | 0.034 | 0.064 | 0.000 |
| ‘EmDsXdD_ATL_1_2’ | 0.077 | 0.071 | 0.138 | 0.000 |
| ‘EmDsXdU_ATL_1_2’ | 0.052 | 0.038 | 0.074 | 0.000 |
| ‘EmUsXdC_ATL_1_2’ | 0.153 | 0.127 | 1.520 | 12.000 |
| ‘EmUsXdD_ATL_1_2’ | 0.261 | 0.259 | 1.347 | 13.000 |
| ‘EmUsXdU_ATL_1_2’ | 0.196 | 0.148 | 0.487 | 5.000 |
| ‘WmCsXdC_ATL_1_2’ | 0.133 | 0.140 | 1.704 | 16.000 |
| ‘WmCsXdD_ATL_1_2’ | 0.200 | 0.178 | 1.362 | 15.000 |
| ‘WmCsXdU_ATL_1_2’ | 0.190 | 0.209 | 3.216 | 22.000 |
| ‘WmDsXdC_ATL_1_2’ | 0.063 | 0.064 | 0.046 | 0.000 |
| ‘WmDsXdD_ATL_1_2’ | 0.106 | 0.093 | 0.102 | 0.000 |
| ‘WmDsXdU_ATL_1_2’ | 0.083 | 0.086 | 0.052 | 0.000 |
| ‘WmUsXdC_ATL_1_2’ | 0.270 | 0.292 | 1.900 | 16.000 |
| ‘WmUsXdD_ATL_1_2’ | 0.355 | 0.304 | 1.496 | 15.000 |
| ‘WmUsXdU_ATL_1_2’ | 0.400 | 0.458 | 3.717 | 22.000 |
| ‘SmCsXdC_ATL_1_2’ | 0.091 | 0.070 | 0.499 | 9.000 |
| ‘SmCsXdD_ATL_1_2’ | 0.154 | 0.133 | 0.609 | 9.000 |
| ‘SmCsXdU_ATL_1_2’ | 0.110 | 0.084 | 1.328 | 15.000 |
| ‘SmDsXdC_ATL_1_2’ | 0.047 | 0.037 | 0.055 | 0.000 |
| ‘SmDsXdD_ATL_1_2’ | 0.083 | 0.072 | 0.195 | 0.000 |
| ‘SmDsXdU_ATL_1_2’ | 0.055 | 0.042 | 0.081 | 0.000 |
| ‘SmUsXdC_ATL_1_2’ | 0.172 | 0.130 | 0.763 | 7.000 |
| ‘SmUsXdD_ATL_1_2’ | 0.284 | 0.244 | 1.573 | 15.000 |
| ‘SmUsXdU_ATL_1_2’ | 0.215 | 0.163 | 2.614 | 20.000 |
| ‘NmCsXdC_ATL_1_2’ | 0.146 | 0.147 | 1.080 | 13.000 |
| ‘NmCsXdD_ATL_1_2’ | 0.212 | 0.167 | 1.424 | 15.000 |
| ‘NmCsXdU_ATL_1_2’ | 0.195 | 0.259 | 3.152 | 22.000 |
| ‘NmDsXdC_ATL_1_2’ | 0.071 | 0.067 | 0.068 | 0.000 |
| ‘NmDsXdD_ATL_1_2’ | 0.116 | 0.093 | 0.156 | 0.000 |
| ‘NmDsXdU_ATL_1_2’ | 0.084 | 0.094 | 0.061 | 0.000 |
| ‘NmUsXdC_ATL_1_2’ | 0.283 | 0.308 | 3.321 | 23.000 |
| ‘NmUsXdD_ATL_1_2’ | 0.366 | 0.287 | 2.844 | 22.000 |
| ‘NmUsXdU_ATL_1_2’ | 0.409 | 0.533 | 3.698 | 23.000 |
Table A3.
Mean normalized difference of maximum height and of arrival time for scenarios with varying dip.
Table A3.
Mean normalized difference of maximum height and of arrival time for scenarios with varying dip.
| Free Parameter: Magnitude | Normalized Difference of Maximum Height (m) | Normalized Difference of Arrival Time (s) | ||
|---|---|---|---|---|
| Name of Case | Mean | STD | Mean | STD |
| ‘CCmCsCdX_ATL_1_2’ | 0.269 | 0.196 | 1.452 | 15.000 |
| ‘CCmCsDdX_ATL_1_2’ | 0.262 | 0.194 | 1.389 | 15.000 |
| ‘CCmCsUdX_ATL_1_2’ | 0.273 | 0.176 | 1.427 | 16.000 |
| ‘CCmDsCdX_ATL_1_2’ | 0.146 | 0.108 | 0.152 | 0.000 |
| ‘CCmDsDdX_ATL_1_2’ | 0.140 | 0.105 | 0.133 | 0.000 |
| ‘CCmDsUdX_ATL_1_2’ | 0.147 | 0.098 | 0.157 | 0.000 |
| ‘CCmUsCdX_ATL_1_2’ | 0.491 | 0.352 | 3.366 | 22.000 |
| ‘CCmUsDdX_ATL_1_2’ | 0.490 | 0.359 | 3.286 | 21.000 |
| ‘CCmUsUdX_ATL_1_2’ | 0.499 | 0.316 | 3.295 | 20.000 |
| ‘EmCsCdX_ATL_1_2’ | 0.209 | 0.144 | 1.545 | 14.000 |
| ‘EmCsDdX_ATL_1_2’ | 0.201 | 0.140 | 0.887 | 10.000 |
| ‘EmCsUdX_ATL_1_2’ | 0.222 | 0.151 | 1.505 | 14.000 |
| ‘EmDsCdX_ATL_1_2’ | 0.115 | 0.082 | 0.173 | 0.000 |
| ‘EmDsDdX_ATL_1_2’ | 0.112 | 0.080 | 0.157 | 0.000 |
| ‘EmDsUdX_ATL_1_2’ | 0.119 | 0.081 | 0.170 | 0.000 |
| ‘EmUsCdX_ATL_1_2’ | 0.382 | 0.259 | 3.180 | 20.000 |
| ‘EmUsDdX_ATL_1_2’ | 0.362 | 0.248 | 3.896 | 23.000 |
| ‘EmUsUdX_ATL_1_2’ | 0.410 | 0.280 | 3.128 | 21.000 |
| ‘WmCsCdX_ATL_1_2’ | 0.331 | 0.240 | 4.705 | 28.000 |
| ‘WmCsDdX_ATL_1_2’ | 0.341 | 0.265 | 4.934 | 29.000 |
| ‘WmCsUdX_ATL_1_2’ | 0.331 | 0.228 | 2.523 | 20.000 |
| ‘WmDsCdX_ATL_1_2’ | 0.170 | 0.129 | 0.128 | 0.000 |
| ‘WmDsDdX_ATL_1_2’ | 0.171 | 0.140 | 0.097 | 0.000 |
| ‘WmDsUdX_ATL_1_2’ | 0.170 | 0.118 | 0.119 | 0.000 |
| ‘WmUsCdX_ATL_1_2’ | 0.657 | 0.489 | 6.061 | 30.000 |
| ‘WmUsDdX_ATL_1_2’ | 0.691 | 0.547 | 7.669 | 35.000 |
| ‘WmUsUdX_ATL_1_2’ | 0.648 | 0.465 | 4.945 | 26.000 |
| ‘SmCsCdX_ATL_1_2’ | 0.250 | 0.178 | 0.541 | 8.000 |
| ‘SmCsDdX_ATL_1_2’ | 0.240 | 0.175 | 1.404 | 15.000 |
| ‘SmCsUdX_ATL_1_2’ | 0.257 | 0.180 | 0.600 | 9.000 |
| ‘SmDsCdX_ATL_1_2’ | 0.135 | 0.100 | 0.195 | 0.000 |
| ‘SmDsDdX_ATL_1_2’ | 0.129 | 0.096 | 0.149 | 0.000 |
| ‘SmDsUdX_ATL_1_2’ | 0.139 | 0.100 | 0.182 | 0.000 |
| ‘SmUsCdX_ATL_1_2’ | 0.450 | 0.309 | 2.084 | 15.000 |
| ‘SmUsDdX_ATL_1_2’ | 0.434 | 0.308 | 3.742 | 25.000 |
| ‘SmUsUdX_ATL_1_2’ | 0.466 | 0.315 | 2.435 | 16.000 |
| ‘NmCsCdX_ATL_1_2’ | 0.347 | 0.264 | 1.819 | 17.000 |
| ‘NmCsDdX_ATL_1_2’ | 0.378 | 0.355 | 3.230 | 23.000 |
| ‘NmCsUdX_ATL_1_2’ | 0.331 | 0.222 | 0.816 | 10.000 |
| ‘NmDsCdX_ATL_1_2’ | 0.182 | 0.143 | 0.151 | 0.000 |
| ‘NmDsDdX_ATL_1_2’ | 0.184 | 0.157 | 0.125 | 0.000 |
| ‘NmDsUdX_ATL_1_2’ | 0.177 | 0.125 | 0.150 | 0.000 |
| ‘NmUsCdX_ATL_1_2’ | 0.699 | 0.571 | 5.747 | 29.000 |
| ‘NmUsDdX_ATL_1_2’ | 0.784 | 0.799 | 3.932 | 24.000 |
| ‘NmUsUdX_ATL_1_2’ | 0.644 | 0.470 | 5.637 | 30.000 |
Table A4.
Mean normalized difference of maximum height and arrival time for scenarios with varying magnitude.
Table A4.
Mean normalized difference of maximum height and arrival time for scenarios with varying magnitude.
| Free Parameter: Magnitude | Normalized Difference of Maximum Height (m) | Normalized Difference of Arrival Time (s) | ||
|---|---|---|---|---|
| Name of Case | Mean | STD | Mean | STD |
| ‘CCmXsCdC_ATL_1_2’ | 1.078 | 0.486 | 8.207 | 33.000 |
| ‘CCmXsCdD_ATL_1_2’ | 0.813 | 0.428 | 7.144 | 31.000 |
| ‘CCmXsCdU_ATL_1_2’ | 1.126 | 0.520 | 8.105 | 33.000 |
| ‘CCmXsDdC_ATL_1_2’ | 1.128 | 0.510 | 8.061 | 33.000 |
| ‘CCmXsDdD_ATL_1_2’ | 0.885 | 0.462 | 7.478 | 33.000 |
| ‘CCmXsDdU_ATL_1_2’ | 1.182 | 0.560 | 8.443 | 36.000 |
| ‘CCmXsUdC_ATL_1_2’ | 1.080 | 0.492 | 8.813 | 35.000 |
| ‘CCmXsUdD_ATL_1_2’ | 0.801 | 0.412 | 7.262 | 32.000 |
| ‘CCmXsUdU_ATL_1_2’ | 1.125 | 0.525 | 8.702 | 34.000 |
| ‘EmXsCdC_ATL_1_2’ | 0.965 | 0.501 | 7.831 | 34.000 |
| ‘EmXsCdD_ATL_1_2’ | 0.747 | 0.440 | 6.552 | 30.000 |
| ‘EmXsCdU_ATL_1_2’ | 0.977 | 0.531 | 8.139 | 35.000 |
| ‘EmXsDdC_ATL_1_2’ | 1.009 | 0.527 | 8.055 | 35.000 |
| ‘EmXsDdD_ATL_1_2’ | 0.821 | 0.495 | 6.331 | 30.000 |
| ‘EmXsDdU_ATL_1_2’ | 1.024 | 0.559 | 8.323 | 36.000 |
| ‘EmXsUdC_ATL_1_2’ | 0.948 | 0.482 | 7.910 | 34.000 |
| ‘EmXsUdD_ATL_1_2’ | 0.702 | 0.385 | 6.698 | 31.000 |
| ‘EmXsUdU_ATL_1_2’ | 0.960 | 0.507 | 7.851 | 33.000 |
| ‘WmXsCdC_ATL_1_2’ | 1.349 | 0.676 | 10.457 | 39.000 |
| ‘WmXsCdD_ATL_1_2’ | 0.992 | 0.533 | 7.134 | 31.000 |
| ‘WmXsCdU_ATL_1_2’ | 1.461 | 0.783 | 12.950 | 45.000 |
| ‘WmXsDdC_ATL_1_2’ | 1.382 | 0.722 | 11.314 | 41.000 |
| ‘WmXsDdD_ATL_1_2’ | 1.045 | 0.570 | 7.337 | 32.000 |
| ‘WmXsDdU_ATL_1_2’ | 1.542 | 0.877 | 14.345 | 47.000 |
| ‘WmXsUdC_ATL_1_2’ | 1.348 | 0.670 | 9.254 | 36.000 |
| ‘WmXsUdD_ATL_1_2’ | 0.981 | 0.515 | 7.171 | 31.000 |
| ‘WmXsUdU_ATL_1_2’ | 1.435 | 0.763 | 10.581 | 38.000 |
| ‘SmXsCdC_ATL_1_2’ | 0.937 | 0.450 | 7.208 | 31.000 |
| ‘SmXsCdD_ATL_1_2’ | 0.698 | 0.393 | 7.471 | 34.000 |
| ‘SmXsCdU_ATL_1_2’ | 0.962 | 0.472 | 6.993 | 31.000 |
| ‘SmXsDdC_ATL_1_2’ | 0.988 | 0.472 | 7.442 | 32.000 |
| ‘SmXsDdD_ATL_1_2’ | 0.777 | 0.420 | 6.748 | 31.000 |
| ‘SmXsDdU_ATL_1_2’ | 1.019 | 0.508 | 5.049 | 26.000 |
| ‘SmXsUdC_ATL_1_2’ | 0.933 | 0.452 | 7.194 | 31.000 |
| ‘SmXsUdD_ATL_1_2’ | 0.669 | 0.387 | 7.610 | 34.000 |
| ‘SmXsUdU_ATL_1_2’ | 0.955 | 0.468 | 6.865 | 29.000 |
| ‘NmXsCdC_ATL_1_2’ | 1.281 | 0.647 | 12.678 | 44.000 |
| ‘NmXsCdD_ATL_1_2’ | 0.917 | 0.508 | 9.379 | 38.000 |
| ‘NmXsCdU_ATL_1_2’ | 1.404 | 0.790 | 12.338 | 42.000 |
| ‘NmXsDdC_ATL_1_2’ | 1.364 | 0.720 | 11.417 | 41.000 |
| ‘NmXsDdD_ATL_1_2’ | 0.986 | 0.520 | 9.082 | 36.000 |
| ‘NmXsDdU_ATL_1_2’ | 1.549 | 0.985 | 12.151 | 42.000 |
| ‘NmXsUdC_ATL_1_2’ | 1.279 | 0.643 | 11.345 | 41.000 |
| ‘NmXsUdD_ATL_1_2’ | 0.935 | 0.533 | 8.197 | 35.000 |
| ‘NmXsUdU_ATL_1_2’ | 1.371 | 0.745 | 10.026 | 37.000 |
Table A5.
Mean normalized difference of maximum height and of arrival time for scenarios with varying source location.
Table A5.
Mean normalized difference of maximum height and of arrival time for scenarios with varying source location.
| Free Parameter: Location | Normalized Difference of Maximum Height (m) | Normalized Difference of Arrival Time (s) | ||
|---|---|---|---|---|
| Name of Case | Mean | STD | Mean | STD |
| ‘lXmCsCdC_ATL_1_2’ | 0.468 | 0.329 | 5.274 | 29.000 |
| ‘lXmCsCdD_ATL_1_2’ | 0.370 | 0.284 | 2.480 | 19.000 |
| ‘lXmCsCdU_ATL_1_2’ | 0.516 | 0.365 | 6.300 | 33.000 |
| ‘lXmCsDdC_ATL_1_2’ | 0.494 | 0.358 | 5.597 | 30.000 |
| ‘lXmCsDdD_ATL_1_2’ | 0.379 | 0.306 | 2.592 | 20.000 |
| ‘lXmCsDdU_ATL_1_2’ | 0.576 | 0.458 | 5.327 | 30.000 |
| ‘lXmCsUdC_ATL_1_2’ | 0.454 | 0.322 | 5.640 | 31.000 |
| ‘lXmCsUdD_ATL_1_2’ | 0.367 | 0.276 | 3.077 | 22.000 |
| ‘lXmCsUdU_ATL_1_2’ | 0.488 | 0.343 | 5.491 | 30.000 |
| ‘lXmDsCdC_ATL_1_2’ | 0.222 | 0.159 | 0.151 | 0.000 |
| ‘lXmDsCdD_ATL_1_2’ | 0.176 | 0.138 | 0.253 | 1.000 |
| ‘lXmDsCdU_ATL_1_2’ | 0.239 | 0.174 | 0.167 | 0.000 |
| ‘lXmDsDdC_ATL_1_2’ | 0.235 | 0.171 | 0.162 | 0.000 |
| ‘lXmDsDdD_ATL_1_2’ | 0.182 | 0.150 | 0.195 | 0.000 |
| ‘lXmDsDdU_ATL_1_2’ | 0.260 | 0.204 | 0.194 | 0.000 |
| ‘lXmDsUdC_ATL_1_2’ | 0.218 | 0.159 | 0.152 | 0.000 |
| ‘lXmDsUdD_ATL_1_2’ | 0.177 | 0.139 | 0.235 | 0.000 |
| ‘lXmDsUdU_ATL_1_2’ | 0.228 | 0.164 | 0.172 | 0.000 |
| ‘lXmUsCdC_ATL_1_2’ | 0.852 | 0.590 | 7.342 | 34.000 |
| ‘lXmUsCdD_ATL_1_2’ | 0.646 | 0.474 | 6.396 | 33.000 |
| ‘lXmUsCdU_ATL_1_2’ | 1.007 | 0.765 | 9.032 | 37.000 |
| ‘lXmUsDdC_ATL_1_2’ | 0.902 | 0.659 | 6.546 | 31.000 |
| ‘lXmUsDdD_ATL_1_2’ | 0.656 | 0.508 | 6.070 | 31.000 |
| ‘lXmUsDdU_ATL_1_2’ | 1.128 | 0.953 | 10.335 | 42.000 |
| ‘lXmUsUdC_ATL_1_2’ | 0.816 | 0.568 | 5.703 | 30.000 |
| ‘lXmUsUdD_ATL_1_2’ | 0.644 | 0.458 | 6.930 | 34.000 |
| ‘lXmUsUdU_ATL_1_2’ | 0.946 | 0.704 | 6.511 | 31.000 |
References
- Santos, A.; Tavares, A.O.; Queirós, M. Numerical modelling and evacuation strategies for tsunami awareness: Lessons from the 2012 Haida Gwaii Tsunami. Geomatics. Nat. Hazards Risk 2016, 7, 1442–1459. [Google Scholar] [CrossRef] [Green Version]
- Marshall, M. Mystery of deadly Indonesian tsunami cracked using social-media videos. Nature 2019, 569, 463–464. [Google Scholar] [CrossRef] [PubMed]
- National Geophysical Data Center/World Data Service: NCEI/WDS Global Historical Tsunami Database. NOAA National Centers for Environmental Information. Available online: https://doi.org/10.7289/V5PN93H7 (accessed on 1 February 2021).
- Maramai, A.; Brizuela, B.; Graziani, L. The Euro-Mediterranean Tsunami Catalogue. Ann. Geophys. 2014, 57, S0435. [Google Scholar] [CrossRef]
- Baptista, M.A.; Miranda, J.M. Revision of the Portuguese catalogue of tsunamis. Nat. Hazards Earth Syst. Sci. 2009, 1932, 25–42. [Google Scholar] [CrossRef] [Green Version]
- Abe, K. Size of great earthquakes of 1837–1974 inferred from tsunami data. J. Geophys. Res. 1979, 84, 1561. [Google Scholar] [CrossRef]
- Martínez-Solares, J.M. Los Efectos en España del Terremoto de Lisboa (1 de Noviembre de 1755). Monografía Número 19; Instituto Geográfico Nacional: Madrid, Spain, 2001; 756p. [Google Scholar]
- Martínez-Solares, J.M.; López Arroyo, A. The great historical 1755 earthquake. Effects and damage in Spain. J. Seismol. 2004, 8, 275–294. [Google Scholar] [CrossRef]
- Fonseca, J.F.B.D. A reassessment of the magnitude of the 1755 Lisbon earthquake. BSSA 2020, 110, 1–17. [Google Scholar] [CrossRef]
- Clouard, V.; Roger, M.J.; Moizan, E. Tsunami deposits in Martinique related to the 1755 Lisbon earthquake. Nat. Hazards Earth Syst. Sci. Discuss 2017, 5, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Roger, J.; Baptista, M.A.; Sahal, A.; Accary, F.; Allgeyer, S.; Hébert, H. The transoceanic 1755 Lisbon Tsunami in Martinique. Pure Appl. Geophys. 2011, 168, 1015–1031. [Google Scholar] [CrossRef] [Green Version]
- Satake, K.; Ishibe, T.; Murotani, S.; Mulia, I.E.; Gusman, A.R. Effects of uncertainty in fault parameters on deterministic tsunami hazard assessment: Examples for active faults along the eastern margin of the Sea of Japan. Earth Planets Space 2022, 74, 1–20. [Google Scholar] [CrossRef]
- Tinti, S.; Graziani, L.; Brizuela, B.; Maramai, A.; Gallazi, S. Applicability of the Decision Matrix of North Eastern Atlantic, Mediterranean and connected seas Tsunami Warning System to the Italian tsunamis. Nat. Hazards Earth Syst. Sci. 2012, 12, 843–857. [Google Scholar] [CrossRef] [Green Version]
- Molinari, I.; Tonini, R.; Lorito, S.; Piatanesi, A.; Romano, F.; Melini, D.; Hoechner, A.; Gonzàlez Vida, J.M.; Maciás, J.; Castro, M.J.; et al. Fast evaluation of tsunami scenarios: Uncertainty assessment for a Mediterranean Sea database. Nat. Hazards Earth Syst. Sci. 2016, 16, 2593–2602. [Google Scholar] [CrossRef] [Green Version]
- Kanamori, H.; Rivera, L. Source inversion of W phase: Speeding up tsunami warning. Geophys. J. Int. 2008, 175, 222–238. [Google Scholar] [CrossRef]
- Lomax, A.; Michellini, A. Mwpd: A duration-amplitude procedure for rapid determination of earthquake magnitude and tsunamigenic potential from P waveforms. Geophys. J. Int. 2009, 176, 200–214. [Google Scholar] [CrossRef] [Green Version]
- Hirshorn, B.; Weinstein, S.; Tsuboi, S. On the application of MWp in the near field and the March 11, 2011 Tohoku earthquake. Pure Appl. Geophys. 2013, 170, 975–991. [Google Scholar] [CrossRef]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Plag, H.; Stein, S.; Okal, E. Rapid determination of earthquake magnitude using GPS for tsunami warning systems, Geophys. Res. Lett. 2006, 33, L11309. [Google Scholar] [CrossRef] [Green Version]
- Angove, M.; Arcas, D.; Bailey, R.; Carrasco, P.; Coetzee, D.; Fry, B.; Gledhill, K.; Harada, S.; Von Hillebrandt-Andrade, C.; Kong, L.; et al. Ocean Observations Required to Minimize Uncertainty in Global Tsunami Forecasts, Warnings, and Emergency Response. Front. Mar. Sci. 2019, 6, 350. [Google Scholar] [CrossRef] [Green Version]
- Heidarzadeh, M.; Wang, Y.; Satake, K.; Mulia, I.E. Potential deployment of offshore bottom pressure gauges and adoption of data assimilation for tsunami warning system in the western Mediterranean Sea. Geosci. Lett. 2019, 6, 19. [Google Scholar] [CrossRef]
- Howe, B.M.; Arbic, B.K.; Aucan, J.; Barnes, C.R.; Bayliff, N.; Becker, N.; Butler, R.; Doyle, L.; Elipot, S.; Johnson, G.C.; et al. SMART Cables for Observing the Global Ocean: Science and Implementation. Front. Mar. Sci. 2019, 6, 424. [Google Scholar] [CrossRef] [Green Version]
- Selva, J.; Lorito, S.; Volpe, M.; Romano, F.; Tonini, R.; Perfetti, P.; Amato, A. Probabilistic tsunami forecasting for early warning. Nat. Commun. 2021, 12, 5677. [Google Scholar] [CrossRef]
- PD2—Faster Than Real Time (FTRT) Live Demo—European Project ChEESE—In ChEESE Project Web Page. Available online: https://cheese-coe.eu/media/news/cheese-conducts-live-demo-faster-real-time-tsunami-simulations (accessed on 28 February 2022).
- Live Demo Recording. Available online: https://www.youtube.com/watch?v=rkruUHAaleA (accessed on 28 February 2022).
- Cantavella, J.V.; Gaite, B.; González, C.; Naveiras, F.; Ros, E.; Sáenz, L. Plan Estatal de Protección Civil Ante el Riesgo de Maremotos. Edición Comentada; Publicación Instituto Geográfico Nacional: Madrid, Spain, 2021; 112p. [Google Scholar]
- Santos, A.; Koshimura, S.; andImamura, F. The 1755 Lisbon Tsunami: Tsunami Source Determination and its Validation. J. Disaster Res. 2009, 4, 41–52. [Google Scholar] [CrossRef]
- Martínez-Loriente, S.; Sallarés, V.; Gracia, E. The Horseshoe abyssal plain thrust could be the source of the 1755 Lisbon earthquake and tsunami. Commun. Earth Environ. 2021, 2, 145. [Google Scholar] [CrossRef]
- Baptista, M.A.; Miranda, J.M.; Luis, J.F. In Search of the 31 March 1761 Earthquake and Tsunami Source. Bull. Seism. Soc. Am. 2006, 96, 713–721. [Google Scholar] [CrossRef]
- Fukao, Y. Thrust faulting at a lithospheric plate boundary the Portugal earthquake of 1969. Earth Planet. Sci. Lett. 1973, 18, 205–216. [Google Scholar] [CrossRef]
- Mezcua, J.; Martínez Solares, J.M. Sismicidad del Área Ibero-Mogrebí, Publicación 203; Instituto Geográfico Nacional: Madrid, Spain, 1983; 301p. [Google Scholar]
- Instituto Geográfico Nacional (IGN). Spanish Seismic Catalogue. Available online: https://doi.org/10.7419/162.03.2022 (accessed on 1 May 2022).
- Demets, C.; Gordon, R.G.; Argus, D.F. Geologically current plate motions. Geophys. J. Int. 2010, 181, 1–80. [Google Scholar] [CrossRef] [Green Version]
- Sartori, R.; Torelli, L.; Zitellini, N.; Peis, D.; Lodolo, E. Eastern segment of the Azores-Gibraltar line (central-eastern Atlantic): An oceanic plate boundary with diffuse compressional deformation. Geology 1994, 22, 555–558. [Google Scholar] [CrossRef]
- Martínez-Loriente, S.; Gracia, E.; Bartolome, R.; Sallarès, V.; Connors, C.; Perea, H.; Lo Iacono, C.; Klaeschen, D.; Terrinha, P.; Danobeitia, J.J.; et al. Active deformation in old oceanic lithosphere and significance for earthquake hazard: Seismic imaging of the Coral Patch Ridge area and neighbouring abyssal plains (SW Iberian margin). Geochem. Geophys. Geosyst. 2013, 14, 2206–2231. [Google Scholar] [CrossRef] [Green Version]
- Gaite, B.; Cantavella, J.V.; González, C.; Rodríguez, B.; Robledano, A.; Carreño, E. Marine-fault and magnitude-scaling law database as input for real-time tsunami propagation computation. In Proceedings of the Iberfault 2018, Alicante, Spain, 11–13 June 2018. [Google Scholar]
- Instituto Geográfico Nacional (IGN). Digital Terrain Model MDT200. Available online: https://centrodedescargas.cnig.es/CentroDescargas (accessed on 1 May 2022).
- NASA JPL NASA Shuttle Radar Topography Mission Global 1 Arc Second. Distributed by NASA EOSDIS Land Processes DAAC. 2013. Available online: https://doi.org/10.5067/MEaSUREs/SRTM/SRTMGL1.003 (accessed on 27 April 2022).
- Interim Operational Users Guide for NEAMTWS, Version 1.10. Available online: http://www.ioc-tsunami.org/index.php?option=com_oe&task=viewDocumentRecord&docID=8129 (accessed on 1 February 2021).
- Schindelé, F.; Gailler, A.; Hébert, H.; Loevenbruck, A.; Gutierrez, E.; Monnier, A.; Roudil, P.; Reymond, D.; Rivera, L. Implementation and Challenges of the Tsunami Warning System in the Western Mediterranean. Pure Appl. Geophys. 2015, 172, 821–833. [Google Scholar] [CrossRef] [Green Version]
- Amato, A.; Avallone, A.; Basili, R.; Bernardi, F.; Brizuela, B.; Graziani, L.; Herrero, A.; Lorenzino, M.C.; Lorito, S.; Mele, F.M.; et al. From Seismic Monitoring to Tsunami Warning in the Mediterranean Sea. Seismol. Res. Lett. 2021, 92, 1796–1816. [Google Scholar] [CrossRef]
- Necmioğlu, Ö.; Turhan, F.; Özer Sözdinler, C.; Yılmazer, M.; Güneş, Y.; Cambaz, M.D.; Özener, H. Koeri’s tsunami warning system in the eastern mediterranean and its connected seas: A decade of achievements and challenges. Appl. Sci. 2021, 11, 11247. [Google Scholar] [CrossRef]
- Matias, L.; Baptista, M.A.; Omira, R.; Annunziato, A.; Franchello, G.; Carrilho, F. Third Generation Tsunami scenario matrix for the Portuguese Tsunami Early Warning System. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Matias, L.; Cunha, T.A.; Annunziato, A.; Baptista, M.A.; Carrilho, F. Tsunamigenic earthquakes in the Gulf of Cadiz: Fault model and recurrence. Nat. Hazards Earth Syst. Sci. 2013, 13, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Echave Lezcano, J. Elaboración de la Metodología y Base de Datos Numérica de Tsunamis Para el Sistema de Alerta de Tsunamis Español; Universidad de Cantabria: Santander, Spain, 2016. [Google Scholar]
- Bernard, E.; Titov, V. Evolution of tsunami warning systems and products. Philos. Trans. R. Soc. Lond. A 2015, 373, 20140371. [Google Scholar] [CrossRef] [PubMed]
- Macías, J.; Castro, M.J.; Ortega, S.; Escalante, C.; González-Vida, J.M. Performance benchmarking of Tsunami-HySEA model for NTHMP’s inundation mapping activities. Pure Appl. Geophys. 2017, 174, 3147–3183. [Google Scholar] [CrossRef] [Green Version]
- Macías, J.; Castro, M.J.; Escalante, C. Performance assessment of Tsunami-HySEA model for NTHMP tsunami currents benchmarking. Laboratory data. Coast Eng. 2020, 158, 103667. [Google Scholar] [CrossRef]
- Macías, J.; Ortega, S.; Castro, M.J.; González-Vida, J.M. Performance assessment of Tsunami-HySEA model for NTHMP tsunami currents benchmarking. Field cases. Ocean Model 2020, 152, 101645. [Google Scholar] [CrossRef]
- Álvarez-Gómez, J.A.; Aniel-Quiroga, Í.; González, M.; Otero, L. Tsunami hazard at the Western Mediterranean Spanish coast from seismic sources. Nat. Hazards Earth Syst. Sci. 2011, 11, 227–240. [Google Scholar] [CrossRef]
- García-Mayordomo, J.; Insua-Arévalo, J.M.; Martínez-Díaz, J.J.; Jiménez-Díaz, A.; Martín-Banda, R.; Martín-Alfageme, S.; Álvarez-Gómez, J.A.; Rodríguez-Peces, M.; Pérez-López, R.; Rodríguez-Pascua, M.A.; et al. The Quaternary Faults Database of Iberia (QAFI v.2.0). J. Iber. Geol. 2012, 38, 285–302. [Google Scholar] [CrossRef]
- Hayes, G. The finite, kinematic rupture properties of great-sized earthquakes since 1990. Earth Planet. Sci. Lett. 2017, 468, 94–100. [Google Scholar] [CrossRef]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library. Open Source Geospatial Foundation. Available online: https://gdal.org (accessed on 1 November 2021).
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools version 6. Geochem. Geophys. 2019, 20, 5556–5564. [Google Scholar] [CrossRef] [Green Version]
- QGIS.org. QGIS Geographic Information System. QGIS Association. Available online: http://www.qgis.org (accessed on 1 November 2021).
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 1 November 2021).
- Green, G. On the motion of waves in a variable canal of small depth and width. Trans. Camb. Philos. Soc. 1837, 6, 457–462. [Google Scholar]
Figure 2.
Map of tsunami alert zones (red polygons) to disseminate tsunami warnings to Civil Protection by the Spanish TWS. (a) Shows tsunami alert zones in the Iberian peninsula and vicinity, and (b) in the Canary islands.
Figure 2.
Map of tsunami alert zones (red polygons) to disseminate tsunami warnings to Civil Protection by the Spanish TWS. (a) Shows tsunami alert zones in the Iberian peninsula and vicinity, and (b) in the Canary islands.
Figure 3.
(a) Atlantic computational domain (ATL) at 1/2 arcmin resolution, scenario epicenter locations (red stars), and FCPs (circles); (b) epicenter locations (CC, N, E, S, W) and strikes of the computed scenarios; and (c) the four rectangular domains with different resolutions used in this study: Atlantic (ATL), Gulf of Cadiz and Canary Islands (GCIC), Gulf of Cadiz and north of the Iberian peninsula (GCN), and Gulf of Cadiz (GC). Domain boundary coordinates are given in Table 2.
Figure 3.
(a) Atlantic computational domain (ATL) at 1/2 arcmin resolution, scenario epicenter locations (red stars), and FCPs (circles); (b) epicenter locations (CC, N, E, S, W) and strikes of the computed scenarios; and (c) the four rectangular domains with different resolutions used in this study: Atlantic (ATL), Gulf of Cadiz and Canary Islands (GCIC), Gulf of Cadiz and north of the Iberian peninsula (GCN), and Gulf of Cadiz (GC). Domain boundary coordinates are given in Table 2.
Figure 4.
Synthetic results for all FCPs and scenarios: (a) for tsunami maximum height; (b) for tsunami arrival time. Scen0, in blue circles, denotes the results of the reference scenario, red circles the mean, and black triangles the value at the 95th percentile at each FCP. (c,d) black dots show standard deviation for every FCP for the tsunami maximum height and arrival time, respectively, (e,f) are maps of FCPs with color-coded mean standard deviation of tsunami maximum height and arrival time, respectively. Color-coded scale limits have been defined as the mean and 95th percentile of all the values.
Figure 4.
Synthetic results for all FCPs and scenarios: (a) for tsunami maximum height; (b) for tsunami arrival time. Scen0, in blue circles, denotes the results of the reference scenario, red circles the mean, and black triangles the value at the 95th percentile at each FCP. (c,d) black dots show standard deviation for every FCP for the tsunami maximum height and arrival time, respectively, (e,f) are maps of FCPs with color-coded mean standard deviation of tsunami maximum height and arrival time, respectively. Color-coded scale limits have been defined as the mean and 95th percentile of all the values.
Figure 5.
Black dots indicate normalized largest differences of maximum height in FCPs for cases corresponding to scenarios where one source parameter takes different values in the range defined in this study from the scenario of reference: varying (a) strike, (b) dip, (c) magnitude and (d) location.
Figure 5.
Black dots indicate normalized largest differences of maximum height in FCPs for cases corresponding to scenarios where one source parameter takes different values in the range defined in this study from the scenario of reference: varying (a) strike, (b) dip, (c) magnitude and (d) location.
Figure 6.
Geographic distribution of normalized largest differences in maximum height and arrival time for the same cases as in Figure 5, varying one source parameter from the reference scenario. (a,e) Differences between cases in which the strike is varied; (b,f) the dip is varied; (c,g) the magnitude is varied; (d,h) the location is varied. The differences are normalized with respect to the values of the reference scenario. The color of the circles indicates the ratio between the largest differences for each case and the values of the reference scenario in each FCP.
Figure 6.
Geographic distribution of normalized largest differences in maximum height and arrival time for the same cases as in Figure 5, varying one source parameter from the reference scenario. (a,e) Differences between cases in which the strike is varied; (b,f) the dip is varied; (c,g) the magnitude is varied; (d,h) the location is varied. The differences are normalized with respect to the values of the reference scenario. The color of the circles indicates the ratio between the largest differences for each case and the values of the reference scenario in each FCP.
Figure 7.
Tsunami warning maps obtained from the maximum tsunami height at close-to-the-coast FCPs computed with the (a) decision matrix, (b) scenario of reference, (c) mean, (d) 90th percentile, and (e) maximum of all 135 scenario results, computed at 1/2 arcmin domain resolution.
Figure 7.
Tsunami warning maps obtained from the maximum tsunami height at close-to-the-coast FCPs computed with the (a) decision matrix, (b) scenario of reference, (c) mean, (d) 90th percentile, and (e) maximum of all 135 scenario results, computed at 1/2 arcmin domain resolution.
Figure 8.
Tsunami warning maps obtained from the results of the 135 scenarios computed at different domain resolutions: (a,d) 1/2 arcmin, (b,e) 1/4 arcmin, and (c) 1/8 arcmin. The warning level is computed as the 90th percentile of maximum height of FCPs belonging to a specific coastal region.
Figure 8.
Tsunami warning maps obtained from the results of the 135 scenarios computed at different domain resolutions: (a,d) 1/2 arcmin, (b,e) 1/4 arcmin, and (c) 1/8 arcmin. The warning level is computed as the 90th percentile of maximum height of FCPs belonging to a specific coastal region.
Table 1.
Tsunami alert levels considered on the NEAMTWS and used in the Spanish TWS.
| Alert Level | Tsunami Height (m) | Run-Up (m) | Coastal Effects |
|---|---|---|---|
| WATCH | >0.5 | >1 | Coastal flooding |
| ADVISORY | 0.2–0.5 | <1 | Currents, retreat from the sea, damage to ports, small flooding on beaches |
| INFORMATION | <0.2 | No tsunami hazard |
Table 2.
Comparison of operational parameters at the National Tsunami Warning System of Spain for tsunamis generated in the Gulf of Cadiz and at the ChEESE live demo.
Table 2.
Comparison of operational parameters at the National Tsunami Warning System of Spain for tsunamis generated in the Gulf of Cadiz and at the ChEESE live demo.
| Operational at IGN | ChEESE Live Demo | |
|---|---|---|
| Model | Tsunami-HySEA v-3.6.1 | Tsunami-HySEA v-3.8.1_MC |
| Target area | Area of the Gulf of Cádiz (Atlantic ocean): from −18.5° W to −1° W in longitude and from 27° N to 45° N in latitude. | |
| Computational domain | One computational domain with one numerical resolution: ATL (−21°, 26°; 1°, 45°) | Four computational domains with three numerical resolutions 1. ATL ½ arcmin (−18.5°, 27°; −1°, 45°) 2. GCN ¼ arcmin (−13°, 33.5°; −1°, 45°) 3. GCIC ¼ arcmin (−18.5°, 27°; −5°, 38°) 4. GC ⅛ arcmin (−13°, 33.5°; −4°, 38°) (left-bottom; right-top corners coordinates in longitude, latitude) |
| Model resolution | ½ arcmin | ½–¼–⅛ arcmin |
| Size of the problem (number of volumes) | 5,472,000 | ATL—4,536,000 GCN—7,948,800 GCIC—8,553,600 GC—9,331,200 |
| Simulated time | 8 h | 4 h |
| Storage frequency for time series | 30 s | 15 s |
| Number of simulations | 1 | 135 × 4 |
| Computational resources | Two nodes/two NVIDIA V100 GPUs | 68 nodes/272 NVIDIA V100 GPUs |
| Time to solution | 2.5 min | 1 min—ATL 3 min—GCN & GCIC 7 min—GC Total time: ≈7 min (parallel) |
| Deterministic products | Tsunami arrival time Maximum tsunami height Alert levels | Tsunami arrival time Maximum tsunami height Alert levels |
| Include uncertainty | No | Yes |
Table 3.
Mean of normalized greatest maximum height differences and of normalized arrival time differences for all FCPs and cases varying one of the four source parameters.
Table 3.
Mean of normalized greatest maximum height differences and of normalized arrival time differences for all FCPs and cases varying one of the four source parameters.
| Cases with Varying Parameter | Mean of Normalized Difference on Maximum Height (m) | Mean of Normalized Difference on Arrival Time (min) |
|---|---|---|
| Strike | 0.163 ± 0.151 | 1.150 ± 9.356 |
| Dip | 0.324 ± 0.241 | 2.076 ± 13.333 |
| Location | 0.505 ± 0.377 | 4.012 ± 20.296 |
| Magnitude | 1.065 ± 0.556 | 8.659 ± 34.956 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Gaite, B.; Macías, J.; Cantavella, J.V.; Sánchez-Linares, C.; González, C.; Puertas, L.C. Analysis of Faster-Than-Real-Time (FTRT) Tsunami Simulations for the Spanish Tsunami Warning System for the Atlantic. GeoHazards 2022, 3, 371-394. https://doi.org/10.3390/geohazards3030019
AMA Style
Gaite B, Macías J, Cantavella JV, Sánchez-Linares C, González C, Puertas LC. Analysis of Faster-Than-Real-Time (FTRT) Tsunami Simulations for the Spanish Tsunami Warning System for the Atlantic. GeoHazards. 2022; 3(3):371-394. https://doi.org/10.3390/geohazards3030019
Chicago/Turabian StyleGaite, Beatriz, Jorge Macías, Juan Vicente Cantavella, Carlos Sánchez-Linares, Carlos González, and Luis Carlos Puertas. 2022. "Analysis of Faster-Than-Real-Time (FTRT) Tsunami Simulations for the Spanish Tsunami Warning System for the Atlantic" GeoHazards 3, no. 3: 371-394. https://doi.org/10.3390/geohazards3030019
APA StyleGaite, B., Macías, J., Cantavella, J. V., Sánchez-Linares, C., González, C., & Puertas, L. C. (2022). Analysis of Faster-Than-Real-Time (FTRT) Tsunami Simulations for the Spanish Tsunami Warning System for the Atlantic. GeoHazards, 3(3), 371-394. https://doi.org/10.3390/geohazards3030019
