Extending the Quality of Secure Service Model to Multi-Hop Networks

Abstract

Rarely are communications networks point-to-point. In most cases, transceiver relay stations exist between transmitter and receiver end-points. These relay stations, while essential for controlling cost and adding flexibility to network architectures, reduce the overall security of the respective network. In an effort to quantify that reduction, we extend the Quality of Secure Service (QoSS) model to these complex networks, specifically multi-hop networks. In this approach, the quantification of security is based upon probabilities that adversarial listeners and disruptors gain access to or manipulate transmitted data on one or more of these multi-hop channels. Message fragmentation and duplication across available channels provides a security performance trade-space, with its consequent QoSS. This work explores that trade-space and the corresponding QoSS model to describe it.

1. Introduction

The concept of Quality of Service (QoS) is well understood as providing objective metrics to describe the traditional performance characteristics of a communication network, the set of wired or wireless channels that may exist between a transmitter and receiver. A network, though, may be vulnerable to either malicious disruptors or unauthorized listeners. Hence, metrics to describe the security of a communication network, including aspects, such as confidentiality and integrity, are also needed. Although investigated [1,2,3], such metrics have generally eluded researchers and service providers. In a recent publication, the Quality of Secure Service (QoSS) model was derived as a baseline approach to define the static security characteristics of a point-to-point network [4].

QoSS describes in measurable and repeatable terms the security available to an end-user of a communication network. Security, in this context, refers to the ability to maintain a high-level of the traditional Information Technology (IT) qualities of confidentiality, integrity, and availability for a communication network. A communication network relies on one or more wired or wireless channels between intermediate nodes. In addition to noise, these channels may be affected by any combination of three malicious attack vectors: Denial of Service (DoS), data injection, or eavesdropping (data extraction). Managing those threats requires an ability to accurately gauge the likelihood and severity of the threat, and adapt the security features available in the system to mitigate the threat.

Understanding that few communication networks are completely point-to-point, it is essential to examine the effect that multiple intermediaries, with varying levels of security, will have on the overall network QoSS. This paper details, adapts, and extends the QoSS model to multi-hop networks, and demonstrates the potential improvement in security when multiple channels are used throughout a complex communication network while also creating a broad foundation for the development of a simulation environment for the verification and validation of the model. This document illustrates an extension of the mathematical framework and analysis needed to define design requirements for multi-hop communication networks. It takes into consideration the probability of exploitation, and provides a foundation for subsequent work analyzing network security performance in the presence of varied environmental characteristics.

The primary contribution of this work is the extension of the QoSS model to a multi-hop scenario, wherein multiple parallel heterogeneous physical channels may exist between source and destination end points. Section 2 of this paper presents related work and previously derived calculations of the QoSS metrics for single-channel and multiple channel, point-to-point communication architectures. Section 3 extends the calculations to cover multi-hop communication architectures. Section 4 provides case study examples for complex multi-channel and multi-hop communication architectures. Section 5 details future research and provides a conclusion.

2. Related Work

Network architects need methods to quantify the security available in their systems. Ideally, those methods could also help to increase security, without impacting flexibility. Incorporating more security or reliability mechanisms into a system is much easier than it is to quantify the resulting security. By analogy, consider computer performance metrics. To quantify the performance of a computer, it is generally accepted that “the only consistent and reliable measure of performance is the execution time of real programs, and that all proposed alternatives to time as the metric or to real programs as the items measured have eventually led to misleading claims or even mistakes in computer design” [5]. With such a clear metric, it is unsurprising that computer performance has steadily improved over several decades.

One technique that has demonstrably improved reliability, as well as potentially improved security based on the specific applications, is to fragment and distribute data across communication channels [6,7]. Signaling System Number 7 (SS7) [8,9], Redundant Array of Inexpensive Disks (RAID) [5], transmission diversity within 5G cellular networks [10], and Perfectly Secure Message Transmission (PSMT) [11,12,13,14] are all examples of using two or more channels to increase system reliability. Research has also evaluated multiple channels for sensor networks [15]. These examples are inspiration for the multi-channel architecture introduced in conjunction with the QoSS model. Directly comparing the security of those respective applications, including an arbitrary multi-channel communication architecture, is challenging without the QoSS modeling framework.

There are some similarities between the proposed fragmentation of data across multiple communication channels and Multiple-Input Multiple-Output (MIMO) wireless communication architectures as defined by various standards [16]. MIMO exploits multi-path propagation within the radio frequency spectral medium to enhance the performance of a single data signal. The channels referred to in the QoSS model can be considered logical channels, as opposed to their physical implementations, because the QoSS model resides at a higher layer of the networking stack. With that, the QoSS model may utilize any possible physical medium for connectivity to the fragment and spread the data across the multiple connections as a technique to increase the security of the transmissions.

To compare the security of one network to another, a set of quantifiable and repeatable metrics that account for the confidentiality, integrity, and availability of the network is essential. Methods already exist for assessing and improving the availability of a network. These are conveyed in traditional QoS metrics [17]. Metrics that measure confidentiality and integrity can be derived using a probabilistic model that considers data leakage and data corruption in place of confidentiality and integrity, and thereby quantify the QoSS. As shown in Figure 1, a communication network provides a channel for a user to send data across, and that channel may be comprised of one or multiple channels, which should be transparent to the end-user. The QoSS model allows the direct and repeatable quantification of the security, specifically the confidentiality and integrity, available in a single or multi-channel network under static configurations. Authentication, which is based upon and derivative of confidentiality and integrity, has been demonstrated to be feasible using multiple transmission paths [18]. In this approach, the quantification of security is based upon probabilities that attackers, whether they are adversarial listeners or disruptors, are able to gain access to or change the original message. The attackers may also only have access to a portion of the channels within the network. Message fragmentation and duplication across the available channels provide demonstrably improved theoretical performances at the expense of the increased complexity of the network architecture.

Rather than quantify confidentiality directly, the probability of confidentiality is quantified as a surrogate. The probability of confidentiality, $P\left(C\right)$, is related to another new metric, the probability of leakage, $P\left(l\right)$, as follows:

$$P\left(C\right)=1-P\left(l\right).$$

(1)

For leakage to occur, a listener must intercept a message, decrypt it (if applicable), and decode the data contained in the message. The probability of interception, $P\left(int\right)$, quantifies the probability that a listener with channel access will receive the message. The probability of decryption, $P\left(dcr\right)$, quantifies the probability that the adversary will decrypt it. Finally, the probability of decoding, $P\left(dco\right)$, quantifies the probability that an adversary will decode the message.

Similarly, the probability of integrity is quantified instead of attempting to quantify integrity directly. The probability of integrity, $P\left(I\right)$, is related to the probability of corruption, $P\left(c\right)$, as follows:

$$P\left(I\right)=1-P\left(c\right).$$

(2)

According to [19], and followed in [4], corruption is considered to have three components: noise, active data injection, and data suppression. The probability of noise occurring in a message, $P\left(n\right)$, is the probability that a message will be adversely affected by noise. Noise is a natural phenomenon that happens regardless of the transmitter’s capability. The probability of injection, $P\left(inj\right)$, quantifies the probability that an adversary will inject false or misleading data into the message. Finally, the probability of suppression, $P\left(s\right)$, quantifies the probability that an adversary will actively suppress or jam the message, thus preventing the receiver from getting the message. This point is somewhat unconventional with respect to the generally accepted concept that suppression, specifically DoS attacks on a network, influence the availability of a network. While true that a DoS attack on a network affects the availability of the network, the active adversarial contamination of a network by injecting so much false data to disable communications, as is the case with a traditional DoS attack, or to overtly jamming a network signal with a false signal, as is the case for a traditional RF jamming attack, relates more directly to the definition of corruption. Therefore, using this approach, all forms of jamming, to include DoS attacks, are considered attacks on the integrity of the data or message, not as an attack on the availability of the network. Conveniently, this groups all adversarial influences under the metrics for confidentiality and integrity.

For the QoSS model, the metrics used to describe availability are already conveyed in QoS metrics. This is reflected as $A=QoS$, where $QoS$ is the set of metrics that include cost, jitter, latency, bandwidth, and bit rate, which already provide a repeatable method of measuring availability. These metrics reflect the basic network characteristics without adversarial influence.

The probability of leakage for each channel within a communication architecture is defined in [4] as:

$$P\left(l\right)=\frac{P\left(int\right)·P\left(dcr\right)·P\left(dco\right)·\sigma }{n}.$$

(3)

This equation considers the number of listeners, $\sigma$, that may be accessing the network and the number of channels, n, between the transmitter and receiver. The number of channels also directly influences the Average Channel Loading (AL) and Duplication Factor (DF) for a communication system, specifically whether the message is fragmented across the n channels, what size those fragments may be, and how many times those specific fragments are duplicated, either on one channel or across multiple channels.

The probability of corruption for each channel, n, between the transmitter and receiver in a communication architecture is defined as:

$$P\left(c\right)=\frac{\left(\begin{array}{c}\left(1-P(n)\right)P(inj)AL+\left(P(n)+\frac{P(s)}{DF}\right)-\left(P(n)\frac{P(s)}{DF}\right)\\ -\left(1-P(n)\right)\left(P(n)+\frac{P(s)}{DF}\right)P(inj)AL\end{array}\right)\rho }{n},$$

(4)

which, in this case, considers the number of disruptors, $\rho$, that have access to network. Again, the number of channels, n, directly influences the factors AL and DF for a communication system, and whether the message is fragmented, the size of the fragments, and how many times those specific fragments are duplicated, either on one channel or across multiple channels.

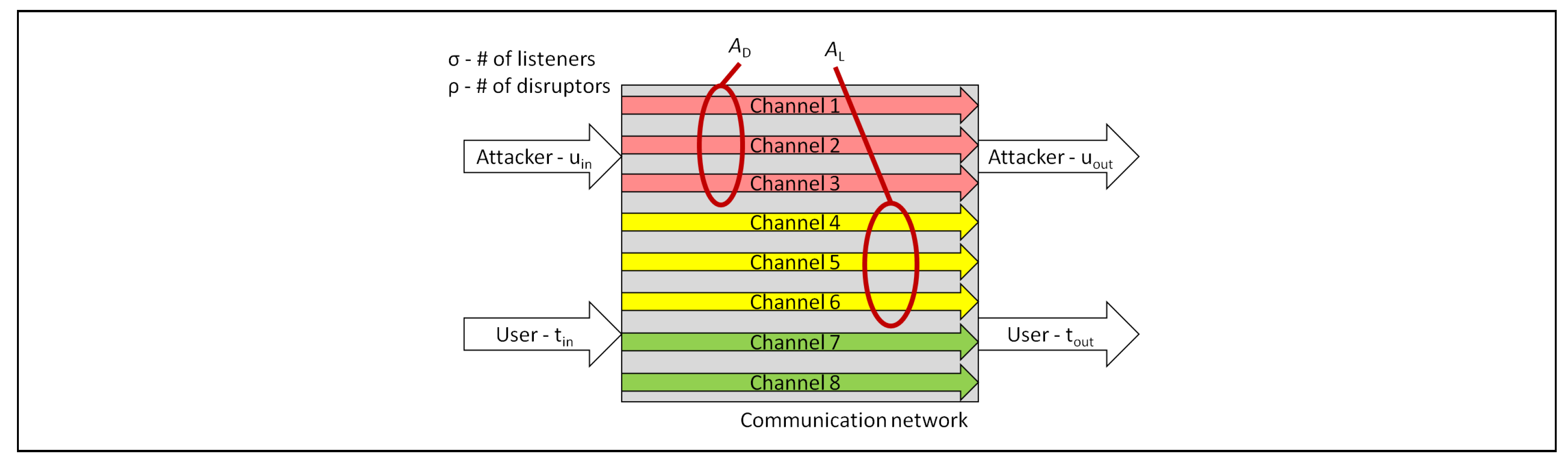
3. QoSS Applied to a Multi-Hop Network

3.1. Reliability of Systems

Reliability is defined as the “ability of an item to perform a required function, under given environmental and operational conditions and for a stated period of time” [20]. For the purposes of QoSS, the item is a communication network, and the required function is to transmit data in a secure manner. Additionally, the definition of security is the “availability of performance with respect to prevention of deliberate hostile actions”, where availability of performance includes reliability performance, maintainability performance, and maintenance support performance. With that, the reliability function is the “probability that the item survives” over a specific period of time [20]. For the concept of unconditional reliability to be possible, both reliability and security are necessary. The message must be correct and must not be intercepted; in other words, both the disruptor and the listener must fail to achieve their objectives [21].

Calculation of the reliability of a system varies, depending on whether the system is constructed in series, parallel, or is a hybrid, containing a combination of series and parallel items. Series systems have items, elements, or devices connected in series, and the entire system fails if any of the individual elements fail. The reliability of such a system is calculated as the product of each element’s reliability in the series, or specifically:

$$R_{series}=R_1\times R_2\times R_3\times \cdots \times R_n=\prod _{j=1}^n{R}_j,$$

(5)

where R represents the reliability of each element. The practical implication is that the reliability of a series system is always lower than the reliability of any of its components. The reliability of a parallel system represents the reliability of mutually independent elements such that all must fail for the entire system to fail. The reliability of a parallel system is therefore calculated as:

$$R_{parallel}=1-\prod _{j=1}^n(1-R_j),$$

(6)

where, again, R represents the reliability of each element [22]. In contrast to a series system, the reliability of a parallel system is always higher than the reliability of any of its components. Hybrid systems will, of course, vary, depending on their construction.

3.2. Reliability Applied to QoSS

Applying the definitions from Section 3.1 to the QoSS model, a failure is any event where data fail to be transmitted across some portion of a network, securely or otherwise. Any failure will affect the confidentiality, integrity, or availability of the network, both individually and collectively. In terms of QoSS, confidentiality and integrity are affected by adversarial actions, whereas availability is affected by natural or non-adversarial events. The QoSS model presents a method to quantify security based measures of system reliability, specifically confidentiality, integrity, and availability. As the probability of failure is complimentary to the reliability, then, by extrapolation, the probability of confidentiality and the probability of integrity can both be viewed as measures of reliability in addition to the typical availability metrics.

Iteratively, each hop in a series may be calculated and then, using typical reliability calculations for a system of components may be multiplied to yield the reliability of the system. To obtain the reliability of the larger system, the probability of interception, decryption, decoding, noise, suppression, and injection may all be multiplied by each other and the full QoSS may be calculated in the same manner. Each hop has the similar cumulative effect of reducing the reliability of the network in terms of security because an adversarial listener or disruptor has additional opportunities to infiltrate. A naive approach would simply average the values together, but that overlooks the cumulative effect of multiple hops. The architecture presented here makes the assumption that message packets are reformed and retransmitted at each hop. As such, signal degradation is only a concern on a per-hop basis. Admittedly, this view is overly conservative in that the possibility of a listener obtaining a message at one or more hops may be counted multiple times.

3.3. Combinational Considerations such as Fragmentation and Duplication

To compute an overall QoSS value of a network composed of multi-hop and parallel logical channels, it is necessary to consider the effects of the fragmentation and duplication of messages on the QoSS metrics.

Consider a simple point-to-point network with one channel and perfect, unbreakable encryption. What if that system were to instead have two parallel channels, one with perfect encryption, and the other with no encryption? How should the summary QoSS values then be computed? If the data were fragmented into equally-sized portions, and an adversarial listener has access to both of those channels, then they would have unencrypted access to exactly half of the data. However, equal sized portions is not the only way to split the data. A “single fragment could represent a single bit of a message while the maximally-sized fragment could contain the entire message” [23]. Therefore, the amount of data accessible to an adversary is based upon the proportions of data that are transmitted across the two parallel channels, and would be represented as a weighted average.

The previous example assumed that the message was split evenly and without any duplication. If only a single copy of each bit from a given message is sent, either physically via multiple channels or temporally via repeated messages, then there is zero duplication. Conversely, “full duplication indicates that the entire message is sent across each of the available channels” [23], which would lead, in the previous example, to the adversary having full access to the message via the unencrypted channel.

If the data is unevenly or non-uniformly split among the channels, in a similar manner to RAID architectures [5], or data are duplicated across the channels, then the amount of data accessible to the adversary would be a weighted average based upon the proportional splitting and the DF of the channel(s), which in turn causes the broader QoSS metrics to utilize a weighted average across the available channels.

To maintain simplicity in the example cases, data is assumed to be split equally and without duplication across parallel links. However, the model can support more elaborate combinations when needed.

3.4. Calculation of Multi-Hop Network QoSS

When reducing a complex equation in algebra, specific rules dictate which operations are solved first, thus simplifying to a more easily-solvable equation. The same is true when reducing the complexity of a communications network into an equivalent single-channel, point-to-point network. Through similar decomposition, it is possible to analyze a complex communication network that utilizes multiple intermediary nodes and multiple channels, similar to the example network link nodes A and D as shown in Figure 2, and to quickly compare the QoSS metrics to another network. When data are split across multiple channels, the end-user may remain agnostic to how the data is handled between the end-points within the larger, end-to-end network, in the same manner as an end-user is agnostic to multiple intermediary hops in current network architectures.

3.4.1. Step 1

The initial step in reducing complexity is to assess how the two end-points are connected, if there are multiple intermediary nodes, and whether the network utilizes multiple channels. In the reduction and simplification process, the primary goal is to derive an equivalent point-to-point network by reducing the number of hops or multi-channel connections between end-points thus leading to an equivalent point-to-point link. To begin, the QoSS metrics, specifically $P\left(C\right)$ and $P\left(I\right)$, must be calculated for all intermediary connections between nodes. This is accomplished by applying Equations (3) and (4) and solving for $P\left(C\right)$ and $P\left(I\right)$, respectively. Using the example of Figure 2, this would require calculating $P\left(C\right)$ and $P\left(I\right)$ for the eight individual links.

3.4.2. Step 2

For the next step, if the link between two nodes contains multiple channels, for example, between nodes X and Y in Figure 2, then the respective QoSS metrics for those two links are averaged. To be precise, a weighted average of the links is applied based on AL and DF as described in Section 3.3. If, on the other hand, the link between two nodes contains multiple hops, for example, link $\langle \mathbf{A}\mathbf{2}\text{-}\mathbf{B},\mathbf{B}\text{-}\mathbf{C},\mathbf{C}\text{-}\mathbf{D}\mathbf{2}\rangle$ in Figure 2, then the respective QoSS metrics for those three links are multiplied together, as detailed by Equation (5). It is not possible to apply Equation (5) if there are multiple channels between the end-points, thus collapsing multi-channel connections into an equivalent single channel takes president, after which Equation (5) may be applied. This is the process for finding the QoSS equivalent for nodes $\left[\mathbf{A}>\mathbf{X}>\mathbf{Y}>\mathbf{D}\right]$ in Figure 2.

3.4.3. Step 3

Repeat steps 1 and 2 as necessary to further reduce the system in Figure 2 to one, point-to-point connection. By following these steps, the point-to-point equivalent QoSS for a complex network may be derived. For example, once the two links between nodes X and Y have been collapsed into one equivalent QoSS value by weighted average, then the series of three links of $\langle \mathbf{A}\mathbf{3}\text{-}\mathbf{X},\mathbf{X}\text{-}\mathbf{Y},\mathbf{Y}\text{-}\mathbf{D}\mathbf{3}\rangle$ may be multiplied together per (5), at which point the system may be fully reduced to one point-to-point link.

4. Case Studies of Multi-Channel and Multi-Hop QoSS

The following case studies will provide detail as to how to calculate the probability of confidentiality and the probability of integrity for various network configurations. Several intermediary steps may be necessary to reach the equivalent single-channel, point-to-point network, which provides the most direct method of comparison.

4.1. Single-Channel, Point-to-Point Network

As the simplest case, a single-channel point-to-point network provides a starting point for developing the QoSS model. This case, as depicted in Figure 3, is similar to the baseline example presented in [4]. Since there is only one channel and one point-to-point connection, there is only one set of QoSS characteristics. For the single-channel point-to-point network, those arbitrary characteristics are also shown in Figure 3, complete with the calculated Probability of Confidentiality and Probability of Integrity. This first case is intended to be somewhat representative of a simple, yet realistic, communication network and its characteristics. As such, this network is presented without encryption or unusual encoding. This network is assumed to be wireless, and will be assigned a probability of interception of $0.5$ and, because noise is a natural phenomena, the probability of noise will be assigned as $0.25$. Finally, because it is wireless, the network is also susceptible to jamming and, to a much lesser degree, spoofing. With there being only one channel, that implies the number of listeners and disruptors is at most one each. These QoSS values will also serve as a baseline comparison for the multi-hop and multi-channel networks.

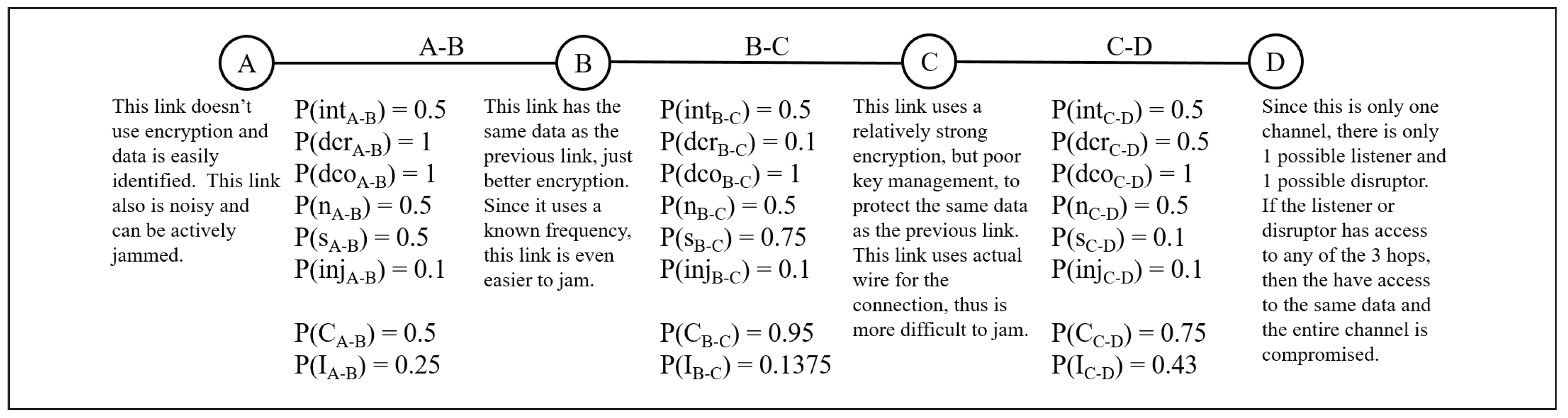
4.2. Single-Channel, Three-Hop Network

A more realistic example is a network that employs several intermediary nodes to forward data, as shown in Figure 4. For this example, two intermediary nodes relay the data, making it a four-node network, with three independent links between the end points. Each section of the communication network, $\langle \mathbf{A}\text{-}\mathbf{B},\mathbf{B}\text{-}\mathbf{C},\mathbf{C}\text{-}\mathbf{D}\rangle$, may have different characteristics because they may traverse different interconnecting channels or they may travel different distances. Those characteristics are also shown in Figure 4, with notionally assigned values for illustration. To calculate the QoSS for each link between hops, the values may be handled in the same manner as the single channel in Figure 3. However, to calculate the equivalent single channel point-to-point network, as shown in Figure 5, the equivalent $P\left(C\right)$ and $P\left(I\right)$ are simply calculated by multiplying each of the component probabilities of the confidentiality or probability of integrity values, respectively. This final value of the equivalent single-channel, point-to-point network is shown in Figure 5.

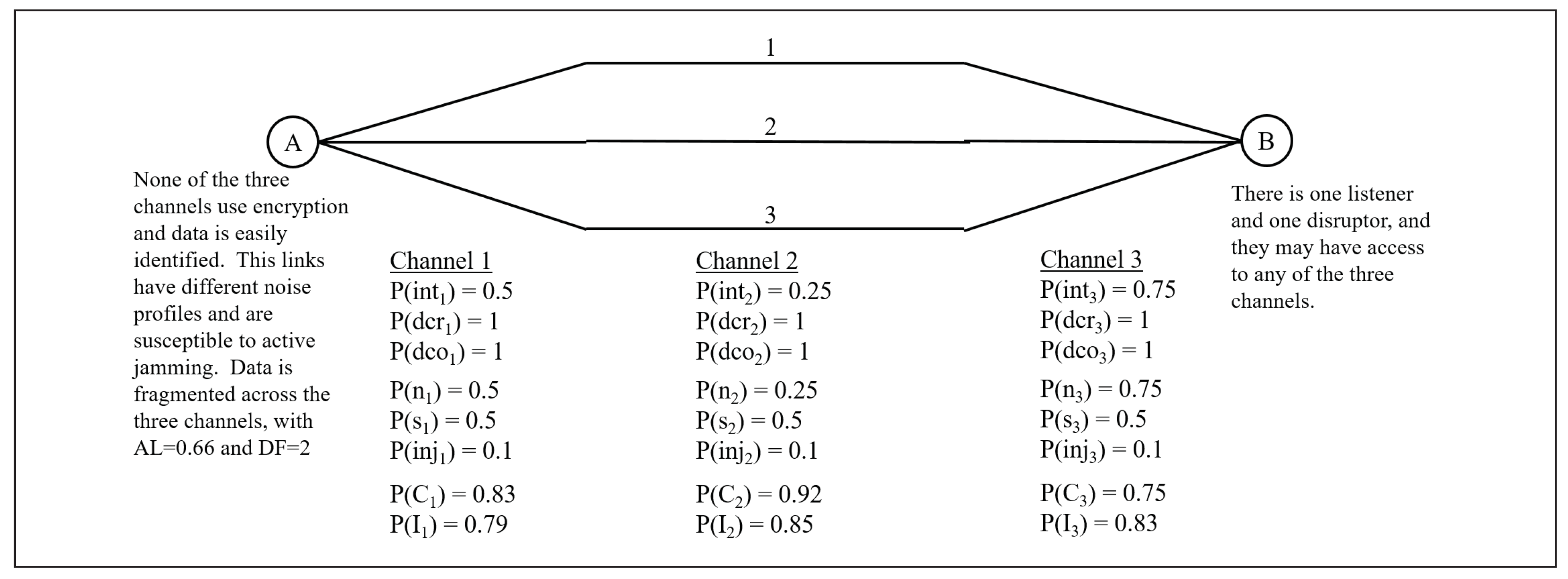
4.3. Three-Channel, Point-to-Point Network

A third example network incorporates the concept of multiple channels between the two end-points, as described by the theory of Perfectly Secure Message Transmission [11,12,13,14] and as shown in Figure 6. This third example network follows the calculations for multi-channel QoSS as detailed in [4]. In this example, there is $\rho =1$ listener and $\sigma =1$ disruptor with access to the network, and they may have access to any of the channels. The data are fragmented across the three channels such that the AL, the average percent of the message on any of the channels, is $0.66$ and the DF, the average number of times a given fragment is transmitted, is 2. The QoSS is similar to that of Figure 3 with some minor variations in the characteristics to highlight the possibility that the three channels cross different network infrastructures. The network equivalent, shown in Figure 7 is represented as a single-channel network with average QoSS characteristics of $P\left(C\right)=0.833$ and $P\left(I\right)=0.789$. Compared to the single-channel point-to-point network in Figure 3 or the single-channel three-hop equivalent network in Figure 5, this network has a significantly improved probability of confidentiality and probability of integrity despite being more complex.

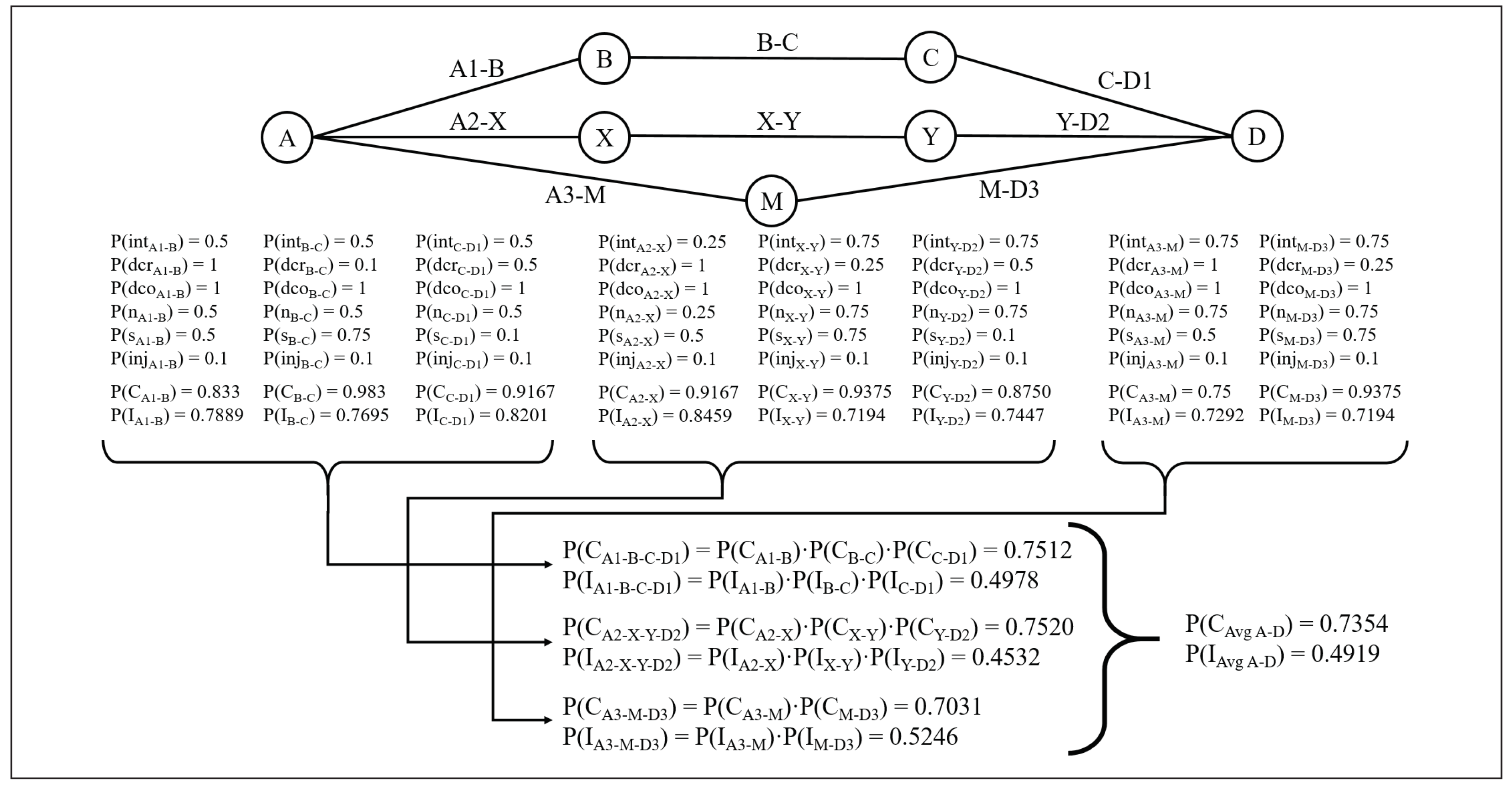
4.4. 3-Channel, 3-Hop Network

This final example incorporates the previous two examples to create a realistic network, to highlight the order needed to reduce the complexity, and to demonstrate the QoSS analysis process. The final example features three channels, two of which have two intermediate nodes and the third with only one intermediate node, thus creating a three-channel, multi-hop network, as shown in Figure 8. In the same manner in which the network shown in Figure 4 may utilize three different interconnecting channels for each of the intermediate links and the network shown in Figure 6 may utilize three different interconnecting paths or media for each channel, so too may Figure 8 utilize different interconnecting channels, which may feature different distances, architectures, or technologies, for each of the eight different, independent links. Most important is the fact that the end-user must remain agnostic of the underlying architecture.

In this example, and providing continuity with the example network shown in Figure 4, there is $\rho =1$ listener and $\sigma =1$ disruptor with access to the network, and they may have access to any of the channels. The data are fragmented across the three channels such that the AL, the average percentage of the message on any of the channels, is $0.66$ and the DF, the average number of times a given fragment is transmitted, is 2. The QoSS is again similar to all of the previous examples with some minor variations in the characteristics to highlight the possibility that each of the eight different, independent links feature different distances, architectures, or technologies.

The first step, as detailed in Section 3.4, calculates the QoSS for each independent link. The next step eliminates the intermediary nodes from each of the three channels. The final step consolidates the multi-channel architecture into one point-to-point connection. With the single point-to-point connection, it becomes trivial to compare the QoSS characteristics of Figure 8 to the more simple system architectures presented in Figure 3, Figure 4, and Figure 6 and their respective single-channel, point-to-point equivalents.

Based on the comparison of the equivalent QoSS characteristics of Figure 8 to the QoSS characteristics of Figure 3, Figure 4, and Figure 6, there are several details that must be highlighted. The example that has, after reduction, the highest probability of confidentiality and probability of integrity is Figure 6 primarily because it employs three channels that feature message fragmentation and duplication across the three available channels. It is observed that simply splitting the data across the available channels, with some duplication, provides a significant increase to the available security of the system, despite the number of potential listeners and disruptors. Conversely, the example that has, after reduction, the lowest probability of confidentiality and probability of integrity is Figure 4 because it employs a single channel with two intermediate nodes. The intermediate nodes provide opportunities for adversarial intervention in the transmission. Furthermore, since there is only one channel, there is no benefit of message fragmentation and duplication, and any listener or disruptor has just the one channel to target. As an adequate median example, Figure 8 demonstrates the improved QoSS characteristics of utilizing multiple channels and message fragmentation and duplication across the three available channels while also demonstrating some of the potentially degraded QoSS because of the multiple intermediary nodes.

4.5. Implications of Results

Setting up the QoSS model requires making some assumptions about network characteristics, though that is a challenging task. For example, when $P\left(int\right)=1$ is used in the case study, it is assumed that an adversary would be able to intercept all critical data in that link, whereas when $P\left(int\right)=0.1$, it is assumed that an adversary is not likely to intercept any critical data in that link. When $P\left(dcr\right)=1$, the assumption implies that no encryption is used, and when $P\left(dcr\right)=0$, the assumption implies a somewhat unrealistic perfectly strong encryption algorithm and strong password are used to protect the data. These assumptions further imply knowledge about the adversary’s fullest capabilities and intentions. Typically, those cannot be fully known. Despite that, the adversary’s capabilities and intentions must be considered and included in the probabilistic aspect of these metrics. This model provides a framework to estimate what is possible within the current state-of-the-art and under a set of operational characteristics.

Another complicating factor is that adversarial intentions or capabilities may rapidly change or may be influenced by different situations. Because the QoSS model reflects a single moment in time, it may not capture those dynamic changes, or even the technical and environmental conditions within the network. New information, refined research, or updated environmental and systemic conditions may be used to update the model. These iterations point to the need for a model that is able to capture both the single snapshot in time and the dynamic, time-varying characteristics. The differences in static and dynamic results highlight the need for a simulation environment, which is the focus of future work. This simulation environment requires significant investment in understanding the network architectures and supporting protocols. Simulating the adversarial actor will provide further insight into a realistic perception of security.

5. Conclusions and Future Work

The concept of security contained within the QoSS model is based directly upon the probabilities that adversarial listeners and disruptors are able to gain access to or change the original message. Probabilistic performance for data leakage and data corruption, as defined in the QoSS model, provides a foundation to compare the confidentiality and integrity available in a communication network. By combining those probabilistic characteristics and using QoS metrics as a baseline for availability in a network, the QoSS model was derived to describe static security characteristics of a point-to-point network. In this paper, those static security characteristics are extended to include complex, multi-hop and multi-channel networks, thus expanding the fidelity of the QoSS model to more complex and realistic network architectures. The expanded QoSS model allows the repeatable quantification and comparison of the security of a variety of communication system architectures under static configurations. Message fragmentation and duplication, as available features of multi-channel communication, provides a demonstrably improved theoretical performance to counteract the possible security concerns created by multi-hop architectures, thus improving the overall QoSS performance. A robust model such as this expanded QoSS model requires a fully developed simulation environment that would confirm the modeled results. (Such a simulation environment featuring a real network with all the aspects of the QoSS model is currently in development and will be the subject of a follow on paper). This tool must include the specific data-handling protocols, adjustable network characteristics, and performance monitors that display how the network end-points respond. Upon completion of that simulation, the extent of an adversary’s influence and the performance of fragmentation and duplication within a multi-channel network may be evaluated.