Tsallis Statistics in High Energy Physics: Chemical and Thermal Freeze-Outs
Abstract
1. Introduction
“Fermi originated the ingenious idea of considering the collision process at very high energies by the use of thermodynamic methods.”
2. Thermal Freeze-Out
- Use Equation (6) to fit the transverse momentum distributions. This determines the three parameters , q and .
- Fix the parameter q thus obtained.
- Perform a new fit to the transverse momentum distributions using Equation (2) keeping q as determined in the previous step. This determines the parameters T and V and the chemical potential .
- Check the consistency with Equations (4) and (5).
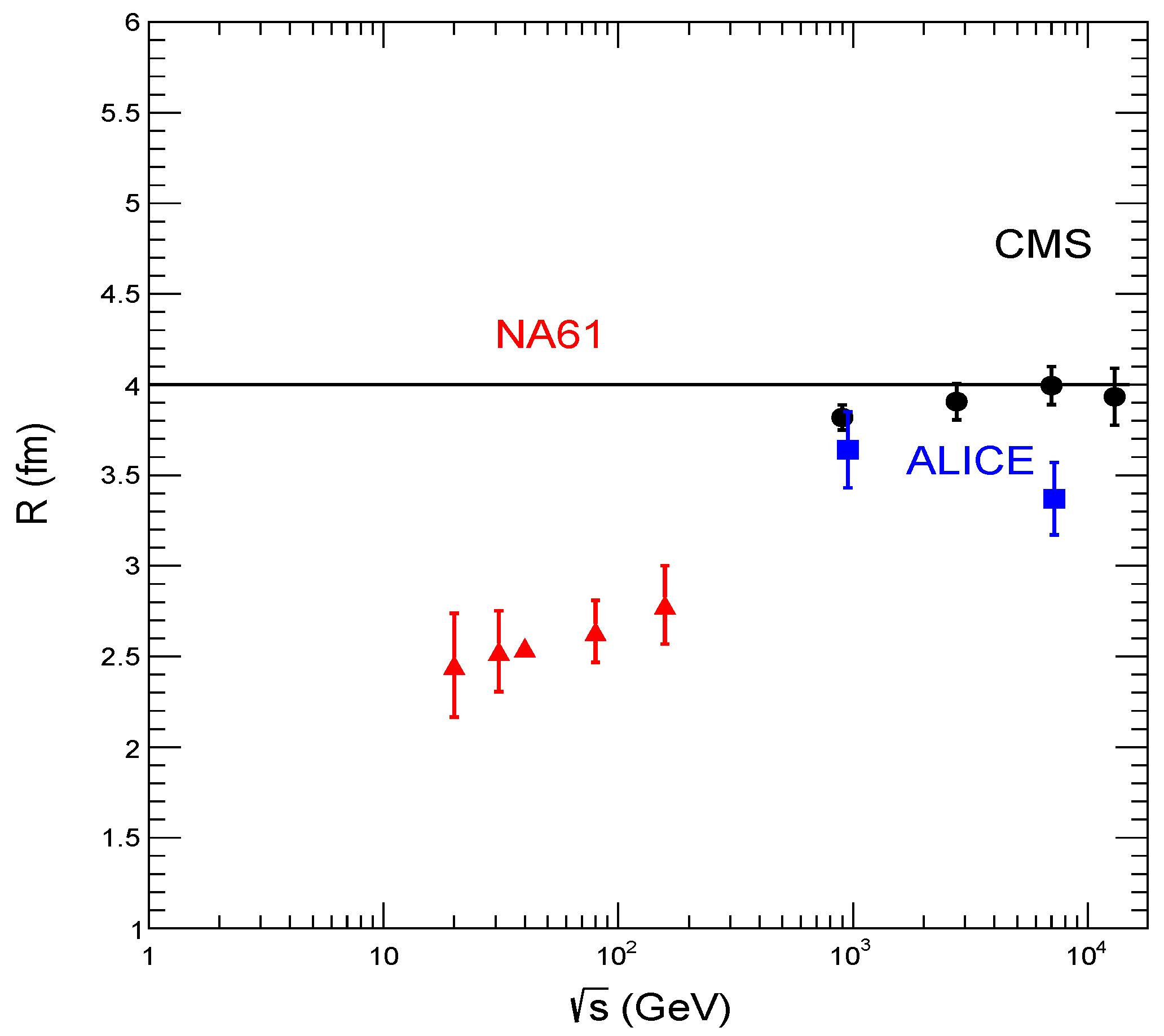
3. Comparison of Fit Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agrawal, N.; Ahammed, Z.; Ahmad, S.F.; Ahn, S.U.; Aimo, I.; Akindinov, A.; Alam, S.N.; et al. Centrality dependence of the pseudorapidity density distribution for charged particles in Pb-Pb collisions at = 5.02 TeV. Phys. Lett. B 2017, 772, 567–577. [Google Scholar] [CrossRef]
- Fermi, E. High-energy nuclear events. Prog. Theor. Phys. 1950, 5, 570–583. [Google Scholar] [CrossRef]
- Fermi, E. Angular Distribution of the Pions Produced in High Energy Nuclear Collisions. Phys. Rev. 1951, 81, 683–687. [Google Scholar] [CrossRef]
- Heisenberg, W. Mesonenerzeugung als Stosswellenproblem. Z. Phys. 1952, 133, 65. [Google Scholar] [CrossRef]
- Landau, L. On the multiparticle production in high-energy collisions. Izv. Akad. Nauk Ser. Fiz. 1953, 17, 51–64. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of particle physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Andronic, A.; Braun-Munzinger, P.; Friman, B.; Lo, P.M.; Redlich, K.; Stachel, J. The thermal proton yield anomaly in Pb-Pb collisions at the LHC and its resolution. Phys. Lett. B 2019, 792, 304–309. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Karthik, N.; Laermann, E.; Lahiri, A.; Larsen, R.; Li, S.T.; et al. Chiral crossover in QCD at zero and non-zero chemical potentials. Phys. Lett. B 2019, 795, 15–21. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Guenther, J.N.; Kara, R.; Katz, S.D.; Parotto, P.; Pasztor, A.; Ratti, C.; Szabo, K.K. The QCD crossover at finite chemical potential from lattice simulations. Phys. Rev. Lett. 2020, 125, 052001. [Google Scholar] [CrossRef]
- Sollfrank, J.; Koch, P.; Heinz, U.W. The Influence of resonance decays on the Pt spectra from heavy ion collisions. Phys. Lett. B 1990, 252, 256–264. [Google Scholar] [CrossRef]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Statist. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Cleymans, J.; Paradza, M. Determination of the Chemical Potential in the Tsallis Distribution at LHC Energies. arXiv 2010, arXiv:2010.05565. [Google Scholar]
- Abgrall, N.; Aduszkiewicz, A.; Ali, Y.; Anticic, T.; Antoniou, N.; Baatar, B.; Bay, F.; Blondel, A.; Blumer, J.; Bogomilov, M.; et al. Measurement of negatively charged pion spectra in inelastic p+p interactions at plab = 20, 31, 40, 80 and 158 GeV/c. Eur. Phys. J. C 2014, 74, 2794. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis Distribution in Proton-Proton Collisions at = 0.9 TeV at the LHC. J. Phys. G 2012, 39, 025006. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. Relativistic Thermodynamics: Transverse Momentum Distributions in High-Energy Physics. Eur. Phys. J. A 2012, 48, 160. [Google Scholar] [CrossRef]
- Cleymans, J.; Lykasov, G.; Parvan, A.; Sorin, A.; Teryaev, O.; Worku, D. Systematic properties of the Tsallis Distribution: Energy Dependence of Parameters in High-Energy p-p Collisions. Phys. Lett. B 2013, 723, 351–354. [Google Scholar] [CrossRef]
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S. Tsallis-thermometer: A QGP indicator for large and small collisional systems. arXiv 2020, arXiv:2003.03278. [Google Scholar]
- Aamodt, K.; Abel, N.; Abeysekara, U.; Quintana, A.A.; Abramyan, A.; Adamova, D.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; et al. Production of pions, kaons and protons in pp collisions at = 900 GeV with ALICE at the LHC. Eur. Phys. J. C 2011, 71, 1655. [Google Scholar] [CrossRef]
- Abelev, B.B.; Adam, J.; Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agostinelli, A.; Agrawal, N.; Ahammed, Z.; Ahmad, N.; et al. Production of charged pions, kaons and protons at large transverse momenta in pp and Pb–Pb collisions at = 2.76 TeV. Phys. Lett. B 2014, 736, 196–207. [Google Scholar] [CrossRef]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Aiola, S.; et al. Multiplicity dependence of charged pion, kaon, and (anti)proton production at large transverse momentum in p-Pb collisions at = 5.02 TeV. Phys. Lett. B 2016, 760, 720–735. [Google Scholar] [CrossRef]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmed, I.; Ahn, S.U.; Aimo, I.; et al. Measurement of pion, kaon and proton production in proton–proton collisions at = 7 TeV. Eur. Phys. J. C 2015, 75, 226. [Google Scholar] [CrossRef] [PubMed]
- James, F.; Roos, M. Minuit: A System for Function Minimization and Analysis of the Parameter Errors and Correlations. Comput. Phys. Commun. 1975, 10, 343. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; et al. Charged particle transverse momentum spectra in pp collisions at = 0.9 and 7 TeV. JHEP 2011, 8, 86. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Study of the Inclusive Production of Charged Pions, Kaons, and Protons in pp Collisions at = 0.9, 2.76, and 7 TeV. Eur. Phys. J. C 2012, 72, 2164. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; Flechl, M.; et al. Measurement of charged pion, kaon, and proton production in proton-proton collisions at = 13 TeV. Phys. Rev. D 2017, 96, 112003. [Google Scholar] [CrossRef]
- Rybczynski, M.; Wlodarczyk, Z. Tsallis statistics approach to the transverse momentum distributions in p-p collisions. Eur. Phys. J. C 2014, 74, 2785. [Google Scholar] [CrossRef]
- Awes, T.C.; Read, K.F., Jr.; Silvermyr, D.O.; Alice, C. Femtoscopy of pp collisions at = 0.9 and 7 TeV at the LHC with two-pion Bose-Einstein correlations. Phys. Rev. D 2011, 84, 112004. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; et al. Strange hadron production in Au + Au collisions at = 7.7, 11.5, 19.6, 27, and 39 GeV. Phys. Rev. C 2020, 102, 034909. [Google Scholar] [CrossRef]





| (TeV) | Particle | (fm) | q | (GeV) | /NDF |
|---|---|---|---|---|---|
| 0.9 | 4.83 ± 0.14 | 1.148 ± 0.005 | 0.070 ± 0.002 | 22.73/30 | |
| 4.74 ± 0.13 | 1.145 ± 0.005 | 0.072 ± 0.002 | 15.83/30 | ||
| 4.52 ± 1.30 | 1.175 ± 0.017 | 0.057 ± 0.013 | 13.02/24 | ||
| 3.96 ± 0.96 | 1.161 ± 0.016 | 0.064 ± 0.013 | 6.21/24 | ||
| p | 42.7 ± 19.8 | 1.158 ± 0.006 | 0.020 ± 0.004 | 14.29/21 | |
| 7.44 ± 3.95 | 1.132 ± 0.014 | 0.052 ± 0.016 | 13.82/21 | ||
| 2.76 | 4.80 ± 0.10 | 1.149 ± 0.002 | 0.077 ± 0.001 | 20.64/60 | |
| 2.51 ± 0.13 | 1.144 ± 0.002 | 0.096 ± 0.004 | 2.46/55 | ||
| 4.01 ± 0.62 | 1.121 ± 0.005 | 0.086 ± 0.008 | 3.51/46 | ||
| 5.02 | 5.02 ± 0.11 | 1.155 ± 0.002 | 0.076 ± 0.002 | 20.13/55 | |
| 2.44 ± 0.17 | 1.15 ± 0.005 | 0.099 ± 0.006 | 1.52/48 | ||
| 3.60 ± 0.55 | 1.126 ± 0.005 | 0.091 ± 0.009 | 2.56/46 | ||
| 7.0 | 5.66 ± 0.17 | 1.179 ± 0.003 | 0.066 ± 0.002 | 14.14/38 | |
| 2.51 ± 0.15 | 1.158 ± 0.005 | 0.097 ± 0.005 | 3.11/45 | ||
| 3.07 ± 0.41 | 1.124 ± 0.005 | 0.101 ± 0.008 | 6.03/43 |
| (TeV) | Particle | R (fm) | (GeV) | T (GeV) | /NDF |
|---|---|---|---|---|---|
| 0.9 | 3.64 ± 0.21 | 0.055 ± 0.012 | 0.079 ± 0.002 | 3.66/30 | |
| 3.53 ± 0.21 | 0.059 ± 0.012 | 0.080 ± 0.002 | 2.18/30 | ||
| 3.76 ± 0.33 | 0.029 ± 0.017 | 0.062 ± 0.003 | 5.31/24 | ||
| 3.89 ± 0.35 | 0.003 ± 0.018 | 0.065 ± 0.003 | 3.38/24 | ||
| p | 3.34 ± 0.27 | 0.233 ± 0.020 | 0.057 ± 0.007 | 7.44/21 | |
| 3.93 ± 0.33 | 0.097 ± 0.024 | 0.065 ± 0.002 | 7.69/21 | ||
| 2.76 | 4.32 ± 2.68 | 0.022 ± 0.130 | 0.080 ± 0.019 | 20.48/60 | |
| 4.75 ± 0.03 | −0.140 ± 0.008 | 0.075 ± 0.004 | 2.48/55 | ||
| 4.47 ± 5.50 | −0.071 ± 0.253 | 0.077 ± 0.030 | 3.52/46 | ||
| 5.02 | 4.19 ± 2.64 | 0.038 ± 0.134 | 0.082 ± 0.021 | 20.14/55 | |
| 4.49 ± 0.03 | −0.142 ± 0.009 | 0.078 ± 0.0005 | 1.52/48 | ||
| 4.00 ± 4.48 | −0.075 ± 0.243 | 0.081 ± 0.031 | 2.56/46 | ||
| 7.0 | 3.67 ± 0.02 | 0.081 ± 0.141 | 0.081 ± 0.003 | 14.15/38 | |
| 3.80 ± 0.22 | −0.098± 0.014 | 0.082 ± 0.002 | 3.13/55 | ||
| 4.07 ± 0.27 | −0.127± 0.018 | 0.085 ± 0.002 | 6.03/43 |
| (TeV) | Particle | T (MeV) | q | R (fm) | (MeV) | |
|---|---|---|---|---|---|---|
| [24] | ||||||
| [25] | ||||||
| [25] | ||||||
| [26] | ||||||
| (GeV) | Particle | (MeV) | q | (fm) | |
|---|---|---|---|---|---|
| 20 | |||||
| 31 | |||||
| 40 | |||||
| 80 | |||||
| 158 |
| (GeV) | Particle | R (fm) | (GeV) | T (GeV) | |
|---|---|---|---|---|---|
| 20 | |||||
| 31 | |||||
| 40 | |||||
| 80 | |||||
| 158 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cleymans, J.; Paradza, M.W. Tsallis Statistics in High Energy Physics: Chemical and Thermal Freeze-Outs. Physics 2020, 2, 654-664. https://doi.org/10.3390/physics2040038
Cleymans J, Paradza MW. Tsallis Statistics in High Energy Physics: Chemical and Thermal Freeze-Outs. Physics. 2020; 2(4):654-664. https://doi.org/10.3390/physics2040038
Chicago/Turabian StyleCleymans, Jean, and Masimba Wellington Paradza. 2020. "Tsallis Statistics in High Energy Physics: Chemical and Thermal Freeze-Outs" Physics 2, no. 4: 654-664. https://doi.org/10.3390/physics2040038
APA StyleCleymans, J., & Paradza, M. W. (2020). Tsallis Statistics in High Energy Physics: Chemical and Thermal Freeze-Outs. Physics, 2(4), 654-664. https://doi.org/10.3390/physics2040038





