Trends in the Structure of Nuclei near 100Sn
Abstract
1. Introduction and Ground-State Properties
2. Experimental Methods
2.1. Low Energy Facilities
2.2. High-Energy Fragmentation and ISOL Facilities
3. Theoretical Approaches
4. Results
4.1. Nuclei below 100Sn, A ≤ 100
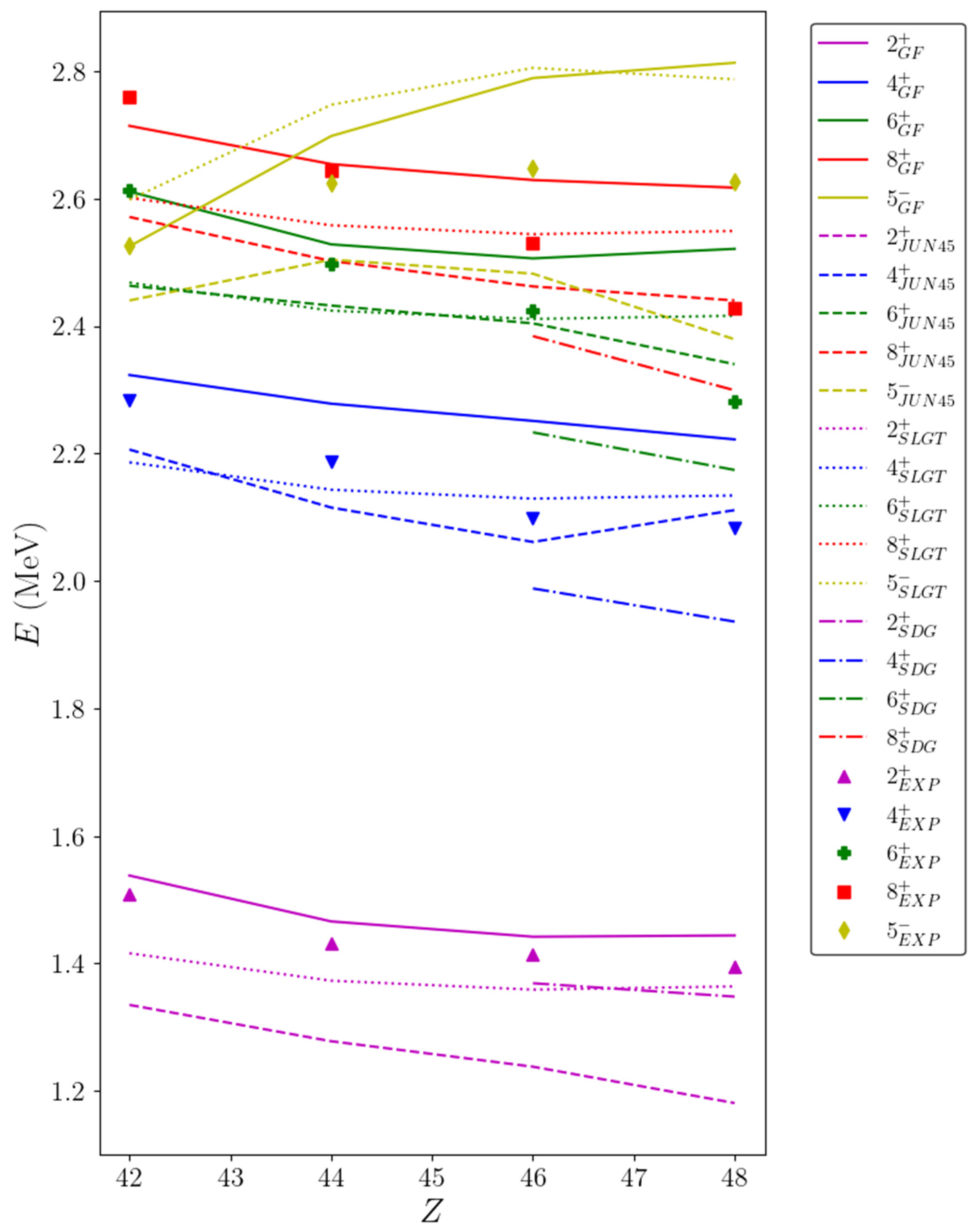
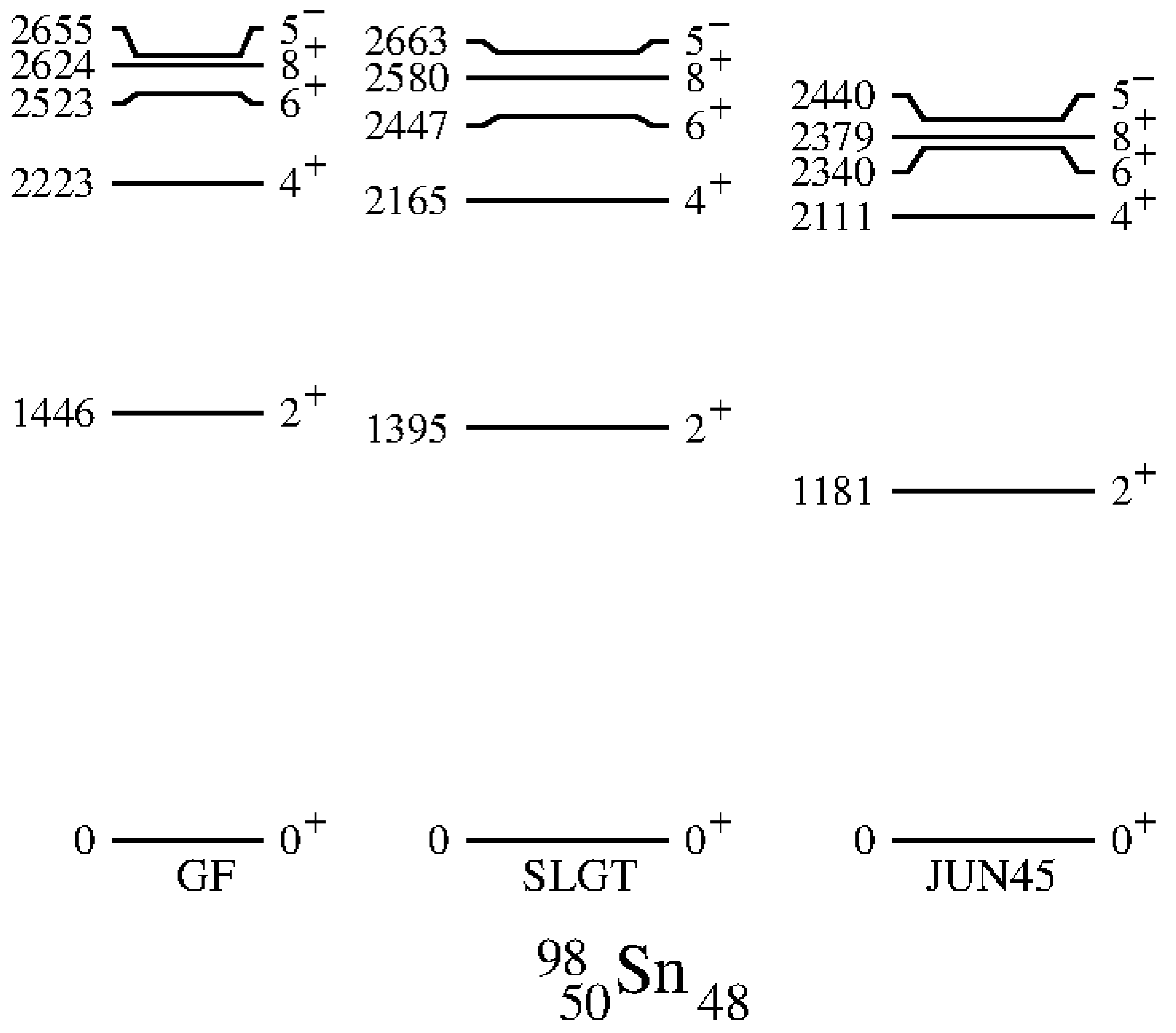
4.1.1. Even-Even N = 50 Isotones of the g9/2 Shell
4.1.2. N = Z Chain from 100Sn to 80Zr
4.2. Nuclei with N > 50
5. Summary and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faestermann, T.; Górska, M.; Grawe, H. The structure of 100Sn and neighbouring nuclei. Prog. Part. Nucl. Phys. 2013, 69, 85–130. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Nazarewicz, W. Limits of proton stability near 100Sn. Phys. Rev. C 1995, 51, R1070–R1073. [Google Scholar] [CrossRef] [PubMed]
- Neufcourt, L.; Cao, Y.; Giuliani, S.; Nazarewicz, W.; Olsen, E.; Tarasov, O.B. Beyond the proton drip line: Bayesian analysis of proton-emitting nuclei. Phys. Rev. C 2020, 101, 014319. [Google Scholar] [CrossRef]
- Arthuis, P.; Barbieri, C.; Vorabbi, M.; Finelli, P. Ab Initio Computation of Charge Densities for Sn and Xe Isotopes. Phys. Rev. Lett. 2020, 125, 182501. [Google Scholar] [CrossRef] [PubMed]
- Reponen, M.; de Groote, R.P.; Al Ayoubi, L.; Beliuskina, O.; Bissell, M.L.; Campbell, P.; Cañete, L.; Cheal, B.; Chrysalidis, K.; Delafosse, C.; et al. Evidence of a sudden increase in the nuclear size of proton-rich silver-96. Nat. Commun. 2021, 12, 4596. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, R.; Bree, N.; Cocolios, T.E.; Darby, I.; De Witte, H.; Dexters, W.; Diriken, J.; Elseviers, J.; Franchoo, S.; Huyse, M.; et al. In-gas-cell laser ionization spectroscopy in the vicinity of 100Sn: Magnetic moments and mean-square charge radii of N = 50–54 Ag. Phys. Lett. B 2014, 728, 191–197. [Google Scholar] [CrossRef]
- Brown, B. The nuclear shell model towards the drip lines. Prog. Part. Nucl. Phys. 2001, 47, 517–599. [Google Scholar] [CrossRef]
- Brown, B.A.; Rykaczewski, K. Gamow-Teller strength in the region of 100Sn. Phys. Rev. C 1994, 50, R2270–R2273. [Google Scholar] [CrossRef]
- Hinke, C.B.; Böhmer, M.; Boutachkov, P.; Faestermann, T.; Geissel, H.; Gerl, J.; Gernhäuser, R.; Górska, M.; Gottardo, A.; Grawe, H.; et al. Superallowed Gamow–Teller decay of the doubly magic nucleus 100Sn. Nature 2012, 486, 341–345. [Google Scholar] [CrossRef]
- Lubos, D.; Park, J.; Faestermann, T.; Gernhäuser, R.; Krücken, R.; Lewitowicz, M.; Nishimura, S.; Sakurai, H.; Ahn, D.S.; Baba, H.; et al. Improved Value for the Gamow-Teller strength of the 100Sn beta decay. Phys. Rev. Lett. 2019, 122, 222502. [Google Scholar] [CrossRef]
- Konieczka, M.; Satuła, W.; Kortelainen, M. Gamow-Teller response in the configuration space of a density-functional-theory–rooted no-core configuration-interaction model. Phys. Rev. C 2018, 97, 034310. [Google Scholar] [CrossRef]
- Morris, T.D.; Simonis, J.; Stroberg, S.R.; Stumpf, C.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Papenbrock, T.; Roth, R.; Schwenk, A. Structure of the Lightest Tin Isotopes. Phys. Rev. Lett. 2018, 120, 152503. [Google Scholar] [CrossRef]
- Gysbers, P.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Morris, T.; Navrátil, P.; Papenbrock, T.; Quaglioni, S.; Schwenk, A.; Stroberg, S.R.; et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat. Phys. 2019, 15, 428–431. [Google Scholar] [CrossRef]
- Mougeot, M.; Atanasov, D.; Karthein, J.; Wolf, R.N.; Ascher, P.; Blaum, K.; Chrysalidis, K.; Hagen, G.; Holt, J.D.; Huang, W.J.; et al. Mass measurements of 99–101In challenge ab initio nuclear theory of the nuclide 100Sn. Nat. Phys. 2021, 17, 1099–1103. [Google Scholar] [CrossRef]
- Hornung, C.; Amanbayev, D.; Dedes, I.; Kripko-Koncz, G.; Miskun, I.; Shimizu, N.; Andrés, S.A.S.; Bergmann, J.; Dickel, T.; Dudek, J.; et al. Isomer studies in the vicinity of the doubly-magic nucleus 100Sn: Observation of a new low-lying isomeric state in 97Ag. Phys. Lett. B 2020, 802, 135200. [Google Scholar] [CrossRef]
- Yang, S.; Xu, C.; Röpke, G.; Schuck, P.; Ren, Z.; Funaki, Y.; Horiuchi, H.; Tohsaki, A.; Yamada, T.; Zhou, B. α decay to a doubly magic core in the quartetting wave function approach. Phys. Rev. C 2020, 101, 024316. [Google Scholar] [CrossRef]
- Clark, R.M.; Macchiavelli, A.O.; Crawford, H.L.; Fallon, P.; Rudolph, D.; Såmark-Roth, A.; Campbell, C.M.; Cromaz, M.; Morse, C.; Santamaria, C. Enhancement of α-particle formation near 100Sn. Phys. Rev. C 2020, 101, 034313. [Google Scholar] [CrossRef]
- Muir, D.; Pastore, A.; Dobaczewski, J.; Barton, C. Bootstrap technique to study correlation between neutron skin thickness and the slope of symmetry energy in atomic nuclei. Acta Phys. Pol. B 2018, 49, 359. [Google Scholar] [CrossRef]
- Blazhev, A.; Górska, M.; Grawe, H.; Nyberg, J.; Palacz, M.; Caurier, E.; Dorvaux, O.; Gadea, A.; Nowacki, F.; Andreoiu, C.; et al. Observation of a core-excited E4 isomer in 98Cd. Phys. Rev. C 2004, 69, 064304. [Google Scholar] [CrossRef]
- Blazhev, A.; Braun, N.; Grawe, H.; Boutachkov, P.; Singh, B.S.N.; Brock, T.; Liu, Z.; Wadsworth, R.; Gorska, M.; Jolie, J.; et al. High-energy excited states in98Cd. J. Phys. Conf. Ser. 2010, 205, 012035. [Google Scholar] [CrossRef]
- Boutachkov, P.; Górska, M.; Grawe, H.; Blazhev, A.; Braun, N.; Brock, T.S.; Liu, Z.; Singh, B.S.N.; Wadsworth, R.; Pietri, S.; et al. High-spin isomers in 96Ag: Excitations across the Z = 38 and Z = 50, N = 50 closed shells. Phys. Rev. C 2011, 84, 044311. [Google Scholar] [CrossRef]
- Davies, P.J.; Park, J.; Grawe, H.; Wadsworth, R.; Gernhäuser, R.; Krücken, R.; Nowacki, F.; Ahn, D.S.; Ameil, F.; Baba, H.; et al. Toward the limit of nuclear binding on the N = Z line: Spectroscopy of 96Cd. Phys. Rev. C 2019, 99, 021302. [Google Scholar] [CrossRef]
- Cederwall, B.; Moradi, F.G.; Bäck, T.; Johnson, A.; Blomqvist, J.; Clement, E.; de France, G.; Wadsworth, R.; Andgren, K.; Lagergren, K.; et al. Evidence for a spin-aligned neutron–proton paired phase from the level structure of 92Pd. Nature 2010, 469, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Zamick, L.; Escuderos, A. Single j-shell studies of cross-conjugate nuclei and isomerism: (2j − 1)Rule. Nucl. Phys. A 2012, 889, 8–17. [Google Scholar] [CrossRef][Green Version]
- Goutte, H.; Navin, A. Microscopes for the physics at the femtoscale: GANIL-SPIRAL2. Nucl. Phys. News 2021, 31, 5–12. [Google Scholar] [CrossRef]
- Nuclear Physics Facilities—Department of Physics. Available online: https://www.jyu.fi/en/frontpage (accessed on 1 August 2021).
- Argonne Tandem Linac Accelerator System—Argonne National Laboratory. Available online: https://www.anl.gov/ (accessed on 1 August 2021).
- Home INFN Legnaro—National Institute for Nuclear Physics. Available online: https://www.lnl.infn.it/en/welcome-on-the-site-of-the-national-laboratories-of-legnaro/ (accessed on 1 August 2021).
- Siciliano, M.; Valiente-Dobón, J.; Goasduff, A.; Nowacki, F.; Zuker, A.; Bazzacco, D.; Lopez-Martens, A.; Clément, E.; Benzoni, G.; Braunroth, T.; et al. Pairing-quadrupole interplay in the neutron-deficient tin nuclei: First lifetime measurements of low-lying states in 106,108Sn. Phys. Lett. B 2020, 806, 135474. [Google Scholar] [CrossRef]
- Akkoyun, S.; Algora, A.; Alikhani, B.; Ameil, F.; de Angelis, G.; Arnold, L.; Astier, A.; Ataç, A.; Aubert, Y.; Aufranc, C.; et al. AGATA—Advanced GAmma Tracking Array. Nucl. Instr. Meth. A 2012, 668, 26. [Google Scholar] [CrossRef]
- Clément, E.; Michelagnoli, C.; de France, G.; Li, H.J.; Lemasson, A.; Barthe Dejean, C.; Beuzard, M.; Bougault, P.; Cacitti, J.; Foucher, J.-L.; et al. Conceptual design of the AGATA π1 array at GANIL. Nucl. Instr. Meth. A 2017, 855, 1. [Google Scholar] [CrossRef]
- Scheurer, J.; Aiche, M.; Aleonard, M.M.; Barreau, G.; Bourgine, F.; Boivin, D.; Cabaussel, D.; Chemin, J.F.; Doan, T.P.; Goudour, J.P.; et al. Improvements in the in-beam y-ray spectroscopy provided by an ancillary detector coupled to a Ge y-spectrometer: The Diamant-Eurogam II example. Nucl. Instr. Meth. A 1997, 385, 501. [Google Scholar] [CrossRef]
- Gál, J.; Hegyesi, G.; Molnár, J.; Nyakó, B.; Kalinka, G.; Scheurer, J.; Aléonard, M.; Chemin, J.; Pedroza, J.; Juhász, K.; et al. The VXI electronics of the DIAMANT particle detector array. Nucl. Instrum. Methods Phys. Res. Sect. A 2004, 516, 502–510. [Google Scholar] [CrossRef]
- Hüyük, T.; Di Nitto, A.; Jaworski, G.; Gadea, A.; Valiente-Dobón, J.J.; Nyberg, J.; Palacz, M.; Söderström, P.-A.; Aliaga-Varea, R.J.; De Angelis, G.; et al. Conceptual design of the early implementation of the NEutron Detector Array (NEDA) with AGATA. Eur. Phys. J. A 2016, 52, 55. [Google Scholar] [CrossRef]
- Valiente-Dobón, J.J.; Jaworski, G.; Goasduff, A.; Egea, F.J.; Modamio, V.; Hüyük, T.; Triossi, A.; Jastrząb, M.; Söderström, P.A.; Di Nitto, A.; et al. NEDA—NEutron Detector Array. Nucl. Instr. Meth. A 2019, 927, 81. [Google Scholar] [CrossRef]
- Pullanhiotan, S.; Chatterjee, A.; Jacquot, B.; Navin, A.; Rejmund, M. Improvement in the reconstruction method for VAMOS spectrometer. Nucl. Instrum. Methods Phys. Res. Sect. B 2008, 266, 4148–4152. [Google Scholar] [CrossRef]
- Rejmund, M.; Lecornu, B.; Navin, A.; Schmitt, C.; Damoy, S.; Delaune, O.; Enguerrand, J.; Fremont, G.; Gangnant, P.; Gaudefroy, L.; et al. Performance of the improved larger acceptance spectrometer: VAMOS++. Nucl. Instrum. Methods Phys. Res. Sect. A 2011, 646, 184–191. [Google Scholar] [CrossRef]
- Vandebrouck, M.; Lemasson, A.; Rejmund, M.; Fremont, G.; Pancin, J.; Navin, A.; Michelagnoli, C.; Goupil, J.; Spitaels, C.; Jacquot, B. Dual Position Sensitive MWPC for tracking reaction products at VAMOS++. Nucl. Instrum. Methods Phys. Res. Sect. A 2016, 812, 112–117. [Google Scholar] [CrossRef]
- Mass Analysing Recoil Apparatus (MARA)—Department of Physics. Available online: https://www.jyu.fi/science/en/physics/research/infrastructures/accelerator-laboratory/nuclear-physics-facilities/recoil-separators/mara-mass-analysing-recoil-apparatus (accessed on 1 November 2021).
- Davids, C.N.; Larson, J.D. The argonne fragment mass analyzer. Nucl. Instr. Meth. B 1989, 40–41, 1224. [Google Scholar] [CrossRef]
- Kalandarov, S.A.; Adamian, G.G.; Antonenko, N.V.; Wieleczko, J.P. Production of the doubly magic nucleus 100Sn in fusion and quasifission reactions via light particle and cluster emission channels. Phys. Rev. C 2014, 90, 024609. [Google Scholar] [CrossRef]
- Cederwall, B.; Liu, X.; Aktas, Ö.; Ertoprak, A.; Zhang, W.; Qi, C.; Clément, E.; de France, G.; Ralet, D.; Gadea, A.; et al. Isospin properties of nuclear pair correlations from the level structure of the self-conjugate nucleus 88Ru. Phys. Rev. Lett. 2020, 124, 062501. [Google Scholar] [CrossRef]
- Auranen, K. Superallowed α decay to doubly magic 100Sn. Phys. Rev. Lett. 2018, 121, 182501. [Google Scholar] [CrossRef]
- Seweryniak, D.; Carpenter, M.P.; Gros, S.; Hecht, A.A.; Hoteling, N.; Janssens, R.V.F.; Khoo, T.L.; Lauritsen, T.; Lister, C.J.; Lotay, G.; et al. Single-neutron states in 101Sn. Phys. Rev. Lett. 2007, 99, 022504. [Google Scholar] [CrossRef]
- Xiao, Y.; Go, S.; Grzywacz, R.; Orlandi, R.; Andreyev, A.N.; Asai, M.; Bentley, M.A.; de Angelis, G.; Gross, C.J.; Hausladen, P.; et al. Search for α decay of 104Te with a novel recoil-decay scintillation detector. Phys. Rev. C 2019, 100, 034315. [Google Scholar] [CrossRef]
- Darby, I.G.; Grzywacz, R.K.; Batchelder, J.C.; Bingham, C.R.; Cartegni, L.; Gross, C.J.; Hjorth-Jensen, M.; Joss, D.T.; Liddick, S.N.; Nazarewicz, W.; et al. Orbital dependent nucleonic pairing in the lightest known Isotopes of Tin. Phys. Rev. Lett. 2010, 105, 162502. [Google Scholar] [CrossRef] [PubMed]
- Erler, J.; Birge, N.; Kortelainen, M.; Nazarewicz, W.; Olsen, E.; Perhac, A.M.; Stoitsov, M. The limits of the nuclear landscape. Nature 2012, 486, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Kubo, T.; Kameda, D.; Suzuki, H.; Fukuda, N.; Takeda, H.; Yanagisawa, Y.; Ohtake, M.; Kusaka, K.; Yoshida, K.; Inabe, N.; et al. BigRIPS separator and ZeroDegree spectrometer at RIKEN RI Beam Factory. Prog. Theor. Exp. Phys. 2012, 2012, 03C003. [Google Scholar] [CrossRef]
- RIKEN. Euroball-RIKEN Cluster Array (EURICA) Project Unveiled. Available online: https://www.riken.jp/en/news_pubs/news/2012/20120326_4/index.html (accessed on 1 August 2021).
- Takeuchi, S.; Motobayashi, T.; Togano, Y.; Matsushita, M.; Aoi, N.; Demichi, K.; Hasegawa, H.; Murakami, H. DALI2: A NaI(Tl) detector array for measurements of γ-rays from fast nuclei. Nucl. Instr. Meth. A 2014, 763, 596. [Google Scholar] [CrossRef]
- Čeliković, I.; Lewitowicz, M.; Gernhäuser, R.; Krücken, R.; Nishimura, S.; Sakurai, H.; Ahn, D.; Baba, H.; Blank, B.; Blazhev, A.; et al. New isotopes and proton emitters–Crossing the drip line in the vicinity of 100Sn. Phys. Rev. Lett. 2016, 116, 162501. [Google Scholar] [CrossRef]
- Park, J.; Krücken, R.; Lubos, D.; Gernhäuser, R.; Lewitowicz, M.; Nishimura, S.; Ahn, D.S.; Baba, H.; Blank, B.; Blazhev, A.; et al. New and comprehensive β- and βp-decay spectroscopy results in the vicinity of 100Sn. Phys. Rev. C 2019, 99, 034313. [Google Scholar] [CrossRef]
- Park, J.; Krücken, R.; Blazhev, A.; Lubos, D.; Gernhäuser, R.; Lewitowicz, M.; Nishimura, S.; Ahn, D.; Baba, H.; Blank, B.; et al. Spectroscopy of 99Cd and 101In from β decays of 99In and 101Sn. Phys. Rev. C 2020, 102, 014304. [Google Scholar] [CrossRef]
- Davies, P.; Grawe, H.; Moschner, K.; Blazhev, A.; Wadsworth, R.; Boutachkov, P.; Ameil, F.; Yagi, A.; Baba, H.; Bäck, T.; et al. The role of core excitations in the structure and decay of the 16+ spin-gap isomer in 96Cd. Phys. Lett. B 2017, 767, 474–479. [Google Scholar] [CrossRef]
- Häfner, G.; Moschner, K.; Blazhev, A.; Boutachkov, P.; Davies, P.J.; Wadsworth, R.; Ameil, F.; Baba, H.; Bäck, T.; Dewald, M.; et al. Properties of γ-decaying isomers in the 100Sn region populated in fragmentation of a 124Xe beam. Phys. Rev. C 2019, 100, 024302. [Google Scholar] [CrossRef]
- Park, J.; Krücken, R.; Lubos, D.; Gernhäuser, R.; Lewitowicz, M.; Nishimura, S.; Ahn, D.S.; Baba, H.; Blank, B.; Blazhev, A.; et al. Properties of γ -decaying isomers and isomeric ratios in the 100Sn region. Phys. Rev. C 2017, 96, 044311. [Google Scholar] [CrossRef]
- Doornenbal, P. In-beam gamma-ray spectrometer at the RIBF. Prog. Theor. Exp. Phys. 2012, 2012, 03C004. [Google Scholar] [CrossRef]
- Loruso, G.; Becerril, A.D.; Amthor, A.M.; Baumann, T. β-delayed proton emission in the 100Sn region. Phys. Rev. C 2012, 86, 014313. [Google Scholar] [CrossRef]
- Cerizza, G.; Ayres, A.; Jones, K.L.; Grzywacz, R.; Bey, A.; Bingham, C.; Cartegni, L.; Miller, D.; Padgett, S.; Baugher, T.; et al. Structure of 107Sn studied through single-neutron knockout reactions. Phys. Rev. C 2016, 93, 021601. [Google Scholar] [CrossRef]
- Hamaker, A.; Leistenschneider, E.; Jain, R.; Bollen, G.; Giuliani, S.A.; Lund, K.; Nazarewicz, W.; Neufcourt, L.; Nicoloff, C.R.; Puentes, D.; et al. Precision mass measurement of lightweight self-conjugate nucleus 80Zr. Nat. Phys. 2021, 17 1408, 1–5. [Google Scholar] [CrossRef]
- Grawe, H.; Straub, K.; Faestermann, T.; Górska, M.; Hinke, C.; Krücken, R.; Nowacki, F.; Böhmer, M.; Boutachkov, P.; Geissel, H.; et al. The (6+) isomer in 102Sn revisited: Neutron and proton effective charges close to the double shell closure. Phys. Lett. B 2021, 820, 136591. [Google Scholar] [CrossRef]
- Pietri, S.; Regan, P.H.; Podolyak, Z.; Rudolph, D.; Steer, S.; Garnsworthy, A.B.; Werner-Malento, E.; Hoischen, R.; Górska, M.; Gerl, J.; et al. Recent results in fragmentation isomer spectroscopy with rising. Nucl. Instr. Met. B 2007, 261, 1079. [Google Scholar] [CrossRef]
- Geissel, G.; Armbruster, P.; Behr, K.H.; Brünle, A.; Burkard, K.; Chen, M.; Folger, H.; Franczak, B.; Keller, H.; Klepperet, O.; et al. The GSI projectile fragment separator (FRS): A versatile magnetic system for relativistic heavy ions. Nucl. Instr. Meth. B 1992, 70, 286. [Google Scholar] [CrossRef]
- Mistry, A.K.; Albers, H.M.; Arıcı, T.; Banerjee, A.; Benzoni, G.; Cederwall, B.; Gerl, J.; Górska, M.; Hall, O.; Hubbard, N.; et al. The DESPEC setup for GSI and FAIR. Nucl. Inst. Meth. B, in print.
- Technical Report for the Design, Construction and Commissioning of FATIMA, the FAst TIMing Array (2015). Available online: https://edms.cern.ch/document/1865981/1 (accessed on 1 August 2021).
- Kester, O.; Sieber, T.; Emhofer, S.; Ames, F.; Reisinger, K.; Reiter, P.; Thirolf, P.; Lutter, R.; Habs, D.; Wolf, B.; et al. Accelerated radioactive beams from REX-ISOLDE. Nucl. Instrum. Methods Phys. Res. Sect. B 2002, 204, 20–30. [Google Scholar] [CrossRef]
- Borge, M. Highlights of the ISOLDE facility and the HIE-ISOLDE project. Nucl. Instrum. Methods Phys. Res. Sect. B 2016, 376, 408–412. [Google Scholar] [CrossRef]
- Eberth, J.; Pascovici, G.; Thomas, H.; Warr, N.; Weisshaar, D.; Habs, D.; Reiter, P.; Thirolf, P.; Schwalm, D.; Gund, C.; et al. MINIBALL A Ge detector array for radioactive ion beam facilities. Prog. Part. Nucl. Phys. 2001, 46, 389–398. [Google Scholar] [CrossRef]
- Warr, N.; Van De Walle, J.; Albers, M.; Ames, F.; Bastin, B.; Bauer, C.; Bildstein, V.; Blazhev, A.; Bönig, S.; Bree, N.; et al. The Miniball spectrometer. Eur. Phys. J. A 2013, 49, 40. [Google Scholar] [CrossRef]
- Ekström, A.; Cederkäll, J.; DiJulio, D.D.; Fahlander, C.; Hjorth-Jensen, M.; Blazhev, A.; Bruyneel, B.; Butler, P.A.; Davinson, T.; Eberth, J.; et al. Electric quadrupole moments of the 21+states in Cd100,102,104. Phys. Rev. C 2009, 80, 054302. [Google Scholar] [CrossRef]
- Ekstrom, A.; Cederkall, J.; Fahlander, C.; Hjorth-Jensen, M.; Engeland, T.; Blazhev, A.; Butler, P.A.; Davinson, T.; Eberth, J.; Finke, F.; et al. Coulomb excitation of the odd-odd isotopes 106, 108In. Eur. Phys. J. A 2010, 44, 355–361. [Google Scholar] [CrossRef]
- DiJulio, D.D.; Cederkall, J.; Fahlander, C.; Ekstrom, A.; Hjorth-Jensen, M.; Albers, M.; Bildstein, V.; Blazhev, A.; Darby, I.; Davinson, T.; et al. Excitation strengths in 109Sn: Single-neutron and collective excitations near 100Sn. Phys. Rev. C 2012, 86, 031302. [Google Scholar] [CrossRef]
- DiJulio, D.D.; Cederkall, J.; Fahlander, C.; Ekstrom, A.; Hjorth-Jensen, M.; Albers, M.; Bildstein, V.; Blazhev, A.; Darby, I.; Davinson, T.; et al. Coulomb excitation of 107Sn. Eur. Phys. J. A 2012, 48, 105. [Google Scholar] [CrossRef]
- DiJulio, D.; Cederkall, J.; Fahlander, C.; Ekström, A. Coulomb excitation of 107In. Phys. Rev. C 2013, 87, 017301. [Google Scholar] [CrossRef]
- Lunderberg, E.; Belarge, J.; Bender, P.; Bucher, B.; Cline, D.; Elman, B.; Gade, A.; Liddick, S.; Longfellow, B.; Prokop, C.; et al. JANUS—A setup for low-energy Coulomb excitation at ReA3. Nucl. Instrum. Methods Phys. Res. Sect. A 2018, 885, 30–37. [Google Scholar] [CrossRef]
- Rhodes, D.; Brown, B.A.; Henderson, J.; Gade, A.; Ash, J.; Bender, P.C.; Elder, R.; Elman, B.; Grinder, M.; Hjorth-Jensen, M.; et al. Exploring the role of high-j configurations in collective observables through the Coulomb excitation of 106Cd. Phys. Rev. C 2021, 103, L051301. [Google Scholar] [CrossRef]
- Togashi, T.; Tsunoda, Y.; Otsuka, T.; Shimizu, N.; Honma, M. Novel shape evolution in Sn isotopes from magic numbers 50 to 82. Phys. Rev. Lett. 2018, 121, 062501. [Google Scholar] [CrossRef] [PubMed]
- Honma, M.; Otsuka, T.; Mizusaki, T.; Hjorth-Jensen, M. New effective interaction for f5 pg9-shell nuclei. Phys. Rev. C 2009, 80, 064323. [Google Scholar] [CrossRef]
- Zuker, A.P.; Poves, A.; Nowacki, F.; Lenzi, S.M. Nilsson-SU3 self-consistency in heavy N = Z nuclei. Phys. Rev. C 2015, 92, 024320. [Google Scholar] [CrossRef]
- Gargano, A.; Coraggio, L.; Covello, A.; Itaco, N. Investigating neutron-deficient tin isotopes via realistic shell-model calculations. AIP Conf. Proc. 2015, 1681, 020007. [Google Scholar]
- Coraggio, L.; Gargano, A.; Itaco, N. Double-step truncation procedure for large-scale shell-model calculations. Phys. Rev. C 2016, 93, 064328. [Google Scholar] [CrossRef]
- Zucker, A. Quadrupole dominance in the light Sn and in the Cd isotope. Phys. Rev. C 2021, 103, 024322. [Google Scholar] [CrossRef]
- Coraggio, L.; Itaco, N. Perturbative approach to effective shell-model hamiltonians and operators. Front. Phys. 2020, 8, 345. [Google Scholar] [CrossRef]
- Gargano, A.; Coraggio, L.; Itaco, N. Effectively-truncated large-scale shell-model calculations and nuclei around 100Sn. Phys. Scr. 2017, 92, 094003. [Google Scholar] [CrossRef]
- Gross, R.; Frenkel, A. Effective interaction of protons and neutrons in the 2p12-1g92 subshells. Nucl. Phys. A 1976, 267, 85. [Google Scholar] [CrossRef]
- Serduke, F.J.D.; Lawson, R.D.; Gloeckner, D.H. Shell-modelstudy of the N = 49 isotones. Nucl. Phys. A 1976, 256, 45. [Google Scholar] [CrossRef]
- Brown, B.A.; Rae, W.D.M. The Shell-Model Code NuShellX@MSU. Nucl. Data Sheets 2014, 120, 115. [Google Scholar] [CrossRef]
- Hjorth-Jensen, M.; Kuo, T.T.; Osnes, E. Realistic effective interactions for nuclear systems. Phys. Rep. 1995, 261, 125–270. [Google Scholar] [CrossRef]
- Grawe, H.; Blazhev, A.; Górska, M. Correspondence Affiliation: GSI Darmstadt, Darmstadt, Germany. Empirically-modified realistic intereraction for the 100Sn region. 2021. to be published. [Google Scholar]
- Yordanov, D.T.; Balabanski, D.L.; Bissell, M.L.; Blaum, K.; Blazhev, A.; Budinčević, I.; Frömmgen, N.; Geppert, C.; Grawe, H.; Hammen, M.; et al. Spins and electromagnetic moments of 101–109Cd. Phys. Rev. C 2018, 98, 011303. [Google Scholar] [CrossRef]
- Coombes, B.J.; Stuchbery, A.E.; Blazhev, A.; Grawe, H.; Reed, M.W.; Akber, A.; Dowie, J.T.H.; Gerathy, M.S.M.; Gray, T.J.; Kibedi, T.; et al. Spectroscopy and excited-state g factors in weakly collective 111Cd: Confronting collective and micro-scopic models. Phys. Rev. C 2019, 100, 024322. [Google Scholar] [CrossRef]
- Nowacki, F. (Institut Pluridisciplinaire Hubert Curien, Strasbourg, France). Updated calculations with t=5. Private communication, 2021. [Google Scholar]
- Arnswald, K.; Blazhev, A.; Nowacki, F.; Petkov, P.; Reiter, P.; Braunroth, T.; Dewald, A.; Droste, M.; Fransen, C.; Hirsch, R.; et al. Enhanced quadrupole collectivity in doubly-magic 56Ni: Lifetime measurements of the 41+ and 61+ states. Phys. Lett. B 2021, 820, 136592. [Google Scholar] [CrossRef]
- Derbali, E.; van Isacker, P.; Tellili, B.; Souga, C. Effective operators in a single-j orbital. J. Phys. G Nucl. Part. Phys. 2018, 45, 035102. [Google Scholar] [CrossRef]
- Romero, A.; Dobaczewski, J.; Pastore, A. Symmetry restoration in the mean-field description of proton-neutron pairing. Phys. Lett. B 2019, 795, 177–182. [Google Scholar] [CrossRef]
- Idini, A.; Potel, G.; Barranco, F.; Vigezzi, E.; Broglia, R.A. Interweaving of elementary modes of excitation in superfluid nuclei through particle-vibration coupling: Quantitative account of the variety of nuclear structure observables. Phys. Rev. C 2015, 92, 031304. [Google Scholar] [CrossRef]
- Nomura, K.; Jolie, J. Structure of even-even cadmium isotopes from the beyond-mean-field interacting boson model. Phys. Rev. C 2018, 98, 024303. [Google Scholar] [CrossRef]
- Sun, Z.H.; Hagen, G.; Jansen, G.R.; Papenbrock, T. Effective shell-model interaction for nuclei “southeast” of 100Sn. Phys. Rev. C 2021, 104, 064310. [Google Scholar] [CrossRef]
- De-Shalit, A.; Talmi, I.; Wigner, E.P. Review of “Nuclear Shell Theory”. In Historical and Biographycal Reflections and Syntheses; Mehra, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 494–495. [Google Scholar] [CrossRef]
- Mach, H.; Korgul, A.; Górska, M.; Grawe, H. Ultrafast-timing lifetime measurements in 94Ru and 96Pd: Breakdown of the seniority scheme in N = 50 iso-tones. Phys. Rev. C 2017, 95, 014313. [Google Scholar] [CrossRef]
- National Nuclear Data Center, NuDat 3. Available online: https://www.bnl.gov/world/ (accessed on 1 August 2021).
- Jin, S.Y.; Wang, S.T.; Lee, J.; Corsi, A.; Wimmer, K.; Browne, F.; Chen, S.; Cortés, M.L.; Doornenbal, P.; Koiwai, T.; et al. Spectroscopy of 98Cd by two-nucleon removal from 100In. Phys. Rev. C 2021, 104, 024302. [Google Scholar] [CrossRef]
- Qi, C. Partial conservation of seniority and its unexpected influence on E2 transitions in g9/2 nuclei. Phys. Lett. B 2017, 773, 616. [Google Scholar] [CrossRef]
- Pérez-Vidal, R.M. Collectivity along N=50: Nuclear Structure studies on the neutron-magic nuclei 92Mo and 94Ru with AGATA and VAMOS++. Ph.D. Thesis, Universidad de Valencia, València, Spain, 2019. Available online: https://roderic.uv.es/handle/10550/72450 (accessed on 1 November 2021).
- Das, B.; Cederwall, B.; Qi, C.; Górska, M.; Regan, P.H.; Aktas, Ö.; Albers, H.M.; Banerjee, A.; Chishti, M.M.R.; Gerl, J.; et al. Nature of seniority symmetry breaking in the semimagic nucleus 94Ru. Phys. Rev. C, in print.
- Lorusso, G.; Becerril, A.; Amthor, A.; Baumann, T.; Bazin, D.; Berryman, J.; Brown, B.; Cyburt, R.; Crawford, H.; Estrade, A.; et al. Half-lives of ground and isomeric states in 97Cd and the astrophysical origin of 96Ru. Phys. Lett. B 2011, 699, 141–144. [Google Scholar] [CrossRef][Green Version]
- Robinson, S.J.Q.; Hoang, T.; Zamick, L.; Escuderos, A.; Sharon, Y.Y. Shell model calculations of B(E2) values, static quadrupole moments, and g factors for a number of N = Z nuclei. Phys. Rev. C 2014, 89, 014316. [Google Scholar] [CrossRef]
- Kingan, A.; Zamick, L. Odd-J states of isospin zero and one for 4-nucleon systems: Near-degeneracies. Phys. Rev. C 2018, 98, 014301. [Google Scholar] [CrossRef]
- Fu, G.J.; Cheng, Y.Y.; Zhao, Y.M.; Arima, A. Shell model study of T = 0 states for 96Cd by the nucleon-pair approximation. Phys. Rev. C 2016, 94, 024336. [Google Scholar] [CrossRef]
- Nara Singh, B.S.; Liu, Z.; Wadsworth, R.; Grawe, H.; Brock, T.S.; Boutachkov, P.; Braun, N.; Blazhev, A.; Górska, M.; Pietri, S.; et al. 16+ spin-gap isomer in 96Cd. Phys. Rev. Lett. 2011, 107, 172502. [Google Scholar] [CrossRef]
- Zerguine, S.; Van Isacker, P. Spin-aligned neutron-proton pairs in N = Z nuclei. Phys. Rev. C 2011, 83, 064314. [Google Scholar] [CrossRef]
- Xu, Z.; Qi, C.; Blomqvist, J.; Liotta, R.; Wyss, R. Multistep shell model description of spin-aligned neutron–proton pair coupling. Nucl. Phys. A 2012, 877, 51–58. [Google Scholar] [CrossRef]
- Qi, C.; Blomqvist, J.; Bäck, T.; Cederwall, B.; Johnson, A.; Liotta, R.J.; Wyss, R. Spin-aligned neutron-proton pair mode in atomic nuclei. Phys. Rev. C 2011, 84, 021301. [Google Scholar] [CrossRef]
- Van Isacker, P. Neutron–proton pairs in nuclei. Int. J. Mod. Phys. 2013, E22, 1330028. [Google Scholar] [CrossRef]
- Marginean, N.; Bucurescu, D.; Alvarez, C.R.; Ur, C.A. Delayed alignments in the N = Z nuclei 84Mo and 88Ru. Phys. Rev. C 2002, 65, 051303. [Google Scholar] [CrossRef]
- Sun, Y. Projected shell model study on nuclei near the N = Z line. Eur. Phys. J. A 2003, 20, 133–138. [Google Scholar] [CrossRef]
- Sun, Y.; Sheikh, J. Anomalous rotational alignment in N = Z nuclei and residual neutron-proton interaction. Phys. Rev. C 2001, 64, 162031302. [Google Scholar] [CrossRef]
- Kaneko, Y.S.K.; de Angelis, G. Enhancement of high-spin collectivity in N = Z nuclei by the isoscalar neutron–proton pairing. Nucl. Phys. A 2017, 957, 144. [Google Scholar] [CrossRef]
- Kaneko, Y.S.K.; Mizusaki, T.; Sun, Y.; Tazaki, S. Toward a unified realistic shell-model Hamiltonian with the mono-pole-based universal force. Phys. Rev. C 2014, 89, 011302. [Google Scholar] [CrossRef]
- Fu, G.J.; Johnson, C.W. Nucleon-pair approximation for nuclei from spherical to deformed regions. Phys. Rev. C 2021, 104, 024312. [Google Scholar] [CrossRef]
- Corsi, A.; Obertelli, A.; Doornenbal, P.; Nowacki, F.; Sagawa, H.; Tanimura, Y.; Aoi, N.; Baba, H.; Bednarczyk, P.; Boissinot, S.; et al. Spectroscopy of nuclei around 100Sn populated via two-neutron knockout reactions. Phys. Rev. C 2018, 97, 044321. [Google Scholar] [CrossRef]
- Banu, A.; Gerl, J.; Fahlander, C.; Górska, M.; Grawe, H.; Saito, T.R.; Wollersheim, H.-J.; Caurier, E.; Engeland, T.; Gniady, A.; et al. 108Sn studied with intermediate-energy Coulomb excitation. Phys. Rev. C 2005, 72, 061305. [Google Scholar] [CrossRef]
- Maheshwari, B. A unified view of the first-excited 2+ and 3− states of Cd, Sn and Te isotopes. Eur. Phys. J. Spéc. Top. 2020, 229, 2485–2495. [Google Scholar] [CrossRef]
- Guastalla, G.; DiJulio, D.D.; Górska, M.; Cederkall, J.; Boutachkov, P.; Golubev, P.; Pietri, S.; Grawe, H.; Nowacki, F.; Sieja, K.; et al. Coulomb Excitation of 104Sn and the Strength of the 100Sn Shell Closure. Phys. Rev. Lett. 2013, 110, 172501. [Google Scholar] [CrossRef]
- Jonsson, N.-G.; Bäcklin, A.; Kantele, J.; Julin, R.; Luontama, M.; Passoja, A. Collective states in even Sn nuclei. Nucl. Phys. A 1981, 371, 333–348. [Google Scholar] [CrossRef]
- Vaman, C.; Andreoiu, C.; Bazin, D.; Becerril, A.; Brown, B.A.; Campbell, C.M.; Chester, A.; Cook, J.M.; Dinca, D.C.; Gade, A.; et al. Z = 50 shell gap near 100Sn from intermediate-energy Coulomb excitations in even-mass 106–112Sn isotopes. Phys. Rev. Lett. 2007, 99, 162501. [Google Scholar] [CrossRef]
- Cederkall, J.; Ekstrom, A.; Fahlander, C.; Hurst, A.M.; Hjorth-Jensen, M.; Ames, F.; Banu, A.; Butler, P.A.; Davinson, T.; Pramanik, U.D.; et al. Sub-barrier Coulomb excitation of 110Sn and its implications for the 100Sn shell closure. Phys. Rev. Lett. 2007, 98, 172501. [Google Scholar] [CrossRef]
- Ekström, A.; Cederkäll, J.; Fahlander, C.; Hjorth-Jensen, M.; Ames, F.; Butler, P.A.; Davinson, T.; Eberth, J.; Fincke, F.; Görgen, A.; et al. transition strengths in 106Sn and 108Sn. Phys. Rev. Lett. 2008, 101, 012502. [Google Scholar] [CrossRef]
- Orce, J.N.; Choudry, S.N.; Crider, B.; Elhami, E.; Mukhopadhyay, S.; Scheck, M.; McEllistrem, M.T.; Yates, S.W. → transition strengths in Sn nuclei. Phys. Rev. C 2007, 76, 021302. [Google Scholar] [CrossRef]
- Bader, V.M.; Gade, A.; Weisshaar, D.; Brown, B.A.; Baugher, T.; Bazin, D.; Berryman, J.S.; Ekstrom, A.; Hjorth-Jensen, M.; Stroberg, R.; et al. Quadrupole collectivity in neutron-deficient Sn nuclei: 104Sn and the role of proton excitations. Phys. Rev. C 2013, 88, 051301. [Google Scholar] [CrossRef]
- Doornenbal, P.; Reiter, P.; Grawe, H.; Wollersheim, H.J.; Bednarczyk, P.; Caceres, L.; Cederkäll, J.; Ekström, A.; Gerl, J.; Górska, M.; et al. Enhanced strength of the transition in 114Sn studied via Coulomb excitation in inverse kinematics. Phys. Rev. C 2008, 78, 031303. [Google Scholar] [CrossRef]
- Kumar, R.; Doornenbal, P.; Jhingan, A.; Bhowmik, R.K.; Muralithar, S.; Appannababu, S.; Garg, R.; Gerl, J.; Górska, M.; Kaur, J.; et al. Enhanced E2 transition strength in 112Sn. Phys. Rev. C 2010, 81, 024306. [Google Scholar] [CrossRef]
- Kumar, R.; Saxena, M.; Doornenbal, P.; Jhingan, A.; Banerjee, A.; Bhowmik, R.K.; Dutt, S.; Garg, R.; Joshi, C.; Mishra, V.; et al. No evidence of reduced collectivity in Coulomb-excited Sn isotopes. Phys. Rev. C 2017, 96, 054318. [Google Scholar] [CrossRef]
- Allmond, J.M.; Radford, D.C.; Baktash, C.; Batchelder, J.C.; Galindo-Uribarri, A.; Gross, C.J.; Hausladen, P.; Lagergren, K.; LaRochelle, Y.; Padilla-Rodal, E.; et al. Coulomb excitation of 124,126,128Sn. Phys. Rev. C 2011, 84, 061303. [Google Scholar] [CrossRef]
- Allmond, J.M.; Stuchbery, A.E.; Galindo-Uribarri, A.; Padilla-Rodal, E.; Radford, D.C.; Batchelder, J.C.; Bingham, C.R.; Howard, M.E.; Liang, J.F.; Manning, B.; et al. Investigation into the semimagic nature of the tin isotopes through electromagnetic moments. Phys. Rev. C 2015, 92, 041303. [Google Scholar] [CrossRef]
- Jungclaus, A.; Walker, J.; Leske, J.; Speidel, K.-H.; Stuchbery, A.; East, M.; Boutachkov, P.; Cederkall, J.; Doornenbal, P.; Egido, J.L.; et al. Evidence for reduced collectivity around the neutron mid-shell in the stable even-mass Sn isotopes from new lifetime measurements. Phys. Lett. B 2011, 695, 110–114. [Google Scholar] [CrossRef]
- Kumbartzki, G.J. Transient field g factor and mean-life measurements with a rare isotope beam of 126Sn. Phys. Rev. C 2012, 86, 034319. [Google Scholar] [CrossRef]
- Kumbartzki, G.J.; Benczer-Koller, N.; Speidel, K.-H.; Torres, D.A.; Allmond, J.M.; Fallon, P.; Abramovic, I.; Bernstein, L.A.; Bevins, J.E.; Crawford, H.; et al. Z = 50 core stability in 110Sn from magnetic-moment and lifetime measurements. Phys. Rev. C 2016, 93, 044316. [Google Scholar] [CrossRef]
- Doornenbal, P.; Takeuchi, S.; Aoi, N.; Matsushita, M.; Obertelli, A.; Steppenbeck, D.; Wang, H.; Audirac, L.; Baba, H.; Bednarczyk, P.; et al. Intermediate-energy Coulomb excitation of 104Sn: Moderate E2 strength decrease approaching 100Sn. Phys. Rev. C 2014, 90, 061302. [Google Scholar] [CrossRef]
- Radford, D.C.; Baktash, C.; Barton, C.J.; Batchelder, J.; Beene, J.R.; Bingham, C.R.; Caprio, M.A.; Danchev, M.; Fuentes, B.; Galindo-Uribarri, A.; et al. Coulomb excitation and transfer reactions with neutron-rich radioactive beams. Int. Conf. Exot. Nucl. At. Masses 2005, 746, 383–387. [Google Scholar] [CrossRef]
- Radford, D.; Baktash, C.; Barton, C.; Batchelder, J.; Beene, J.; Bingham, C.; Caprio, M.; Danchev, M.; Fuentes, B.; Galindo-Uribarri, A.; et al. Coulomb excitation and transfer reactions with rare neutron-rich isotopes. Nucl. Phys. A 2005, 752, 264–272. [Google Scholar] [CrossRef]
- Spieker, M.; Petkov, P.; Litvinova, E.; Müller-Gatermann, C. Shape coexistence and collective low-spin states in 112,114Sn studied with the (p, p’γ ) Doppler-shift at-tenuation coincidence technique. Phys. Rev. C 2018, 97, 054319. [Google Scholar] [CrossRef]
- Berger, M. Kernstrukturuntersuchungen bis zur Teilchenseparationsschwelle mit der Methode der Kernresonanzfluoreszen. Ph.D. Thesis, Technical University of Darmstadt, Darmstadt, Germany, 2020. [Google Scholar] [CrossRef]
- Rosiak, D.; Seidlitz, M.; Reiter, P.; Naïdja, H.; Tsunoda, Y.; Togashi, T.; Nowacki, F.; Otsuka, T.; Colò, G.; Arnswald, K.; et al. Enhanced quadrupole and octupole strength in doubly magic 132Sn. Phys. Rev. Lett. 2018, 121, 252501. [Google Scholar] [CrossRef]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T.T.S. Shell-model study of quadrupole collectivity in light tin isotopes. Phys. Rev. C 2015, 91, 041301. [Google Scholar] [CrossRef]
- Cortes, L.M. (INFN Legnro, Italy). Data analysis of the Coulomb excitations of 102Sn experiment. Private communication, 2021. [Google Scholar]
- Wimmer, K. (GSI Darmstadt, Germany). Review submitted to Prog. Part. Nucl. Phys. Private communication, 2021. [Google Scholar]
- Siciliano, M.; Valiente-Dobón, J.J.; Goasduff, A.; Rodríguez, T.R.; Bazzacco, D.; Benzoni, G.; Braunroth, T.; Cieplicka-Oryńczak, N.; Clément, E.; Crespi, F.C.L.; et al. Lifetime measurements in the even-even 102–108Cd isotopes. Phys. Rev. C 2021, 104, 034320. [Google Scholar] [CrossRef]
- Górska, M.; Lipoglavsek, M.; Grawe, H.; Nyberg, J.; Atac, A.; Axelsson, A.; Bark, R.; Blomqvist, J.; Cederkäll, A.; Cederwall, B.; et al. 9848Cd50: The two-proton-hole spectrum in 10050Sn50. Phys. Rev. Lett. 1997, 79, 2415. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Górska, M. Trends in the Structure of Nuclei near 100Sn. Physics 2022, 4, 364-382. https://doi.org/10.3390/physics4010024
Górska M. Trends in the Structure of Nuclei near 100Sn. Physics. 2022; 4(1):364-382. https://doi.org/10.3390/physics4010024
Chicago/Turabian StyleGórska, Magdalena. 2022. "Trends in the Structure of Nuclei near 100Sn" Physics 4, no. 1: 364-382. https://doi.org/10.3390/physics4010024
APA StyleGórska, M. (2022). Trends in the Structure of Nuclei near 100Sn. Physics, 4(1), 364-382. https://doi.org/10.3390/physics4010024




