The Nuclear Shell Model towards the Drip Lines
Abstract
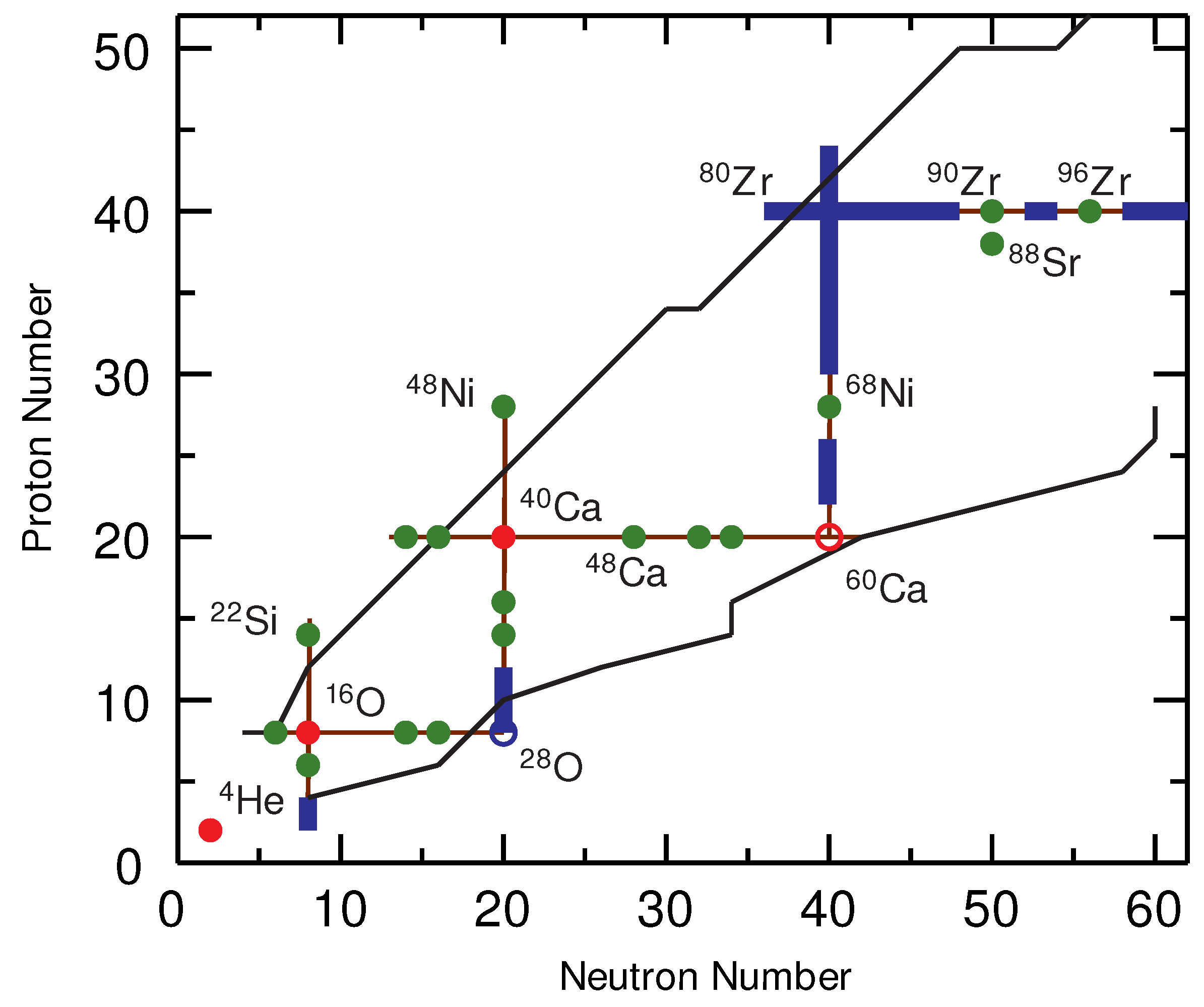
:1. Introduction
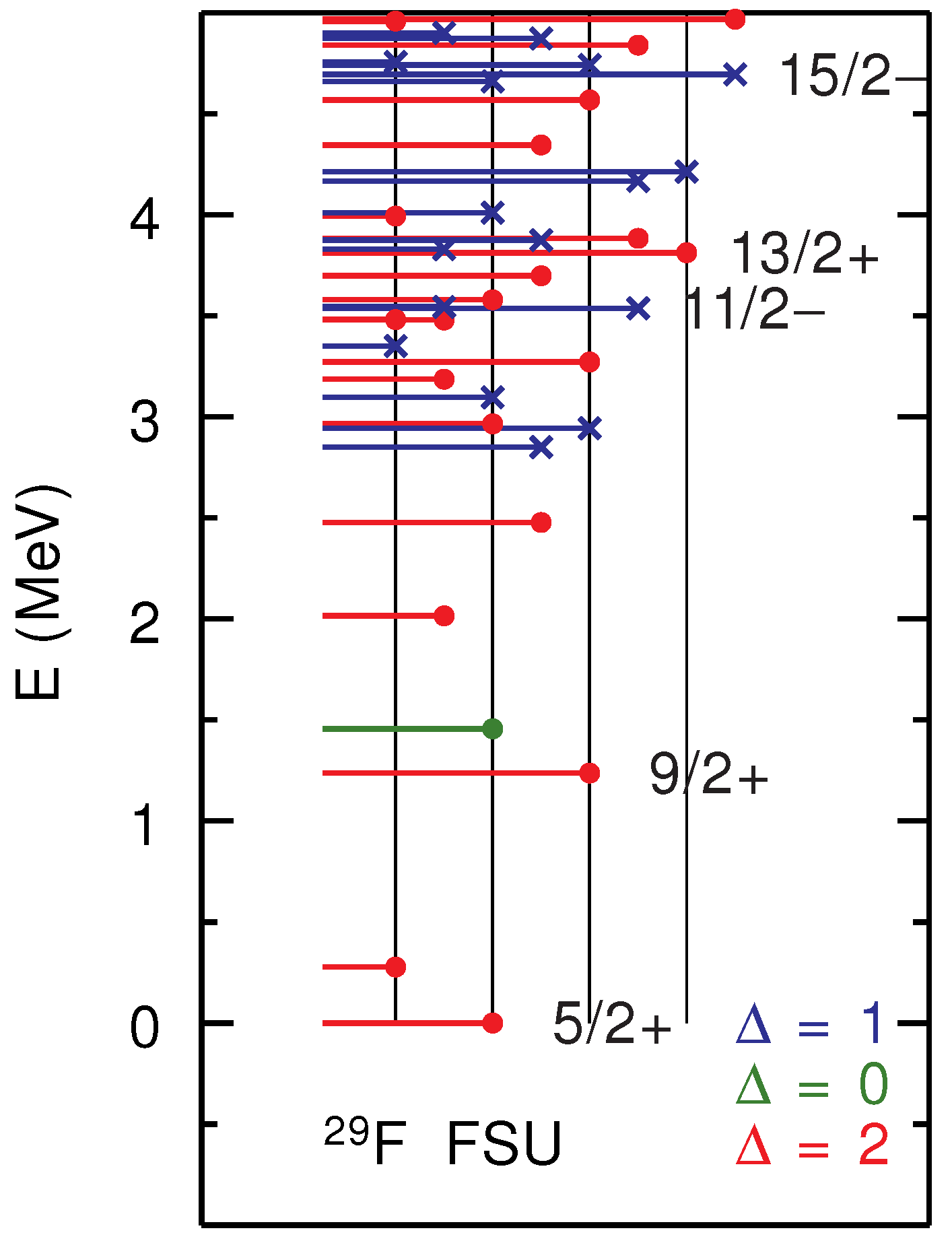
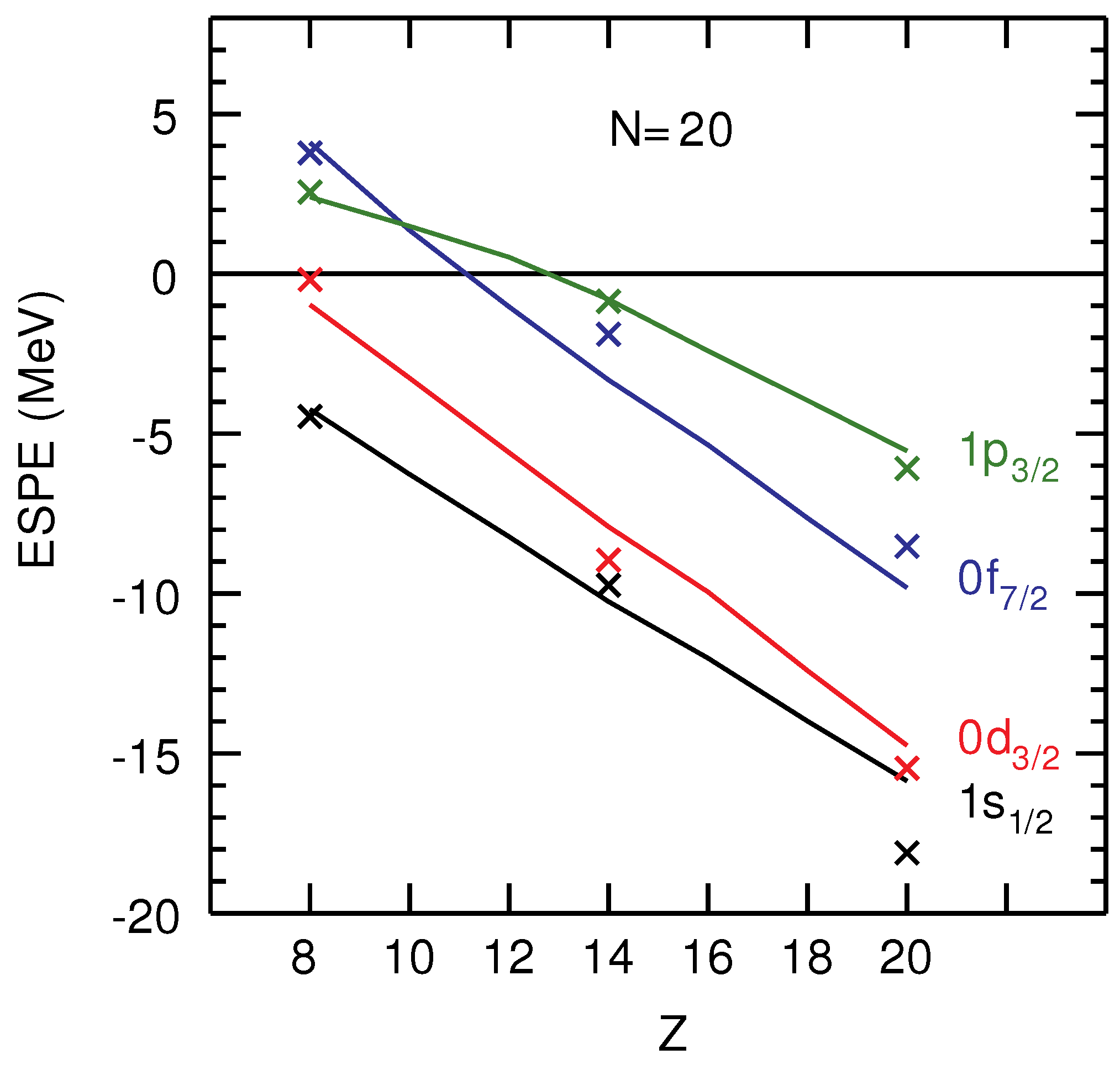
2. The Region of O
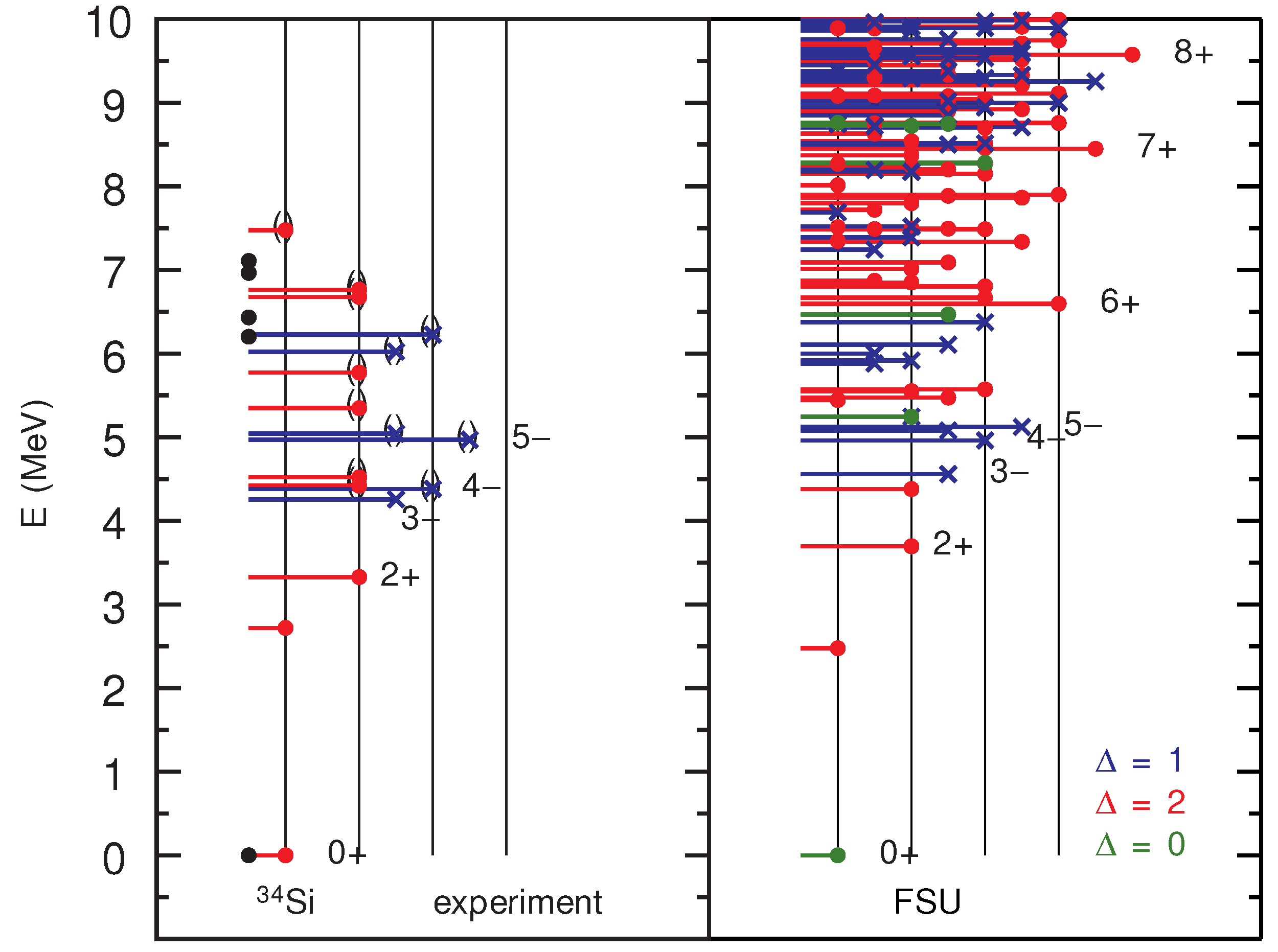
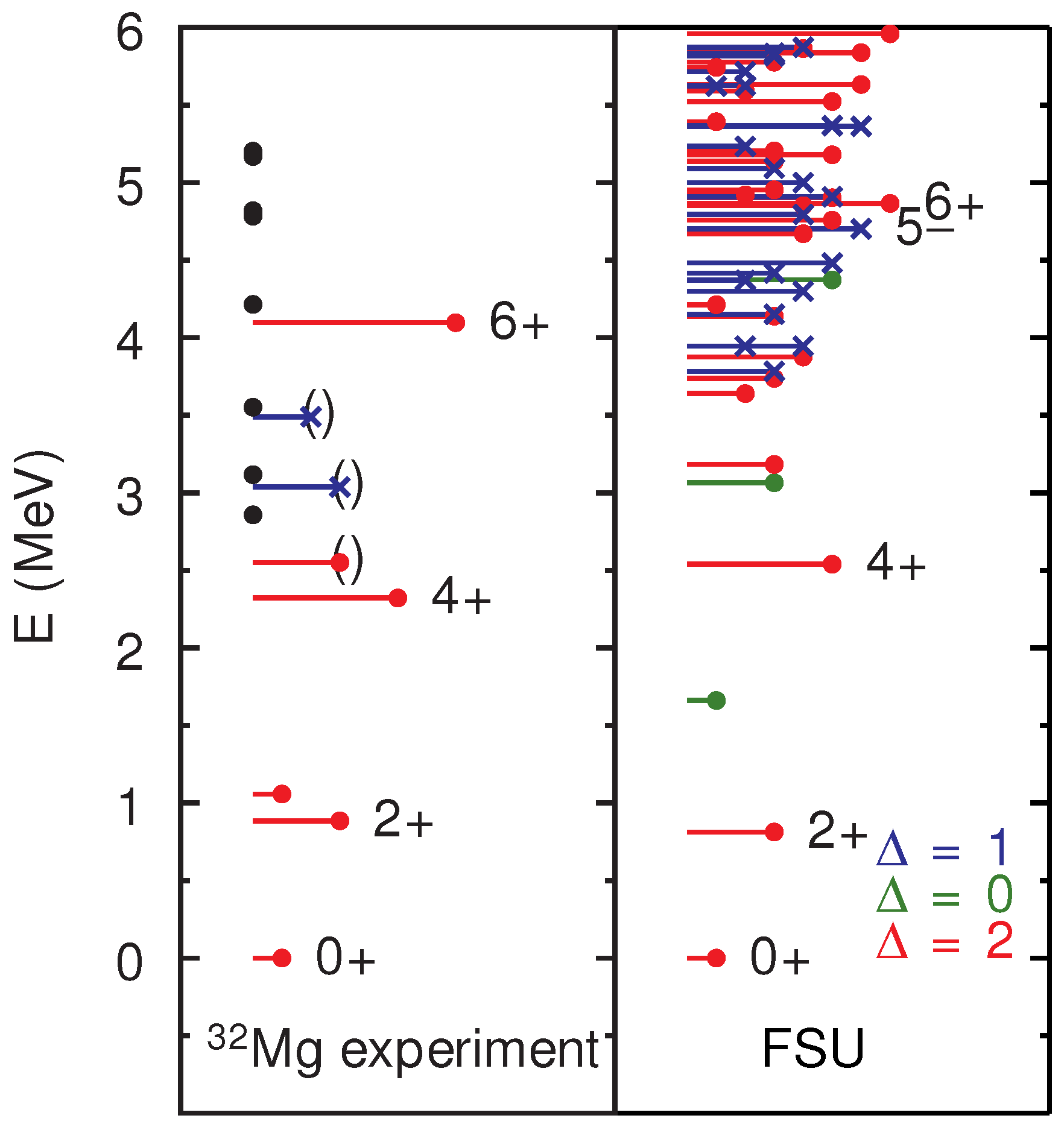
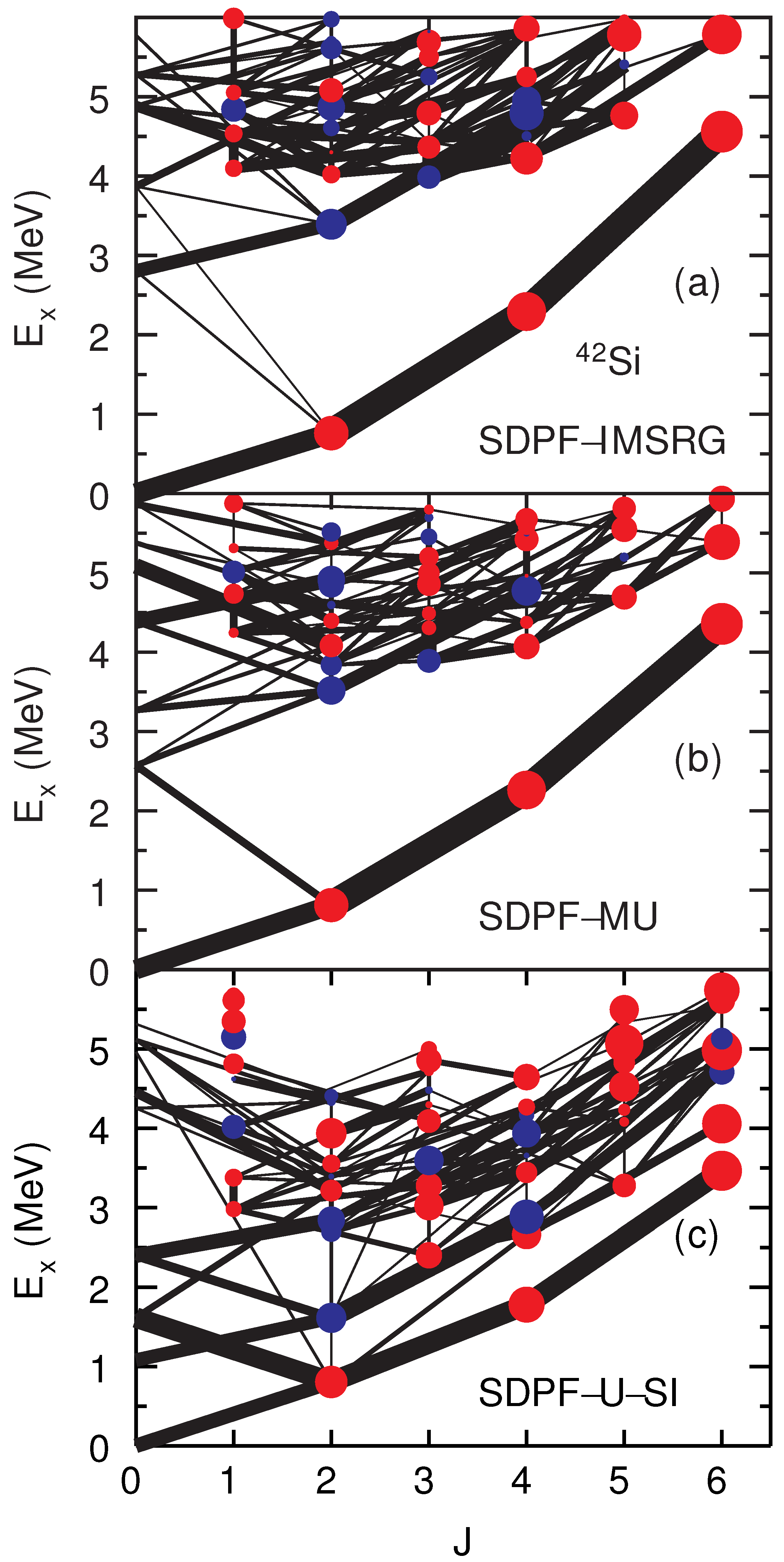
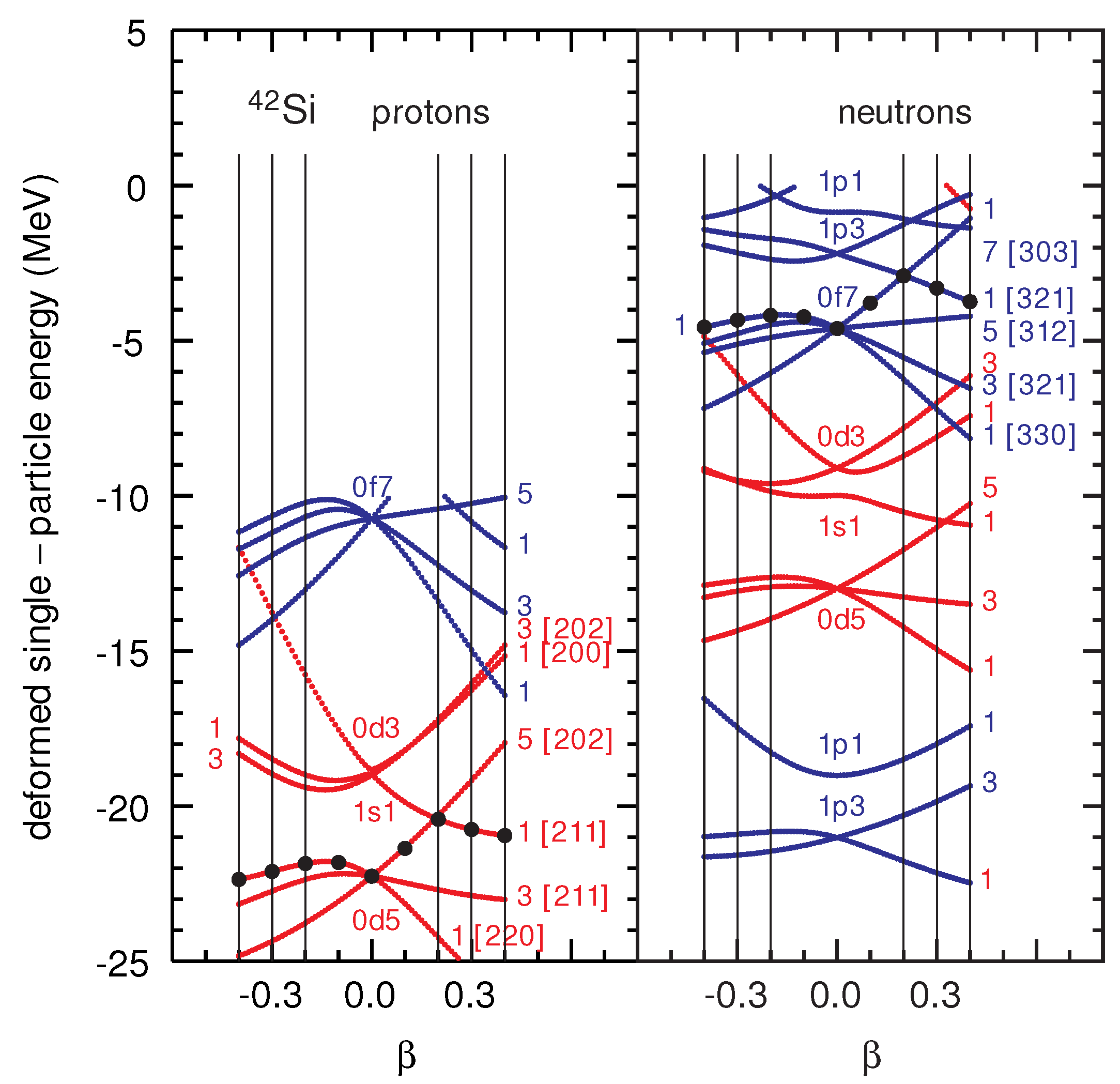
3. The Region of Si
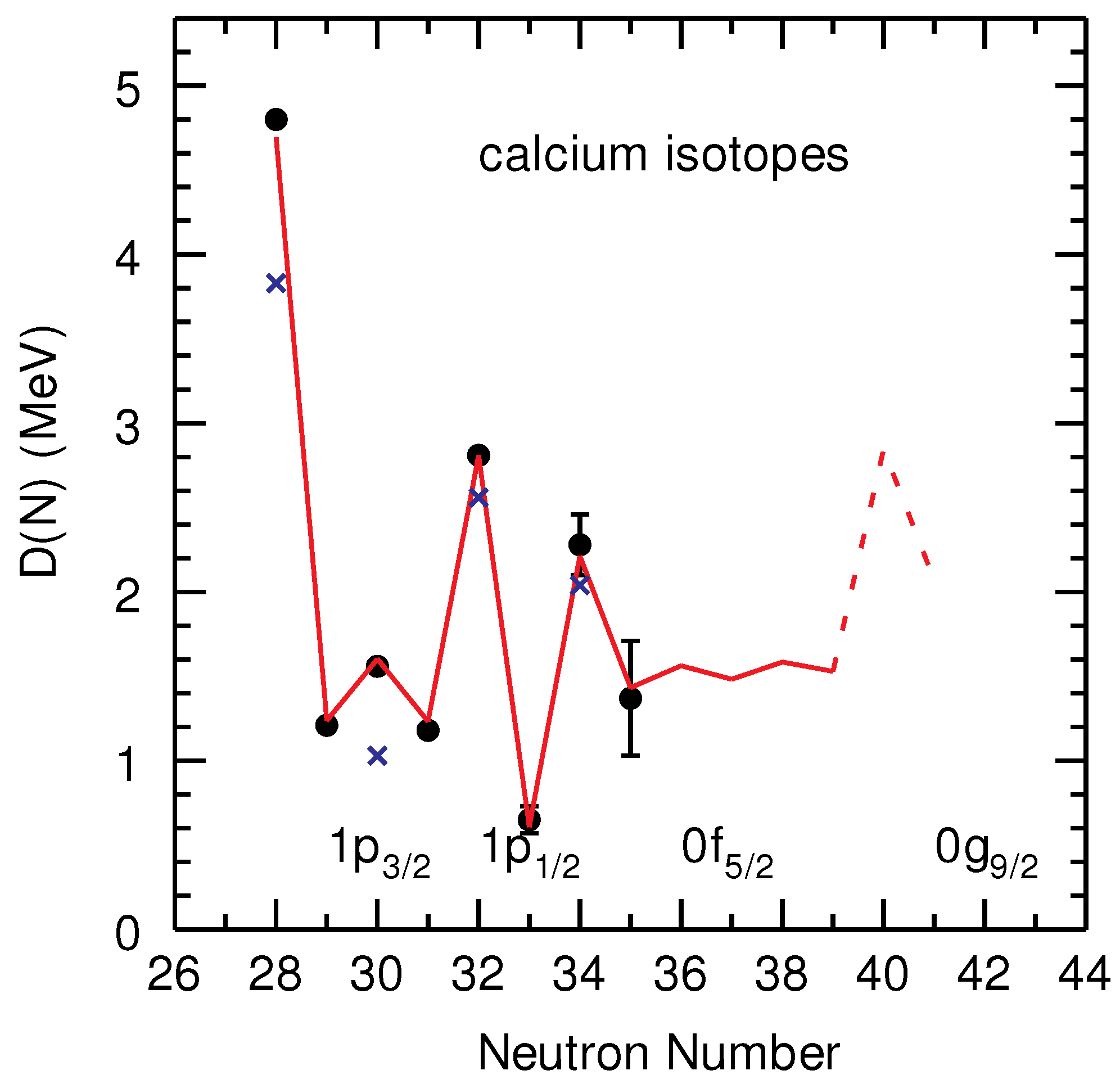
4. The Region of Ca
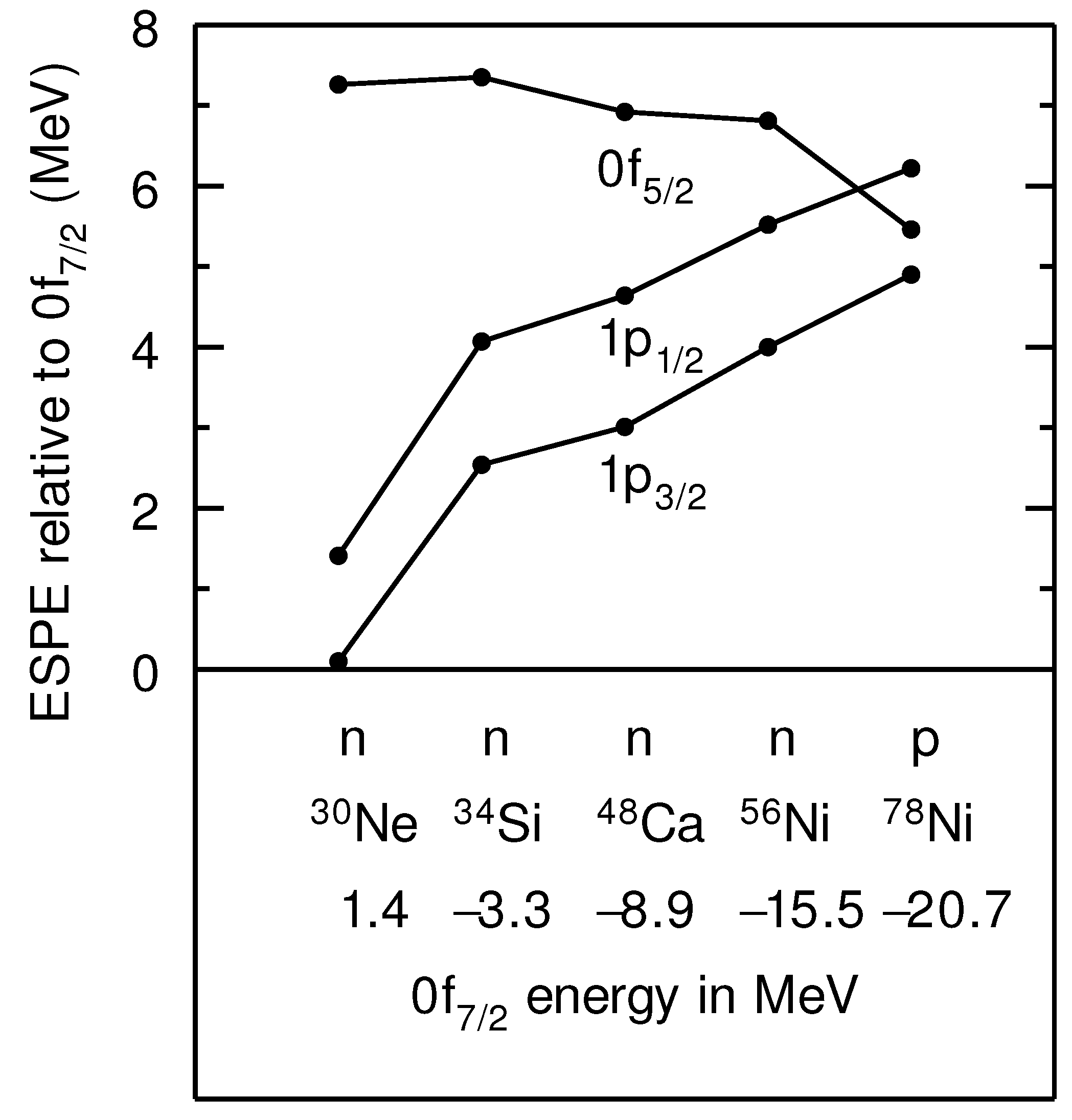
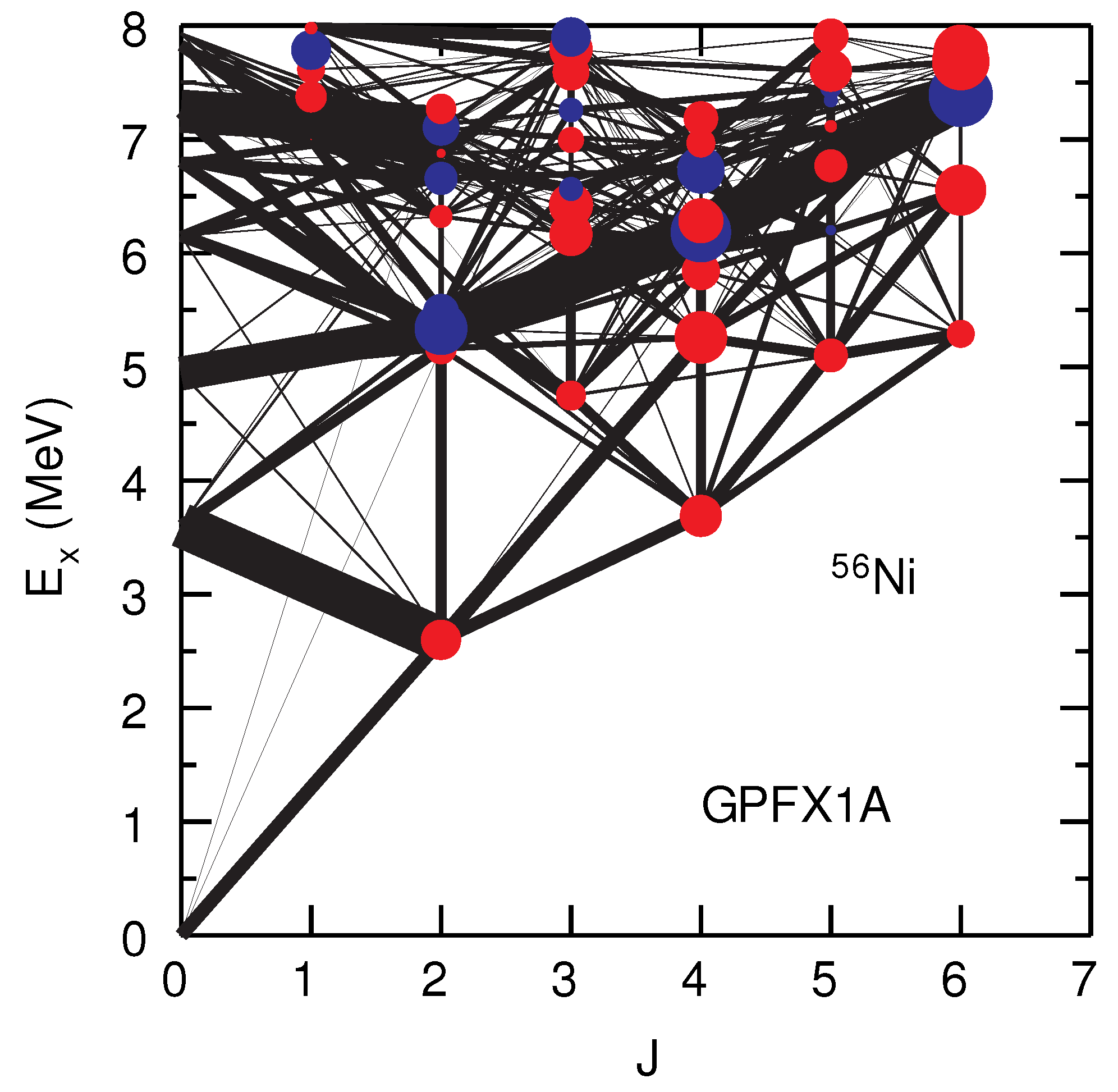
5. The Region of Ni
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, B.A.; Wildenthal, B.H. Status of the nuclear shell model. Ann. Rev. Nucl. Part. Sci. 1988, 38, 29–66. [Google Scholar] [CrossRef]
- Brown, B.A. The nuclear shell model towards the drip lines. Prog. Part. Nucl. Phys. 2001, 47, 517–599. [Google Scholar] [CrossRef]
- Caurier, E.; Martinez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef] [Green Version]
- Stroberg, S.R.; Hergert, H.; Bogner, S.K.; Holt, J.D. Nonempirical interactions for the nuclear shell model: An update. Ann. Rev. Nucl. Part. Sci. 2019, 69, 307–362. [Google Scholar] [CrossRef] [Green Version]
- Otsuka, T.; Gade, A.; Sorlin, O.; Suzuki, T.; Utsuno, Y. Evolution of shell structure in exotic nuclei. Rev. Mod. Phys. 2020, 92, 015002. [Google Scholar] [CrossRef] [Green Version]
- Brown, B.A. Nuclear pairing gap: How low can it go? Phys. Rev. Lett. 2013, 111, 162502. [Google Scholar] [CrossRef] [Green Version]
- Audi, G. The history of nuclidic masses and of their evaluation. Int. J. Mass Spec. 2006, 251, 85–94. [Google Scholar] [CrossRef] [Green Version]
- Pritychenko, B.; Birch, M.; Singh, B.; Horoi, M. Tables of E2 transition probabilities from the first 2+ states in even-even nuclei. Atom. Data Nucl. Data Tables 2016, 107, 1–139. [Google Scholar] [CrossRef] [Green Version]
- Crawford, H.L.; Fallon, P.; Macchiavelli, A.O.; Doornenbal, P.; Aoi, N.; Browne, F.; Campbell, C.M.; Chen, S.; Clark, R.M.; Cortes, M.L.; et al. First spectroscopy of the near drip-line nucleus 40Mg. Phys. Rev. Lett. 2019, 122, 052501. [Google Scholar] [CrossRef] [Green Version]
- Cortes, M.L.; Rodriguez, W.; Doornenbal, P.; Obertelli, A.; Holt, J.D.; Lenzi, S.M.; Menendez, J.; Nowacki, F.; Ogata, K.; Poves, A.; et al. Shell evolution of N = 40 isotones towards 60Ca: First spectroscopy of 62Ti. Phys. Lett. B 2020, 800, 135071. [Google Scholar] [CrossRef]
- Santamaria, C.; Louchart, C.; Obertelli, A.; Werner, V.; Doornenbal, P.; Nowacki, F.; Authelet, G.; Baba, H.; Calvet, D.; Chateau, F.; et al. Extension of the N = 40 island of inversion towards N = 50: Spectroscopy of 66Cr, 70Fe, 72Fe. Phys. Rev. Lett. 2015, 115, 192501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Magilligan, A.; Brown, B.A.; Stroberg, S.R. Data-driven configuration-interaction Hamiltonian extrapolation to 60Ca. Phys. Rev. C 2021, 104, L051302. [Google Scholar] [CrossRef]
- Mass Explorer. Available online: http://massexplorer.frib.msu.edu/ (accessed on 10 April 2022).
- Morris, T.D.; Simonis, J.; Stroberg, S.R.; Stumpf, C.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Papenbrock, T.; Roth, R.; Schwenk, A. Structure of the lightest tin isotopes. Phys. Rev. Lett. 2018, 120, 152503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Warburton, E.K.; Becker, J.A.; Brown, B.A. Mass systematics for A = 29–44 nuclei: The deformed A∼32 region. Phys. Rev. C 1990, 41, 1147–1166. [Google Scholar] [CrossRef] [Green Version]
- Serduke, F.J.D.; Lawson, R.D.; Gloeckner, D.H. Shell-model study of N = 49 isotones. Nucl. Phys. A 1976, 256, 45–86. [Google Scholar] [CrossRef]
- Ji, X.D.; Wildenthal, B.H. Shell-model calculations for the energy-levels of the N = 50 isotones with A = 80–87. Phys. Rev. C 1989, 40, 389–398. [Google Scholar] [CrossRef]
- Lisetskiy, A.; Brown, B.; Horoi, M.; Grawe, H. New T = 1 effective interactions for the f5/2p3/2p1/2g9/2 model space: Implications for valence-mirror symmetry and seniority isomers. Phys. Rev. C 2004, 70, 044314. [Google Scholar] [CrossRef] [Green Version]
- Magilligan, A.; Brown, B.A. New isospin-breaking “USD” Hamiltonians for the sd shell. Phys. Rev. C 2020, 101, 064312. [Google Scholar] [CrossRef]
- Stroberg, S.R.; Holt, J.D.; Schwenk, A.; Simonis, J. Ab initio limits of atomic nuclei. Phys. Rev. Lett. 2021, 126, 022501. [Google Scholar] [CrossRef]
- Forssén, C.; Hagen, G.; Hjorth-Jensen, M.; Nazarewicz, W.; Rotureau, J. Living on the edge of stability, the limits of the nuclear landscape. Physica Scripta 2013, 2013, 014022. [Google Scholar] [CrossRef] [Green Version]
- Rotureau, J.; Michel, N.; Nazarewicz, W.; Płoszajczak, M.; Dukelsky, J. Density matrix renormalization group approach for many-body open quantum systems. Phys. Rev. Lett. 2006, 97, 110603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rotureau, J.; Michel, N.; Nazarewicz, W.; Płoszajczak, M.; Dukelsky, J. Density matrix renormalization group approach to two-fluid open many-fermion systems. Phys. Rev. C 2009, 79, 014304. [Google Scholar] [CrossRef] [Green Version]
- Bertulani, C.; Hammer, H.W.; Van Kolck, U. Effective field theory for halo nuclei: Shallow p-wave states. Nucl. Phys. A 2002, 712, 37–58. [Google Scholar] [CrossRef] [Green Version]
- Bedaque, P.; Hammer, H.W.; Van Kolck, U. Narrow resonances in effective field theory. Phys. Lett. B 2003, 569, 159–167. [Google Scholar] [CrossRef] [Green Version]
- Id Betan, R.; Liotta, R.J.; Sandulescu, N.; Vertse, T. Two-particle resonant states in a many-body mean field. Phys. Rev. Lett. 2002, 89, 042501. [Google Scholar] [CrossRef] [Green Version]
- Michel, N.; Nazarewicz, W.; Płoszajczak, M.; Bennaceur, K. Gamow shell model description of neutron-rich nuclei. Phys. Rev. Lett. 2002, 89, 042502. [Google Scholar] [CrossRef] [Green Version]
- Michel, N.; Nazarewicz, W.; Płoszajczak, M.; Vertse, T. Shell model in the complex energy plane. J. Phys. G: Nucl Part. Phys. 2009, 36, 013101. [Google Scholar] [CrossRef] [Green Version]
- Berggren, T.; Lind, P. Resonant state expansion of the resolvent. Phys. Rev. C 1993, 47, 768–778. [Google Scholar] [CrossRef]
- Lind, P. Completeness relations and resonant state expansions. Phys. Rev. C 1993, 47, 1903–1920. [Google Scholar] [CrossRef]
- Volya, A.; Zelevinsky, V. Discrete and continuum spectra in the unified shell model approach. Phys. Rev. Lett. 2005, 94, 052501. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ma, Y.; Michel, N.; Hu, B.; Sun, Z.; Zuo, W.; Xu, F. Recent progress in Gamow shell model calculations of drip line nuclei. Physics 2021, 3, 977–997. [Google Scholar] [CrossRef]
- Tanihata, I.; Savajols, H.; Kanungo, R. Recent experimental progress in nuclear halo structure studies. Prog. Part. Nucl. Phys. 2013, 68, 215–313. [Google Scholar] [CrossRef]
- Tanihata, I.; Hamagaki, H.; Hashimoto, O.; Shida, Y.; Yoshikawa, N.; Sugimoto, K.; Yamakawa, O.; Kobayashi, T.; Takahashi, N. Measurements of interaction cross-sections and nuclear radii in the light p-shell region. Phys. Rev. Lett. 1985, 55, 2676–2679. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olivier, L.; Franchoo, S.; Niikura, M.; Vajta, Z.; Sohler, D.; Doornenbal, P.; Obertelli, A.; Tsunoda, Y.; Otsuka, T.; Authelet, G.; et al. Persistence of the Z = 28 shell gap around 78Ni: First spectroscopy of 79Cu. Phys. Rev. Lett. 2017, 119, 192501. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, O.B.; Ahn, D.S.; Bazin, D.; Fukuda, N.; Gade, A.; Hausmann, M.; Inabe, N.; Ishikawa, S.; Iwasa, N.; Kawata, K.; et al. Discovery of 60Ca and implications for the stability of 70Ca. Phys. Rev. Lett. 2018, 121, 022501. [Google Scholar] [CrossRef] [Green Version]
- Brown, B.A.; Blank, B.; Giovinazzo, J. Hybrid model for two-proton radioactivity. Phys. Rev. C 2019, 100, 054332. [Google Scholar] [CrossRef]
- Jin, Y.; Niu, C.Y.; Brown, K.W.; Li, Z.H.; Hua, H.; Anthony, A.K.; Barney, J.; Charity, R.J.; Crosby, J.; Dell’Aquila, D.; et al. First observation of the four-proton unbound nucleus 18Mg. Phys. Rev. Lett. 2021, 127, 262502. [Google Scholar] [CrossRef]
- Tostevin, J.A.; Gade, A. Updated systematics of intermediate-energy single-nucleon removal cross sections. Phys. Rev. C 2021, 103, 054610. [Google Scholar] [CrossRef]
- Paschalis, S.; Petri, M.; Macchiavelli, A.O.; Hen, O.; Piasetzky, E. Nucleon-nucleon correlations and the single-particle strength in atomic nuclei. Phys. Lett. B 2020, 800, 135110. [Google Scholar] [CrossRef]
- Hen, O.; Miller, G.A.; Piasetzky, E.; Weinstein, L.B. Nucleon-nucleon correlations, short-lived excitations, and the quarks within. Rev. Mod. Phys. 2017, 89, 045002. [Google Scholar] [CrossRef] [Green Version]
- Panin, V.; Taylor, J.T.; Paschalis, S.; Wamers, F.; Aksyutina, Y.; Alvarez-Pol, H.; Aumann, T.; Bertulani, C.A.; Boretzky, K.; Caesar, C.; et al. Exclusive measurements of quasi-free proton scattering reactions in inverse and complete kinematics. Phys. Lett. B 2016, 753, 204–210. [Google Scholar] [CrossRef]
- Jensen, O.; Hagen, G.; Hjorth-Jensen, M.; Brown, B.A.; Gade, A. Quenching of spectroscopic factors for proton removal in oxygen isotopes. Phys. Rev. Lett. 2011, 107, 032501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wylie, J.; Okołowicz, J.; Nazarewicz, W.; Płoszajczak, M.; Wang, S.M.; Mao, X.; Michel, N. Spectroscopic factors in dripline nuclei. Phys. Rev. C 2021, 104, L061301. [Google Scholar] [CrossRef]
- Brown, B.A. The oxygen isotopes. Int. J. Mod. Phys. E 2017, 26, 1740003. [Google Scholar] [CrossRef]
- Wildenthal, B.H. Empirical strengths of spin operators in nuclei. Prog. Part. Nucl. Phys. 1984, 11, 5–51. [Google Scholar] [CrossRef]
- Kanungo, R.; Nociforo, C.; Prochazka, A.; Aumann, T.; Boutin, D.; Cortina-Gil, D.; Davids, B.; Diakaki, M.; Farinon, F.; Geissel, H.; et al. One-neutron removal measurement reveals 24O as a new doubly magic nucleus. Phys. Rev. Lett. 2009, 102, 152501. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, C.R.; Baumann, T.; Bazin, D.; Brown, J.; Christian, G.; Denby, D.H.; DeYoung, P.A.; Finck, J.E.; Frank, N.; Hinnefeld, J.; et al. Evidence for a doubly magic 24O. Phys. Lett. B 2009, 672, 17–21. [Google Scholar] [CrossRef] [Green Version]
- Janssens, R.V.F. Unexpected doubly magic nucleus. Nature 2009, 459, 1069–1070. [Google Scholar] [CrossRef]
- Kondo, Y.; Nakamura, T.; Tanaka, R.; Minakata, R.; Ogoshi, S.; Orr, N.A.; Achouri, N.L.; Aumann, T.; Baba, H.; Delaunay, F.; et al. Nucleus 26O: A barely unbound system beyond the drip line. Phys. Rev. Lett. 2016, 116, 102503. [Google Scholar] [CrossRef] [Green Version]
- Thibault, C.; Klapisch, R.; Rigaud, C.; Poskanzer, A.M.; Prieels, R.; Lessard, L.; Reisdorf, W. Direct measurement of the masses of 11Li and 26–32Na with an on-line mass spectrometer. Phys. Rev. C 1975, 12, 644–657. [Google Scholar] [CrossRef] [Green Version]
- Campi, X.; Flocard, H.; Kerman, A.K.; Koonin, S. Shape transition in the neutron rich sodium isotopes. Nucl. Phys. A 1975, 251, 193–205. [Google Scholar] [CrossRef]
- Wildenthal, B.H.; Chung, W. Collapse of the conventional shell-model ordering in the very-neutron-rich isotopes of Na and Mg. Phys. Rev. C 1980, 22, 2260–2262. [Google Scholar] [CrossRef]
- Wildenthal, B.H.; Curtin, M.S.; Brown, B.A. Predicted features of the decay-decay of neutron-rich sd-shell nuclei. Phys. Rev. C 1983, 28, 1343–1366. [Google Scholar] [CrossRef]
- Poves, A.; Retamosa, J. The onset of deformation at the N = 20 neutron shell closure far from stability. Phys. Lett. B 1987, 184, 311–315. [Google Scholar] [CrossRef]
- Lubna, R.S.; Kravvaris, K.; Tabor, S.L.; Tripathi, V.; Volya, A.; Rubino, E.; Allmond, J.M.; Abromeit, B.; Baby, L.T.; Hensley, T.C. Structure of 38Cl and the quest for a comprehensive shell model interaction. Phys. Rev. C 2019, 100, 034308. [Google Scholar] [CrossRef] [Green Version]
- Brown, B.A.; Rae, W.D.M. The Shell-model code NuShellX@MSU. Nucl. Data Sheets 2014, 120, 115–118. [Google Scholar] [CrossRef]
- Gloeckner, D.H.; Lawson, R.D. Spurious center-of-mass motion. Phys. Lett. B 1974, 53, 313–318. [Google Scholar] [CrossRef]
- Brown, B.A.; Etchegoyen, A.; Godwin, N.S.; Rae, W.D.M.; Richter, W.A.; Ormand, W.E.; Warburton, E.K.; Winfield, J.S.; Zhao, L.; Zimmerman, C.H. Oxbash for Windows PC; MSU-NSCL Report 1289; National Superconducting Cyclotron Laboratory MSU: East Lansing, MI, USA, 2004. [Google Scholar]
- Caurier, E.; Nowacki, F.; Poves, A. Merging of the islands of inversion at N = 20 and N = 28. Phys. Rev. C 2014, 90, 014302. [Google Scholar] [CrossRef] [Green Version]
- Utsuno, Y.; Otsuka, T.; Mizusaki, T.; Honma, M. Varying shell gap and deformation in N∼20 unstable nuclei studied by the Monte Carlo shell model. Phys. Rev. C 1999, 60, 054315. [Google Scholar] [CrossRef]
- Otsuka, T.; Honma, M.; Mizusaki, T.; Shimizu, N.; Utsuno, Y. Monte Carlo shell model for atomic nuclei. Prog. Part. Nucl. Phys. 2001, 47, 319–400. [Google Scholar] [CrossRef]
- Fifield, L.K.; Woods, C.L.; Bark, R.A.; Drumm, P.V.; Hotchkis, M.A.C. Masses and level schemes of 33Si and 34Si. Nucl. Phys. A 1985, 440, 531–542. [Google Scholar] [CrossRef]
- Brown, B.A.; Richter, W.A. New “USD” Hamiltonians for the sd shell. Phys. Rev. C 2006, 74, 034315. [Google Scholar] [CrossRef] [Green Version]
- Lica, R.; Rotaru, F.; Borge, M.J.G.; Grevy, S.; Negoita, F.; Poves, A.; Sorlin, O.; Andreyev, A.N.; Borcea, R.; Costache, C.; et al. Normal and intruder configurations in 34Si populated in the β− decay of 34Mg and 34Al. Phys. Rev. C 2019, 100, 034306. [Google Scholar] [CrossRef] [Green Version]
- Elder, R.; Iwasaki, H.; Ash, J.; Bazin, D.; Bender, P.C.; Braunroth, T.; Brown, B.A.; Campbell, C.M.; Crawford, H.L.; Elman, B.; et al. Intruder dominance in the 02+ state of 32Mg studied with a novel technique for in-flight decays. Phys. Rev. C 2019, 100, 041301. [Google Scholar] [CrossRef]
- Wimmer, K.; Kroell, T.; Kruecken, R.; Bildstein, V.; Gernhaeuser, R.; Bastin, B.; Bree, N.; Diriken, J.; Van Duppen, P.; Huyse, M.; et al. Discovery of the shape coexisting 0+ state in 34Mg by a two neutron transfer reaction. Phys. Rev. Lett. 2010, 105, 252501. [Google Scholar] [CrossRef] [Green Version]
- Macchiavelli, A.O.; Crawford, H.L.; Campbell, C.M.; Clark, R.M.; Cromaz, M.; Fallon, P.; Jones, M.D.; Lee, I.Y.; Salathe, M.; Brown, B.A.; et al. The 30Mg(t, p)32Mg “puzzle” reexamined. Phys. Rev. C 2016, 94, 051303. [Google Scholar] [CrossRef] [Green Version]
- Kitamura, N.; Wimmer, K.; Poves, A.; Shimizu, N.; Tostevin, J.A.; Bader, V.M.; Bancroft, C.; Barofsky, D.; Baugher, T.; Bazin, D.; et al. Coexisting normal and intruder configurations in 32Mg. Phys. Lett. B 2021, 822, 136682. [Google Scholar] [CrossRef]
- Kitamura, N.; Wimmer, K.; Miyagi, T.; Poves, A.; Shimizu, N.; Tostevin, J.A.; Bader, V.M.; Bancroft, C.; Barofsky, D.; Baugher, T.; et al. In-beam gamma-ray spectroscopy of 32Mg via direct reactions. Phys. Rev. C 2022, 105, 034318. [Google Scholar] [CrossRef]
- Fortunato, L.; Casal, J.; Horiuchi, W.; Singh, J.; Vitturi, A. The 29F nucleus as a lighthouse on the coast of the island of inversion. Nat. Comm. Phys. 2020, 3, 132. [Google Scholar] [CrossRef]
- Doornenbal, P.; Scheit, H.; Takeuchi, S.; Utsuno, Y.; Aoi, N.; Li, K.; Matsushita, M.; Steppenbeck, D.; Wang, H.; Baba, H.; et al. Low-Z shore of the “island of inversion” and the reduced neutron magicity toward 28O. Phys. Rev. C 2017, 95, 041301. [Google Scholar] [CrossRef] [Green Version]
- Bagchi, S.; Kanungo, R.; Tanaka, Y.K.; Geissel, H.; Doornenbal, P.; Horiuchi, W.; Hagen, G.; Suzuki, T.; Tsunoda, N.; Ahn, D.S.; et al. Two-neutron halo is unveiled in 29F. Phys. Rev. Lett. 2020, 124, 222504. [Google Scholar] [CrossRef] [PubMed]
- Brown, B. New Skyrme interaction for normal and exotic nuclei. Phys. Rev. C 1998, 58, 220–231. [Google Scholar] [CrossRef]
- MacGregor, P.T.; Sharp, D.K.; Freeman, S.J.; Hoffman, C.R.; Kay, B.P.; Tang, T.L.; Gaffney, L.P.; Baader, E.F.; Borge, M.J.G.; Butler, P.A.; et al. Evolution of single-particle structure near the N = 20 island of inversion. Phys. Rev. C 2021, 104, L051301. [Google Scholar] [CrossRef]
- Otsuka, T.; Tsunoda, Y. The role of shell evolution in shape coexistence. J. Phys. G: Nucl Part. Phys. 2016, 43, 024009. [Google Scholar] [CrossRef]
- Chrisman, D.; Kuchera, A.N.; Baumann, T.; Blake, A.; Brown, B.A.; Brown, J.; Cochran, C.; DeYoung, P.A.; Finck, J.E.; Frank, N.; et al. Neutron-unbound states in 31Ne. Phys. Rev. C 2021, 104, 034313. [Google Scholar] [CrossRef]
- Thoennessen, M.; Baumann, T.; Brown, B.A.; Enders, J.; Frank, N.; Hansen, R.G.; Heckman, P.; Luther, B.A.; Seitz, J.; Stolz, A.; et al. Single proton knock-out reactions from 24F, 25F, 26F. Phys. Rev. C 2003, 68, 044318. [Google Scholar] [CrossRef] [Green Version]
- Tang, T.L.; Uesaka, T.; Kawase, S.; Beaumel, D.; Dozono, M.; Fujii, T.; Fukuda, N.; Fukunaga, T.; Galindo-Uribarri, A.; Hwang, S.H.; et al. How different is the core of 25F from 24Og.s. ? Phys. Rev. Lett. 2020, 124, 212502. [Google Scholar] [CrossRef]
- Grigorenko, L.V.; Mukha, I.G.; Scheidenberger, C.; Zhukov, M.V. Two-neutron radioactivity and four-nucleon emission from exotic nuclei. Phys. Rev. C 2011, 84, 021303. [Google Scholar] [CrossRef] [Green Version]
- Lepailleur, A.; Wimmer, K.; Mutschler, A.; Sorlin, O.; Thomas, J.C.; Bader, V.; Bancroft, C.; Barofsky, D.; Bastin, B.; Baugher, T.; et al. Spectroscopy of 28Na: Shell evolution toward the drip line. Phys. Rev. C 2015, 92, 054309. [Google Scholar] [CrossRef] [Green Version]
- Utsuno, Y.; Otsuka, T.; Brown, B.A.; Honma, M.; Mizusaki, T.; Shimizu, N. Shape transitions in exotic Si and S isotopes and tensor-force-driven Jahn-Teller effect. Phys. Rev. C 2012, 86, 051301. [Google Scholar] [CrossRef] [Green Version]
- Nowacki, F.; Poves, A. New effective interaction for 0ℏω shell-model calculations in the sd–pf valence space. Phys. Rev. C 2009, 79, 014310. [Google Scholar] [CrossRef] [Green Version]
- Morris, L.; Jenkins, D.G.; Harakeh, M.N.; Isaak, J.; Kobayashi, N.; Tamii, A.; Adachi, S.; Adsley, P.; Aoi, N.; Bracco, A.; et al. Search for in-band transitions in the candidate superdeformed band in 28Si. Phys. Rev. C 2021, 104, 054323. [Google Scholar] [CrossRef]
- Sagawa, H.; Zhou, X.; Zhang, X.Z. Deformations and electromagnetic moments in carbon and neon isotopes. Phys. Rev. C 2004, 70, 054316. [Google Scholar] [CrossRef]
- Petri, M.; Fallon, P.; Macchiavelli, A.O.; Paschalis, S.; Starosta, K.; Baugher, T.; Bazin, D.; Cartegni, L.; Clark, R.M.; Crawford, H.L.; et al. Lifetime measurement of the 21+ state in 20C. Phys. Rev. Lett. 2011, 107, 102501. [Google Scholar] [CrossRef] [Green Version]
- Cwiok, S.; Dudek, J.; Nazarewicz, W.; Skalski, J.; Werner, T. Single-particle energies, wave-functions, quadrupole-moments and g-factors in an axially deformed Woods-Saxson potential with applications to the 2-center-type nuclear problems. Comp. Phys. Comm. 1987, 46, 379–399. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Brown, B.; Mizusaki, T. New effective interaction for pf-shell nuclei and its implications for the stability of the N = Z = 28 closed core. Phys. Rev. C 2004, 69, 034335. [Google Scholar] [CrossRef] [Green Version]
- Honma, M.; Otsuka, T.; Brown, B.; Mizusaki, T. Shell-model description of neutron-rich pf-shell nuclei with a new effective interaction GXPF1. Eur. Phys. J. A 2005, 25, 499–502. [Google Scholar] [CrossRef]
- Warburton, E.; Brown, B. Effective interactions for the 0p1s0d nuclear shell-model space. Phys. Rev. C 1992, 46, 923–944. [Google Scholar] [CrossRef]
- Richter, W.A.; Mkhize, S.; Brown, B.A. sd-shell observables for the USDA and USDB Hamiltonians. Phys. Rev. C 2008, 78, 064302. [Google Scholar] [CrossRef] [Green Version]
- du Rietz, R.; Ekman, J.; Rudolph, D.; Fahlander, C.; Dewald, A.; Moller, O.; Saha, B.; Axiotis, M.; Bentley, M.; Chandler, C.; et al. Effective charges in the fp shell. Phys. Rev. Lett. 2004, 93, 222501. [Google Scholar] [CrossRef] [Green Version]
- Bohr, A.; Mottelson, B.R. Nuclear Structure; W. A. Benjamin, Inc.: New York, NY, USA, 1975; Volume 2. [Google Scholar]
- Brown, B.A.; Arima, A.; McGrory, J.B. E2 core-polarization charge for nuclei near 16O and 40Ca. Nucl. Phys. A 1977, 277, 77–108. [Google Scholar] [CrossRef]
- Longfellow, B.; Weisshaar, D.; Gade, A.; Brown, B.A.; Bazin, D.; Brown, K.W.; Elman, B.; Pereira, J.; Rhodes, D.; Spieker, M. Quadrupole collectivity in the neutron-rich sulfur isotopes 38S, 40S, 42S, 44S. Phys. Rev. C 2021, 103, 054309. [Google Scholar] [CrossRef]
- Heil, S.; Petri, M.; Vobig, K.; Bazin, D.; Belarge, J.; Bender, P.; Brown, B.A.; Elder, R.; Elman, B.; Gade, A.; et al. Electromagnetic properties of 21O for benchmarking nuclear Hamiltonians. Phys. Lett. B 2020, 809, 135678. [Google Scholar] [CrossRef]
- Lobner, K.; Vetter, M.; Honig, V. Nuclear intrinsic quadrupole moments and deformation paramters. Atom. Data Nucl. Data Tables 1970, 7, 495–520. [Google Scholar] [CrossRef]
- Tostevin, J.A.; Brown, B.A.; Simpson, E.C. Two-proton removal from 44S and the structure of 42Si. Phys. Rev. C 2013, 87, 027601. [Google Scholar] [CrossRef] [Green Version]
- Gade, A.; Brown, B.A.; Tostevin, J.A.; Bazin, D.; Bender, P.C.; Campbell, C.M.; Crawford, H.L.; Elman, B.; Kemper, K.W.; Longfellow, B.; et al. Is the structure of 42Si understood? Phys. Rev. Lett. 2019, 122, 222501. [Google Scholar] [CrossRef] [Green Version]
- Utsuno, Y.; Shimizu, N.; Otsuka, T.; Yoshida, T.; Tsunoda, Y. Nature of Isomerism in Exotic Sulfur Isotopes. Phys. Rev. Lett. 2015, 114. [Google Scholar] [CrossRef] [Green Version]
- Santiago-Gonzalez, D.; Wiedenhoever, I.; Abramkina, V.; Avila, M.L.; Baugher, T.; Bazin, D.; Brown, B.A.; Cottle, P.D.; Gade, A.; Glasmacher, T.; et al. Triple configuration coexistence in 44S. Phys. Rev. C 2011, 83, 061305. [Google Scholar] [CrossRef] [Green Version]
- Longfellow, B.; Weisshaar, D.; Gade, A.; Brown, B.A.; Bazin, D.; Brown, K.W.; Elman, B.; Pereira, J.; Rhodes, D.; Spieker, M. Shape changes in the N = 28 island of inversion: Collective structures built on configuration-coexistingsStates in 43S. Phys. Rev. Lett. 2020, 125, 232501. [Google Scholar] [CrossRef]
- Sharon, Y.Y.; Benczer-Koller, N.; Kumbartzki, G.J.; Zamick, L.; Casten, R.F. Systematics of the ratio of electric quadrupole moments Q(21+) to the square root of the reduced transition probabilities B(E2;01+→21+) in even-even nuclei. Nucl. Phys. A 2018, 980, 131–142. [Google Scholar] [CrossRef]
- Brown, B.; Richter, W. Shell-model plus Hartree-Fock calculations for the neutron-rich Ca isotopes. Phys. Rev. C 1998, 58, 2099–2107. [Google Scholar] [CrossRef] [Green Version]
- Poves, A.; Sanchez-Solano, J.; Caurier, E.; Nowacki, F. Shell model study of the isobaric chains A = 50, A = 51 and A = 52. Nucl. Phys. A 2001, 694, 157–198. [Google Scholar] [CrossRef] [Green Version]
- Browne, F.; Chen, S.; Doornenbal, P.; Obertelli, A.; Ogata, K.; Utsuno, Y.; Yoshida, K.; Achouri, N.L.; Baba, H.; Calvet, D.; et al. Pairing forces govern population of doubly magic 54Ca from direct reactions. Phys. Rev. Lett. 2021, 126, 252501. [Google Scholar] [CrossRef] [PubMed]
- Bhoy, B.; Srivastava, P.C.; Kaneko, K. Shell model results for 47–58Ca isotopes in the fp, fpg9/2 and fpg9/2d5/2 model spaces. J. Phys. G: Nucl. Part. Phys. 2020, 47, 065105. [Google Scholar] [CrossRef] [Green Version]
- Lenzi, S.M.; Nowacki, F.; Poves, A.; Sieja, K. Island of inversion around Cr-64. Phys. Rev. C 2010, 82, 054301. [Google Scholar] [CrossRef]
- Gade, A. Reaching into the N = 40 Island of inversion with nucleon removal reactions. Physics 2021, 3, 1226–1236. [Google Scholar] [CrossRef]
- Zamora, J.C.; Zegers, R.G.T.; Austin, S.M.; Bazin, D.; Brown, B.A.; Bender, P.C.; Crawford, H.L.; Engel, J.; Falduto, A.; Gade, A.; et al. Experimental constraint on stellar electron-capture rates from the 88Sr(t,3He+γ)88Rb reaction at 115 MeV/u. Phys. Rev. C 2019, 100, 032801. [Google Scholar] [CrossRef] [Green Version]
- Titus, E.R.; Ney, E.M.; Zegers, R.G.T.; Bazin, D.; Belarge, J.; Bender, P.C.; Brown, B.A.; Campbell, C.M.; Elman, B.; Engel, J.; et al. Constraints for stellar electron-capture rates on 86Kr via the 86Kr(t,3He+γ)86Br reaction and the implications for core-collapse supernovae. Phys. Rev. C 2019, 100, 045805. [Google Scholar] [CrossRef] [Green Version]
- Stroberg, S.R. Beta decay in medium-mass nuclei with the in-medium similarity renormalization group. Particles 2021, 4, 521–535. [Google Scholar] [CrossRef]
- Lubos, D.; Park, J.; Faestermann, T.; Gernhaeuser, R.; Kruecken, R.; Lewitowicz, M.; Nishimura, S.; Sakurai, H.; Ahn, D.S.; Baba, H.; et al. Improved value for the Gamow-Teller strength of the 100Sn beta decay. Phys. Rev. Lett. 2019, 122, 222502. [Google Scholar] [CrossRef]
- Nowacki, F.; Poves, A.; Caurier, E.; Bounthong, B. Shape coexistence in 78Ni as the portal to the fifth island of inversion. Phys. Rev. Lett. 2016, 117, 272501. [Google Scholar] [CrossRef] [PubMed] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, B.A. The Nuclear Shell Model towards the Drip Lines. Physics 2022, 4, 525-547. https://doi.org/10.3390/physics4020035
Brown BA. The Nuclear Shell Model towards the Drip Lines. Physics. 2022; 4(2):525-547. https://doi.org/10.3390/physics4020035
Chicago/Turabian StyleBrown, B. Alex. 2022. "The Nuclear Shell Model towards the Drip Lines" Physics 4, no. 2: 525-547. https://doi.org/10.3390/physics4020035
APA StyleBrown, B. A. (2022). The Nuclear Shell Model towards the Drip Lines. Physics, 4(2), 525-547. https://doi.org/10.3390/physics4020035




