Abstract
It is well known that singlet state aromaticity is quite insensitive to substituent effects, in the case of monosubstitution. In this work, we use density functional theory (DFT) calculations to examine the sensitivity of triplet state aromaticity to substituent effects. For this purpose, we chose the singlet state antiaromatic cyclopentadienyl cation, antiaromaticity of which reverses to triplet state aromaticity, conforming to Baird’s rule. The extent of (anti)aromaticity was evaluated by using structural (HOMA), magnetic (NICS), energetic (ISE), and electronic (EDDBp) criteria. We find that the extent of triplet state aromaticity of monosubstituted cyclopentadienyl cations is weaker than the singlet state aromaticity of benzene and is, thus, slightly more sensitive to substituent effects. As an addition to the existing literature data, we also discuss substituent effects on singlet state antiaromaticity of cyclopentadienyl cation.
1. Introduction
Aromaticity and antiaromaticity are important concepts in science since they explain the special physical and chemical properties of cyclically delocalized systems. Compounds showing aromaticity delocalize (4n + 2), usually π–electrons, as stated by Hückel’s rule [1,2,3]. They show enhanced thermodynamic stability, develop diamagnetic ring currents when exposed to an external magnetic field, and tend to equalize bond lengths and retain their cyclic delocalization during a chemical reaction [4]. In contrast, compounds that delocalize 4n π–electrons have been named antiaromatic by Breslow et al. since they are unstable and very reactive [5,6]. In addition, they develop paramagnetic ring currents when placed in a magnetic field and are characterized by alternating single and double bonds [4]. Thus, the extent and type of electron delocalization [7], molecular geometry [8], energy [9,10], and magnetic properties [11] are often taken into account when defining a system as aromatic or antiaromatic.
In the first excited triplet state, the electron count is reversed: (4n + 2) π–electron systems are antiaromatic, and 4n π–electron ones are aromatic. This was first pointed out by Baird on the basis of molecular orbital considerations [12] and was extended to the first singlet excited state by Karadakov on the basis of calculated magnetic properties of benzene and cyclobutadiene [13]. Theoretical investigations of electron delocalization [14,15,16], molecular structure [17,18], stabilization energies [17,19,20,21] and magnetic properties [13,17,21,22,23,24,25] supported Baird’s rule, for which experimental lines of evidence also exist [26,27,28]. A few review articles summarize these lines of evidence for the rule and explain earlier reports on various photochemical reactions on the basis of concepts related to excited-state aromaticity and antiaromaticity [29,30]. It is important to mention a recently developed concept of adaptive aromaticity by Zhu et al., referring to the small number of cyclically delocalized compounds, which show aromaticity in both singlet and triplet states [31,32,33].
Since most compounds are derivatives of their basic skeleton, understanding of substituent effects on molecular properties has attracted great attention from scientists. In unsaturated molecules, substituents mostly interact with the π–electronic system, increasing delocalization in conjugated butadiene moiety but decreasing it in an aromatic system [34]. In a competition between aromaticity and substituent effect, the former wins in the case of monosubstitution [35,36]. However, the extent of aromaticity can be decreased upon polysubstitution [37]. On the other hand, antiaromaticity, as a destabilizing effect, is often attenuated by substituent [38,39], particularly in electron-deficient and cationic systems, such as borole [40] and cyclopentadienyl cation [41,42], respectively, where it is significantly reduced by electron-donating groups. Additionally, the recent computational work proved that aromatic benzene is almost insensitive to substituent effect, whereas electron delocalization in its nonaromatic dication is greatly affected by substituent [43].
How similar are singlet- and triplet-state aromaticity and antiaromaticity? Does the former resist the substituent effect, and is the latter influenced by it to the same extent as the singlet-state properties? A few works were aimed to answer these questions. Two substituents, F and CN, were considered when examining the aromaticity of cyclooctatetraene in its triplet state. The authors found a decrease in aromaticity upon increasing the number of substituents [39]. The triplet-state dicationic benzene, formally 4n π–electronic system, was found to be more delocalized than its singlet state and showed less sensitivity to substituent effect [43]. Recently, it was shown computationally that a single substituent can have a large impact on the triplet-state (anti)aromaticity of benzene. Depending on the substituent’s electronic properties, the triplet state of benzene can be tuned between highly antiaromatic and strongly aromatic [44].
It is the aim of this work to provide more information about the sensitivity of triplet-state aromaticity on substituent effect, which we find important because of the tight relation between aromaticity and molecular properties. The results may be useful for future studies on the possible tuning of triplet state aromaticity and, thus, physical and chemical properties of organic compounds. We chose the antiaromatic cyclopentadienyl cation as a model system and introduced a substituent at its most cationic C-5 atom (Figure 1). The substituents were chosen to cover the most important electronic effects, such as the π–electron-donating effect (NH2, OH, and F), σ–electron-donating effect (CH3), σ–electron-withdrawing effect (CF3) and π–electron-withdrawing effect (NO2, NO, CN, CHO, COCH3, COOCH3, and CONH2). The π–electron-donating/-withdrawing abilities vary between the studied groups.
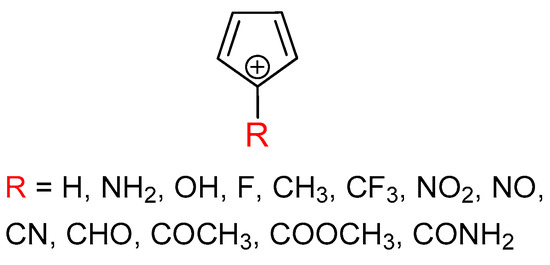
Figure 1.
Molecules examined in this work.
The cyclopentadienyl cation, itself, is an unstable, antiaromatic compound [45], which has a triplet ground state detected by EPR studies [46]. The triplet ground state was also observed for its several derivatives [47,48,49]. Recently, the unstable, antiaromatic singlet tetrachlorocyclopentadienyl cation connected to the negatively charged BF3 was isolated in a low-temperature matrix [50].
2. Computational Details and Methods
All calculations were performed at the DFT level of theory by using B3LYP functional and 6-311 + G(d,p) basis set, for closed-shell species, and its unrestricted version UB3LYP, for open-shell species [51,52,53]. Geometries were fully optimized by using the Gaussian 09 package [54], followed by frequency calculations in order to verify that all obtained structures correspond to energy minima, Nimag = 0. The stability of wave functions was checked by using the “stable” keyword. Instability appeared for R = H, F, CH3, CF3, NO2, CN, CHO, and COOCH3, and these compounds were also analyzed as open-shell singlet states by using the UB3LYP and “guess = mix” keyword. To reduce spin contamination of this type of calculation, all open-shell singlet state energies were corrected by employing the approximate spin projection technique [55,56], according to Equations (1) and (2), where EOS and ET are calculated energies of open-shell singlet and triplet states, respectively, and S2 is the spin-squared expectation value.
The degree of (anti)aromaticity of the studied compounds was evaluated by using geometric, energetic, magnetic, and electronic criteria. For the first, the harmonic oscillator model of aromaticity (HOMA) index [8,57,58] was calculated by using the Multiwfn program [59], according to Equation (3). In the equation, Ropt refers to the optimal bond length taken as 1.388 Å for the CC bond. Ri is an individual bond length, n is the number of bonds taken up in the summation and α is an empirical constant taken to give HOMA = 1 for an aromatic system, and HOMA = 0 for nonaromatic one. Antiaromatic molecules usually show negative HOMA values. For the CC bond, α = 257.7 was used. The idea behind the HOMA index is that an aromatic system tends to equalize its bond lengths, whereas nonaromatic and antiaromatic molecules, as more localized, have alternating single and double bonds. We note that HOMA was parametrized to assess the aromaticity of molecules in their closed-shell state and should be considered by taking other electronic states into account.
To estimate aromaticity from an energetic point of view, the isomerization stabilization energy (ISE) method was applied for singlet and triplet states by using the chemical Equation (4) [19,25,60]. The structure on the left side of the equation has disrupted cyclic conjugation and that on the right side is cyclically conjugated. Thus, aromatic compounds have negative ISE values, antiaromatic ones have positive, and nonaromatic molecules have ISE values close to zero. The ISE was not calculated for open-shell singlets, because most of the calculations converged into the closed-shell states.

As a magnetic criterion of aromaticity, the NICS-based scan and ACID calculations were used. The nucleus independent chemical shift (NICS) represents the chemical shielding of a point in the vicinity of a molecule, usually in the center of a ring or 1 Å above it for aromaticity studies [61,62]. Extraction of the π–electron contribution from the all-orbital shielding values is more relevant for aromaticity [63,64] and, particularly, the out-of-plane component of it, since ring currents are induced when a ring is perpendicularly oriented with respect to the magnetic field direction [65,66,67,68]. Thus, the π–electron contribution to the out-of-plane component of magnetic shielding tensor was used in this work, and NICS values were calculated along a line traversing perpendicularly from the ring plane center up to 4 Å, with the step width of 0.1 Å. This procedure [69,70] is more reliable than the calculation of a single NICS value [71]. Negative NICS values indicate diatropic ring currents and aromaticity, positive ones indicate paratropic ring currents and antiaromaticity, and values close to zero indicate a nonaromatic molecule. Magnetic shieldings were calculated by employing the GIAO method [72,73] and Aroma 1.0 program package [74]. In the package, we used the σ-only method to extract the π–electron contribution to the shielding values [75].
The anisotropy of the induced current density (ACID) method calculates delocalization pathways in molecules, aromaticity, and antiaromaticity [76,77], which can be pictorially represented. In this kind of calculation, the CSGT method was used to obtain chemical shielding values [78], and ACID plots were created by using the POV-Ray, v. 3.7 [79].
The electron density of the delocalized bonds (EDDB) index quantifies the number of delocalized electrons in a molecule [80,81,82,83]. For the purpose of this work, only delocalization along the specific path, the five-membered ring, was considered and is labeled as EDDBp. Calculations were performed by using the NBO 3.1 version [84], implemented in Gaussian 09, and RunEDDB software [85].
Charge and spin distribution in the studied compounds were obtained by the Hirshfeld population analysis [86].
3. Results
Table 1 lists the main characteristics of optimized geometries of the studied molecules and calculated aromaticity indices (the maximum NICS values were observed at 0.5 Å above the ring planes and they are given in the table). Substituent orientation with respect to the plane of the ring is also shown in Figure 2, along with the charge and spin distributions. The full NICS scans are presented in Figure 3, and the ACID plots are shown in the Supplementary Materials Figures S1–S13. Molecular orbitals (MO) involved in electronic state transitions are shown in Figures S14 and S15 in the Supplementary Materials. All transitions are related to π-type orbitals and, thus, should conform to Baird’s rule, except when R = NO. In this case, the transition occurs between the π-type and substituent orbitals (Figure S14), and this compound is predicted to behave differently, as will be discussed. In the text below, we also analyze and discuss the substituent effect on singlet states and compare our results with the literature data. To the best of our knowledge, no such data exist for the triplet state of cyclopentadienyl cation.

Table 1.
Symmetry point groups, substituent (R) orientation with respect to the ring plane, relative energies of singlet (S), triplet (T), and open-shell singlet states (OS), HOMA, NICS, ISE, and EDDBp data for the studied compounds.
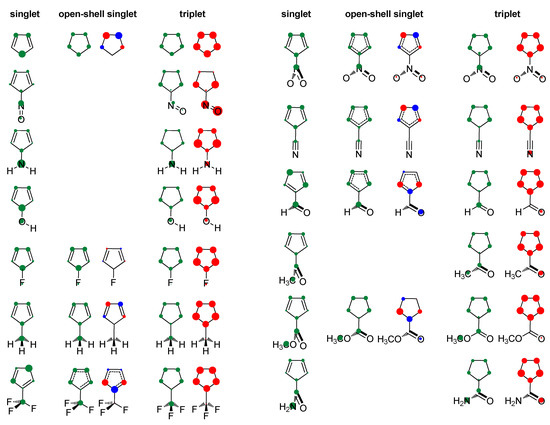
Figure 2.
Positive charge distribution with hydrogens summed into heavy atoms (green circles) and spin density distribution (red and blue circles for α and β spins) in the studied molecules obtained by the Hirshfeld population analysis. The area of circles is proportional to the amount of charge/spin density.
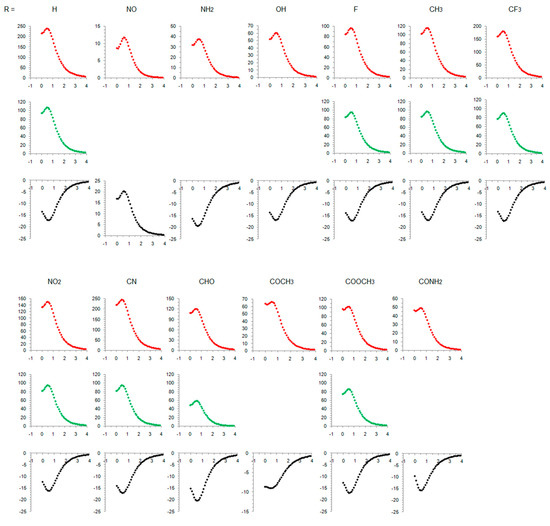
Figure 3.
NICS scans of the studied compounds. Red-colored curves refer to singlet states, green-colored curves refer to open-shell singlets, and black curves refer to triplet states. Horizontal axis: distance in Å, vertical axis: NICS values in ppm.
3.1. Cyclopentadienyl Cation
Our result on relative adiabatic energies of singlet and triplet states of cyclopentadienyl cation, 10.5 kcal/mol in favor of triplet, agrees with the experimental finding that triplet is its ground state and the value is in close agreement with the previous calculations: 11.3 kcal/mol, B3LYP/6-31G(d)//B3LYP/6-31G(d) [41], 42.4 kJ/mol (10.1 kcal/mol), B3LYP/def2-TZVP//M06-2X/def2-TZVP [87], and 3.4–11.6 kcal/mol, using various ab initio methods [88]. The triplet state is of D5h symmetry with equal bond lengths, which is a characteristic of aromatic molecules. This triplet-state aromaticity, according to HOMA, NICS, ISE (Table 1, R = H), and NICS scan (Figure 3), is smaller than the ground-state aromaticity of benzene, HOMA = 0.990, NICS(0.5)πzz = −38.5 ppm, and ISE = −33.9 kcal/mol. Singlet state of cyclopentadienyl cation with C2v symmetry is clearly antiaromatic, having negative HOMA and positive ISE values (Table 1), large positive NICS (Table 1 and Figure 3), and strong paramagnetic ring currents (the ACID plot in Figure S1). The EDDBp = 0.639 e also indicates little electron delocalization. The broken symmetry calculations [89], applied to produce open-shell singlet, resulted in a more bond-equalized system (HOMA in Table 1) with slightly lower energy (OS in Table 1) and weaker antiaromaticity (NICS in Table 1 and Figure 3). The weakly delocalized charge density in the closed-shell state becomes (almost) equally delocalized on each carbon atom in open-shell states, and spin density is unsymmetrically distributed in two allyl-like substructures (Figure 2). The EDDBp = 0.472 e (0.236 for alpha electrons and 0.236 for beta electrons) calculated for open-shell singlet cyclopentadienyl cation points to the conclusion that the drop in antiaromaticity, inferred from HOMA and NICS, comes from the smaller portion of delocalized electron density. In the triplet state, the spin density is fully delocalized (Figure 2).
3.2. Singlet State of Substituted Cyclopentadienyl Cations
As positively charged, the closed-shell cyclopentadienyl cation behaves as an electron-withdrawing system and strongly interacts with groups that can donate a pair of electrons: lone pair donors (NO, NH2, OH, and F) and σ-bond donor (CH3). Thus, in five-substituted derivatives, the NO group adopts a linear structure, NH2 and OH are coplanar with the ring, and one of the three C–H bonds of the methyl group is perpendicular to the ring plane, which allows the strongest hyperconjugative interaction (Figure 2, symmetry point groups and R–ring dihedral angles in Table 1). Aromaticity indices in Table 1 show that electron donation to the cyclopentadienyl system decreases its singlet-state antiaromaticity and, thus, decreases (in absolute value) or reverses the singlet-triplet energy splitting, compared with the unsubstituted ring. In the case of the NH2 group, the singlet is more stable than the triplet by 16.7 kcal/mol, and this energy difference, in favor of the singlet, drops to 9.7 kcal/mol for OH substituent and to only 1.7 kcal/mol for the still less electron-donating fluorine atom. In the case of the σ–electron-donating CH3 group, the triplet state is just slightly more stable, by 1.5 kcal/mol, whereas in NO-substituted compound triplet is favored by 5.8 kcal/mol. The amount of singlet–triplet energy splitting nicely correlates with the π–electron substituent effect (Figure 4a), represented by the π–electron donor-acceptor (pEDA) values, which show how easy a substituent donates its electrons to the π–electronic system of the ring (developed for benzene): NH2 (0.145) > OH (0.121) > F (0.078) > CH3 (0.014) > H (0.000) > NO (−0.129) [90]. Aromaticity indices, however, show, with small discrepancies, that the most effective in reducing antiaromaticity of closed-shell singlet state cyclopentadienyl cation is the NO group, and then the effect follows a decrease in the electron-donating ability of substituent (Figure 4b–d). The same is clearly visible from the NICS scans in Figure 3 and the ACID plots in Figures S2–S6. Only the EDDBp places the NO group as the weakest donor among the studied electron-donating substituents (Table 1 and Figure 4e). It also reveals that a decrease in electron delocalization is the source of attenuated antiaromaticity. Figure 5 shows that the singlet–triplet energy splitting is strongly dependent on the extent of antiaromaticity, and it increases with a decrease in antiaromaticity. The peculiar behavior of the NO group, represented by the blue dot in graphs, can be interpreted by its dual electronic effects: it is basically an electron-withdrawing substituent with a negative pEDA value, but it can also donate the nitrogen lone pair to stabilize a neighboring positive charge. In a highly localized cyclopentadienyl cation, its donor ability prevails.
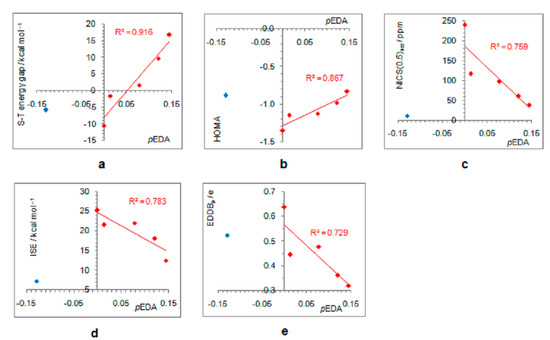
Figure 4.
Dependence of singlet–triplet energy gaps (a) and extent of antiaromaticity evaluated by HOMA (b), NICS (c), ISE (d), and EDDBp (e), on π–electron substituent effect (pEDA). Red–colored dots represent H, NH2, OH, F, and CH3 substituents, and blue–colored dot represents the NO substituent.
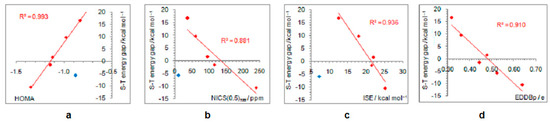
Figure 5.
Correlations between the singlet–triplet energy gaps and extent of antiaromaticity evaluated by HOMA (a), NICS (b), ISE (c), and EDDBp (d). Red–colored dots represent H, NH2, OH, F, and CH3 substituents, and blue–colored dot represents the NO substituent, except in the last graph where all compounds are included in correlation.
The finding that electron-donating groups reduce the antiaromaticity of cyclopentadienyl cation agrees with previous results [41,42].
On the other hand, electron-withdrawing substituents tend to avoid electronic interactions with the positively charged, closed-shell ring system. Thus, the CF3 group has one of the C–F bonds coplanar with the ring, and the other two form dihedral angles of about 60° with the ring plane. The planes of NO2, COCH3, COOCH3, and CONH2 adopt perpendicular orientation relative to the ring plane, which disables any interaction between the two π systems, that of the ring and the substituent, which become orthogonal. The plane of the CHO group is by 15° tilted from the plane of the ring, whereas the linear CN group cannot avoid interaction with the ring. Thus, the singlet–triplet energy splitting, in favor of triplet, is the closest to the parent molecule in the case of CN and CF3 substituents (8.7 kcal/mol and 8.6 kcal/mol, respectively), followed by the CHO group (7.2 kcal/mol). In the latter two cases, optimizations ended in a two-substituted cyclopentadienyl cation with partial substituent–ring interactions (Figure 2). The rest of the substituents reduce the singlet–triplet energy gap relative to the parent molecule, and all favor triplet state. Due to the absence or decrease in substituent–ring π–electronic interaction, there are almost no correlations of singlet–triplet energy splitting and antiaromaticity with the π–electron-withdrawing ability, represented by the negative pEDA values [90] (Figure 6). However, even in this case, singlet–triplet energy gaps are dependent on antiaromaticity degree (Figure 7), though less so than for electron donors. According to aromaticity measures given in Table 1 and shown in Figure 3 and Figures S7–S10, the extent of antiaromaticity decreases with a decrease in substituent–ring π–electronic interactions, which are dependent on substituent–ring orientation.
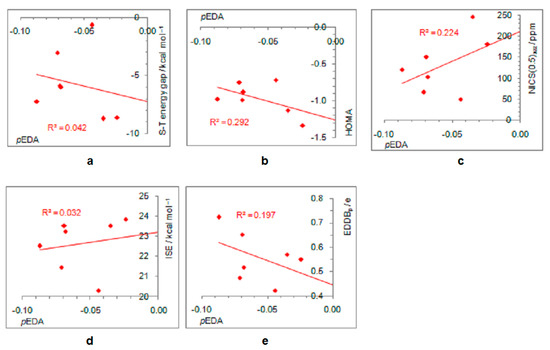
Figure 6.
Dependence of singlet–triplet energy gaps (a) and extent of antiaromaticity evaluated by HOMA (b), NICS (c), ISE (d), and EDDBp (e) on π–electron substituent effect (pEDA) for cyclopentadienyl cation substituted with electron–withdrawing groups. For the ester group, the pEDA of COOH was taken from the original reference.
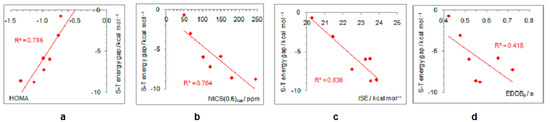
Figure 7.
Correlations between the singlet–triplet energy gaps and extent of antiaromaticity evaluated by HOMA (a), NICS (b), ISE (c), and EDDBp (d) for cyclopentadienyl cation substituted with electron–withdrawing groups.
Similarly, the singlet dication of benzene strongly interacts with electron-donating substituents but not with electron-withdrawing ones [43].
Our calculations suggest that the formation of open-shell singlet species has little effect on energy (Table 1), decreases bond length alternation (HOMA values), and decreases antiaromaticity (NICS data in Table 1 and Figure 3, and ACID plots shown in the Supplementary Materials Section). Figures S14 and S15 show that the extension of the singly occupied MOs does not change greatly, compared with that of the HOMOs, though they can involve different atoms. The EDDBp data in Table 1 point, again, that the drop in the extent of antiaromaticity should be related to the slight drop in electron delocalization (with exception of CH3 substituent). As can be seen in Figure 2 (charge density distribution) and from HOMA data, electron-withdrawing groups create more bond-equalized systems than electron donors, but their antiaromaticity degree does not differ significantly (ΔNICS(0.5)πzz = 38.4 ppm, compared with (ΔNICS(0.5)πzz = 148.7 ppm for singlet state, and similar EDDBp values), even though (partial) interaction of substituent and ring π system is possible regarding molecular conformation.
3.3. Triplet State of Substituted Cyclopentadienyl Cations
In the optimized triplet state geometries, when possible, the substituent is coplanar with the cyclopentadienyl ring. Exceptions are NO2, COCH3, and CONH2 groups, presumably due to steric reasons, whereas in CH3 and CF3 groups, one of the C–H and C–F bonds is perpendicular to the ring plane (Figure 2, symmetry point groups and R–ring dihedral angles in Table 1). Thus, all substituents are positioned so that they can (partially) interact with the π system of the ring. In the triplet state, the NO group has an angular geometry, which means that it behaves as an electron-withdrawing group rather than electron-donating in the singlet state. The charge density distribution is shown in Figure 2, in which positive HOMA values ranging from 0.560 to 0.707 and EDDBp data spanning the range of 1.102 e to 2.955 e indicate a significant increase in electron delocalization relative to singlet state (HOMA = −1.346–0.721, EDDBp = 0.318–0.723).
Figure 2 shows that the majority of spin density is located in the ring in all but one compound (R = NO), where it is mainly positioned at the substituent, which is a consequence of the involvement of substituent’s orbital in singlet/triplet electronic transition (Figure S14). According to negative NICS and ISE values (Table 1 and Figure 3), all compounds with the spin density in the ring are aromatic, though to a lesser extent than benzene, NICS(0.5)πzz = −38.5 ppm and ISE = −33.9 kcal/mol. The ACID plots in Figures S2–S13, showing diatropic ring currents for triplet states, agree with this conclusion, as well as the large EDDBp values, which are all between 2.183 e and 2.955 e. The 5-nitroso cyclopentadienyl cation has positive NICS and ISE values (Table 1 and Figure 3) and is, thus, antiaromatic in both singlet and triplet state (slightly more in the triplet state). The ACID plot in Figure S2 shows paratropic ring currents for this compound, thus supporting the previous conclusion. The EDDBp = 1.102 e for this compound is clearly much less than for all other triplet states, and an increase in the density of delocalized electrons relative to the closed-shell state (Table 1) is in accordance with the slight increase in antiaromaticity. Therefore, increased spin density in the ring in the triplet state of substituted 4π–electronic cyclopentadienyl cation means aromaticity, whereas increased spin density at substituent means antiaromaticity. Similarly, in substituted benzene, accumulation of spin density in the ring creates triplet state antiaromaticity, whereas accumulation of spin density at substituent enables benzene to be (weakly) aromatic in both singlet and triplet state (R = CHO, COCH3, NO2, and NO) [44].
Due to the increased π–electron delocalization in the triplet state, structural and magnetic aromaticity descriptors do not correlate with the electron-withdrawing/-donating ability of substituents (Figure 8a,b,e,f). However, moderate-to-good correlations exist between pEDA values and energetic and electronic aromaticity measures (ISE and EDDBp, respectively), showing that aromaticity degree decreases with increasing electron-donating or electron-withdrawing power of substituent (Figure 8c,d,g,h).
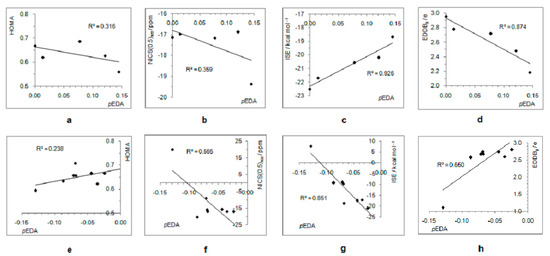
Figure 8.
Correlations between the extent of aromaticity (evaluated by HOMA, NICS, ISE, and EDDBp) and π–electron substituent effect (pEDA) for triplet state cyclopentadienyl cation substituted with electron-donating groups (a–d) and electron–withdrawing groups (e–h). For the ester group, the pEDA of COOH was taken from the original reference.
3.4. Comparison of the Results with the CAM-B3LYP Calculations
It was reported recently that the local character of the exchange–correlation functional, such as B3LYP, may lead to an inconsistent picture of aromaticity due to the overestimation of electron delocalization [91]. To test the correctness of our results, we selected a small set of compounds, which was also examined by using the long-range corrected exchange–correlation functional, CAM-B3LYP [92]. The test set comprised cyclopentadienyl cations substituted with an electron-donating group (NH2), electron-withdrawing group (CHO), electron-withdrawing/-donating group (NO), and the parent cation.
The only difference in optimized molecular geometry was observed for R = CHO, which (1) in the closed-shell singlet-state substituent was found in the same plane as the ring (tilted by 15° when using B3LYP), and (2) in the UCAM-B3LYP open-shell singlet calculation converged to the same geometry as RCAM-B3LYP calculation, with S2 = 0 (the UB3LYP calculation ended in the structure with slightly lower energy, Table 1).
Comparison of calculated aromaticity indices is presented in Table 2, and ACID plots are included in Supplementary Materials (Figures S1–S3 and S10). Inspection of data shows that the two functionals provide exactly the same trend and, thus, would lead to the same conclusions. Only NICS(0.5) value for the closed-shell singlet, when R = CHO, points to somewhat increased antiaromaticity, compared with the B3LYP, which can be ascribed to the difference in molecular geometry, where substituent can interact with the π system of the ring.

Table 2.
Comparison of relative energies of singlet (S), triplet (T), and open-shell singlet-state (OS), HOMA, NICS, ISE, and EDDBp data for test set examined with both (U)B3LYP and (U)CAM-B3LYP functionals (data for the latter are given in italics).
4. Discussion
In this section, we answer the question posed in the Introduction: How similar are singlet and triplet state aromaticity with respect to their sensitivity to substituent effects? The results presented in Section 3.3 show that the structural aromaticity index, HOMA, span a rather narrow range of 0.147 for the triplet state of substituted cyclopentadienyl cation, compared with 0.625 for the closed-shell singlet state. For monosubstituted benzene, which is a prototypical aromatic compound, this range is still narrower, 0.030 [43] or 0.022 [44]. This means that different substituents have a small effect on the extent of bond length equalization in the aromatic triplet state of cyclopentadienyl cation but larger than in the ground state of benzene.
The NICS scans in Figure 3 for substituted triplet-state cyclopentadienyl cation are somewhat similar on the NICS scale from 0 ppm to −25 ppm, with two exceptions: acetylcyclopentadienyl cation, which is less magnetically aromatic, and nitrosocyclopentadienyl cation, which becomes slightly more antiaromatic in the triplet state. In contrast, the NICS scale for closed-shell singlet states ranges from 0–15 ppm, when R = NO, to 0–250 ppm when R = H and CN. Similarly, the single NICS(0.5) values span a range of 233.9 ppm for antiaromatic closed-shell singlet states but only 11.4 ppm for aromatic triplet states (or only 4.6 ppm excluding the COCH3-substituted molecule with unusually low magnetic aromaticity). As a comparison, the range of NICS(1)zz values for variously monosubstituted benzenes is 4.6 ppm [34] and of NICS(1)πzz is 4.7 ppm [44]. Thus, the triplet state aromaticity appears quite insensitive to substituent effects on the basis of magnetic criterion. The ACID plots also show little difference between the amount of diatropicity of triplet states of studied compounds (Figures S1–S13).
The range of EDDBp values of 0.772 e for substituted aromatic triplet cyclopentadienylcations is a bit larger than the range for the ground-state-substituted benzenes [82], and with the same substituents as considered here, ΔEDDBp = 0.480 e. Therefore, according to the density of delocalized electrons, the triplet state aromaticity appears slightly more sensitive to substituent effect.
However, the range of ISEs, 13.5 kcal/mol, for aromatic triplet states is just slightly lower than the range for antiaromatic closed-shell singlet states, 17.9 kcal/mol. For substituted benzene, some energetic aromaticity measures span the following ranges: 4.5 kcal/mol for aromatic stabilization energies (ASE) [35] and 6.5 kcal/mol for Gibbs energy of hydrogenation [44]. Thus, on the basis of the presented data, it can be concluded that the energetic stabilization of a system due to aromaticity in triplet state is more sensitive to substituent effects than singlet state aromaticity, also supported by the good correlations shown in Figure 8c,g. However, this topic needs more future studies.
Here, we wish to point out that we used the pEDA values developed for the ground singlet state of benzene [90] to examine correlations between substituent effect and aromaticity as a triplet state property, which may not be transferable, as discussed for monosubstituted benzene [93]. However, benzene changes its aromaticity to antiaromaticity upon singlet–triplet excitation, which may be accompanied by significant geometrical changes. Thus, in the case of triplet benzene, pEDA values do not depend only on substituent properties, but also on ring geometry [93]. In this work, however, the pEDA values were used in the analysis of triplet-state aromaticity, and no significant differences in ring geometry between singlet and triplet states were observed, except changes in bond lengths which, certainly, are a consequence of a change in π–electron delocalization.
We find that with an increase in electron delocalization upon going from closed-shell to open-shell triplet state substituent effects weaken so that the triplet-state aromaticity of the studied model system is little sensitive to substituent effect. A similar conclusion was drawn for the triplet state of benzene dication [43].
5. Conclusions
In this work, we used quantum chemical calculations to analyze the sensitivity of triplet state aromaticity to substituent effects by using cyclopentadienyl cation as a model compound. We also provided a discussion on substituent effects on its singlet state antiaromaticity for comparison purposes and as an addition to the existing literature data, and we examined open-shell singlet states for molecules whose closed-shell states had unstable wave function (R = H, F, CH3, CF3, NO2, CN, CHO, and COOCH3). The main conclusions are summarized as follows:
- In its closed-shell singlet state, the positively charged and antiaromatic cyclopentadienyl cation strongly interacts with electron-donating substituents, such as NH2, OH, F, CH3, and NO, but does not interact with electron-withdrawing groups, which orient themselves in such a position to diminish or fully avoid interaction with the π system of the ring. As a consequence, the extent of antiaromaticity nicely correlates with the π–electron substituent effect, represented by the pEDA values, for electron-donors but not for electron acceptors. Although the NO group is basically an electron-withdrawing substituent, it strongly donates its lone pair to the cyclopentadienyl ring, diminishing its antiaromaticity to the largest extent.
- The singlet–triplet energy gaps, favoring triplet in the parent molecule, show a good correlation with the extent of antiaromaticity. They increase with a decrease in antiaromaticity and favor singlet state for strong donors, such as NH2 and OH.
- The formation of an open-shell singlet state has little effect on energy. The slight change in MO extensions and drop in EDDBp values indicates that the decrease in the extent of antiaromaticity, as evidenced from the decrease in NICS values, should have its source in the weaker density of delocalized electrons.
- The triplet state is characterized as aromatic in all but one case (R = NO), which conforms to Baird’s rule. Increased electron delocalization, that is, aromaticity, decreases substituent–ring electronic interactions. Thus, in the absence of steric effects, all substituents adopt a conformation that allows their interaction with the π system of the ring, but it is weak so that the triplet state aromaticity of this chosen model compound is just weakly sensitive to substituent effects. This can be explained by the fact that this triplet state aromaticity is not as large as that of singlet benzene, the aromaticity of which almost resists substituent effects.
- The spin density distribution determines whether the cyclopentadienyl ring is triplet state aromatic or antiaromatic: if it is accumulated in the ring, the system is aromatic, but if it is accumulated at the substituent, the system is antiaromatic. The latter was found for the NO group only so that 5-nitrosocyclopentadienyl cation, according to our calculations, is antiaromatic in both singlet and triplet states. Similarly, our previous calculations indicated that nitrosobenzene would be aromatic in both singlet and triplet states [44]. This is reminiscent of adaptive aromaticity [31,32,33], which here, was enabled by the introduction of a substituent.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/chemistry3030055/s1, Figures S1–S13: ACID plots of studied compounds, Figures S14 and S15: Molecular orbitals involved in the studied electronic state transitions, absolute energies, and x, y, z coordinates of optimized structures.
Author Contributions
Conceptualization, methodology, visualization, data curation, writing—original draft preparation, M.B.-S.; validation, formal analysis, investigation, writing—review and editing M.S., J.A. and M.B.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education, Science and Technological Development of the Republic of Serbia, Contract Number: 451-03-9/2021-14/200168.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hückel, E. Quantum Theoretical Contributions to the Benzene Problem. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Hückel, E. Broad Theory of Unsaturated and Aromatic Compounds; Verlag Chemie: Berlin, Germany, 1938; pp. 77–85. [Google Scholar]
- Von Eggers Doering, W.; Detert, F.L. Cycloheptatrienylium Oxide. J. Am. Chem. Soc. 1951, 73, 876–877. [Google Scholar] [CrossRef]
- IUPAC. Compendium of Chemical Terminology, the Gold Book; IUPAC: Zurich, Switzerland, 2014; Available online: https://goldbook.iupac.org/files/pdf/goldbook.pdf (accessed on 30 January 2020).
- Breslow, R.; Brown, J.; Gajewski, J.J. Antiaromaticity of CyclopropenylAnions. J. Am. Chem. Soc. 1967, 89, 4383–4390. [Google Scholar] [CrossRef]
- Breslow, R. Antiaromaticity. Acc. Chem. Res. 1973, 6, 393–398. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying Aromaticity with Electron Delocalization Measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef] [Green Version]
- Krygowski, T.M.; Szatylowicz, H.; Stasyuk, O.A.; Dominikowska, J.; Palusiak, M. Aromaticity from the Viewpoint of Molecular Geometry: Application to Planar Systems. Chem. Rev. 2014, 114, 6383–6422. [Google Scholar] [CrossRef] [PubMed]
- Cyrański, M.K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. [Google Scholar] [CrossRef]
- Mo, Y.; von Ragué Schleyer, P. An Energetic Measure of Aromaticity and Antiaromaticity Based on the Pauling–Wheland Resonance Energies. Chem. Eur. J. 2006, 12, 2009–2020. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R.; Stanger, A. Magnetic Criteria of Aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef]
- Baird, C. Quantum Organic Photochemistry. II. Resonance and Aromaticity in the Lowest 3ππ* State of Cyclic Hydrocarbons. J. Am. Chem. Soc. 1972, 94, 4941–4948. [Google Scholar] [CrossRef]
- Karadakov, P. Ground- and Excited-State Aromaticity and Antiaromaticity in Benzene and Cyclobutadiene. J. Phys. Chem. A 2008, 112, 7303–7309. [Google Scholar] [CrossRef]
- Villaume, S.; Fogarty, H.A.; Ottosson, H. Triplet-State Aromaticity of 4nπ-Electron Monocycles: Analysis of Bifurcation in the π Contribution to the Electron Localization Function. Chem. Phys. Chem. 2008, 9, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Feixas, F.; Matito, E.; Solà, M.; Poater, J. Patterns of π-Electron Delocalization in Aromatic and Antiaromatic Organic Compounds in the Light of Hückel’s 4n + 2 rule. Phys. Chem. Chem. Phys. 2010, 12, 7126–7137. [Google Scholar] [CrossRef] [Green Version]
- Feixas, F.; Vandenbussche, J.; Bultinck, P.; Matito, E.; Solà, M. Electron Delocalization and Aromaticity in Low-Lying Excited States of Archetypal Organic Compounds. Phys. Chem. Chem. Phys. 2011, 13, 20690–20703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gogonea, V.; von Ragué Schleyer, P.; Schreiner, P.R. Consequences of Triplet Aromaticity in 4nπ-Electron Annulenes: Calculation of Magnetic Shieldings for Open-Shell Species. Angew. Chem. Int. Ed. 1998, 37, 1945–1948. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M.K. Two Sources of the Decrease of Aromaticity: Bond Length Alternation and Bond Elongation. Part II. An Analysis Based on Geometry of the Singlet and Triplet States of 4nπ Annulenes: C4H4, C5H5 +, C6H62+, C7H7−, C8H8, C9H9+. Tetrahedron 1999, 55, 11143–11148. [Google Scholar] [CrossRef]
- Zhu, J.; An, K.; von Ragué Schleyer, P. Evaluation of Triplet Aromaticity by the Isomerization Stabilization Energy. Org. Lett. 2013, 15, 2442–2445. [Google Scholar] [CrossRef] [PubMed]
- An, K.; Zhu, J. Evaluation of Triplet Aromaticity by the Indene–Isoindene Isomerization Stabilization Energy Method. Eur. J. Org. Chem. 2014, 2764–2769. [Google Scholar] [CrossRef]
- Baranac-Stojanović, M. Triplet-State Structures, Energies, and Antiaromaticity of BN Analogues of Benzene and Their Benzo-Fused Derivatives. J. Org. Chem. 2019, 84, 13582–13594. [Google Scholar] [CrossRef]
- Fowler, P.W.; Steiner, E.; Jenneskens, L.W. Ring-Current Aromaticity in Triplet States of 4nπ Electron Monocycles. Chem. Phys. Lett. 2003, 371, 719–723. [Google Scholar] [CrossRef] [Green Version]
- Karadakov, P.B. Aromaticity and Antiaromaticity in the Low-Lying Electronic States of Cyclooctatetraene. J. Phys. Chem. A 2008, 112, 12707–12713. [Google Scholar] [CrossRef] [PubMed]
- Karadakov, P.B.; Hearnshaw, P.; Horner, K.E. Magnetic Shielding, Aromaticity, Antiaromaticity, and Bonding in the Low-Lying Electronic States of Benzene and Cyclobutadiene. J. Org. Chem. 2016, 81, 11346–11352. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; An, K.; Zhu, J. Triplet State Aromaticity: NICS Criterion, Hyperconjugation, and Charge Effects. Chem. Asian J. 2016, 11, 234–240. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, R.; Li, H.; Bergman, J.; Lundstedt, A.; Jorner, K.; Ayub, R.; Haldar, S.; Jahn, B.O.; Denisova, A.; Zietz, B.; et al. Metal-Free Photochemical Silylations and Transfer Hydrogenations of Benzenoid Hydrocarbons and Graphene. Nat. Commun. 2016, 7, 12962. [Google Scholar] [CrossRef]
- Ueda, M.; Jorner, K.; Sung, Y.M.; Mori, T.; Xiao, Q.; Kim, D.; Ottosson, H.; Aida, T.; Itoh, Y. Energetics of Baird Aromaticity Supported by Inversion of Photoexcited Chiral [4n] Annulene Derivatives. Nat. Commun. 2017, 8, 346. [Google Scholar] [CrossRef] [Green Version]
- Oh, J.; Sung, Y.M.; Hong, Y.; Kim, D. Spectroscopic Diagnosis of Excited-State Aromaticity: Capturing Electronic Structures and Conformations upon Aromaticity Reversal. Acc. Chem. Res. 2018, 51, 1349–1358. [Google Scholar] [CrossRef]
- Rosenberg, M.; Dahlstrand, C.; Kilså, K.; Ottosson, H. Excited State Aromaticity and Antiaromaticity: Opportunities for Photophysical and Photochemical Rationalizations. Chem. Rev. 2014, 114, 5379–5425. [Google Scholar] [CrossRef]
- Papadakis, R.; Ottosson, H. The Excited State Antiaromatic Benzene Ring: A Molecular Mr Hyde? Chem. Soc. Rev. 2015, 44, 6472–6493. [Google Scholar] [CrossRef] [Green Version]
- Shen, T.; Chen, D.; Lin, L.; Zhu, J. Dual Aromaticity in Both the T0 and S1 States: Osmapyridinium with Phosphonium Substituents. J. Am. Chem. Soc. 2019, 141, 5720–5727. [Google Scholar] [CrossRef]
- Dai, C.; Chen, D.; Zhu, J. Achieving Adaptive Aromaticity in Cyclo [10] carbon by Screening Cyclo [n] carbon (n = 8–24). Chem. Asian J. 2020, 15, 2187–2191. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Chen, D.; Zhu, J. Adaptive Aromaticity in Metallasilapentalynes. Organometallics 2021, 40, 899–906. [Google Scholar] [CrossRef]
- Siodla, T.; Szatylowicz, H.; Varaksin, K.S.; Krygowski, T.M. Difference in pi-electron delocalization for monosubstituted olefinic and aromatic systems. RSC Adv. 2016, 6, 96527–96530. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Ejsmont, K.; Stepień, B.T.; Cyrański, M.K.; Poater, J.; Solà, M. Relation between the Substituent Effect and Aromaticity. J. Org. Chem. 2004, 69, 6634–6640. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Stępień, B.T. Sigma- and Pi-Electron Delocalization: Focus on Substituent Effects. Chem. Rev. 2005, 105, 3482–3512. [Google Scholar] [CrossRef] [PubMed]
- Omelchenko, I.V.; Shishkin, O.V.; Gorb, L.; Hill, F.C.; Leszczynksi, J. Properties, aromaticity, and substituents effects in poly nitro- and amino-substituted benzenes. Struct. Chem. 2012, 23, 1585–1597. [Google Scholar] [CrossRef]
- Palusiak, M.; Krygowski, T.M. Substituent Effects in Mono- and Disubstituted 1,3,5,7-Cyclooctatetraene Derivatives in Natural and Planar Conformations. New J. Chem. 2009, 33, 1753–1759. [Google Scholar] [CrossRef]
- Sánchez-Sanz, G.; Trujillo, C.; Rozas, I.; Alkorta, I. Influence of Fluoro and Cyano Substituents in the Aromatic and Antiaromatic Characteristics of Cyclooctatetraene. Phys. Chem. Chem. Phys. 2015, 17, 14961–14971. [Google Scholar] [CrossRef] [Green Version]
- Jimenez-Halla, J.O.C.; Matito, E.; Solà, M.; Braunschweig, H.; Hörl, C.; Krummenacher, I.; Wahler, J. A Theoretical Study of the Aromaticity in Neutral and Anionic Borole Compounds. Dalton Trans. 2015, 44, 6740–6747. [Google Scholar] [CrossRef] [Green Version]
- Pincock, J.A.; Speed, A.W.H. The Aromatic Character and Resonance Stabilization Energies of Substituted Cyclopentadienyl and Indenyl Cations. Can. J. Chem. 2005, 83, 1287–1298. [Google Scholar] [CrossRef]
- Alonso, M.; Herradón, B. Substituent Effects on the Aromaticity of Carbocyclic Five-Membered Rings. Phys. Chem. Chem. Phys. 2010, 12, 1305–1317. [Google Scholar] [CrossRef]
- Palusiak, M.; Domagała, M.; Dominikowska, J.; Bickelhaupt, F.M. The Substituent Effect on Benzene Dications. Phys. Chem. Chem. Phys. 2014, 16, 4752–4763. [Google Scholar] [CrossRef] [Green Version]
- Baranac-Stojanović, M. Substituent Effect on Triplet State Aromaticity of Benzene. J. Org. Chem. 2020, 85, 4289–4297. [Google Scholar] [CrossRef]
- Breslow, R.; Hoffman, J.M., Jr. Antiaromaticity in the Parent Cyclopentadienyl Cation. Reaction of 5-Iodocyclopentadiene with Silver Ion. J. Am. Chem. Soc. 1972, 94, 2110–2111. [Google Scholar] [CrossRef]
- Saunders, M.; Berger, R.; Jaffe, A.; McBride, J.M.; O’Neill, J.; Breslow, R.; Hoffman, J.N., Jr.; Perchonock, C.; Wasserman, E.; Hutton, R.S.; et al. Unsubstituted Cyclopentadienyl Cation, a Ground State Triplet. J. Am. Chem. Soc. 1973, 95, 3017–3018. [Google Scholar] [CrossRef]
- Breslow, R.; Chang, H.W.; Yager, W.A. A Stable Triplet State of Pentaphenylcyclopentadienyl Cation. J. Am. Chem. Soc. 1963, 85, 2033–2034. [Google Scholar] [CrossRef]
- Breslow, R.; Hill, R.; Wasserman, E. Pentachlorocyclopentadienyl Cation, a Ground State Triplet. J. Am. Chem. Soc. 1964, 86, 5349–5350. [Google Scholar] [CrossRef]
- Sitzmann, H.; Bock, H.; Boese, R.; Dezember, T.; Havlas, Z.; Kaim, W.; Moscherosch, M.; Zanathy, L. Pentaisopropylcyclopentadienyl: Singlet Anion, Doublet Radical, and Triplet Cation of a Carbocyclic π System. J. Am. Chem. Soc. 1993, 115, 12003–12009. [Google Scholar] [CrossRef]
- Costa, P.; Trosien, I.; Mieres-Perez, J.; Sander, W. Isolation of an Antiaromatic Singlet Cyclopentadienyl Zwitterion. J. Am. Chem. Soc. 2017, 139, 13024–13030. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation Energy Formula into a Functional of the Electron Density. Phys. Rev. B Condens. Matter Mater. Phys. 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Foresman, J.B.; Frisch, A. Exploring Chemistry with Electronic Structure Methods, 2nd ed.; Gaussian, Inc.: Pittsburgh, CA, USA, 1996. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 (Revision D.01); Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Takano, Y.; Taniguchi, T.; Isobe, H.; Kubo, T.; Morita, Y.; Yamamoto, K.; Nakasuji, K.; Takui, T.; Yamaguchi, K. Hybrid Density Functional Theory Studies on the Magnetic Interactions and the Weak Covalent Bonding for the Phenalenyl Radical Dimeric Pair. J. Am. Chem. Soc. 2002, 124, 11122–11130. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Saito, T.; Yamaguchi, K. Approximate Spin Projection for Broken-Symmetry Method and Its Application. In Symmetry (Group Theory) and Mathematical Treatment in Chemistry; Akitsu, T., Ed.; IntechOpen: London, UK, 2018; Chapter 7. [Google Scholar] [CrossRef] [Green Version]
- Kruszewski, J.; Krygowski, T.M. Definition of Aromaticity Basing on the Harmonic Oscillator Model. Tetrahedron Lett. 1972, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1419. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Von Ragué Schleyer, P.; Puhlhofer, F. Recommendations for the Evaluation of Aromatic Stabilization Energies. Org. Lett. 2002, 4, 2873–2876. [Google Scholar] [CrossRef]
- Von Ragué Schleyer, P.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shift: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; von Ragué Schleyer, P. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Von Ragué Schleyer, P.; Jiao, H.; van Eikema Hommes, N.J.R.; Malkin, V.G.; Malkina, O.L. An Evaluation of the Aromaticity of Inorganic Rings: Refined Evidence from Magnetic Properties. J. Am. Chem. Soc. 1997, 119, 12669–12670. [Google Scholar] [CrossRef]
- Von Ragué Schleyer, P.; Manoharan, M.; Wang, Z.-X.; Kiran, B.; Jiao, H.; Puchta, R.; van Eikema Hommes, N.J.R. Dissected Nucleus Independent Chemical Shift Analysis of π-Aromaticity and Antiaromaticity. Org. Lett. 2001, 3, 2465–2468. [Google Scholar] [CrossRef]
- Viglione, R.G.; Zanasi, R.; Lazzeretti, P. Are Ring Currents Still Useful to Rationalize the Benzene Proton Magnetic Shielding? Org. Lett. 2004, 6, 2265–2267. [Google Scholar] [CrossRef]
- Lazzeretti, P. Assessment of Aromaticity via Molecular Response Properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. [Google Scholar] [CrossRef]
- Faglioni, F.; Ligabue, A.; Pelloni, S.; Soncini, A.; Viglione, R.G.; Ferraro, M.B.; Zanasi, R.; Lazzeretti, P. Why Downfield Proton Chemical Shifts Are Not Reliable Aromaticity Indicators. Org. Lett. 2005, 7, 3457–3460. [Google Scholar] [CrossRef] [PubMed]
- Fallah-Bagher-Shaidaei, H.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; von Ragué Schleyer, P. Which NICS Aromaticity Index for Planar π Rings is Best? Org. Lett. 2006, 8, 863–866. [Google Scholar] [CrossRef] [PubMed]
- Stanger, A. Nucleus-Independent Chemical Shifts (NICS): Distance Dependence and Revised Criteria for Aromaticity and Antiaromaticity. J. Org. Chem. 2006, 71, 883–893. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Halla, J.O.C.; Matito, E.; Robles, J.; Solà, M. Nucleus-Independent Chemical Shift (NICS) Profiles in a Series of Monocyclic Planar Inorganic Compounds. J. Organomet. Chem. 2006, 691, 4359–4366. [Google Scholar] [CrossRef]
- Stanger, A. Reexamination of NICSπzz: Height Dependence, Off-Center Values, and Integration. J. Phys. Chem. A 2019, 123, 3922–3927. [Google Scholar] [CrossRef]
- Ditchfeld, R. Self-Consistent Perturbation Theory of Diamagnetism. 1. Gauge-Invariant LCAO Method for N.M.R. Chemical Shifts. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Rahalkar, A.; Stanger, A. Aroma. Available online: http://chemistry.technion.ac.il/members/amnon-stanger/ (accessed on 30 January 2020).
- Stanger, A. Obtaining Relative Induced Ring Currents Quantitatively from NICS. J. Org. Chem. 2010, 75, 2281–2288. [Google Scholar] [CrossRef]
- Herges, R.; Geuenich, D. Delocalization of Electrons in Molecules. J. Phys. Chem. A 2001, 105, 3214–3220. [Google Scholar] [CrossRef]
- Geuenich, D.; Hess, K.; Köhler, F.; Herges, R. Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Calculation of magnetic response properties using a continuous set of gauge transformations. Chem. Phys. Lett. 1993, 210, 223–231. [Google Scholar] [CrossRef]
- Cason, C.; Froehlich, T.; Lipka, C. POV-Ray 3.7.0.msvc10.win64. Persistence of Vision; Raytracer Pty. Ltd.: Fortitude Valley, Australia, 2013. [Google Scholar]
- Szczepanik, D.W.; Andrzejak, M.; Dyduch, K.; Żak, E.; Makowski, M.; Mazur, G.; Mrozek, J. A Uniform Approach to the Description of Multicenter Bonding. Phys. Chem. Chem. Phys. 2014, 16, 20514–20523. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik, D.W. A New Perspective on Quantifying Electron Localization and Delocalization in Molecular Systems. Comput. Theor. Chem. 2016, 1080, 33–37. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Andrzejak, M.; Dominikowska, J.; Pawełek, B.; Krygowski, T.M.; Szatylowicz, H.; Solà, M. The Electron Density of Delocalized Bonds (EDDB) Applied for Quantifying Aromaticity. Phys. Chem. Chem. Phys. 2017, 19, 28970–28981. [Google Scholar] [CrossRef] [Green Version]
- Szczepanik, D.W.; Solà, M. The Electron Density of Delocalized Bonds(EDDBs) as a Measure of Local and Global Aromaticity. In Aromaticity. Modern Computational Methods and Applicattions; Fernandez, I., Ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2021; pp. 259–284. [Google Scholar] [CrossRef]
- Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO Version 3.1.; Gaussian Inc.: Pittsburgh, CA, USA, 2003. [Google Scholar]
- Available online: http://www.eddb.pl/runeddb/ (accessed on 8 July 2021).
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Iversen, K.J.; Wilson, D.J.D.; Dutton, J.L. A Computational Study on a Strategy for Isolating a Stable Cyclopentadienyl Cation. Chem. Eur. J. 2014, 20, 14132–14138. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.P.F.; Wright, T.G. A Study of the Lowest-Lying Triplet and Singlet States of the Cyclopentadienyl Cation (c-C5H5+). Phys. Chem. Chem. Phys. 1999, 1, 219–225. [Google Scholar] [CrossRef]
- Saito, T.; Nishihara, S.; Yamanaka, S.; Kitagawa, Y.; Kawakumi, T.; Yamada, S.; Isobe, H.; Okumura, M.; Yamaguchi, K. Symmetry and Broken Symmetry in Molecular Orbital Description of Unstable Molecules IV: Comparison Between Single- and Multi-Reference Computational Results for Antiaromatic Molecules. Theor. Chem. Acc. 2011, 130, 749–763. [Google Scholar] [CrossRef]
- Ozimiński, W.P.; Dobrowolski, J.C. σ- and π-Electron Contributions to the Substituent Effect: Natural Population Analysis. J. Phys. Org. Chem. 2009, 22, 769–778. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Solà, M.; Andrzejak, M.; Pawełek, B.; Dominikowska, J.; Kukułka, M.; Dyduch, K.; Krygowski, T.M.; Szatylowicz, H. The Role of the Long-Range Exchange Corrections in the Description of Electron Delocalization in Aromatic Species. J. Comput. Chem. 2017, 38, 1640–1654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Dobrowolski, J.C.; Karpińska, G. Substituent Effect in the First Excited Triplet State of Monosubstituted Benzenes. ACS Omega 2020, 16, 9477–9490. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).