The Inert Pair Effect: An Analysis Using the Chemdex Database
Abstract
1. Introduction
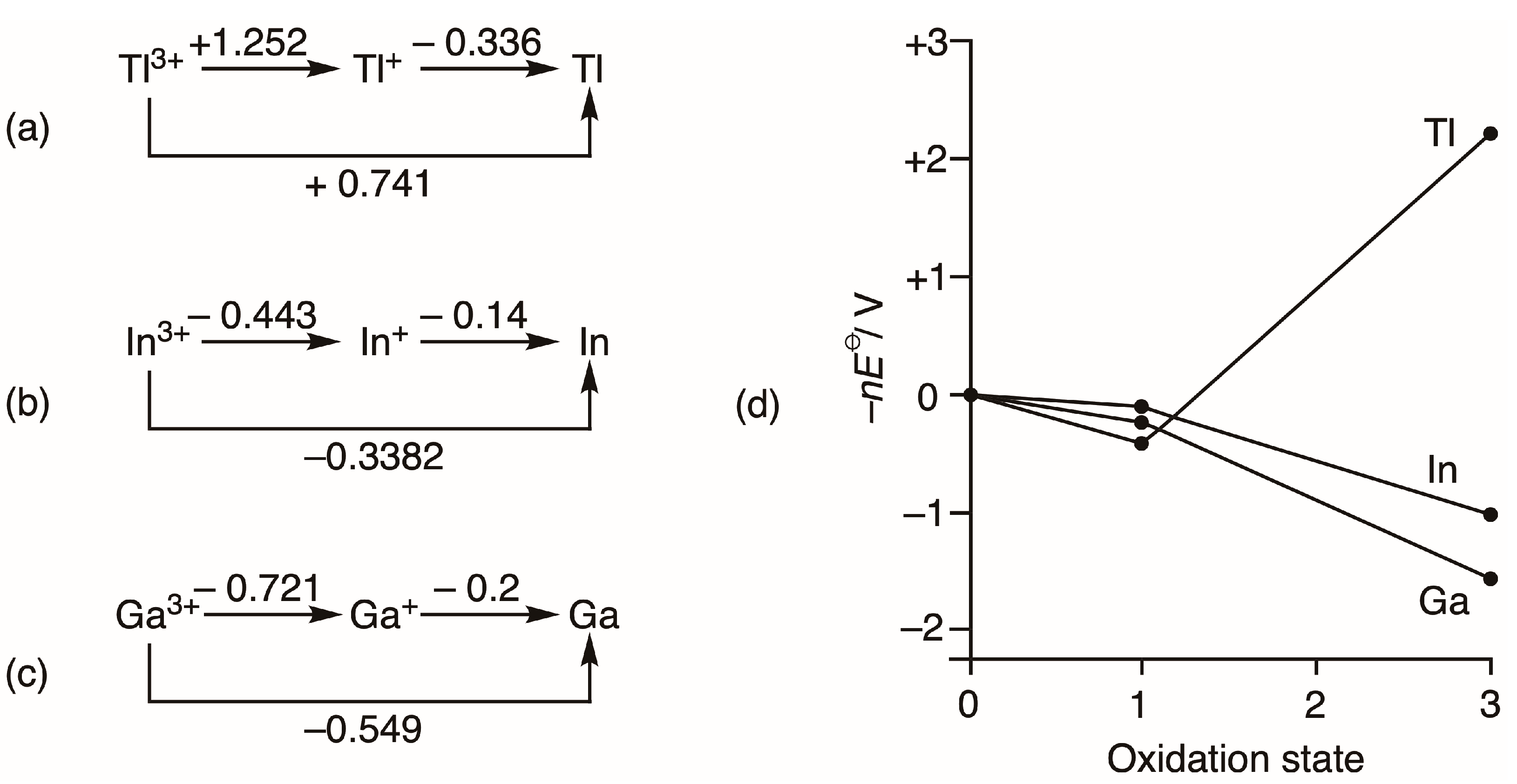
We conclude that, at least for the compounds studied here, there is no special 6s inert pair effect. In short, the ns2 pair is not especially inert for heavy element hydrides and fluorides. The low valency in the heavy element compounds arises naturally as a periodic trend towards weaker bonding, which cannot be explained either in terms of trends in atomic s ionization potentials or by s-p separations, but may be attributed to a decrease in metal–ligand covalent bond character, as suggested by Drago.
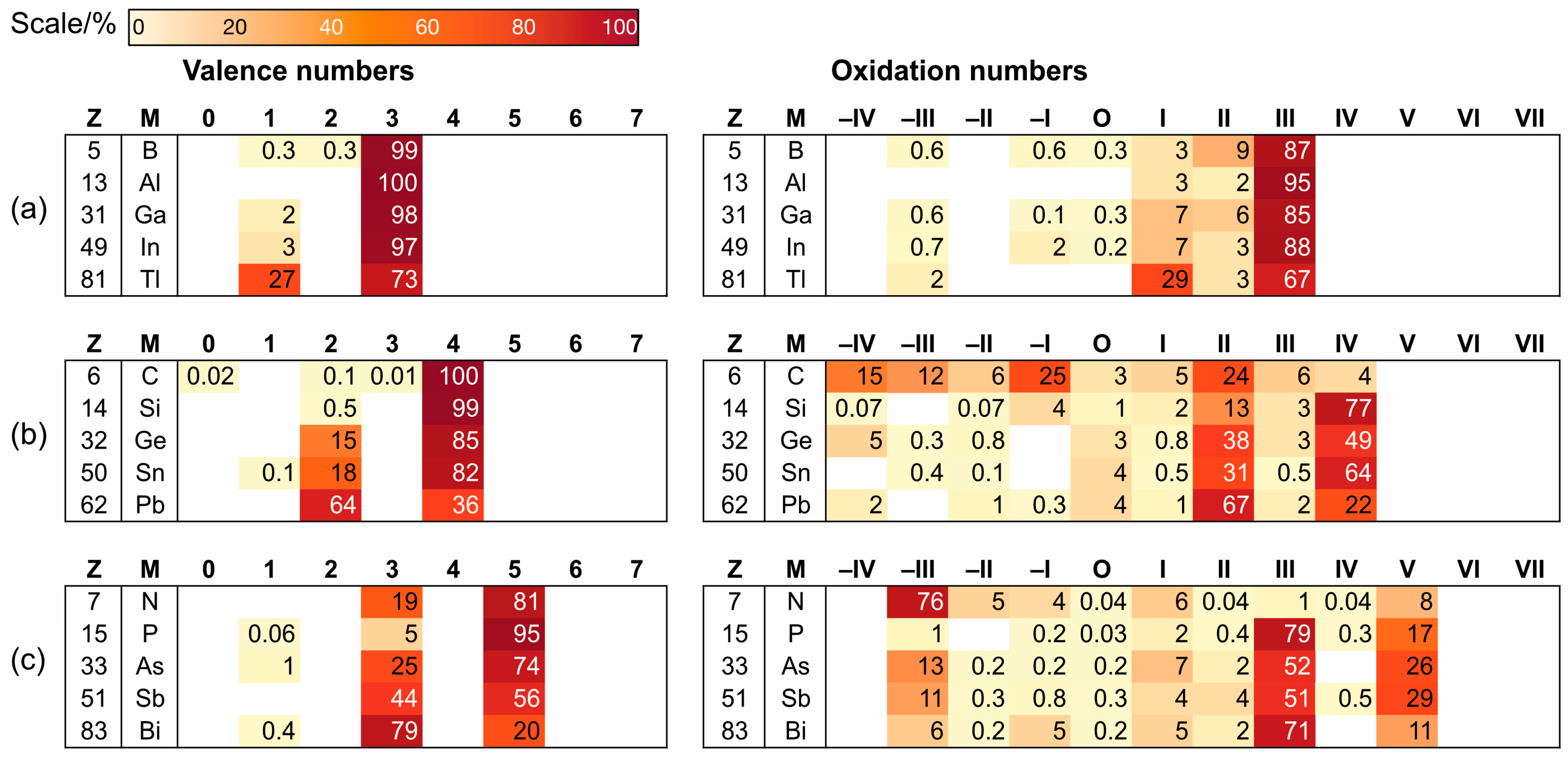
2. A Chemdex Database Analysis
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Notes
- Sidgwick used the term 611 rather than 6s. He also recognised the prior work of Grimm and Sommerfeld on the stability of s pairs of electrons, but the credit belongs to Sidgwick for bringing this matter to the attention of inorganic chemists.
- PbCl4 (a yellow oil) can be stored below 0 °C but decomposes to PbCl2 and Cl2 above 50 °C.
- The electronic configurations 6s16p2 for thallium and 6s16p3 for lead following promotion of an electron from a ground state 6s2 configuration are sometimes referred to as the valence state.
- For a subsequent study by Schwerdtfeger and co-workers that considered the thermodynamic and kinetic stability of the Group 13 trihydrides and covered a number of general points about the inert pair effect, see ref. [11], and for some early references (included in ref. [11]) to the importance of relativistic effects, see refs. [12] and [13]. Ref. [14] considers the electronegativity differences between Tl(I) and Tl(III) and between Pb(II) and Pb(IV), which are relevant to the values for the respective element–chlorine bond dissociation energies shown in Table 2.
- Chemdex employs the term oxidation number (ON) rather than oxidation state (OS), although for the purposes of this paper, the two terms should be considered synonymous. Thus, while Figure 2 uses the term ‘oxidation numbers’ in the heading, the term oxidation state is employed in the text.
- Examples of divalent carbon include N-heterocyclic carbenes (NHCs) and cyclic alkylamino carbenes (CAACs).
- A survey of some other organothallium(I) species that have been reported is provided in ref. [11].
References
- Sidgwick, N.V. The Electronic Theory of Valency; Oxford University Press: Oxford, UK, 1927. [Google Scholar]
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Pu, L.; Twamley, B.; Power, P.P. Terphenyl Ligand Stabilized Lead(II) Derivatives of Simple Organic Groups: Characterization of Pb(R)C6H3-2,6-Trip2 (R = Me, t-Bu, or Ph; Trip = C6H2-2,4,6-i-Pr3), {Pb(μ-Br)C6H3-2,6-Trip2}2, py·Pb(Br)C6H3-2,6-Trip2 (py = Pyridine), and the Bridged Plumbylyne Complex [{W(CO)4}2(μ-Br)(μ-PbC6H3-2,6-Trip2)]. Organometallics 2000, 19, 2874–2881. [Google Scholar]
- Winter, M.J. Chemdex Quantification and Distributions of Valence Numbers, Oxidation Numbers, Coordination Numbers, Electron Numbers, and Covalent Bond Classes for the Elements. Dalton Trans. 2024, 53, 493–511. [Google Scholar] [CrossRef]
- Winter, M.J. Chemdex. Available online: https://winter.group.shef.ac.uk/chemdex/ (accessed on 8 October 2025).
- Drago, R.S. Thermodynamic Evaluation of the Inert Pair Effect. J. Phys. Chem. 1958, 62, 353–357. [Google Scholar] [CrossRef]
- Dasent, W.E. Nonexistent Compounds: Compounds of Low Stability; Marcel Dekker: New York, NY, USA, 1965. [Google Scholar]
- Mingos, D.M.P. Essential Trends in Inorganic Chemistry; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Rumble, J.R. (Ed.) Handbook of Chemistry and Physics; 104th Edition 2023–2024; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Schwerdtfeger, P.; Heath, G.A.; Dolg, M.; Bennett, M.A. Low Valencies and Periodic Trends in Heavy Element Chemistry. A Theoretical Study of Relativistic Effects and Electron Correlation Effects in Group 13 and Period 6 Hydrides and Halides. J. Am. Chem. Soc. 1992, 114, 7518–7527. [Google Scholar] [CrossRef]
- Vest, B.; Klinkhammer, K.; Thierfelder, C.; Lein, M.; Schwerdtfeger, P. Kinetic and Thermodynamic Stability of the Group 13 Trihydrides. Inorg. Chem. 2009, 48, 7953–7961. [Google Scholar] [CrossRef]
- Pitzer, K.S. Relativistic Effects on Chemical Properties. Acc. Chem. Res. 1979, 12, 271–276. [Google Scholar] [CrossRef]
- Pyykkö, P.; Desclaux, J.-P. Relativity and the Periodic System of Elements. Acc. Chem. Res. 1979, 12, 276–281. [Google Scholar] [CrossRef]
- Sanderson, R.T. The “Inert-Pair Effect” on Electronegativity. Inorg. Chem. 1986, 25, 1856–1858. [Google Scholar] [CrossRef]
- Kaupp, M.; Schleyer, P.v.R. Ab Initio Study of Structures and Stabilities of Substituted Lead Compounds. Why is Inorganic Lead Chemistry Dominated by PbII but Organolead Chemistry by PbIV? J. Am. Chem. Soc. 1993, 115, 1061–1073. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Chemical Bonding in Higher Main Group Elements. Angew. Chem. Int. Ed. Engl. 1984, 23, 272–295. [Google Scholar] [CrossRef]
- Housecroft, C.E.; Sharpe, A.G. Inorganic Chemistry, 5th ed.; Pearson: London, UK, 2018. [Google Scholar]
- Downs, A.J. (Ed.) Chemistry of the Group 13 Metals. Chapter 1: Some Themes and Variations. In Chemistry of Aluminium, Gallium, Indium and Thallium; Blackie Academic & Professional (Chapman & Hall): New York, NY, USA, 1993. [Google Scholar]
- Bagnall, K.W. The Chemistry of Polonium. Adv. Inorg. Chem. Radiochem. 1962, 4, 197–230. [Google Scholar]
- Bandeira, N.A.G.; Marçalo, J. The Inert Pair Effect on Heavy Noble Gases: Insights from Radon Tetroxide. Phys. Chem. Chem. Phys. 2023, 25, 14084–14088. [Google Scholar] [CrossRef]
- Karen, P.; McArdle, P.; Takats, J. Toward a Comprehensive Definition of Oxidation State (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 1017–1081. [Google Scholar] [CrossRef]
- Karen, P.; McArdle, P.; Takats, J. Comprehensive Definition of Oxidation State (IUPAC Recommendations 2016). Pure Appl. Chem. 2016, 88, 831–839. [Google Scholar] [CrossRef]
- Parkin, G. Valence, Oxidation Number, and Formal Charge: Three Related but Fundamentally Different Concepts. J. Chem. Educ. 2006, 83, 791–799. [Google Scholar] [CrossRef]
- Smith, D.W. Valence, Covalence, Hypervalence, Oxidation State and Coordination Number. J. Chem. Educ. 2005, 82, 1202–1204. [Google Scholar] [CrossRef]
- Norman, N.C.; Pringle, P.G. Valence and Oxidation State: A Comparison of Their Value and Limitations as Simple Chemical Models. Organometallics 2025, 44, 1315–1336. [Google Scholar] [CrossRef]
- Norman, N.C.; Pringle, P.G. In Defence of Oxidation States. Dalton Trans. 2022, 51, 400–410. [Google Scholar] [CrossRef]
- Green, M.L.H.; Parkin, G. Application of the Covalent Bond Classification Method for the Teaching of Inorganic Chemistry. J. Chem. Educ. 2014, 91, 807–816. [Google Scholar] [CrossRef]
- Häring, M.; Kerpen, C.; Ribbeck, T.; Hennig, P.T.; Bertermann, R.; Ignat’ev, N.V.; Finze, M. Dismutation of Tricyanoboryllead Compounds: The Homoleptic Tetrakis(tricyanoboryl)plumbate Tetraanion. Angew. Chem. Int. Ed. 2022, 61, e202202882. [Google Scholar] [CrossRef]
- Protchenko, A.V.; Dange, D.; Schwarz, A.D.; Tang, C.Y.; Phillips, N.; Mountford, P.; Jones, C.; Aldridge, S. Heavy Metal Boryl Chemistry: Complexes of Cadmium, Mercury and Lead. Chem. Commun. 2014, 50, 3841–3844. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Pan, S.; Holzmann, N.; Schwerdtfeger, P.; Frenking, G. Chemical Bonding and Bonding Models in Main-Group Chemistry. Chem. Rev. 2019, 119, 8781–8845. [Google Scholar] [CrossRef] [PubMed]
- Wolczanski, P.T. Elemental Aspects of Transition Metals Pertinent to Organometallic Chemistry: Properties, Periodicity, Curiosities, and Related Main Group Issues. Organometallics 2024, 43, 787–801. [Google Scholar] [CrossRef]
| Group 13 | Promotion Energy kJ mol–1 | Group 14 | Promotion Energy kJ mol–1 |
|---|---|---|---|
| Al | 347 | Si | 399 |
| Ga | 454 | Ge | 502 |
| In | 418 | Sn | 474 |
| Tl | 541 | Pb | 607 |
| M–Cl | Bond Dissociation Energy kJ mol–1 | M–Cl | Bond Dissociation Energy kJ mol–1 |
|---|---|---|---|
| Ga(I)–Cl | 463 | Ge(II)–Cl | 385 |
| Ga(III)–Cl | 360 | Ge(IV)–Cl | 349 |
| In(I)–Cl | 435 | Sn(II)–Cl | 386 |
| In(III)–Cl | 328 | Sn(IV)–Cl | 323 |
| Tl(I)–Cl | 364 | Pb(II)–Cl | 304 |
| Tl(III)–Cl | 260 | Pb(IV)–Cl | 243 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norman, N.C.; Winter, M.J. The Inert Pair Effect: An Analysis Using the Chemdex Database. Chemistry 2025, 7, 170. https://doi.org/10.3390/chemistry7050170
Norman NC, Winter MJ. The Inert Pair Effect: An Analysis Using the Chemdex Database. Chemistry. 2025; 7(5):170. https://doi.org/10.3390/chemistry7050170
Chicago/Turabian StyleNorman, Nicholas C., and Mark J. Winter. 2025. "The Inert Pair Effect: An Analysis Using the Chemdex Database" Chemistry 7, no. 5: 170. https://doi.org/10.3390/chemistry7050170
APA StyleNorman, N. C., & Winter, M. J. (2025). The Inert Pair Effect: An Analysis Using the Chemdex Database. Chemistry, 7(5), 170. https://doi.org/10.3390/chemistry7050170






