Theoretical Analysis of Intermolecular Interactions in Cationic π-Stacked Dimer Models of Antiaromatic Molecules
Abstract
1. Introduction
2. Computational Details
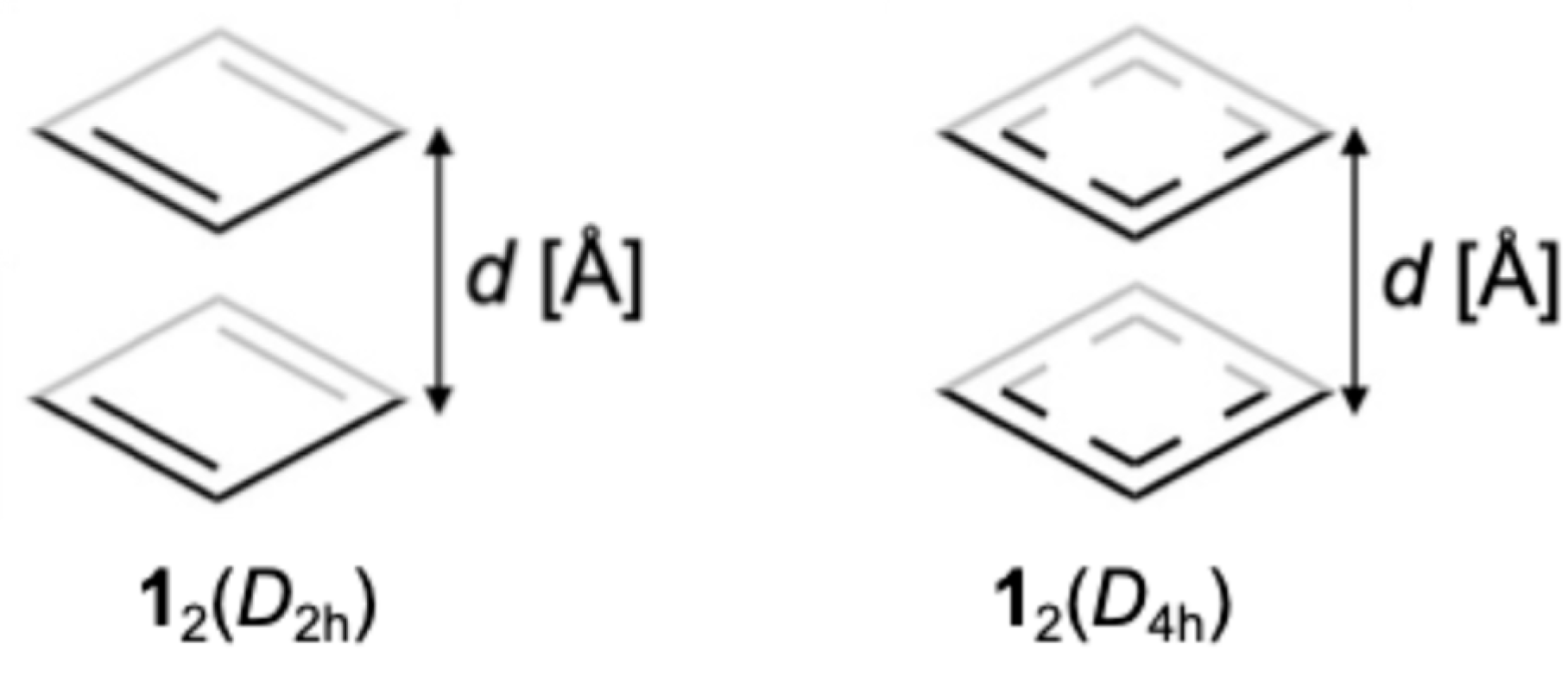
2.1. Calculated Models
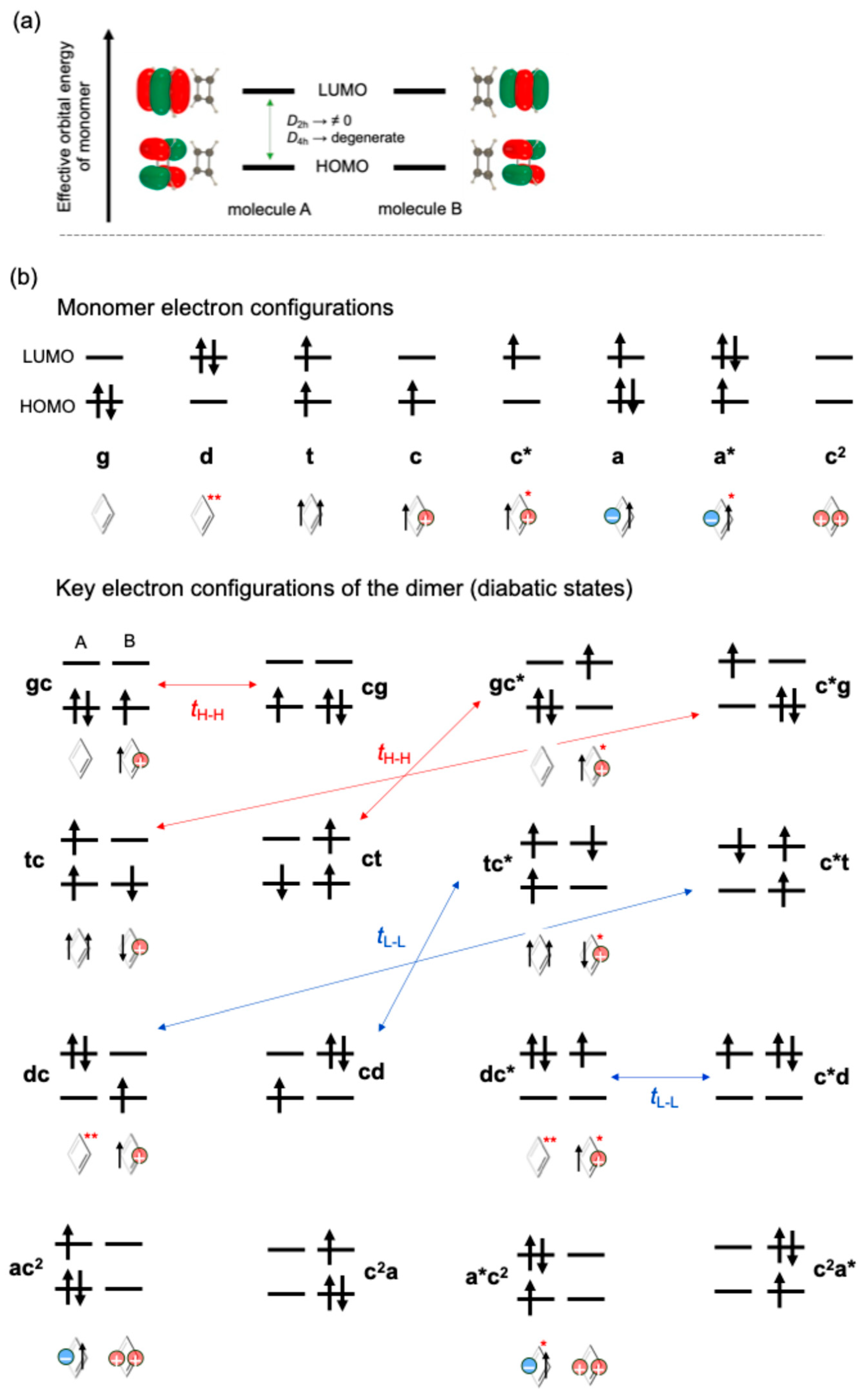
2.2. Calculation and Analysis Methods
3. Results and Discussion
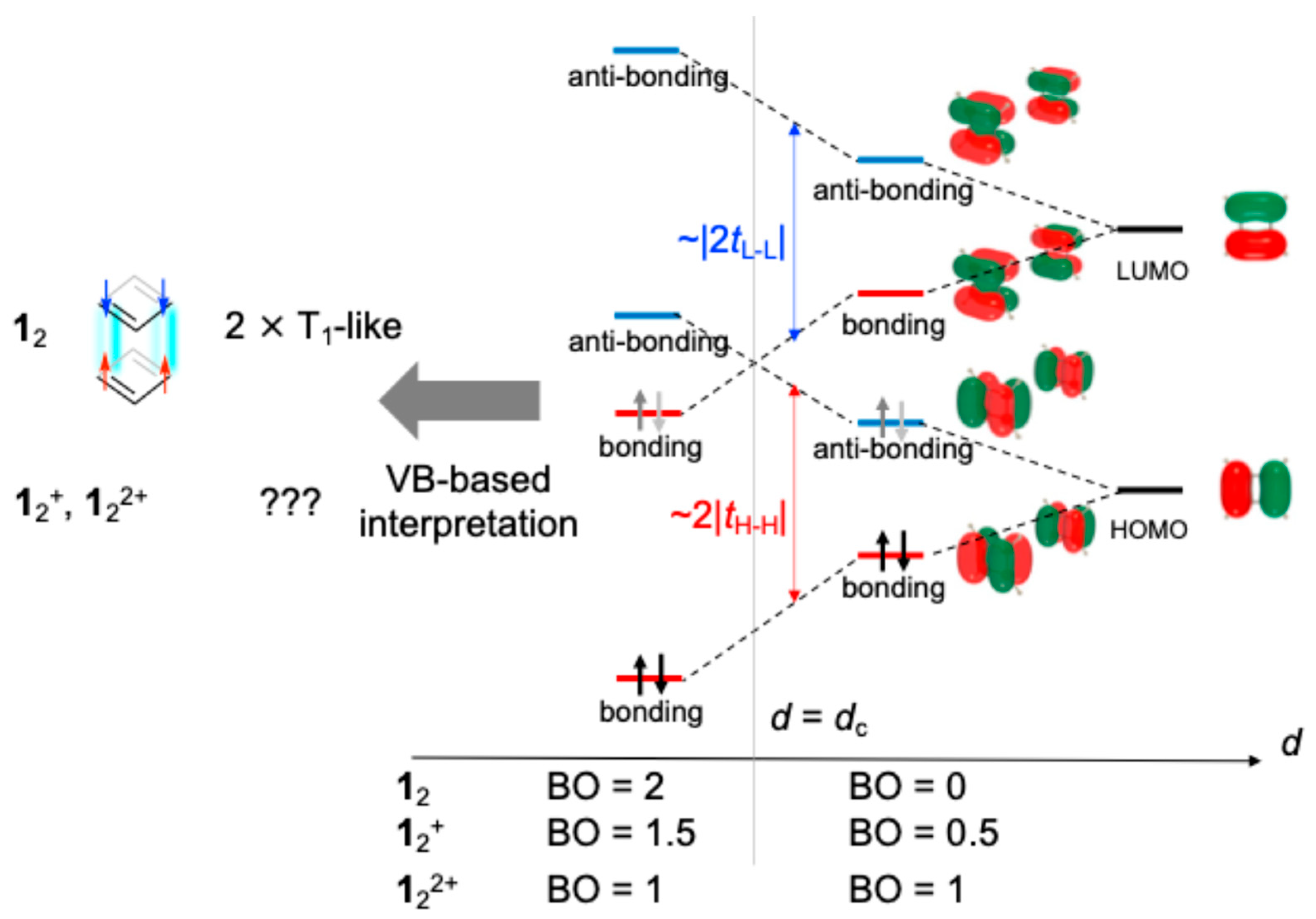
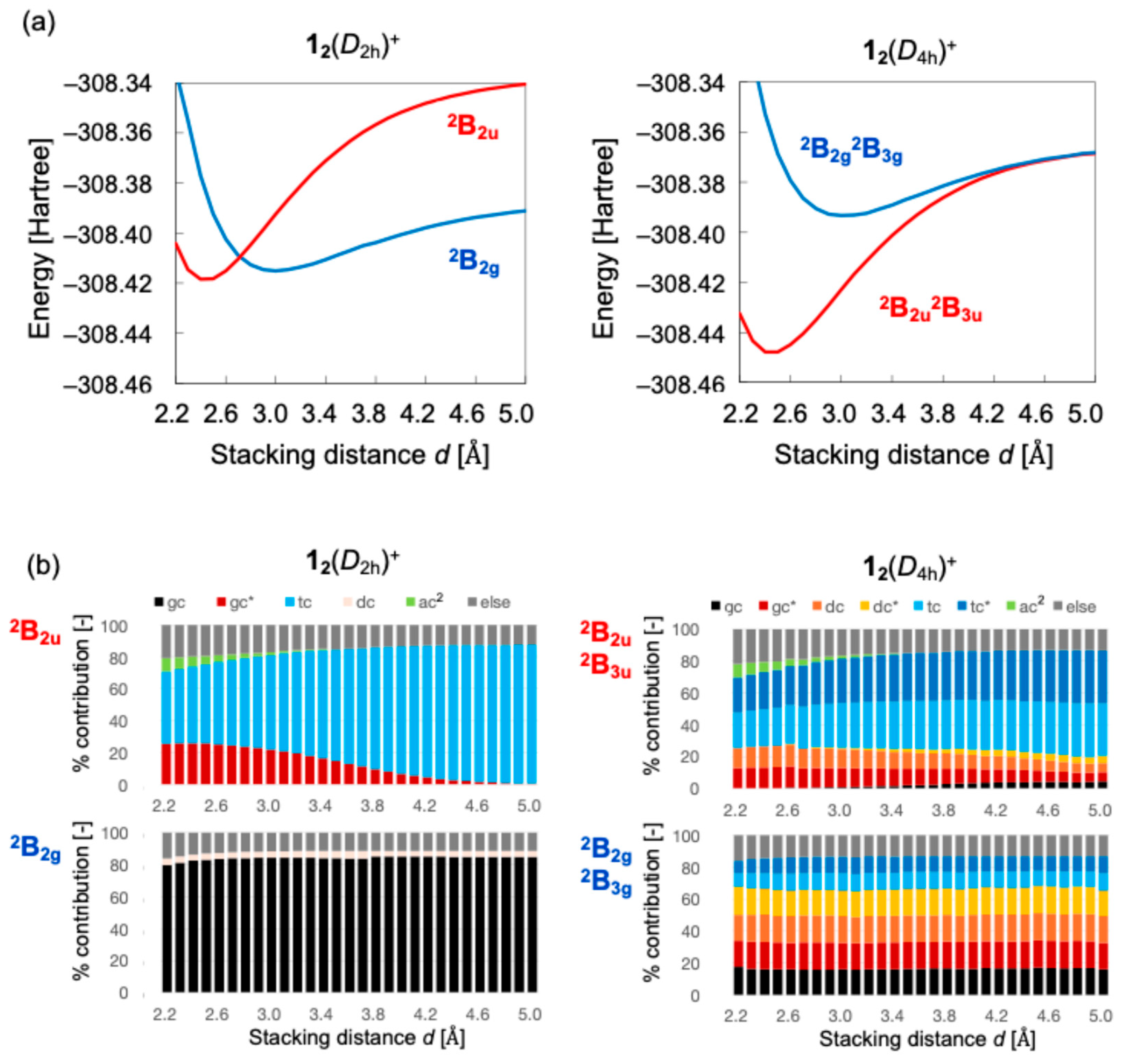
3.1. Monocationic π-Dimer Models
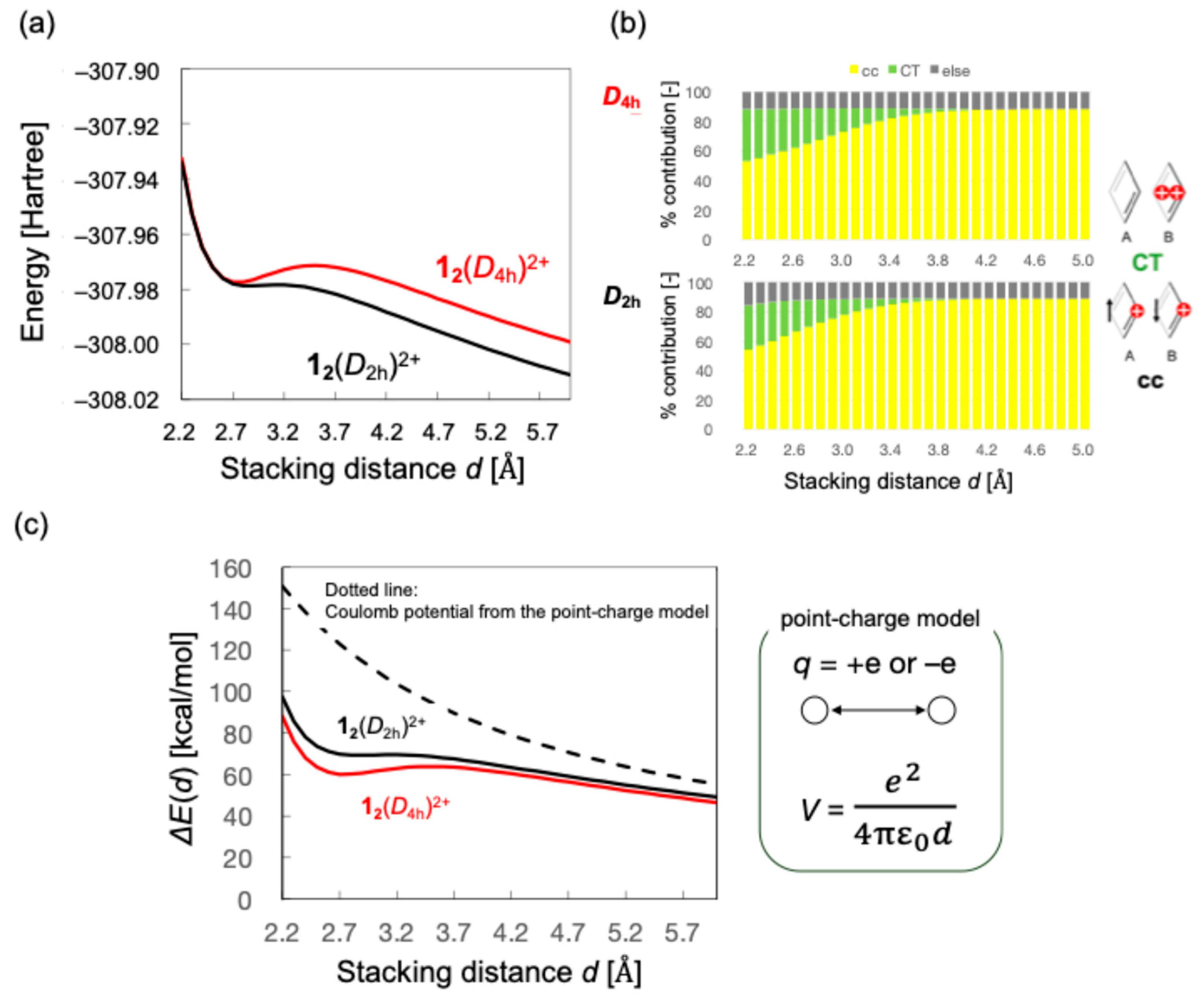
3.2. Dicationic π-Dimer Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salonen, L.M.; Ellermann, M.; Diederich, F. Aromatic Rings in Chemical and Biological Recognition: Energetics and Structures. Angew. Chem. Int. Ed. 2011, 50, 4808–4842. [Google Scholar] [CrossRef]
- Tsuzuki, S. Interactions with Aromatic Rings. In Intermolecular Forces and Clusters I; Wales, D.J., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 149–193. [Google Scholar]
- Ninković, D.B.; Blagojević Filipović, J.P.; Hall, M.B.; Brothers, E.N.; Zarić, S.D. What Is Special about Aromatic–Aromatic Interactions? Significant Attraction at Large Horizontal Displacement. ACS Cent. Sci. 2020, 6, 420–425. [Google Scholar] [CrossRef]
- Bhattacharjee, R.; Lischka, H.; Kertesz, M. Pancake Bonding in the Stabilization of Cationic Acene Dimers. ACS Mater. Au 2025, 5, 365–376. [Google Scholar] [CrossRef]
- Matsumoto, M.; Inokuchi, Y.; Ohashi, K.; Nishi, N. Charge Delocalization in Benzene−Naphthalene Hetero-Dimer Cation. J. Phys. Chem. A 1997, 101, 4574–4578. [Google Scholar] [CrossRef]
- Martinez, C.R.; Iverson, B.L. Rethinking the Term “Pi-Stacking”. Chem. Sci. 2012, 3, 2191–2201. [Google Scholar] [CrossRef]
- Badger, B.; Brocklehurst, B. Formation of Dimer Cations of Aromatic Hydrocarbons. Nature 1968, 219, 263. [Google Scholar] [CrossRef]
- Meot-Ner, M. Dimer Cations of Polycyclic Aromatics. Experimental Bonding Energies and Resonance Stabilization. J. Phys. Chem. 1980, 84, 2724–2728. [Google Scholar] [CrossRef]
- Hübler, P.; Heinze, J. Kinetic Studies on Reversible Dimerization of Thianthrene and 2,3,7,8-Tetramethoxythianthrene Radical Cations. Berichte Bunsenges. Für Phys. Chem. 1998, 102, 1506–1509. [Google Scholar] [CrossRef]
- Small, D.; Zaitsev, V.; Jung, Y.; Rosokha, S.V.; Head-Gordon, M.; Kochi, J.K. Intermolecular π-to-π Bonding between Stacked Aromatic Dyads. Experimental and Theoretical Binding Energies and Near-IR Optical Transitions for Phenalenyl Radical/Radical versus Radical/Cation Dimerizations. J. Am. Chem. Soc. 2004, 126, 13850–13858. [Google Scholar] [CrossRef]
- Rhee, Y.M.; Lee, T.J.; Gudipati, M.S.; Allamandola, L.J.; Head-Gordon, M. Charged Polycyclic Aromatic Hydrocarbon Clusters and the Galactic Extended Red Emission. Proc. Natl. Acad. Sci. USA 2007, 104, 5274–5278. [Google Scholar] [CrossRef] [PubMed]
- Kochi, J.K.; Rathore, R.; Maguères, P.L. Stable Dimeric Aromatic Cation−Radicals. Structural and Spectral Characterization of Through-Space Charge Delocalization. J. Org. Chem. 2000, 65, 6826–6836. [Google Scholar] [CrossRef]
- Attah, I.K.; Platt, S.P.; Meot-Ner (Mautner), M.; El-Shall, M.S.; Peverati, R.; Head-Gordon, M. What Is the Structure of the Naphthalene–Benzene Heterodimer Radical Cation? Binding Energy, Charge Delocalization, and Unexpected Charge-Transfer Interaction in Stacked Dimer and Trimer Radical Cations. J. Phys. Chem. Lett. 2015, 6, 1111–1118. [Google Scholar] [CrossRef] [PubMed]
- Slater, J.C. The Normal State of Helium. Phys. Rev. 1928, 32, 349–360. [Google Scholar] [CrossRef]
- Pauling, L. The Normal State of the Helium Molecule-Ions He2+ and He2++. J. Chem. Phys. 1933, 1, 56–59. [Google Scholar] [CrossRef]
- Guilhaus, M.; Brenton, A.G.; Beynon, J.H.; Rabrenović, M.; von Ragué Schleyer, P. He22+, the Experimental Detection of a Remarkable Molecule. J. Chem. Soc. Chem. Commun. 1985, 4, 210–211. [Google Scholar] [CrossRef]
- Callear, A.B.; Hedges, R.E.M. Metastability of Rotationally Hot Dihelium at 77° K. Nature 1967, 215, 1267–1268. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond. Application of Results Obtained From the Quantum Mechanics and From a Theory of Paramagnetic Susceptibility to the Structure of Molecules. J. Am. Chem. Soc. 1931, 53, 1367–1400. [Google Scholar] [CrossRef]
- Harris, M.L. Chemical Reductionism Revisited: Lewis, Pauling and the Physico-Chemical Nature of the Chemical Bond. Stud. Hist. Philos. Sci. Part A 2008, 39, 78–90. [Google Scholar] [CrossRef]
- Wu, W.; Su, P.; Shaik, S.; Hiberty, P.C. Classical Valence Bond Approach by Modern Methods. Chem. Rev. 2011, 111, 7557–7593. [Google Scholar] [CrossRef]
- Shaik, S.; Hiberty, P.C. Valence Bond Theory, Its History, Fundamentals, and Applications: A Primer. In Reviews in Computational Chemistry; John Wiley & Sons, Inc.: Hoboken, NY, USA, 2004; pp. 1–100. [Google Scholar]
- McWeeny, R. The Valence Bond Theory of Molecular Structure—I. Orbital Theories and the Valence-Bond Method. Proc. Roy. Soc. Lond. A Math. Phys. Sci. 1997, 223, 63–79. [Google Scholar]
- Sugimori, R.; Okada, K.; Kishi, R.; Kitagawa, Y. Stacked-Ring Aromaticity from the Viewpoint of the Effective Number of π-Electrons. Chem. Sci. 2025, 16, 1707–1715. [Google Scholar] [CrossRef]
- Sugimori, R.; Kishi, R.; Shinokubo, H.; Kitagawa, Y. Diradical Character View of Energy Stabilization in π-Stacked Dimers of Antiaromatic Molecules. Chem. Lett. 2024, 53, upae224. [Google Scholar] [CrossRef]
- Sugimori, R.; Ikeuchi, M.; Kishi, R.; Kitagawa, Y. Theoretical Study on Aromatic Characters in π-Stacked Multimers Composed of Antiaromatic Molecules. Bull. Chem. Soc. Jpn. 2024, 97, uoae133. [Google Scholar] [CrossRef]
- Corminboeuf, C.; von Ragué Schleyer, P.; Warner, P. Are Antiaromatic Rings Stacked Face-to-Face Aromatic? Org. Lett. 2007, 9, 3263–3266. [Google Scholar] [CrossRef]
- Bean, D.E.; Fowler, P.W. Stacked-Ring Aromaticity: An Orbital Model. Org. Lett. 2008, 10, 5573–5576. [Google Scholar] [CrossRef]
- Wang, Q.; Sundholm, D.; Gauss, J.; Nottoli, T.; Lipparini, F.; Kino, S.; Ukai, S.; Fukui, N.; Shinokubo, H. Changing Aromatic Properties through Stacking: The Face-to-Face Dimer of Ni(Ii) Bis(Pentafluorophenyl)Norcorrole. Phys. Chem. Chem. Phys. 2024, 26, 14777–14786. [Google Scholar] [CrossRef]
- Alonso, M.; Poater, J.; Solà, M. Aromaticity Changes along the Reaction Coordinate Connecting the Cyclobutadiene Dimer to Cubane and the Benzene Dimer to Hexaprismane. Struct. Chem. 2007, 18, 773–783. [Google Scholar] [CrossRef]
- Okazawa, K.; Tsuji, Y.; Yoshizawa, K. Frontier Orbital Views of Stacked Aromaticity. J. Phys. Chem. A 2023, 127, 4780–4786. [Google Scholar] [CrossRef] [PubMed]
- Orozco-Ic, M.; Restrepo, A.; Muñoz-Castro, A.; Merino, G. Molecular Helmholtz Coils. J. Chem. Phys. 2019, 151, 014102. [Google Scholar] [CrossRef] [PubMed]
- Kino, S.; Ukai, S.; Fukui, N.; Haruki, R.; Kumai, R.; Wang, Q.; Horike, S.; Phung, Q.M.; Sundholm, D.; Shinokubo, H. Close Stacking of Antiaromatic Ni(II) Norcorrole Originating from a Four-Electron Multicentered Bonding Interaction. J. Am. Chem. Soc. 2024, 146, 9311–9317. [Google Scholar] [CrossRef]
- Tsuji, Y.; Okazawa, K.; Yoshizawa, K. Hückel Molecular Orbital Analysis for Stability and Instability of Stacked Aromatic and Stacked Antiaromatic Systems. J. Org. Chem. 2023, 88, 14887–14898. [Google Scholar] [CrossRef]
- Orozco-Ic, M.; Sundholm, D. On the Antiaromatic–Aromatic–Antiaromatic Transition of the Stacked Cyclobutadiene Dimer. Phys. Chem. Chem. Phys. 2023, 25, 12777–12782. [Google Scholar] [CrossRef]
- Nozawa, R.; Tanaka, H.; Cha, W.-Y.; Hong, Y.; Hisaki, I.; Shimizu, S.; Shin, J.-Y.; Kowalczyk, T.; Irle, S.; Kim, D.; et al. Stacked Antiaromatic Porphyrins. Nat. Commun. 2016, 7, 13620. [Google Scholar] [CrossRef]
- Aihara, J. Origin of Stacked-Ring Aromaticity. J. Phys. Chem. A 2009, 113, 7945–7952. [Google Scholar] [CrossRef]
- Kawashima, H.; Ukai, S.; Nozawa, R.; Fukui, N.; Fitzsimmons, G.; Kowalczyk, T.; Fliegl, H.; Shinokubo, H. Determinant Factors of Three-Dimensional Aromaticity in Antiaromatic Cyclophanes. J. Am. Chem. Soc. 2021, 143, 10676–10685. [Google Scholar] [CrossRef] [PubMed]
- Nozawa, R.; Kim, J.; Oh, J.; Lamping, A.; Wang, Y.; Shimizu, S.; Hisaki, I.; Kowalczyk, T.; Fliegl, H.; Kim, D.; et al. Three-Dimensional Aromaticity in an Antiaromatic Cyclophane. Nat. Commun. 2019, 10, 3576. [Google Scholar] [CrossRef]
- Tada, K.; Sugimori, R.; Kishi, R.; Kitagawa, Y. Unveiled Open-Shell Nature of an Antiaromatic Molecule by Surface–Molecule Interaction: A Concept Suggestion by Spin-Projected Density Functional Theory. Chem. Commun. 2025, 61, 11758–11761. [Google Scholar] [CrossRef]
- Fujiyoshi, J.-Y.; Tonami, T.; Yamane, M.; Okada, K.; Kishi, R.; Muhammad, S.; Al-Sehemi, A.G.; Nozawa, R.; Shinokubo, H.; Nakano, M. Theoretical Study on Open-Shell Singlet Character and Second Hyperpolarizabilities in Cofacial π-Stacked Dimers Composed of Weak Open-Shell Antiaromatic Porphyrins. ChemPhysChem 2018, 19, 2863–2871. [Google Scholar] [CrossRef] [PubMed]
- Joseph, J.; Berville, M.; Wytko, J.; Weiss, J.; Jacquot de Rouville, H.-P. π-Mers and π-Dimers: Two Radical Supramolecular Interactions—A Tutorial Review. Chem. Eur. J. 2025, 31, e202403115. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of N-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. N-Electron Valence State Perturbation Theory: A Fast Implementation of the Strongly Contracted Variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. N-Electron Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A Quasidegenerate Formulation of the Second Order N-Electron Valence State Perturbation Theory Approach. J. Chem. Phys. 2004, 121, 4043–4049. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Monino, E.; Boggio-Pasqua, M.; Scemama, A.; Jacquemin, D.; Loos, P.-F. Reference Energies for Cyclobutadiene: Automerization and Excited States. J. Phys. Chem. A 2022, 126, 4664–4679. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishino, K.; Okada, K.; Sugimori, R.; Tada, K.; Kishi, R.; Kitagawa, Y. Theoretical Analysis of Intermolecular Interactions in Cationic π-Stacked Dimer Models of Antiaromatic Molecules. Chemistry 2025, 7, 171. https://doi.org/10.3390/chemistry7060171
Nishino K, Okada K, Sugimori R, Tada K, Kishi R, Kitagawa Y. Theoretical Analysis of Intermolecular Interactions in Cationic π-Stacked Dimer Models of Antiaromatic Molecules. Chemistry. 2025; 7(6):171. https://doi.org/10.3390/chemistry7060171
Chicago/Turabian StyleNishino, Kosei, Kenji Okada, Ryota Sugimori, Kohei Tada, Ryohei Kishi, and Yasutaka Kitagawa. 2025. "Theoretical Analysis of Intermolecular Interactions in Cationic π-Stacked Dimer Models of Antiaromatic Molecules" Chemistry 7, no. 6: 171. https://doi.org/10.3390/chemistry7060171
APA StyleNishino, K., Okada, K., Sugimori, R., Tada, K., Kishi, R., & Kitagawa, Y. (2025). Theoretical Analysis of Intermolecular Interactions in Cationic π-Stacked Dimer Models of Antiaromatic Molecules. Chemistry, 7(6), 171. https://doi.org/10.3390/chemistry7060171









