Optimal Design of Practical Quantum Key Distribution Backbones for Securing CoreTransport Networks

Abstract

We describe two mixed-integer linear programming formulations, one a faster version of a previous proposal, the other a slower but better performing new model, for the design of Quantum Key Distribution (QKD) sub-networks dimensioned to secure existing core fiber plants. We exploit existing technologies, including non-quantum repeater nodes and multiple disjoint QKD paths to overcome reach limitations while maintaining security guarantees. We examine the models’ performance using simulations on both synthetic and real topologies, quantifying their time and resulting QKD network cost compared to our previous proposal.

1. Introduction

Recent advances towards the realization of practical quantum computers with a large number of qbits, and hence the looming threat of fast implementations of Shor’s and Grover’s quantum algorithms, have spurned the research and security communities into looking for secure replacements to parts of the modern computer security infrastructure which rely on soon to be vulnerable mathematical problems (prime factorization and discrete logarithms). Two main avenues have been identified to prevent this issue, namely Post-Quantum Cryptography (PQC), and Quantum-secured Communications via Quantum Key Distribution (QKD); each presents advantages and disadvantages.

Briefly, PQC comprises new mathematical techniques to replace the vulnerable ones, which are believed to be secure even against a quantum computer. While it promises to be a practical drop-in replacement for outgoing crypto, there is, unfortunately, no guarantee that its mathematical underpinnings are indeed secure.

In contrast, QKD is an unwieldy physical solution to the problem of sharing random bit strings (i.e., secret keys). It comprises a set of protocols and devices (some, notably, already commercially available, e.g., [1]) that exploit the weird properties of quantum mechanics to achieve the exchange of a random bit stream between two communicating parties, with an arbitrarily low upper bound on the probability that an adversary silently eavesdropped the communication, making it an ideal choice to generate key material for cryptography (especially session keys), which can then be used with symmetric ciphers, which are known to be relatively unaffected by quantum computing, or even One-Time Pads (OTPs) for short, provably secure communications. The key advantage of QKD over PQC is that it can be mathematically proven to be secure, even independently of the security of the QKD devices (via Measurement Device Independent QKD, or MDI-QKD [2]). On the other hand, this reliance on physical properties, and hence specialized hardware with many limitations despite significant advances [3], makes QKD impractical in the vast majority of use cases.

In this paper we focus on QKD, imagining how to use it to securely encrypt the data crossing large core transport optical networks, the kind of networks that cross countries, continents and oceans to interconnect the world. While metro-sized experimental QKD networks already exist [4], the reach limitations of current QKD devices have so far discouraged the adoption of such technology for nation- and continent-wide networks. To cross such distances with high capacity, high reliability and low latency, there is only one economically viable technology: optical communications in fibers. And while we realize that in-network encryption is no guarantee of end-to-end privacy of security, the ease with which traffic can be spoofed from a fiber, even from underwater cables, has led operators to begin to consider how to secure their networks (to protect control traffic vital to their functioning, if nothing else). With the speed of modern transceivers exceeding 400 Gb/s per connection, and that of QKD in the order of Mb/s, a direct application of information-theoretically secure OTPs is clearly out of the question, unless used only to secure the small subset of control traffic. Outside of that, QKD could be used for continuous key regeneration, which for AES-256 operating in hardware at line rate may or may not be a concern even at these high data transmission rates, or it could even be a new value-added service for telecom operators, replacing human secure couriers with faster delivery and better guarantees of key secrecy [5].

As mentioned, QKD has several limitations, chief among which are relatively low key generation rates (in the order of 1 Mb/s for distances <100 Km), and short reach (100–150 Km, twice that with schemes where the measuring device is in the middle like MDI-QKD), owing to relatively weak laser pulses, fiber losses and environmental noise. To overcome the latter limitation, which is vital to successfully deploy this technology in geographically wide networks, two possible solutions have been identified: satellite QKD, where the atmosphere-less space between satellites offers a much better propagation medium than terrestrial fibers, but which suffers from significant issues in ground-to-satellite links (e.g., loss-of-signal during bad weather [6]), and the use of repeaters to regenerate the quantum signal. Regarding the latter, one possibility touted in research papers is to use Quantum Repeaters [7], which would guarantee the security of the key material even as it passes through intermediate sites. Unfortunately, no such device has, so far, been demonstrated to work in field conditions.

In the absence of quantum repeaters, we are currently limited to ‘trusted’ repeaters, i.e., nodes (of degree two) where one QKD instance is terminated and another initiated, with classical crypto-based security in the middle. Note that having to monitor a few sites instead of hundreds of kilometers of underground fibers is already a vast security improvement over the current situation, and the nodes themselves need not expose clear-text key material if they use OTPs to simply re-encrypt an arbitrary bit string (the key) with a local key that is the XOR of the link-local QKD keys produced by its two sides [8]. Since the key generation rate decays with distance, the next obvious question pertains to where to place how many repeaters on any particular link to achieve sufficient key generation at optimal, i.e., minimal cost. This has already been studied [9], but due to practical constraints, such as the need for power, shelf space and physical security at repeater nodes, it also has a holistic answer: at least for existing networks, we would expect repeaters to be co-located with existing amplification stations, with the overall effectiveness of the chain being determined largely by its least efficient span (the longest, barring other sources of noise).

So we know how to organize a chain of QKD repeaters to traverse a long link. Which links in a network should we augment with such repeaters in order to connect all nodes that need secure communications? Ref. [9] provides some answers rooted in geometric modeling for simple topologies, which however are quite hard to apply directly to real networks. Fortunately, there exists a case where the answer is indeed quite simple: if the required key rate is very low, much lower than that generated by even the least effective QKD chain in the topology, then the set of links to be augmented is simply the minimum spanning tree that connects all the required nodes on the topology graph, where the link weights represent the cost to deploy a QKD chain on those links.

If, instead, the required key rate is comparable or higher than that of the chains, i.e., multiple parallel chains might be required, the answer is slightly more complicated, as it may, in some instances, be cheaper to install fewer but more efficient chains on one link instead of more on another.

Repeater chains, however, do not prevent an attacker that manages to compromise a node from eventually reading the messages passing through it, and hence discovering the keys being passed through that node. A relatively simple way to foil this attack is to split the key over messages sent over multiple, disjoint paths, forcing an attacker to compromise at least that many nodes to recover a whole key, which is the idea we exploit in this work. A more thorough theoretical justification for this idea can be found in [10], where multiple parallel trusted repeaters are traversed in an information-theoretic secure way by distributing the key via network coding. An additional benefit of a multi-path approach is that it also ameliorates the service disruption caused by fiber cuts, or even targeted attacks against the QKD infrastructure. QKD exchanges are delicate processes, quite vulnerable to ambient noise; therefore, an attacker can simply inject random noise in a fiber used for QKD to all but interrupt the process, which in turn forces the remote security endpoints to stretch their use of existing keys or rely on less secure classical key refresh mechanisms. With the proposed approach, the impact of such failures or attacks would be reduced at least proportionally to the number of available parallel paths.

In this paper we expand on a previous answer [11] to the question: if we were to deploy QKD in a terrestrial core transport network tomorrow, how could we do it effectively? That is, if the threat of quantum computers and/or the emergence of some new attack on Public Key Infrastructure forced us to deploy QKD technology in the short term, how could we do it in a manner that is both economical and guarantees adequate security in the presence of (classical) repeater sites? Which links should we secure, and with how many QKD chains each? Given multiple QKD paths between nodes, which routes should every QKD session follow?

While we hope to never actually need to, to answer these questions we formulate optimization models that, given a medium-large distance fiber plant graph and a matrix of QKD traffic demands, minimize the use of costly QKD devices and compute the routes taken by the key material over the resulting QKD-enabled sub-graph such that all demands are satisfied and utilize a desired (input) number of disjoint paths. Notably, the contours of our questions prevent us to assume the existence of unproven technology: we have to rely only on the technology available today, i.e., BB84-like [12] point to point devices and trusted (not quantum) repeaters. We present two answers to these questions, in the form of two Mixed-Integer Linear Programming (MILP) formulations. The first is an improvement over our previous solution [11] in terms of execution time, due to using many fewer integer variables; the second new model accounts for the fact that key distribution need not follow the direction of the traffic, and, despite being significantly more complex and hence slower, can produce better (i.e., cheaper) QKD configurations which may well be significant if the cost of devices remains high.

We present these formulations, and our assumptions in their design, in Section 2, and we quantify their performance advantages compared to our previous proposal, on both random and realistic topologies, in Section 3, before summarizing the work, its findings and potential future extensions in Section 4.

2. MILP Formulations for QKD Subnetwork Design

In this section, we present two Mixed-Integer Linear Programming (MILP) formulations to solve the problem of finding the optimal placement of QKD devices, and the routes taken by the end-to-end QKD exchanges. Both formulations take the following items as input:

• A directed graph $G=(V,E)$, representing an existing or planned fiber plant.
• An integer N representing the desired path multiplicity, i.e., the minimum number of parallel disjoint paths that each end-to-end QKD session must support in order to offer protection from attackers compromising some repeater nodes.
• A set of directed demands $\mathcal{D}\subseteq E$, and a function (or table of weights) $C:\mathcal{D}\to {\mathbb{R}}^{+}$ specifying, for each demand, the requested key bit-rate between the two terminal nodes of the demand.
• A function (or table of weights) $L:E\to \mathbb{N}$ mapping each edge to the number of devices needed to realize a QKD chain on that edge; in practice, given the current reach of QKD devices, they are likely to be co-located with optical line amplifiers serving the data fibers, which translates to somewhere in the neighborhood of 80–100 Km; we assume that the best placement of QKD repeater nodes on a link, e.g., matching the location of amplification sites, has been pre-computed, and encoded in this function.
• A function (or table of weights) $Q:E\to {\mathbb{R}}^{+}$ mapping each edge to the key bit-rate provided by a QKD chain established on that edge, pre-computed under the same distance considerations used to compute L.

We summarized this and other notations in

Table 1. Main notation used throughout the paper.

Symbol	Meaning
$G=(V,E)$	Fiber plant graph, with $E\subseteq V\times V$
${\mathcal{N}}^{out}\left(v\right)$	$\{u\in V|(v,u)\in E\}$, i.e., outgoing neighbours of v
${\mathcal{N}}^{in}\left(v\right)$	$\{u\in V|(u,v)\in E\}$, i.e., incoming neighbours of v
N	Desired path multiplicity, i.e., how many separate paths are required
$L(u,v)$	Number of device pairs to realize a QKD chain on edge $(u,v)\in E$
$C(s,d)$	Required key bit-rate between s and d
$Q(u,v)$	Key bit-rate generated by the QKD chain on edge $(u,v)\in E$

. Note that the L and Q functions encode the potentially complex inter-relation between number (i.e., cost) and placement of QKD devices on a particular link, and the corresponding key generation rate. Holistically, assuming uniform fiber quality and ambient noise, the bottleneck with respect to capacity is going to be the longest span between QKD devices. This implies that denser chains (with shorter links), while more costly, would exhibit a higher key rate. The optimal placement can be computed, if the required key rate is known, as in [9]. For our models, which actually need to decide the key rate, we assume that practical considerations take precedence and so the QKD carrying capacity of each link can be computed in advance. The joint optimization of internal link QKD placement and network-wide QKD routes is an interesting problem left for future research on this subject.

2.1. Forced Direction MILP Model

The first formulation we discuss, an improvement over the one we presented in [11] and which we named Forced Direction (MForced) model, contains two types of variables: (i) $S_{(u,v)}^{s,d}$, continuous variables representing the amount of the $(s,d)$ demand passing through the edge $(u,v)\in E$, and (ii) $C_{(u,v)}$, integer variables counting the number of parallel QKD chains deployed on edge $(u,v)\in E$. The complete formulation is then given by the following problem:

$$\begin{array}{cc}\hfill \mathrm{minimize}:& \sum _{(u,v)\in E}L(u,v)C_{(u,v)}\hfill \\ \mathrm{subject} \mathrm{to}:\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & \hfill C_{(u,v)}\ge \frac{1}{Q(u,v)}\sum _{(s,d)\in \mathcal{D}}{S}_{(u,v)}^{s,d},\forall (u,v)\in E\end{array}$$

(2)

$$\begin{array}{cc}\hfill & \hfill C_{(u,v)}\le \frac{1}{Q(u,v)}\sum _{(s,d)\in \mathcal{D}}{S}_{(u,v)}^{s,d}+1-\epsilon ,\forall (u,v)\in E\end{array}$$

(3)

$$\begin{array}{cc}\hfill & \hfill \sum _{v\in {\mathcal{N}}^{in}\left(u\right)}{S}_{(v,u)}^{s,d}=\sum _{v\in {\mathcal{N}}^{out}\left(u\right)}{S}_{(u,v)}^{s,d},\forall u\in V\backslash \left\{u\right\},\forall (s,d)\in \mathcal{D}\end{array}$$

(4)

$$\begin{array}{cc}\hfill & \hfill \sum _{v\in {\mathcal{N}}^{out}\left(s\right)}{S}_{(s,v)}^{s,d}\ge C(s,d),\forall (s,d)\in \mathcal{D}\end{array}$$

(5)

$$\begin{array}{cc}\hfill & \hfill \sum _{v\in {\mathcal{N}}^{in}\left(d\right)}{S}_{(v,d)}^{s,d}\ge C(s,d),\forall (s,d)\in \mathcal{D}\end{array}$$

(6)

$$\begin{array}{cc}\hfill & \hfill S_{(u,v)}^{s,d}\le \frac{C(s,d)}{N},\forall (s,d)\in \mathcal{D},\forall (u,v)\in E\end{array}$$

(7)

$$\begin{array}{cc}\hfill & \hfill \sum _{v\in {\mathcal{N}}^{in}\left(s\right)}{S}_{(v,s)}^{s,d}=0,\forall (s,d)\in \mathcal{D}\end{array}$$

(8)

$$\begin{array}{cc}\hfill & \hfill \sum _{v\in {\mathcal{N}}^{out}\left(d\right)}{S}_{(d,v)}^{s,d}=0,\forall (s,d)\in \mathcal{D}\end{array}$$

(9)

$$\begin{array}{cc}\hfill & \hfill S_{(u,v)}^{s,d}\ge 0,\forall (s,d)\in \mathcal{D},\forall (u,v)\in E\end{array}$$

(10)

$$\begin{array}{cc}\hfill & \hfill C_{(u,v)}\in \mathbb{N},\forall (u,v)\in E.\end{array}$$

(11)

The objective, expressed in (1), is to minimize the number of parallel QKD chains traversing each edge, as that implies minimizing the capital expenditure in equipment. Each link-chain counter is weighted by the number of devices required to actually traverse that link (based on link length, reach limitation and trade-off between reach and key generation rate of QKD). Constraints (2) and (3) (where $ϵ\in (0,0.01]$) connect the two different of decision variables and linearise the ceiling relation (12):

$$C_{(u,v)}=\lceil \frac{1}{Q(u,v)}\sum _{(s,d)\in \mathcal{D}}{S}_{(u,v)}^{s,d}\rceil .$$

(12)

I.e., the number of chains on a link must have sufficient capacity to carry all the QKD traffic insisting on said link. Constraint (4) expresses the flow conservation condition, i.e., as much non-locally-terminated QKD traffic must exit a node as it enters it. Constraints (5) and (6) ensure that sufficient key material exits the source node and enters the destination one to satisfy the rate required between those two nodes, respectively. Constraint (7) limits the quantity of QKD traffic from each demand crossing each edge of the network to be at most $1/N$; this enforces the instantiation of at least N disjoint QKD paths to serve each demand, but still allows multiple paths serving different demands to share the same QKD devices. Note that we could rewrite constraint (7) as an equality to enforce the instantiation of exactly N disjoint QKD paths, but this comes at the price of additional $\left|E\right|\left|\mathcal{D}\right|$ constraints, which increase the computation time [13]; furthermore, since we are minimizing the cost of deployed chains, in practice the computed solutions almost never contain more than the strictly required number of QKD paths (and if they did, it would be at no additional cost). Finally, constraints (8) and (9) prevent the instantiation of short loops around the source and destination nodes, forcing the model to actually select an entire path connecting them.

The size of the resulting problem instances is dominated by the number of $S_{(u,v)}^{s,d}$ variables, which is upper-bounded by ${\left|V\right|}^2\left|E\right|={O\left(\right|V|}^4)$, and the number of constraints that is $O\left(\right|V{|}^4+|V{|}^3+|V{|}^2)$. These sizes are large but still manageable for design problems (which afford significant running time), especially with modern, efficient solvers like Gurobi [14], which we used to obtain our results.

Note that, once a solution is found, it is trivial to extract the routes followed by each demand sub-path by examining the values of the corresponding $S_{(u,v)}^{s,d}$ variables.

Compared to our previous model in [11], this one is similar (and indeed computes the same optimal solutions) but forgoes the need for a large number of binary variables, which ought to result in non-trivial execution speed gains.

2.2. Free Direction MILP Model

A careful observer may have noticed that the MILP problem formulated above considers demands to be directed, i.e., key material generated to protect traffic from s to d is completely unrelated to that generated for the protection of traffic from d to s. Clearly, this is not really the case in real networks, although the two directions may exhibit large differences in traffic load, and hence required key rate. For our purposes, this limitation entails that, in the MForced model, we need to set up two separate directed paths between each couple of communicating nodes (as communication is in general bidirectional, if asymmetric). But, based on the observation above, we only need one QKD path between each two nodes, in whatever direction, to establish secret key material between them. This could lead to better utilization of QKD devices, and hence cheaper deployments.

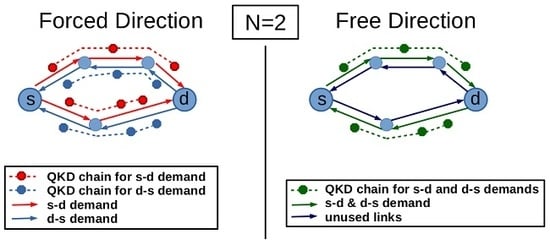
The idea is graphically represented in Figure 1, showing the difference between how MForced and a model exploiting this observation would behave on a simple example. For a required QKD path multiplicity $N=2$ and two demands, one from s to d and the other from d to s, MForced establishes two QKD chains per direction for a total of four (12 QKD devices), while the other model could make do with just two (only six devices), running the deployed QKD devices hotter.

This observation led us to develop the Free Direction (MFree) model, which, in addition to those already in MForced, relies on a third type of variable: binary variables $y_{u,v}$ encoding the direction in which the QKD session is ‘flowing’ (practically, in which of the fiber plant’s fiber, which is generally directed, the QKD photons are traveling). Furthermore, this model has an additional pre-processing step that sums the directed demands in D for each node couple. The whole model is represented by the following problem (constraints in bold are new):

$$\begin{array}{cc}\hfill \mathrm{minimize}:& \sum _{(u,v)\in E}L(u,v)C_{(u,v)}\hfill \\ \mathrm{subject} \mathrm{to}:\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & C_{(u,v)}\ge \frac{1}{Q(u,v)}\sum _{(s,d)\in \mathcal{D}}{S}_{(u,v)}^{s,d},\forall (u,v)\in E\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & C_{(u,v)}\le \frac{1}{Q(u,v)}\sum _{(s,d)\in \mathcal{D}}{S}_{(u,v)}^{s,d}+1-\epsilon ,\forall (u,v)\in E\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \sum _{v\in {\mathcal{N}}^{in}\left(u\right)}{S}_{(v,u)}^{s,d}=\sum _{v\in {\mathcal{N}}^{out}\left(u\right)}{S}_{(u,v)}^{s,d},\forall u\in V\backslash \left\{u\right\},\forall (s,d)\in \mathcal{D}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \mathbf{\sum }_{\mathbf{v}\mathbf{\in }{\mathcal{N}}^{\mathit{out}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{\mathit{S}}_{\mathbf{(}\mathit{s}\mathbf{,}\mathit{v}\mathbf{)}}^{\mathit{s},\mathit{d}}\mathbf{+}\mathbf{\sum }_{\mathbf{v}\mathbf{\in }{\mathcal{N}}^{\mathit{in}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{\mathit{S}}_{\mathbf{(}\mathit{v}\mathbf{,}\mathit{s}\mathbf{)}}^{\mathit{s}\mathbf{,}\mathit{d}}\mathbf{\ge }\mathit{C}\mathbf{(}\mathit{s}\mathbf{,}\mathit{d}\mathbf{)}\mathbf{,}\mathbf{\forall }\mathbf{(}\mathit{s}\mathbf{,}\mathit{d}\mathbf{)}\mathbf{\in }\mathbf{𝒟}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \mathbf{\sum }_{\mathit{v}\mathbf{\in }{\mathcal{N}}^{\mathit{out}}\mathbf{\left(}\mathit{d}\mathbf{\right)}}{\mathit{S}}_{\mathbf{(}\mathit{d}\mathbf{,}\mathit{v}\mathbf{)}}^{\mathit{s}\mathbf{,}\mathit{d}}\mathbf{+}\mathbf{\sum }_{\mathit{v}\mathbf{\in }{\mathcal{N}}^{\mathit{in}}\mathbf{\left(}\mathit{d}\mathbf{\right)}}{\mathit{S}}_{\mathbf{(}\mathit{v}\mathbf{,}\mathit{d}\mathbf{)}}^{\mathit{s}\mathbf{,}\mathit{d}}\mathbf{\ge }\mathit{C}\mathbf{(}\mathit{s}\mathbf{,}\mathit{d}\mathbf{)}\mathbf{,}\mathbf{\forall }\mathbf{(}\mathit{s}\mathbf{,}\mathit{d}\mathbf{)}\mathbf{\in }\mathbf{𝒟}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & S_{(u,v)}^{s,d}\le \frac{C(s,d)}{N},\forall (s,d)\in \mathcal{D},\forall (u,v)\in E\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \mathbf{\sum }_{\mathit{v}\mathbf{\in }{\mathcal{N}}^{\mathit{out}}\left(\mathit{s}\right)}{\mathit{S}}_{(\mathit{s},\mathit{v})}^{\mathit{s},\mathit{d}}\mathbf{-}\mathbf{\sum }_{\mathit{v}\in {\mathcal{N}}^{\mathit{in}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{\mathit{S}}_{\mathbf{(}\mathit{v}\mathbf{,}\mathit{s}\mathbf{)}}^{\mathit{s},\mathit{d}}\mathbf{+}\mathit{M}{\mathit{y}}_{\mathit{s},\mathit{d}}\mathbf{\ge }\mathit{C}(\mathit{s},\mathit{d}),\mathbf{\forall }\mathbf{(}\mathit{s}\mathbf{,}\mathit{d}\mathbf{)}\mathbf{\in }\mathbf{𝒟}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \mathbf{\sum }_{\mathit{v}\mathbf{\in }{\mathcal{N}}^{\mathit{in}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{\mathit{S}}_{\mathbf{(}\mathit{v}\mathbf{,}\mathit{s}\mathbf{)}}^{\mathit{s},\mathit{d}}\mathbf{-}\mathbf{\sum }_{\mathit{v}\mathbf{\in }{\mathcal{N}}^{\mathit{out}}\mathbf{\left(}\mathit{s}\mathbf{\right)}}{\mathit{S}}_{\mathbf{(}\mathit{s}\mathbf{,}\mathit{v}\mathbf{)}}^{\mathit{s}\mathbf{,}\mathit{d}}\mathbf{+}\mathit{M}(\mathbf{1}\mathbf{-}{\mathit{y}}_{\mathit{s}\mathbf{,}\mathit{d}}\mathbf{)}\mathbf{\ge }\mathit{C}\mathbf{(}\mathit{s},\mathit{d}\mathbf{)}\mathbf{,}\mathbf{\forall }\mathbf{(}\mathit{s}\mathbf{,}\mathit{d}\mathbf{)}\mathbf{\in }\mathbf{𝒟}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & S_{(u,v)}^{s,d}\ge 0,\forall (s,d)\in \mathcal{D},\forall (u,v)\in E\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & C_{(u,v)}\in \mathbb{N},\forall (u,v)\in E\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & {\mathit{y}}_{\mathit{s},\mathit{d}}\mathbf{\in }\{\mathbf{0},\mathbf{1}\},\mathbf{\forall }(\mathit{s},\mathit{d})\mathbf{\in }\mathbf{𝒟}.\hfill \end{array}$$

(24)

The objective, expressed in (13), is identical to that of the MForced formulation, as are constraints (14)–(16) and (19). The significant differences are encoded in constraints (17) and (18), which now ensure that there is sufficient key material entering or exiting the terminal nodes of each demand (without caring for which direction it is traveling in, or whether it is split among both), and in constraints (20) and (21), which perform a similar function to constraints (8) and (9) in MForced, by linearising the relation (25):

$$|\sum _{v\in {\mathcal{N}}^{out}\left(s\right)}{S}_{(s,v)}^{s,d}-\sum _{v\in {\mathcal{N}}^{in}\left(s\right)}{S}_{(v,s)}^{s,d}|\ge C(s,d),\forall (s,d)\in \mathcal{D}.$$

(25)

In words, the sum of key material traveling, in either direction, through the neighbours of the source node of a demand must be sufficient to satisfy said demand. In conjunction with constraint (16), this extends to all non-terminal nodes of a demand. This trick allows us to more efficiently use the QKD devices we choose to deploy, as it removes the constraint of directionality, leading to a lower number of required QKD devices, as evidenced in Section 3. M needs to be a large enough number for the relationships to hold, in this case $M\ge {\sum }_{(s,d)\in \mathcal{D}}C(s,d)$.

As before, also in this formulation the problem size is dominated by the number of $S_{(u,v)}^{s,d}$ variables, $O\left(\right|V{|}^4)$, and the number of constraints that is $O\left(\right|V{|}^4+|V{|}^3+|V{|}^2)$. Time-wise, however, solving this model requires dealing with a large ($O\left(\right|V{|}^2)$) number of binary variables $y_{s,d}$, whose value strongly impacts the feasible assignments to the remaining families of variables. As solving integer (or binary) linear problems is much less efficient that solving continuous ones [15], this has a large impact on computation time, as also shown in Section 3. Nonetheless, the advantages in terms of the number of required (expensive, in the order of tens of thousands of Euros) QKD devices can more than justify the investment of additional design (computational) resources.

3. Performance Evaluation and Results

In this section, we evaluate the performance of the two proposed MILP models, and compare it to that of a previously published model from literature [11], which we named ‘SoA’ in this work.

3.1. Synthetic Topologies

Firstly, we examined the performance of the models on a number of randomly-generated graphs, in an attempt to understand their average behavior. We generated 10 families of graphs using the Erdos-Rényi model and known seeds, with each family consisting of 30 instances with a fixed number of nodes, and an average nodal degree of 3, with edge lengths drawn uniformly from $[50,350]$ Km. These numbers were arbitrarily chosen to generate somewhat realistic national transport network topologies. We assumed the need for a trusted QKD repeater every 80 Km, a distance that would allow to co-locate such repeaters with existing amplification infrastructure for the ‘data’ fibers. We further assumed that the key rate of each QKD-secured link can provide material for securing 10 optical ‘data’ connections. Again, this is a largely arbitrary number, and may need to be tweaked on a real scenario; the important point is that a single QKD device (or chain of devices) should be over-dimensioned compared to the key-rate required to secure a single data connection. We also assumed a uniform data traffic matrix between all nodes, which we know is unrealistic, but unfortunately, realistic data is nearly impossible to come by and publish, as it is considered a trade secret, while this choice permits the easy reproduction and verification of our results by other researchers. Note that the chosen scenarios are the worst cases in terms of computational complexity, involving $O\left(\right|V{|}^2)$ demands. Fairly realistic cases such as hub-and-spoke-like traffic matrices would result in faster computations since the number of demands would be only slightly superlinear in $\left|V\right|$. All experiments were performed on a 12 core (Intel Xeon E5-2420 clocked at 2.20 GHz) server with 64 GB of RAM. Each data point depicts results averaged over all 30 instances in a family of the corresponding network size, along with the corresponding 95% confidence interval.

In Figure 2a we report the fraction of feasible instances, i.e., the instances that could be solved by each formulation as a function of the random network size (in terms of number of nodes, as $\left|E\right|=3\left|V\right|$). We remark that the MForced and MFree models can solve the exact same instances of the SoA model. It is clear from the figure that at multiplicity $N=3$ it becomes hard to find sufficient paths as the network size increases since the existence of nodes with degree 2 (too low to support three disjoint paths for all demands) becomes proportionally more common.

Figure 2b–d show instead the average running time of the models, for a required number of parallel disjoint paths (path multiplicity) of 1, 2 and 3, respectively. All clearly exhibit a non-trivial gain, approaching an order of magnitude, for the MForced model compared to SoA (note the log scale on the Y-axis). Reasonably, the MFree model takes significantly more time than the other two models because of the presence of additional hard-to-optimize binary variables. ILP problem solving is known to be NP-complete, thus excluding the existence of a polynomial-time algorithm (as the input size increases) for the problem resolution unless P = NP [15]. The introduction of integer and binary variables to a linear program increases the complexity of the overall problem since we do not have a well-known characterization of the solution for such problems like the one we have for LP problems (i.e., purely linear, based only on continuous variables) [16]. Consequently, the majority of existing solvers are based on some combinations of LP relaxations and heuristic methods in order to find exact integer solution for integer and mixed programming problems. For example, the Gurobi solver [17] (which we use) applies, after a pre-solve step to reduce the problem size, an improved version of the well-known branch-and-bound algorithm [18] where at each step a linear programming relaxation of the problem together with cutting planes constraints are applied to find a lower bound for the objective value. At each step, if an integer solution for all the integer variables is found then the algorithm stops, otherwise, if there exists at least one integer variable x with a continuous value $a\in \mathbb{R}$ it splits the computation in two nodes containing the previous relaxed problem with the additional constraints $x\le \lfloor a\rfloor$ and $x\le \lceil a\rceil$, respectively. This explains the fluctuation of the MFree average time in Figure 2b: based on the particular problem instance and the additional cutting planes constraints, the branch and bound can suddenly find an exact solution at the early levels of the search tree built during the overall solving process, or waste an extremely long time exploring branches that do not lead to the optimal solution (i.e., time to solve does not depend solely on instance size).

In Figure 3a–c we report the average value of the objective function, i.e., the number of QKD device couples needed to deploy the designed QKD sub-network, vs. the graph size for a required path multiplicity of 1, 2 and 3. As expected, the SoA and MForced models have the same behavior in terms of deployed devices in all cases. The MFree model, instead, consistently requires a smaller number of QKD devices, validating the observation that using both directions from the source and the destination of each demand can lead to cheaper QKD networks. As shown earlier, this comes at a significant but possibly tolerable increase in computation time (or, equivalently, investment in computational resources). We can also notice that, despite the number of required QKD devices increasing with higher path multiplicities, the increment is relatively modest for significant network sizes; this implies that our design models are doing a good job of packing together QKD routes to fully exploit the deployed devices.

3.2. Real Topologies

Finally, to confirm our findings from the previous section, and to verify that we had chosen sensible parameters for the generation of random topologies, we applied our design algorithms on two realistic national transport network topologies, ‘DT14’ from Germany [19] and ‘TID30’ from Spain [20]. We forced a time limit of one hour (*), but otherwise used the same assumptions as for the synthetic topologies study (QKD repeaters every 80 Km, uniform demand matrix). The related results are reported in

Table 2. Mixed-Integer Linear Programming (MILP) models performance on two real transport network topologies with one-hour time limit. The MForced model, while equivalent to SoA at the optimum, can find better solutions under time constraints because of its faster optimization time, while, if ample time is available, the MFree model can produce better optimal solutions, but suffers significantly under such a relatively short time constraint. * Experiment artificially limited to one hour.

Topology		SoA Model		MForced Model		MFree Model
		Sol. (Dev. Pairs)	Time (s)	Sol. (Dev. Pairs)	Time (s)	Sol. (Dev. Pairs)	Time (s)
GER [19]	$N=1$	234	213	234	74	219 (gap 2.28%)	3600 *
	$N=2$	303	97	303	93	291 (gap 8.59%)	3600 *
SPA [20]	$N=1$	649 (gap 4.16%)	3600 *	655 (gap 5.04%)	3600 *	1119 (gap 45.58%)	3600 *
	$N=2$	758 (gap 1.98%)	3600 *	742 (gap 1.48%)	3600 *	1015 (gap 32.02%)	3600 *

. There too we observe that SoA and MForced reach the same optimal conclusion, and that MForced is faster, sometimes significantly so, than SoA, while MFree can design cheaper networks but is much, much slower. Indeed, for the DT14 network instances, which SoA and MForced could solve optimally under the time limit, MFree could not, exhibiting a worst-case gap to the optimal solution of 2.28% and 8.59% for $N=1$ and $N=2$, respectively. Yet, despite these gaps, the solutions it computed are better than those of the other models, which translates to significant capital savings. On the other hand, on the much more complex TID30 network, one hour is not even remotely sufficient for MFree to find even a half-decent solution (30% gaps), so the simpler MFree and SoA produce better configurations.

4. Conclusions

We presented two Mixed Integer Linear Programming models for the design of QKD sub-networks dimensioned around the requirements for securing, and embedded in, existing national transport networks. We proved, using simulations, that one model (MForced) produces equivalent solutions to one previously presented in literature while being faster, while the other (MFree) is slower but can produce cheaper configurations. The former should be fast enough to be compatible with the time frame of procuring and installing a sufficient number of QKD devices (weeks to months); the latter isn’t, but suggests that further savings can be achieved. While we hope this work will never be truly needed, we believe it is important to have such design tools ready should deploying QKD become our last defense for secure communications. To that end, as the technology matures we expect to need to update this work with models able to exploit the emergence of novel QKD methods, such as MDI-QKD, and foresee the need for approximate but faster design algorithms to actually be able to exploit the advantages of the MFree model.